Monazite-Type SmPO4 as Potential Nuclear Waste Form: Insights into Radiation Effects from Ion-Beam Irradiation and Atomistic Simulations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Preparation and Characterisation
2.2. Ion-Beam Irradiation
2.3. SRIM/TRIM Calculations and Simulation of Threshold Displacement Energies
3. Results
3.1. Material Characterisation
3.2. Simulation of Threshold Displacement Energies
3.3. SRIM/TRIM Simulations
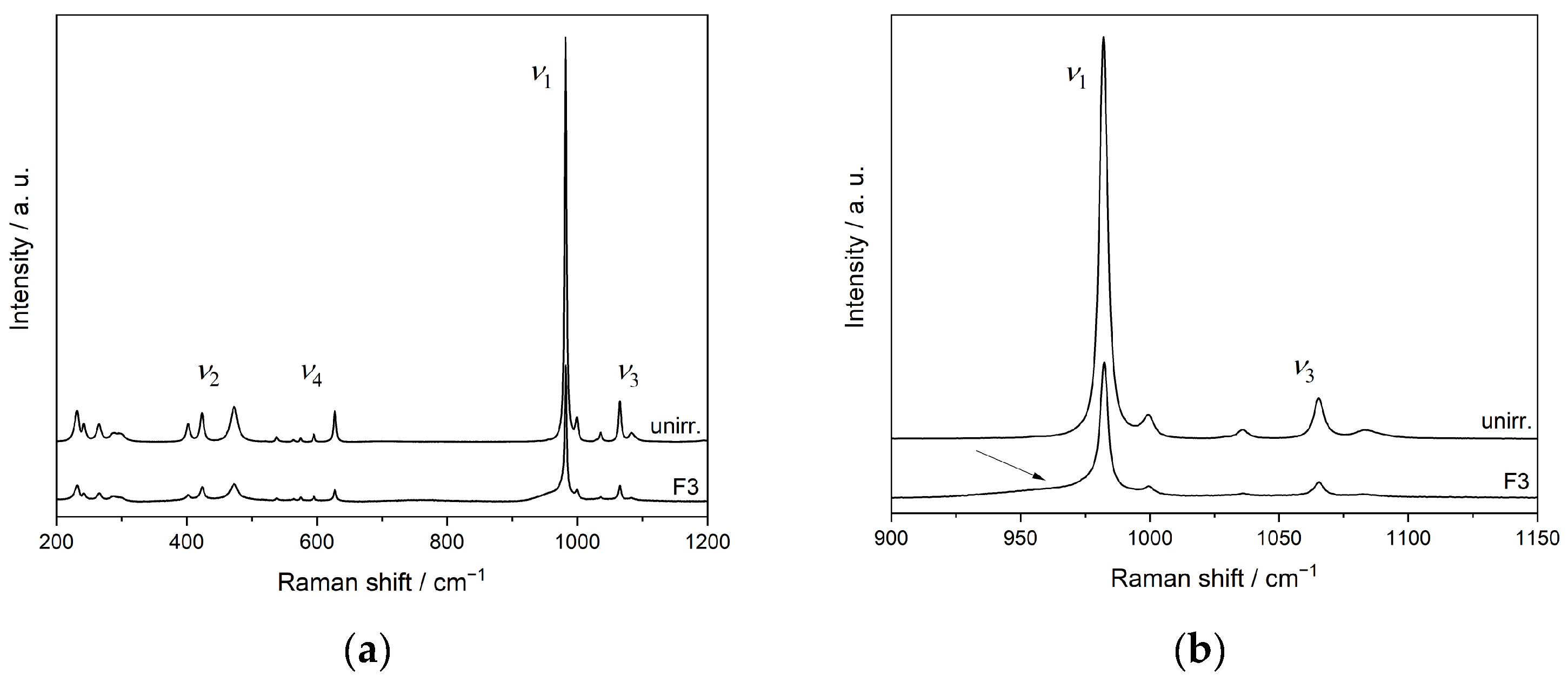
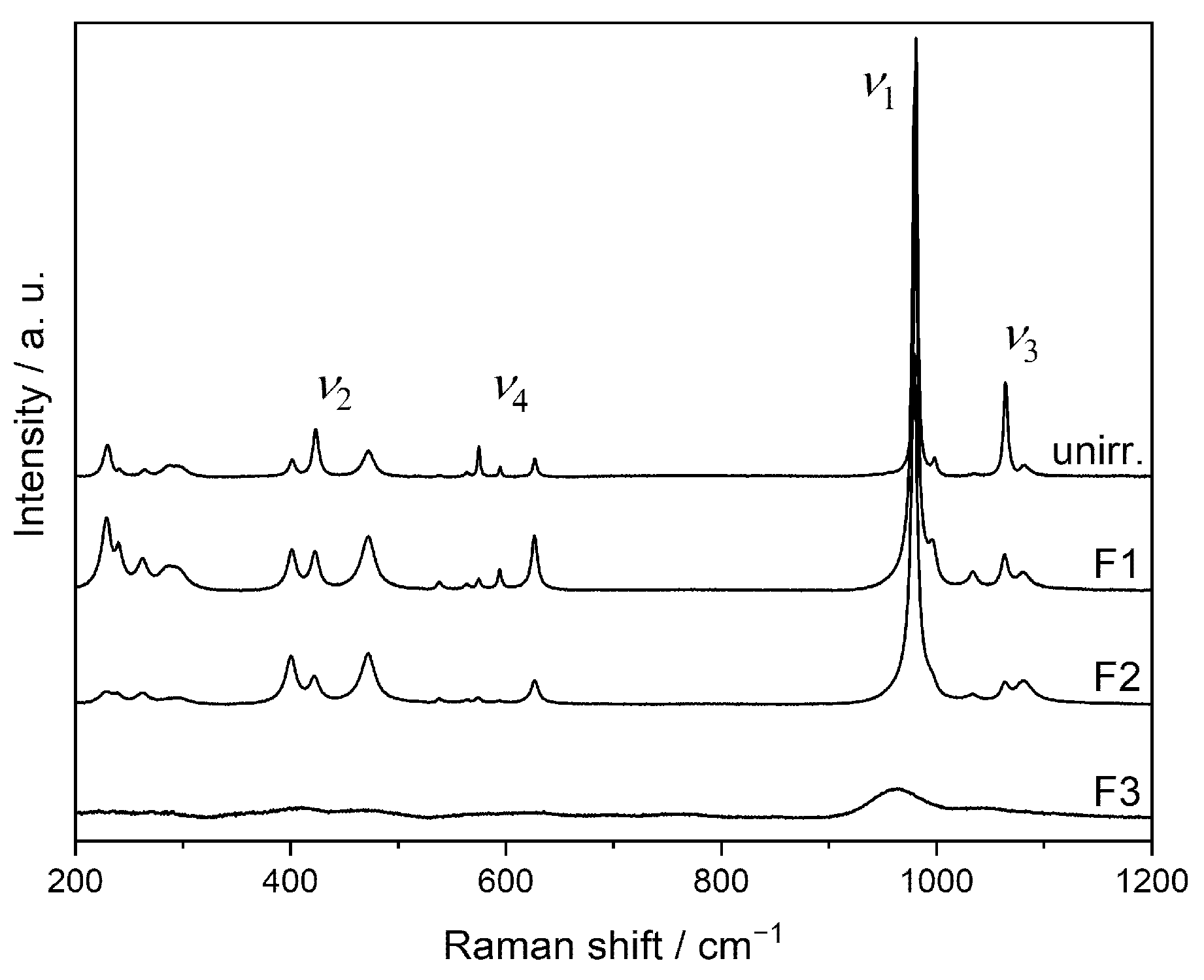
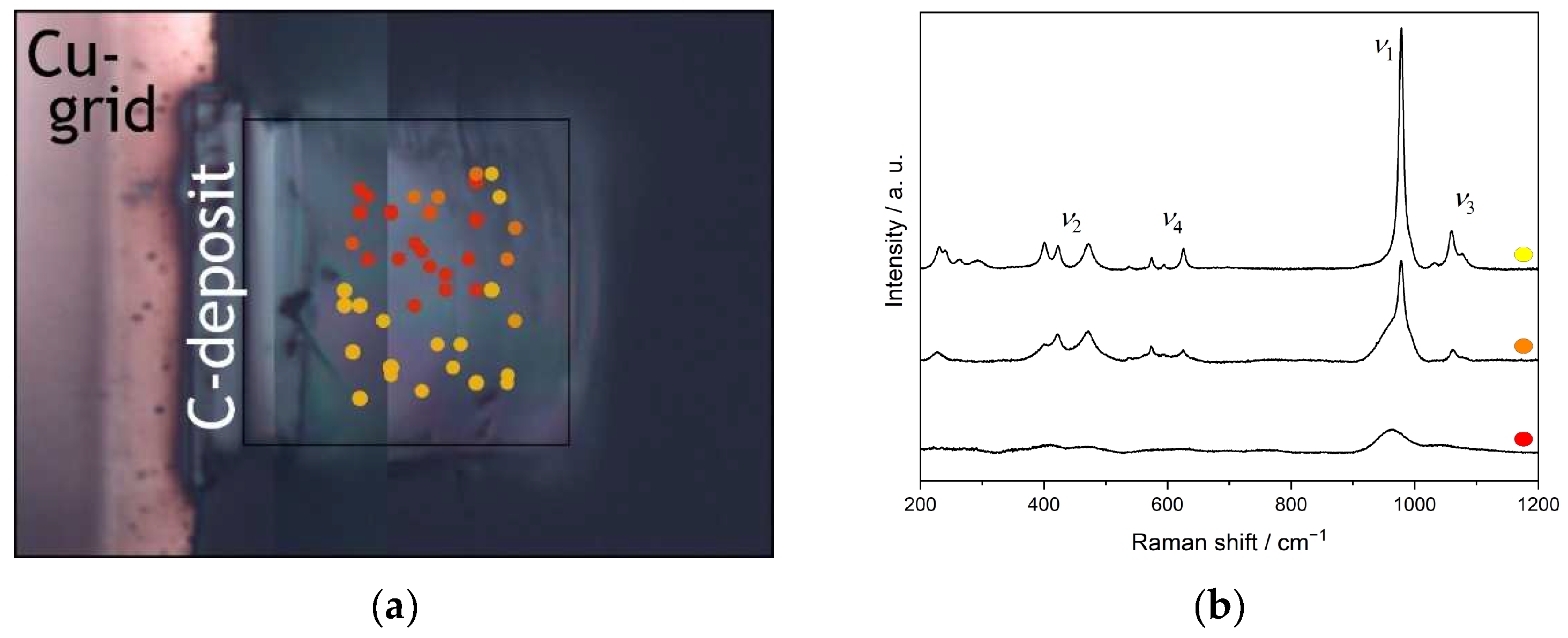
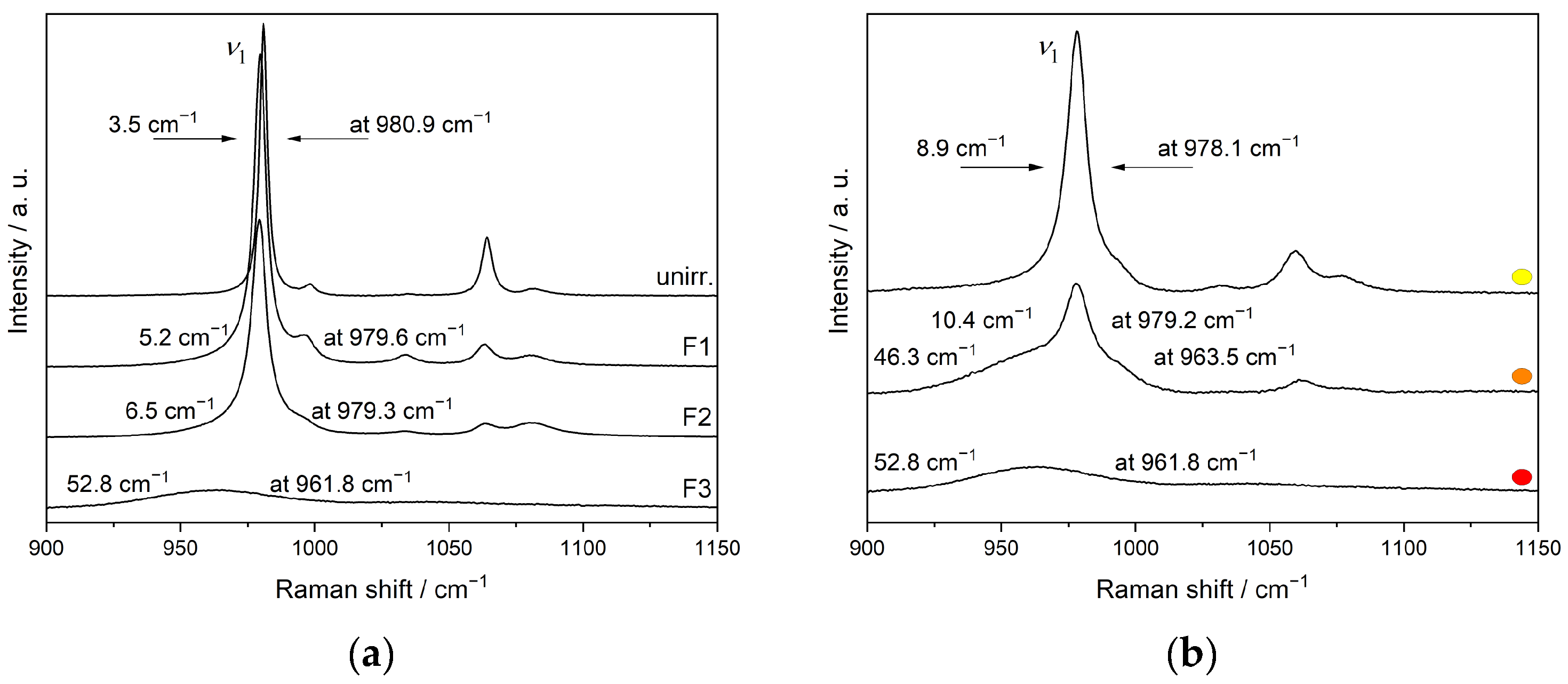
3.4. Ion-Beam Irradiation of SmPO4
4. Discussion
4.1. Radiation Damage in Monazite-Type LnPO4
4.2. Implications for SmPO4 as Waste Form for Actinides
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ringwood, A.E.; Kesson, S.E.; Reeve, K.D.; Levins, D.M.; Ramm, E.J. Synroc. In Radioactive Waste Forms for the Future; Lutze, W., Ewing, R.C., Eds.; North-Holland: Amsterdam, The Netherlands, 1988; pp. 233–334. [Google Scholar]
- Harker, A.B. Tailored Ceramics. In Radioactive Waste Forms for the Future; Lutze, W., Ewing, R.C., Eds.; North-Holland: Amsterdam, The Netherlands, 1988; pp. 335–392. [Google Scholar]
- Ewing, R.; Weber, W.; Clinard, F. Radiation effects in nuclear waste forms for high level radioactive waste. Prog. Nucl. Energy 1995, 29, 63–127. [Google Scholar] [CrossRef]
- Weber, W.J.; Ewing, R.C.; Catlow, C.R.A.; de la Rubia, T.D.; Hobbs, L.W.; Kinoshita, C.; Matzke, H.; Motta, A.T.; Nastasi, M.; Salje, E.K.H.; et al. Radiation effects in crystalline ceramics for the immobilization of high-level nuclear waste and plutonium. J. Mater. Res. 1998, 13, 1434–1484. [Google Scholar] [CrossRef] [Green Version]
- Ewing, R.C. Nuclear waste forms for actinides. Proc. Natl. Acad. Sci. USA 1999, 96, 3432–3439. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lumpkin, G.R. Ceramic waste forms for actinides. Elements 2006, 2, 365–372. [Google Scholar] [CrossRef]
- Ewing, R.C. Ceramic matrices for plutonium disposition. Prog. Nucl. Energy 2007, 49, 635–643. [Google Scholar] [CrossRef]
- Weber, W.J.; Navrotsky, A.; Stefanovsky, S.; Vance, E.R.; Vernaz, E. Materials science of high-level nuclear waste immobilization. MRS Bull. 2009, 34, 46–53. [Google Scholar] [CrossRef] [Green Version]
- Ewing, R.C. Actinides and radiation effects: Impact on the back-end of the nuclear fuel cycle. Mineral. Mag. 2011, 75, 2359–2377. [Google Scholar] [CrossRef]
- Deissmann, G.; Neumeier, S.; Modolo, G.; Bosbach, D. Durability of potential plutonium wasteforms under repository conditions. Mineral. Mag. 2012, 76, 2911–2918. [Google Scholar] [CrossRef]
- Boatner, L.; Beall, G.; Abraham, M.; Finch, C.; Huray, P.; Rappaz, M. Scientific Basis for Nuclear Waste Management; Springer: Boston, MA, USA, 1980; pp. 289–296. [Google Scholar]
- Boatner, L.; Sales, B. Monazite. In Radioactive Waste Forms for the Future; Lutze, W., Ewing, R.C., Eds.; North-Holland: Amsterdam, The Netherlands, 1988; pp. 495–564. [Google Scholar]
- Ewing, R.C.; Wang, L. Phosphates as nuclear waste forms. Rev. Mineral. Geochem. 2002, 48, 673–699. [Google Scholar] [CrossRef]
- Terra, O.; Dacheux, N.; Audubert, F.; Podor, R. Immobilization of tetravalent actinides in phosphate ceramics. J. Nucl. Mater. 2006, 352, 224–232. [Google Scholar] [CrossRef]
- Oelkers, E.; Montel, J.M. Phosphates and nuclear waste storage. Elements 2008, 4, 113–116. [Google Scholar] [CrossRef]
- Clavier, N.; Podor, R.; Dacheux, N. Crystal chemistry of the monazite structure. J. Eur. Ceram. Soc. 2011, 31, 941–976. [Google Scholar] [CrossRef]
- Dacheux, N.; Clavier, N.; Podor, R. Monazite as a promising long-term radioactive waste matrix: Benefits of high-structural flexibility and chemical durability. Am. Mineral. 2013, 98, 833–847. [Google Scholar] [CrossRef]
- Schlenz, H.; Heuser, J.; Neumann, A.; Schmitz, S.; Bosbach, D. Monazite as a suitable actinide waste form. Cryst. Mater. 2013, 228, 113–123. [Google Scholar] [CrossRef]
- Heuser, J.; Bukaemskiy, A.; Neumeier, S.; Neumann, A.; Bosbach, D. Raman and infrared spectroscopy of monazite-type ceramics used for nuclear waste conditioning. Prog. Nucl. Energy 2014, 72, 149–155. [Google Scholar] [CrossRef]
- Neumeier, S.; Arinicheva, Y.; Ji, Y.; Heuser, J.M.; Kowalski, P.M.; Kegler, P.; Schlenz, H.; Bosbach, D.; Deissmann, G. New insights into phosphate based materials for the immobilisation of actinides. Radiochim. Acta 2017, 105, 961–984. [Google Scholar] [CrossRef]
- Schlenz, H.; Neumeier, S.; Hirsch, A.; Peters, L.; Roth, G. Highlights in Applied Mineralogy; de Gruyter: Berlin, Germany, 2017; pp. 171–196. [Google Scholar]
- Arinicheva, Y. Monazite-Type Ceramics as Nuclear Waste Form: Crystal Structure, Microstructure and Properties; Schriften des Forschungszentrums Jülich Reihe Energie & Umwelt/Energy & Environment; Forschungszentrum Jülich GmbH Zentralbibliothek, Verlag: Jülich, Germany, 2019; Volume 459, pp. 1–194. [Google Scholar]
- Ji, Y.; Kowalski, P.M.; Kegler, P.; Huittinen, N.; Marks, N.A.; Vinograd, V.L.; Arinicheva, Y.; Neumeier, S.; Bosbach, D. Rare-earth orthophosphates from atomistic simulations. Front. Chem. 2019, 7, 197. [Google Scholar] [CrossRef] [Green Version]
- Ni, Y.; Hughes, J.M.; Mariano, A.N. Crystal-chemistry of the monazite and xenotime structures. Am. Mineral. 1995, 80, 21–26. [Google Scholar] [CrossRef]
- Boatner, L.A. Synthesis, structure and properties of monazite, pretulite, and xenotime. Rev. Mineral. Geochem. 2002, 48, 87–121. [Google Scholar] [CrossRef]
- Montel, J.-M.; Devidal, J.-L.; Avignant, D. X-ray diffraction study of brabantite-monazite solid solution. Chem. Geol. 2002, 191, 89–104. [Google Scholar] [CrossRef]
- Ewing, R.C.; Meldrum, A.; Wang, L.; Wang, S. Radiation-induced amorphization. Rev. Mineral. Geochem. 2000, 39, 319–361. [Google Scholar] [CrossRef]
- Ewing, R.C.; Weber, W.J. The Chemistry of the Actinide and Transactinide Elements; Springer: Dordrecht, The Netherlands, 2010; pp. 3813–3887. [Google Scholar]
- Meldrum, A.; Cherniak, D. Materials science with ion beams. In Topics in Applied Physics; Springer: Berlin/Heidelberg, Germany, 2009; Volume 116, pp. 317–343. [Google Scholar]
- Grammacioli, C.M.; Segalstad, T.V. A uranium- and thorium-rich monazite from a south-alpine pegmatite at Piona, Italy. Am. Mineral. 1978, 63, 757–761. [Google Scholar]
- Lumpkin, G.R. Rare-element mineralogy and internal evolution of the Rutherford #2 pegmatite, Amelia County, Virginia: A classic locality revisited. Can. Mineral. 1998, 36, 339–353. [Google Scholar]
- Hoshino, M.; Sanematsu, K.; Watanabe, Y. REE mineralogy and resources. Handb. Phys. Chem. Rare Earths 2016, 49, 129–291. [Google Scholar]
- Seydoux-Guillaume, A.-M.; Wirth, R.; Nasdala, L.; Gottschalk, M.; Montel, J.M.; Heinrich, W. An XRD, TEM and Raman study of experimentally annealed natural monazite. Phys. Chem. Miner. 2002, 29, 240–253. [Google Scholar] [CrossRef]
- Seydoux-Guillaume, A.-M.; Wirth, R.; Deutsch, A.; Schärer, U. Microstructure of 24-1928 Ma concordant monazites: Implications for geochronology and nuclear waste deposits. Geochim. Cosmochim. Acta 2004, 68, 2517–2527. [Google Scholar] [CrossRef]
- Seydoux-Guillaume, A.-M.; David, M.-L.; Alix, K.; Datas, L.; Bingen, B. Trapping of helium in nano-bubbles in euxenite: Positive identification and implications. Earth Planet. Sci. Lett. 2016, 448, 133–139. [Google Scholar] [CrossRef]
- Ruschel, K.; Nasdala, L.; Kronz, A.; Hanchar, J.; Többens, D.; Skoda, R.; Finger, F.; Möller, A. A Raman spectroscopic study on the structural disorder of monazite-(Ce). Miner. Petrol. 2012, 105, 41–55. [Google Scholar] [CrossRef]
- Ewing, R.C.; Haaker, R.F. The metamict state: Implications for radiation damage in crystalline waste forms. Nucl. Chem. Waste Manag. 1980, 1, 51–57. [Google Scholar] [CrossRef]
- Black, L.P.; Fitzgerald, J.D.; Harley, S.L. Pb isotopic composition, colour, and microstructure of monazites from a polymetamorphic rock in Antarctica. Contrib. Mineral. Petrol. 1984, 85, 141–148. [Google Scholar] [CrossRef]
- Meldrum, A.; Boatner, L.A.; Weber, W.J.; Ewing, R.C. Radiation damage in zircon and monazite. Geochim. Cosmochim. Acta 1998, 62, 2509–2520. [Google Scholar] [CrossRef]
- Montel, J.-M.; Razafimahatratra, D.; de Parseval, P.; Poitrasson, F.; Moine, B.; Seydoux-Guillaume, A.-M.; Pik, R.; Arnaud, N.; Gibert, F. The giant monazite crystals from Manangotry (Madagascar). Chem. Geol. 2018, 484, 36–50. [Google Scholar] [CrossRef]
- Seydoux-Guillaume, A.-M.; Deschanels, X.; Baumier, C.; Neumeier, S.; Weber, W.J.; Peuget, S. Why natural monazite never becomes amorphous: Experimental evidence for alpha self-healing. Am. Mineral. 2018, 103, 824–827. [Google Scholar] [CrossRef]
- Nasdala, L.; Akhmadaliev, S.; Artac, A.; Chanmuang, N.C.; Habler, G.; Lenz, C. Irradiation effects in monazite–(Ce) and zircon: Raman and photoluminescence study of Au-irradiated FIB foils. Phys. Chem. Miner. 2018, 45, 855–871. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Masau, M.; Černý, P.; Cooper, M.A.; Chapman, R. Monazite-(Sm), a new member of the monazite group from the Annie Claim #3 granitic pegmatite, southwestern Manitoba. Can. Mineral. 2002, 40, 1649–1655. [Google Scholar]
- Meldrum, A.; Wang, L.M.; Ewing, R.C. Ion beam induced amorphization of monazite. Nucl. Instrum. Meth. B 1996, 116, 220–224. [Google Scholar] [CrossRef]
- Meldrum, A.; Boatner, L.A.; Wang, L.M.; Ewing, R.C. Ion-beam-induced amorphization of LaPO4 and ScPO4. Nucl. Instrum. Meth. B 1997, 127, 160–165. [Google Scholar] [CrossRef]
- Meldrum, A.; Boatner, L.A.; Ewing, R.C. Displacive radiation effects in the monazite- and zircon-structure orthophosphates. Phys. Rev. B 1997, 56, 13805–13814. [Google Scholar] [CrossRef]
- Meldrum, A.; Boatner, L.A.; Ewing, R.C. A comparison of radiation effects in crystalline ABO4-type phosphates and silicates. Mineral. Mag. 2000, 64, 185–194. [Google Scholar] [CrossRef]
- Picot, V.; Deschanels, X.; Peuget, S.; Glorieux, B.; Seydoux-Guillaume, A.-M.; Wirth, R. Ion beam radiation effects in monazite. J. Nucl. Mater. 2008, 381, 290–296. [Google Scholar] [CrossRef] [Green Version]
- Nasdala, L.; Grotzschel, R.; Probst, S.; Bleisteiner, B. Irradiation damage in Monazite-(Ce): An example to establish the limits of Raman confocality and depth resolution. Can. Mineral. 2010, 48, 351–359. [Google Scholar] [CrossRef]
- Deschanels, X.; Seydoux-Guillaume, A.-M.; Magnin, V.; Mesbah, A.; Tribet, M.; Moloney, M.; Serruys, Y.; Peuget, S. Swelling induced by alpha decay in monazite and zirconolite ceramics: A XRD and TEM comparative study. J. Nucl. Mater. 2014, 448, 184–194. [Google Scholar] [CrossRef]
- Karioris, F.G.; Gowda, K.A.; Cartz, L. Heavy ion bombardement of monoclinic ThSiO4, ThO2 and monazite. Radiat. Eff. Lett. 1981, 58, 1–3. [Google Scholar] [CrossRef]
- Ehlert, T.C.; Gowda, K.A.; Karioris, F.G.; Cartz, L. Differential scanning calorimetry of heavy ion bombarded synthetic monazite. Radiat. Eff. 1983, 70, 173–181. [Google Scholar] [CrossRef]
- Meldrum, A.; Boatner, L.A.; Ewing, R.C. Electron-irradiation-induced nucleation and growth in amorphous LaPO4, ScPO4, and zircon. J. Mater. Res. 1997, 12, 1816–1927. [Google Scholar] [CrossRef]
- Seydoux-Guillaume, A.-M.; Wirth, R.; Ingrin, J. Contrasting response of ThSiO4 and monazite to natural irradiation. Eur. J. Mineral. 2007, 19, 7–14. [Google Scholar] [CrossRef]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. 1976, A32, 751–767. [Google Scholar] [CrossRef]
- Heuser, J.M. Keramiken des Monazit-Typs zur Immobilisierung von Minoren Actinoiden und Plutonium; Schriften des Forschungszentrums Jülich Reihe Energie & Umwelt/Energy & Environment; Forschungszentrum Jülich GmbH Zentralbibliothek, Verlag: Jülich, Germany, 2015; Volume 278, pp. 1–212. [Google Scholar]
- Heuser, J.M.; Palomares, R.I.; Bauer, J.D.; Lozano Rodriguez, J.M.; Cooper, J.; Lang, M.; Scheinost, A.C.; Schlenz, H.; Winkler, B.; Bosbach, D.; et al. Structural characterisation of (Sm,Tb)PO4 solid solutions and pressure-induced phase transitions. J. Eur. Ceram. Soc. 2018, 38, 4018–4070. [Google Scholar] [CrossRef]
- Kinchin, G.H.; Pease, R.S. The displacement of atoms in solids by radiation. Rep. Prog. Phys. 1955, 18, 1. [Google Scholar] [CrossRef]
- Brinkman, J.A. Production of atomic displacements by high-energy particles. Am. J. Phys. 1956, 24, 246–267. [Google Scholar] [CrossRef]
- Nastasi, M.; Mayer, J.W.; Hirvonen, J.K. Ion-Solid Interactions—Fundamentals and Applications; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Smith, R. (Ed.) Atomic and Ion Collisions in Solids and at Surfaces: Theory, Simulation and Applications; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Biersack, J.P.; Haggmark, L.G. A Monte Carlo computer program for the transport of energetic ions in amorphous targets. Nucl. Instrum. Meth. 1980, 174, 257–269. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Biersack, J.P.; Ziegler, M.D. SRIM: The Stopping and Range of Ions in Matter; SRIM Company: Chester, MD, USA, 2008. [Google Scholar]
- Lunéville, L.; Simeone, D.; Jouanne, C. A new tool to compare neutron and ion irradiation in materials. Nucl. Instrum. Meth. B 2006, 250, 71–75. [Google Scholar] [CrossRef]
- Lunéville, L.; Simeone, D.; Jouanne, C. Calculation of radiation damage induced by neutrons in compound materials. J. Nucl. Mater. 2006, 353, 89–100. [Google Scholar] [CrossRef]
- Lunéville, L.; Simeone, D. DART, a BCA code to assess and compare primary irradiation damage in nuclear materials submitted to neutron and ion flux. EPJ Web Conf. 2016, 115, 02002. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Kowalski, P.M.; Beridze, G.; Blanca-Romero, A.; Ji, Y.; Vinograd, V.L.; Gale, J.; Bosbach, D. Atomistic simulations of ceramic materials relevant for nuclear waste management: Cases of monazite and pyrochlore. Ceram. Trans. 2016, 255, 165–175. [Google Scholar]
- Ji, Y.; Kowalski, P.M.; Neumeier, S.; Deissmann, G.; Kulriya, P.K.; Gale, J.D. Atomistic modeling and experimental studies of radiation damage in monazite-type LaPO4 ceramics. Nucl. Instrum. Meth. B 2017, 393, 54–58. [Google Scholar] [CrossRef] [Green Version]
- Boakye, E.E.; Mogilevsky, P.; Hay, R.S.; Fair, G.E. Synthesis and phase composition of lanthanide phosphate nanoparticles LnPO4 (Ln = La, Gd, Tb, Dy, Y) and solid solutions for fiber coatings. J. Am. Ceram. Soc. 2008, 91, 3841–3849. [Google Scholar] [CrossRef]
- Rietveld, H.M. Line profiles of neutron powder-diffraction peaks for structure refinement. Acta Crystallogr. 1967, 22, 151–152. [Google Scholar] [CrossRef]
- Coelho, A. TOPAS Academic User Manual, version 4.1; Coelho Software: Brisbane, Australia, 2007. [Google Scholar]
- Cheary, R.W.; Coelho, A. A fundamental parameters approach to x-ray line-profile fitting. J. Appl. Crystallogr. 1992, 25, 109–121. [Google Scholar] [CrossRef]
- Dijkman, F.G.; van der Maas, J.H. Dependence of bandshape and depolarization ratio on slitwidth. Appl Spectrosc. 1976, 30, 545–546. [Google Scholar] [CrossRef]
- Irmer, G. Zum Einfluss der Apparatefunktion auf die Bestimmung von Streuquerschnitten und Lebensdauern aus optischen Phononenspektren. Exp. Tech. Phys. 1985, 33, 501–506. [Google Scholar]
- Nasdala, L.; Wenzel, M.; Vavra, G.; Irmer, G.; Wenzel, T.; Kober, B. Metamictisation of natural zircon: Accumulation versus thermal annealing of radioactivity-induced damage. Contrib. Mineral. Petr. 2001, 141, 125–144. [Google Scholar] [CrossRef]
- Váczi, T. A new, simple approximation for the deconvolution of instrumental broadening in spectroscopic band profiles. Appl. Spectrosc. 2014, 68, 1274–1278. [Google Scholar] [CrossRef] [PubMed]
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM—The stopping and range of ions in matter (2010). Nucl. Instrum. Meth. B 2010, 268, 1818–1823. [Google Scholar] [CrossRef] [Green Version]
- Robinson, M.T. The binary collision approximation: Background and introduction. Radiat. Eff. Defects Solids 1994, 130–131, 3–20. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Robinson, M.; Marks, N.A.; Whittle, K.R.; Lumpkin, G.R. Systematic calculation of threshold displacement energies: Case study in rutile. Phys. Rev. B 2012, 85, 104105. [Google Scholar] [CrossRef]
- Buckingham, R.A. The classical equation of state of gaseous helium, neon and argon. Proc. R. Soc. Lond. A 1938, 168, 264–283. [Google Scholar]
- Blanca-Romero, A.; Kowalski, P.M.; Beridze, G.; Schlenz, H.; Bosbach, D. Performance of DFT+U method for prediction of structural and thermodynamic parameters of monazite-type ceramics. J. Comput. Chem. 2014, 35, 1339–1346. [Google Scholar] [CrossRef]
- Gale, J.D.; Henson, N.J. Derivation of interatomic potentials for microporous aluminophosphates from the structure and properties of berlinite. J. Chem. Soc. Faraday Trans. 1994, 90, 3175–3179. [Google Scholar] [CrossRef]
- Girard, S.; Gale, J.D.; Mellot-Draznieks, C.; Ferey, G. Derivation of interatomic potentials for gallophosphates from the GaPO4−quartz structure: Transferability study to gallosilicates and zeotype gallophosphates. Chem. Mater. 2001, 13, 1732–1738. [Google Scholar] [CrossRef]
- Robinson, M.; Marks, N.A.; Lumpkin, G.R. Sensitivity of the threshold displacement energy to temperature and time. Phys. Rev. B 2012, 86, 134105. [Google Scholar] [CrossRef]
- Mullica, D.F.; Grossie, D.A.; Boatner, L.A. Coordination geometry and structural determinations of samarium orthophosphate, europium orthophosphate, and gadolinium orthophosphate. Inorg. Chim. Acta 1985, 109, 105–110. [Google Scholar] [CrossRef]
- Ushakov, S.; Helean, K.; Navrotsky, A.; Boatner, L. Thermochemistry of rare-earth orthophosphates. J. Mater. Res. 2001, 16, 2623–2633. [Google Scholar] [CrossRef]
- Popa, K.; Konings, R. High-temperature heat capacities of EuPO4 and SmPO4 synthetic monazites. Thermochim. Acta 2006, 445, 49–52. [Google Scholar] [CrossRef]
- Rustad, J.R. Density functional calculations of the enthalpies of formation of rare-earth orthophosphates. Am. Mineral. 2012, 97, 791–799. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef] [Green Version]
- Kowalski, P.M.; Ji, Y.; Li, Y.; Arinicheva, Y.; Beridze, G.; Neumeier, S.; Bukaemskiy, A.; Bosbach, D. Simulation of ceramic materials relevant for nuclear waste management: Case of La1-xEuxPO4 solid solution. Nucl. Instrum. Meth. B 2017, 393, 68–72. [Google Scholar] [CrossRef]
- Gouadec, G.; Colomban, P. Raman spectroscopy of nanomaterials: How spectra relate to disorder, particle size and mechanical properties. Prog. Cryst. Growth Charact. Mater. 2007, 53, 1–56. [Google Scholar] [CrossRef] [Green Version]
- Begun, G.M.; Beall, G.W.; Boatner, L.A.; Gregor, W.J. Raman spectra of the rare earth orthophosphates. J. Raman Spectrosc. 1981, 11, 273–278. [Google Scholar] [CrossRef]
- Silva, E.; Ayala, A.; Guedes, I.; Paschoal, C.; Moreira, R.; Loong, C.-K.; Boatner, L. Vibrational spectra of monazite-type rare-earth orthophosphates. Opt. Mater. 2006, 29, 224–230. [Google Scholar] [CrossRef]
- Salje, E. Experimentelle Untersuchung der Ramanstreuung an Kristallpulvern. J. Appl. Cryst. 1973, 6, 442–446. [Google Scholar] [CrossRef]
- Shimizu, R.; Ogasawara, Y. Radiation damage to Kokchetav UHPM diamonds in zircon: Variations in Raman, photoluminescence, and cathodoluminescence spectra. Lithos 2014, 206–207, 201–213. [Google Scholar] [CrossRef]
- Popovic, L.; de Waal, D.; Boeyens, J.C.A. Correlation between Raman wavenumbers and P-O bond lengths in crystalline inorganic phosphates. J. Raman Spectrosc. 2005, 36, 2–11. [Google Scholar] [CrossRef]
- Williford, R.E.; Devanathan, R.; Weber, W.J. Computer simulation of displacement energies for several ceramic materials. Nucl. Instrum. Meth. B 1998, 141, 94–98. [Google Scholar] [CrossRef]
- Park, B.; Weber, W.J.; Corrales, L.R. Molecular-dynamics simulation study of threshold displacements and defect formation in zircon. Phys. Rev. B 2001, 64, 174108. [Google Scholar] [CrossRef]
- Lang, M.; Zhang, F.; Ewing, R.; Lian, J.; Trautmann, C.; Wang, Z. Structural modifications of Gd2Zr2-xTixO7 pyrochlore induced by swift heavy ions: Disordering and amorphization. J. Mater. Res. 2009, 24, 1322–1334. [Google Scholar] [CrossRef]
- Burakov, B.E.; Yagovkina, M.A.; Garbuzov, V.M.; Kitsay, A.A.; Zirlin, V.A. Self-irradiation of monazite ceramics: Contrasting behavior of PuPO4 and (La,Pu)PO4 doped with Pu-238. Mater. Res. Soc. Symp. Proc. 2004, 824, 219–224. [Google Scholar] [CrossRef]
- Brown, D.A.; Chadwick, M.B.; Capote, R.; Kahler, A.C.; Trkov, A.; Herman, M.W.; Sonzogni, A.A.; Danon, Y.; Carlson, A.D.; Dunn, M.; et al. ENDF/B-VIII.0: The 8th major releae of the Nuclear Reaction Data Library with CIELO-project cross sections, new standards and thermal scattering data. Nucl. Data Sheets 2018, 148, 1–142. [Google Scholar] [CrossRef]
- Luo, J.S.; Liu, G.K. Microscopic effects of self-radiation damage in 244Cm-doped LuPO4 crystals. J. Mater. Res. 2001, 16, 366–372. [Google Scholar] [CrossRef]
- Nasdala, L.; Grambole, D.; Ruschel, K. Review of effects of radiation damage on the luminescence emission of minerals, and the example of He-irradiated CePO4. Mineral. Petrol. 2013, 107, 441–454. [Google Scholar] [CrossRef]
- Hyatt, N.C. Plutonium management policy in the United Kingdom: The need for a dual track strategy. Energy Policy 2017, 101, 303–309. [Google Scholar] [CrossRef] [Green Version]
- Arinicheva, Y.; Popa, K.; Scheinost, A.C.; Rossberg, A.; Dieste-Blanco, O.; Raison, P.; Cambriani, A.; Somers, J.; Bosbach, D.; Neumeier, S. Structural investigations of (La,Pu)PO4 monazite solid solutions: XRD and XAFS study. J. Nucl. Mater. 2017, 493, 404–411. [Google Scholar] [CrossRef]
- International Atomic Energy Agency (IAEA). Safe Handling and Storage of Plutonium; Safety Reports Series No. 9; IAEA: Vienna, Austria, 1998. [Google Scholar]
- Nasdala, L.; Akhmadaliev, S.; Burakov, B.E.; Chanmuang, N.C.; Škoda, R. The absence of metamictisation in natural monazite. Sci. Rep. 2020, 10, 14676. [Google Scholar] [CrossRef]
- Mir, A.H.; Peuget, S. Using external ion irradiations for simulating self-irradiation damage in nuclear waste glasses: State of the art, recommendations and prospects. J. Nucl. Mater. 2020, 539, 152246. [Google Scholar] [CrossRef]
- Shiryaev, A.A.; Burakov, B.E.; Nickolsky, M.S.; Yapaskurt, V.O.; Pavlushin, A.D.; Grigoriev, M.S.; Vlasova, I.E. Surface features on aged 238Pu-doped Eu-monazite. Radiochim. Acta 2020, 108, 353–360. [Google Scholar] [CrossRef]
- Shiryaev, A.A.; Burakov, B.E.; Yapaskurt, V.O.; Egorov, A.V.; Vlasova, I.E. Microstructure of aged 238Pu-doped La-monazite ceramic and peculiarities of its X-ray emission spectra. MRS Adv. 2020, 5, 1–7. [Google Scholar] [CrossRef]
- OECD-NEA. Plutonium Fuel: An Assessment; OECD Nuclear Energy Agency: Paris, France, 1989. [Google Scholar]
- Wallenius, M.; Peerani, P.; Koch, L. Origin determination of plutonium material in nuclear forensics. J. Radioanal. Nucl. Chem. 2000, 246, 317–321. [Google Scholar] [CrossRef]
- OECD-NEA. Physics of Plutonium Recycling, Vol. 1—Issues and Perspectives; OECD Nuclear Energy Agency: Paris, France, 1995. [Google Scholar]
- Kang, J.; von Hippel, F.N.; MacFarlane, A.; Nelson, R. Storage MOX: A third way for plutonium disposal? Sci. Glob. Secur. 2002, 10, 85–101. [Google Scholar] [CrossRef]
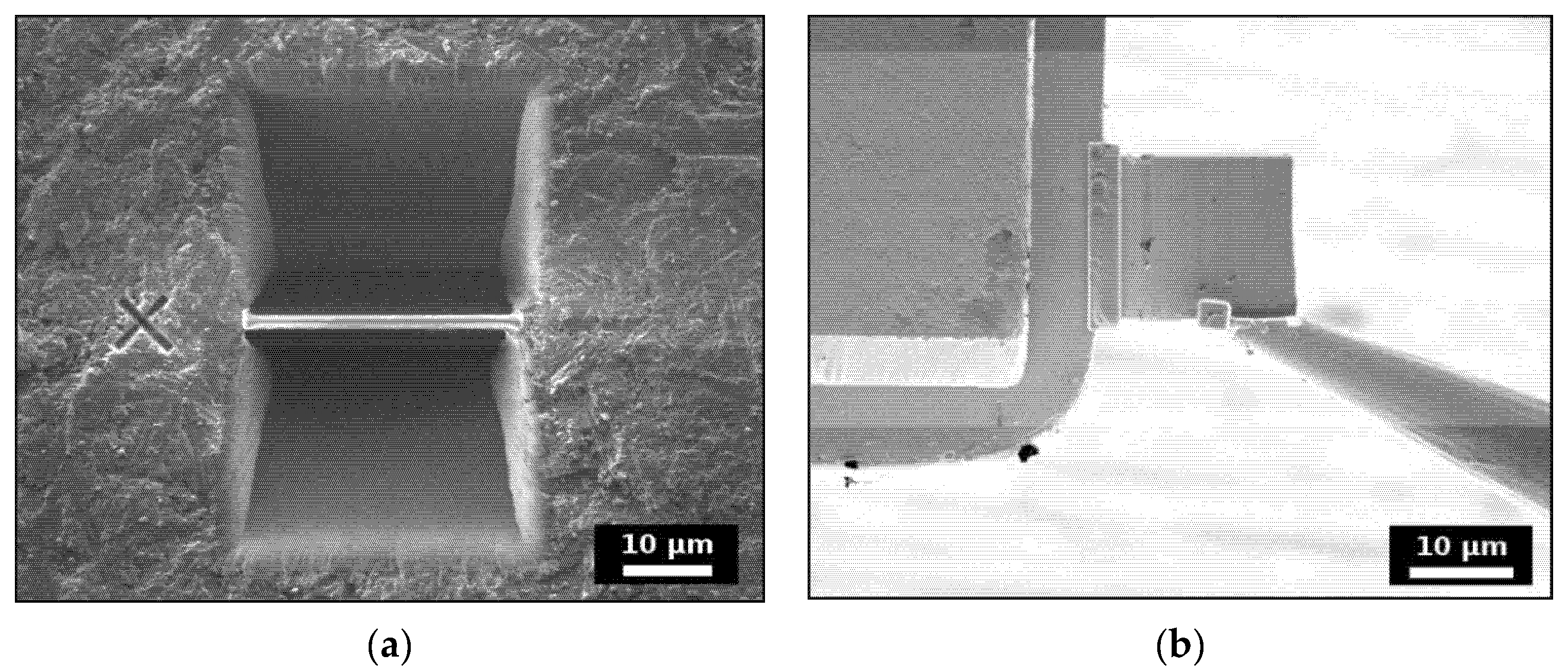
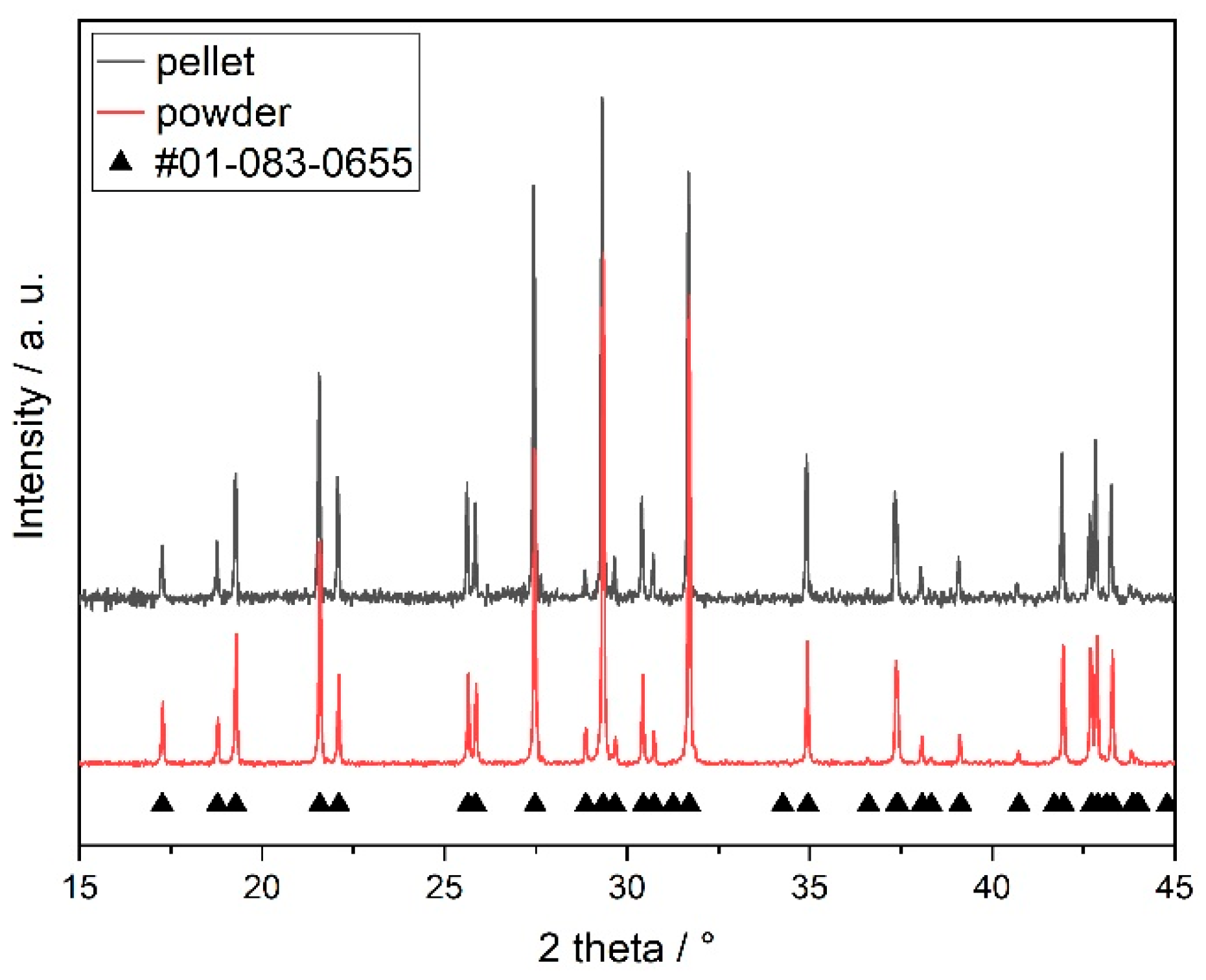


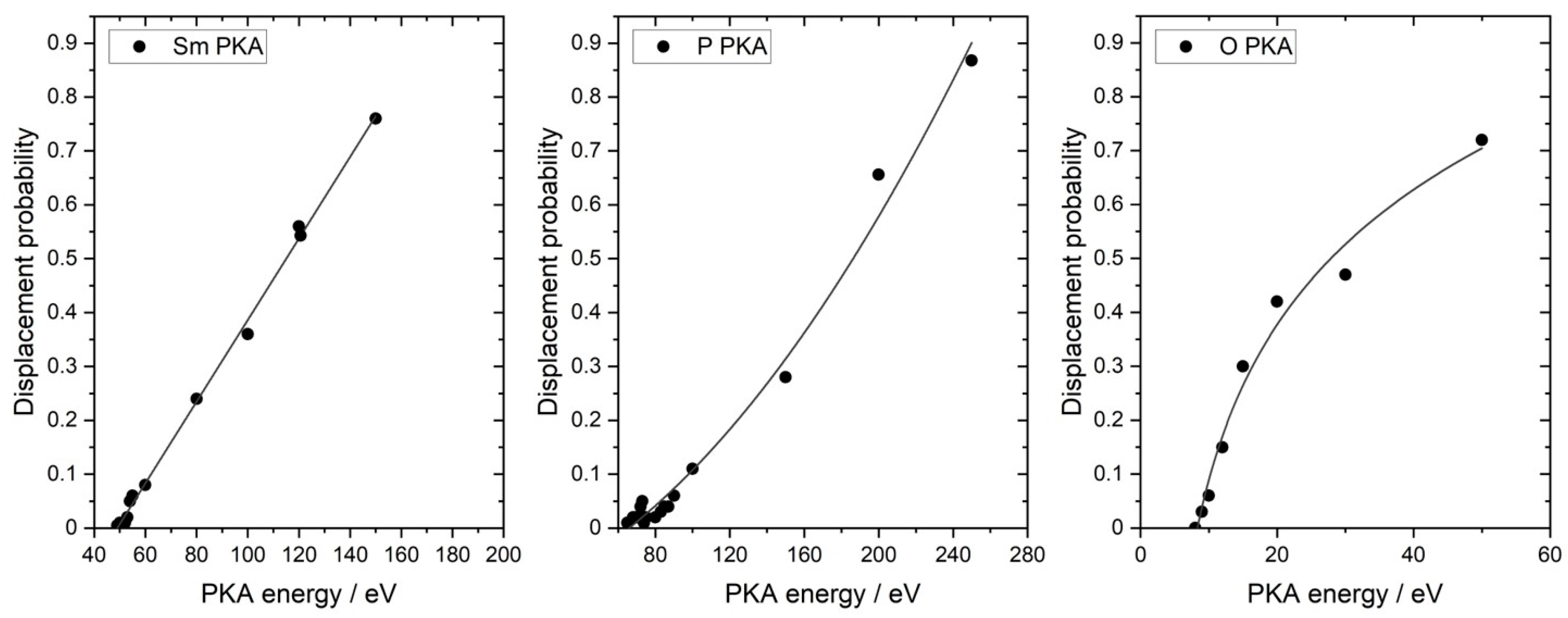
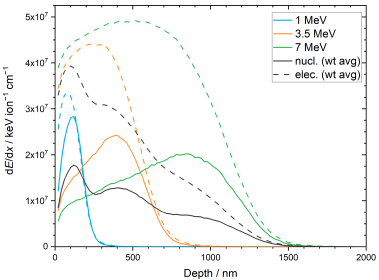

| A/eV | B/Å–1 | C/Å6 eV | |
|---|---|---|---|
| Sm–O | 14,794.52 | 0.26 | 0.00 |
| P–O | 877.3 | 0.3594 | 0.0000 |
| O–O | 22,764.3 | 0.1390 | 27.879 |
| Reference | a/Å | b/Å | c/Å | β/° | V/Å3 |
|---|---|---|---|---|---|
| This work | 6.69035 (4) | 6.89207 (4) | 6.37219 (4) | 103.8632 (4) | 285.2647 (3) |
| [24] | 6.6818 (12) | 6.8877 (9) | 6.3653 (9) | 103.86 (1) | 284.42 |
| [87] | 6.6891 (3) | 6.8958 (3) | 6.3770 (6) | 103.9 (1) | 285.54 |
| [88] | 6.6902 (9) | 6.8935 (5) | 6.3714 (3) | 103.871 (9) | 285.30 |
| [18] | 6.6888 (3) | 6.8948 (2) | 6.3725 (3) | 103.87 (1) | 285.32 (5) |
| [89] | 6.803 | 6.961 | 6.394 | 104.2 | 293.52 |
| [82] * | 6.731 | 6.923 | 6.383 | 104.081 | 288.523 |
| [67] * | 6.686 | 6.880 | 6.344 | 104.032 | 283.128 |
| Fluence/Ions cm−2 | Average Energy Deposition/keV cm−3 | Average Dose/MGy | |||||
|---|---|---|---|---|---|---|---|
| Total | Nuclear | Electronic | Total | Nuclear | Electronic | ||
| F1 | 6.0 × 1012 | 1.57 × 1020 | 4.85 × 1019 | 1.09 × 1020 | 4.8 | 1.5 | 3.3 |
| F2 | 1.8 × 1013 | 4.72 × 1020 | 1.45 × 1020 | 3.26 × 1020 | 14.3 | 4.4 | 9.9 |
| F3 | 5.1 × 1014 | 1.34 × 1022 | 4.12 × 1021 | 9.24 × 1021 | 403.9 | 124.5 | 279.4 |
| Pellet Samples | Lamellae | |||||
|---|---|---|---|---|---|---|
| F1 | F2 | F3 | F1 | F2 | F3 | |
| Fluence/ions cm−2 | 6.0 × 1012 | 1.8 × 1013 | 5.1 × 1014 | 6.1 × 1012 | 1.8 × 1013 | 5.1 × 1014 |
| dpa(max) | 0.06 | 0.19 | 5.44 | 0.06 | 0.19 | 5.44 |
| dpa(avg) | 0.03 * | 0.08 * | 2.13 * | 0.05 | 0.15 | 3.81 |
| Pellet Samples | Lamellae | |||||||
|---|---|---|---|---|---|---|---|---|
| F1 | F2 | F3 | F1 | F2 | F3 | |||
| Fluence/ions cm−2 | 0 | 6.0 × 1012 | 1.8 × 1013 | 5.1 × 1014 | 0 | 6.1 × 1012 | 1.8 × 1013 | 5.1 × 1014 |
| ν1/cm−1 | 982.0 | 981.8 | 981.6 | 982.4 | 980.9 | 979.6 | 979.3 | 961.8 |
| FWHM/cm−1 | 4.3 | 3.6 | 3.5 | 3.4 | 3.5 | 5.2 | 6.5 | >>10 |
| Phase | Ed/eV | Used by | Comment | |||
|---|---|---|---|---|---|---|
| Ln | P | O | Σ | |||
| Monazite (natural) | 25 | 25 | 25 | 150 | [44] | |
| Monazite (natural) | 79 | 23 | 47 | 290 | [39] | analogy to ZrSiO4 [4] |
| LnPO4 (Ln: La—Lu) | 20 | 20 | 20 | 120 | [46] | |
| LaPO4 | 20 | 20 | 20 | 120 | [45] | |
| LaPO4 | 79 | 23 | 47 | 290 | [39,47] | analogy to ZrSiO4 [4] |
| LaPO4 | 25 | 25 | 25 | 150 | [50] | |
| LaPO4 | 56 | 75 | 8 | 163 | [68] | derived from MD simulations |
| CePO4 | 25 | 25 | 28 | 162 | [42,49] | SRIM/TRIM default [77] |
| SmPO4 | 49 | 65 | 8 | 146 | this work | derived from MD simulations |
| GdPO4 | 51 | 75 | 8 | 158 | [68] | derived from MD simulations |
| Material | Dalpha/α g−1 | Dose Rate/α g−1 s−1 | Source |
|---|---|---|---|
| Pu wasteform (10 wt% Pu) | 1 × 1020 to 4 × 1020 (1 Ma) | ~1 × 107 | this work (cf. Table S4) |
| Monazite-(Sm) (natural) | 2.9 × 1020 to 3.7 × 1020 (2640 Ma) | 3471 to 4492 | [43] |
| Monazite-(Ce) (natural) | 2.43 × 1019 (474 to 479 Ma) | 1618 | [33] |
| Monazites (natural) | 1.3 × 1018 to 1.7 × 1020 (24 to 1928 Ma) | 1718 to 3561 | [34] |
| Monazites (natural) | 6.0 × 1018 to 1.1 × 1020 (101 to 1391 Ma) | 379 to 4973 | [36] |
| Monazite-(Ce) (natural) | 2.4 × 1019 to 1.7 × 1020 (500 to 1928 Ma) | 1522 to 2796 | [35] |
| 244Cm-doped LuPO4 | 5.0 × 1019 (18 a) | 8.8 × 1010 | [103] |
| 238Pu-doped (La,Pu)PO4 | 2.5 × 1018 | [101] | |
| 238Pu-doped (La,Ca,Th)PO4 | 7.5 × 1018 (5 a) | 4.7 × 1010 | [50] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leys, J.M.; Ji, Y.; Klinkenberg, M.; Kowalski, P.M.; Schlenz, H.; Neumeier, S.; Bosbach, D.; Deissmann, G. Monazite-Type SmPO4 as Potential Nuclear Waste Form: Insights into Radiation Effects from Ion-Beam Irradiation and Atomistic Simulations. Materials 2022, 15, 3434. https://doi.org/10.3390/ma15103434
Leys JM, Ji Y, Klinkenberg M, Kowalski PM, Schlenz H, Neumeier S, Bosbach D, Deissmann G. Monazite-Type SmPO4 as Potential Nuclear Waste Form: Insights into Radiation Effects from Ion-Beam Irradiation and Atomistic Simulations. Materials. 2022; 15(10):3434. https://doi.org/10.3390/ma15103434
Chicago/Turabian StyleLeys, Julia M., Yaqi Ji, Martina Klinkenberg, Piotr M. Kowalski, Hartmut Schlenz, Stefan Neumeier, Dirk Bosbach, and Guido Deissmann. 2022. "Monazite-Type SmPO4 as Potential Nuclear Waste Form: Insights into Radiation Effects from Ion-Beam Irradiation and Atomistic Simulations" Materials 15, no. 10: 3434. https://doi.org/10.3390/ma15103434
APA StyleLeys, J. M., Ji, Y., Klinkenberg, M., Kowalski, P. M., Schlenz, H., Neumeier, S., Bosbach, D., & Deissmann, G. (2022). Monazite-Type SmPO4 as Potential Nuclear Waste Form: Insights into Radiation Effects from Ion-Beam Irradiation and Atomistic Simulations. Materials, 15(10), 3434. https://doi.org/10.3390/ma15103434







