Influence of Water-Induced Degradation of Polytetrafluoroethylene (PTFE)-Coated Woven Fabrics Mechanical Properties
Abstract
:1. Introduction
2. Materials and Methods
3. Laboratory Test Results and Discussion
3.1. Measurements of Surface Weight
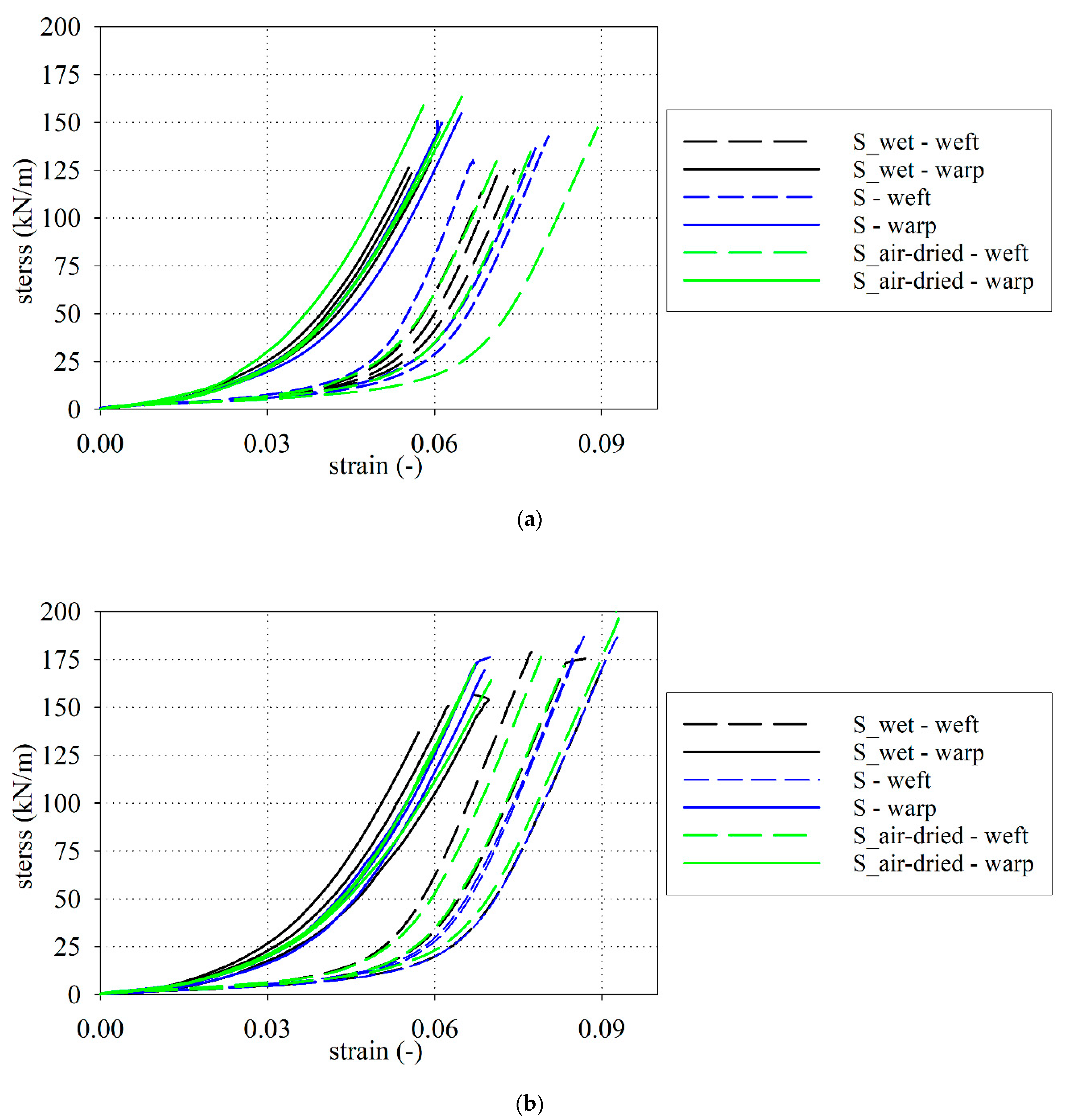
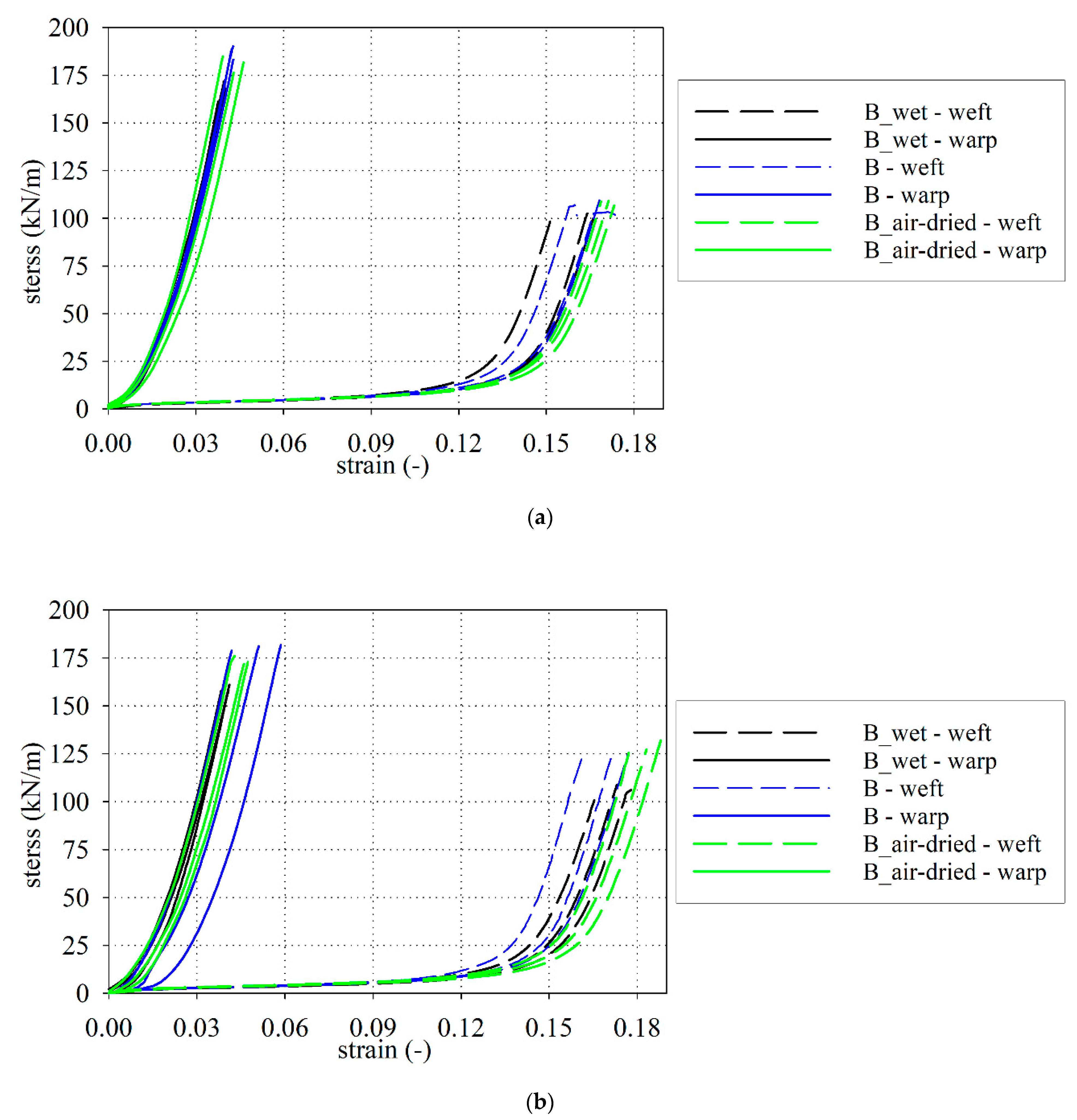
3.2. Uniaxial Tensile Tests
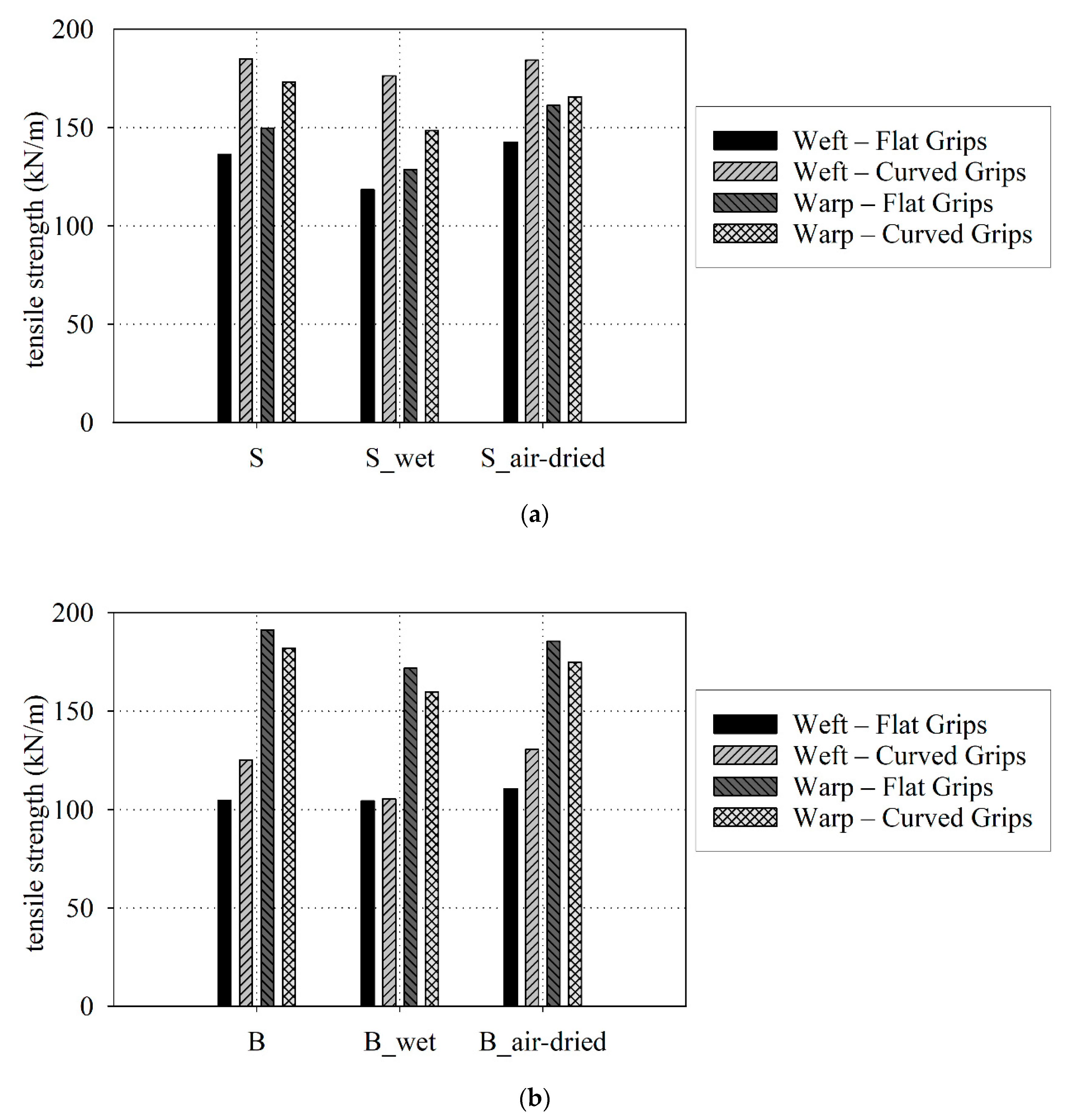
3.3. Elongation at Break and Tensile Strength
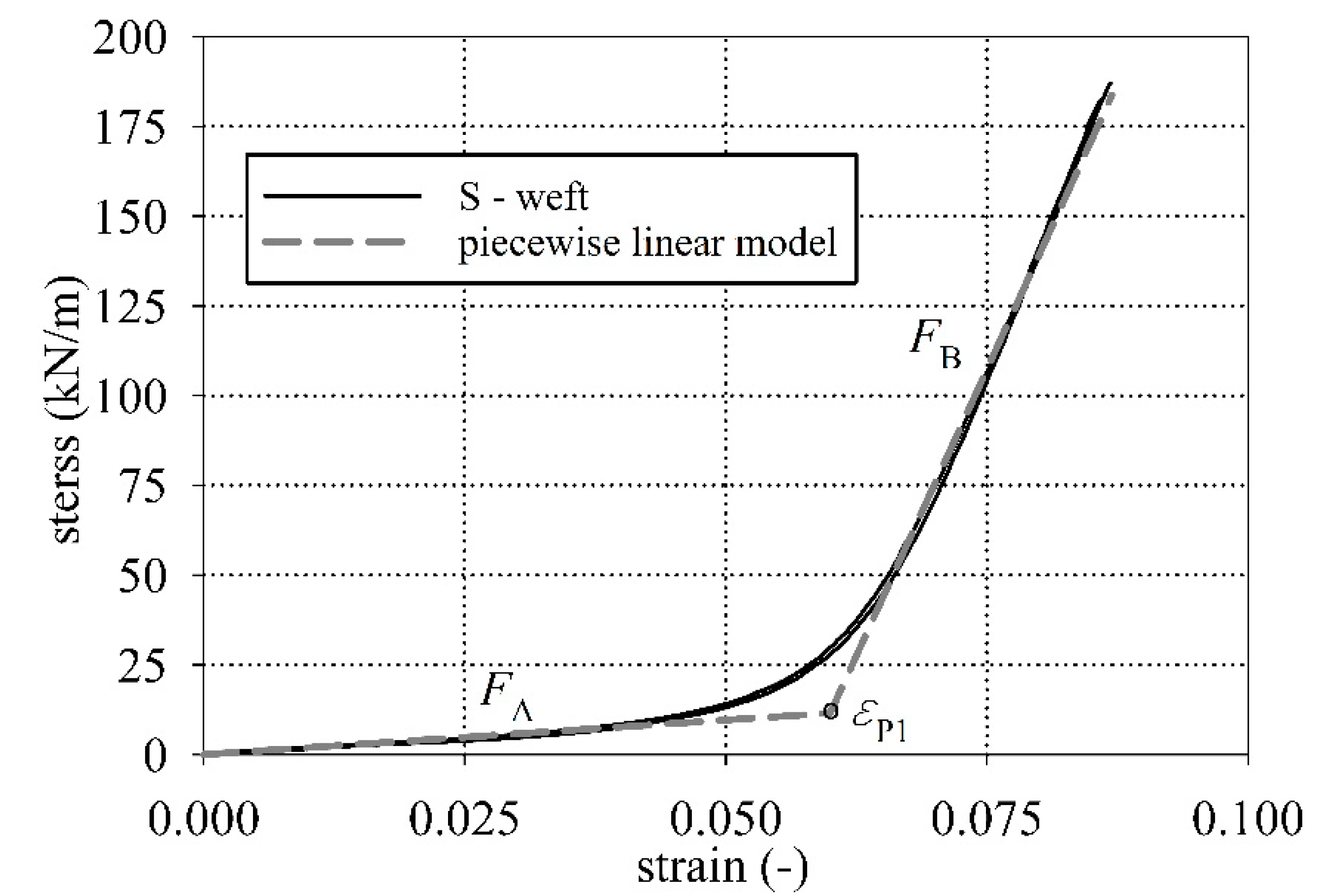
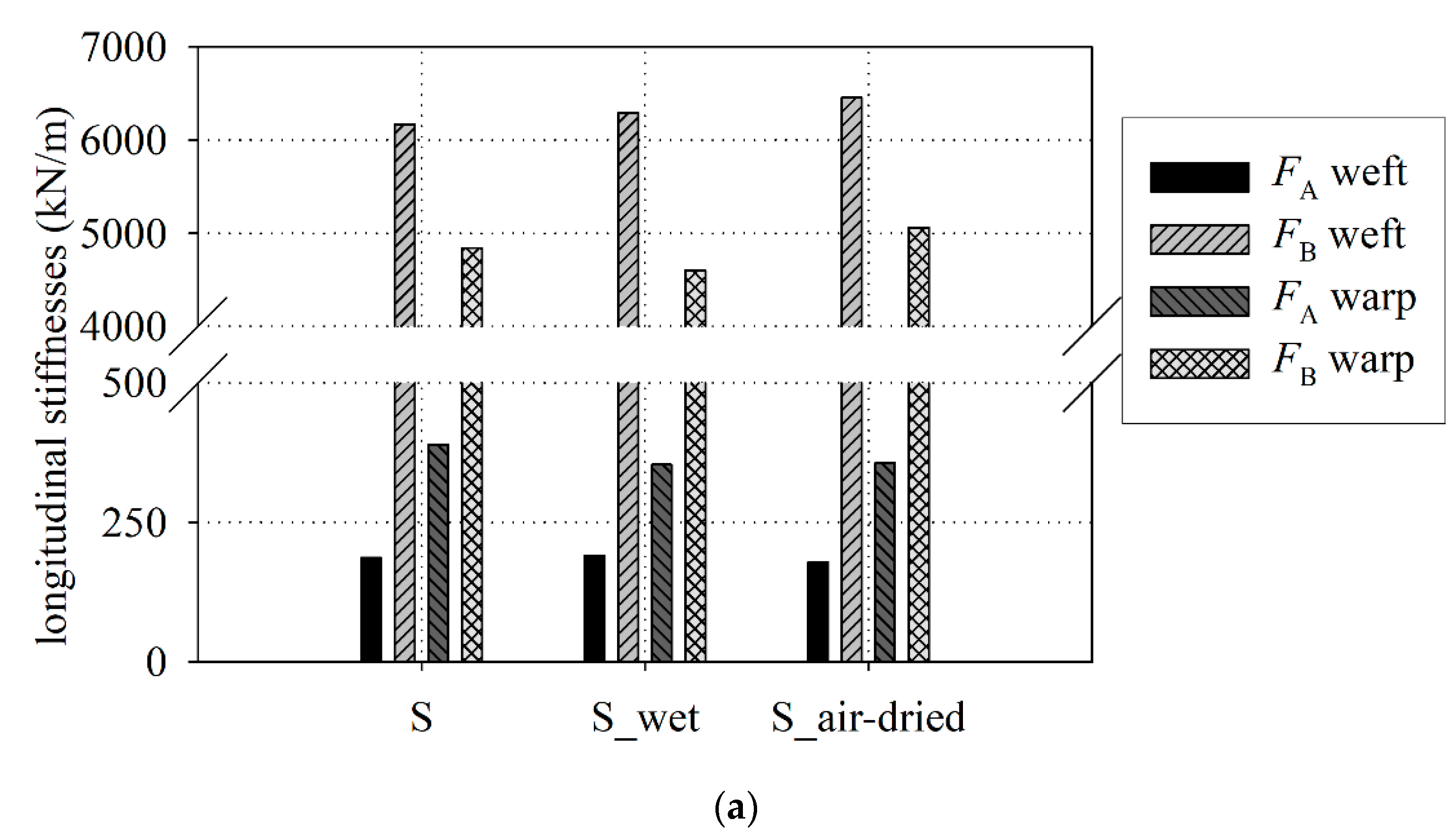
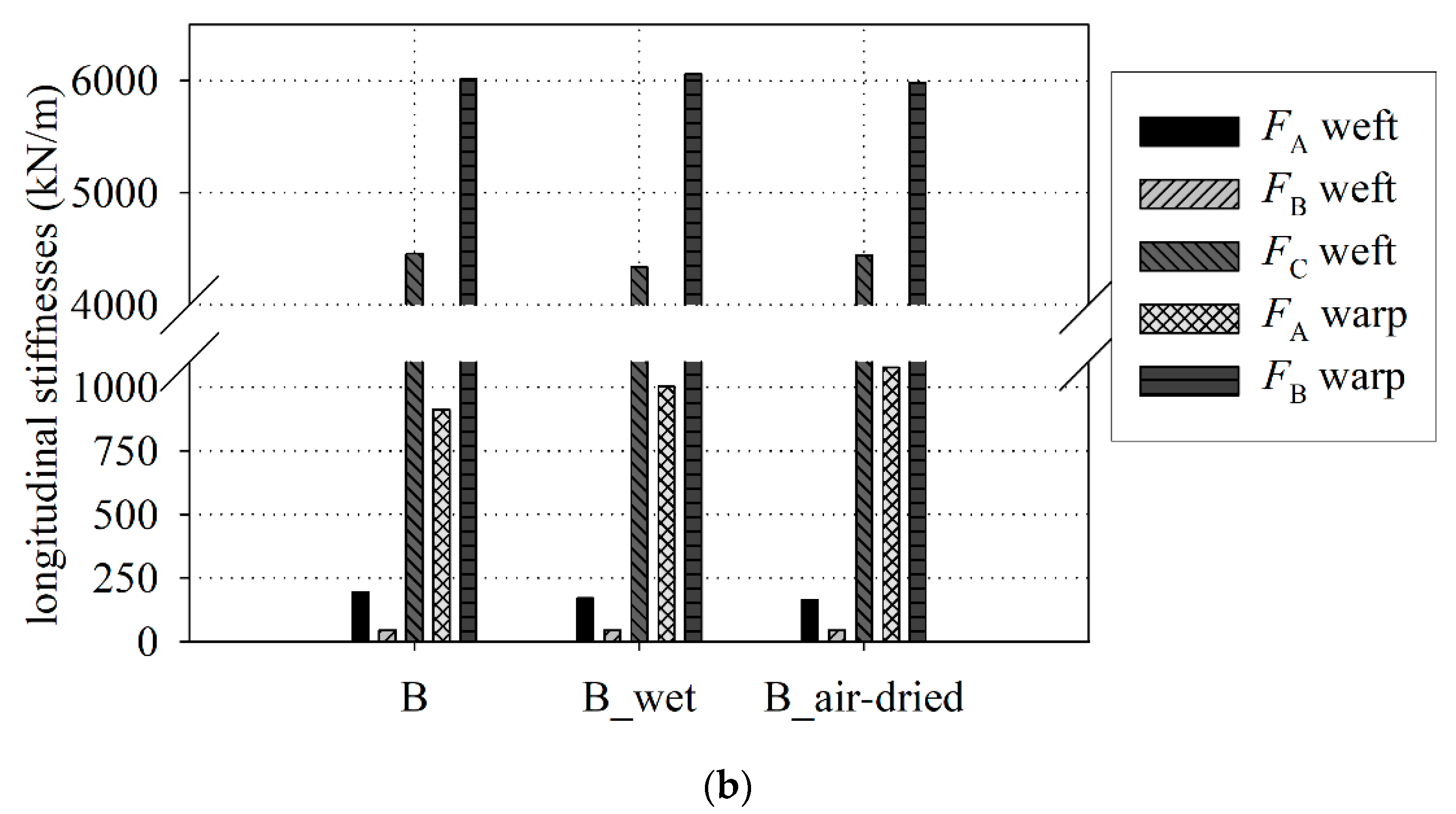
3.4. Determination of the Longitudinal Stiffnesses
4. Conclusions
- The reduction in the tensile strength resulting under waterlogged was observed in the range from 5% (for weft) to 14% (for warp) for S-type fabric and from 16% (for weft) to 10% (for warp) for B-type fabric, respectively. A similar conclusion came from the authors of [94], where the change in the tensile strength under influence of water was specified nearby 20%.
- The mechanical properties of investigated PTFE coated fabric under water-induced are degraded not only via in-plane watering at unsealed cut edges but also via out-of-plane watering through the coating.
- The influence of moisture is not the same for different physical parameters. The most sensitive is the tensile strength.
- Even small moisture changes as it has been reported between the base fabric and air-dried material cause statistically important changes in the tensile strength. The changes in fabric stiffness are much less sensitive and from the statistical point of view, they can be neglected.
- The ANOVA analysis indicated that the longitudinal stiffnesses differences among the investigated groups (dry, wet, and air-dry) are not statistically significant. Future investigations should take into account a more large number of specimens to confirm differences.
- Types of grips used in tensile tests influenced the determined values of the tensile strength. The type of grips is not important during the stiffness of fabric determination. Determination of the tensile strength should be rather performed by using the curved grips to avoid the close-to-grip breaks in coated fabric specimens that are often observed when the flat grips are used. Such close-to-grip breaks reduce the tensile strength value.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Specimens No. | Weft—Flat Grips SWp | Weft—Curved Grips SW | Warp—Flat Grips SOp | Warp—Curved Grips SO | ||||
|---|---|---|---|---|---|---|---|---|
| Rupture Strain | Tensile Strength | Rupture Strain | Tensile Strength | Rupture Strain | Tensile Strength | Rupture Strain | Tensile Strength | |
| - | kN/m | - | kN/m | - | kN/m | - | kN/m | |
| 1 | 0.0804 | 142.5 | 0.0859 | 182.2 | 0.0622 | 147.7 | 0.0694 | 171.0 |
| 2 | 0.0670 | 128.7 | 0.0929 | 187.0 | 0.0689 | 156.2 | 0.0745 | 171.3 |
| 3 | 0.0784 | 138.0 | 0.0868 | 187.1 | 0.0567 | 145.6 | 0.0723 | 177.2 |
| mean | 0.0753 ± 0.0042 | 136.4 ± 4 | 0.0885 ± 0.0022 | 185 ± 2 | 0.0626 ± 0.0035 | 149.8 ± 3 | 0.0721 ± 0.0015 | 173.1 ± 2 |
| Specimens No. | Weft—Flat Grips SWp_Wet | Weft—Curved Grips SW_Wet | Warp—Flat Grips SOp_Wet | Warp—Curved Grips SO_Wet | ||||
|---|---|---|---|---|---|---|---|---|
| Rupture Strain | Tensile Strength | Rupture Strain | Tensile Strength | Rupture Strain | Tensile Strength | Rupture Strain | Tensile Strength | |
| - | kN/m | - | kN/m | - | kN/m | - | kN/m | |
| 1 | 0.0738 | 112.4 | 0.0939 | 175.1 | 0.0508 | 129.6 | 0.0573 | 138.0 |
| 2 | 0.0905 | 122.1 | 0.0776 | 180.3 | 0.0485 | 122.4 | 0.0625 | 151.1 |
| 3 | 0.0989 | 120.8 | 0.1253 | 173.8 | 0.0448 | 134.1 | 0.0700 | 156.9 |
| mean | 0.0878 ± 0.0074 | 118.5 ± 3 | 0.0989 ± 0.0140 | 176.4 ± 2 | 0.0480 ± 0.0018 | 128.7 ± 3 | 0.0633 ± 0.0037 | 148.6 ± 6 |
| Specimens No. | Weft—Flat Grips SWp_Air-Dried | Weft—Curved Grips SW_Air-Dried | Warp—Flat Grips SOp_Air-Dried | Warp—Curved Grips SO_Air-Dried | ||||
|---|---|---|---|---|---|---|---|---|
| Rupture Strain | Tensile Strength | Rupture Strain | Tensile Strength | Rupture Strain | Tensile Strength | Rupture Strain | Tensile Strength | |
| - | kN/m | - | kN/m | - | kN/m | - | kN/m | |
| 1 | 0.0896 | 149.4 | 0.0800 | 177.0 | 0.0659 | 169.8 | 0.0705 | 166.1 |
| 2 | 0.0718 | 134.7 | 0.1290 | 202.5 | 0.0619 | 150.8 | 0.0651 | 158.5 |
| 3 | 0.0782 | 143.7 | 0.0835 | 173.5 | 0.0584 | 163.6 | 0.0913 | 172.4 |
| mean | 0.0799 ± 0.0052 | 142.6 ± 4 | 0.0975 ± 0.0158 | 184.3 ± 9 | 0.0480 ± 0.0018 | 161.4 ± 6 | 0.0757 ± 0.0079 | 165.7 ± 4 |
| Specimens No. | Weft—Flat Grips BWp | Weft—Curved Grips BW | Warp—Flat Grips BOp | Warp—Curved Grips BO | ||||
|---|---|---|---|---|---|---|---|---|
| Rupture Strain | Tensile Strength | Rupture Strain | Tensile Strength | Rupture Strain | Tensile Strength | Rupture Strain | Tensile Strength | |
| - | kN/m | - | kN/m | - | kN/m | - | kN/m | |
| 1 | 0.1736 | 101.8 | 0.1761 | 126.3 | 0.0436 | 189.0 | 0.0592 | 184.1 |
| 2 | 0.1684 | 111.0 | 0.1755 | 123.4 | 0.0432 | 192.4 | 0.0401 | 179.7 |
| 3 | 0.1606 | 101.4 | 0.1768 | 125.6 | 0.0387 | 192.5 | 0.0512 | 181.7 |
| mean | 0.1675 ± 0.0038 | 104.7 ± 3 | 0.1761 ± 0.0007 | 125.1 ± 1 | 0.0418 ± 0.0016 | 191.3 ± 1 | 0.0502 ± 0.0055 | 181.9 ± 1 |
| Specimens No. | Weft—Flat Grips BWp_Wet | Weft—Curved Grips BW_Wet | Warp—Flat Grips BOp_Wet | Warp—Curved Grips BO_Wet | ||||
|---|---|---|---|---|---|---|---|---|
| Rupture Strain | Tensile Strength | Rupture Strain | Tensile Strength | Rupture Strain | Tensile Strength | Rupture Strain | Tensile Strength | |
| - | kN/m | - | kN/m | - | kN/m | - | kN/m | |
| 1 | 0.1673 | 107.8 | 0.1731 | 108.7 | 0.0428 | 174.7 | 0.0759 | 159.0 |
| 2 | 0.2261 | 104.6 | 0.1860 | 106.1 | 0.0388 | 168.3 | 0.0357 | 158.0 |
| 3 | 0.1570 | 101.2 | 0.1655 | 101.9 | 0.0403 | 172.3 | 0.0417 | 162.8 |
| mean | 0.1835 ± 0.0215 | 104.5 ± 2 | 0.1749 ± 0.0104 | 105.5 ± 3 | 0.0407 ± 0.0011 | 171.8 ± 2 | 0.0511 ± 0.0125 | 159.9 ± 1 |
| Specimens No. | Weft—Flat Grips BWp_Air-Dried | Weft—Curved Grips BW_Air-Dried | Warp—Flat Grips BOp_Air-Dried | Warp—Curved Grips BO_Air-Dried | ||||
|---|---|---|---|---|---|---|---|---|
| Rupture Strain | Tensile Strength | Rupture Strain | Tensile Strength | Rupture Strain | Tensile Strength | Rupture Strain | Tensile Strength | |
| - | kN/m | - | kN/m | - | kN/m | - | kN/m | |
| 1 | 0.1702 | 111.9 | 0.1834 | 133.4 | 0.0430 | 183.2 | 0.0477 | 174.7 |
| 2 | 0.1736 | 108.1 | 0.1834 | 128.5 | 0.0485 | 185.8 | 0.0429 | 176.0 |
| 3 | 0.1745 | 112.0 | 0.1780 | 130.3 | 0.0397 | 187.4 | 0.0463 | 173.6 |
| mean | 0.1728 ± 0.0013 | 110.7 ± 1 | 0.1816 ± 0.0018 | 130.7 ± 1 | 0.0437 ± 0.0026 | 185.5 ± 1 | 0.0456 ± 0.0014 | 174.8 ± 1 |
| S | S_Wet | S_Air-Dried | ||||
|---|---|---|---|---|---|---|
| Weft | Warp | Weft | Warp | Weft | Warp | |
| (kN/m) (-) | (kN/m) (-) | (kN/m) (-) | (kN/m) (-) | (kN/m) (-) | (kN/m) (-) | |
| FA | 187 ± 5 0.059 ± 0.002 | 390 ± 12 0.035 ± 0.001 | 191 ± 5 0.056 ± 0.002 | 354 ± 12 0.035 ± 0.002 | 179 ± 5 0.059 ± 0.002 | 357 ± 4 0.037 ± 0.001 |
| FB | 6168 ± 63 | 4842 ± 137 | 6294 ± 102 | 4603 ± 92 | 6454 ± 101 | 5064 ± 60 |
| B | B_Wet | B_Air-Dried | ||||
|---|---|---|---|---|---|---|
| Weft | Warp | Weft | Warp | Weft | Warp | |
| (kN/m) (-) | (kN/m) (-) | (kN/m) (-) | (kN/m) (-) | (kN/m) (-) | (kN/m) (-) | |
| FA | 196 ± 8 0.009 ± 0.0003 | 913 ± 135 0.019 ± 0.002 | 172 ± 10 0.01± 0.001 | 1004 ± 41 0.016 ± 0.0005 | 165 ± 6 0.010 ± 0.002 | 1079 ± 72 0.018 ± 0.001 |
| FB | 47 ± 1 0.144 ± 0.002 | 6014 ± 180 | 46 ± 2 0.149 ± 0.003 | 6060 ± 173 | 46 ± 1 0.153 ± 0.002 | 5986 ± 209 |
| FC | 4459 ± 88 | - | 4338 ± 64 | - | 4441 ± 71 | - |
References
- Stimpfle, B. Recent developments in architectural fabric structures: Shopping mall Titan Plaza, Bogotá, Columbia. In Fabric Structures in Architecture; Llorens, J., Ed.; Woodhead Publishing: Sawston, UK, 2015; pp. 727–747. [Google Scholar]
- Birchall, M. Recent developments in architectural fabric structures in Europe: The design and construction of the London 2012 Olympic Stadium and its context in the European fabric structures market. In Fabric Structures in Architecture; Llorens, J., Ed.; Woodhead Publishing: Sawston, UK, 2015; pp. 773–817. [Google Scholar]
- Lombardi, S.; Monticelli, C. Recent developments in architectural fabric structures in Europe: The example of Winter Garden, Verona, Italy. In Fabric Structures in Architecture; Llorens, J., Ed.; Woodhead Publishing: Sawston, UK, 2015; pp. 749–771. [Google Scholar]
- Ambroziak, A.; Kłosowski, P. Review of constitutive models for technical woven fabrics in finite element analysis. AATCC Rev. 2011, 5–6, 58–67. [Google Scholar]
- Haas, R. The Stretching of the Fabric and the Shape of the Envelope. Natl. Advis. Comm. Aeronaut. Rep. 1918, 16, 155–250. [Google Scholar]
- Peirce, F.T. The geometry of cloth structure. J. Text. Inst. Trans. 1937, 28, T45–T96. [Google Scholar] [CrossRef]
- Argyris, J.; St. Doltsinis, I.; da silva, V.D. Constitutive modelling and computation of non-linear viscoelastic solids. Part I: Rheological models and numerical integration techniques. Comput. Methods Appl. Mech. Eng. 1991, 88, 135–163. [Google Scholar] [CrossRef]
- Szostkiewicz-Chatain, C.; Hamelin, P. Numerical and experimental stiffness characterisations applied to soft textile composites for tensile structures. Mater. Struct. 1998, 31, 118–125. [Google Scholar] [CrossRef]
- Bridgens, B.N.; Gosling, P.D. Direct stress–strain representation for coated woven fabrics. Comput. Struct. 2004, 82, 1913–1927. [Google Scholar] [CrossRef]
- Pargana, J.B.; Lloyd-Smith, D.; Izzuddin, B.A. Advanced material model for coated fabrics used in tensioned fabric structures. Eng. Struct. 2007, 29, 1323–1336. [Google Scholar] [CrossRef]
- Galliot, C.; Luchsinger, R.H. The shear ramp: A new test method for the investigation of coated fabric shear behaviour – Part II: Experimental validation. Compos. Part A Appl. Sci. Manuf. 2010, 41, 1750–1759. [Google Scholar] [CrossRef]
- Derewonko, A.; Baranowski, P.; Rudnik, D. Simulation of Rubber-Coated Fabric Material Damage. Key Eng. Mater. 2011, 488–489, 585–588. [Google Scholar] [CrossRef]
- Meng, L.; Wu, M. Study on stress relaxation of membrane structures in the prestress state by considering viscoelastic properties of coated fabrics. Thin-Walled Struct. 2016, 106, 18–27. [Google Scholar] [CrossRef]
- Jekel, C.F.; Venter, G.; Venter, M.P. Obtaining a hyperelastic non-linear orthotropic material model via inverse bubble inflation analysis. Struct. Multidiscip. Optim. 2016, 54, 927–935. [Google Scholar] [CrossRef]
- Hegyi, D.; Halász, M.; Molnár, K.; Szebenyi, G.; Sipos, A.A. An elastic phenomenological material law for textile composites and it’s fitting to experimental data. J. Reinf. Plast. Compos. 2017, 36, 1343–1354. [Google Scholar] [CrossRef] [Green Version]
- Jekel, C.F.; Venter, G.; Venter, M.P. Modeling PVC-coated polyester as a hypoelastic non-linear orthotropic material. Compos. Struct. 2017, 161, 51–64. [Google Scholar] [CrossRef]
- Dib, W.; Bles, G.; Blaise, A.; Tourabi, A. Modelling of cyclic visco-elasto-plastic behaviour of coated woven fabrics under biaxial loading and finite strain. Int. J. Solids Struct. 2018, 154, 147–167. [Google Scholar] [CrossRef] [Green Version]
- Motevalli, M.; Uhlemann, J.; Stranghöner, N.; Balzani, D. Geometrically nonlinear simulation of textile membrane structures based on orthotropic hyperelastic energy functions. Compos. Struct. 2019, 223, 110908. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, Y.; Wu, M.; Zhao, Y. A phenomenological material model for PTFE coated fabrics. Constr. Build. Mater. 2020, 237, 117667. [Google Scholar] [CrossRef]
- Zhao, B.; Hu, J.; Chen, W.; Chen, J.; Jing, Z. A nonlinear uniaxial stress-strain constitutive model for viscoelastic membrane materials. Polym. Test. 2020, 90, 106633. [Google Scholar] [CrossRef]
- Reinhardt, H.W. On the biaxial testing and strength of coated fabrics. Exp. Mech. 1976, 16, 71–74. [Google Scholar] [CrossRef]
- Day, A.S. Stress strain equations for non-linear behaviour of coated woven fabrics. In Proceedings of the IASS Symposium: Shells, Membranes and Space Frames; Elsevier: Osaka, Japan, 1986; pp. 17–24. [Google Scholar]
- Chen, S.; Ding, X.; Fangueiro, R.; Yi, H.; Ni, J. Tensile behavior of PVC-coated woven membrane materials under uni- and bi-axial loads. J. Appl. Polym. Sci. 2008, 107, 2038–2044. [Google Scholar] [CrossRef]
- Zouari, R.; Amar, S.B.; Dogui, A. Experimental and numerical analyses of fabric off-axes tensile test. J. Text. Inst. 2010, 101, 58–68. [Google Scholar] [CrossRef]
- El-Messiry, M.; Youssef, S. Analysis of stress-strain of architect woven fabric strength under biaxial extensions. Alexandria Eng. J. 2011, 50, 297–303. [Google Scholar] [CrossRef]
- Derewońko, A.; Niezgoda, T.; Bogusz, P. Uniaxial Tests of Limp Elastic Multi-Layer Materials. In Proceedings of the 9th International Conference On Composite Science And Technology: 2020-Scientific And Industrial Challenges, Naples, Italy, 24–26 April 2013; Meo, M., Ed.; University of Bath: Naples, Italy, 2013; pp. 745–754. ISBN 9781605951133. [Google Scholar]
- Ambroziak, A.; Kłosowski, P. Mechanical properties for preliminary design of structures made from PVC coated fabric. Constr. Build. Mater. 2014, 50, 74–81. [Google Scholar] [CrossRef]
- Chen, J.; Chen, W.; Zhang, D. Experimental study on uniaxial and biaxial tensile properties of coated fabric for airship envelopes. J. Reinf. Plast. Compos. 2014, 33, 630–647. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, W. Deformation evaluation due to poisson’s ratio variation of coated fabric for airship envelope. Res. J. Appl. Sci. Eng. Technol. 2014, 7, 1101–1107. [Google Scholar] [CrossRef]
- Bögner-Balz, H.; Blum, R.; Köhnlein, J. Structural behaviour of fabrics and coatings for architectural fabric structures. In Fabric Structures in Architecture; Woodhead Publishing: Sawston, UK, 2015; pp. 123–157. [Google Scholar]
- Ambroziak, A. Mechanical properties of Precontraint 1202S coated fabric under biaxial tensile test with different load ratios. Constr. Build. Mater. 2015, 80, 210–224. [Google Scholar] [CrossRef]
- Ambroziak, A. Mechanical Properties of Polyester Coated Fabric Subjected to Biaxial Loading. J. Mater. Civ. Eng. 2015, 27, 04015012. [Google Scholar] [CrossRef]
- Chen, J.; Chen, W. Central Crack Tearing Testing of Laminated Fabric Uretek3216LV under Uniaxial and Biaxial Static Tensile Loads. J. Mater. Civ. Eng. 2016, 28, 04016028. [Google Scholar] [CrossRef]
- Wu, M.; Li, Y.; Shang, Y. Statistical Characteristics of Ethylene Tetrafluoroethylene Foil’s Mechanical Properties and Its Partial Safety Factors. J. Mater. Civ. Eng. 2016, 28, 04016004. [Google Scholar] [CrossRef]
- Shi, T.; Chen, W.; Gao, C.; Hu, J.; Zhao, B.; Zhang, D.; Qiu, Z. Shear behavior of architectural coated fabrics under biaxial bias-extension. Constr. Build. Mater. 2018, 187, 964–973. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, H.; Chen, W.; Wang, M.; Zhao, B.; Sun, W. Full-strain range characteristics of the Poisson’s ratio for coated biaxial warp-knitted fabrics under bias tensile loading. Text. Res. J. 2019, 89, 1997–2009. [Google Scholar] [CrossRef]
- Shi, T.; Hu, J.; Chen, W.; Gao, C. Biaxial tensile behavior and strength of architectural fabric membranes. Polym. Test. 2020, 82, 106230. [Google Scholar] [CrossRef]
- Chen, J.; Luo, F.; Fan, J.; Chen, W.; Wang, M.; Xia, Y. Detailed Deformation Behaviors and Tensile Parameters for Coated Warp-Knitted Fabrics in 2D Stress Space. J. Mater. Civ. Eng. 2021, 33, 04021333. [Google Scholar] [CrossRef]
- Gao, C.; Chen, W.; Hu, J.; Zhao, B. A new constitutive model on biaxial tensile behavior of architectural fabrics. Polym. Test. 2020, 87, 106519. [Google Scholar] [CrossRef]
- Ansell, M.P.; Hill, C.A.S.; Allgood, C. Architectural PTFE-Coated Glass Fabrics—Their Structure and Limitations. Text. Res. J. 1983, 53, 692–700. [Google Scholar] [CrossRef]
- Ambroziak, A.; Kłosowski, P. Mechanical properties of polyvinyl chloride-coated fabric under cyclic tests. J. Reinf. Plast. Compos. 2014, 33, 225–234. [Google Scholar] [CrossRef]
- Yingying, Z.; Qilin, Z.; Ke, L.; Bei-lei, K. Experimental analysis of tensile behaviors of polytetrafluoroethylene-coated fabrics subjected to monotonous and cyclic loading. Text. Res. J. 2014, 84, 231–245. [Google Scholar] [CrossRef]
- Wang, F.; Chen, Y.; Xu, W.; Song, Z.; Fu, G. Experimental study on uniaxial tensile and welding performance of a new coated fabric for airship envelopes. J. Ind. Text. 2017, 46, 1474–1497. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, Y.; Xue, J. Off-axial failure analysis of polytetrafluoroethylene-coated woven glass fibers under different loading rates. J. Ind. Text. 2017, 47, 310–330. [Google Scholar] [CrossRef]
- Żerdzicki, K.; Kłosowski, P.; Woznica, K. Analysis of the cyclic load-unload-reload tests of VALMEX aged fabric. In Shell Structures: Theory and Applications; Pietraszkiewicz, W., Witkowski, W., Eds.; CRC Press: London, UK, 2018; Volume 4, pp. 477–480. [Google Scholar]
- Zhao, B.; Hu, J.; Chen, W.; Chen, J.; Jing, Z. Simultaneous uniaxial creep testing of time-dependent membrane materials with optical devices. Mater. Today Commun. 2019, 21, 100655. [Google Scholar] [CrossRef]
- Uhlemann, J.; Surholt, F.; Westerhoff, A.; Stranghöner, N.; Motevalli, M.; Balzani, D. Saturation of the stress-strain behaviour of architectural fabrics. Mater. Des. 2020, 191, 108584. [Google Scholar] [CrossRef]
- Eun, J.H.; Kim, M.S.; Sung, S.M.; Choi, B.K.; Jang, I.U.; Kim, D.; Lee, J.S. Effect of the viscosity of polyvinyl chloride resin and weaving structures of polyester fabric on the off-axis mechanical properties of PVC coated fabric. J. Ind. Text. 2020, 152808372098017. [Google Scholar] [CrossRef]
- Chen, J.; Chen, W.; Zhou, H.; Zhao, B.; Ding, Y.; Zhang, N. Central tearing characteristics of laminated fabrics: Effect of slit parameter, off-axis angle, and loading speed. J. Reinf. Plast. Compos. 2017, 36, 921–941. [Google Scholar] [CrossRef]
- Eltahan, E. Structural parameters affecting tear strength of the fabrics tents. Alexandria Eng. J. 2018, 57, 97–105. [Google Scholar] [CrossRef]
- Chen, J.; Chen, W.; Zhou, H.; Zhao, B.; Wang, M.; Sun, W.; He, S. Fracture failure analysis and bias tearing strength criterion for a laminated fabric. J. Ind. Text. 2018, 47, 1496–1527. [Google Scholar] [CrossRef]
- Sun, X.; He, R.; Wu, Y. A novel tearing residual strength model for architectural coated fabrics with central crack. Constr. Build. Mater. 2020, 263, 120133. [Google Scholar] [CrossRef]
- He, R.; Sun, X.; Wu, Y.; Tang, G.; Carvelli, V. Biaxial tearing properties of woven coated fabrics using digital image correlation. Compos. Struct. 2021, 272, 114206. [Google Scholar] [CrossRef]
- Sun, X.; He, R.; Wu, Y.; Wang, T. Uniaxial tearing properties and the tearing residual strength models of PTFE coated fabric. Structures 2021, 33, 1354–1364. [Google Scholar] [CrossRef]
- Xu, J.; Zhang, Y.; Song, J.; Zhao, Y.; Zhang, L. Quasi-static puncture resistance behaviors of architectural coated fabric. Compos. Struct. 2021, 114307. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Xu, J.; Zhang, L.; Wu, M.; Zhao, Q. Central tearing behavior of PVDF coated fabrics with multiple initial notches. Polym. Compos. 2021, 42, 1049–1058. [Google Scholar] [CrossRef]
- Chen, Y.; Lloyd, D.W.; Harlock, S.C. Mechanical Characteristics of Coated Fabrics. J. Text. Inst. 1995, 86, 690–700. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, Y. The Tensile Strength of Neat and Coated Woven Fabrics. Key Eng. Mater. 2011, 480–481, 448–452. [Google Scholar] [CrossRef]
- Wang, P.; Sun, B.; Gu, B. Comparison of stab behaviors of uncoated and coated woven fabrics from experimental and finite element analyses. Text. Res. J. 2012, 82, 1337–1354. [Google Scholar] [CrossRef]
- Bassett, R.J.; Postle, R.; Pan, N. Experimental Methods for Measuring Fabric Mechanical Properties: A Review and Analysis. Text. Res. J. 1999, 69, 866–875. [Google Scholar] [CrossRef]
- Klosowski, P.; Zagubien, A.; Woznica, K. Investigation on rheological properties of technical fabric Panama. Arch. Appl. Mech. 2004, 73, 661–681. [Google Scholar] [CrossRef]
- Kłosowski, P.; Komar, W.; Woźnica, K. Finite element description of nonlinear viscoelastic behaviour of technical fabric. Constr. Build. Mater. 2009, 23, 1133–1140. [Google Scholar] [CrossRef]
- Żerdzicki, K.; Kłosowski, P.; Woźnica, K. Application of the Bodner-Partom constitutive equations for modelling the technical fabric Valmex used for the hanging roof of the Forest Opera in Sopot. In Proceedings of the Shell structures: Theory and Applications; Pietraszkiewicz, W., Gorski, J., Eds.; Taylor & Francis/Balkema: London, UK, 2014; pp. 579–582. [Google Scholar]
- Uhlemann, J.; Stranghöner, N.; Saxe, K. Stiffness parameters for architectural fabrics: An analysis of two determination procedures. Struct. Eng. Int. J. Int. Assoc. Bridg. Struct. Eng. 2015, 25, 9–19. [Google Scholar] [CrossRef]
- Chen, W.; Hao, H.; Irawan, P.; Chen, S.; Meng, Q. Experimental investigations of fabric material against projectile impacts. Constr. Build. Mater. 2016, 104, 142–153. [Google Scholar] [CrossRef]
- Van Craenenbroeck, M.; Puystiens, S.; De Laet, L.; Van Hemelrijck, D.; Van Paepegem, W.; Mollaert, M. Integrated analysis of kinematic form active structures for architectural applications: Experimental verification. Eng. Struct. 2016, 123, 59–70. [Google Scholar] [CrossRef]
- Meng, J.; Lv, M.; Tan, D.; Li, P. Mechanical properties of woven fabric composite for stratospheric airship envelope based on stochastic simulation. J. Reinf. Plast. Compos. 2016, 35, 1434–1443. [Google Scholar] [CrossRef]
- Meng, J.; Lv, M.; Qu, Z.; Li, P. Mechanical Properties and Strength Criteria of Fabric Membrane for the Stratospheric Airship Envelope. Appl. Compos. Mater. 2017, 24, 77–95. [Google Scholar] [CrossRef]
- Zhao, B.; Chen, W.; Hu, J.; Chen, J.; Qiu, Z.; Zhou, J. In Situ Determination of Stress Distribution of Inflatable Membrane Structure Using Force Finding Method. J. Eng. Mech. 2017, 143, 04017042. [Google Scholar] [CrossRef]
- Dinh, T.D.; Rezaei, A.; Linthout, T.; Mollaert, M.; Van Hemelrijck, D.; Van Paepegem, W. A computational compensation method for fabric panels of tensioned membrane structures using a shape optimization method based on gradientless algorithms. Int. J. Solids Struct. 2017, 112, 16–24. [Google Scholar] [CrossRef]
- Klosowski, P.; Zerdzicki, K.; Woznica, K. Identification of Bodner-Partom model parameters for technical fabrics. Comput. Struct. 2017, 187, 114–121. [Google Scholar] [CrossRef]
- Chen, J.; Chen, W.; Wang, M.; Ding, Y.; Zhou, H.; Zhao, B.; Fan, J. Mechanical Behaviors and Elastic Parameters of Laminated Fabric URETEK3216LV Subjected to Uniaxial and Biaxial Loading. Appl. Compos. Mater. 2017, 24, 1107–1136. [Google Scholar] [CrossRef]
- Ambroziak, A.; Kłosowski, P. Polyester sail technical woven fabric behaviour under uniaxial and biaxial tensile tests. J. Theor. Appl. Mech. 2018, 56, 227–238. [Google Scholar] [CrossRef] [Green Version]
- Xu, J.; Zhang, Y.; Wu, M.; Zhao, Y. Experimental analysis of off-axis mechanical behaviors of PVC coated fabrics subjected to cyclic loading. Polym. Test. 2019, 80, 106090. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, B.; Chen, W.; Wang, M.; Guan, X.; Wu, S. Response surface analysis of biaxial mechanical properties and elastic parameters for woven fabric composites. J. Ind. Text. 2019, 49, 219–242. [Google Scholar] [CrossRef]
- Khaothong, K. Analysis of failing load and optimization of hot air welding parameters on PVC-acrylic coated polyester fabric by Taguchi and ANOVA technique. Eng. J. 2019, 23, 331–344. [Google Scholar] [CrossRef]
- Yingying Zhang; Qilin Zhang; Chuanzhi Zhou; Ying Zhou Mechanical properties of PTFE coated fabrics. J. Reinf. Plast. Compos. 2010, 29, 3624–3630. [CrossRef]
- Ambroziak, A.; Kosowski, P. Influence of thermal effects on mechanical properties of PVDF-coated fabric. J. Reinf. Plast. Compos. 2014, 33. [Google Scholar] [CrossRef]
- Jabbari, M.; Åkesson, D.; Skrifvars, M.; Taherzadeh, M.J. Novel lightweight and highly thermally insulative silica aerogel-doped poly(vinyl chloride)-coated fabric composite. J. Reinf. Plast. Compos. 2015, 34, 1581–1592. [Google Scholar] [CrossRef]
- Zhang, Y.; Xu, S.; Zhang, Q.; Zhou, Y. Experimental and Theoretical Research on the Stress-Relaxation Behaviors of PTFE Coated Fabrics under Different Temperatures. Adv. Mater. Sci. Eng. 2015, 2015, 319473. [Google Scholar] [CrossRef] [Green Version]
- Meng, J.; Cao, S.; Qu, Z.; Li, J.; Lv, M. Thermoelasticity of a Fabric Membrane Composite for the Stratospheric Airship Envelope Based on Multiscale Models. Appl. Compos. Mater. 2017, 24, 209–220. [Google Scholar] [CrossRef]
- Yu, Y.; Cao, Z.; Sun, Y. Mechanical properties of four types of PVC-coated woven fabrics at high-temperature and after exposure to high-temperature. Structures 2021, 33, 830–840. [Google Scholar] [CrossRef]
- Sun, G.; Li, L.; Xue, S.; Yang, Y.; Wu, M. Mechanical Properties of Polyester-Coated Fabric Membrane Material Subjected to Uniaxial Loading at Elevated Temperatures. J. Mater. Civ. Eng. 2021, 33, 04021169. [Google Scholar] [CrossRef]
- Li, Y.; Liu, T.; Yang, B.; Zhang, Q.; Zhang, Y. Effects of natural ageing on mechanical properties of PVDF-coated fabrics. Struct. Eng. Int. 2016, 26, 348–356. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, M. Aging Properties of Polyvinylidenefluoride-Coated Polyesters Used in Tensioned Membrane Structure: Effect of Loading Protocol and Environment. Adv. Mater. Sci. Eng. 2017, 2017, 8789247. [Google Scholar] [CrossRef] [Green Version]
- Zerdzicki, K.; Klosowski, P.; Woznica, K. Influence of service ageing on polyester-reinforced polyvinyl chloride-coated fabrics reported through mathematical material models. Text. Res. J. 2019, 89, 1472–1487. [Google Scholar] [CrossRef]
- João, L.S.; Carvalho, R.; Fangueiro, R. A Study on the Durability Properties of Textile Membranes for Architectural Purposes. Procedia Eng. 2016, 155, 230–237. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.; Shang, Y.; Wu, M.; Yu, Z.; Qu, X. Statistical characteristics of naturally aged PVDF-coated fabrics’ mechanical properties and structural reliability index. Polym. Test. 2019, 80, 106143. [Google Scholar] [CrossRef]
- Klosowski, P.; Zerdzicki, K.; Woznica, K. Influence of artificial thermal ageing on polyester-reinforced and polyvinyl chloride coated AF9032 technical fabric. Text. Res. J. 2019, 89, 4632–4646. [Google Scholar] [CrossRef]
- Dobilaitė, V.; Jucienė, M.; Bliūdžius, R.; Šveikauskaitė, L. Investigation of some weathering impacts on tearing properties of PVC-coated fabrics used for architectural purposes. J. Ind. Text. 2020, 152808372098238. [Google Scholar] [CrossRef]
- Shang, Y.; Yang, B.; Wu, M.; Tao, Y.; Qin, J. Degradation of PVDF-Coated Fabrics after Engineering Applications: Correlations between Surface Microstructure, Physical Properties, and Mechanical Properties Based on Statistical Analysis. Adv. Polym. Technol. 2021, 2021, 9345451. [Google Scholar] [CrossRef]
- Toyoda, H.; Sakabe, H.; Itoh, T.; Konishi, T. Degradation of Polytetrafluoroethylene-Coated Glass Fiber Fabrics by Hot Water Treatment. Sen’i Gakkaishi 1995, 51, 282–286. [Google Scholar] [CrossRef] [Green Version]
- Razak, H.A.; Chua, C.S.; Toyoda, H. Weatherability of coated fabrics as roofing material in tropical environment. Build. Environ. 2004, 39, 87–92. [Google Scholar] [CrossRef]
- Asadi, H.; Uhlemann, J.; Stranghoener, N.; Ulbricht, M. Water influence on the uniaxial tensile behavior of polytetrafluoroethylene-coated glass fiber fabric. Materials 2021, 14, 846. [Google Scholar] [CrossRef]
- ISO (International Organization for Standardization). ISO 1421 Rubber or Plastics-Coated Fabrics—Determination of Tensile Strength and Elongation at Brake; International Organization for Standardization: Geneva, Switzerland, 2016. [Google Scholar]
- Heiberger, R.M.; Neuwirth, E. One-Way ANOVA. In R Through Excel; Springer New York: New York, NY, USA, 2009; pp. 165–191. [Google Scholar]
- Górecki, T.; Smaga, Ł. A comparison of tests for the one-way ANOVA problem for functional data. Comput. Stat. 2015, 30, 987–1010. [Google Scholar] [CrossRef] [Green Version]
- Hanusz, Z.; Tarasinska, J.; Zieliński, W. Shapiro—Wilk Test with Known Mean. REVSTAT—Stat. J. 2016, 14, 89–100. [Google Scholar]
- Gamage, J.; Weerahandi, S. Size performance of some tests in one-way ANOVA. Commun. Stat. Part B Simul. Comput. 1998, 27, 625–640. [Google Scholar] [CrossRef]



| Properties | S Type | B Type |
|---|---|---|
| Total Mass per Unit Area (g/m2) | 1540 | 1550 |
| Tensile Strength (kN/m): Warp | 170 | 160 |
| Tensile Strength (kN/m): Weft | 156 | 140 |
| Base Coat | PTFE | PTFE |
| Weight per Unit Area of Base Fabric (g/m2) | 625 | 670 |
| Yarn Count (yarn/cm): Warp | 7.1 | 8 |
| Yarn Count (yarn/cm): Weft | 7.5 | 7.5 |
| Translucency at 550 nm (%) | 9 | 8–11 |
| Dry (Base Specimens) | Wet | Air-Dried | |
|---|---|---|---|
| S-type | 1511 ± 4 | 1532 ± 4 | 1503 ± 5 |
| B-type | 1638 ± 4 | 1670 ± 4 | 1625 ± 4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ambroziak, A.; Kłosowski, P. Influence of Water-Induced Degradation of Polytetrafluoroethylene (PTFE)-Coated Woven Fabrics Mechanical Properties. Materials 2022, 15, 1. https://doi.org/10.3390/ma15010001
Ambroziak A, Kłosowski P. Influence of Water-Induced Degradation of Polytetrafluoroethylene (PTFE)-Coated Woven Fabrics Mechanical Properties. Materials. 2022; 15(1):1. https://doi.org/10.3390/ma15010001
Chicago/Turabian StyleAmbroziak, Andrzej, and Paweł Kłosowski. 2022. "Influence of Water-Induced Degradation of Polytetrafluoroethylene (PTFE)-Coated Woven Fabrics Mechanical Properties" Materials 15, no. 1: 1. https://doi.org/10.3390/ma15010001
APA StyleAmbroziak, A., & Kłosowski, P. (2022). Influence of Water-Induced Degradation of Polytetrafluoroethylene (PTFE)-Coated Woven Fabrics Mechanical Properties. Materials, 15(1), 1. https://doi.org/10.3390/ma15010001







