Abstract
The PU (partition-of-unity) based FE-RPIM QUAD4 (4-node quadrilateral) element was proposed for statics problems. In this element, hybrid shape functions are constructed through multiplying QUAD4 shape function with radial point interpolation method (RPIM). In the present work, the FE-RPIM QUAD4 element is further applied for structural dynamics. Numerical examples regarding to free and forced vibration analyses are presented. The numerical results show that: (1) If CMM (consistent mass matrix) is employed, the FE-RPIM QUAD4 element has better performance than QUAD4 element under both regular and distorted meshes; (2) The DLMM (diagonally lumped mass matrix) can supersede the CMM in the context of the FE-RPIM QUAD4 element even for the scheme of implicit time integration.
1. Introduction
The FEM (finite element method) [1] has been widely adopted to model structural dynamics. The problem domain to be considered is discretized by a series of elements of simple shapes. In a two-dimensional problem domain, finite elements are either triangles or quadrilaterals [2]. TRIG3 (3-node triangular) element is much easier than QUAD4 element in mesh generation but has poorer accuracy. The QUAD4 element can generally obtain satisfactory results for regular mesh but performs badly for distorted mesh. Often in practice, the generation of a high-quality quadrilateral mesh is a time-consuming task for problems with complex geometric boundary.
A lot of work has been done in the past several decades to develop more powerful numerical methods than the FEM for the analysis of time-dependent problems. Due to the use of higher-order interpolation with specific quadrature formulae [3,4], the spectral finite element method (SFEM) is capable of simulating dynamic problems, such as wave propagation, and has better convergent rate than FEM [5]. The meshless methods, was also expected to become an effective procedure since the mesh is not needed [6,7,8,9,10,11,12,13,14,15,16]. However, some meshless methods’ shape functions have no Kronecker-delta character, which means special treatment is required for essential boundary condition implementation. Moreover, the computational cost to form the trial functions of meshless methods cannot be neglected [17]. Hence, several schemes were proposed to optimize meshless methods [18,19].
In other front, a class of PU [20] based methods were proposed, such as the PUFEM (PU FEM) [21], the GFEM (generalized FEM) [22] and the NMM (numerical manifold method) [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45]. In these methods, global approximations with high order are usually built by using high order local approximations. However, the LD (linear dependence) problem [20] will arise if the local approximations and the PU functions were simultaneously constructed using explicit polynomials [21]. For the purpose of eliminating the LD problem, a lot of efforts have been made [46,47,48].
Recently, a series of FE-Meshfree elements including FE-LSPIM QUAD4 element [46], were proposed. In the FE-LSPIM QUAD4 element, shape functions are usually built through multiplying the FE shape function (QUAD4) and the meshfree shape functions (LSPIM). As a result, good properties of meshless method and FEM are inherited [46]. Compared to FEM, higher accuracy can be obtained by FE-LSPIM QUAD4 element, because global approximations with high order are constructed. In contrast to meshless method, FE-LSPIM QUAD4 shape functions have Kronecker-delta character, which means special treatment is not needed for essential boundary condition implementation. Moreover, the FE-LSPIM QUAD4 element is immune to LD problem. However, since a pure polynomial basis is adopted in the LSPIM, the moment matrix singularity may arise if the polynomial basis functions were inappropriately employed [14,49].
To avoid the drawback of LSPIM, the RPIM (radial point interpolation method) [14] has been employed to replace it, resulting in a new FE-RPIM QUAD4 element [49]. According to the report from Xu and Rajendran [49], FE-RPIM QUAD4 element has higher accuracy than FE-LSPIM QUAD4 element for linear and geometry nonlinear static problems if the same number of polynomial terms are employed. Apart from FE-LSPIM QUAD4 and FE-RPIM QUAD4 elements, there are also other types of FE-Meshfree elements [50,51,52,53].
The FE-RPIM QUAD4 element is further applied for structural dynamics in the present work. After the statement of the formulations related to FE-RPIM QUAD4 element in Section 2, equations related to elastodynamic problems are presented in Section 3. Besides, the expressions for the stiffness matrix, the CMM and the DLMM are given. In Section 4, five numerical examples are investigated using the FE-RPIM QUAD4 element. At the last section, some conclusions will be presented.
2. Shape Functions for FE-RPIM QUAD4 Element
2.1. Formulation of Shape Functions
Before expounding formulation of the shape functions, two important concepts, namely, the nodal support domain () and the element support domain (), are introduced. The nodal support domain is adopted to determine all the support nodes of a given node (also named as central node) to construct its local approximation. According to the scope of the support domain, we can define different order of nodal support domain (). The nodal support domain of first order is determined through the nodal connectivity of first order. Figure 1 shows an example for the nodal support domain of first order for node 1, where 9 support nodes are obtained in Figure 1a and Figure 4 support nodes are determined in Figure 1b. Similarly, the nodal support domain of second order or third order can be defined. As shown in Figure 2, is the union of 4 nodal support domains (), which is defined as .
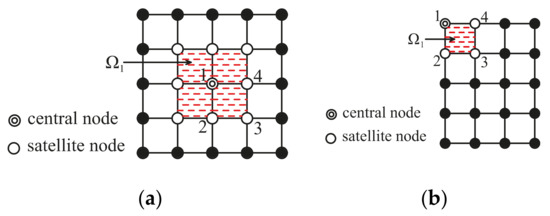
Figure 1.
The nodal support domain of first order () for a central node 1: (a) central node within computational domain; (b) central node on computational boundary.
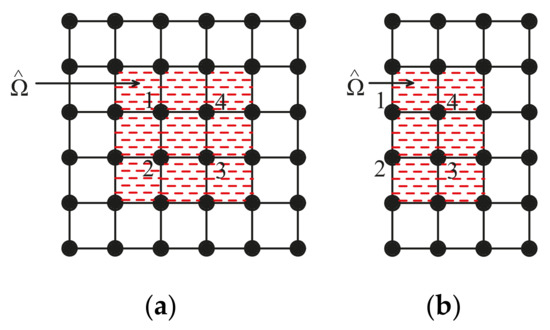
Figure 2.
Element support domain: (a) central node within computational domain; (b) central node on computational boundary.
Let domain be defined with nodes {P1 P2 P3 P4}. The global approximation uh(x) of FE-RPIM QUAD4 element can be simply written as [49]
where represents PU function, while represents local approximation function related to node i. Since quadrilateral mesh is employed, is equivalent to QUAD4 shape function. It is noticed that the global approximation of QUAD4 element can be considered as a special case of FE-RPIM QUAD4 element. If is set as a constant, then in Equation (1) becomes the global approximation for QUAD4 element.
The local approximation functions are obtained by the RPIM [14], which is defined with:
where M and n[i] represent the specified polynomial term number and the number of nodes within Ωi. a and b are two unknown vectors. r represents the radial basis functions, while p represents the polynomial functions formulated as:
p(x) = {1 x y} for M = 3;
p(x) = {1 x y xy} for M = 4;
p(x) = {1 x y xy x2 y2} for M = 6.
According to the discussion in [49], the FE-RPIM QUAD4 element with three- or four-term basis can give as accurate results as with six-term basis for static problems. Furthermore, the computational cost of six-term basis or four-term basis is more than that of three-term basis. Hence, in the present paper, we set M = 3, namely, a three-term basis is used; r(x, y) can be formulated with [14,16]:
in which
in which . The numerical values of q and c have an influence on the accuracy of RPIM, which have been discussed in great details in [49]. In the present work, q and c are separately set to 2.01 and 0.0001 according to the recommendation in [49].
Enforcing Equation (2) to pass through all the nodes in within Ωi, the following equations are obtained:
where is a vector of corresponding nodal displacements of all the nodes in Ωi, and
Obviously, there are totally (M + n[i]) parameters in Equation (8). However, only n[i] equations are available. Nevertheless, according to the work finished in [14,54], vectors of a and b can be eliminated as proposed in their work and local approximation function in Equation (2) is eventually expressed as [14]:
with
Note that Wendland [55] has presented the evident of the existence of for any scattered nodes.
2.2. Properties of Shape Functions
Through substituting Equation (11) into Equation (1), for the FE-RPIM QUAD4 element can then be formulated with a more compact form:
where and represent a shape function and nodal displacement associated with node i. p represents node number within .
The attractive properties of in Equation (19) can be listed as follows [49]:
- (i)
- Kronecker-delta character
- (ii)
- Compatibility property at the interface of elements.
- (iii)
- High order completeness, in other words, reproducibility of all the assumed Cartesian terms (Equation (3)).
To investigate the changes of shape functions within element, we consider a two-dimensional domain discretized with four quadrilateral elements and 9 nodes (Figure 3). The 3D graphics of shape functions of FE-RPIM QUAD4 element for different nodes (node 1, node 2, node 3 and node 5) are plotted in Figure 4. For the purpose of comparison, the 3D graphics of shape functions of QUAD4 element are also plotted, as shown in Figure 5. As can be seen in Figure 4 and Figure 5, the shape function of FE-RPIM QUAD4 element is smoother than that of Quad4 element.
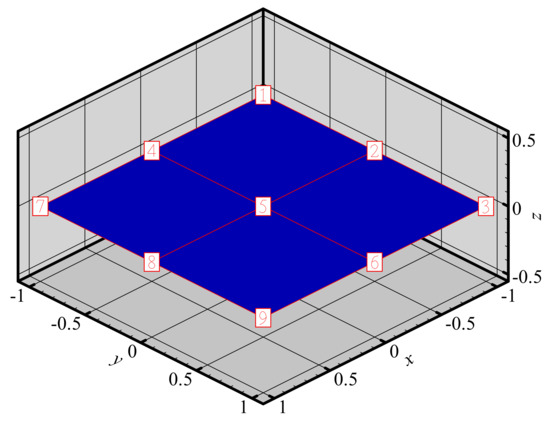
Figure 3.
A two−dimensional domain (2 m× 2 m) discretized with 4 quadrilateral elements and 9 nodes.
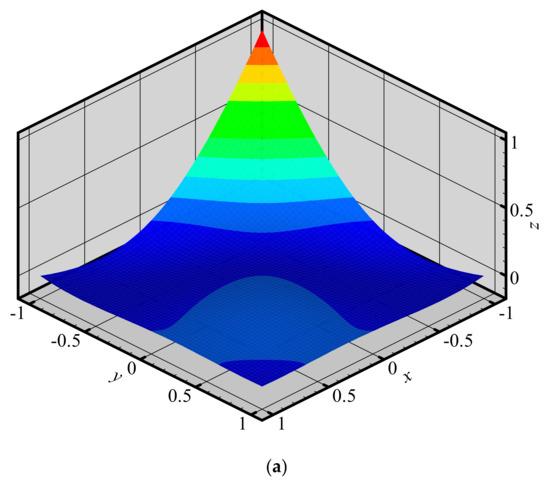
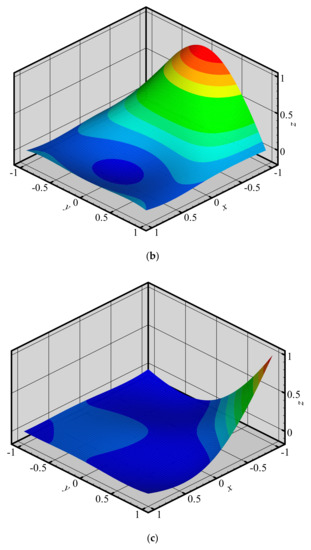
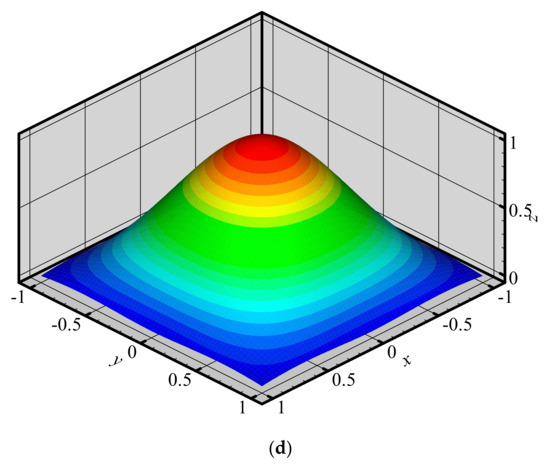
Figure 4.
Shape functions of FE−RPIM QUAD4 element for different nodes at different locations: (a) node 1; (b) node 2; (c) node 3; (d) node 5.
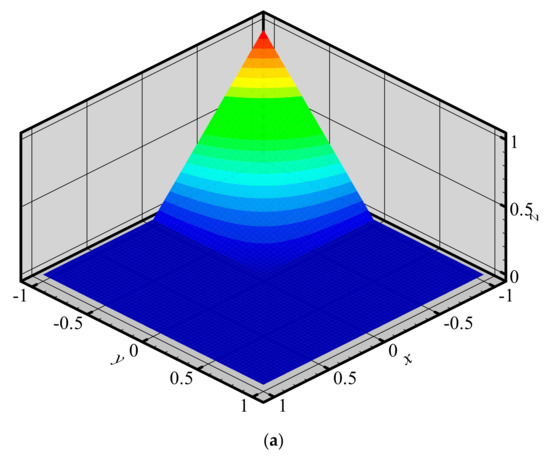
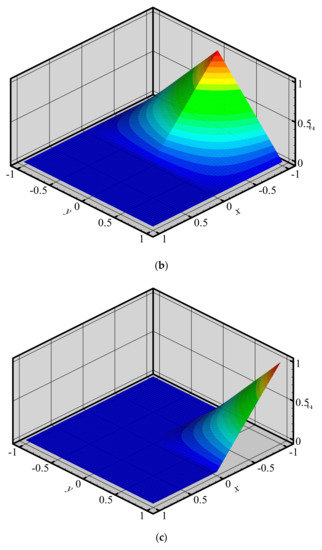
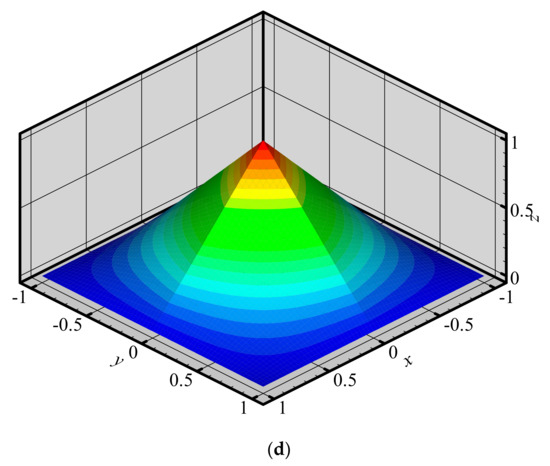
Figure 5.
Shape functions of QUAD4 element for different nodes at different locations. (a) node 1; (b) node 2; (c) node 3; (d) node 5.
3. FE-RPIM QUAD4 for Elastodynamic Problems
3.1. FE-RPIM QUAD4 for Dynamic Analysis
Let the problem domain discretized using a series of QUAD4 elements: In the context of the FE-RPIM QUAD4 element, the discretized form of the system equations about dynamic analysis can be expressed as [56]:
in which M is the global mass matrix, K is the global stiffness matrix, and is the global load vector, which can be computed as:
where
and
in which is the material density, D is the matrix of the elastic constants of the material, is the specified traction vector applied on stress boundary , b is the body force per unit volume, represents the matrix of shape function for , expressed as:
and is the gradient matrix expressed as:
where represent a shape function associated with node i. p represents the node number within .
The Rayleigh damping is adopted in the present work. Hence, the damping matrix C can be formulated into,
in which , represent the coefficients of Rayleigh damping.
3.2. Time Integration Scheme
The Newmark method [56] will be employed in this study to solve Equation (21). Assuming that , and separately represent approximation values of , and . When ,
then the approximations of and are expressed as:
Here, represents the solution of Equation (32).
with
is computed with Equation (35).
It is noticed that obtained from Equations (22) and (24) is named as CMM (consistent mass matrix). If is a diagonally lumped mass matrix (DLMM), solving should be a very easy task. Moreover, if the damping effect is ignored, as is done frequently and = 0, then reduces to . Consequently, if is a positive DLMM whose inverse is easy to calculate, solving Equation (32) for would be very easy.
3.3. Generalized Eigenvalue Problem
If the terms associated to damping matrix and force vector are neglected, Equation (21) will reduce to the following form [14]:
The general solution for Equation (36) is formulated as:
in which t represents time. represents the natural frequency, while represents the eigenvector.
Based on Equations (36) and (37), is obtained from Equation (38).
Here, determines the mode shape related to . Note that it is time-consuming to compute all the modes. Hence, the subspace iteration procedure is usually adopted to obtain only those modes with small values of .
However, if is a DLMM, Equation (38) becomes a standard eigenvalue problem,
where is defined as:
Since is a DLMM, the inversion of , namely, , can be easily obtained. There are more powerful algorithms available to solve the standard eigenvalue problem (Equation (39)) [57].
3.4. Diagonally Lumped Mass Matrix
Here, we propose to use the “special lumping technique” introduced by Hinton et al. [58] to obtain the diagonally lumped mass matrix (DLMM). This procedure always leads to positive lumped masses at the nodes. Moreover, the requirement for mass conservation can be ensured. With little change, this procedure can be used for FE-RPIM QUAD4 element. For the FE-RPIM QUAD4 element, we obtain:
where is the i-th diagonal entry of the element consistent mass matrix (CMM) obtained through Equation (24), is the i-th diagonal entry of the DLMM, is a constant defined as:
where represents the density of material.
4. Numerical Examples
In this section, a static example and five examples regarding to free and forced vibration analyses will be presented to investigate the performance of FE-RPIM QUAD4 element. For comparison, other well-known element types, such as the TRIG3, QUAD4 and QUAD8 (8-node quadrilateral element) will also be used to conduct these tests. In the computation for dynamic problems, both the CMM and the DLMM will be employed in the context of FE-RPIM QUAD4 element, while only the CMM will be employed in the context of QUAD4, TRIG3, and QUAD8.
Physical units in this section will be according to the unit system of international standard without specification. n is the node number within discretized model. Natural frequency’s relative error expressed in Equation (44) is adopted to evaluate the accuracy of the numerical models.
in which “num” and “ref” separately represent the numerical solution and reference solution.
4.1. Cook’s Skew Beam
Before proceeding with dynamic analysis, the well-known example of Cook’s skew beam (Figure 6a) is adopted to test the performance of the FE-RPIM QUAD4 element for static problem. A mesh with 10 × 10 quadrilateral elements and 121 nodes is plotted in Figure 6b. The reference solution for the vertical displacement of point A for Cook’s skew beam is 23.96 [49].
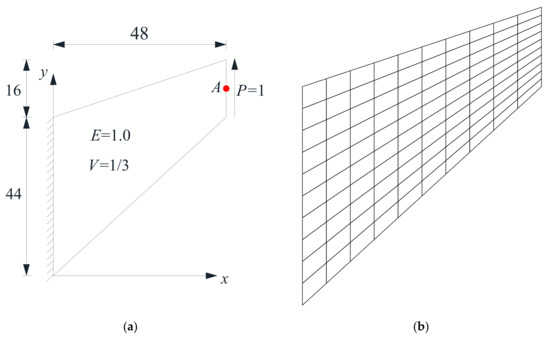
Figure 6.
Cook’s skew beam: (a) geometry and load; (b) a mesh with 10 × 10 elements.
With the mesh presented in Figure 6b, the solutions for the vertical displacement of point A based on the FE-RPIM QUAD4 element is 23.8170, which is better than that based on the QUAD4 element (22.6965). Note that this problem was also solved in [59] by the spectral finite element (SFEM) [60]. If the problem domain is discretized into 10 × 10 elements, where each element has 2 × 2 nodes, the solution based on the SFEM is 22.6940, which is inferior to that based on the FE-RPIM QUAD4 element (23.8170). However, If the problem domain is discretized into 1 element with 11 × 11 nodes, the solution based on the SFEM is 23.9414, which is even slightly better than that based on the FE-RPIM QUAD4 element (23.8170).
4.2. A Slender Rod
Free vibration analysis for a slender rod [61] is conducted, as shown in Figure 7. The ith natural frequency from the analytical solution is [62]:
in which L represents the length of the rod.
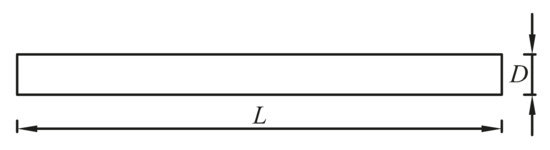
Figure 7.
Free vibration analysis of a slender rod.
Geometric and mechanical parameters used in this example are L = 100, thickness t = 1, D = 1, Poisson’s ratio v = 0, Young’s modulus E = 72 × 109, mass density ρ = 2700. Since L/D = 100 > 10, the geometric parameters used assure that the one-dimensional slender rod can be well represented by the two-dimensional model without causing unacceptable error. In the computation, both upside and down sides of the model are fixed in the normal direction.
For investigating the convergence of the solution, three regular discretized models (Figure 8) are constructed. Table 1 lists the numerical results from different numerical models. According to Table 1, the results from all the listed numerical models approach the analytical solution gradually, as the mesh density increases.
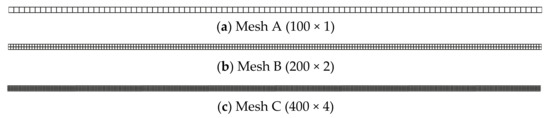
Figure 8.
Normalized mesh for slender rod in Figure 3.

Table 1.
Comparisons of computed frequencies (Hz) for the slender rod with regular.
By using the consistent mass scheme, the result from FE-RPIM QUAD4 element is better than that from QUAD4 element and TRIG3 element, but slightly inferior to that from QUAD8 element. Note that QUAD8 element requires more nodes than FE-RPIM QUAD4 element to discretize the problem domain. In addition, results from the CMM and the DLMM in the context of FE-RPIM QUAD4 element are close to each other.
4.3. An Annulus
As the second example, an annulus without constraint shown in Figure 9 is employed to validate the FE-RPIM QUAD4 element. The geometric and mechanical parameters used in this example are Ra = 0.4, Rb = 0.5, v = 0.33, E = 72 × 109, t = 1, ρ = 2700.
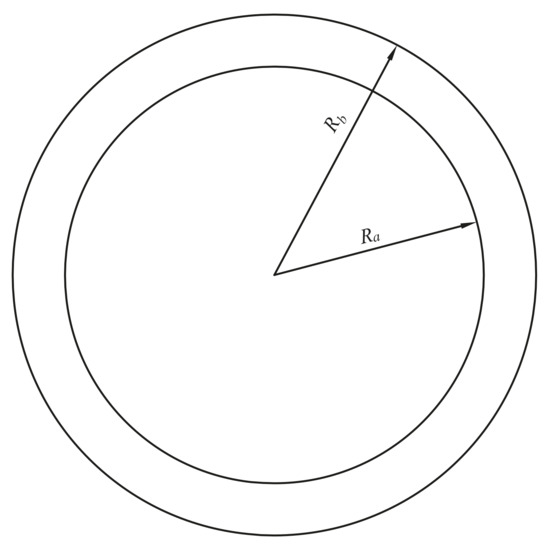
Figure 9.
Free vibration analysis of an annulus.
For the purpose of investigating the convergence of the solution, several regular discretized models shown in Figure 10 and Figure 11 are constructed. Table 2 lists the frequencies assessed by different numerical models. The reference solution for this problem, which is listed in the last column of Table 2, can be found in [61]. According to Table 2, the result from FE-RPIM QUAD4 element is much better than that from QUAD4 and TRIG3 elements, but slightly inferior to that from QUAD8 element, if the CMM was employed.
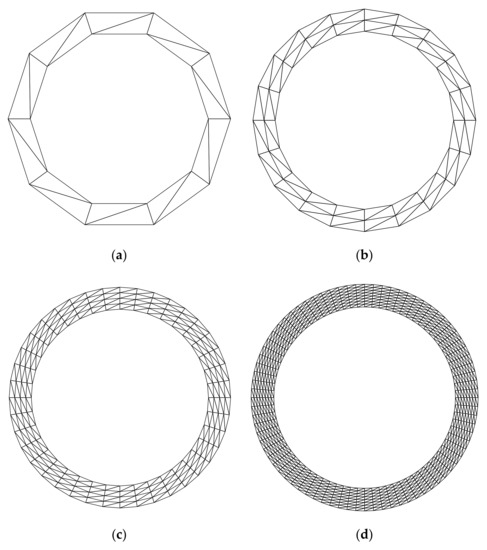
Figure 10.
Triangular meshes for the annulus. (a) Mesh A (20 elements, 20 nodes); (b) Mesh B (80 elements, 60 nodes); (c) Mesh C (320 elements, 200 nodes); (d) Mesh D (1280 elements, 720 nodes).
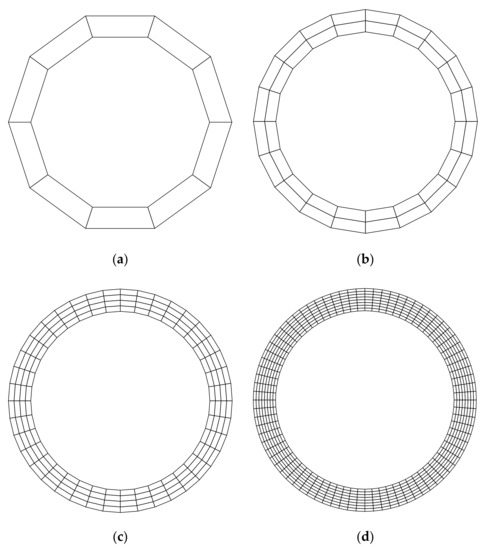
Figure 11.
Quadrilaterial meshes for the annulus: (a) Mesh A (10 elements, 20 nodes); (b) Mesh B (40 elements, 60 nodes); (c) Mesh C (160 elements, 200 nodes); (d) Mesh D (640 elements, 720 nodes).

Table 2.
Comparisons of computed frequencies (Hz) for the annulus.
In addition, FE-RPIM QUAD4 element can obtain better result if the DLMM is employed instead of the CMM.
4.4. Mesh Distortion Test
In the previous two examples, regular meshes are adopted. In this section, mesh distortion test based on the cantilever beam (Figure 12) is conducted. The parameters used are D = 10 mm, L = 100 mm, v = 0.3, E = 2.1 × 104 kg/mm2, = 8.0 × 10−10 kg fs2/mm4, t = 1 mm.
Figure 12.
Free vibration analysis of a 2D cantilever beam.
As shown in Figure 13a,b, the beam is meshed with two elements for QUAD4 element, FE-RPIM QUAD4 element and QUAD8 element. For TRIG3 element, the problem domain is meshed with four elements, as shown in Figure 13c. A distortion parameter, 2d/D, is adopted to control mesh distortion.
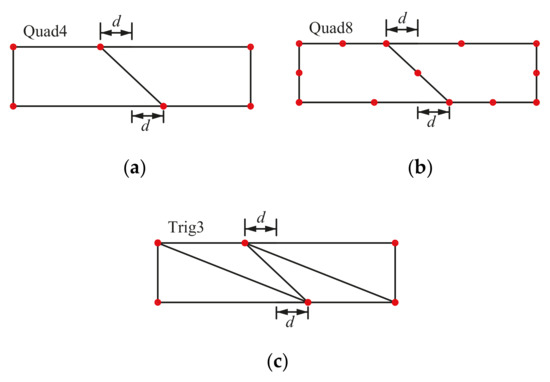
Figure 13.
The mesh used for the distortion sensitivity test: (a) Mesh A; (b) Mesh B; (c) Mesh C.
Table 3 lists the fundamental natural frequency assessed by different numerical models. The corresponding relative errors are plotted in Figure 14. To better see the reached accuracy of FE-RPIM QUAD4(CMM) and FE-RPIM QUAD4(DLMM), Figure 15 is plotted. According to Table 3, Figure 14 and Figure 15, we can draw the following conclusions:

Table 3.
Computed natural frequencies (Hz) of the first mode for the mesh distortion sensitivity test.
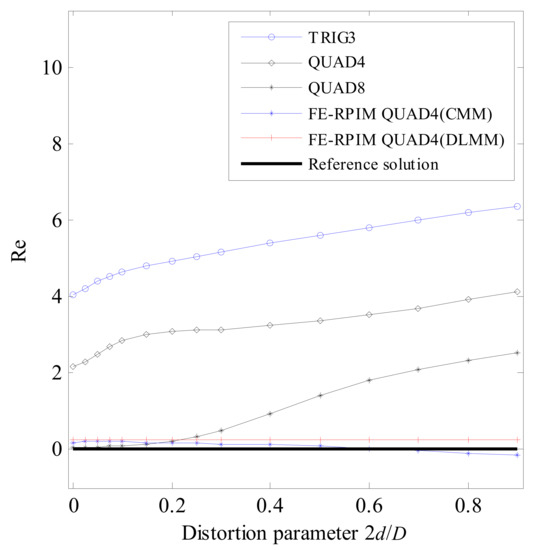
Figure 14.
Error in fundamental natural frequency for mesh distortion sensitivity test.
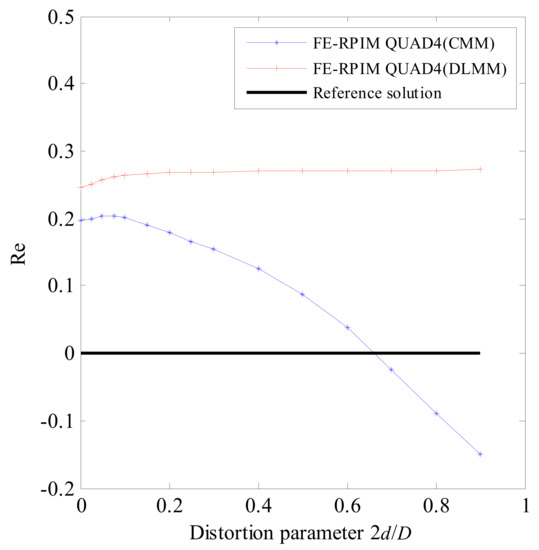
Figure 15.
Comparison of accuracy of FE−RPIM QUAD4 (CMM) and FE−RPIM QUAD4(DLMM) for mesh distortion sensitivity test.
- (1)
- First, as distortion parameter’s value increases, the errors based on FE-RPIM QUAD4 element do not change appreciably, while those based on QUAD4 element, TRIG3 element and QUAD8 elements change rapidly. The FE-RPIM QUAD4 element is immune to mesh distortion.
- (2)
- Second, accuracy of FE-RPIM QUAD4 element is always much higher than QUAD4 and TRIG3 elements.
- (3)
- Third, when 2d/D < 0.2, QUAD8 element’s accuracy is higher than QUAD4, FE-RPIM QUAD4 and TRIG3 elements. However, as the value of 2d/D increases, accuracy through QUAD8 element deteriorates quickly. If meshes used are distorted severely, QUAD8 element’s accuracy is much lower than FE-RPIM QUAD4 element.
- (4)
- Fourth, compared to CMM, FE-RPIM QUAD4 element can achieve better results if DLMM is employed.
4.5. A Plate with Four Holes
In this section, a plate with four holes shown in Figure 16 is considered. The mechanical parameters used are v = 0.3, E = 72 × 109 and ρ = 2700. Left side of the plate is fixed.
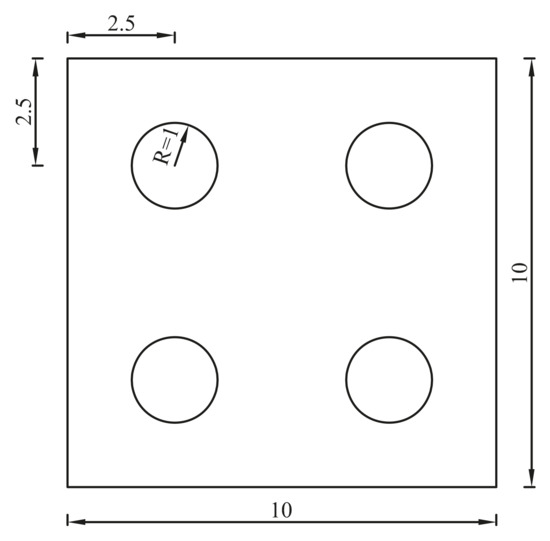
Figure 16.
A plate with four holes.
For the purpose of investigating the convergence of the solution, four discretized models shown in Figure 17 and Figure 18 are constructed. In order to get a reference solution, the QUAD4 element is adopted with a very dense discretized model (43,704 nodes, 43,058 elements). Table 4 lists the results from different numerical models. The results from different numerical models all approach the reference solution gradually, as the mesh density increases. In addition, by using the CMM, FE-RPIM QUAD4 element’s accuracy is much higher than QUAD4 and TRIG3 elements.
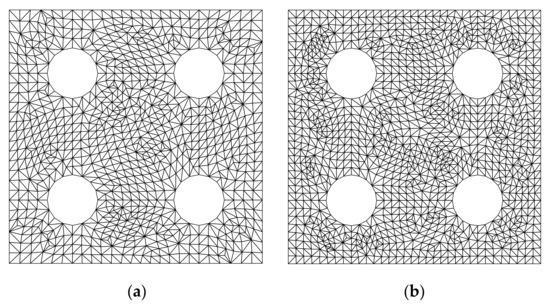
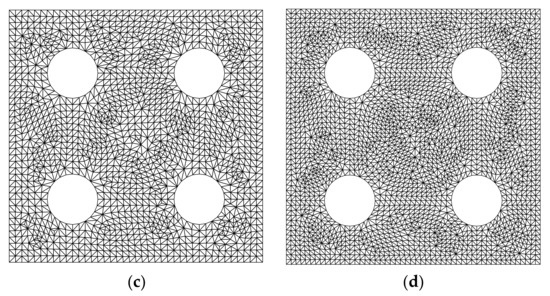
Figure 17.
Triangular mesh for the plate with four holes. (a) Mesh A (1584 elements and 871 nodes); (b) Mesh B (2350 elements and 1278 nodes); (c) Mesh C (3170 elements and 1710 nodes); (d) Mesh D (5302 elements and 2814 nodes).
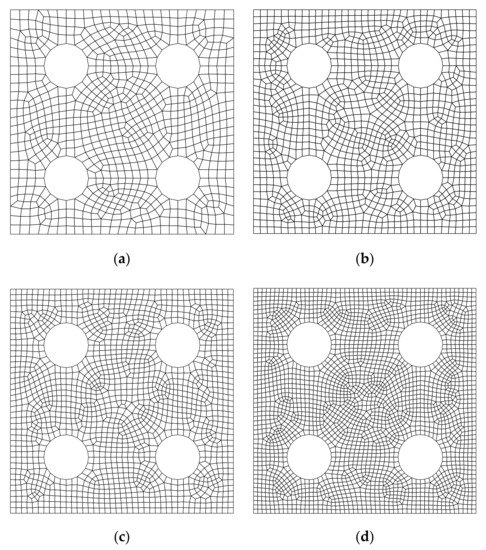
Figure 18.
Quadrilateral mesh for the plate with four holes: (a) Mesh A (792 elements and 871 nodes); (b) Mesh B (1175 elements and 1278 nodes); (c) Mesh C (1585 elements and 1710 nodes); (d) Mesh D (2651 elements and 2814 nodes).

Table 4.
Comparisons of computed frequencies (Hz) for the plate with four holes.
The first six mode shapes obtained through the FE-RPIM QUAD4 element under CMM are presented in Figure 19. Mode shapes through CMM agree well with those through DLMM in the context of FE-RPIM QUAD4 element.
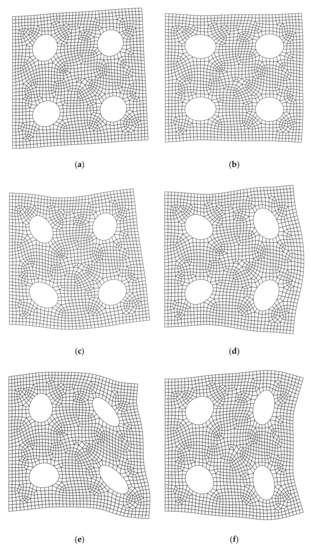
Figure 19.
First 6 mode shapes of the plate with four holes using FE-RPIM QUAD4 element (CMM): (a) Mode 1; (b) Mode 2; (c) Mode 3; (d) Mode 4; (e) Mode 5; (f) Mode 6.
4.6. A Cantilever Beam under Harmonic Load
In the context of FE-RPIM QUAD4 element, accuracy for natural frequencies obtained through the DLMM is as good as or even better than those through the CMM. This conclusion was also hold FEM [61,63]. However, the CMM is considered to be a better choice to calculate deformation and mode shapes [61,63]. In this section, following the same purpose as in [61], an example is employed to show that the FE-RPIM QUAD4 element is able to obtain satisfactory results by employing DLMM even for the scheme of implicit time integration.
A cantilever beam (Figure 20) under harmonic load () on the right end is considered. The parameters used are = 1 kg/m3, D = 1 m, L = 4 m, v = 0.3, E = 1 Pa, , , and .
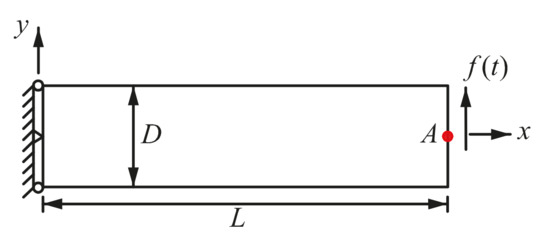
Figure 20.
A 2D cantilever beam subjected to a harmonic loading on the right end.
In the computation, scheme of implicit time integration with and is used. Time step size is adopted. Shown in Figure 21 is the discretized model used by the FE-RPIM QUAD4 element. Apart from the FE-RPIM QUAD4 element, this dynamic problem is also investigated using QUAD4 element (27 nodes, 16 elements), TRIG3 element (27 nodes, 32 elements) and QUAD8 element (69 nodes, 16 elements). In order to compute a reference solution, the QUAD4 element is adopted with a very dense discretized model (6601 nodes, 6400 elements).
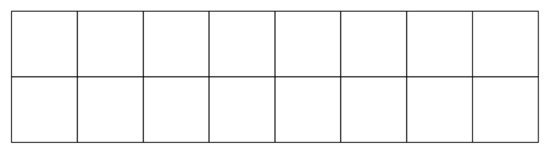
Figure 21.
Discretized model of the 2D cantilever beam subjected to a harmonic loading.
As can be seen from Figure 22, if CMM scheme is employed, FE-RPIM QUAD4 element’s accuracy is higher than QUAD4 and TRIG3 elements. More importantly, the result of FE-RPIM QUAD4 (DLMM) almost coincides with FE-RPIM QUAD4 (CMM), which means DLMM can supersede the CMM in the context of the FE-RPIM QUAD4 element.
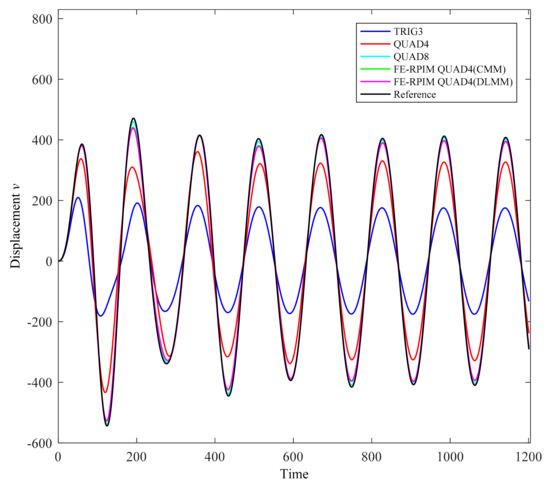
Figure 22.
Transient responses of a cantilever beam subjected to a harmonic loading.
5. Conclusions
FE-RPIM QUAD4 element is further extended for problems of structural dynamics. Some important conclusions, which can be drawn from this work, are as follows:
- (1)
- Based on 4-node quadrilateral mesh, FE-RPIM QUAD4 element’s accuracy is much higher than QUAD4 and TRIG3 elements (Table 2).
- (2)
- Although FE-RPIM QUAD4 element’s accuracy is slightly inferior to QUAD8 element, QUAD8 element requires more nodes than FE-RPIM QUAD4 element to discretize the problem domain. In addition, FE-RPIM QUAD4 element can achieve results closing to the reference solution, even for coarse mesh (Figure 22).
- (3)
- For distorted meshes, FE-RPIM QUAD4 element’s accuracy is always much higher than QUAD4 and TRIG3 elements. Moreover, FE-RPIM QUAD4 element is immune to mesh distortion, but TRIG3, QUAD4 and QUAD8 elements give very bad results as the mesh quality deteriorates (Figure 14).
- (4)
- In the tests associated to the analysis of free vibration, the result based on the DLMM are very close to those based on the CMM in the context of FE-RPIM QUAD4 element. In the test on forced vibration analysis, the result from the DLMM also agrees well with that from the CMM, which means DLMM can supersede the CMM in the context of the FE-RPIM QUAD4 element even for the scheme of implicit time integration.
Author Contributions
Conceptualization, H.L. and G.S.; methodology, G.S.; software, G.S.; validation, H.L. and G.S.; formal analysis, H.L.; investigation, H.L.; resources, H.L.; data curation, G.S.; writing—original draft preparation, G.S.; writing—review and editing, G.S.; visualization, G.S.; supervision, G.S.; project administration, H.L.; funding acquisition, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study is sponsored by the National Natural Sciences Foundation of China, under the grant no. 42077270.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Reddy, J.N. An Introduction to Nonlinear Finite Element Analysis; Oxford University Press: Oxford, UK, 2004. [Google Scholar]
- Song, C. The scaled boundary finite element method in structural dynamics. Int. J. Numer. Methods Eng. 2009, 77, 1139–1171. [Google Scholar] [CrossRef]
- Kim, Y.; Ha, S.; Chang, F.K. Time-domain spectral element method for built-in piezoelectric-actuator-induced lamb wave propagation analysis. Aiaa J. 2008, 46, 591–600. [Google Scholar] [CrossRef]
- He, S.; Ng, C.T. A probabilistic approach for quantitative identification of multiple delaminations in laminated composite beams using guided waves. Eng. Struct. 2016, 127, 602–614. [Google Scholar] [CrossRef]
- Yeung, C.; Ng, C.T. Time-domain spectral finite element method for analysis of torsional guided waves scattering and mode conversion by cracks in pipes. Mech. Syst. Signal Process. 2019, 128, 305–317. [Google Scholar] [CrossRef]
- Nagashima, T. Node-by-node meshless approach and its application to structural analyses. Int. J. Numer. Methods Eng. 1999, 46, 341–385. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission thesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Nayroles, B.; Touzot, G.; Villon, P. Generating the finite element method: Diffuse approximation and diffuse elements. Comput. Mech. 1992, 10, 307–318. [Google Scholar] [CrossRef]
- Belytschko, T.; Lu, Y.Y.; Gu, L. Element-free Galerkin method. Int. J. Numer. Methods Eng. 1994, 37, 229–256. [Google Scholar] [CrossRef]
- Zhuang, X.Y.; Augarde, C. Aspects of the use of orthogonal basis functions in the element free Galerkin method. Int. J. Numer. Methods Eng. 2010, 81, 366–380. [Google Scholar] [CrossRef]
- Rabczuk, T.; Belytschko, T.; Xiao, S.P. Stable particle methods based on Lagrangian kernels. Comput. Methods Appl. Mech. Eng. 2004, 193, 1035–1063. [Google Scholar] [CrossRef]
- Cai, Y.C.; Zhu, H.H. A meshless local natural neighbour interpolation method for stress analysis of solids. Eng. Anal. Bound. Elem. 2004, 28, 607–613. [Google Scholar]
- Liu, G.R.; Gu, Y.T. A point interpolation method for two dimensional solid. Int. J. Numer. Methods Eng. 2001, 50, 937–951. [Google Scholar] [CrossRef]
- Liu, G.; Gu, Y.T. A local radial point interpolation method (LRPIM) for free vibration analyses of 2-d solids. J. Sound Vib. 2001, 246, 29–46. [Google Scholar] [CrossRef]
- Liu, G.R.; Zhang, G.; Gu, Y.T.; Wang, Y. A meshfree radial point interpolation method (rpim) for three-dimensional solids. Comput. Mech. 2005, 36, 421–430. [Google Scholar] [CrossRef]
- Liu, G.R. Mesh Free Methods: Moving Beyond the Finite Element Method; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Zheng, C.; Wu, S.C.; Tang, X.H.; Zhang, J.H. A novel twice-interpolation finite element method for solid mechanics problems. Acta Mech. Sin. 2010, 26, 265–278. [Google Scholar] [CrossRef]
- Liu, G.R.; Gu, Y.T. Meshless local Petrov-Galerkin (MLPG) method in combination with finite element and boundary element approaches. Comput. Mech. 2000, 26, 536–546. [Google Scholar] [CrossRef][Green Version]
- Rabczuk, T.; Xiao, S.P.; Sauer, M. Coupling of mesh-free methods with finite elements: Basic concepts and test results. Commun. Numer. Methods Eng. 2006, 22, 1031–1065. [Google Scholar] [CrossRef]
- Babuška, I.; Melenk, J.M. The partition of unity method. Int. J. Numer. Methods Eng. 1997, 40, 727–758. [Google Scholar] [CrossRef]
- Melenk, J.M.; Babuška, I. The partition of unity finite element method: Basic theory and applications. Comput. Methods Appl. Mech. Eng. 1996, 139, 289–314. [Google Scholar] [CrossRef]
- Strouboulis, T.; Babuška, I.; Copps, K. The design and analysis of the Generalized Finite Element Method. Comput. Methods Appl. Mech. Eng. 2000, 181, 43–69. [Google Scholar] [CrossRef]
- Cai, Y.C.; Zhuang, X.Y.; Zhu, H.H. A generalized and efficient method for finite cover generation in the numerical manifold method. Int. J. Comput. Methods 2013, 10, 1350028. [Google Scholar] [CrossRef]
- Yang, Y.; Tang, X.; Zheng, H.; Liu, Q.; He, L. Three-dimensional fracture propagation with numerical manifold method. Eng. Anal. Bound. Elem. 2016, 72, 65–77. [Google Scholar] [CrossRef]
- Yang, Y.T.; Zheng, H. A three-node triangular element fitted to numerical manifold method with continuous nodal stress for crack analysis. Eng. Fract. Mech. 2016, 162, 51–75. [Google Scholar] [CrossRef]
- Wu, W.A.; Yang, Y.T.; Zheng, H. Hydro-mechanical simulation of the semi-saturated porous soil-rock mixtures using the numerical manifold method. Comput. Methods Appl. Mech. Eng. 2020, 370, 113238. [Google Scholar] [CrossRef]
- Yang, Y.T.; Sun, G.H.; Zheng, H.; Yan, C.Z. An improved numerical manifold method with multiple layers of mathematical cover systems for the stability analysis of soil-rock-mixture slopes. Eng. Geol. 2020, 264, 105373. [Google Scholar] [CrossRef]
- Yang, Y.T.; Tang, X.H.; Zheng, H.; Liu, Q.S.; Liu, Z.J. Hydraulic fracturing modeling using the enriched numerical manifold method. Appl. Math. Modell. 2018, 53, 462–486. [Google Scholar] [CrossRef]
- Yang, Y.T.; Sun, G.H.; Zheng, H. Investigation of the sequential excavation of a soil-rock-mixture slope using the numerical manifold method. Eng. Geol. 2019, 256, 93–109. [Google Scholar] [CrossRef]
- Yang, Y.T.; Sun, Y.H.; Sun, G.H.; Zheng, H. Sequential excavation analysis of soil-rock-mixture slopes using an improved numerical manifold method with multiple layers of mathematical cover systems. Eng. Geol. 2019, 261, 105278. [Google Scholar] [CrossRef]
- Yang, Y.T.; Wu, W.A.; Zheng, H. Searching for critical slip surfaces of slopes using stress fields by numerical manifold method. J. Rock Mech. Geotech. Eng. 2020, 12, 1313–1325. [Google Scholar] [CrossRef]
- Yang, Y.T.; Sun, G.H.; Zheng, H. A high-order numerical manifold method with continuous stress/strain field. Appl. Math. Modell. 2020, 78, 576–600. [Google Scholar] [CrossRef]
- Wu, W.A.; Yang, Y.T.; Zheng, H. Enriched mixed numerical manifold formulation with continuous nodal gradients for dynamics of fractured poroelasticity. Appl. Math. Modell. 2020, 86, 225–258. [Google Scholar] [CrossRef]
- Yang, Y.T.; Xu, D.D.; Sun, G.H.; Zheng, H. Modeling complex crack problems using the three-node triangular element fitted to numerical manifold method with continuous nodal stress. Sci. China Technol. Sci. 2017, 60, 1537–1547. [Google Scholar] [CrossRef]
- Yang, Y.T.; Xu, D.D.; Liu, F.; Zheng, H. Modeling the entire progressive failure process of rock slopes using a strength-based criterion. Comput. Geotech. 2020, 126, 103726. [Google Scholar] [CrossRef]
- Chen, L.; Yang, Y.T.; Zheng, H. Numerical study of soil-rock mixture: Generation of random aggregate structure. Sci. China Technol. Sci. 2018, 61, 359–369. [Google Scholar] [CrossRef]
- Chen, T.; Yang, Y.T.; Zheng, H.; Wu, Z.J. Numerical determination of the effective permeability coefficient of soil-rock mixtures using the numerical manifold method. Int. J. Numer. Anal. Methods Geomech. 2019, 43, 381–414. [Google Scholar] [CrossRef]
- Yang, Y.T.; Sun, G.H.; Zheng, H. Modelling unconfined seepage flow in soil-rock mixtures using the numerical manifold method. Eng. Anal. Bound. Elem. 2019, 108, 60–70. [Google Scholar] [CrossRef]
- Yang, Y.T.; Sun, G.H.; Zheng, H. Stability analysis of soil-rock-mixture slopes using the numerical manifold method. Eng. Anal. Bound. Elem. 2019, 109, 153–160. [Google Scholar] [CrossRef]
- Yang, Y.T.; Chen, T.; Zheng, H. Mathematical cover refinement of the numerical manifold method for the stability analysis of a soil-rock-mixture slope. Eng. Anal. Bound. Elem. 2020, 116, 64–76. [Google Scholar] [CrossRef]
- Yang, Y.T.; Wu, W.A.; Zheng, H.; Liu, X.W. A high-order three dimensional numerical manifold method with continuous stress/strain field. Eng. Anal. Bound. Elem. 2020, 117, 309–320. [Google Scholar] [CrossRef]
- Yang, Y.T.; Wu, W.A.; Zheng, H. Stability analysis of slopes using the vector sum numerical manifold method. Bull. Eng. Geol. Environ. 2021, 80, 345–352. [Google Scholar] [CrossRef]
- Yang, Y.T.; Xu, D.D.; Zheng, H. Explicit discontinuous deformation analysis method with lumped mass matrix for highly discrete block system. Int. J. Geomech. 2018, 18, 04018098. [Google Scholar] [CrossRef]
- Yang, Y.T.; Chen, T.; Wu, W.A.; Zheng, H. Modelling the stability of a soil-rock-mixture slope based on the digital image technology and strength reduction numerical manifold method. Eng. Anal. Bound. Elem. 2021, 126, 45–54. [Google Scholar] [CrossRef]
- Zheng, H.; Yang, Y.T.; Shi, G.H. Reformulation of dynamic crack propagation using the numerical manifold method. Eng. Anal. Bound. Elem. 2019, 105, 279–295. [Google Scholar] [CrossRef]
- Rajendran, S.; Zhang, B.R. A “FE-meshfree” QUAD4 element based on partition of unity. Comput. Methods Appl. Mech. Eng. 2007, 197, 128–147. [Google Scholar] [CrossRef]
- Cai, Y.C.; Zhuang, X.Y.; Augarde, C. A new partition of unity finite element free from linear dependence problem and processing the delta property. Comput. Methods Appl. Mech. Eng. 2010, 199, 1036–1043. [Google Scholar] [CrossRef]
- Tian, R.; Yagawa, G.; Terasaka, H. Linear dependence of unity-based generalized FEMs. Comput. Methods Appl. Mech. Eng. 2006, 195, 4768–4782. [Google Scholar] [CrossRef]
- Xu, J.P.; Rajendran, S. A partition-of-unity based ‘FE-Meshfree’ QUAD4 element with radial-polynomial basis functions for static analyses. Comput. Methods Appl. Mech. Eng. 2011, 200, 3309–3323. [Google Scholar] [CrossRef]
- Xu, J.P.; Rajendran, S. A ‘FE-Meshfree’ TRIA3 element based on partition of unity for linear and geometry nonlinear analyses. Comput. Mech. 2013, 51, 843–864. [Google Scholar] [CrossRef]
- Ooi, E.T.; Rajendran, S.; Yeo, J.H. A mesh distortion tolerant 8-node solid element based on the partition of unity method with inter-element compatibility and completeness properties. Finite Elem. Anal. Des. 2007, 43, 771–787. [Google Scholar] [CrossRef]
- Yang, Y.T.; Tang, X.H.; Zheng, H. Construct ‘FE-Meshfree’ Quad4 using mean value coordinates. Eng. Anal. Bound. Elem. 2015, 59, 78–88. [Google Scholar] [CrossRef]
- Yang, Y.T.; Tang, X.H.; Zheng, H. A three-node triangular element with continuous nodal stress. Comput. Struct. 2014, 141, 46–58. [Google Scholar] [CrossRef]
- Golberg, M.A.; Chen, C.S.; Bowman, H. Some recent results and proposals for the useof radial basis functions in the bem. Eng. Anal. Bound. Elem. 1999, 23, 285–296. [Google Scholar] [CrossRef]
- Wendland, H. Error estimates for interpolation by compactly supported radial basis function s of minimal degree. J. Approx. Theory 1998, 93, 258–272. [Google Scholar] [CrossRef]
- Hughes, T.J.R. The Finite Element Method: Linear Static and Dynamic Finite Element Analysis; Courier Corporation: New York, NY, USA, 2012. [Google Scholar]
- Bathe, K.J. Finite Element Procedure; Prentice-Hall: Englewood Cliffs, NJ, USA, 1996. [Google Scholar]
- Hinton, E.; Rock, T.; Zienkiewicz, O.C. A note on mass lumping and related processes in finite element method. Earthq. Eng. Struct. Dyn. 1976, 4, 245–249. [Google Scholar] [CrossRef]
- Witkowski, W.; Rucka, M.; Chroscielewski, J.; Wilde, K. On some properties of 2D spectral finite elements in problems of wave propagation. Finite Elem. Anal. Des. 2012, 55, 31–41. [Google Scholar] [CrossRef]
- Kudela, P.; Krawczuk, M.; Ostachowicz, W. Wave propagation modelling in 1D structures using spectral finite elements. J. Sound Vib. 2007, 300, 88–100. [Google Scholar] [CrossRef]
- Yang, Y.T.; Zheng, H.; Sivaselvan, M.V. A rigorous and unified mass lumping scheme for higher-order elements. Comput. Methods Appl. Mech. Eng. 2017, 319, 491–514. [Google Scholar] [CrossRef]
- Yang, G.T.; Zhang, S.Y. Elastodynamics; China Railway Publishing House: Beijing, UK, 1988. [Google Scholar]
- Larson, M.G.; Bengzon, F. The Finite Element Method: Theory, Implementation, and Applications; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).