Modeling of the Kinetics of Polyoxymethylene Decomposition under Oxidative and Non-Oxidative Conditions
Abstract
1. Introduction
2. Background
- -
- The reaction is the sum of separate steps in chemical reactions, characterized by a constant value of activation energy and is a mathematical expression of a kinetic model;
- -
- Reactions can take place independently, concurrently, or sequentially;
- -
- The reactions take place in an irreversible manner during the thermal degradation of polymers, because the volatile degradation products formed during the thermogravimetric analysis are continuously removed from the apparatus’ furnace chamber.
3. Materials and Methods
3.1. Materials
- -
- Drying temperature: 80 °C;
- -
- Drying time: 4 h;
- -
- Temperature of feed zone: 190 °C;
- -
- First zone temperature: 200 °C;
- -
- Second zone temperature: 200 °C;
- -
- Third zone temperature: 210 °C;
- -
- Forth zone temperature: 210 °C;
- -
- Extrusion zone temperature: 220 °C;
- -
- Die temperature: 220 °C;
- -
- Screw speed: 120 rpm.
3.2. Differential Scanning Calorimetry (DSC)
- -
- First heating (I) from 25 to 200 °C with a heating rate of 10 °C/min;
- -
- Cooling from 200 to 25 °C with cooling rate 10 °C/min;
- -
- Second heating (II) from 25 to 200 °C with a heating rate of 10 °C/min.
3.3. Thermogravimetric Analysis
3.4. Kinetic Modelling of Thermo-Oxidative Degradation Process
4. Results and Discussion
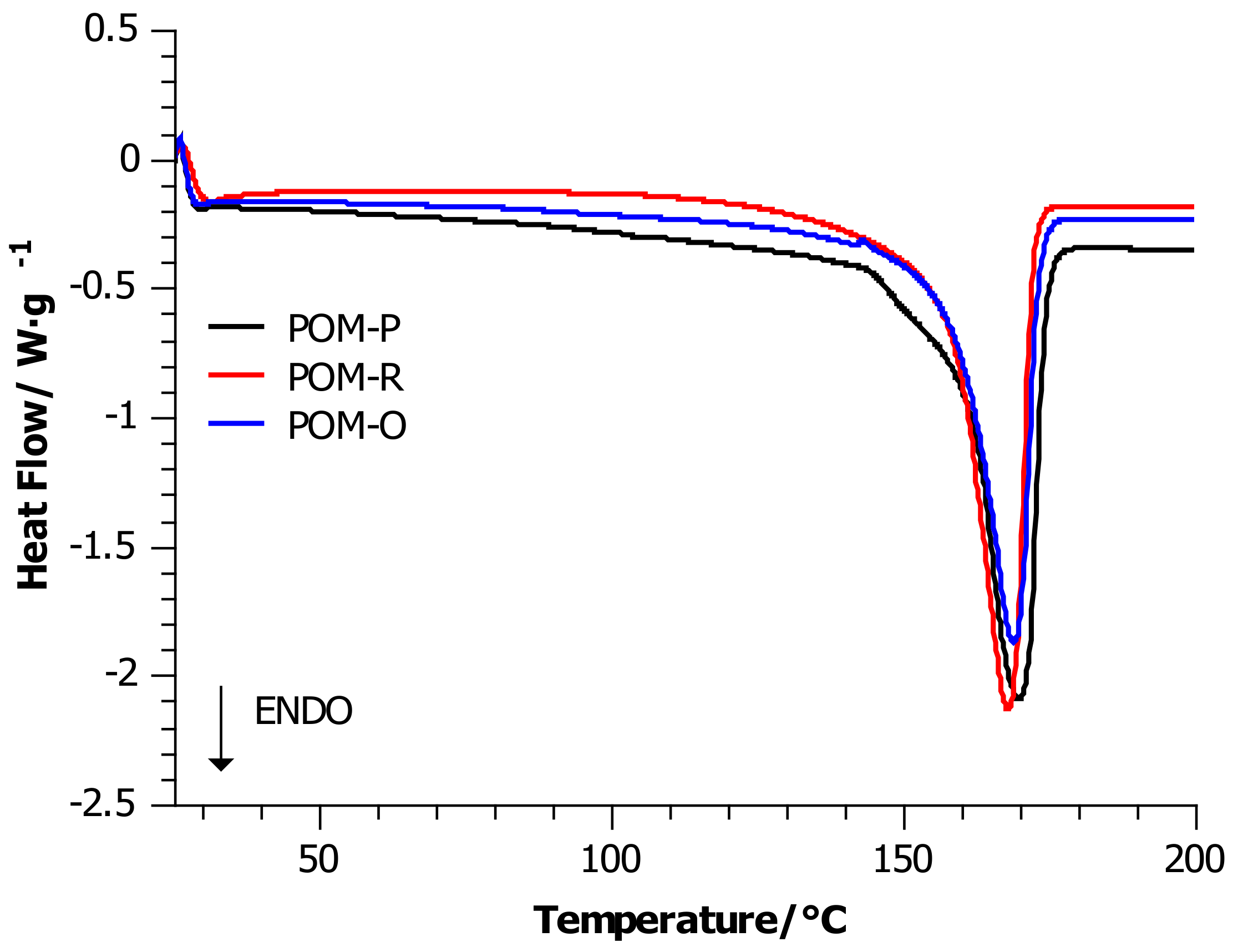
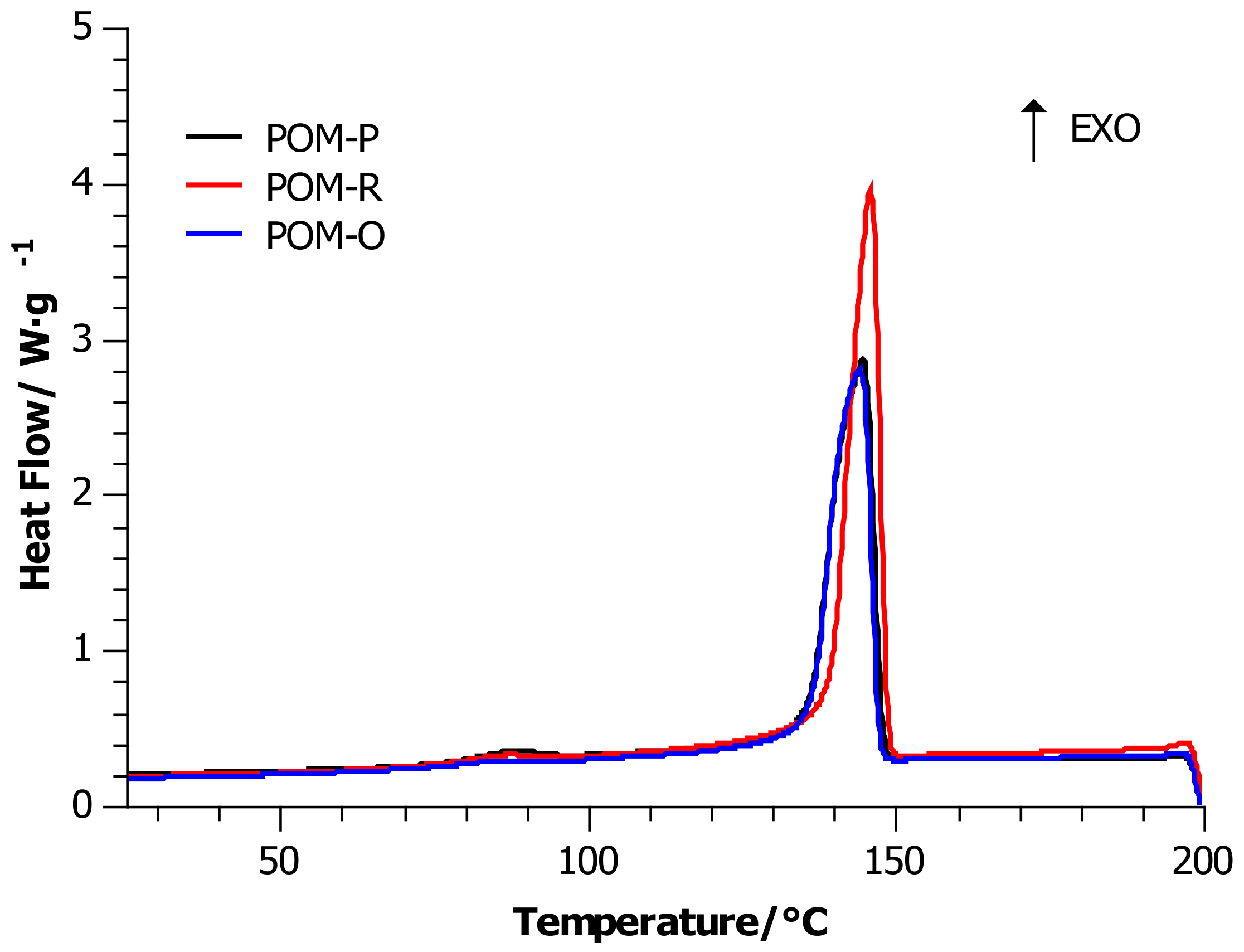
4.1. Differential Scanning Calorimetry (DSC)
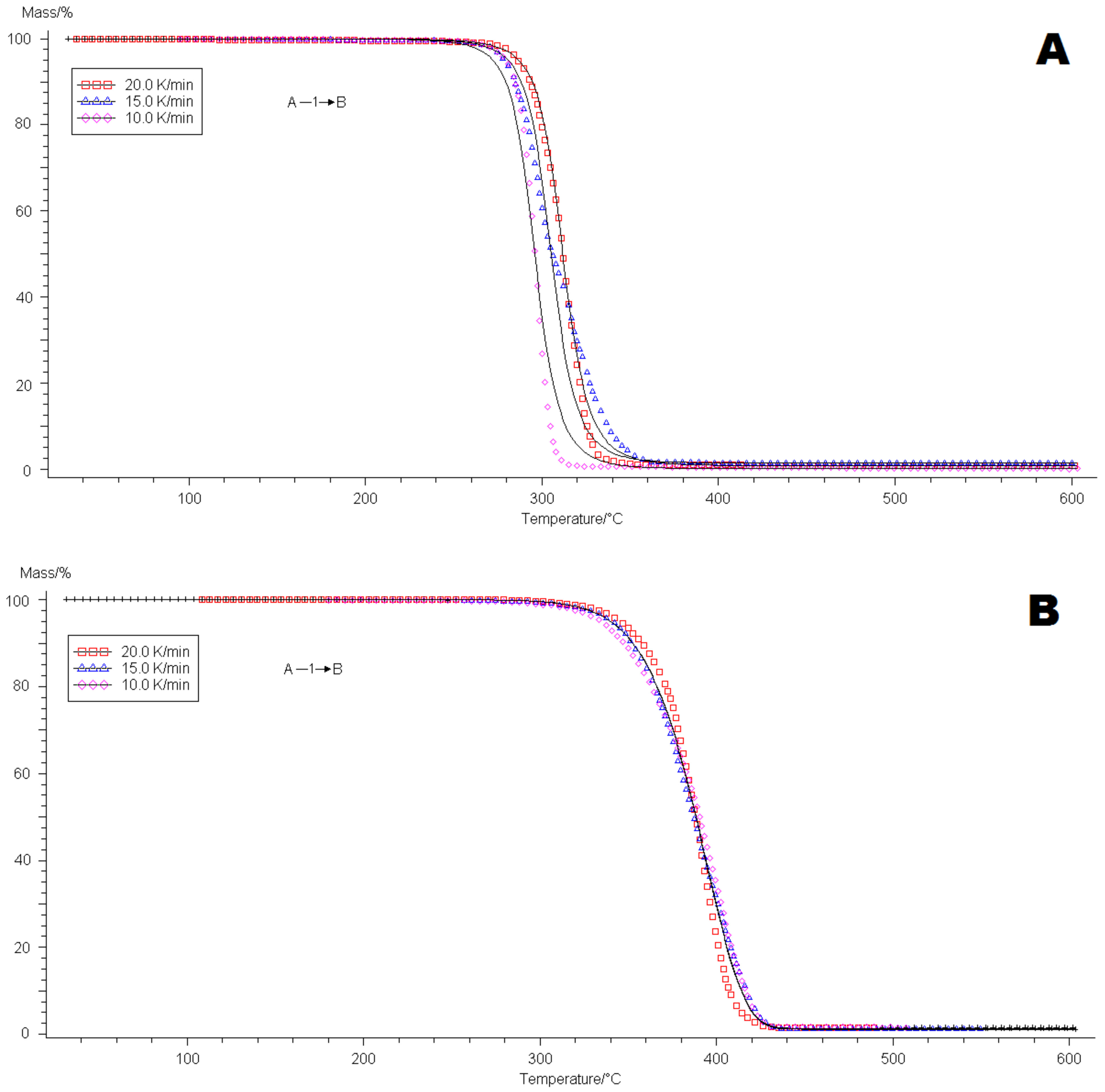
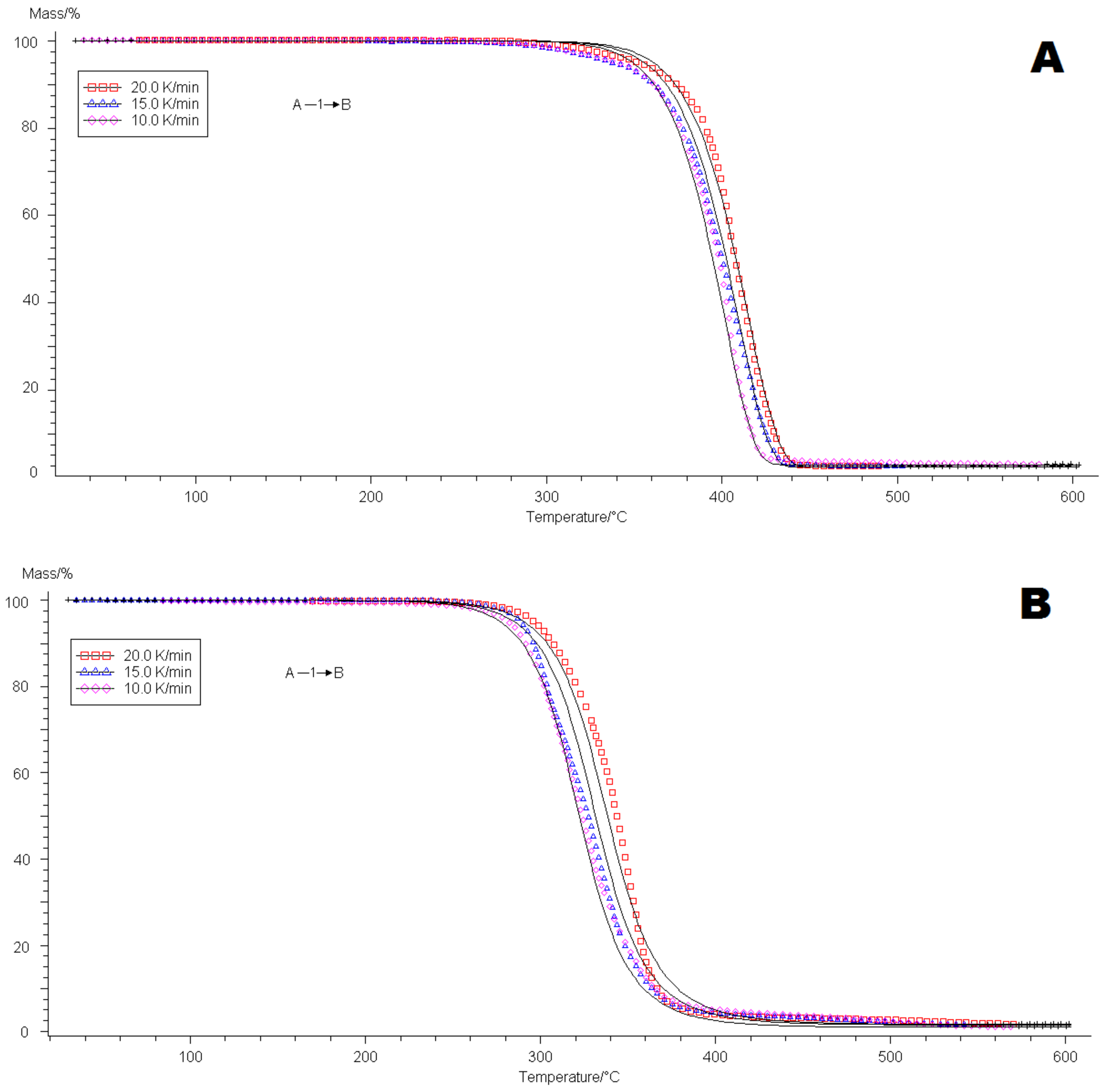
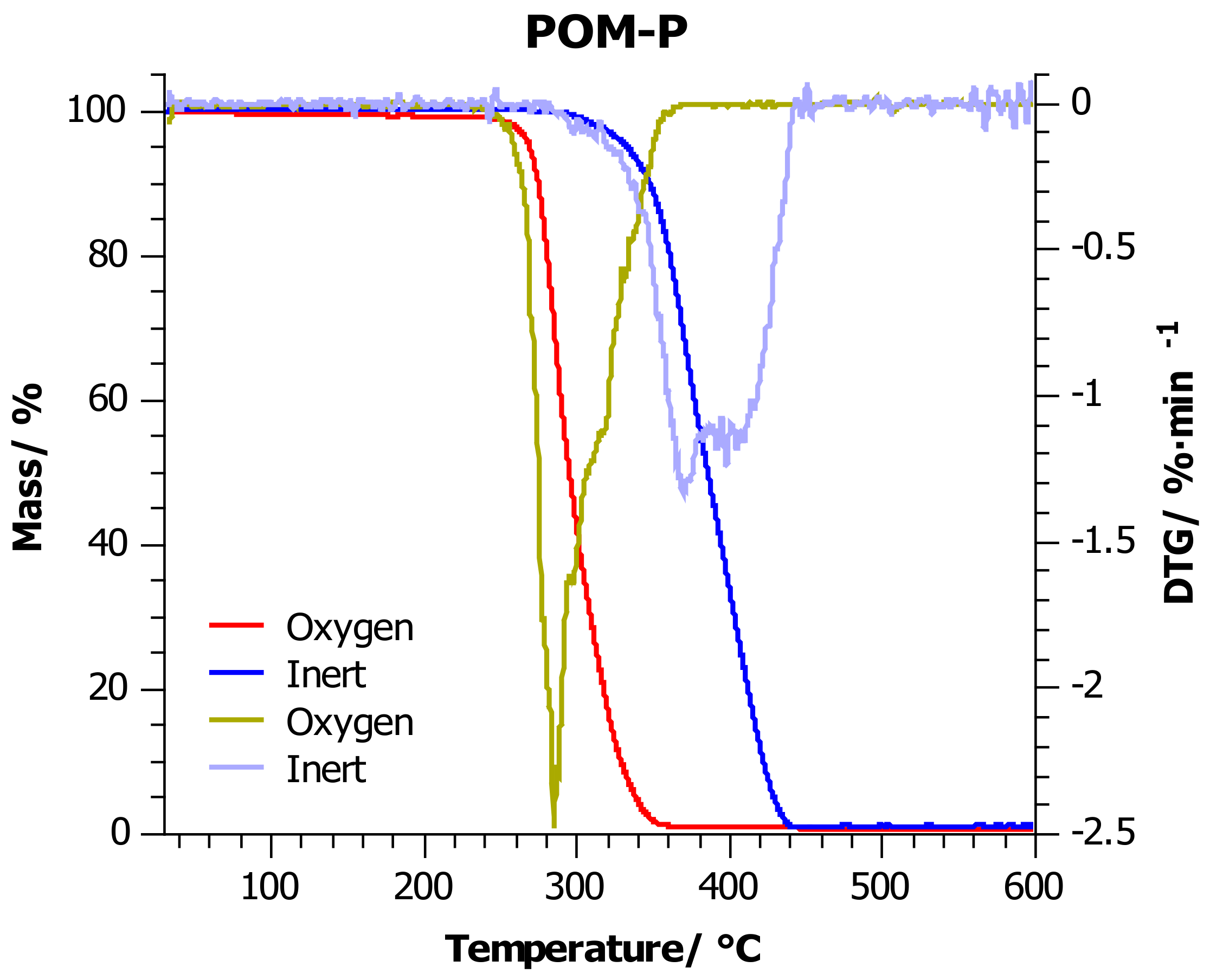
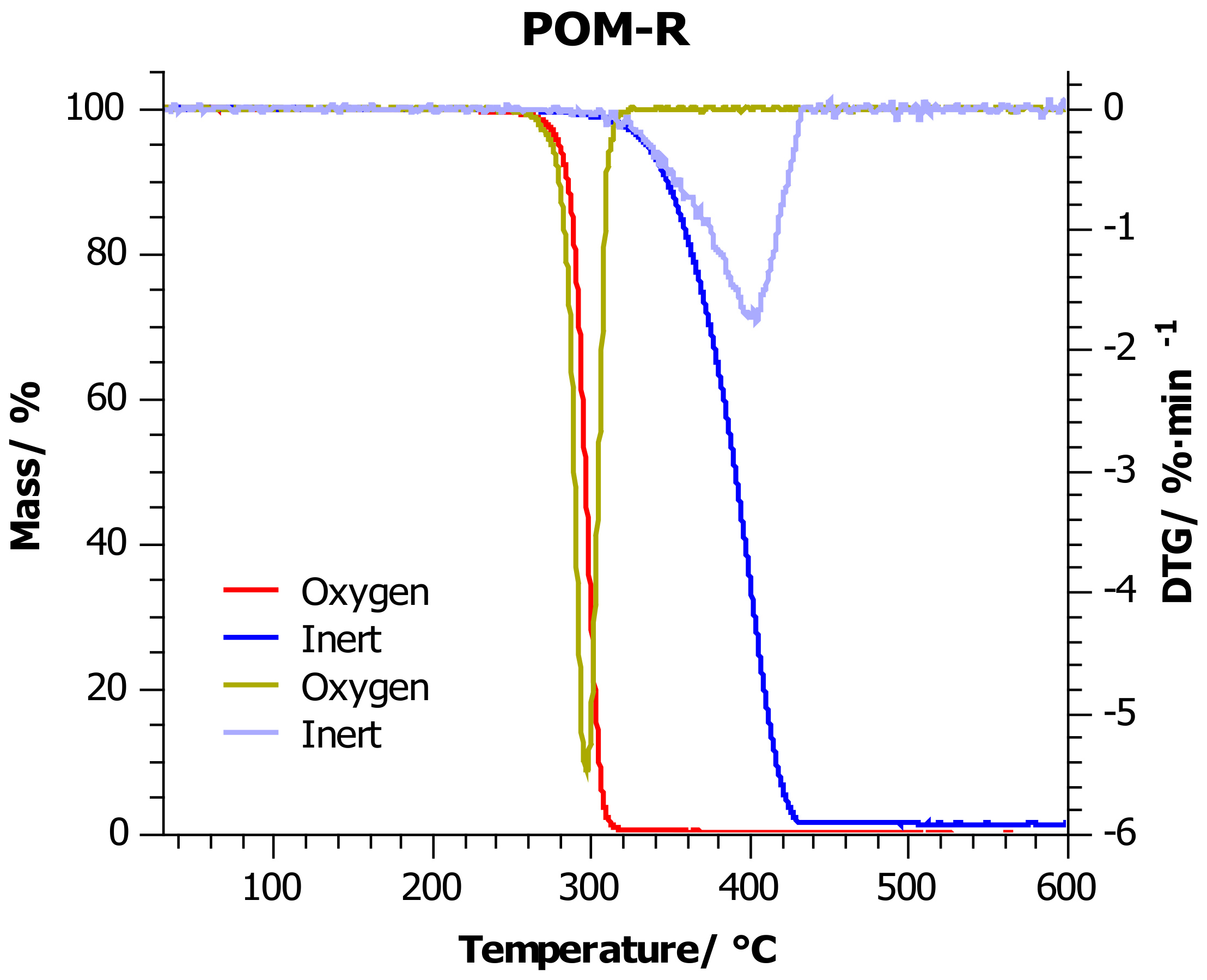
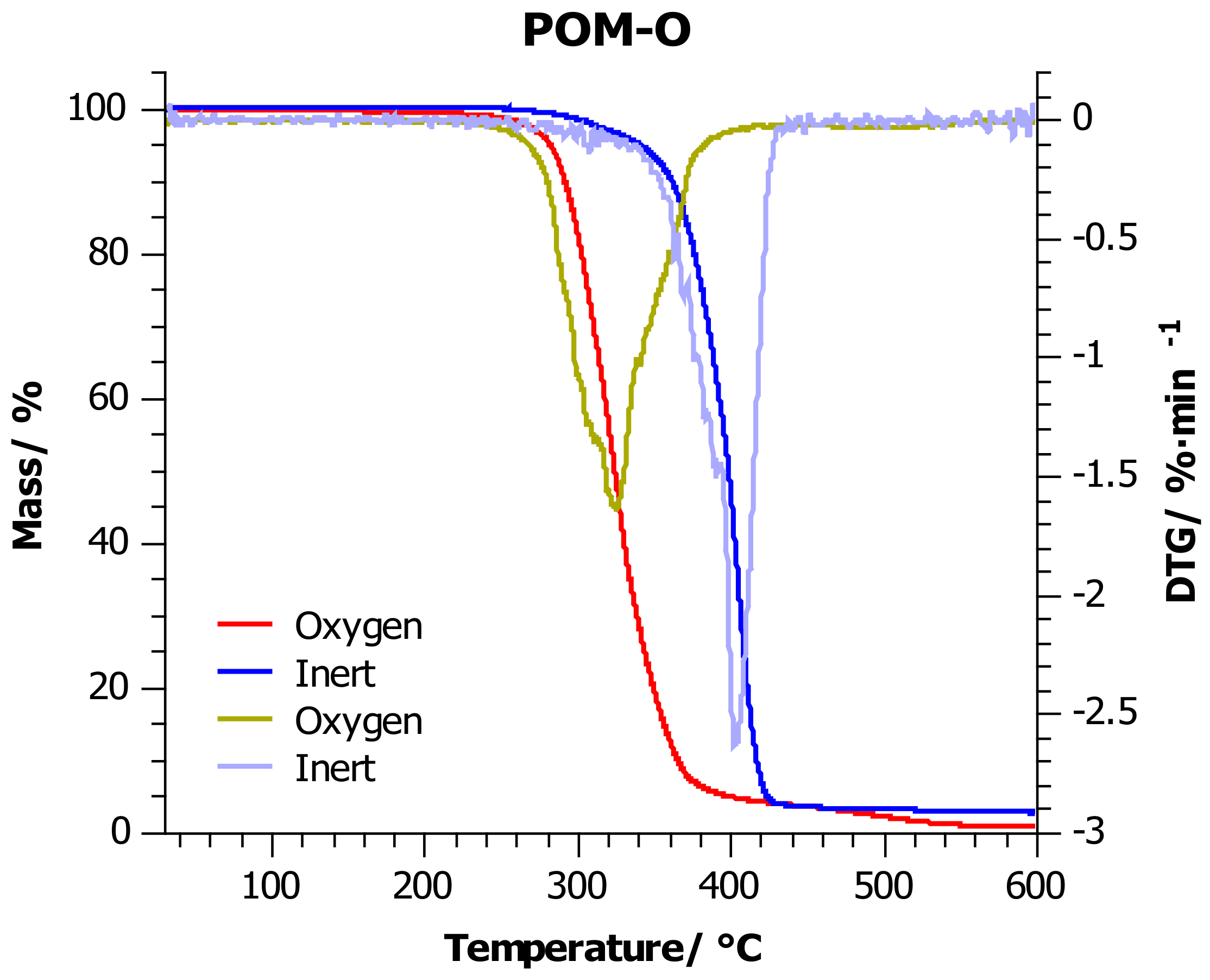
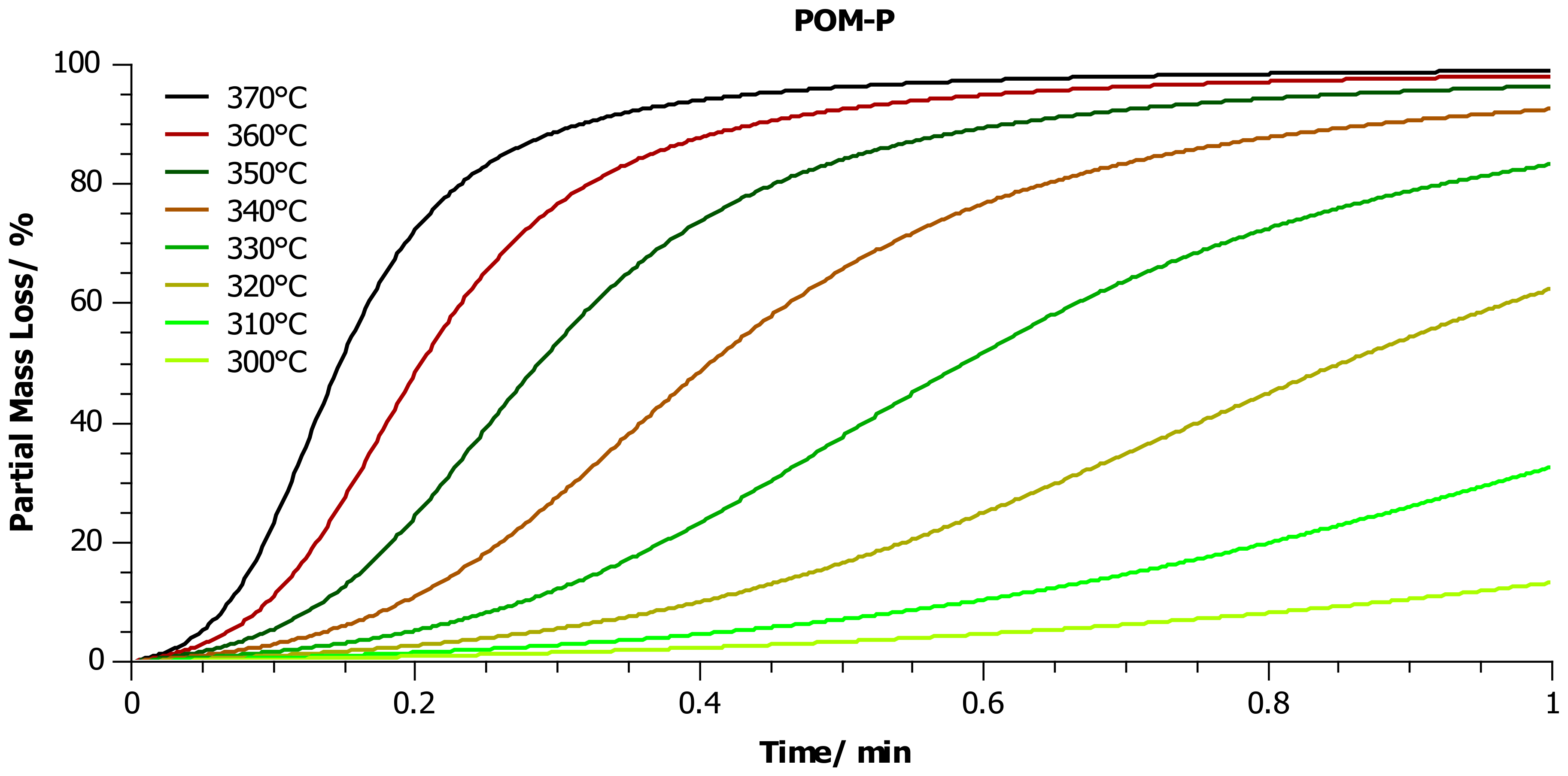
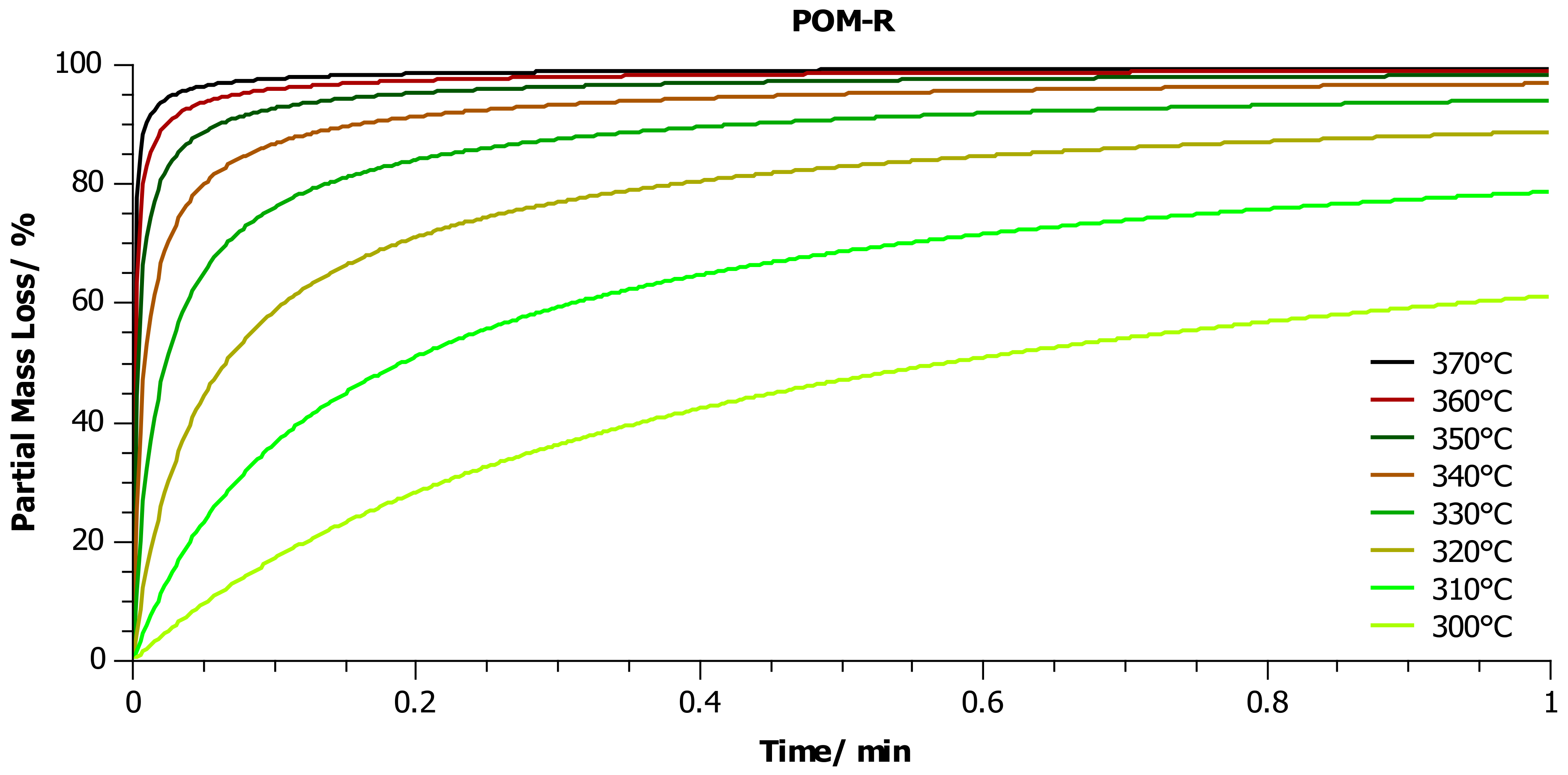
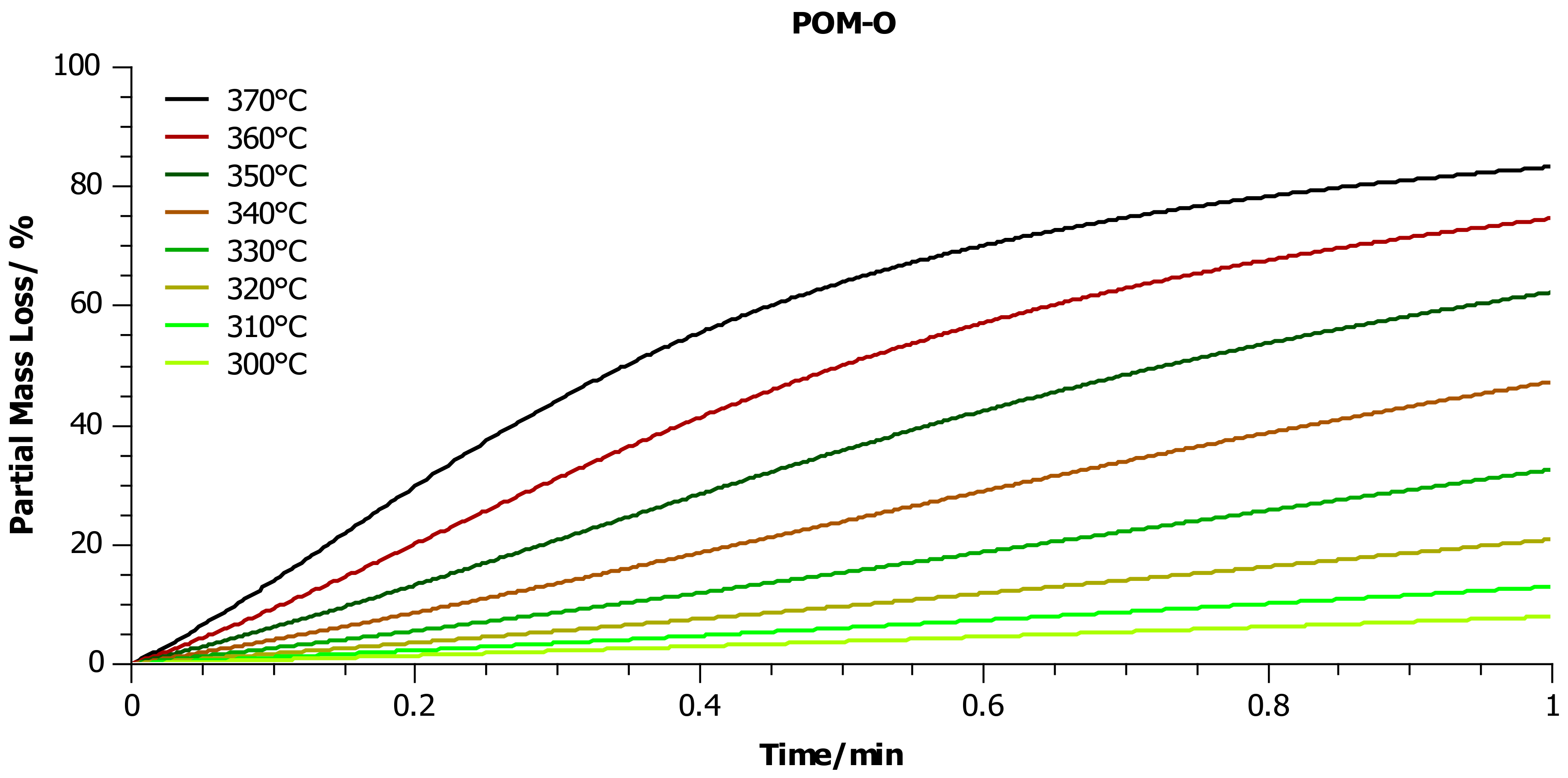
4.2. Thermogravimetric Analysis
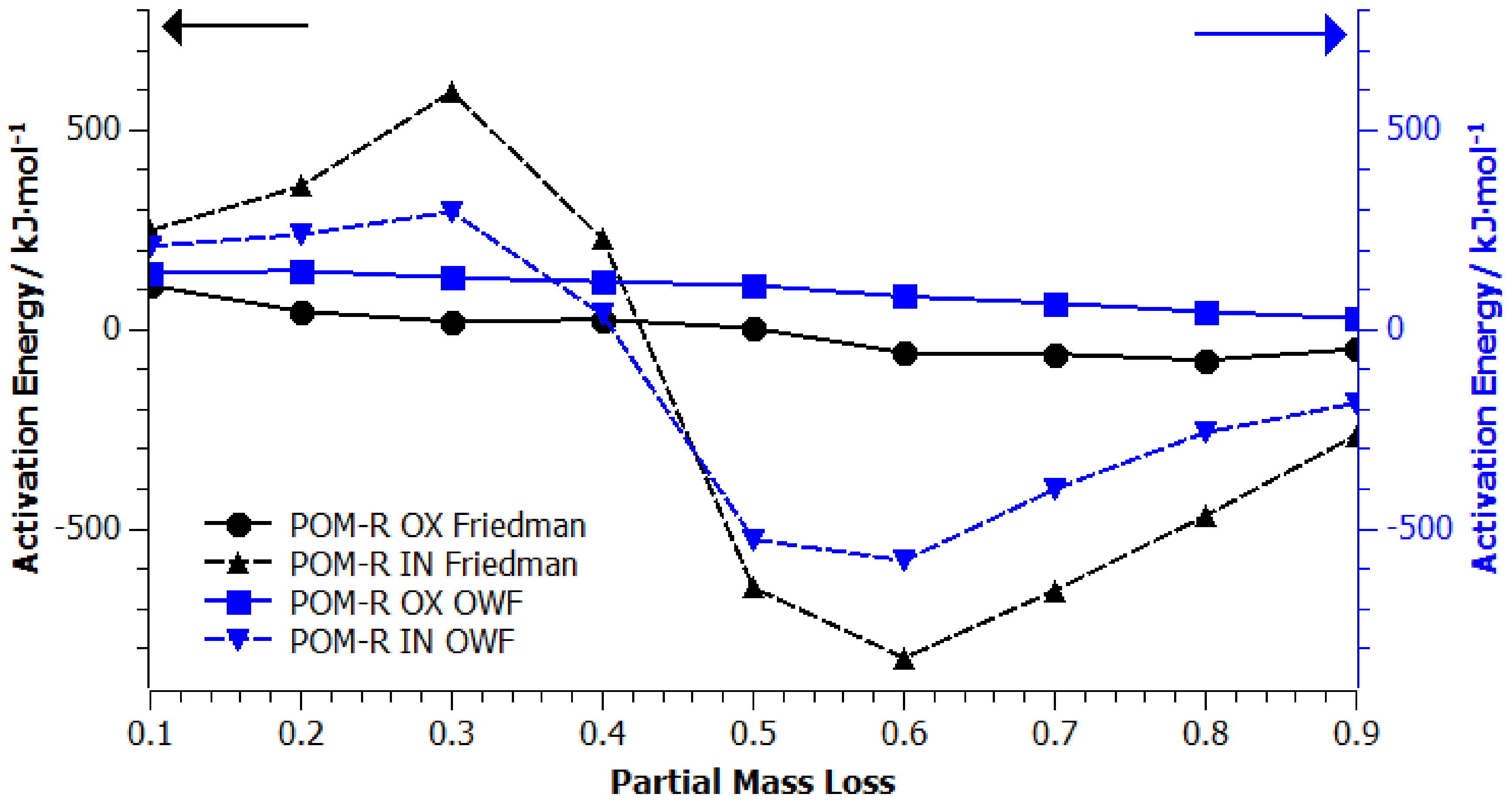
4.3. Kinetic Modelling of Thermo-Oxidative Degradation Process
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

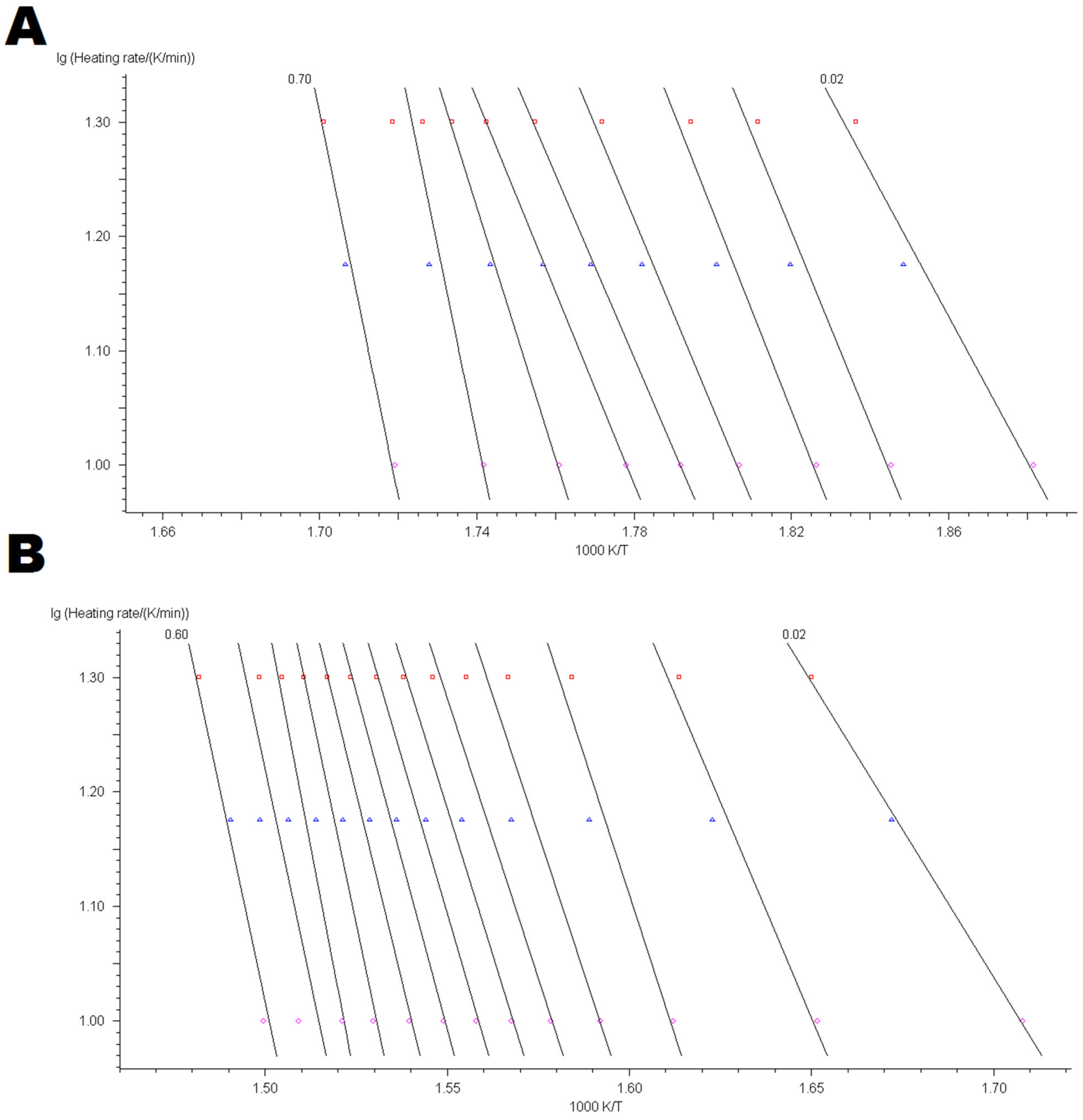
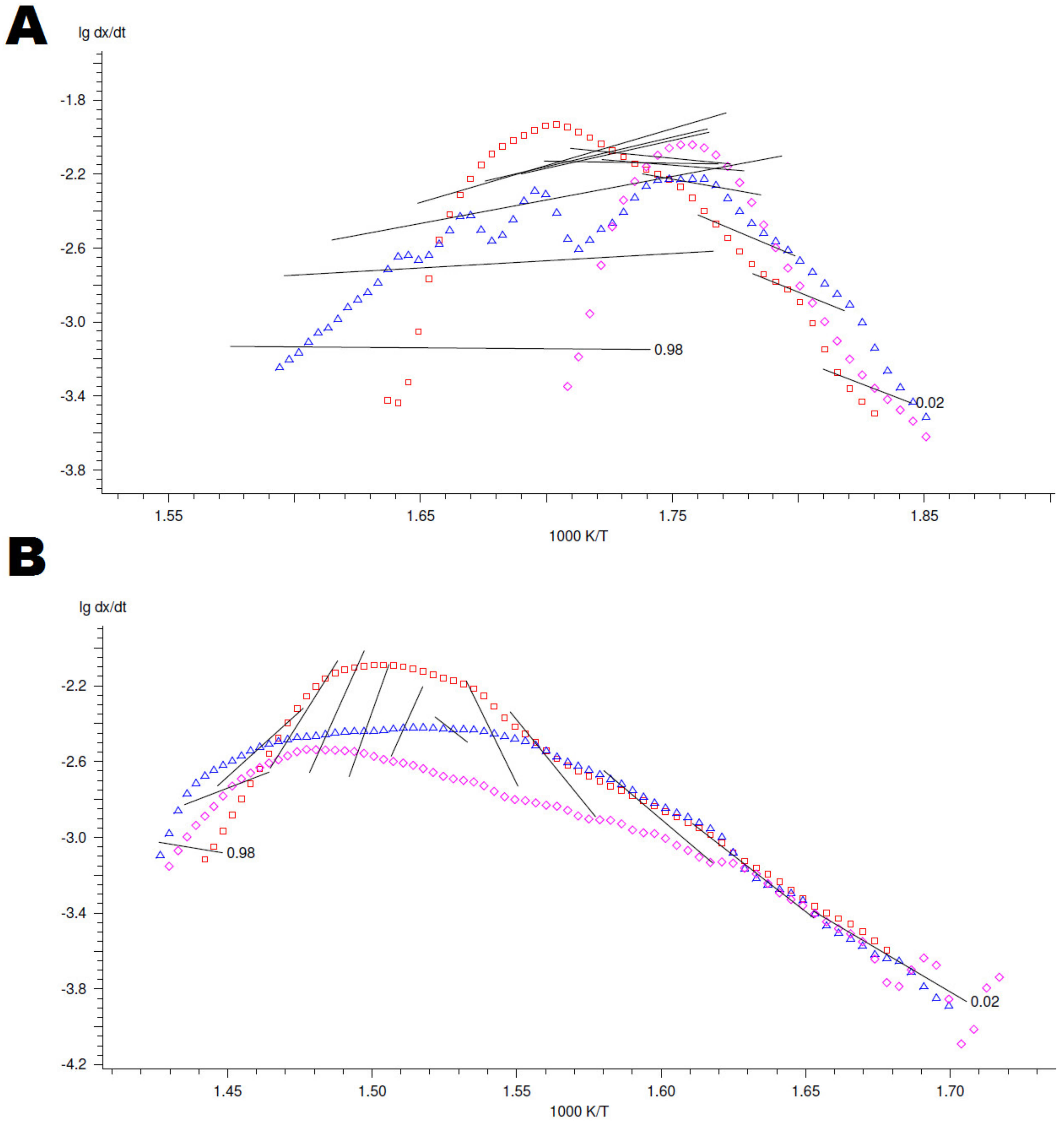
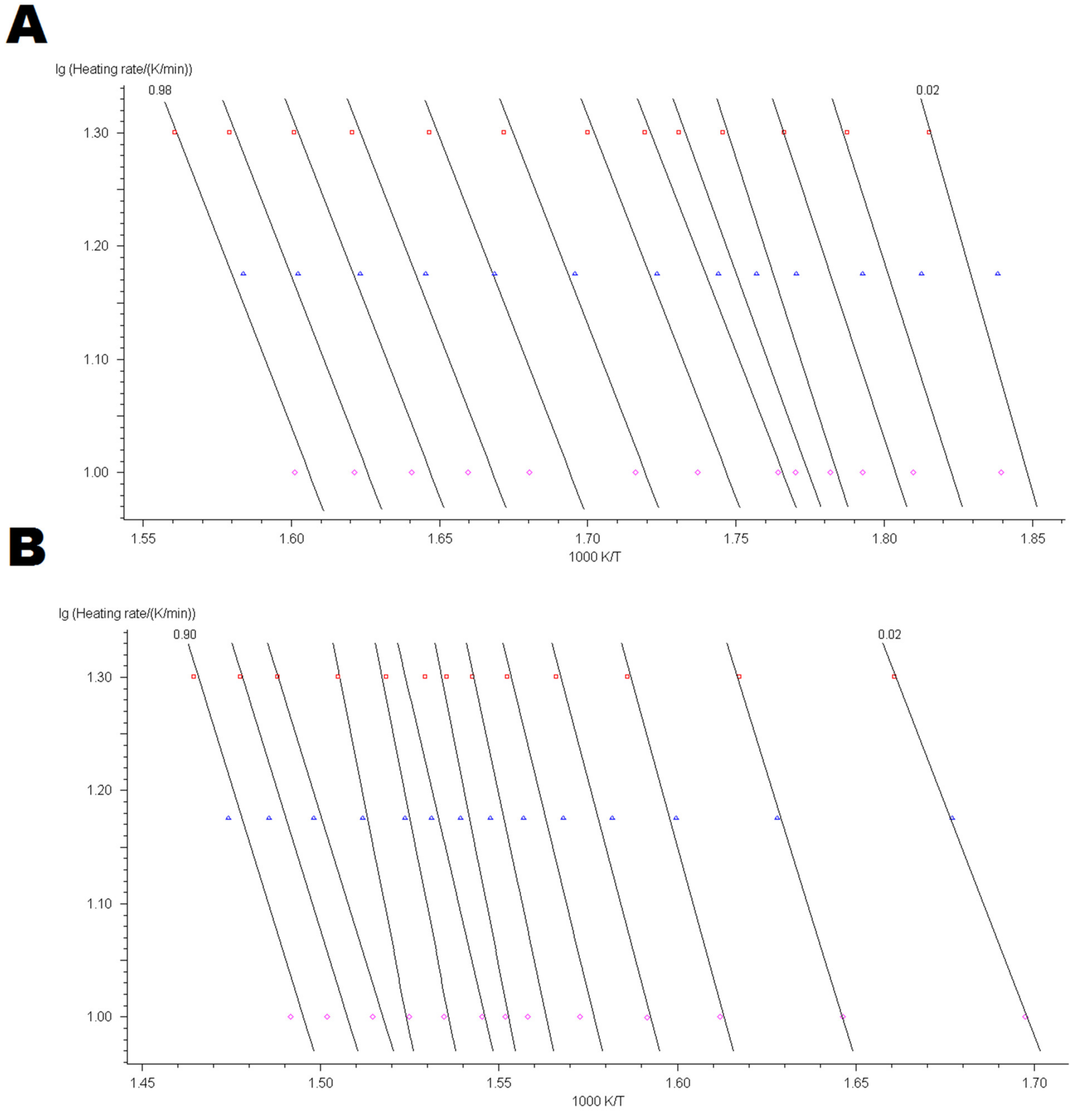
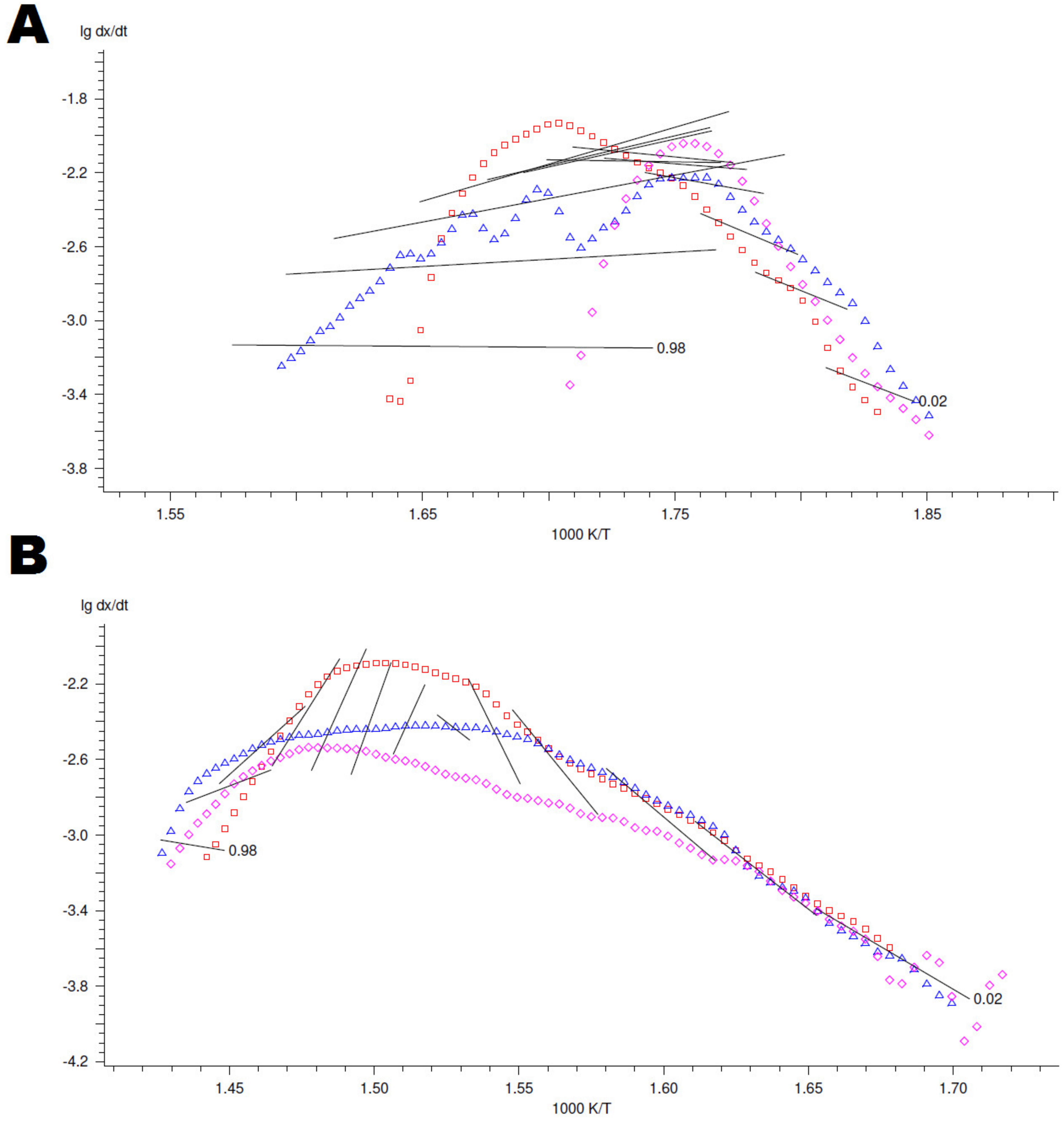
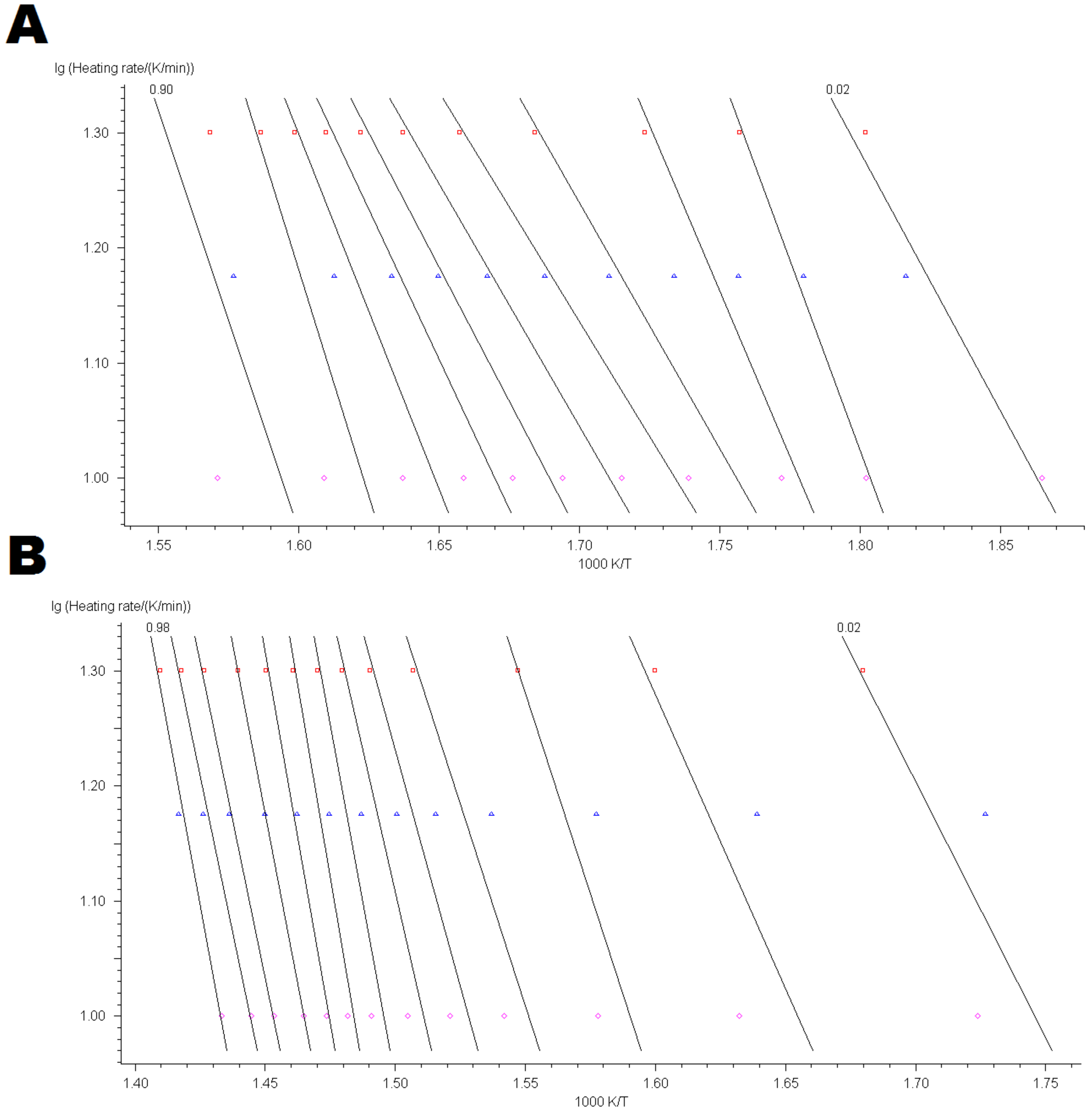
Appendix B

References
- Leszczyńska, A.; Pielichowski, K.; Majka, T.M. The synthesis and investigation of structure–properties relationship in polyoxymethylene (POM)/montmorillonite (MMT) nanocomposites. In Modern Polymeric Materials for Environmental Applications; Pielichowski, K., Ed.; Wydaw. Naukowo-Techniczne TEZA: Warsaw, Poland, 2010; Volume 1, pp. 193–202. [Google Scholar]
- Pielichowska, K.; Król, K.; Majka, T.M. Polyoxymethylene-copolymer based composites with PEG-grafted hydroxyapatite with improved thermal stability. Thermochim. Acta 2016, 633, 98–107. [Google Scholar] [CrossRef]
- Pielichowska, K. The influence of polyoxymethylene molar mass on the oxidative thermal degradation of its nanocomposites with hydroxyapatite. J. Therm. Anal. Calorim. 2016, 124, 751–765. [Google Scholar] [CrossRef]
- Pielichowska, K. Thermooxidative degradation of polyoxymethylene homo- and copolymer nanocomposites with hydroxyapatite: Kinetic and thermoanalytical study. Thermochim. Acta 2015, 600, 7–19. [Google Scholar] [CrossRef]
- Ramirez, N.V.; Sánchez-Soto, M.; Illescas, S. Enhancement of POM thermooxidation resistance through POSS nanoparticles. Polym. Compos. 2011, 32, 1584–1592. [Google Scholar] [CrossRef]
- Yang, F.; Li, H.; Cai, L.; Lan, F.; Xiang, M. Degradation and Stabilization of Co-POM. Polym. Technol. Eng. 2009, 48, 530–534. [Google Scholar] [CrossRef]
- Lüftl, S.; Archodoulaki, V.-M.; Seidler, S. Thermal-oxidative induced degradation behaviour of polyoxymethylene (POM) copolymer detected by TGA/MS. Polym. Degrad. Stab. 2006, 91, 464–471. [Google Scholar] [CrossRef]
- Berkowicz, G.; Majka, T.M.; Żukowski, W. The pyrolysis and combustion of polyoxymethylene in a fluidised bed with the possibility of incorporating CO2. Energy Convers. Manag. 2020, 214, 112888. [Google Scholar] [CrossRef]
- Żukowski, W.; Berkowicz, G.; Majka, T.M. Dataset on flue gas composition during pyrolysis of polyoxymethylene in a fluidised bed with the possibility of incorporating CO2. Data Brief 2020, 31, 105703. [Google Scholar] [CrossRef]
- Burnham, A.K.; Braun, R.L. Global Kinetic Analysis of Complex Materials. Energy Fuels 1999, 13, 1–22. [Google Scholar] [CrossRef]
- Moukhina, E. Determination of kinetic mechanisms for reactions measured with thermoanalytical instruments. J. Therm. Anal. Calorim. 2012, 109, 1203–1214. [Google Scholar] [CrossRef]
- Budrugeac, P. The evaluation of the non-isothermal kinetic parameters of thethermal and thermo-oxidative degradation of polymers andpolymeric materials: Its use and abuse. Polym. Degrad. Stab. 2001, 71, 185–187. [Google Scholar] [CrossRef]
- Opfermann, J.; Blumm, J.; Emmerich, W.-D. Simulation of the sintering behavior of a ceramic green body using advanced thermokinetic analysis. Thermochim. Acta 1998, 318, 213–220. [Google Scholar] [CrossRef]
- Opfermann, J. Kinetic Analysis Using Multivariate Non-linear Regression. I. Basic concepts. J. Therm. Anal. Calorim. 2000, 60, 641–658. [Google Scholar] [CrossRef]
- Opfermann, J.; Kaisersberger, E. An advantageous variant of the Ozawa-Flynn-Wall analysis. Thermochim. Acta 1992, 203, 167–175. [Google Scholar] [CrossRef]
- Herrera, M.; Matuscheka, G.; Kettrup, A. Main products and kinetics of the thermal degradation of polyamides. Chemosphere 2001, 42, 601–607. [Google Scholar] [CrossRef]
- How Fast Are Chemical Reactions? Available online: https://d2brmtk65c6tyc.cloudfront.net/fileadmin/www.netzsch-thermal-analysis.com/Microsites/Kinetics_Neo/Docs/Kinetics_NEO_en_web_2018-09-06.pdf?1558356264 (accessed on 18 December 2020).
- Friedman, H.L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic. J. Polym. Sci. Part C Polym. Symp. 2007, 6, 183–195. [Google Scholar] [CrossRef]
- Doyle, C.D. Estimating isothermal life from thermogravimetric data. J. Appl. Polym. Sci. 1962, 6, 639–642. [Google Scholar] [CrossRef]
- Ozawa, T. A New Method of Analyzing Thermogravimetric Data. Bull. Chem. Soc. Jpn. 1965, 38, 1881–1886. [Google Scholar] [CrossRef]
- Flynn, J.H.; Wall, L.A. A quick, direct method for the determination of activation energy from thermogravimetric data. J. Polym. Sci. Part B Polym. Lett. 1966, 4, 323–328. [Google Scholar] [CrossRef]
- Chrissafis, K. Kinetics of thermal degradation of polymers. Complementary use of isoconversional and model-fitting methods. J. Therm. Anal. Calorim. 2009, 95, 273–283. [Google Scholar] [CrossRef]
- Arshad, M.A.; Maaroufi, A.K. Recent Progress in Kinetics of Thermal Degradation Mechanisms in Polymer Composites. MOJ Polym. Sci. 2017, 1, 120–125. [Google Scholar]
- Al-Salem, S.M. (Ed.) Kinetic Studies Related to Polymer Degradation and Stability. In Plastics to Energy: Fuel, Chemicals, and Sustainability Implications; Elsevier, William Andrew Imprint: Amsterdam, The Netherlands, 2019; pp. 233–268. [Google Scholar]
- Lomakin, S.M.; Novokshonova, L.A.; Brevnov, P.N.; Shchegolikhin, A.N. Thermal properties of polyethylene/montmorillonite nanocomposites prepared by intercalative polymerization. J. Mater. Sci. 2007, 43, 1340–1353. [Google Scholar] [CrossRef]
- Pérez-Maqueda, L.A.; Sánchez-Jiménez, P.E.; Perejón, A.; García-Garrido, C.; Criado, J.M.; Benítez-Guerrero, M. Scission kinetic model for the prediction of polymer pyrolysis curves from chain structure. Polym. Test. 2014, 37, 1–5. [Google Scholar] [CrossRef]
- Navarro, R.; Torre, L.; Kenny, J.; Jiménez, A. Thermal degradation of recycled polypropylene toughened with elastomers. Polym. Degrad. Stab. 2003, 82, 279–290. [Google Scholar] [CrossRef]
- Bordère, S.; Rouquerol, F.; Estienne, J.; Floreancig, A. Kinetical possibilities of controlled transformation Rate Thermal Analysis (CRTA). J. Therm. Anal. Calorim. 1990, 36, 1651–1668. [Google Scholar] [CrossRef]
- Van Krevelen, D.W. (Ed.) Crystallization and recrystalization. In Properties of Polymers; Elsevier Science Imprint: Amsterdam, The Netherlands, 1997; pp. 585–623. [Google Scholar]
- Katoh, Y.; Okamoto, M. Crystallization controlled by layered silicates in nylon 6–clay nano-composite. Polymer 2009, 50, 4718–4726. [Google Scholar] [CrossRef]
- Zhao, R.R. Melt Blowing Polyoxymethylene Copolymer. J. Eng. Fibers Fabr. 2005, 14, 19–24. [Google Scholar] [CrossRef]
- Pielichowska, K. The influence of molecular weight on the properties of polyacetal/hydroxyapatite nanocomposites. Part 1. Microstructural analysis and phase transition studies. J. Polym. Res. 2012, 19, 1–16. [Google Scholar] [CrossRef][Green Version]
- Hihara, L.H.; Adler, R.P.L.; Latanision, R.M. Environmental Degradation of Advanced and Traditional Engineering Materials; CRC Press, Tylor & Francis Group: Boca Raton, FL, USA, 2019. [Google Scholar]
- Khawam, A.; Flanagan, D.R. Solid-State Kinetic Models: Basics and Mathematical Fundamentals. J. Phys. Chem. B 2006, 110, 17315–17328. [Google Scholar] [CrossRef]


| Type of Reaction | Designation | f(α) |
|---|---|---|
| Reaction of 1st order | F1 | 1 − α |
| Reaction of 2nd order | F2 | (1 − α)2 |
| Reaction of nth order | Fn | (1 − α)n |
| One-dimensional diffusion | D1 | 1/(2α) |
| Two-dimensional diffusion | D2 | [−ln(1 − α)]−1 |
| Three-dimensional diffusion—Jander’s type | D3 | 1.5(1 − α)2/3[1 − (1 − α)1/3] |
| Three-dimensional diffusion—Ginstling-Brounstein | D4 | 1.5[(1 − α)−1/3 − 1]−1 |
| Two-dimensional phase boundary | R2 | 2(1 − α)1/2 |
| Three-dimensional phase boundary | R3 | 3(1 − α)2/3 |
| Prout–Tompkins equation | B1 | α(1 − α) |
| Expanded Prout–Tompkins equation | Bna | (1 − α)nαm |
| Reaction of 1st order with autocatalysis by product | C1-X | (1 − α)(1 + KcatX) |
| Reaction of nth order with autocatalysis by product | Cn-X | (1 − α)n(1 + KcatX) |
| Two-dimensional nucleation according to Avrami | A2 | 2(1 − α)[−ln(1 − α)]1/2 |
| Three-dimensional nucleation according to Avrami | A3 | 3(1 − α)[−ln(1 − α)]2/3 |
| n-dimensional nucleation according to Avrami-Erofeev | An | n(1 − α)[−ln(1 − α)](n−1)/n |
| Type of Reaction | Scheme |
|---|---|
| One-step | |
| Independent | |
| Consecutive | |
| Parallel | 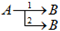 |
| Competitive |  |
| Sample | Tm/ °C | ΔHm/J·g−1 | ∆Cp/J·(g·K)−1 | Xc/ % | Tc/r °C |
|---|---|---|---|---|---|
| POM-P | 167 ± 3 | 153.29 | 0.260 | 47 | 145 ± 2 |
| POM-R | 166 ± 3 | 161.14 | 0.219 | 49 | 147 ± 3 |
| POM-O | 167 ± 4 | 139.39 | 0.224 | 43 | 145 ± 2 |
| Sample | Atmosphere | T5%/°C | T10%/°C | T20%/°C | T50%/°C | Tmax/°C |
|---|---|---|---|---|---|---|
| POM-P | Inert | 332 ± 7 | 348 ± 7 | 361 ± 7 | 386 ± 8 | 370 ± 8 |
| Oxygen | 267 ± 5 | 274 ± 5 | 280 ± 6 | 295 ± 6 | 285 ± 6 | |
| POM-R | Inert | 335 ± 7 | 348 ± 7 | 363 ± 7 | 390 ± 8 | 404 ± 8 |
| Oxygen | 279 ± 6 | 284 ± 6 | 289 ± 6 | 295 ± 6 | 296 ± 6 | |
| POM-O | Inert | 340 ± 7 | 361 ± 7 | 376 ± 8 | 398 ± 8 | 403 ± 8 |
| Oxygen | 282 ± 6 | 291 ± 6 | 302 ± 6 | 324 ± 7 | 324 ± 7 |
| POM-P | ||||||
| # | Oxygen | Inert | ||||
| Type | f-Act | F-Test | Type | f-Act | F-Test | |
| 1 | Cn B | 870 | 1.00 | An | 632 | 1.00 |
| 2 | Bna | 869 | 1.03 | Fn | 632 | 1.52 |
| 3 | Fn | 869 | 1.03 | Cn B | 631 | 1.52 |
| 4 | F2 | 871 | 1.08 | F2 | 633 | 1.55 |
| 5 | An | 870 | 1.63 | Bna | 631 | 1.56 |
| 6 | F1 | 871 | 1.99 | D3 | 633 | 2.00 |
| POM-R | ||||||
| # | Oxygen | Inert | ||||
| Type | f-Act | Fexp | Type | f-Act | Fexp | |
| 1 | Cn B | 1028 | 1.00 | An | 674 | 1.00 |
| 2 | Bna | 1028 | 1.02 | D3 | 675 | 3.36 |
| 3 | A2 | 1039 | 1.22 | D4 | 675 | 4.17 |
| 4 | C1 B | 1029 | 1.26 | F2 | 675 | 4.28 |
| 5 | A3 | 1029 | 1.41 | Fn | 674 | 4.28 |
| 6 | Fn | 1030 | 1.97 | Cn B | 673 | 4.28 |
| POM-O | ||||||
| # | Oxygen | Inert | ||||
| Type | f-Act | Fexp | Type | f-Act | Fexp | |
| 1 | Cn B | 934 | 1.00 | An | 855 | 1.00 |
| 2 | Bna | 934 | 1.03 | Cn B | 854 | 1.00 |
| 3 | Fn | 935 | 1.14 | Bna | 854 | 1.01 |
| 4 | F2 | 936 | 1.19 | Fn | 855 | 1.01 |
| 5 | F1 | 936 | 1.35 | C1 B | 855 | 1.03 |
| 6 | An | 935 | 1.35 | R3 | 856 | 1.05 |
| Factor | POM-P | POM-R | POM-O | |||
|---|---|---|---|---|---|---|
| Oxygen | Inert | Oxygen | Inert | Oxygen | Inert | |
| log A1/s−1 | 26.54 | 30.42 | 6.92 | 10.81 | 8.28 | 12.16 |
| E1/kJ/mol | 307.08 | 366.89 | 111.53 | 172.33 | 122.95 | 183.95 |
| Stand. dev. n1 | 0.41 | 0.26 | 0.23 | 0.07 | 0.35 | 0.19 |
| Correlation coefficient | 0.9998 | 0.9997 | 0.9998 | 0.9993 | 0.9997 | 0.9994 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Majka, T.M.; Berkowicz-Płatek, G.; Żukowski, W. Modeling of the Kinetics of Polyoxymethylene Decomposition under Oxidative and Non-Oxidative Conditions. Materials 2021, 14, 2281. https://doi.org/10.3390/ma14092281
Majka TM, Berkowicz-Płatek G, Żukowski W. Modeling of the Kinetics of Polyoxymethylene Decomposition under Oxidative and Non-Oxidative Conditions. Materials. 2021; 14(9):2281. https://doi.org/10.3390/ma14092281
Chicago/Turabian StyleMajka, Tomasz M., Gabriela Berkowicz-Płatek, and Witold Żukowski. 2021. "Modeling of the Kinetics of Polyoxymethylene Decomposition under Oxidative and Non-Oxidative Conditions" Materials 14, no. 9: 2281. https://doi.org/10.3390/ma14092281
APA StyleMajka, T. M., Berkowicz-Płatek, G., & Żukowski, W. (2021). Modeling of the Kinetics of Polyoxymethylene Decomposition under Oxidative and Non-Oxidative Conditions. Materials, 14(9), 2281. https://doi.org/10.3390/ma14092281








