Strain Localization of Orthotropic Elasto–Plastic Cohesive–Frictional Materials: Analytical Results and Numerical Verification
Abstract
1. Introduction
2. Strain Localization in Elasto-Plastic Solids
2.1. Elasto-Plasticity Model
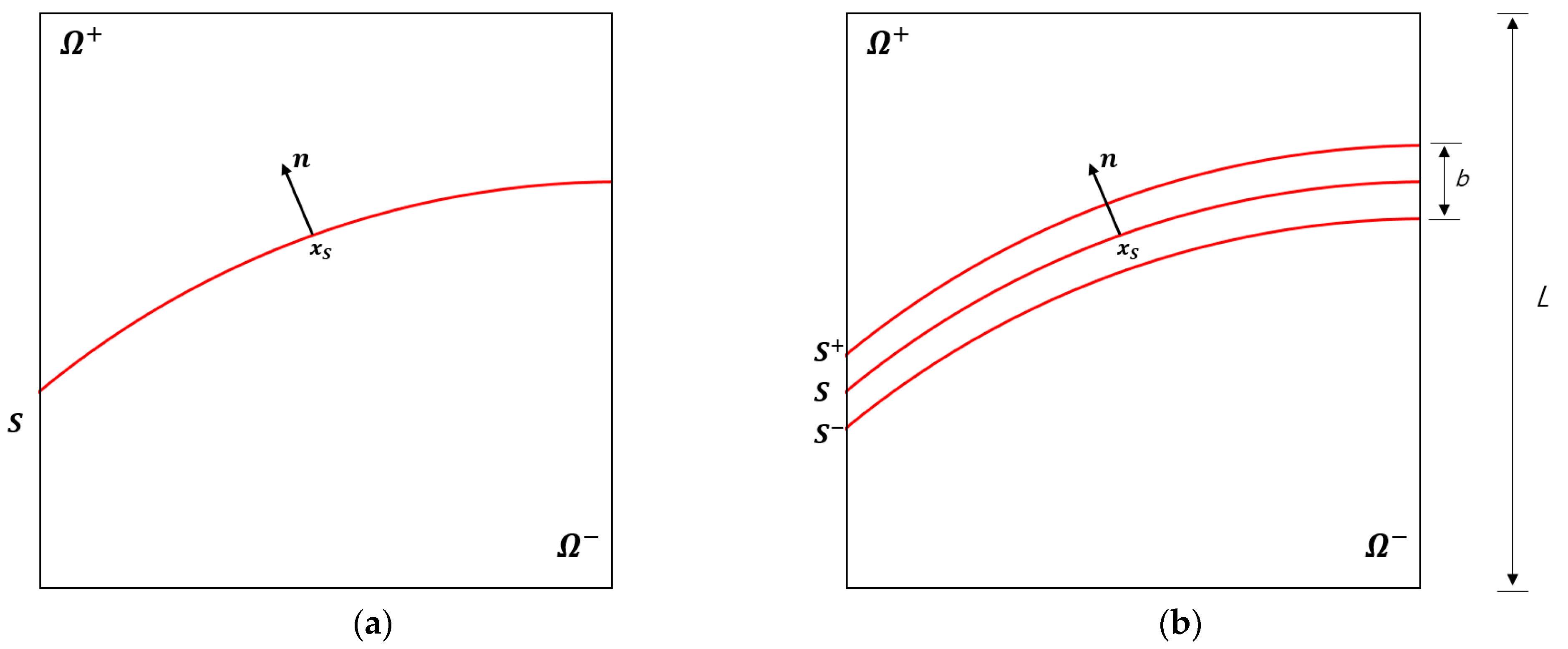
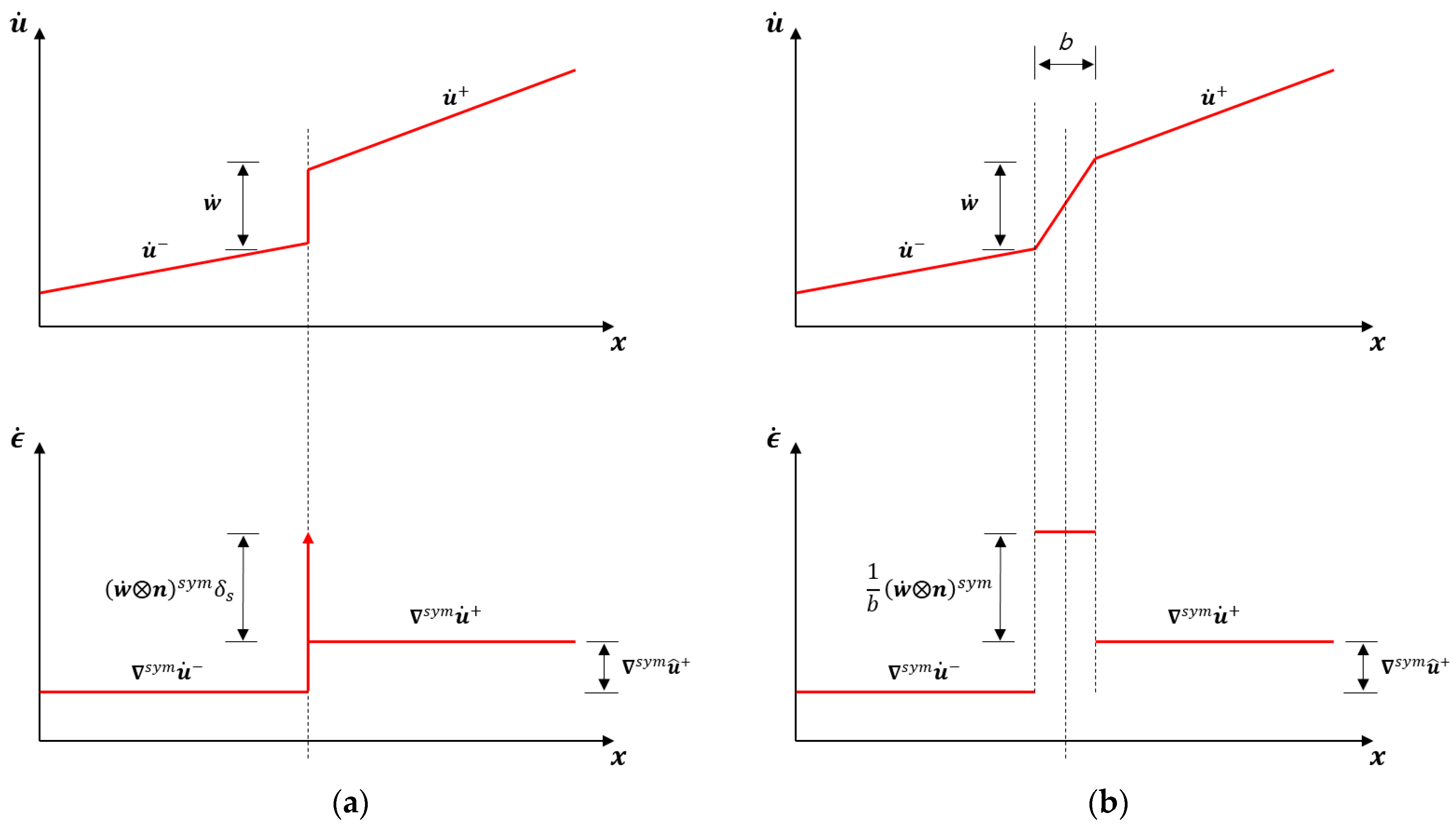
2.2. Kinematics of Strong and Regularized Discontinuities
2.3. Strain Localization and Stress Boundedness
2.4. Strain Localization Plastic Flow Vector and Tensor
3. Application to Orthotropic Cohesive–Frictional Plastic Materials
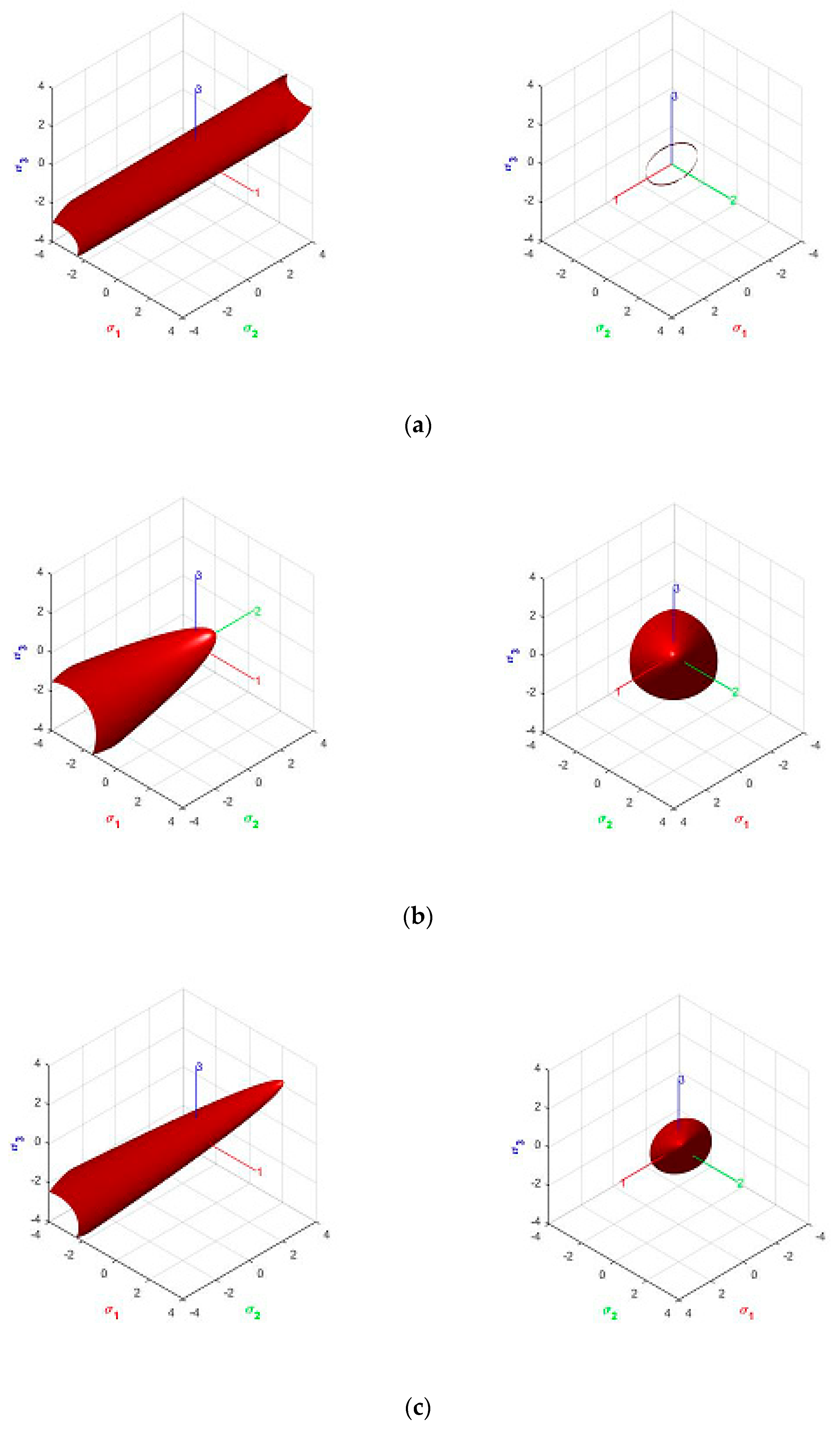
3.1. Orthotropic Cohesive–Frictional Plasticity
3.2. Orthotropic Plastic Flow
3.3. Strain Localization Angle
3.3.1. Plane Stress
3.3.2. Plane Strain
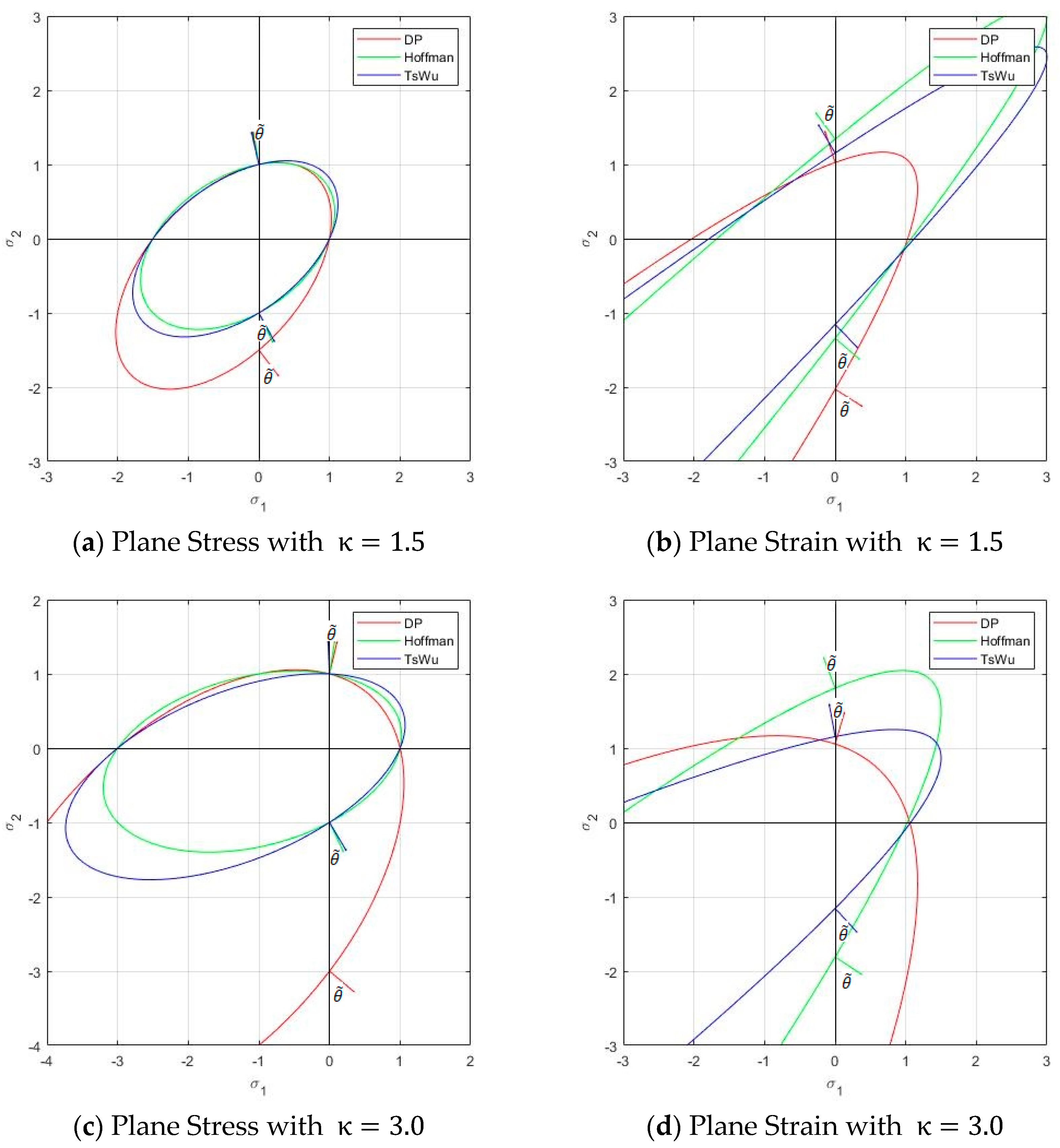
3.4. Geometrical Interpretation of the Strain Localization Angle in the Stress Space
3.5. Uniaxial Tension and Compression: Analytical Strain Localization Angles
3.5.1. Plane Stress
3.5.2. Plane Strain
4. Numerical Verification
4.1. B-Bar Finite Element
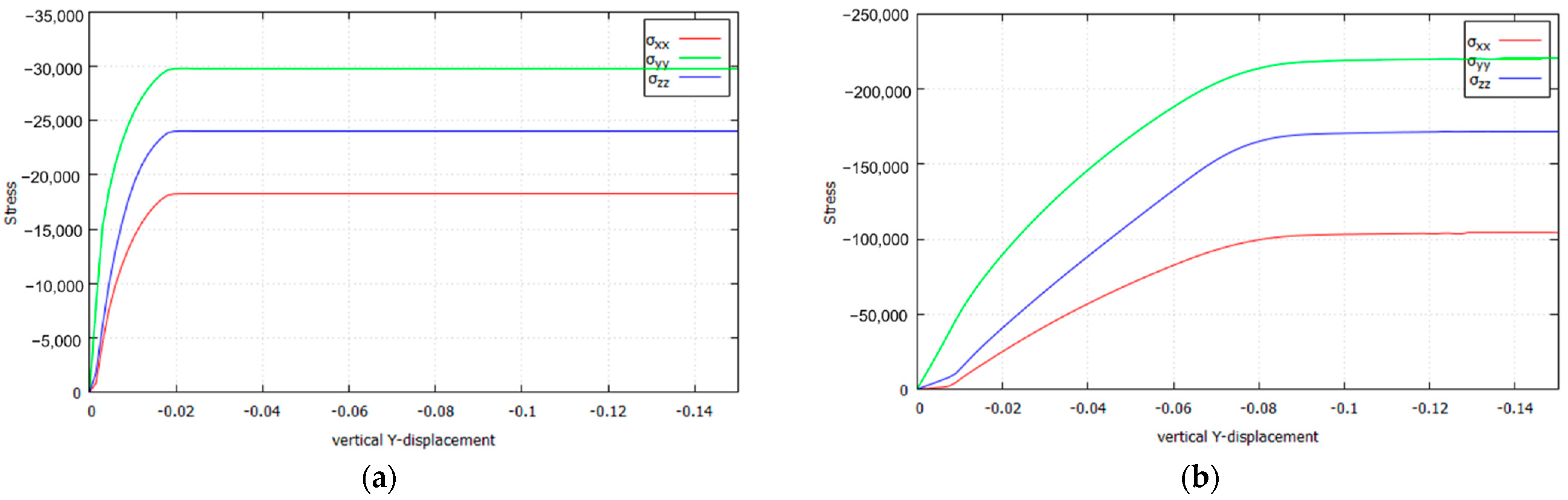
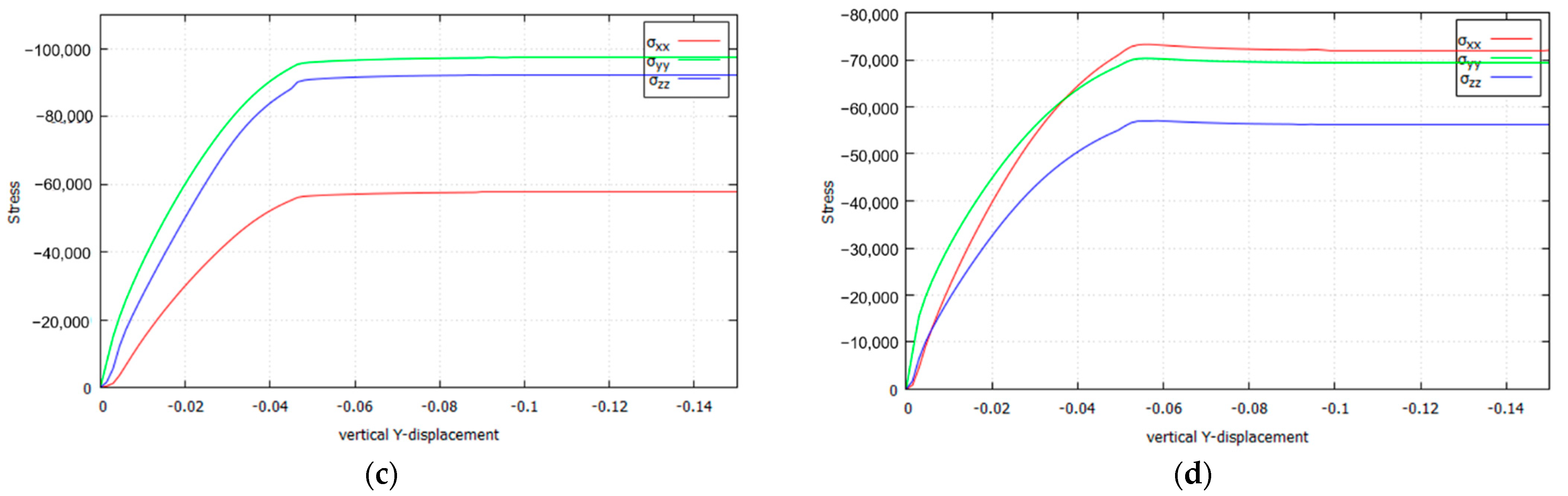
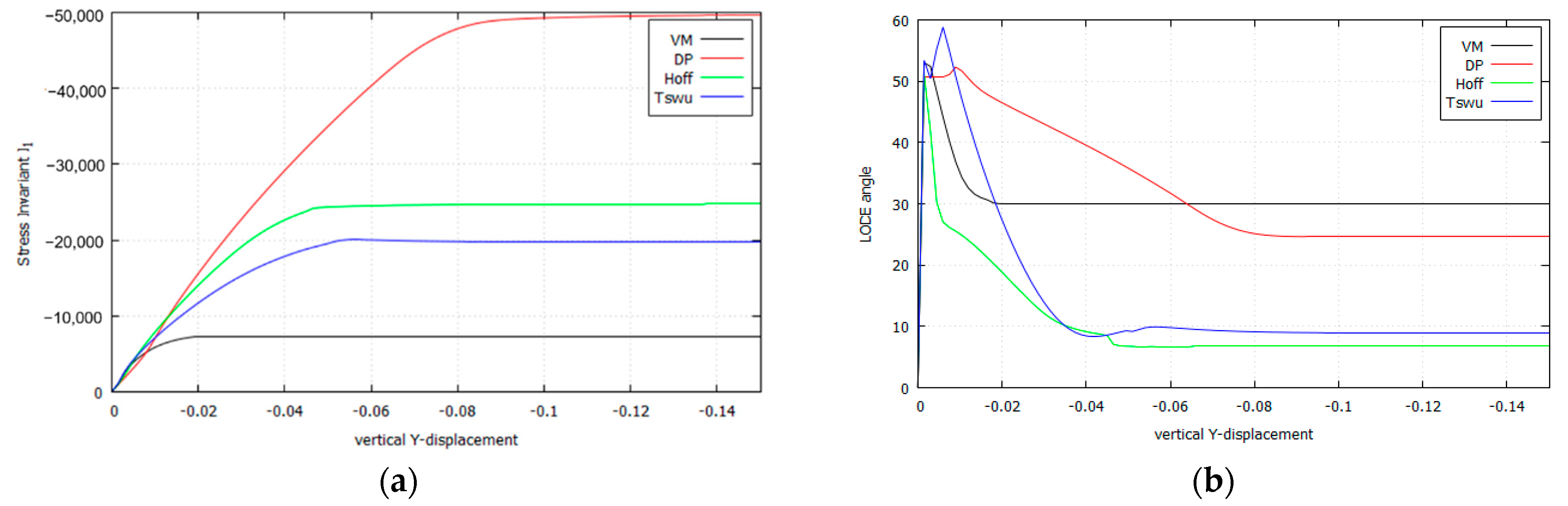
4.2. Uniaxial Tension and Compression: Numerical Verification
4.2.1. Isotropic Incompressible and Cohesive–Frictional Models
4.2.2. Isotropic and Orthotropic Cohesive–Frictional Models
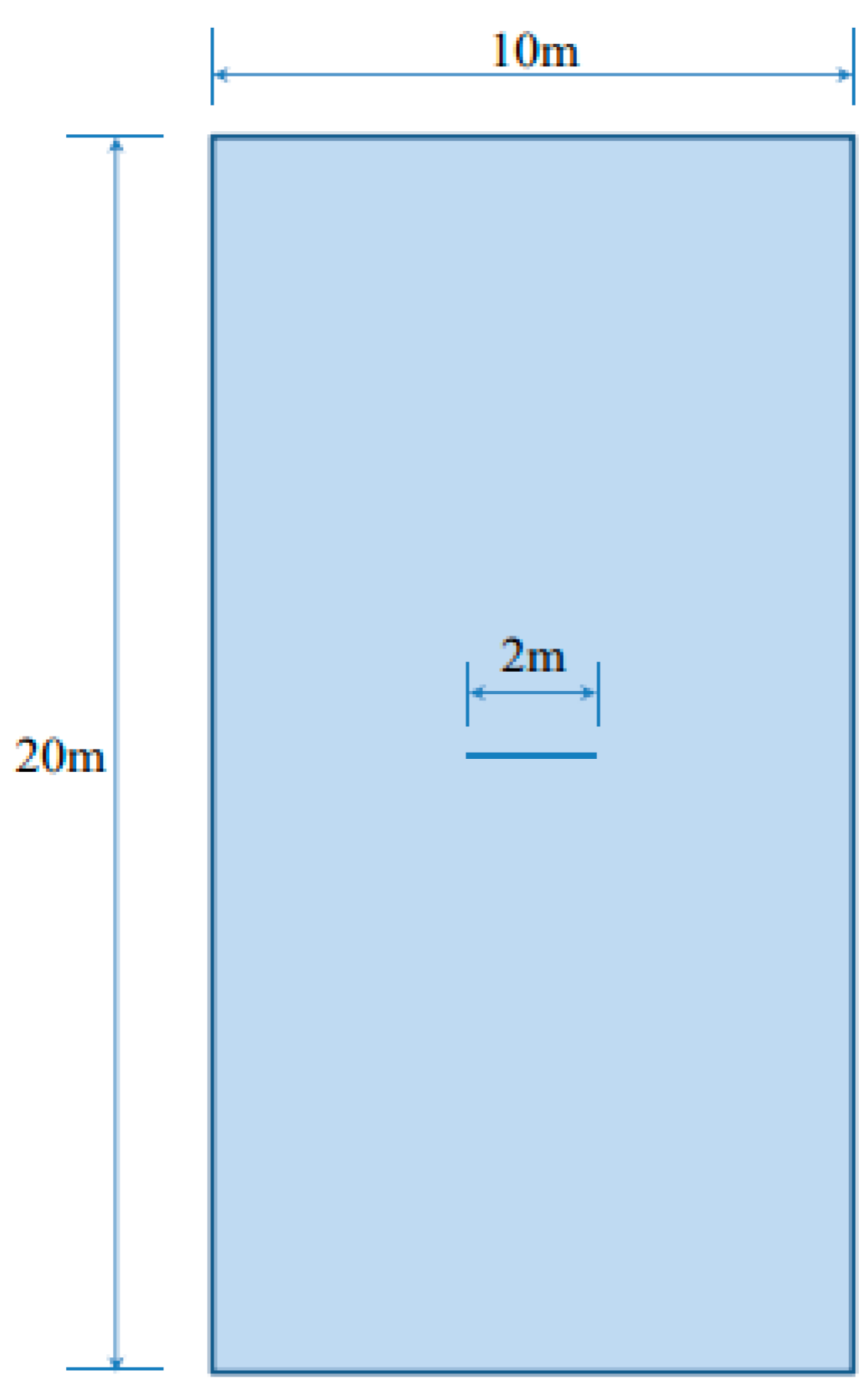
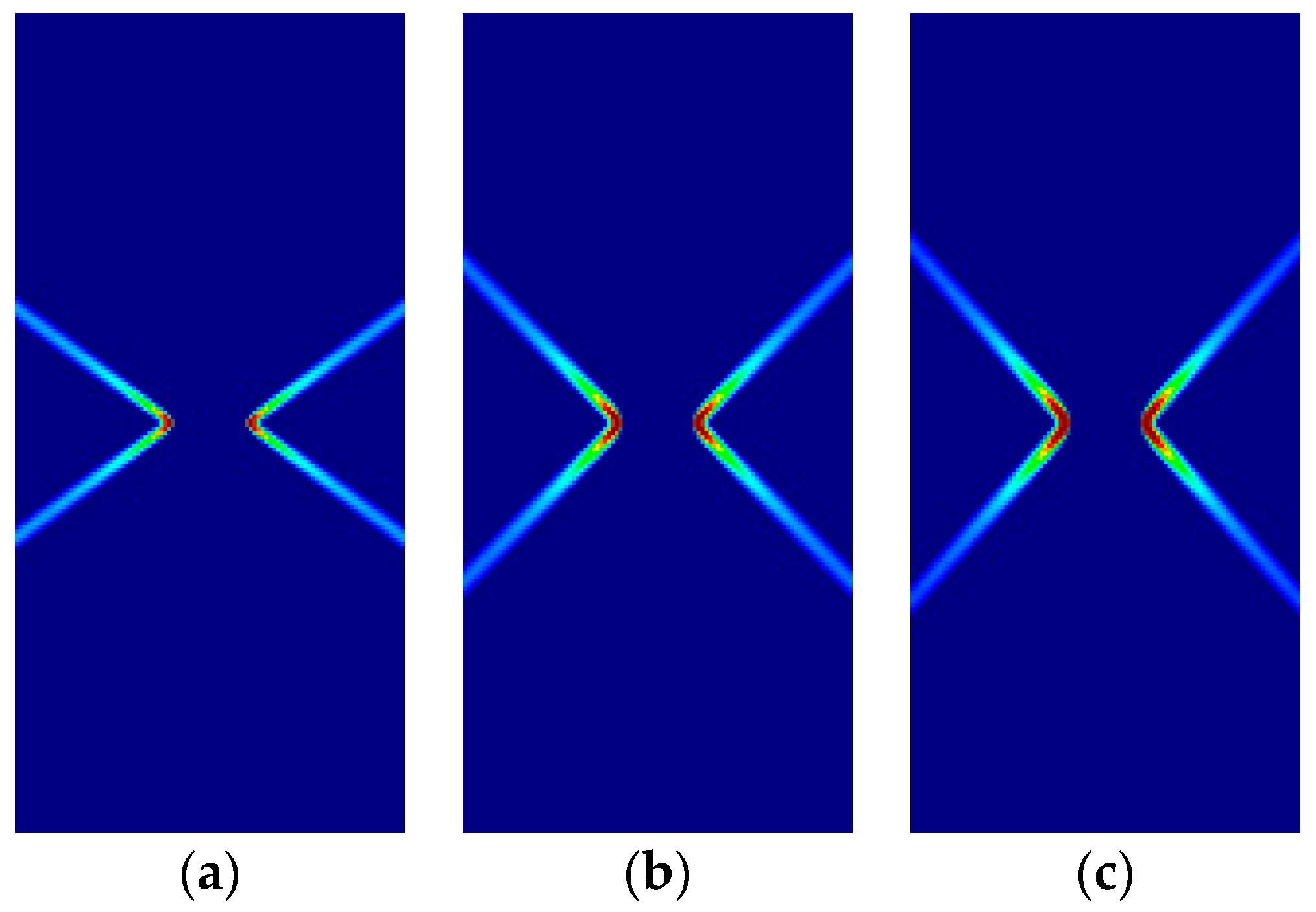
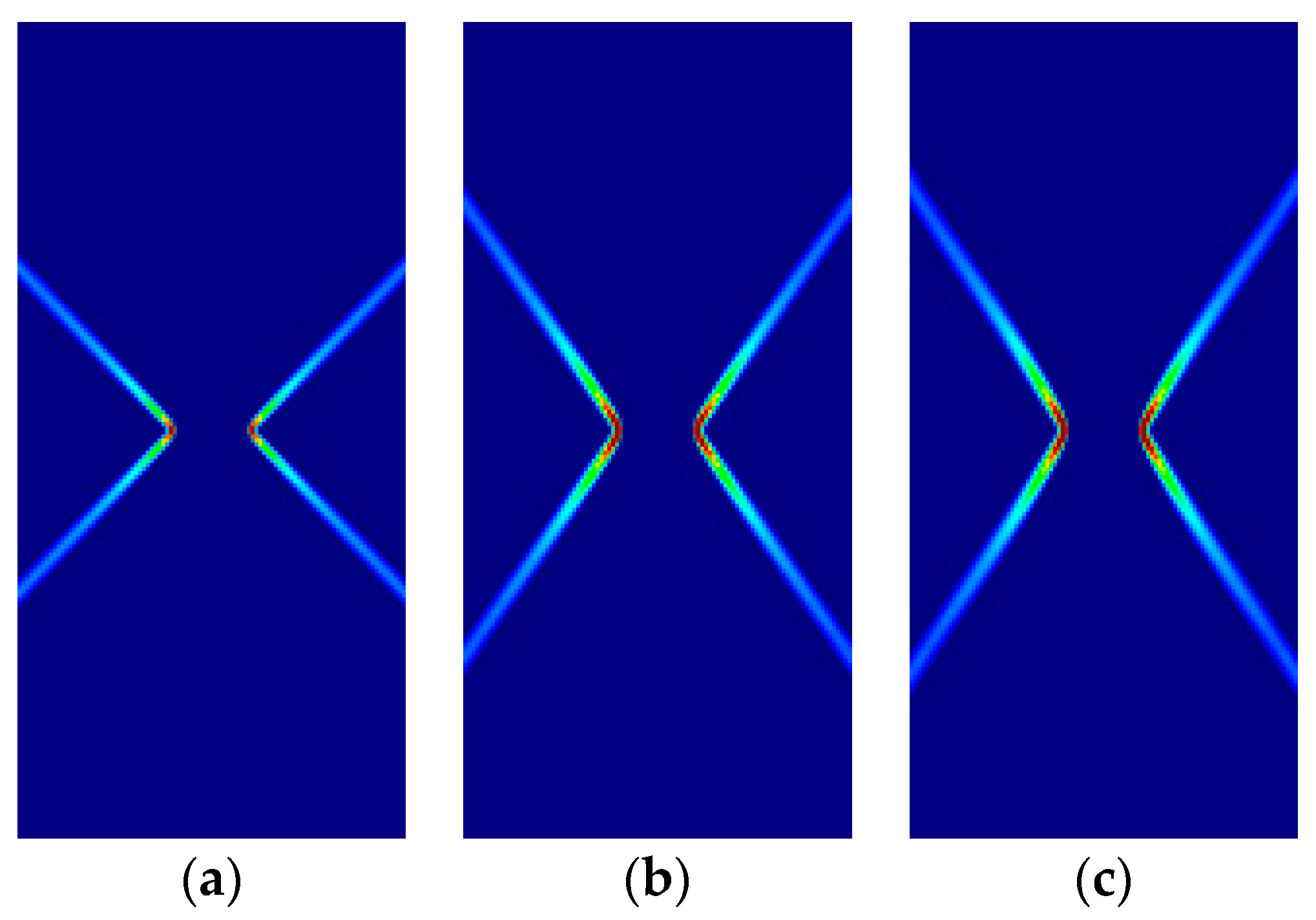
4.3. Prandtl’s Punch Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Stress Invariants and Lode Angle
Appendix B. Tilting of the Material Axes with Respect the Global Axes
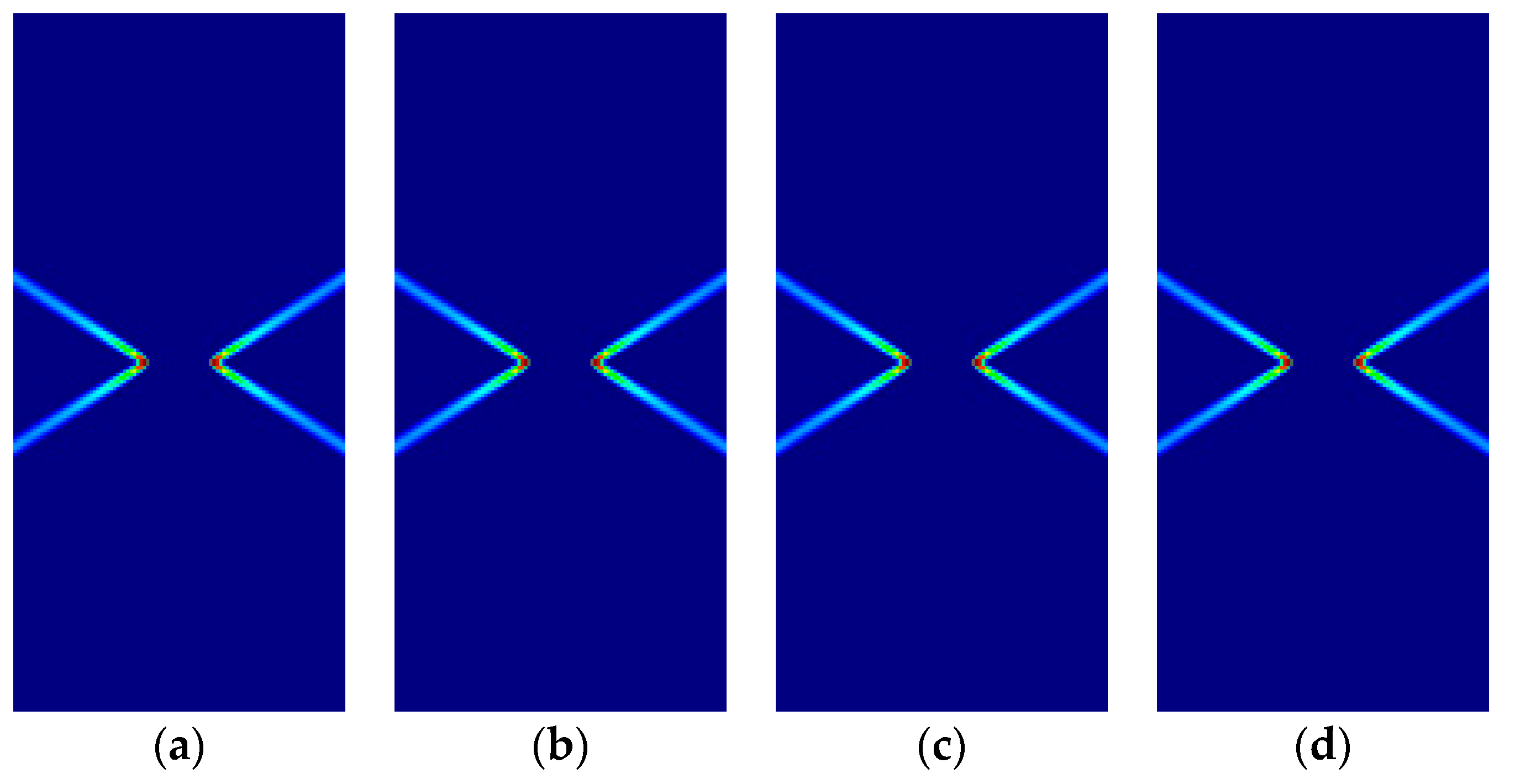
| 14.3077° | 15.9519° | 30.4411° | 31.4875° | |
| 14.3077° | 15.9519° | 30.4411° | 31.4875° | |
| 14.3077° | 15.9519° | 30.4411° | 31.4875° | |
| 14.3077° | 15.9519° | 30.4411° | 31.4875° |

| 40.8934° | 42.5043° | 41.3843°, 41.3843° | 41.5891°, 41.5891° | |
| 35.4964° | 35.5087° | 39.4100°, 43.0613° | 39.5226°, 43.1524° | |
| 30.0000° | 30.0031° | 37.4491°, 45.0000° | 37.7757°, 45.0000° | |
| 24.5036° | 24.8814° | 36.9016°, 45.7565° | 36.8699°, 45.7073° |

References
- Hill, R. Constitutive modelling of orthotropic plasticity in sheet metals. J. Mech. Phys. Solids 1990, 38, 405–417. [Google Scholar] [CrossRef]
- Hill, R. A user-friendly theory of orthotropic plasticity in sheet metals. J. Mech. Phys. Solids 1993, 35, 19–25. [Google Scholar] [CrossRef]
- Hill, R. On the mechanics of localized necking in anisotropic sheet metals. J. Mech. Phys. Solids 2001, 49, 2055–2070. [Google Scholar] [CrossRef]
- Drucker, D.C.; Prager, W.; Greenberg, H. Extended limit design theorems for continuous media. Q. Appl. Math. 1952, 9, 381–389. [Google Scholar] [CrossRef]
- Drucker, D.C.; Prager, W. Soil Mechanics and Plastic Analysis on Limit Design. J. Appl. Math. 1952, 10, 157–165. [Google Scholar] [CrossRef]
- Drucker, D.C. Limit analysis of two and three dimensional soil mechanics problems. J. Mech. Phys. Solids 1953, 1, 217–226. [Google Scholar] [CrossRef]
- Drucker, D.C.; Gibson, R.E.; Henkel, D.J. Soil Mechanics and Work-Hardening Theories of Plasticity. Trans. Am. Soc. Civ. Eng. 1957, 122, 338–346. [Google Scholar] [CrossRef]
- Hoffman, O. The Brittle Strength of Orthotropic Materials. J. Compos. Mater. 1967, 1, 200–206. [Google Scholar] [CrossRef]
- Tsai, S.W.; Wu, E.M. A General Theory of Strength for Anisotropic Materials. J. Compos. Mater. 1971, 5, 58–80. [Google Scholar] [CrossRef]
- Karafillis, A.P.; Boyce, M.C. A general anisotropic yield criterion using bounds and a transformation weighting tensor. J. Mech. Phys. Solids 1993, 41, 1859–1886. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Fleck, N.A.; Ashby, M.F. Effective properties of the octet-truss lattice material. J. Mech. Phys. Solids 2001, 49, 1747–1769. [Google Scholar] [CrossRef]
- Cazacu, O.; Plunkett, B.; Barlat, F. Orthotropic yield criterion for hexagonal closed packed metals. Int. J. Plast. 2001, 22, 1171–1194. [Google Scholar] [CrossRef]
- Gdoutos, E.; Abot, J.L. Indentation of a PVC Cellular Foam. Recent Adv. Exp. Mech. 2002, 55–64. [Google Scholar] [CrossRef]
- Gdoutos, E.; Daniel, I.; Wang, K.-A. Failure of cellular foams under multiaxial loading. Compos. Part A Appl. Sci. Manuf. 2002, 33, 163–176. [Google Scholar] [CrossRef]
- Qiao, Y.; Bisagni, C.; Bai, Y. Experimental investigation and numerical simulation of unidirectional carbon fiber composite under multi-axial loadings. Compos. Part B Eng. 2017, 124, 190–206. [Google Scholar] [CrossRef]
- Zhong, C. Pressure Chamber Experiments to Determine Triaxial Material Properties of Polymer Foams. Ph.D. Thesis, University of Akron, Akron, OH, USA, 2019. [Google Scholar]
- Galavi, V.; Schweiger, H.F. Nonlocal Multilaminate Model for Strain Softening Analysis. Int. J. Geomech. 2010, 10, 30–44. [Google Scholar] [CrossRef]
- Prandtl, L. Über die Härte plastischer Körper. Nachr. Ges. Wiss. Zu Göttingen Math. Phys. Kl. 1920, 74–85. (In German) [Google Scholar] [CrossRef]
- Hencky, H. Über Einige Statisch Bestimmte Fälle Des Gleichgewichts in Plastischen Körpern. Z. Angew. Math. Mech. 1923, 3, 241–251. [Google Scholar] [CrossRef]
- Hencky, H. Zur Theorie plastischer Deformationen und der hierdurch im Material hervorgerufenen Nachspannungen. Z. Für Angew. Math. Und Mech. 1924, 4, 323–334. [Google Scholar] [CrossRef]
- Mandel, J. Sur Les Équilibres Par Tranches Planes Des Corps Solides à La Limite D’écoulement. Thèses de Docteur Ès-sciences, Université De Lyon, Lyon, France. Available online: http://www.numdam.org/issue/THESE_1942__251__1_0.pdf (accessed on 16 April 2021). (In French).
- Hill, R. A general theory of uniqueness and stability in elastic-plastic solids. J. Mech. Phys. Solids 1958, 6, 236–249. [Google Scholar] [CrossRef]
- Hill, R. Acceleration waves in solids. J. Mech. Phys. Solids 1962, 10, 1–16. [Google Scholar] [CrossRef]
- Thomas, T.Y. Plastic Flow and Fracture of Solids; Academic Press: New York, NY, USA, 1961. [Google Scholar]
- Rice, J.R. A path independent integral and the approximate analysis of strain concentration by notches and cracks. J. Appl. Mech. 1968, 35, 379–386. [Google Scholar] [CrossRef]
- Rice, J.R. Plane strain slip line theory for anisotropic rigid/plastic materials. J. Mech. Phys. Solids 1973, 21, 63–74. [Google Scholar] [CrossRef]
- Rudnicki, J.W.; Rice, J.R. Conditions for the localization of deformation in pressure-sensitive dilatant materials. J. Mech. Phys. Solids 1975, 23, 371–394. [Google Scholar] [CrossRef]
- Pietruszczak, S.; Mróz, Z. Finite element analysis of deformation of strain-softening materials. Int. J. Numer. Methods Eng. 1981, 17, 327–334. [Google Scholar] [CrossRef]
- Neilsen, M.K.; Schreyer, H.L. Bifurcations in elastic-plastic materials. Int. J. Solids Struct. 1993, 30, 521–544. [Google Scholar] [CrossRef]
- Leroy, Y.; Ortiz, M. Finite element analysis of transient strain localization phenomena in frictional solids. Int. J. Numer. Anal. Methods Geomech. 1990, 14, 93–124. [Google Scholar] [CrossRef]
- Forest, S.; Blazy, J.-S.; Chastel, Y.; Moussy, F. Continuum modeling of strain localization phenomena in metallic foams. J. Mater. Sci. 2005, 40, 5903–5910. [Google Scholar] [CrossRef]
- Borja, R.I. A finite element model for strain localization analysis of strongly discontinuous fields based on standard Galerkin approximation. Comput. Methods Appl. Mech. Eng. 2000, 190, 1529–1549. [Google Scholar] [CrossRef]
- Borja, R.I. Finite element simulation of strain localization with large deformation: Capturing strong discontinuity using a Petrov–Galerkin multiscale formulation. Comput. Methods Appl. Mech. Eng. 2002, 191, 2949–2978. [Google Scholar] [CrossRef][Green Version]
- Kuhl, E.; Ramm, E.; Willam, K. Failure analysis of elasto-plastic material models on different levels of observation. Int. J. Solids Struct. 2000, 37, 7259–7280. [Google Scholar] [CrossRef]
- Liebe, T.; Willam, K. Localization Properties of Generalized Drucker-Prager Elastoplasticity. J. Eng. Mech. 2001, 127, 616–619. [Google Scholar] [CrossRef]
- Vrech, S.M.; Etse, G. Geometrical localization analysis of gradient-dependent parabolic Drucker–Prager elastoplasticity. Int. J. Plast. 2006, 22, 943–964. [Google Scholar] [CrossRef]
- Zhang, Y.Q.; Lu, Y.; Qiang, H.F. Influence of damage on properties of strain localization in geomaterials at plane stress and plane strain. Arch. Appl. Mech. 2004, 74, 102–117. [Google Scholar] [CrossRef]
- Tasan, C.C.; Hoefnagels, J.P.M.; Diehl, M.; Yan, D.; Roters, F.; Raabe, D. Strain localization and damage in dual phase steels investigated by coupled in-situ deformation experiments and crystal plasticity simulations. Int. J. Plast. 2014, 63, 198–210. [Google Scholar] [CrossRef]
- Simo, J.C.; Oliver, J.; Armero, F. An analysis of strong discontinuities induced by strain-softening in rate-independent inelastic solids. Comput. Mech. 1993, 12, 277–296. [Google Scholar] [CrossRef]
- Oliver, J. Modelling strong discontinuities in solid mechanics via strain softening constitutive equations. Part 1: Fundamentals. Int. J. Numer. Methods Eng. 1996, 39, 3575–3600. [Google Scholar] [CrossRef]
- Oliver, J. Modelling strong discontinuities in solid mechanics via strain softening constitutive equations. Part 2: Numerical simulation. Int. J. Numer. Methods Eng. 1996, 39, 3601–3623. [Google Scholar] [CrossRef]
- Oliver, J.; Cervera, M.; Manzoli, O. Strong discontinuities and continuum plasticity models: The strong discontinuity approach. Int. J. Plast. 1999, 15, 319–351. [Google Scholar] [CrossRef]
- Oliver, J. On the discrete constitutive models induced by strong discontinuity kinematics and continuum constitutive equations. Int. J. Solids Struct. 2000, 37, 7207–7229. [Google Scholar] [CrossRef]
- Cervera, M.; Chiumenti, M.; Capua, D.D. Benchmarking on bifurcation and localization in J2 plasticity for plane stress and plane strain conditions. Comput. Methods Appl. Mech. Eng. 2012, 241–244, 206–224. [Google Scholar] [CrossRef]
- Cervera, M.; Wu, J.Y.; Chiumenti, M.; Kim, S. Strain localization analysis of Hill’s orthotropic elastoplasticity: Analytical results and numerical verification. Comput. Mech. 2020, 65, 533–554. [Google Scholar] [CrossRef]
- Wu, J.Y.; Cervera, M. On the equivalence between traction- and stress-based approaches for the modeling of localized failure in solids. J. Mech. Phys. Solids 2015, 82, 137–163. [Google Scholar] [CrossRef]
- Wu, J.Y.; Cervera, M. A thermodynamically consistent plastic-damage framework for localized failure in quasi-brittle solids: Material model and strain localization analysis. Int. J. Solids Struct. 2016, 88–89. [Google Scholar] [CrossRef]
- Wu, J.Y.; Cervera, M. Strain Localization of Elastic-Damaging Frictional-Cohesive Materials: Analytical Results and Numerical Verification. Materials 2017, 10, 434. [Google Scholar] [CrossRef]
- Hughes, T.J.R. Generalization of selective integration procedures to anisotropic and nonlinear media. Int. J. Numer. Methods Eng. 1980, 15, 1413–1418. [Google Scholar] [CrossRef]




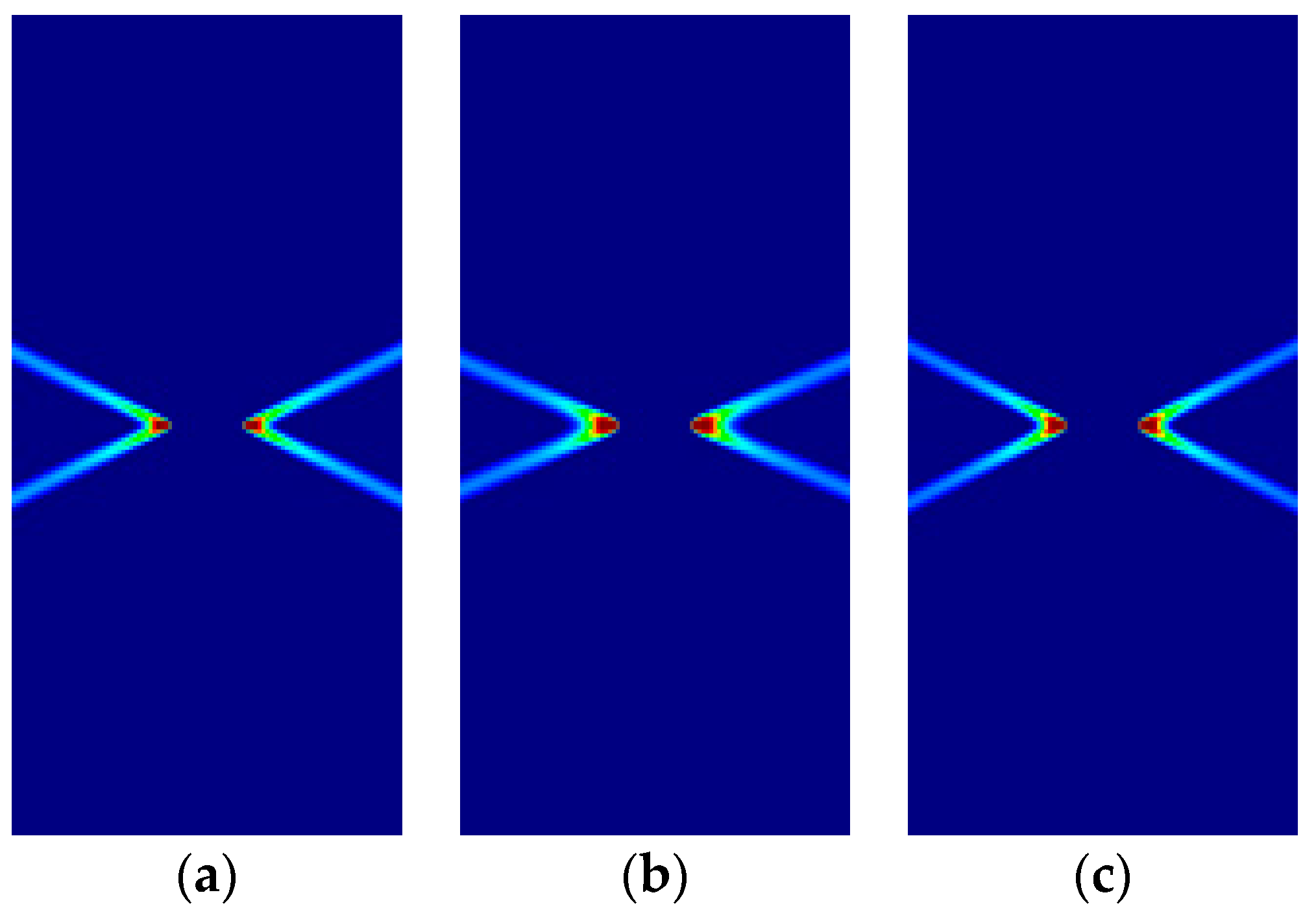
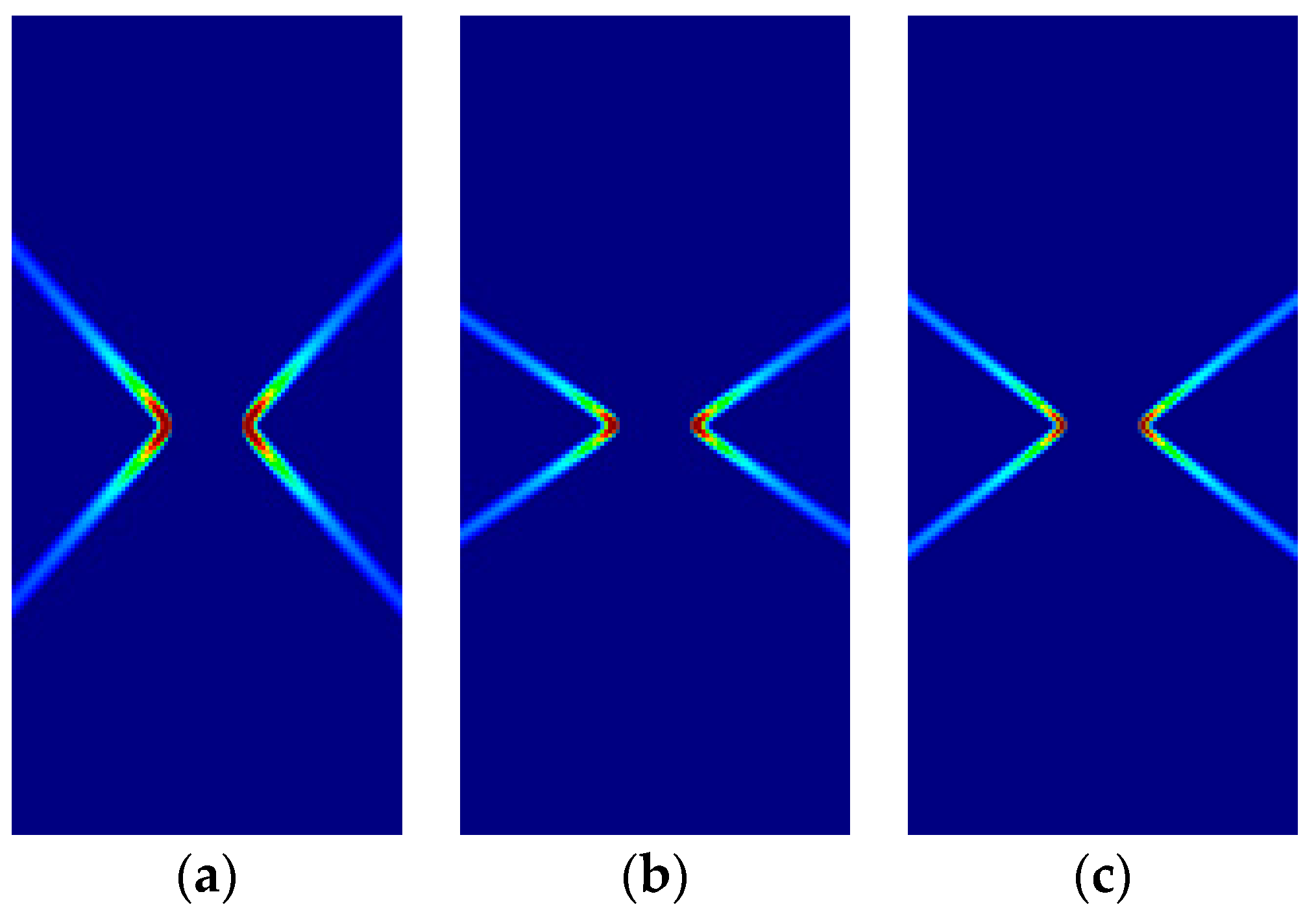
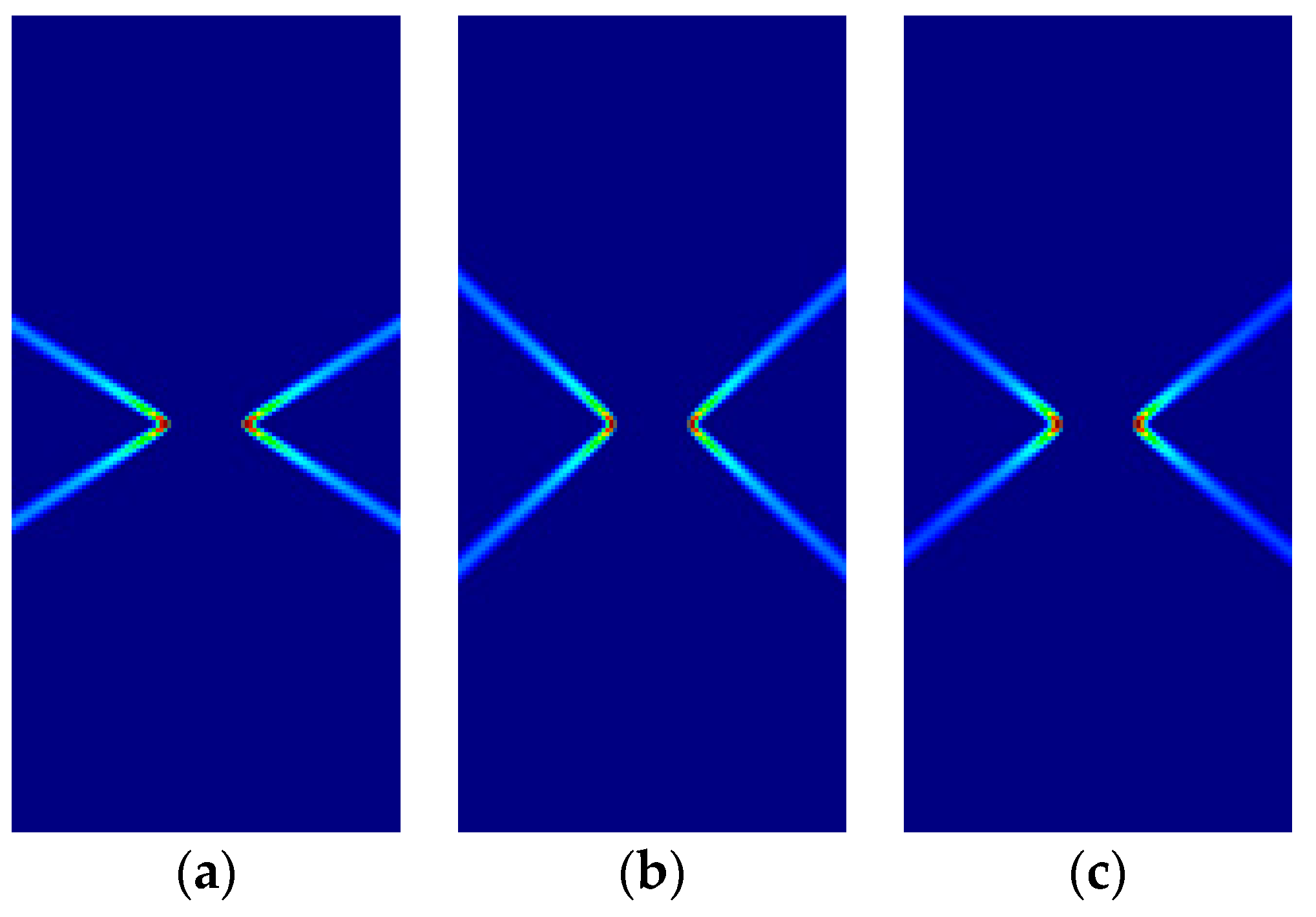
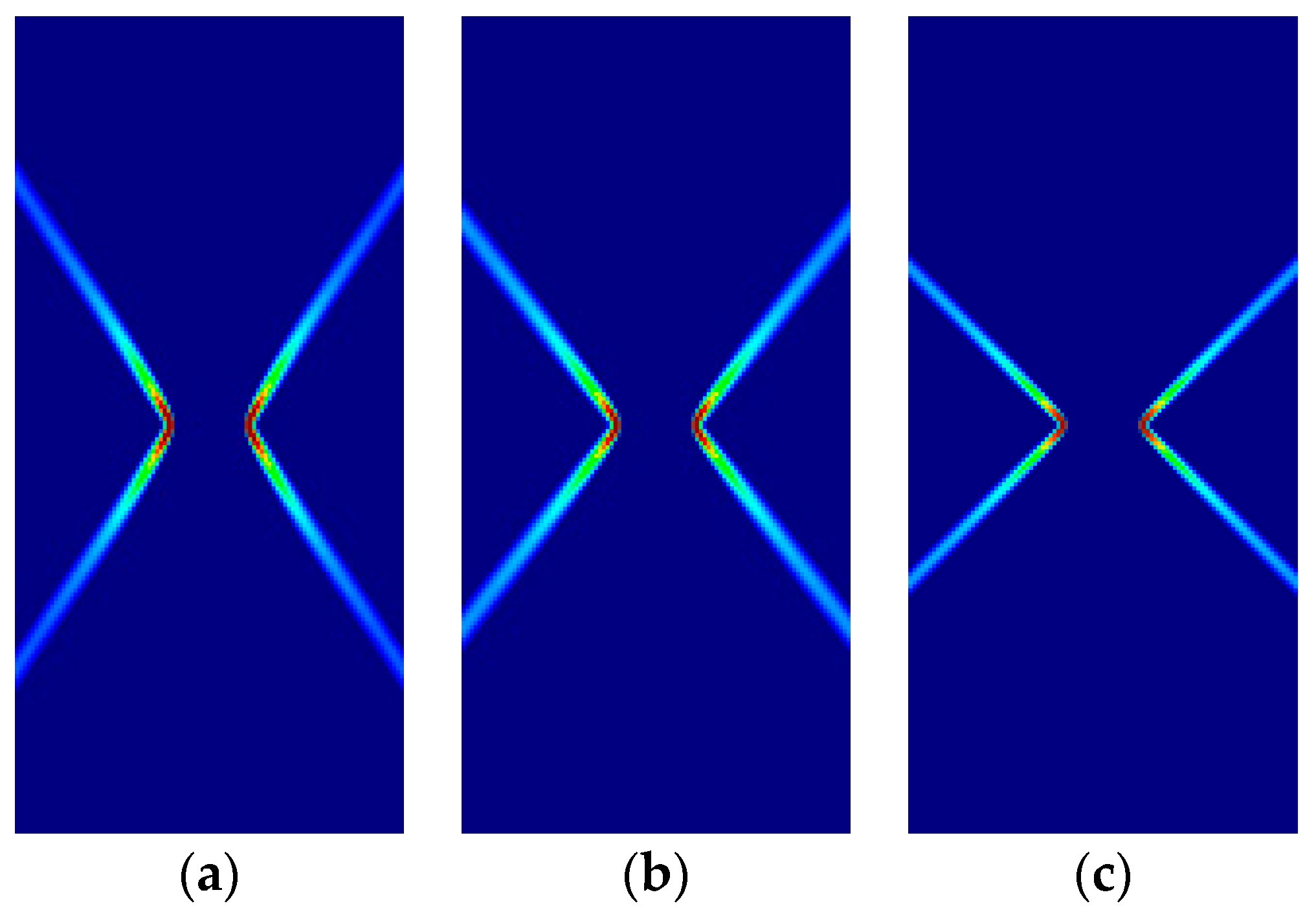



| DP | 1/3 | 1/3 | 1/3 | F | G | H | 1/3 | 1/3 | 1/3 |
| Hoffman | 1/3 | 1/3 | 2/3 | F | G | H | 1/3 | 0 | 0 |
| Tsai–Wu | 1/3 | 1/3 | 2/3 | 0.5 | 1/3 | 0 | 0 |
| Tension | Compression | |||||
|---|---|---|---|---|---|---|
| DP | 1.0000 | 0.0000 | 1.0000 | 0.0000 | ||
| Hoffman | 1.0000 | 0.0000 | ±22.2077° | 1.0000 | 0.0000 | |
| Tsai–Wu | 1.0000 | 0.0000 | 1.0000 | 0.0000 | ||
| Tension | Compression | |||||
|---|---|---|---|---|---|---|
| DP | 1.0275 | 0.2638 | 2.0275 | 1.2638 | ||
| Hoffman | 1.3416 | 0.8944 | 1.3416 | 0.8944 | ||
| Tsai–Wu | 1.1547 | 0.5774 | 1.1547 | 0.5774 | ||
| VM 1.0 | 0.0000° | 0.6459° | 35.2644° | 35.4699° |
| DP 1.25 | 0.0000° | 0.3803° | 30.0000° | 30.4342° |
| DP 1.5 | 0.0000° | 0.7800° | 24.0948° | 24.2277° |
| VM 1.0 | 60.0000° | 59.3541° | 35.2644° | 35.4699° |
| DP 2.0 | 60.0000° | 59.6989° | 45.0000° | 45.0000° |
| DP 3.0 | 60.0000° | 59.6006° | 48.1897° | 48.8141° |
| VM 1.0 | 30.0000° | 30.1669° | 45.0000° | 45.0000° |
| DP 1.25 | 22.3378° | 23.6244° | 38.2626° | 39.0939° |
| DP 1.5 | 14.3077° | 15.9519° | 30.4411° | 31.4875° |
| VM 1.0 | 30.0000° | 30.1669° | 45.0000° | 45.0000° |
| DP 2.0 | 19.1066° | 19.6359° | 54.7356° | 54.2934° |
| DP 3.0 | 17.1330° | 17.6788° | 56.6531° | 57.5289° |
| Drucker–Prager | 0.0000° | 0.7800° | 24.0948° | 24.2277° |
| Hoffman | 0.0000° | 0.5258° | 22.2077° | 22.1355° |
| Tsai–Wu | 0.0000° | 0.3457° | 26.1746° | 26.5651° |
| Drucker–Prager | 60.0000° | 59.6006° | 48.1897° | 48.8141° |
| Hoffman | 60.0000° | 58.6061° | 35.2644° | 35.4699° |
| Tsai–Wu | 60.0000° | 59.8503° | 38.2620° | 37.7757° |
| Drucker–Prager | 14.3077° | 15.9519° | 30.4411° | 31.4875° |
| Hoffman | 40.8934° | 42.5043 | 41.3843° | 41.5891° |
| Tsai–Wu | 30.0000 ° | 30.7240° | 38.3075° | 38.2204° |
| Drucker–Prager | 17.1330° | 17.6788° | 56.6531° | 57.5288° |
| Hoffman | 8.9483° | 7.8626° | 51.6975° | 50.7106° |
| Tsai–Wu | 30.0000° | 29.4419° | 44.4488° | 44.6397° |
| VM | 18286 | 29832 | 24061 | 29.9902° | 45.0000° | 45.0000° |
| Drucker–Prager | 104260 | 220560 | 171920 | 24.6035° | 50.1944° | 49.9512° |
| Hoffman | 57783 | 97541 | 92394 | 6.8372° | 48.9909° | 48.4646° |
| Tsai–Wu | 72007 | 69365 | 56219 | 8.9246° | 41.1859° | 40.6354° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, S.; Cervera, M.; Wu, J.-Y.; Chiumenti, M. Strain Localization of Orthotropic Elasto–Plastic Cohesive–Frictional Materials: Analytical Results and Numerical Verification. Materials 2021, 14, 2040. https://doi.org/10.3390/ma14082040
Kim S, Cervera M, Wu J-Y, Chiumenti M. Strain Localization of Orthotropic Elasto–Plastic Cohesive–Frictional Materials: Analytical Results and Numerical Verification. Materials. 2021; 14(8):2040. https://doi.org/10.3390/ma14082040
Chicago/Turabian StyleKim, Sungchul, Miguel Cervera, Jian-Ying Wu, and Michele Chiumenti. 2021. "Strain Localization of Orthotropic Elasto–Plastic Cohesive–Frictional Materials: Analytical Results and Numerical Verification" Materials 14, no. 8: 2040. https://doi.org/10.3390/ma14082040
APA StyleKim, S., Cervera, M., Wu, J.-Y., & Chiumenti, M. (2021). Strain Localization of Orthotropic Elasto–Plastic Cohesive–Frictional Materials: Analytical Results and Numerical Verification. Materials, 14(8), 2040. https://doi.org/10.3390/ma14082040









