Does the Modification of the Apical Geometry of a Dental Implant Affect Its Primary Stability? A Comparative Ex Vivo Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Implant Design
- while in the J-line the cutting threads extended to the end of the implant, in the K-line they were shortened, resulting in an apical rounding,
- the cutting part of the implant was elongated cranially from J- to K-line and
- in the K-line, a shorter cylindrical portion was designed crestally with a beveling of the former taper there (Figure 1, changes highlighted in red).
2.2. Specimens
2.3. Surgery
2.4. Measurements
- Electromechanical measurement of implant stability using the Periotest® device over 4 s with n = 3 measurements per implant [29,30]. For this purpose, the abutments of the implants were inserted according to the manufacturer’s instructions. The Periotest® value scale ranges from −8 to +50, with smaller Periotest® values representing greater stability of the measured object. Mean values were used for the statistical evaluations.
- Bone resonance frequency measurement (RFA) using the Osstell® resonance frequency analyzer (Integration Diagnostics, Gothenburg, Sweden). For this purpose, the abutments were carefully removed, the corresponding transducers were mounted on the implants and the Ossell® device was positioned at a distance of 3 mm from the transducer. The recorded frequencies (n = 3 in vertical and in horizontal orientation per implant) were automatically converted into ISQ (implant stability coefficient) values in the range of 0–100 (minimum to maximum stability) [27,31]. Mean values were used for the statistical evaluations.
- After performing the aforementioned measurements, all implants were pushed out using a Zwick UPM (Universalprüfmaschine) materials testing machine (Zwick, Atlanta, GA, USA). For this purpose, axial compression forces (continuously 0.5 mm/min) were applied to the cranial end of each implant and the shear force to detach the implant from the bone was recorded in Newtons (N) [22]. Mean values were used for the statistical evaluations.
2.5. Statistics
3. Results
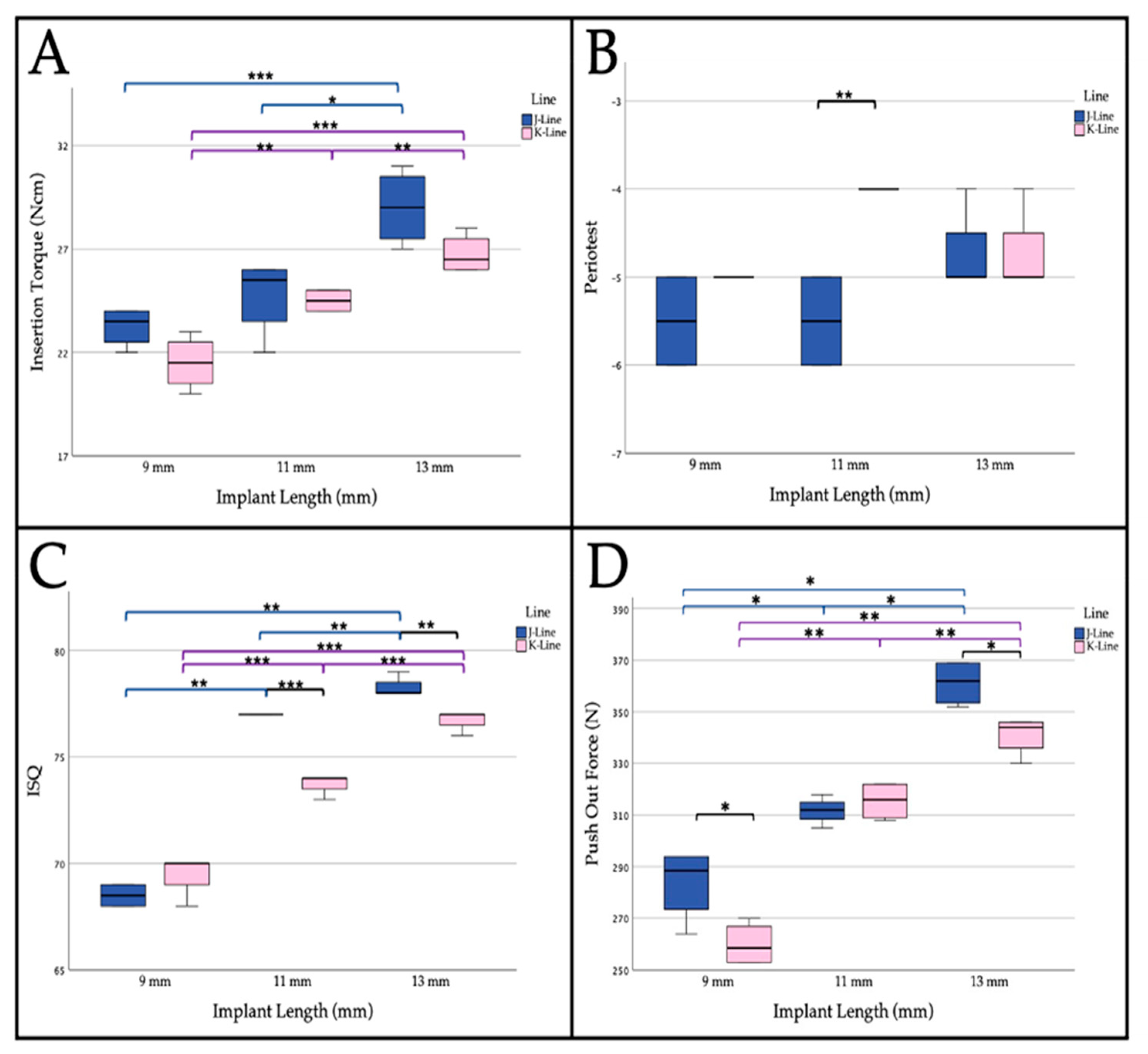
3.1. Part A
3.1.1. Insertion Torque
3.1.2. Periotest® Measurement
3.1.3. Resonance Frequency Analysis
3.1.4. Push-Out Force
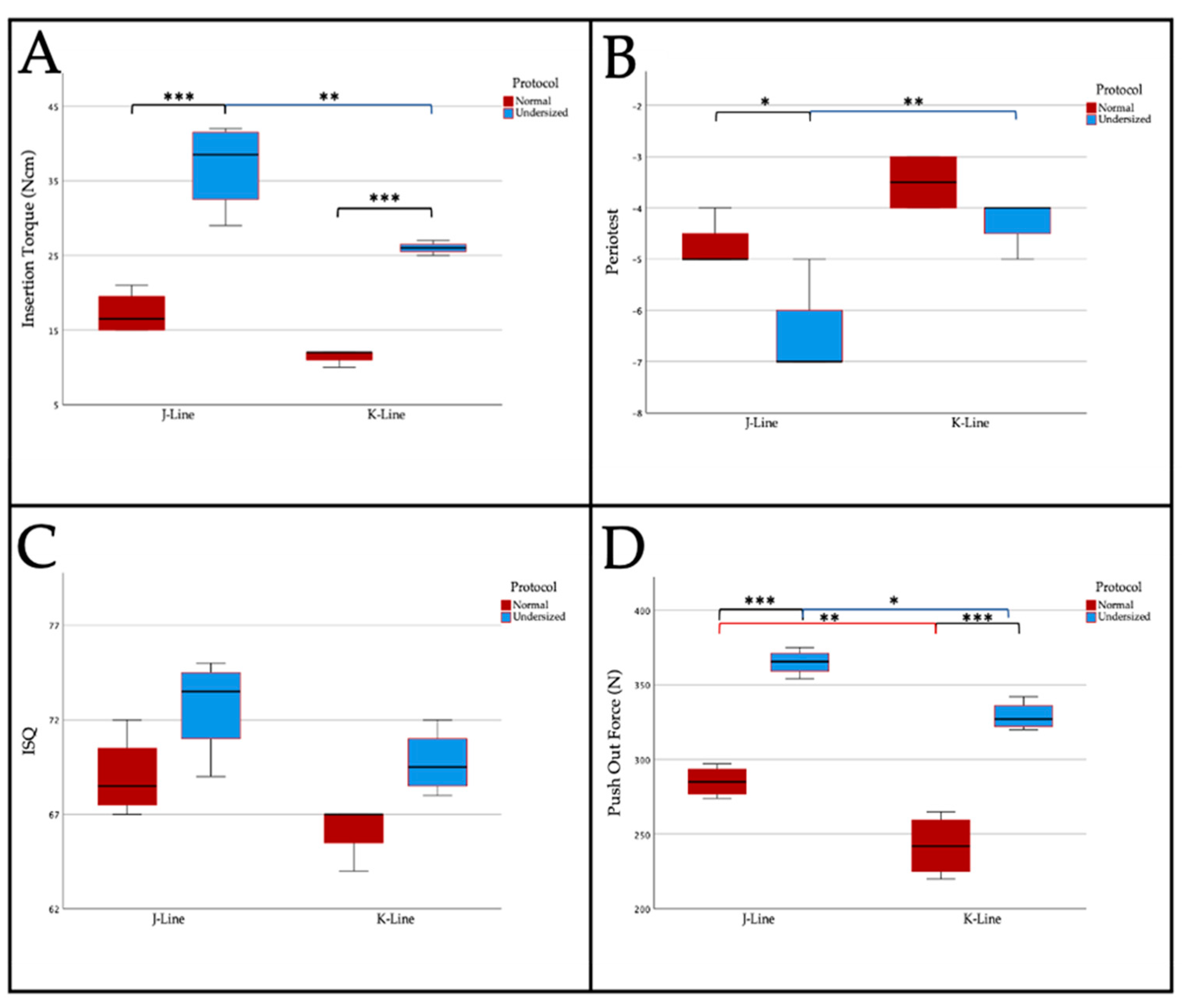
3.2. Part B
3.2.1. Insertion Torque
3.2.2. Periotest® Measurement
3.2.3. Resonance Frequency Analysis
3.2.4. Push-Out Force
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kleis, W.K.; Kämmerer, P.W.; Hartmann, S.; Al-Nawas, B.; Wagner, W. A comparison of three different attachment systems for mandibular two-implant overdentures: One-year report. Clin. Implant Dent. Relat. Res. 2010, 12, 209–218. [Google Scholar] [CrossRef] [PubMed]
- Schiegnitz, E.; Kämmerer, P.W.; Sagheb, K.; Wendt, A.J.; Pabst, A.; Al-Nawas, B.; Klein, M.O. Impact of maxillary sinus augmentation on oral health-related quality of life. Int. J. Implant Dent. 2017, 3, 10. [Google Scholar] [CrossRef] [PubMed]
- Al-Sabbagh, M.; Eldomiaty, W.; Khabbaz, Y. Can Osseointegration Be Achieved Without Primary Stability? Dent. Clin. N. Am. 2019, 63, 461–473. [Google Scholar] [CrossRef]
- Quesada-Garcia, M.P.; Prados-Sanchez, E.; Olmedo-Gaya, M.V.; Munoz-Soto, E.; Gonzalez-Rodriguez, M.P.; Valllecillo-Capilla, M. Measurement of dental implant stability by resonance frequency analysis: A review of the literature. Med. Oral Patol. Oral Cir. Bucal 2009, 14, e538–e546. [Google Scholar] [CrossRef]
- Staedt, H.; Palarie, V.; Staedt, A.; Wolf, J.M.; Lehmann, K.M.; Ottl, P.; Kämmerer, P.W. Primary Stability of Cylindrical and Conical Dental Implants in Relation to Insertion Torque-A Comparative Ex Vivo Evaluation. Implant Dent. 2017, 26, 250–255. [Google Scholar] [CrossRef]
- Lekholm, U. Surgical considerations and possible shortcomings of host sites. J. Prosthet. Dent. 1998, 79, 43–48. [Google Scholar] [CrossRef]
- Chavarri-Prado, D.; Brizuela-Velasco, A.; Dieguez-Pereira, M.; Perez-Pevida, E.; Jimenez-Garrudo, A.; Viteri-Agustin, I.; Estrada-Martinez, A.; Montalban-Vadillo, O. Influence of cortical bone and implant design in the primary stability of dental implants measured by two different devices of resonance frequency analysis: An in vitro study. J. Clin. Exp. Dent. 2020, 12, e242–e248. [Google Scholar] [CrossRef]
- Karl, M.; Grobecker-Karl, T. Effect of bone quality, implant design, and surgical technique on primary implant stability. Quintessence Int. 2018, 189–198. [Google Scholar] [CrossRef]
- Staedt, H.; Rossa, M.; Lehmann, K.M.; Al-Nawas, B.; Kammerer, P.W.; Heimes, D. Potential risk factors for early and late dental implant failure: A retrospective clinical study on 9080 implants. Int. J. Implant Dent. 2020, 6, 81. [Google Scholar] [CrossRef]
- Barbera-Millan, J.; Larrazabal-Moron, C.; Enciso-Ripoll, J.J.; Perez-Pevida, E.; Chavarri-Prado, D.; Gomez-Adrian, M.D. Evaluation of the primary stability in dental implants placed in low density bone with a new drilling technique, Osseodensification: An in vitro study. Med. Oral Patol. Oral Cir. Bucal 2020. [Google Scholar] [CrossRef]
- Lemos, B.F.; Lopez-Jarana, P.; Falcao, C.; Rios-Carrasco, B.; Gil, J.; Rios-Santos, J.V.; Herrero-Climent, M. Effects of Different Undersizing Site Preparations on Implant Stability. Int. J. Environ. Res. Public Health 2020, 17, 8965. [Google Scholar] [CrossRef]
- Campos, F.E.; Jimbo, R.; Bonfante, E.A.; Barbosa, D.Z.; Oliveira, M.T.; Janal, M.N.; Coelho, P.G. Are insertion torque and early osseointegration proportional? A histologic evaluation. Clin. Oral Implant. Res. 2015, 26, 1256–1260. [Google Scholar] [CrossRef] [PubMed]
- Raaj, G.; Manimaran, P.; Kumar, C.D.; Sadan, D.S.; Abirami, M. Comparative Evaluation of Implant Designs: Influence of Diameter, Length, and Taper on Stress and Strain in the Mandibular Segment-A Three-Dimensional Finite Element Analysis. J. Pharm. Bioallied. Sci. 2019, 11, S347–S354. [Google Scholar] [CrossRef] [PubMed]
- Abuhussein, H.; Pagni, G.; Rebaudi, A.; Wang, H.L. The effect of thread pattern upon implant osseointegration. Clin. Oral Implant. Res. 2010, 21, 129–136. [Google Scholar] [CrossRef]
- Lee, S.Y.; Kim, S.J.; An, H.W.; Kim, H.S.; Ha, D.G.; Ryo, K.H.; Park, K.B. The effect of the thread depth on the mechanical properties of the dental implant. J. Adv. Prosthodont. 2015, 7, 115–121. [Google Scholar] [CrossRef] [PubMed]
- Yamaguchi, Y.; Shiota, M.; Fujii, M.; Shimogishi, M.; Munakata, M. Effects of implant thread design on primary stability-a comparison between single- and double-threaded implants in an artificial bone model. Int. J. Implant Dent. 2020, 6, 42. [Google Scholar] [CrossRef] [PubMed]
- Makary, C.; Menhall, A.; Zammarie, C.; Lombardi, T.; Lee, S.Y.; Stacchi, C.; Park, K.B. Primary Stability Optimization by Using Fixtures with Different Thread Depth According To Bone Density: A Clinical Prospective Study on Early Loaded Implants. Materials 2019, 12, 2398. [Google Scholar] [CrossRef]
- Lan, T.H.; Du, J.K.; Pan, C.Y.; Lee, H.E.; Chung, W.H. Biomechanical analysis of alveolar bone stress around implants with different thread designs and pitches in the mandibular molar area. Clin. Oral Investig. 2012, 16, 363–369. [Google Scholar] [CrossRef] [PubMed]
- McCullough, J.J.; Klokkevold, P.R. The effect of implant macro-thread design on implant stability in the early post-operative period: A randomized, controlled pilot study. Clin. Oral Implant. Res. 2017, 28, 1218–1226. [Google Scholar] [CrossRef]
- Menini, M.; Bagnasco, F.; Calimodio, I.; Di Tullio, N.; Delucchi, F.; Baldi, D.; Pera, F. Influence of Implant Thread Morphology on Primary Stability: A Prospective Clinical Study. Biomed. Res. Int. 2020, 2020, 6974050. [Google Scholar] [CrossRef]
- Santamaria-Arrieta, G.; Brizuela-Velasco, A.; Fernandez-Gonzalez, F.J.; Chavarri-Prado, D.; Chento-Valiente, Y.; Solaberrieta, E.; Dieguez-Pereira, M.; Vega, J.A.; Yurrebaso-Asua, J. Biomechanical evaluation of oversized drilling technique on primary implant stability measured by insertion torque and resonance frequency analysis. J. Clin. Exp. Dent. 2016, 8, e307–e311. [Google Scholar] [CrossRef] [PubMed]
- Toyoshima, T.; Wagner, W.; Klein, M.O.; Stender, E.; Wieland, M.; Al-Nawas, B. Primary stability of a hybrid self-tapping implant compared to a cylindrical non-self-tapping implant with respect to drilling protocols in an ex vivo model. Clin. Implant Dent. Relat. Res. 2011, 13, 71–78. [Google Scholar] [CrossRef] [PubMed]
- Olive, J.; Aparicio, C. Periotest method as a measure of osseointegrated oral implant stability. Int. J. Oral Maxillofac. Implant. 1990, 5, 390–400. [Google Scholar]
- MA, A.A.; El Far, M.; Sheta, N.M.; Fayyad, A.; El Desouky, E.; Nabi, N.A.; Ibrahim, M. Correlation of Implant Stability Between Two Noninvasive Methods Using Submerged and Nonsubmerged Healing Protocols: A Randomized Clinical Trial. J Oral Implantol 2020, 46, 571–579. [Google Scholar] [CrossRef]
- Kumar, V.V.; Sagheb, K.; Klein, M.O.; Al-Nawas, B.; Kann, P.H.; Kämmerer, P.W. Relation between bone quality values from ultrasound transmission velocity and implant stability parameters--an ex vivo study. Clin. Oral Implant. Res. 2012, 23, 975–980. [Google Scholar] [CrossRef] [PubMed]
- Kämmerer, P.W.; Kumar, V.V.; Brullmann, D.; Gotz, H.; Kann, P.H.; Al-Nawas, B.; Klein, M.O. Evaluation of ultrasound transmission velocity and 3-dimensional radiology in different bone types for dental implantology: A comparative ex vivo study. Oral Surg. Oral Med. Oral Pathol. Oral Radiol. 2013, 116, e77–e84. [Google Scholar] [CrossRef]
- Staedt, H.; Kämmerer, P.W.; Goetze, E.; Thiem, D.G.E.; Al-Nawas, B.; Heimes, D. Implant primary stability depending on protocol and insertion mode—An ex vivo study. Int. J. Implant Dent. 2020, 6, 49. [Google Scholar] [CrossRef]
- Bolm, I.; Goetze, E.; Kämmerer, P.W.; Sader, R.; Klos, M.; Landes, C.; Al-Nawas, B. Self-drilling and self-tapping miniscrews for osteosynthesis fixture after LeFort I osteotomy: An ex vivo trial for primary stability and a randomized clinical study. J. Surg. Res. 2017, 212, 246–252. [Google Scholar] [CrossRef]
- Lachmann, S.; Jager, B.; Axmann, D.; Gomez-Roman, G.; Groten, M.; Weber, H. Resonance frequency analysis and damping capacity assessment. Part I: An in vitro study on measurement reliability and a method of comparison in the determination of primary dental implant stability. Clin. Oral Implant. Res. 2006, 17, 75–79. [Google Scholar] [CrossRef]
- Palarie, V.; Bicer, C.; Lehmann, K.M.; Zahalka, M.; Draenert, F.G.; Kämmerer, P.W. Early outcome of an implant system with a resorbable adhesive calcium-phosphate coating--a prospective clinical study in partially dentate patients. Clin. Oral Investig. 2012, 16, 1039–1048. [Google Scholar] [CrossRef]
- Sakoh, J.; Wahlmann, U.; Stender, E.; Nat, R.; Al-Nawas, B.; Wagner, W. Primary stability of a conical implant and a hybrid, cylindric screw-type implant in vitro. Int. J. Oral Maxillofac. Implant. 2006, 21, 560–566. [Google Scholar]
- Mardas, N.; Dereka, X.; Donos, N.; Dard, M. Experimental model for bone regeneration in oral and cranio-maxillo-facial surgery. J. Invest. Surg. 2014, 27, 32–49. [Google Scholar] [CrossRef] [PubMed]
- Jackowski, J.; Peters, H.; Hölzle, F. Zahnärztliche Chirurgie; Springer: Berlin, Germany, 2017. [Google Scholar]
- Al-Nawas, B.; Klein, M.O.; Gotz, H.; Vaterod, J.; Duschner, H.; Grotz, K.A.; Kann, P.H. Dental implantation: Ultrasound transmission velocity to evaluate critical bone quality--an animal model. Ultraschall Med. 2008, 29, 302–307. [Google Scholar] [CrossRef]
- Toia, M.; Stocchero, M.; Cecchinato, F.; Corra, E.; Jimbo, R.; Cecchinato, D. Clinical Considerations of Adapted Drilling Protocol by Bone Quality Perception. Int. J. Oral Maxillofac. Implant. 2017, 32, 1288–1295. [Google Scholar] [CrossRef]
- Stocchero, M.; Toia, M.; Cecchinato, D.; Becktor, J.P.; Coelho, P.G.; Jimbo, R. Biomechanical, Biologic, and Clinical Outcomes of Undersized Implant Surgical Preparation: A Systematic Review. Int. J. Oral Maxillofac. Implant. 2016, 31, 1247–1263. [Google Scholar] [CrossRef]
- Chieruzzi, M.; Pagano, S.; Cianetti, S.; Lombardo, G.; Kenny, J.M.; Torre, L. Effect of fibre posts, bone losses and fibre content on the biomechanical behaviour of endodontically treated teeth: 3D-finite element analysis. Mater. Sci. Eng. C Mater. Biol. Appl. 2017, 74, 334–346. [Google Scholar] [CrossRef]
- Arosio, P.; Arosio, F.; Di Stefano, D.A. Implant Diameter, Length, and the Insertion Torque/Depth Integral: A Study Using Polyurethane Foam Blocks. Dent. J. 2020, 8, 56. [Google Scholar] [CrossRef] [PubMed]
- Mesa, F.; Munoz, R.; Noguerol, B.; de Dios Luna, J.; Galindo, P.; O’Valle, F. Multivariate study of factors influencing primary dental implant stability. Clin. Oral Implant. Res. 2008, 19, 196–200. [Google Scholar] [CrossRef] [PubMed]
- Ostman, P.O.; Hellman, M.; Wendelhag, I.; Sennerby, L. Resonance frequency analysis measurements of implants at placement surgery. Int. J. Prosthodont. 2006, 19, 77–83. [Google Scholar]
- Silva, R.; Villalon, P.; Caceres, F. Effect of macro-design in the primary stability of short and extra-short implants using resonance frequency analysis. An ex vivo study. J. Oral Biol. Craniofac. Res. 2020, 10, 603–607. [Google Scholar] [CrossRef]
- Aragoneses, J.M.; Suarez, A.; Brugal, V.A.; Gomez, M. Frequency Values and Their Relationship with the Diameter of Dental Implants. Prospective Study of 559 Implants. Implant Dent. 2019, 28, 279–288. [Google Scholar] [CrossRef]
- Shiffler, K.; Lee, D.; Rowan, M.; Aghaloo, T.; Pi-Anfruns, J.; Moy, P.K. Effect of length, diameter, intraoral location on implant stability. Oral Surg. Oral Med. Oral Pathol. Oral Radiol. 2016, 122, e193–e198. [Google Scholar] [CrossRef]
- Hsieh, M.C.; Huang, C.H.; Lin, C.L.; Hsu, M.L. Effect of implant design on the initial biomechanical stability of two self-tapping dental implants. Clin. Biomech. 2020, 74, 124–130. [Google Scholar] [CrossRef] [PubMed]
- Degidi, M.; Daprile, G.; Piattelli, A. Influence of Stepped Osteotomy on Primary Stability of Implants Inserted in Low-Density Bone Sites: An In Vitro Study. Int. J. Oral Maxillofac. Implant. 2017, 32, 37–41. [Google Scholar] [CrossRef] [PubMed]
- Hansson, S.; Werke, M. The implant thread as a retention element in cortical bone: The effect of thread size and thread profile: A finite element study. J. Biomech. 2003, 36, 1247–1258. [Google Scholar] [CrossRef]
- Ma, P.; Xiong, W.; Tan, B.; Geng, W.; Liu, J.; Li, W.; Li, D. Influence of thread pitch, helix angle, and compactness on micromotion of immediately loaded implants in three types of bone quality: A three-dimensional finite element analysis. Biomed. Res. Int. 2014, 2014, 983103. [Google Scholar] [CrossRef]
- Wentaschek, S.; Scheller, H.; Schmidtmann, I.; Hartmann, S.; Weyhrauch, M.; Weibrich, G.; Lehmann, K.M. Sensitivity and Specificity of Stability Criteria for Immediately Loaded Splinted Maxillary Implants. Clin. Implant Dent. Relat. Res. 2015, 17 (Suppl. 2), e542–e549. [Google Scholar] [CrossRef]
- Hakim, S.G.; Glanz, J.; Ofer, M.; Steller, D.; Sieg, P. Correlation of cone beam CT-derived bone density parameters with primary implant stability assessed by peak insertion torque and periotest in the maxilla. J. Craniomaxillofac. Surg. 2019, 47, 461–467. [Google Scholar] [CrossRef]
- Herrero-Climent, M.; Lemos, B.F.; Herrero-Climent, F.; Falcao, C.; Oliveira, H.; Herrera, M.; Gil, F.J.; Rios-Carrasco, B.; Rios-Santos, J.V. Influence of Implant Design and Under-Preparation of the Implant Site on Implant Primary Stability. An In Vitro Study. Int. J. Environ. Res. Public Health 2020, 17, 4436. [Google Scholar] [CrossRef]
- Unsal, G.S.; Turkyilmaz, I. Analysis of the relationship between a modified method for implant site preparation and primary implant stability: A pilot study. J. Dent. Sci. 2020, 15, 234–235. [Google Scholar] [CrossRef]
- Turkyilmaz, I.; Tozum, T.F. Enhancing primary implant stability by undersizing implant site preparation: A human cadaver study. J. Stomatol. Oral Maxillofac. Surg. 2020, 121, 58–62. [Google Scholar] [CrossRef] [PubMed]
- Griggs, J.A. Dental Implants. Dent. Clin. N. Am. 2017, 61, 857–871. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Staedt, H.; Heimes, D.; Lehmann, K.M.; Ottl, P.; Bjelopavlovic, M.; Wagner, W.; Al-Nawas, B.; Kämmerer, P.W. Does the Modification of the Apical Geometry of a Dental Implant Affect Its Primary Stability? A Comparative Ex Vivo Study. Materials 2021, 14, 1728. https://doi.org/10.3390/ma14071728
Staedt H, Heimes D, Lehmann KM, Ottl P, Bjelopavlovic M, Wagner W, Al-Nawas B, Kämmerer PW. Does the Modification of the Apical Geometry of a Dental Implant Affect Its Primary Stability? A Comparative Ex Vivo Study. Materials. 2021; 14(7):1728. https://doi.org/10.3390/ma14071728
Chicago/Turabian StyleStaedt, Henning, Diana Heimes, Karl M. Lehmann, Peter Ottl, Monika Bjelopavlovic, Wilfried Wagner, Bilal Al-Nawas, and Peer W. Kämmerer. 2021. "Does the Modification of the Apical Geometry of a Dental Implant Affect Its Primary Stability? A Comparative Ex Vivo Study" Materials 14, no. 7: 1728. https://doi.org/10.3390/ma14071728
APA StyleStaedt, H., Heimes, D., Lehmann, K. M., Ottl, P., Bjelopavlovic, M., Wagner, W., Al-Nawas, B., & Kämmerer, P. W. (2021). Does the Modification of the Apical Geometry of a Dental Implant Affect Its Primary Stability? A Comparative Ex Vivo Study. Materials, 14(7), 1728. https://doi.org/10.3390/ma14071728






