Influence of Residual Stress around Constituent Particles on Recrystallization and Grain Growth in Al-Mn-Based Alloy during Annealing
Abstract
1. Introduction
2. Experimental Procedure
3. Results
3.1. Microstructure of Homogenized Specimen
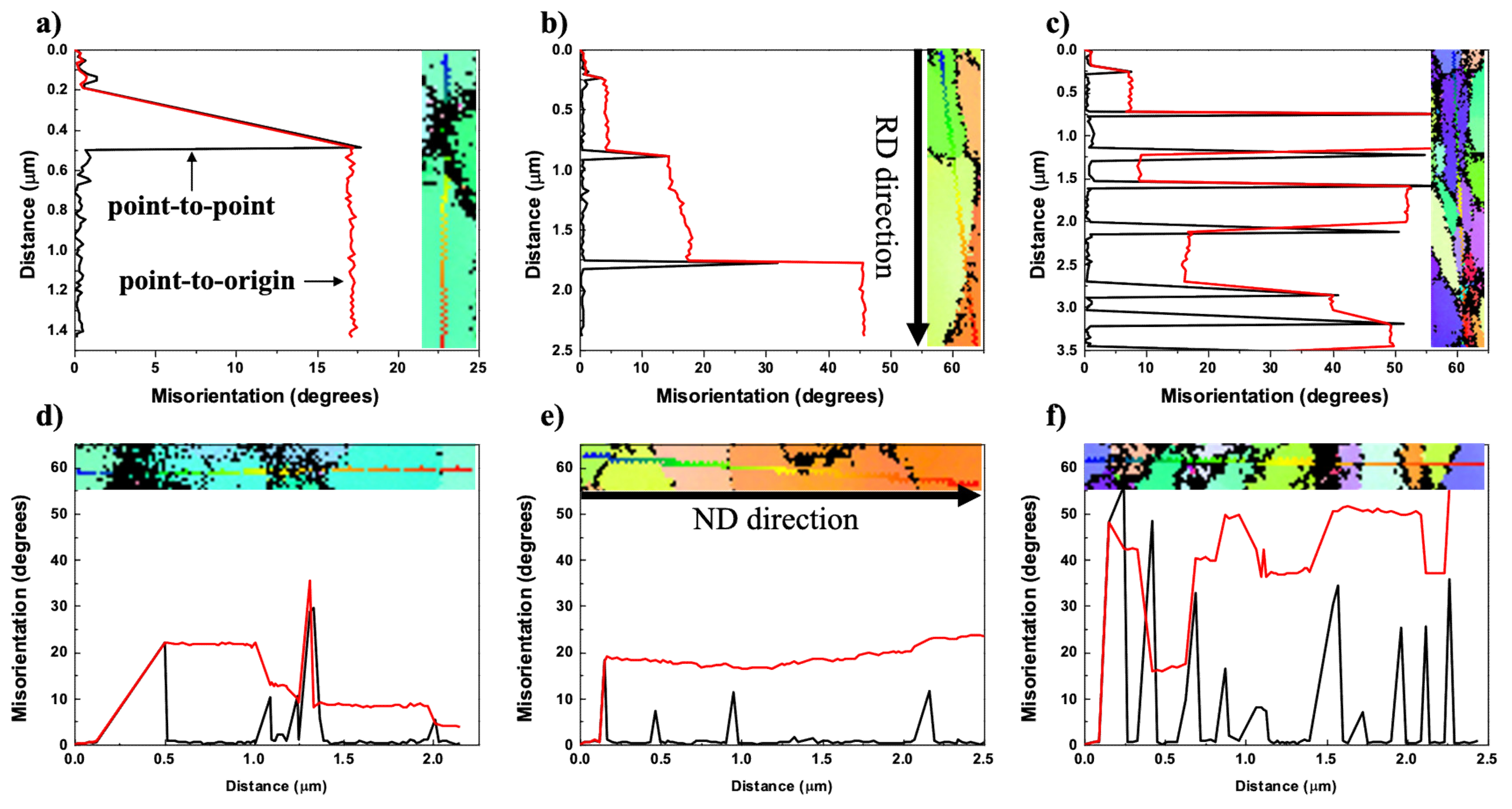
3.2. Change in Microstructure with Increase of Strain
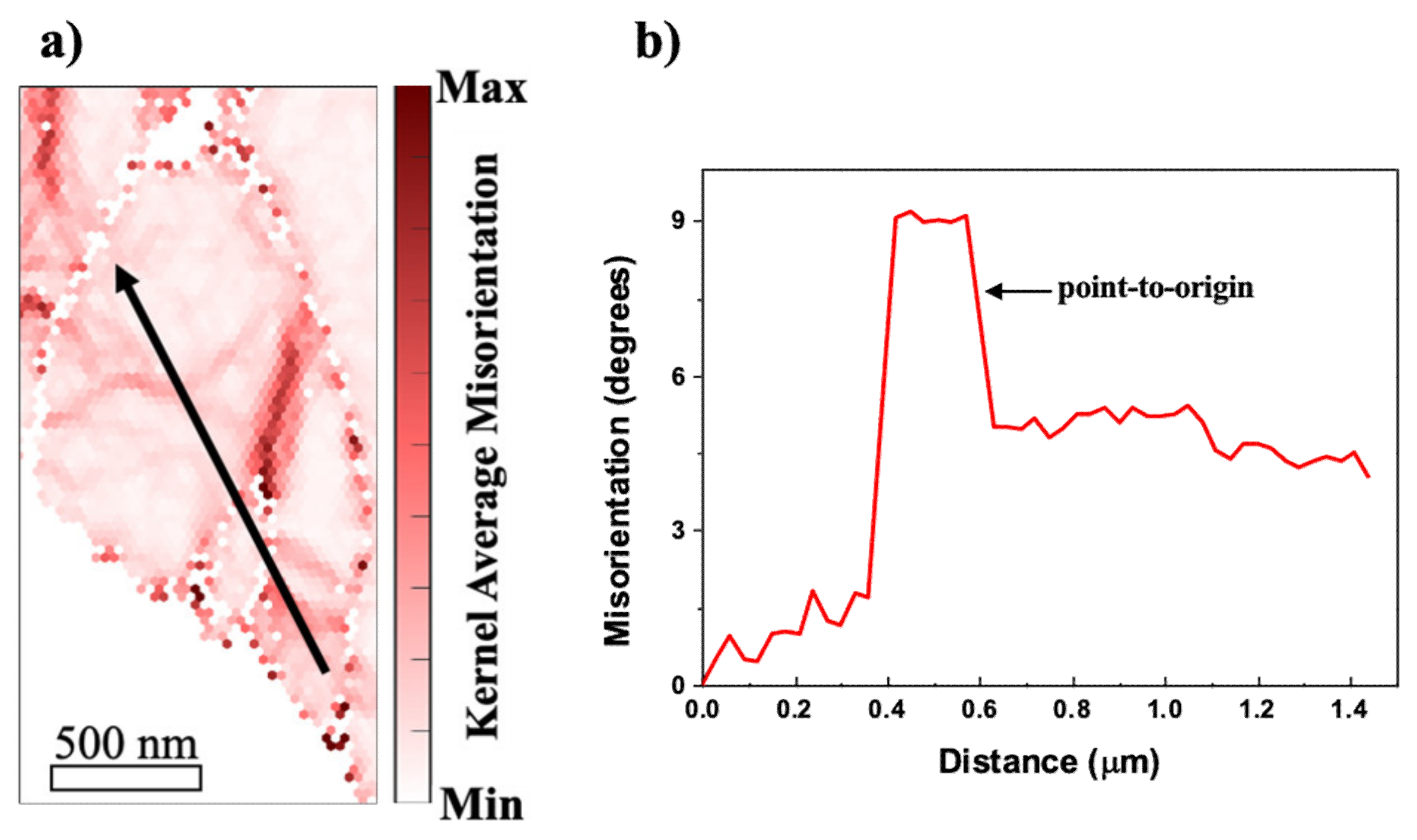
3.3. Deformation Zone around the α-Al(Mn, Fe)Si Precipitate with Increase of Strain
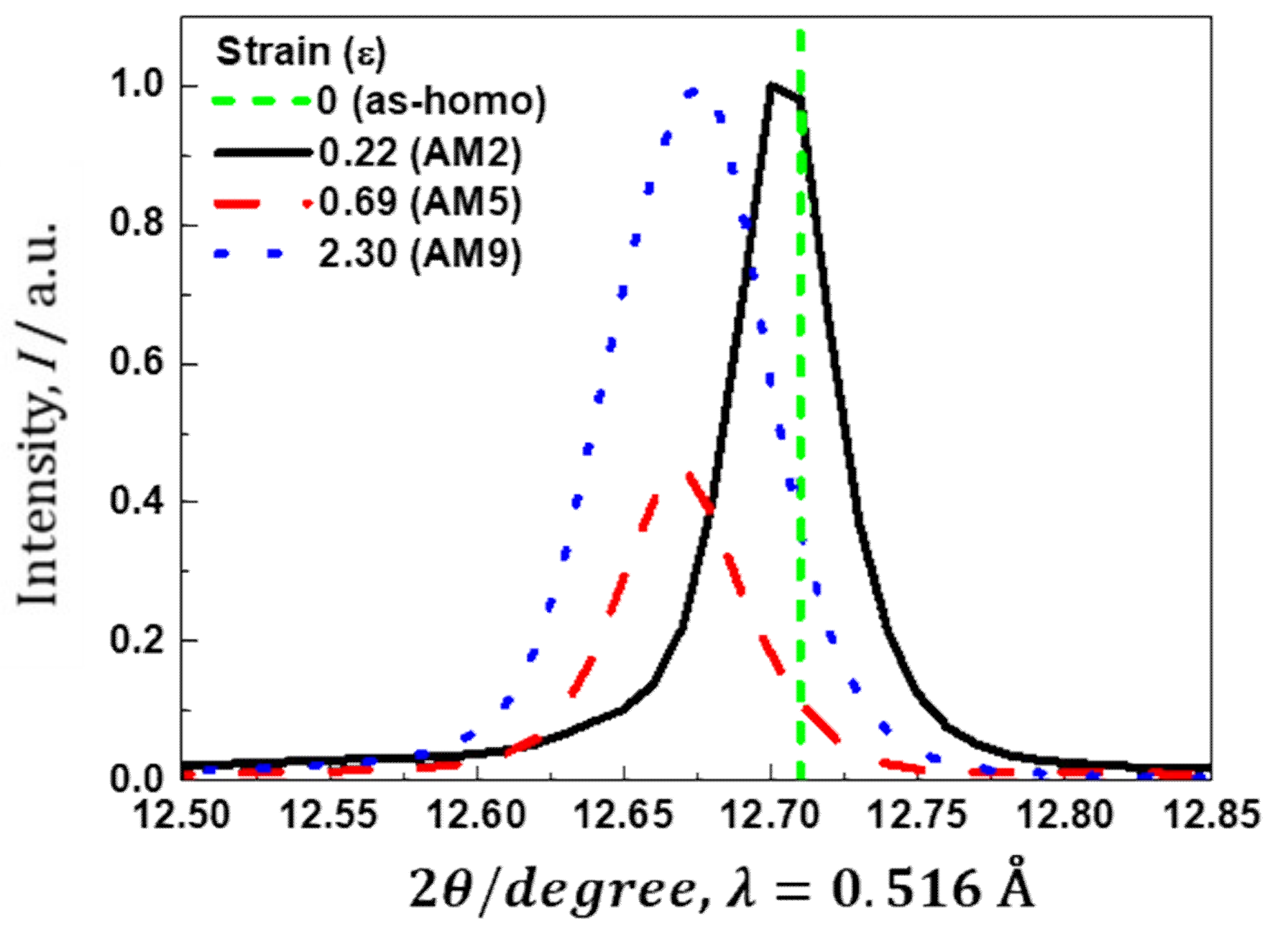
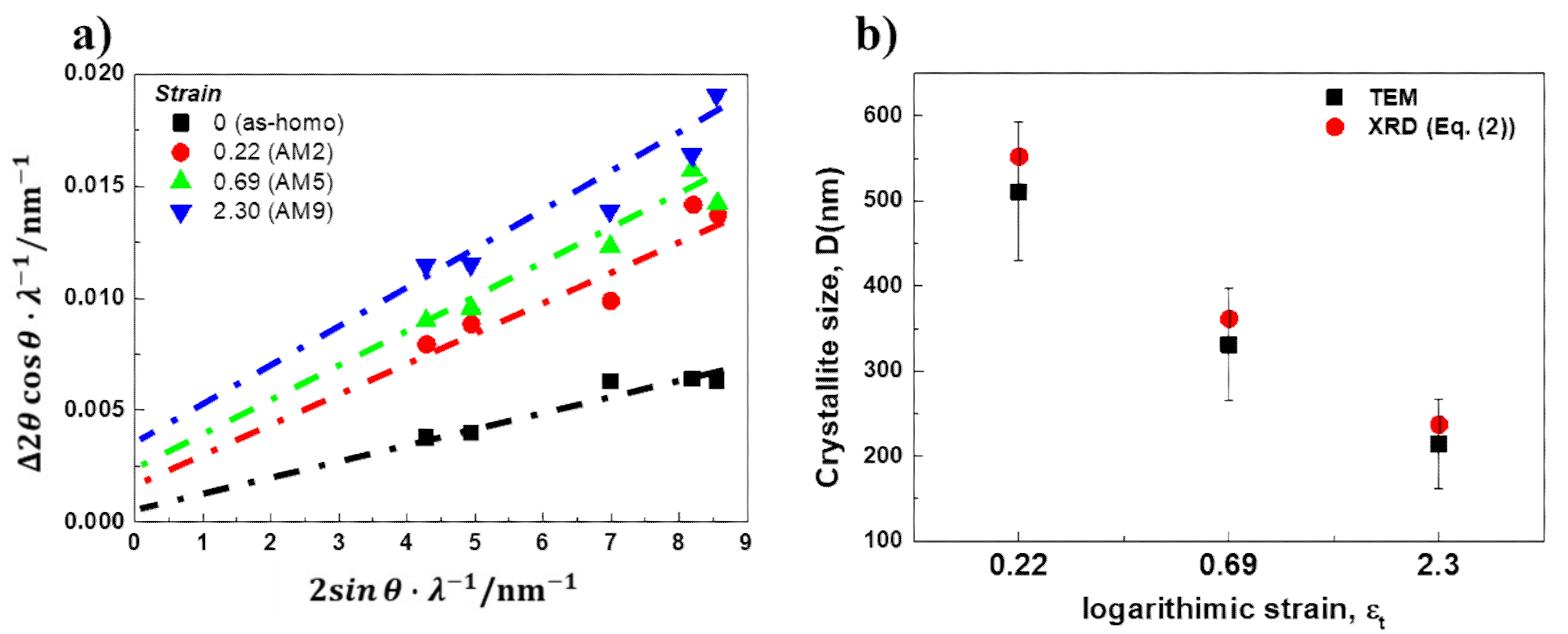
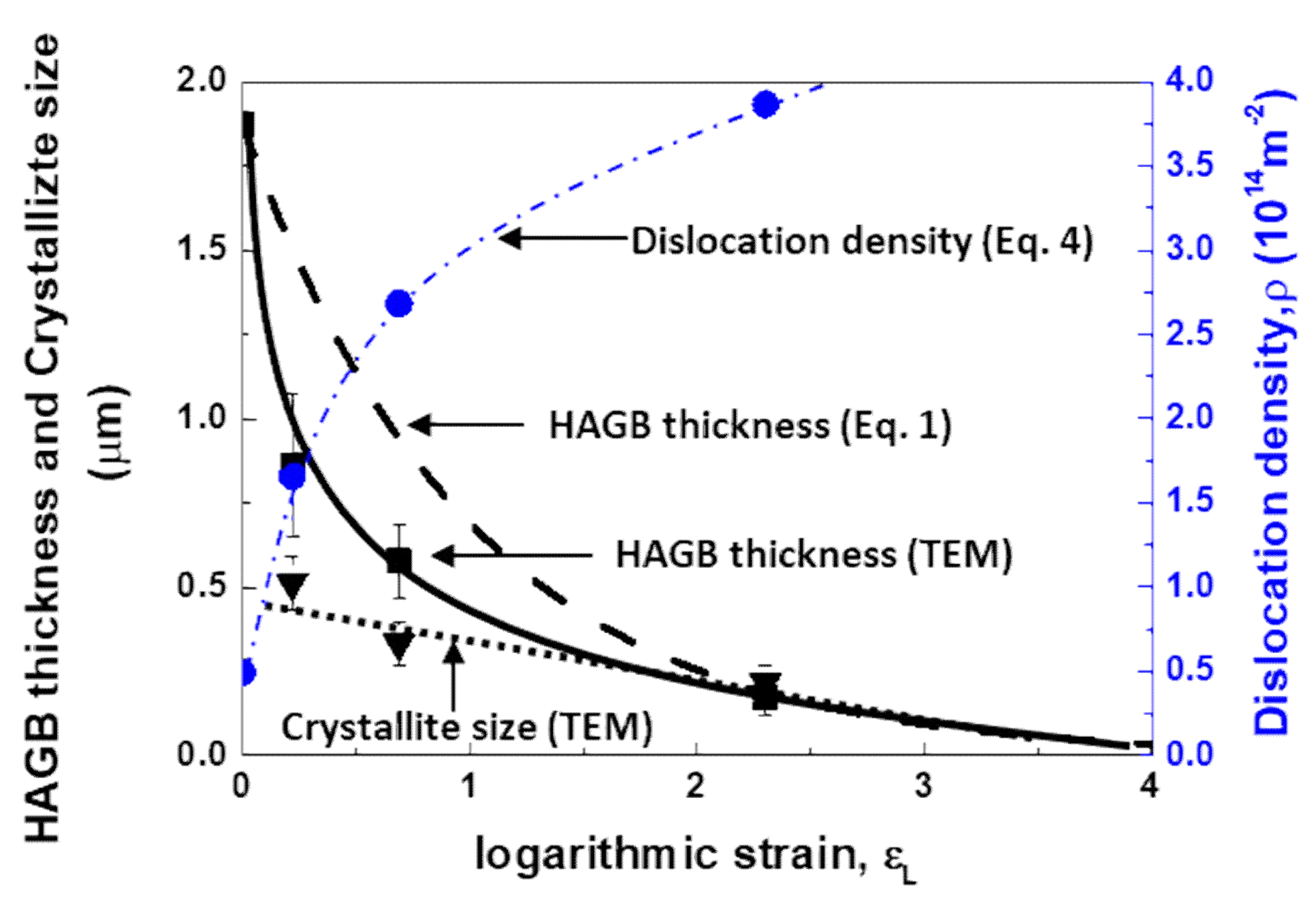
3.4. Evolution of Dislocation Density with Increasing Strain
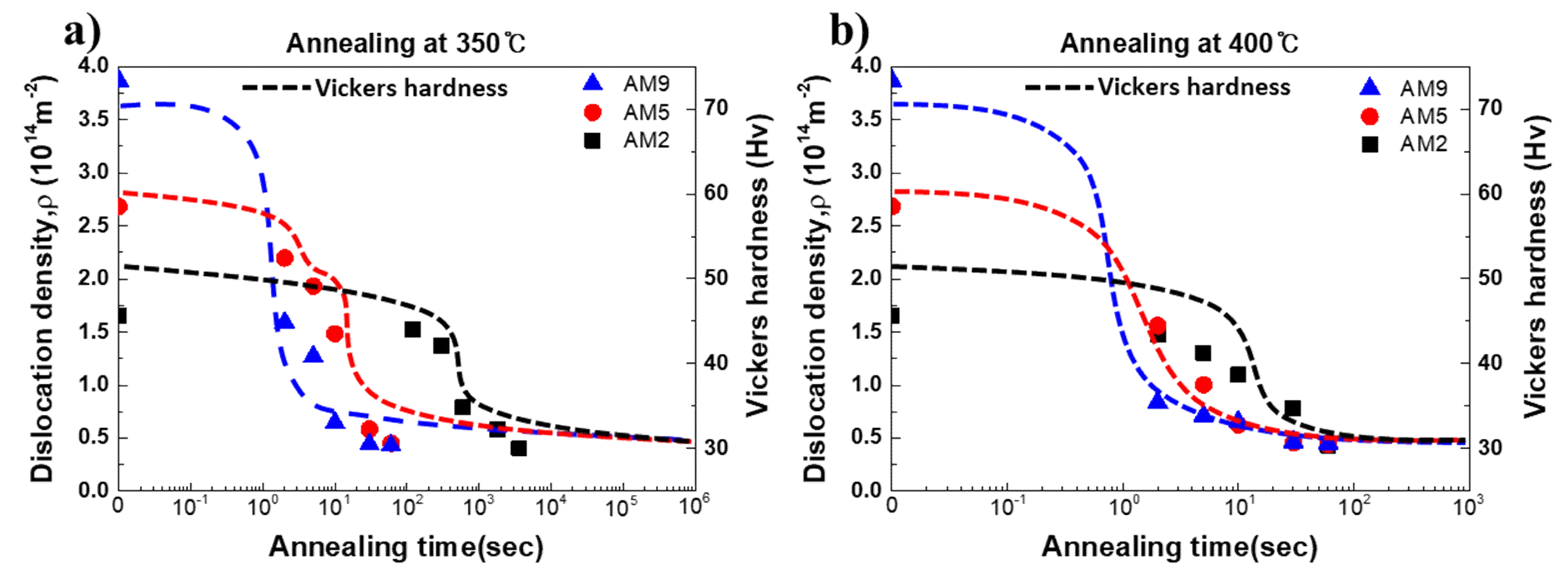
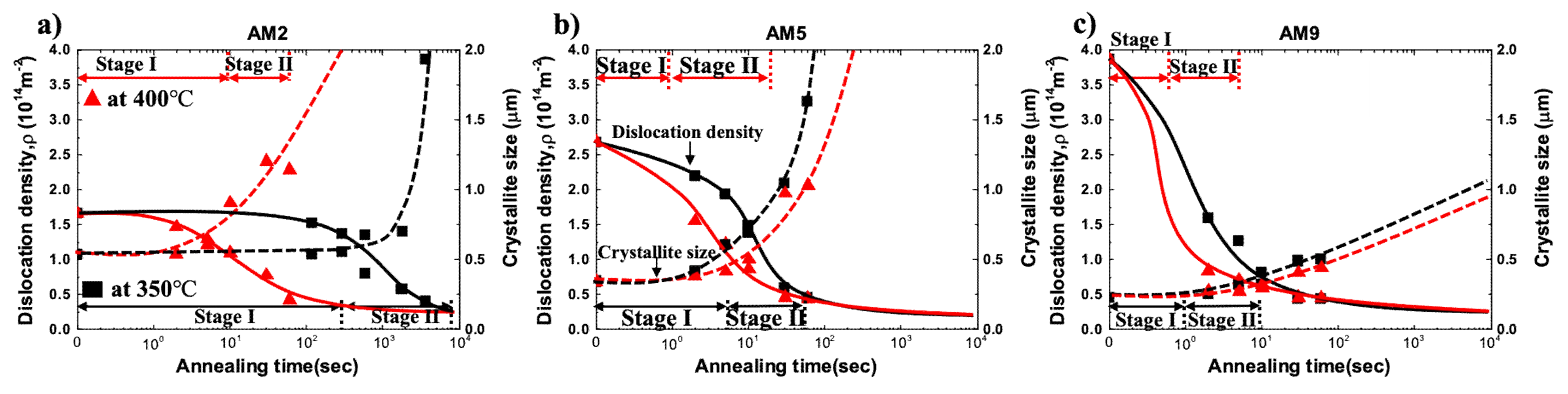
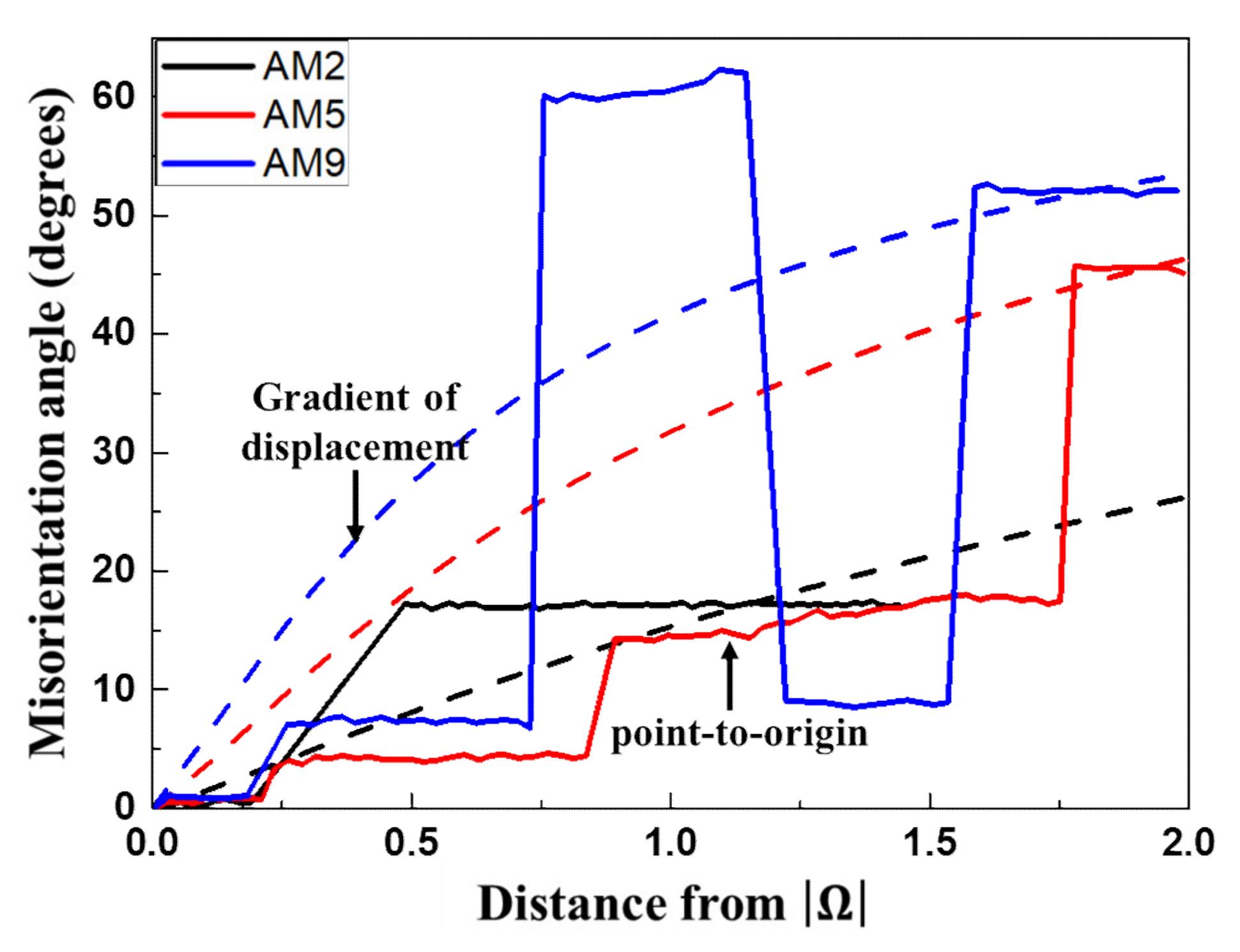
3.5. Recrystallization Behavior in Cold Rolled Specimen with Different Reduction Ratio
4. Discussions
4.1. Evolution of Dislocation Density
4.2. Driving Force for Recrystallization
4.3. Thermodynamic Pressure for Boundary Migration
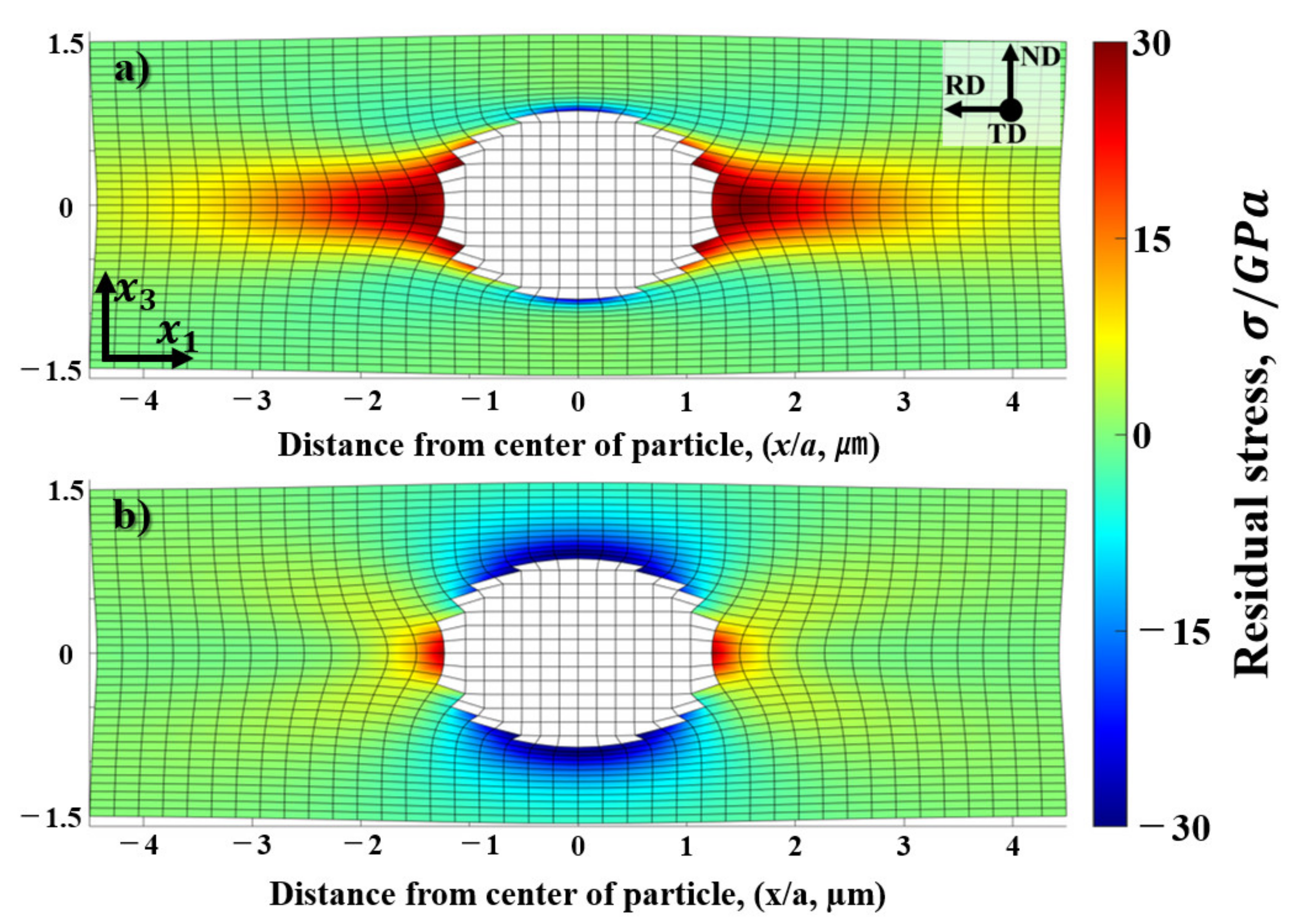
4.4. Residual Stress of α-Al(Mn, Fe)Si Particle
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Humphreys, F.; Rohrer, G.S.; Rollett, A. Recrystallization and Related Annealing Phenomena; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar] [CrossRef]
- Lloyd, D.; Kenny, D. The structure and properties of some heavily cold worked aluminum alloys. Acta Metall. 1980, 28, 639–649. [Google Scholar] [CrossRef]
- Gil Sevillano, J.; van Houtte, P.; Aernoudt, E. Large strain work hardening and textures. Prog. Mater. Sci. 1980, 25, 69–134. [Google Scholar] [CrossRef]
- Gholinia, A.; Humphreys, F.; Prangnell, P. Production of ultra-fine grain microstructures in Al–Mg alloys by coventional rolling. Acta Mater. 2002, 50, 4461–4476. [Google Scholar] [CrossRef]
- Park, S.; Muraishi, S. Effect of reduction rate on the recrystallization behavior in AA3003 aluminum alloy fabricated by DC casting. In Proceedings of the International Conference on the Physical Properties and Application of Advanced Materials (ICPMAT 2019), Daegu, Korea, 1–4 September 2019; pp. 28–29. [Google Scholar]
- Nes, E.; Ryum, N.; Hunderi, O. On the Zener drag. Acta Metall. 1985, 33, 11–22. [Google Scholar] [CrossRef]
- Zhao, Q.; Zhang, H.; Qiu, F.; Jiang, Q. Strain-induced precipitation kinetics during non-isothermal annealing of Al-Mn alloys. J. Alloys Compd. 2018, 735, 2275–2280. [Google Scholar] [CrossRef]
- Simonovic, D.; Sluiter, M.H.F. Impurity diffusion activation energies in Al from first principles. Phys. Rev. B 2009, 79, 1–12. [Google Scholar] [CrossRef]
- Humphreys, F. Inhomogeneous Deformation of Some Aluminium Alloys at Elevated Temperature. In Strength of Metals and Alloys (ICSMA 6); Elsevier: Amsterdam, The Netherlands, 1982; pp. 625–630. [Google Scholar] [CrossRef]
- Humphreys, F. Local lattice rotations at second phase particles in deformed metals. Acta Metall. 1979, 27, 1801–1814. [Google Scholar] [CrossRef]
- Humphreys, F. A unified theory of recovery, recrystallization and grain growth, based on the stability and growth of cellular microstructures—I. The basic model. Acta Mater. 1997, 45, 4231–4240. [Google Scholar] [CrossRef]
- Smith, C.S. Grains, phases, and interfaces: An introduction of microstructure. Trans. Metall. Soc. AIME 1948, 175, 15–51. [Google Scholar]
- Pimenta, F.C., Jr.; Arruda, A.C.; Padilha, A.F. Resistance to recrystallization in Al-1% Mn alloys. Z. Für Met. 1986, 77, 522–528. [Google Scholar]
- Nagahama, K.; Miki, I. Precipitation during recrystallization in Al-Mn and Al-Cr alloys. Trans. Jpn. Inst. Met. 1974, 15, 185–192. [Google Scholar] [CrossRef]
- Sun, N.; Patterson, B.R.; Suni, J.P.; Simielli, E.A.; Weiland, H.; Allard, L.F. Microstructural evolution in twin roll cast AA3105 during homogenization. Mater. Sci. Eng. A 2006, 416, 232–239. [Google Scholar] [CrossRef]
- Sun, N.; Patterson, B.R.; Suni, J.P.; Doherty, R.D.; Weiland, H.; Kadolkar, P.; Blue, C.A.; Thompson, G.B. Effect of Heating Rate on Recrystallization of Twin Roll Cast Aluminum. Metall. Mater. Trans. A 2008, 39, 165–170. [Google Scholar] [CrossRef]
- Vernon-Parry, K.D.; Furu, T.; Jensen, D.J.; Humphreys, F.J. Deformation microstructure and texture in hot worked aluminium alloys. Mater. Sci. Technol. 1996, 12, 889–896. [Google Scholar] [CrossRef]
- McQueen, H.J.; Spigarelli, S.; Kassner, M.E.; Evangelista, E. Hot Deformation and Processing of Aluminum Alloys; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar] [CrossRef]
- Park, S.-J.; Muraishi, S. Micromechanical analysis of residual stress around coarse precipitates under cold rolling conditions. Mech. Mater. 2021, 103841. [Google Scholar] [CrossRef]
- Hielscher, R.; Silbermann, C.B.; Schmidl, E.; Ihlemann, J. Denoising of crystal orientation maps. J. Appl. Crystallogr. 2019, 52, 984–996. [Google Scholar] [CrossRef]
- Zhou, W.; Yu, J.; Lin, J.; Dean, T.A. Manufacturing a curved profile with fine grains and high strength by differential velocity sideways extrusion. Int. J. Mach. Tools Manuf. 2019, 140, 77–88. [Google Scholar] [CrossRef]
- Mura, T. Micromechanics of Defects in Solids; Martinus Nijhoff: Dordrecht, The Netherlands, 1987. [Google Scholar] [CrossRef]
- Ju, J.W.; Sun, L.Z. A Novel Formulation for the Exterior-Point Eshelby’s Tensor of an Ellipsoidal Inclusion. J. Appl. Mech. 1999, 66, 570–574. [Google Scholar] [CrossRef]
- Ju, J.; Sun, L. Effective elastoplastic behavior of metal matrix composites containing randomly located aligned spheroidal inhomogeneities. Part I: Micromechanics-based formulation. Int. J. Solids Struct. 2001, 38, 183–201. [Google Scholar] [CrossRef]
- Kaufman, J.G. Properties of Aluminum Alloys: Tensile, Creep, and Fatigue Data at High and Low Temperatures; ASM International: Almere, The Netherlands, 1999. [Google Scholar]
- Chen, C.-L.; Richter, A.; Thomson, R. Investigation of mechanical properties of intermetallic phases in multi-component Al–Si alloys using hot-stage nanoindentation. Intermetallics 2010, 18, 499–508. [Google Scholar] [CrossRef]
- Tóth, L.; Beausir, B.; Gu, C.; Estrin, Y.; Scheerbaum, N.; Davies, C. Effect of grain refinement by severe plastic deformation on the next-neighbor misorientation distribution. Acta Mater. 2010, 58, 6706–6716. [Google Scholar] [CrossRef]
- Raj, S.V.; Iskovitz, I.S.; Freed, A.D. Modeling the Role of Dislocation Substructure during Class M and Exponential Creep; Academic Press Inc.: Cambridge, MA, USA, 1996. [Google Scholar] [CrossRef]
- Humphreys, F.J. Quantitative metallography by electron backscattered diffraction. J. Microsc. 1999, 195, 170–185. [Google Scholar] [CrossRef]
- Williamson, G.; Hall, W. X-ray line broadening from filed aluminium and wolfram. Acta Metall. 1953, 1, 22–31. [Google Scholar] [CrossRef]
- Ungár, T.; Gubicza, J.; Ribárik, G.; Borbély, A. Crystallite size distribution and dislocation structure determined by diffraction profile analysis: Principles and practical application to cubic and hexagonal crystals. J. Appl. Crystallogr. 2001, 34, 298–310. [Google Scholar] [CrossRef]
- Williamson, G.K.; Smallman, R.E. III. Dislocation densities in some annealed and cold-worked metals from measurements on the X-ray debye-scherrer spectrum. Philos. Mag. 1956, 1, 34–46. [Google Scholar] [CrossRef]
- Williamson, G.K.; Smallman, R.E. The use of Fourier analysis in the interpretation of X-ray line broadening from cold-worked iron and molybdenum. Acta Crystallogr. 1954, 7, 574–581. [Google Scholar] [CrossRef]
- Jones, A.R.; Ralph, B.; Hansen, N. Subgrain coalescence and the nucleation of recrystallization at grain boundaries in aluminium. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1979, 368, 345–357. [Google Scholar] [CrossRef]
- Doherty, R.D.; Cahn, R.W. Nucleation of New Grains in Cold Worked Metals. J. Less Common Met. 1972, 28, 279. [Google Scholar] [CrossRef]
- Bakker, H.; Bonzel, H.P.; Bruff, C.M.; Dayananda, M.A.; Gust, W.; Horvath, J.; Kaur, I.; Kidson, G.V.; LeClaire, A.D.; Mehrer, H.; et al. Diffusion in Solid Metals and Alloys; Springer: Berlin/Heidelberg, Germany, 1990. [Google Scholar] [CrossRef]
- Balluffi, R.W. On measurements of self-diffusion rates along dislocations in F.C.C. Metals. Phys. Status Solidi (b) 1970, 42, 11–34. [Google Scholar] [CrossRef]
- Wilson, A.J.C. Dislocations in Crystals by W. T. Read Jr. Acta Crystallogr. 1954, 7, 384. [Google Scholar] [CrossRef]
- Murr, L.E. Interfacial Phenomena in Metals and Alloys; Addison-Wesley Pub. Co.: London, UK, 1975; ISBN 0201048841. [Google Scholar]
- Muraishi, S. Formulation of Eshelby’s inclusion problem by BIEM (boundary integral equation method) and PDD (parametric dislocation dynamics). Mech. Mater. 2014, 74, 41–55. [Google Scholar] [CrossRef]
- Kalu, P.; Waryoba, D. A JMAK-microhardness model for quantifying the kinetics of restoration mechanisms in inhomogeneous microstructure. Mater. Sci. Eng. A 2007, 464, 68–75. [Google Scholar] [CrossRef]
- Sridharan, N.; Wolcott, P.; Dapino, M.; Babu, S. Microstructure and texture evolution in aluminum and commercially pure titanium dissimilar welds fabricated using ultrasonic additive manufacturing. Scr. Mater. 2016, 117, 1–5. [Google Scholar] [CrossRef]
- Humphreys, F. The nucleation of recrystallization at second phase particles in deformed aluminium. Acta Metall. 1977, 25, 1323–1344. [Google Scholar] [CrossRef]
- Muraishi, S.; Taya, M. Average Eshelby tensor and elastic field for helical inclusion problems. Int. J. Solids Struct. 2019, 180–181, 125–136. [Google Scholar] [CrossRef]
- Tanaka, K.; Mori, T. Note on volume integrals of the elastic field around an ellipsoidal inclusion. J. Elast. 1972, 2, 199–200. [Google Scholar] [CrossRef]
- Muraishi, S.; Taya, M. Eshelby problem in continuous shape transition of helical inclusion. Int. J. Solids Struct. 2020, 199, 36–42. [Google Scholar] [CrossRef]
- Shibata, S.; Taya, M.; Mori, T.; Mura, T. Dislocation punching from spherical inclusions in a metal matrix composite. Acta Metall. et Mater. 1992, 40, 3141–3148. [Google Scholar] [CrossRef]
- Muraishi, S. Efficient interpolation algorithm of electro-elastic Green’s function for boundary integral equation method and Eshelby inclusion problem. Int. J. Solids Struct. 2016, 100–101, 297–306. [Google Scholar] [CrossRef]
- Meng, C.; Heltsley, W.; Pollard, D.D. Evaluation of the Eshelby solution for the ellipsoidal inclusion and heterogeneity. Comput. Geosci. 2012, 40, 40–48. [Google Scholar] [CrossRef]










| Alloy | Mn | Cu | Fe | Si | Ti | Al |
|---|---|---|---|---|---|---|
| AA3003 | 1.15 | 0.16 | 0.52 | 0.28 | 0.01 | bal. |
| Constant | Value | Source |
|---|---|---|
| Em | 69 GPa | [25] |
| vm | 0.33 | |
| Ep | 175 GPa | [26] |
| vp | 0.28 | assumed |
| Condition | Average Grain Size (μm) | Average Primary Particle Size (μm) | Electric Conductivity (%IACS) |
|---|---|---|---|
| As-cast | 140 | 2.8 | 30 |
| As-homo | 160 | 4.1 | 43.5 |
| 0.2 | 8.25 | <10−17 | −8.25 | 14.29 |
| 0.5 | 20.62 | <10−17 | −20.62 | 35.72 |
| 0.9 | 37.12 | <10−17 | −37.12 | 64.29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, S.-J.; Muraishi, S. Influence of Residual Stress around Constituent Particles on Recrystallization and Grain Growth in Al-Mn-Based Alloy during Annealing. Materials 2021, 14, 1701. https://doi.org/10.3390/ma14071701
Park S-J, Muraishi S. Influence of Residual Stress around Constituent Particles on Recrystallization and Grain Growth in Al-Mn-Based Alloy during Annealing. Materials. 2021; 14(7):1701. https://doi.org/10.3390/ma14071701
Chicago/Turabian StylePark, Sung-Jin, and Shinji Muraishi. 2021. "Influence of Residual Stress around Constituent Particles on Recrystallization and Grain Growth in Al-Mn-Based Alloy during Annealing" Materials 14, no. 7: 1701. https://doi.org/10.3390/ma14071701
APA StylePark, S.-J., & Muraishi, S. (2021). Influence of Residual Stress around Constituent Particles on Recrystallization and Grain Growth in Al-Mn-Based Alloy during Annealing. Materials, 14(7), 1701. https://doi.org/10.3390/ma14071701








