Gate Control of Superconductivity in Mesoscopic All-Metallic Devices
Abstract
1. Introduction
2. Gate-Driven Supercurrent Suppression in Nb and V Nanojunctions
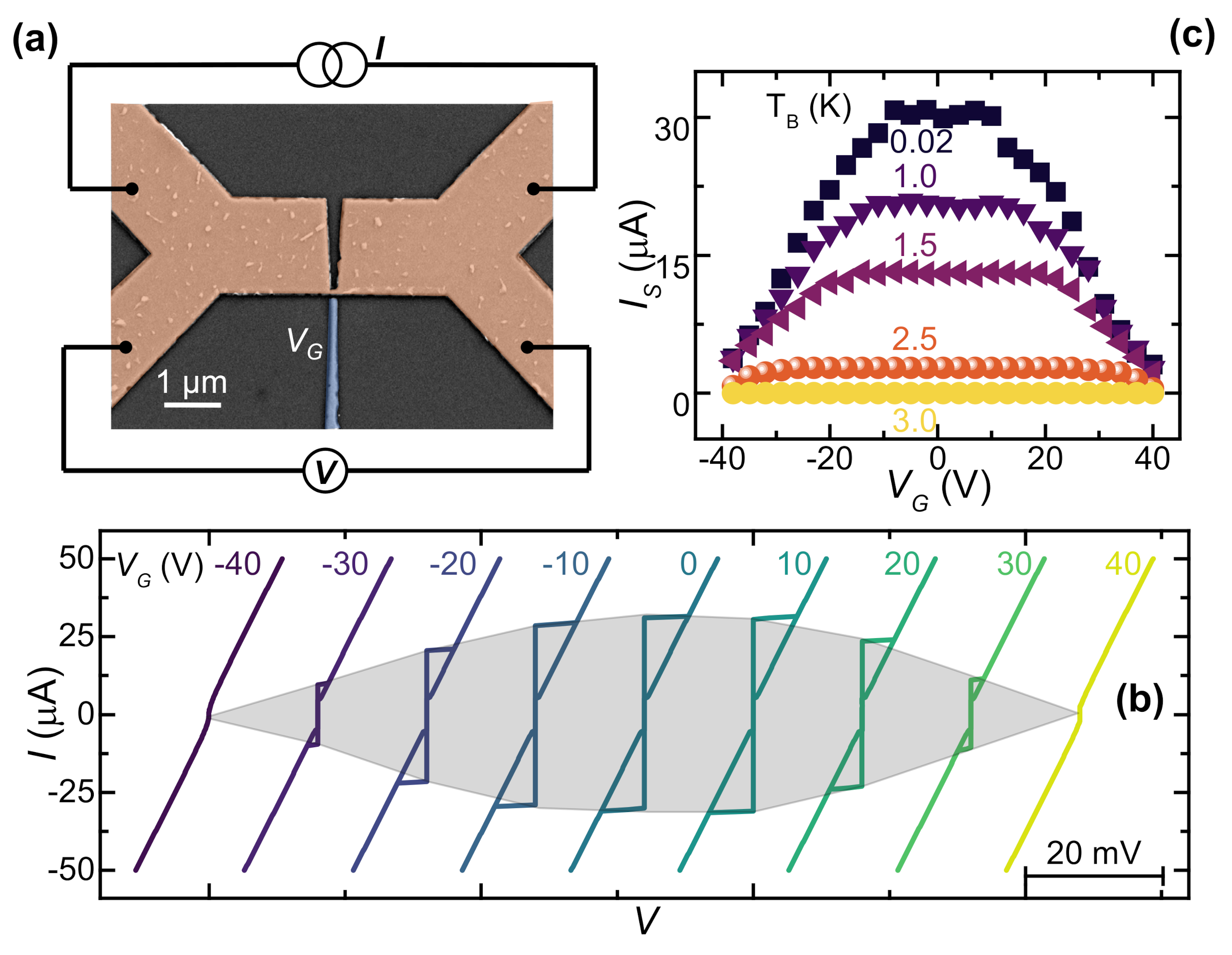
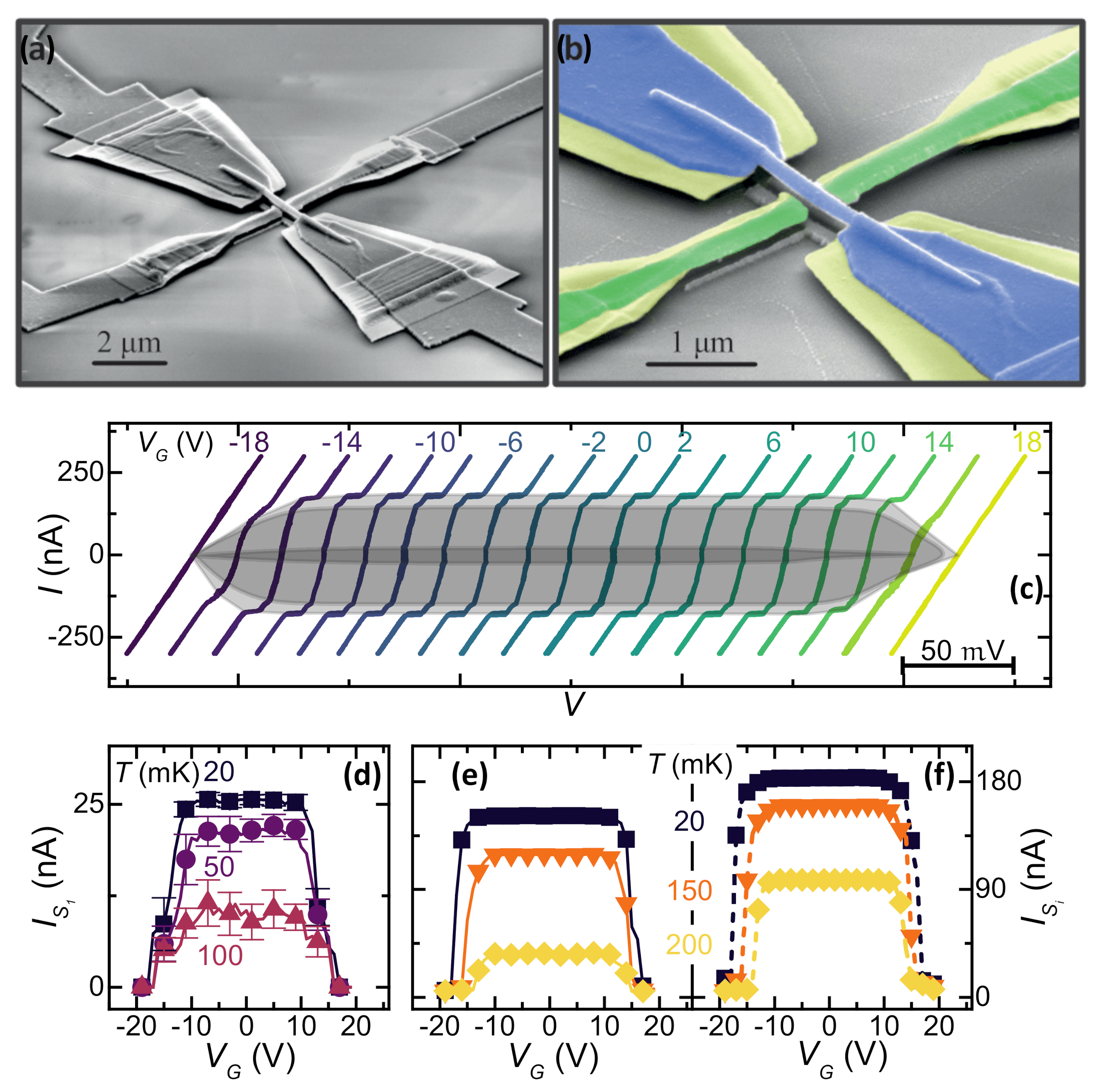
2.1. Niobium Gate-Controlled Transistor
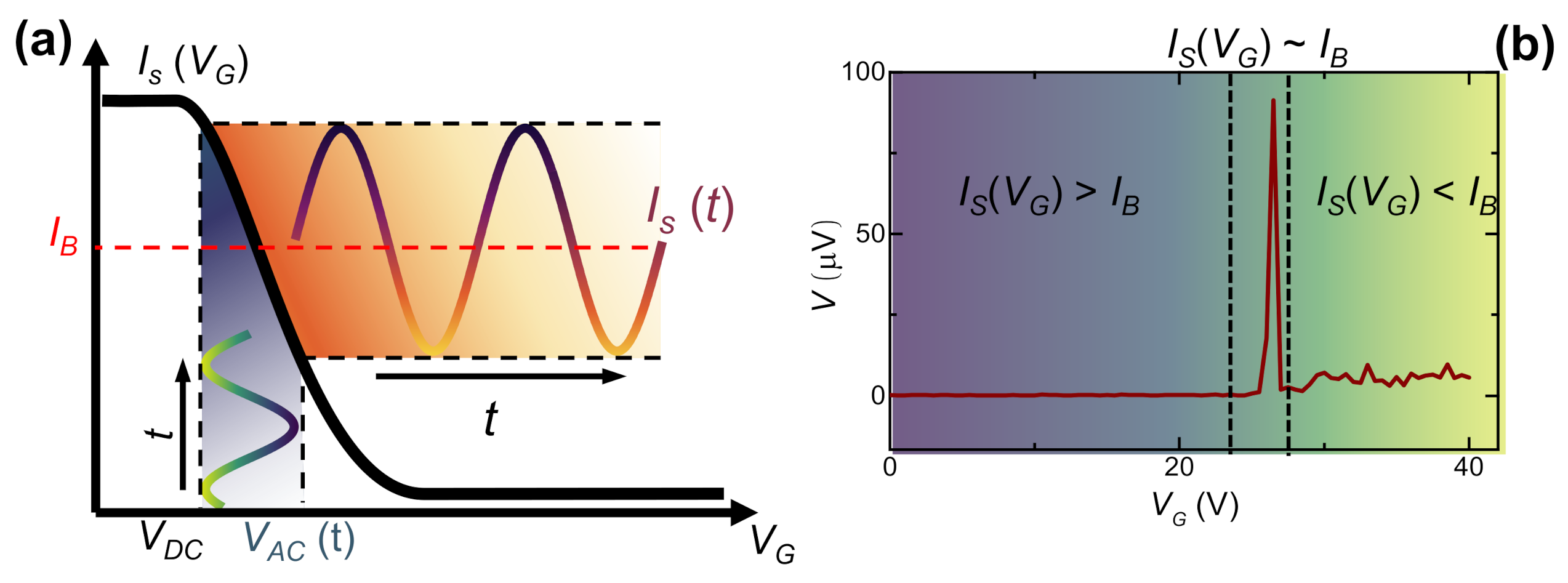
2.1.1. Rectification Properties
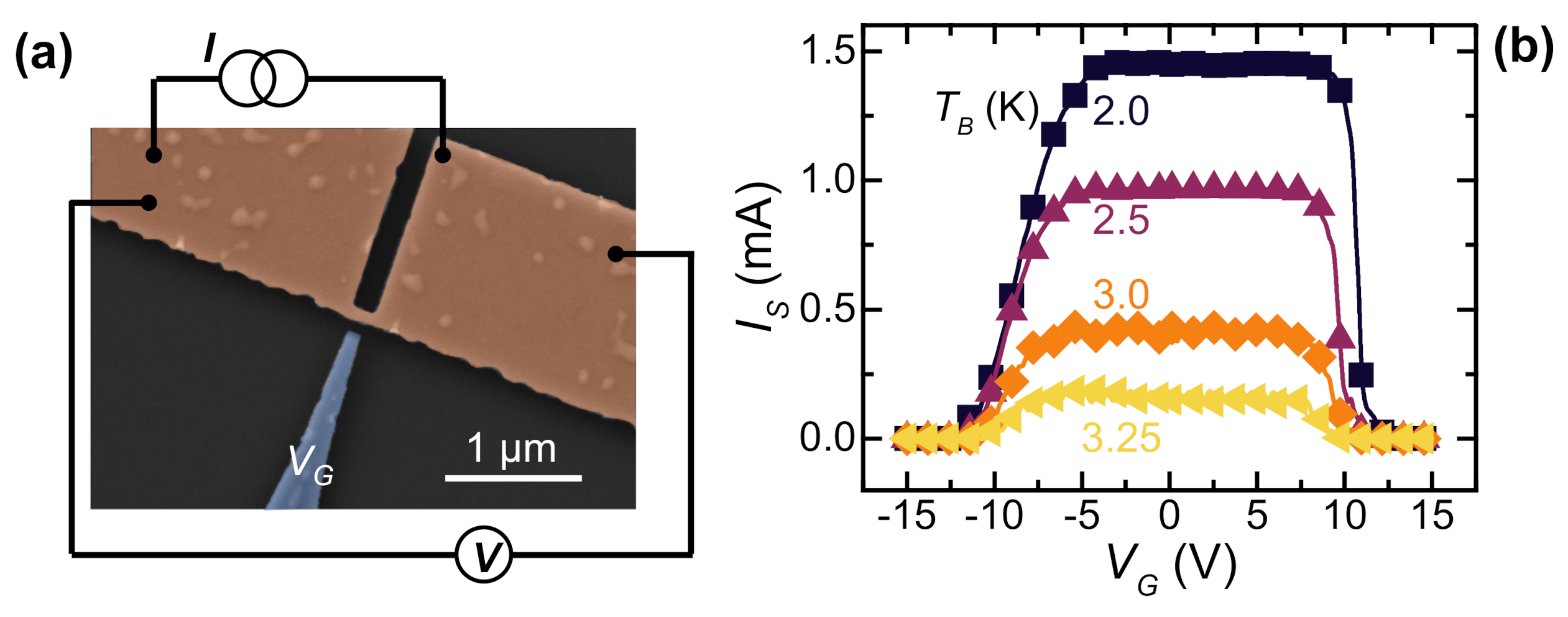
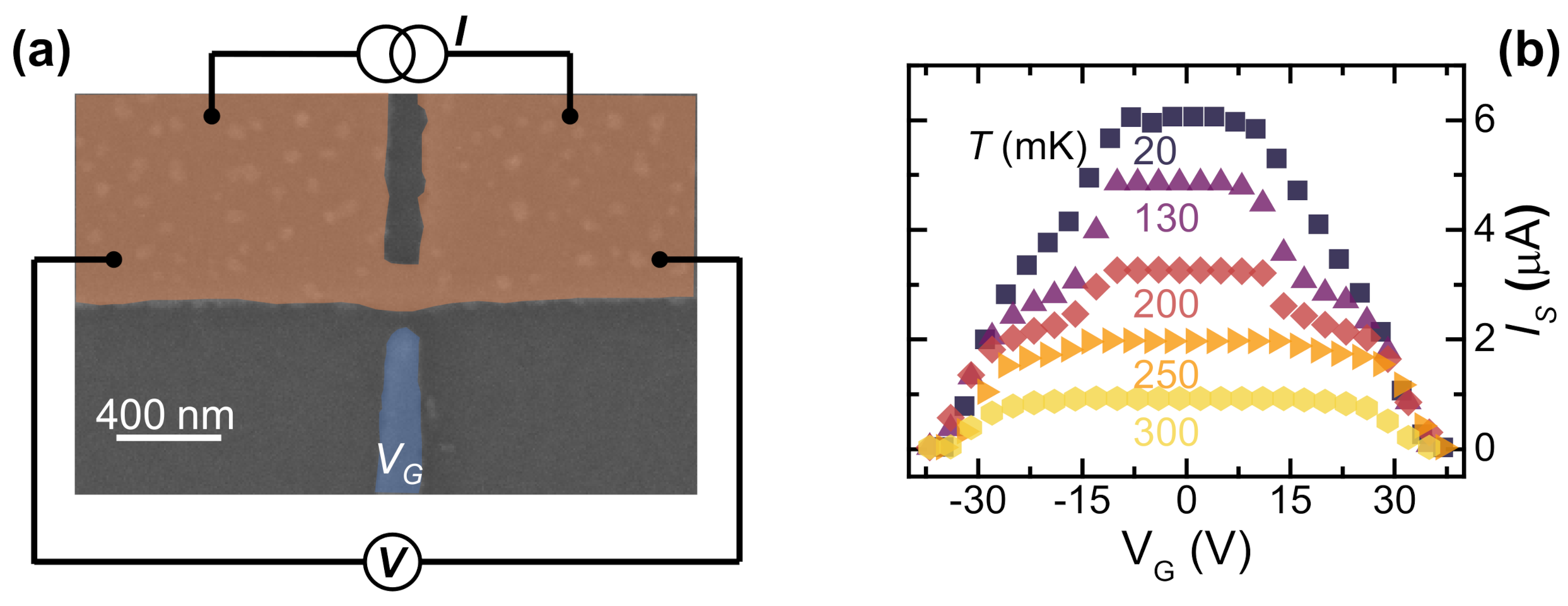
2.2. Vanadium Gate-Controlled Transistor
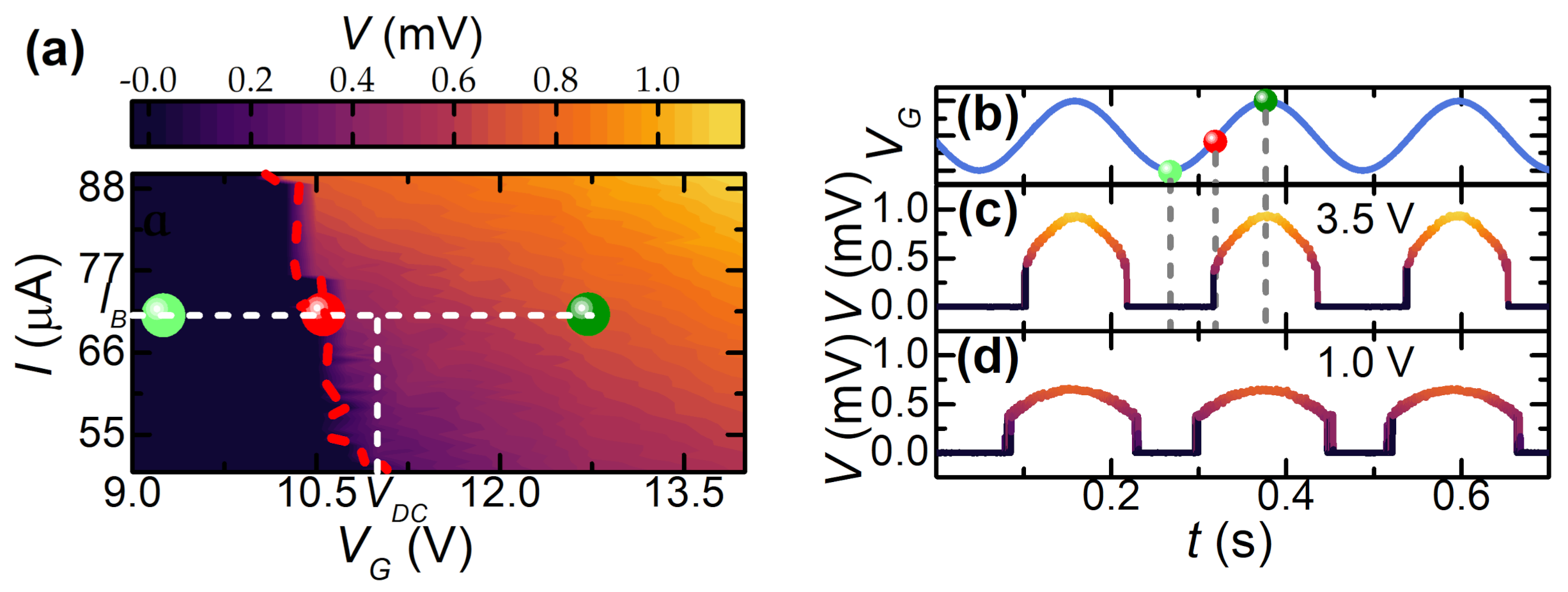
2.2.1. Half-Wave Rectifier
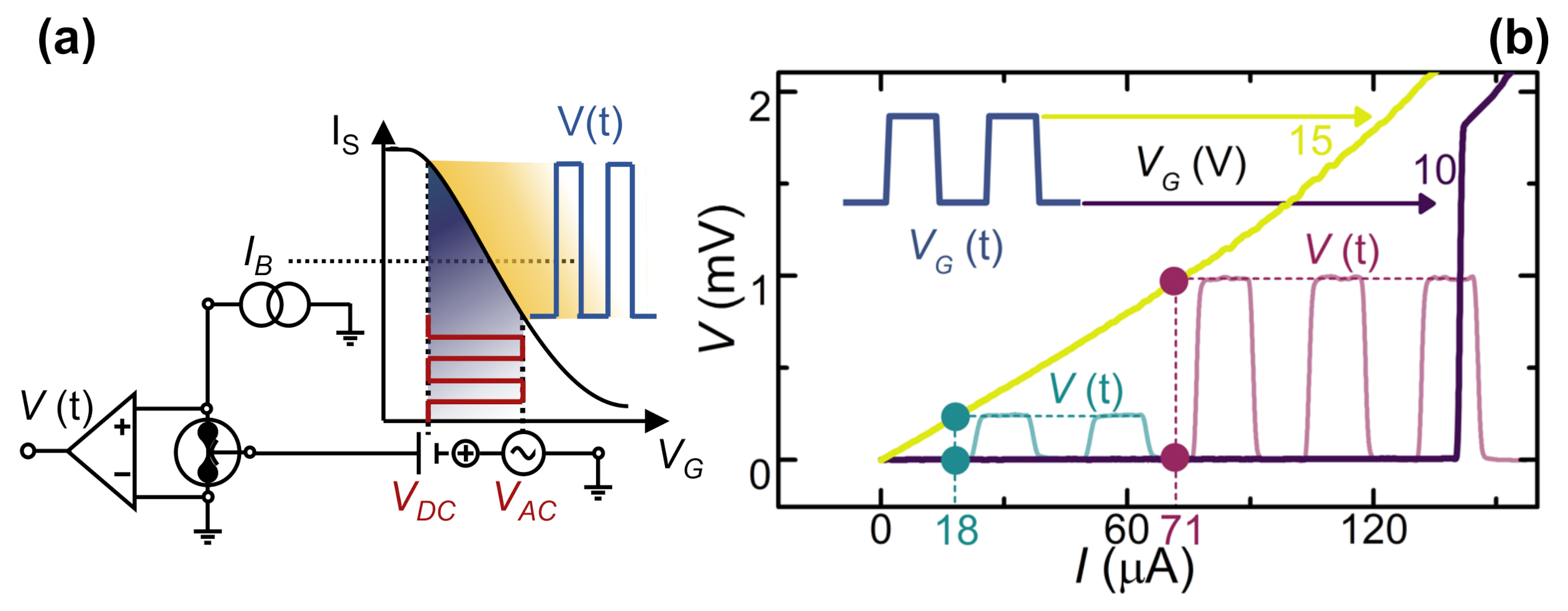
2.2.2. Amplification Properties
3. Nonthermal Origin of Supercurrent Suppression in Gated All-Metallic Superconducting Devices
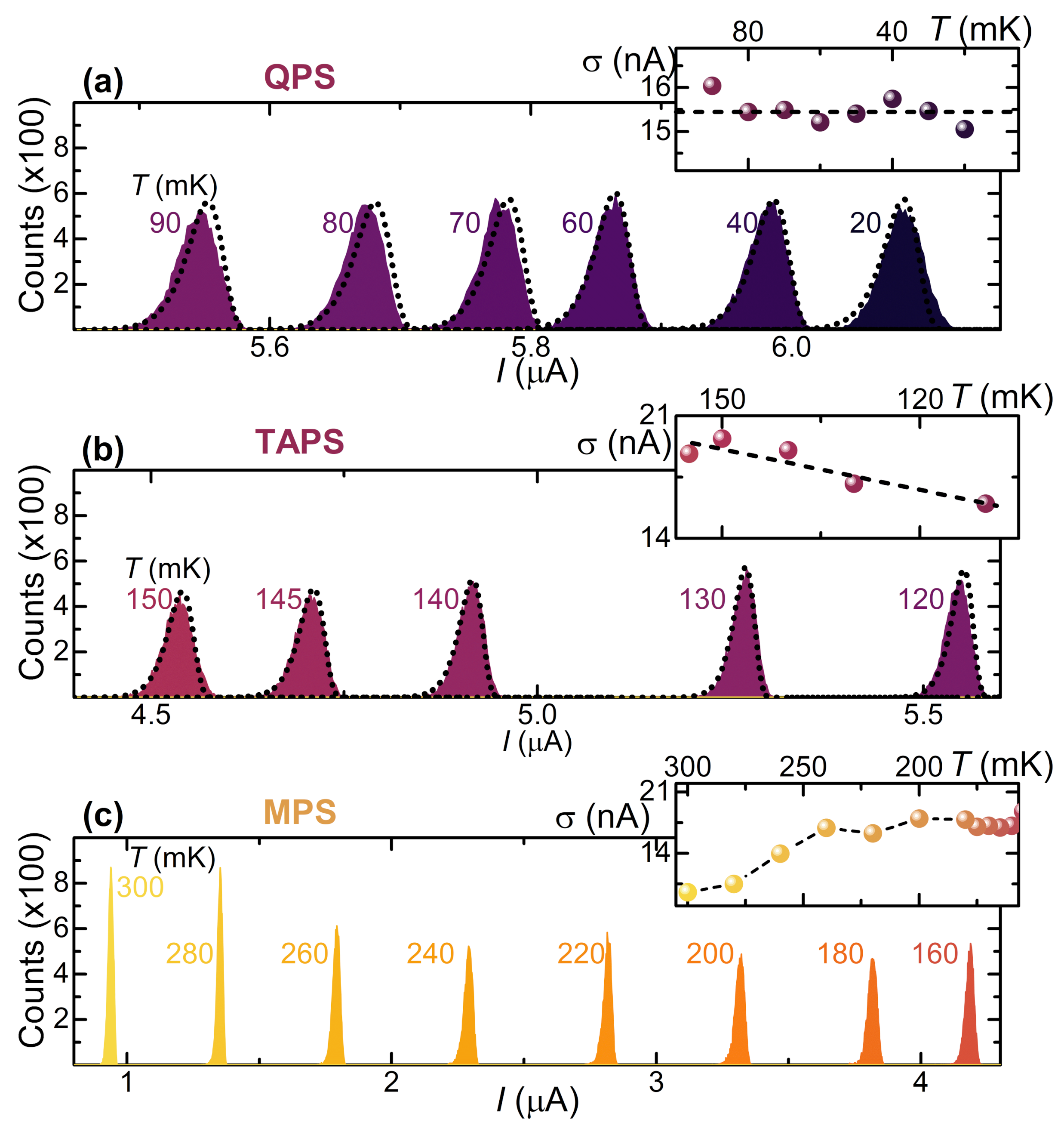
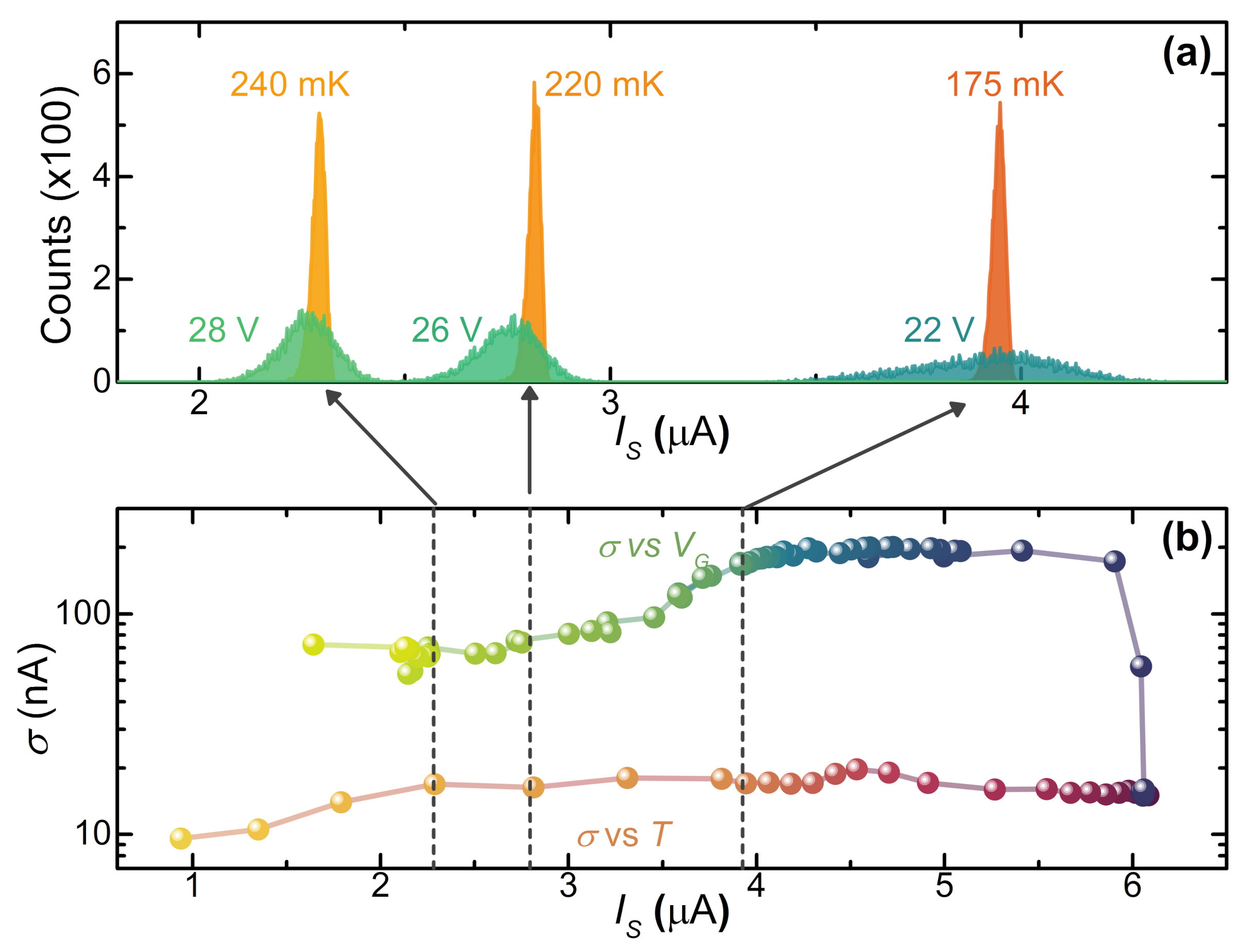
3.1. SCPDs in a Titanium Gate-Controlled Transistor
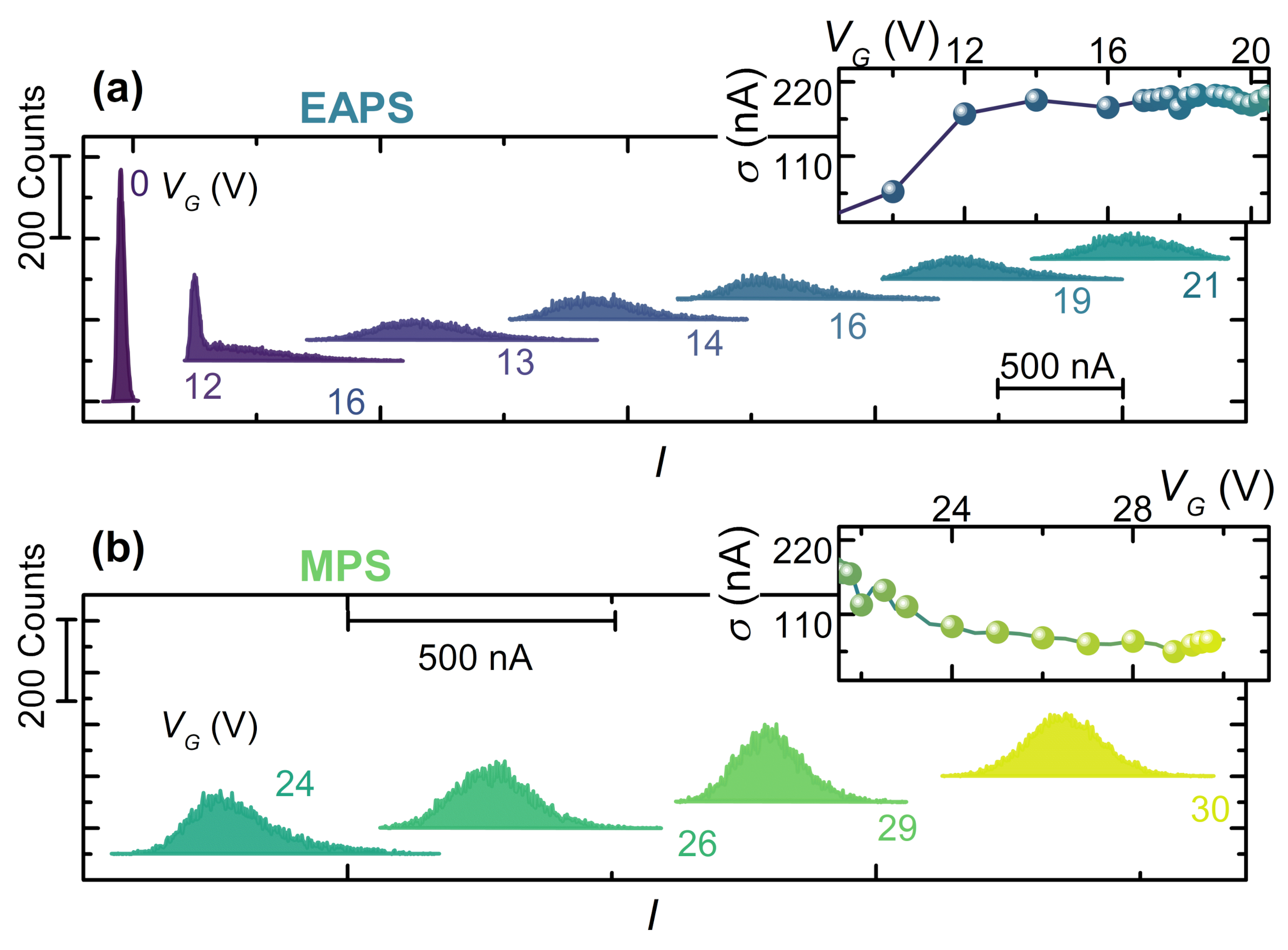
3.2. Suspended Titanium Gate-Controlled Transistor
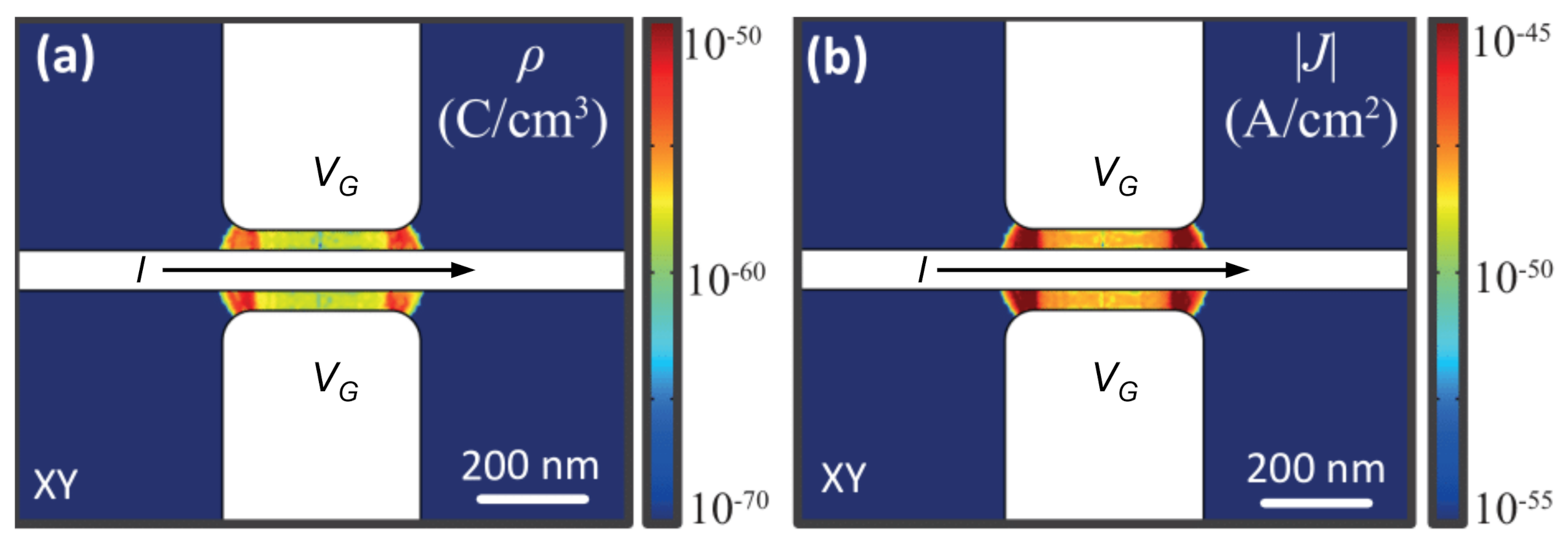
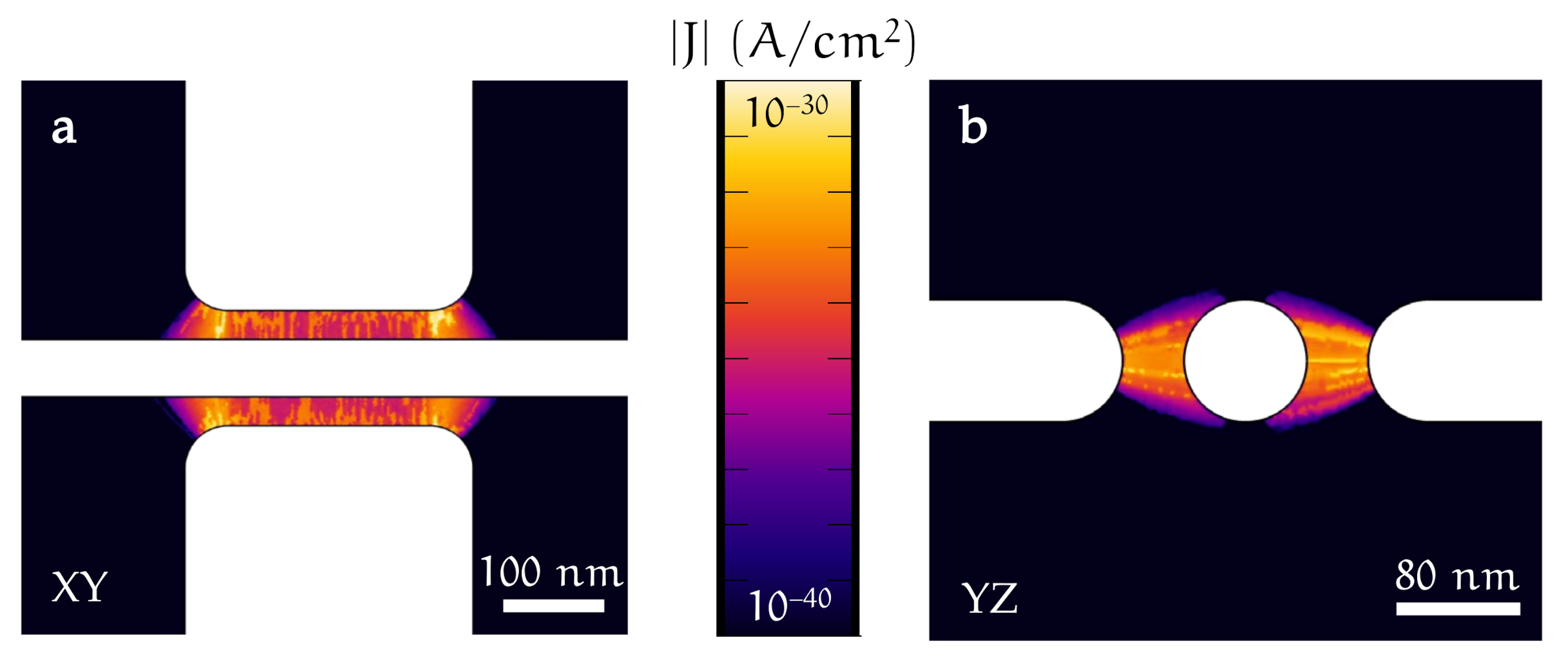
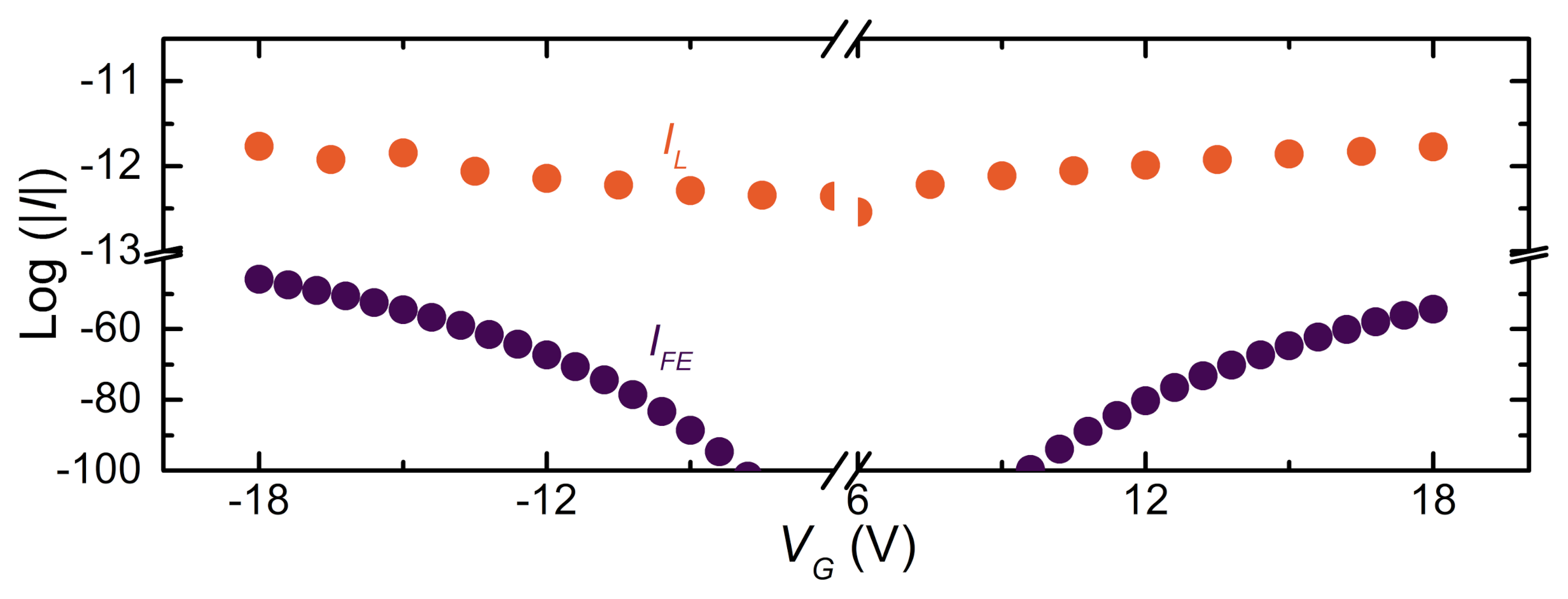
3.3. Leakage Current Finite Element Method Simulations
3.4. Heating through Single Cold-Electron Field Emission or Absorption
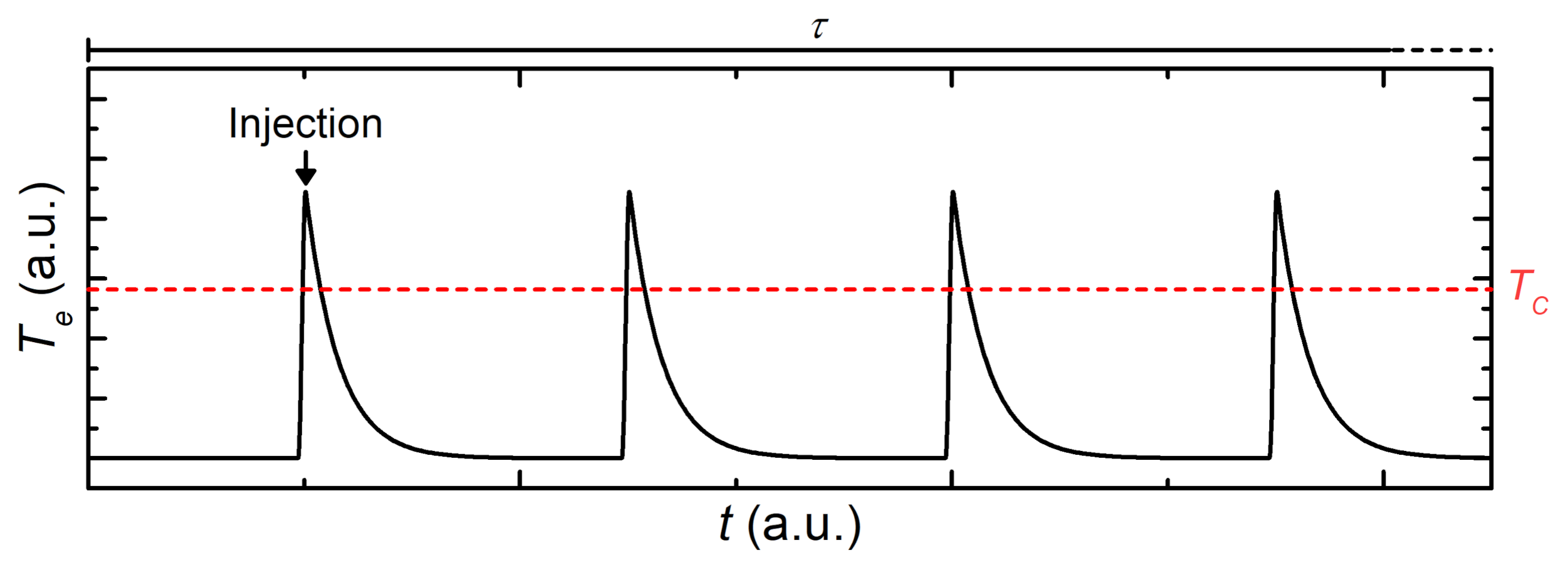
3.5. Continuous Power Injection
3.6. Unconventional Sum Rule
4. Summary and Further Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bardeen, J. Critical Fields and Currents in Superconductors. Rev. Mod. Phys. 1962, 34, 667–681. [Google Scholar] [CrossRef]
- De Simoni, G.; Paolucci, F.; Solinas, P.; Strambini, E.; Giazotto, F. Metallic supercurrent field-effect transistor. Nat. Nanotechnol. 2018, 13, 802–805. [Google Scholar] [CrossRef] [PubMed]
- Paolucci, F.; De Simoni, G.; Strambini, E.; Solinas, P.; Giazotto, F. Ultra-Efficient Superconducting Dayem Bridge Field-Effect Transistor. Nano Lett. 2018, 18, 4195–4199. [Google Scholar] [CrossRef] [PubMed]
- Paolucci, F.; De Simoni, G.; Solinas, P.; Strambini, E.; Ligato, N.; Virtanen, P.; Braggio, A.; Giazotto, F. Magnetotransport Experiments on Fully Metallic Superconducting Dayem-Bridge Field-Effect Transistors. Phys. Rev. Appl. 2019, 11, 024061. [Google Scholar] [CrossRef]
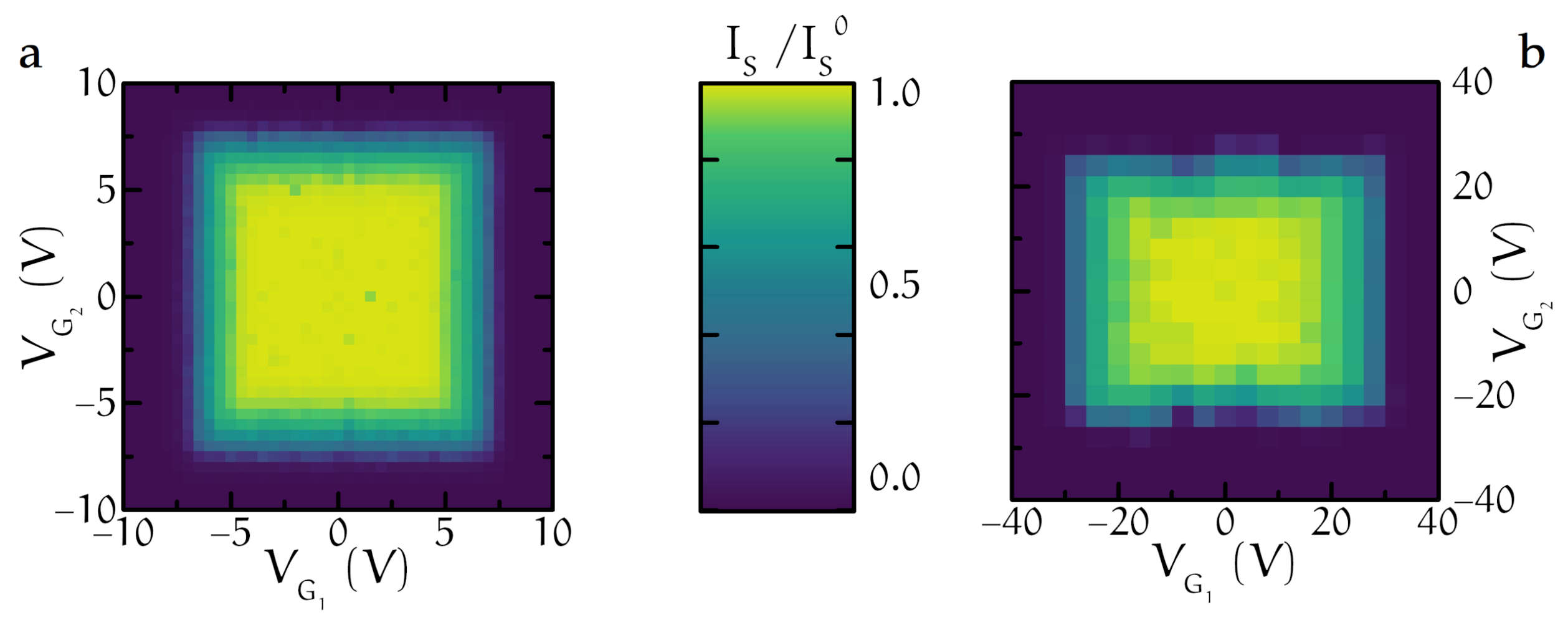
- Paolucci, F.; Vischi, F.; De Simoni, G.; Guarcello, C.; Solinas, P.; Giazotto, F. Field-Effect Controllable Metallic Josephson Interferometer. Nano Lett. 2019, 19, 6263–6269. [Google Scholar] [CrossRef] [PubMed]
- Paolucci, F.; De Simoni, G.; Solinas, P.; Strambini, E.; Puglia, C.; Ligato, N.; Giazotto, F. Field-effect control of metallic superconducting systems. AVS Quantum Sci. 2019, 1, 016501. [Google Scholar] [CrossRef]
- Bours, L.; Mercaldo, M.T.; Cuoco, M.; Strambini, E.; Giazotto, F. Unveiling mechanisms of electric field effects on superconductors by a magnetic field response. Phys. Rev. Res. 2020, 2, 033353. [Google Scholar] [CrossRef]
- Rocci, M.; Suri, D.; Kamra, A.; Gilvânia, V.; Takamura, Y.; Nemes, N.M.; Martinez, J.L.; Hernandez, M.G.; Moodera, J.S. Large Enhancement of Critical Current in Superconducting Devices by Gate Voltage. Nano Lett. 2021, 21, 216–221. [Google Scholar] [CrossRef]
- De Simoni, G.; Paolucci, F.; Puglia, C.; Giazotto, F. Josephson Field-Effect Transistors Based on All-Metallic Al/Cu/Al Proximity Nanojunctions. ACS Nano 2019, 13, 7871–7876. [Google Scholar] [CrossRef]
- Virtanen, P.; Braggio, A.; Giazotto, F. Superconducting size effect in thin films under electric field: Mean-field self-consistent model. Phys. Rev. B 2019, 100, 224506. [Google Scholar] [CrossRef]
- Shmidt, V.V.; Balkov, A.A. The Critical Current in Superconducting Films. Sov. Phys. JETP 1970, 6, 1137–1142. [Google Scholar]
- Shmidt, V.V. Critical Currents in Superconductors. Sov. Phys. Uspekhi 1970, 13, 408–409. [Google Scholar] [CrossRef]
- Aslamazov, L.G.; Larkin, A.I.; Landau, L.D. Josephson effect in wide superconducting bridges. Sov. Phys. JEPT 1975, 41, 381–386. [Google Scholar]
- Kim, P.; Kang, K.T.; Go, G.; Han, J.H. Nature of orbital and spin Rashba coupling in the surface bands of SrTiO3 and KTaO3. Phys. Rev. B 2014, 90, 205423. [Google Scholar] [CrossRef]
- Park, J.H.; Kim, C.H.; Lee, H.W.; Han, J.H. Orbital chirality and Rashba interaction in magnetic bands. Phys. Rev. B 2013, 87, 041301. [Google Scholar] [CrossRef]
- Petersen, L.; Hedegård, P. A simple tight-binding model of spin–orbit splitting of sp-derived surface states. Surf. Sci. 2000, 459, 49–56. [Google Scholar] [CrossRef]
- Mercaldo, M.T.; Solinas, P.; Giazotto, F.; Cuoco, M. Electrically Tunable Superconductivity Through Surface Orbital Polarization. Phys. Rev. Appl. 2020, 14, 034041. [Google Scholar] [CrossRef]
- Sauter, F. Uber das Verhalten eines Elektrons im homogenen elektrischen Feld nach der relativistischen Theorie Diracs. Z. Phys. 1931, 69, 742–764. [Google Scholar] [CrossRef]
- Heisenberg, W.; Euler, H. Folgerungen aus der Diracschen Theorie des Positrons. Z. Phys. 1936, 98, 714–732. [Google Scholar] [CrossRef]
- Solinas, P.; Amoretti, A.; Giazotto, F. Schwinger effect in a Bardeen-Cooper-Schrieffer superconductor. arXiv 2020, arXiv:2007.08323. [Google Scholar]
- Alegria, L.D.; Bøttcher, C.G.L.; Saydjari, A.K.; Pierce, A.T.; Lee, S.H.; Harvey, S.P.; Vool, U.; Yacoby, A. High-energy quasiparticle injection into mesoscopic superconductors. Nat. Nanotechnol. 2021. [Google Scholar] [CrossRef] [PubMed]
- Ritter, M.F.; Fuhrer, A.; Haxell, D.Z.; Hart, S.; Gumann, P.; Riel, H.; Nichele, F. A superconducting switch actuated by injection of high energy electrons. arXiv 2020, arXiv:2005.00462. [Google Scholar]
- Puglia, C.; De Simoni, G.; Giazotto, F. Electrostatic Control of Phase Slips in Ti Josephson Nanotransistors. Phys. Rev. Appl. 2020, 13, 054026. [Google Scholar] [CrossRef]
- Rocci, M.; De Simoni, G.; Puglia, C.; Degli Esposti, D.; Strambini, E.; Zannier, V.; Sorba, L.; Giazotto, F. Gate-Controlled Suspended Titanium Nanobridge Supercurrent Transistor. ACS Nano 2020, 14, 12621–12628. [Google Scholar] [CrossRef] [PubMed]
- Likharev, K.K. Superconductor digital electronics. Phys. C Supercond. Its Appl. 2012, 482, 6–18. [Google Scholar] [CrossRef]
- De Simoni, G.; Puglia, C.; Giazotto, F. Niobium Dayem nano-bridge Josephson gate-controlled transistors. Appl. Phys. Lett. 2020, 116, 242601. [Google Scholar] [CrossRef]
- Stromberg, T.F.; Swenson, C.A. Negative Surface Free-Energy Effects in Superconducting Niobium. Phys. Rev. Lett. 1962, 9, 370–374. [Google Scholar] [CrossRef]
- Finnemore, D.K.; Stromberg, T.F.; Swenson, C.A. Superconducting Properties of High-Purity Niobium. Phys. Rev. 1966, 149, 231–243. [Google Scholar] [CrossRef]
- Giazotto, F.; Heikkilä, T.T.; Luukanen, A.; Savin, A.M.; Pekola, J.P. Opportunities for mesoscopics in thermometry and refrigeration: Physics and applications. Rev. Mod. Phys. 2006, 78, 217–274. [Google Scholar] [CrossRef]
- Tinkham, M. Introduction to Superconductivity; Dover Publications: Mineola, NY, USA, 2004; p. 454. [Google Scholar]
- Puglia, C.; De Simoni, G.; Ligato, N.; Giazotto, F. Vanadium gate-controlled Josephson half-wave nanorectifier. Appl. Phys. Lett. 2020, 116, 252601. [Google Scholar] [CrossRef]
- Barone, A.; Paternò, G. Physics and Applications of the Josephson Effect; Wiley: Hoboken, NJ, USA, 1982. [Google Scholar] [CrossRef]
- Ullom, J.N.; Bennett, D.A. Review of superconducting transition-edge sensors for X-ray and gamma-ray spectroscopy. Supercond. Sci. Technol. 2015, 28, 084003. [Google Scholar] [CrossRef]
- Paolucci, F.; Ligato, N.; Germanese, G.; Buccheri, V.; Giazotto, F. Fully Superconducting Josephson Bolometers for Gigahertz Astronomy. Appl. Sci. 2021, 11, 746. [Google Scholar] [CrossRef]
- Gol’tsman, G.N.; Okunev, O.; Chulkova, G.; Lipatov, A.; Semenov, A.; Smirnov, K.; Voronov, B.; Dzardanov, A.; Williams, C.; Sobolewski, R. Picosecond superconducting single-photon optical detector. Appl. Phys. Lett. 2001, 79, 705–707. [Google Scholar] [CrossRef]
- Ivanov, B.I.; Trgala, M.; Grajcar, M.; Il’ichev, E.; Meyer, H.G. Cryogenic ultra-low-noise SiGe transistor amplifier. Rev. Sci. Instrum. 2011, 82, 104705. [Google Scholar] [CrossRef]
- Oukhanski, N.; Grajcar, M.; Il’ichev, E.; Meyer, H.G. Low noise, low power consumption high electron mobility transistors amplifier, for temperatures below 1 K. Rev. Sci. Instrum. 2003, 74, 1145–1146. [Google Scholar] [CrossRef]
- Clarke, J.; Bragisnki, A.I. The SQUID Handbook; Wiley: Weinheim, Germany, 2004. [Google Scholar]
- Giazotto, F.; Peltonen, J.T.; Meschke, M.; Pekola, J.P. Superconducting quantum interference proximitytransistor. Nat. Phys. 2010, 6, 254–259. [Google Scholar] [CrossRef]
- Giazotto, F.; Martínez-Pérez, M.J. The Josephson heat interferometer. Nature 2012, 492, 401–405. [Google Scholar] [CrossRef] [PubMed]
- Fornieri, A.; Giazotto, F. Towards phase-coherent caloritronics in superconducting circuits. Nat. Nanotechnol. 2017, 12, 944–952. [Google Scholar] [CrossRef]
- McCaughan, A.N. Readout architectures for superconducting nanowire single photon detectors. Supercond. Sci. Technol. 2018, 31, 040501. [Google Scholar] [CrossRef] [PubMed]
- McCaughan, A.N.; Berggren, K.K. A Superconducting-Nanowire Three-Terminal Electrothermal Device. Nano Lett. 2014, 14, 5748–5753. [Google Scholar] [CrossRef] [PubMed]
- Morpurgo, A.F.; Klapwijk, T.M.; van Wees, B.J. Hot electron tunable supercurrent. Appl. Phys. Lett. 1998, 72, 966–968. [Google Scholar] [CrossRef]
- Bezryadin, A. Superconductivity in Nanowires: Fabrication and Quantum Transport; Wiley-VCH: Weinheim, Germany, 2012; p. 282. [Google Scholar]
- Kurkijärvi, J. Intrinsic Fluctuations in a Superconducting Ring Closed with a Josephson Junction. Phys. Rev. B 1972, 6, 832–835. [Google Scholar] [CrossRef]
- Bezryadin, A.; Goldbart, P.M. Superconducting Nanowires Fabricated Using Molecular Templates. Adv. Mater. 2010, 22, 1111–1121. [Google Scholar] [CrossRef]
- Fulton, T.A.; Dunkleberger, L.N.; Dynes, R.C. Quantum Interference Properties of Double Josephson Junctions. Phys. Rev. B 1972, 6, 855–875. [Google Scholar] [CrossRef]
- Fulton, T.; Dynes, R. Switching to zero voltage in Josephson tunnel junctions. Solid State Commun. 1971, 9, 1069–1073. [Google Scholar] [CrossRef]
- Giordano, N. Evidence for Macroscopic Quantum Tunneling in One-Dimensional Superconductors. Phys. Rev. Lett. 1988, 61, 2137–2140. [Google Scholar] [CrossRef] [PubMed]
- Zaikin, A.D.; Golubev, D.S.; van Otterlo, A.; Zimányi, G.T. Quantum Phase Slips and Transport in Ultrathin Superconducting Wires. Phys. Rev. Lett. 1997, 78, 1552–1555. [Google Scholar] [CrossRef]
- Sahu, M.; Bae, M.H.; Rogachev, A.; Pekker, D.; Wei, T.C.; Shah, N.; Goldbart, P.M.; Bezryadin, A. Individual topological tunnelling events of a quantum field probed through their macroscopic consequences. Nat. Phys. 2009, 5, 503–508. [Google Scholar] [CrossRef]
- Golubov, A.; Neurohr, K.; Schäpers, T.; Lüth, H.; Behet, M. Suppression of Josephson currents in ballistic junctions by an injection current. Superlattices Microstruct. 1999, 25, 1033–1040. [Google Scholar] [CrossRef]
- Bezryadin, A.; Lau, C.N.; Tinkham, M. Quantum suppression of superconductivity in ultrathin nanowires. Nature 2000, 404, 971–974. [Google Scholar] [CrossRef]
- Giordano, N.; Schuler, E. Macroscopic quantum tunneling and related effects in a one-dimensional superconductor. Phys. Rev. Lett. 1989, 63, 2417–2420. [Google Scholar] [CrossRef] [PubMed]
- Fulton, T.A.; Dunkleberger, L.N. Lifetime of the zero-voltage state in Josephson tunnel junctions. Phys. Rev. B 1974, 9, 4760–4768. [Google Scholar] [CrossRef]
- Ejrnaes, M.; Salvoni, D.; Parlato, L.; Massarotti, D.; Caruso, R.; Tafuri, F.; Yang, X.Y.; You, L.X.; Wang, Z.; Pepe, G.P.; et al. Superconductor to resistive state switching by multiple fluctuation events in NbTiN nanostrips. Sci. Rep. 2019, 9, 8053. [Google Scholar] [CrossRef]
- Li, Q.; Huang, S.; Pan, D.; Wang, J.; Zhao, J.; Xu, H.Q. Suspended InAs nanowire gate-all-around field-effect transistors. Appl. Phys. Lett. 2014, 105, 113106. [Google Scholar] [CrossRef]
- Iorio, A.; Rocci, M.; Bours, L.; Carrega, M.; Zannier, V.; Sorba, L.; Roddaro, S.; Giazotto, F.; Strambini, E. Vectorial Control of the Spin–Orbit Interaction in Suspended InAs Nanowires. Nano Lett. 2019, 19, 652–657. [Google Scholar] [CrossRef] [PubMed]
- Simmons, J.G. Generalized Formula for the Electric Tunnel Effect between Similar Electrodes Separated by a Thin Insulating Film. J. Appl. Phys. 1963, 34, 1793–1803. [Google Scholar] [CrossRef]
- Fowler, R.H.; Nordheim, L. Electron emission in intense electric fields. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1928, 119, 173–181. [Google Scholar] [CrossRef]
- Wilson, R.G. Vacuum Thermionic Work Functions of Polycrystalline Be, Ti, Cr, Fe, Ni, Cu, Pt, and Type 304 Stainless Steel. J. Appl. Phys. 1966, 37, 2261–2267. [Google Scholar] [CrossRef]
- Bhushan, B. Encyclopedia of Nanotechnology; Springer: Dordrecht, The Netherlands, 2012; pp. 824–837. [Google Scholar]
- Ummarino, G.A.; Piatti, E.; Daghero, D.; Gonnelli, R.S.; Sklyadneva, I.Y.; Chulkov, E.V.; Heid, R. Proximity Eliashberg theory of electrostatic field-effect doping in superconducting films. Phys. Rev. B 2017, 96, 064509. [Google Scholar] [CrossRef]
- Zmuidzinas, J.; Richards, P. Superconducting detectors and mixers for millimeter and submillimeter astrophysics. Proc. IEEE 2004, 92, 1597–1616. [Google Scholar] [CrossRef]
- Gousev, Y.P.; Gol’tsman, G.N.; Semenov, A.D.; Gershenzon, E.M.; Nebosis, R.S.; Heusinger, M.A.; Renk, K.F. Broadband ultrafast superconducting NbN detector for electromagnetic radiation. J. Appl. Phys. 1994, 75, 3695–3697. [Google Scholar] [CrossRef]
- Lösch, S.; Alfonsov, A.; Dobrovolskiy, O.V.; Keil, R.; Engemaier, V.; Baunack, S.; Li, G.; Schmidt, O.G.; Bürger, D. Microwave Radiation Detection with an Ultrathin Free-Standing Superconducting Niobium Nanohelix. ACS Nano 2019, 13, 2948–2955. [Google Scholar] [CrossRef] [PubMed]
- Mukhanov, O.A. Energy-Efficient Single Flux Quantum Technology. IEEE Trans. Appl. Supercond. 2011, 21, 760–769. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Puglia, C.; De Simoni, G.; Giazotto, F. Gate Control of Superconductivity in Mesoscopic All-Metallic Devices. Materials 2021, 14, 1243. https://doi.org/10.3390/ma14051243
Puglia C, De Simoni G, Giazotto F. Gate Control of Superconductivity in Mesoscopic All-Metallic Devices. Materials. 2021; 14(5):1243. https://doi.org/10.3390/ma14051243
Chicago/Turabian StylePuglia, Claudio, Giorgio De Simoni, and Francesco Giazotto. 2021. "Gate Control of Superconductivity in Mesoscopic All-Metallic Devices" Materials 14, no. 5: 1243. https://doi.org/10.3390/ma14051243
APA StylePuglia, C., De Simoni, G., & Giazotto, F. (2021). Gate Control of Superconductivity in Mesoscopic All-Metallic Devices. Materials, 14(5), 1243. https://doi.org/10.3390/ma14051243







