Vibration and Damping Analysis of Pipeline System Based on Partially Piezoelectric Active Constrained Layer Damping Treatment
Abstract
1. Introduction
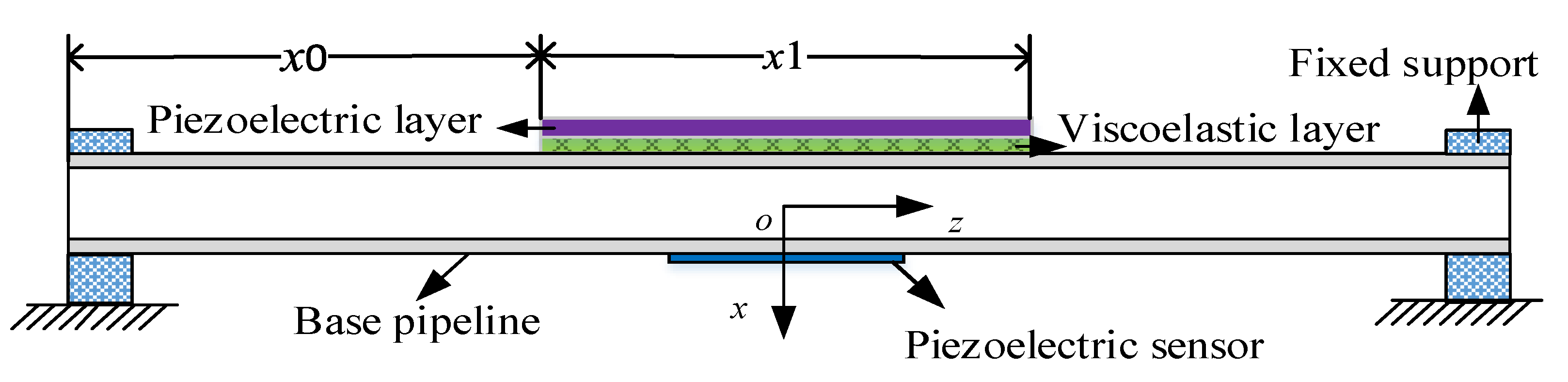
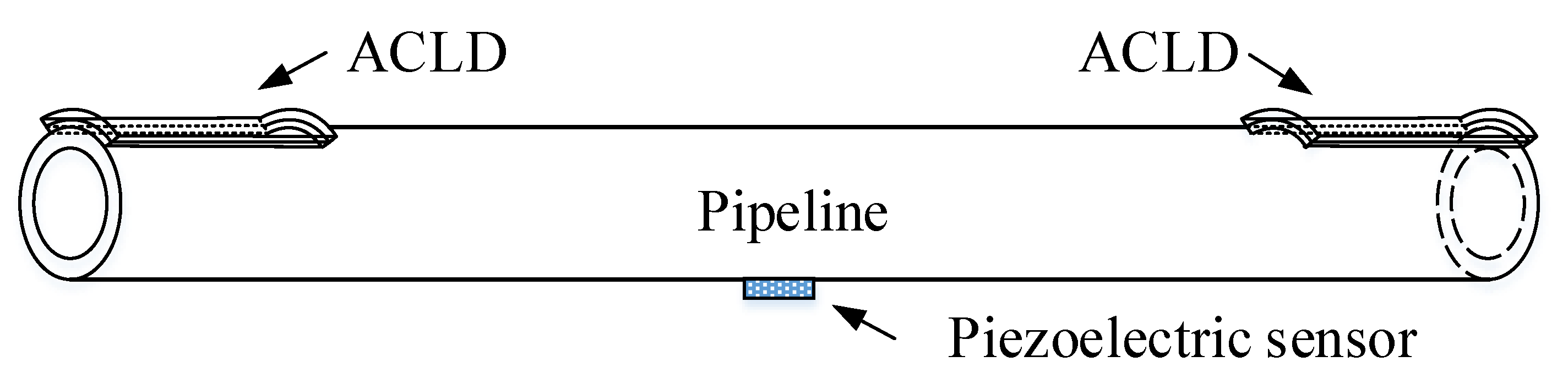
2. Finite Element Model of the Pipeline
- The rotation and shear deformation of piezoelectric layer and base pipeline are not considered;
- The viscoelastic layer has a transverse variable, but the normal stress is negligible;
- The pipeline, viscoelastic damping layer, and piezoelectric layer are all in the linear elastic range;
- There is no relative slip between the layers and the interfaces have a perfect continuity;
- The potential distribution of piezoelectric layer is linear along the thickness direction;
- The complex shear modulus of viscoelastic material is independent of temperature.
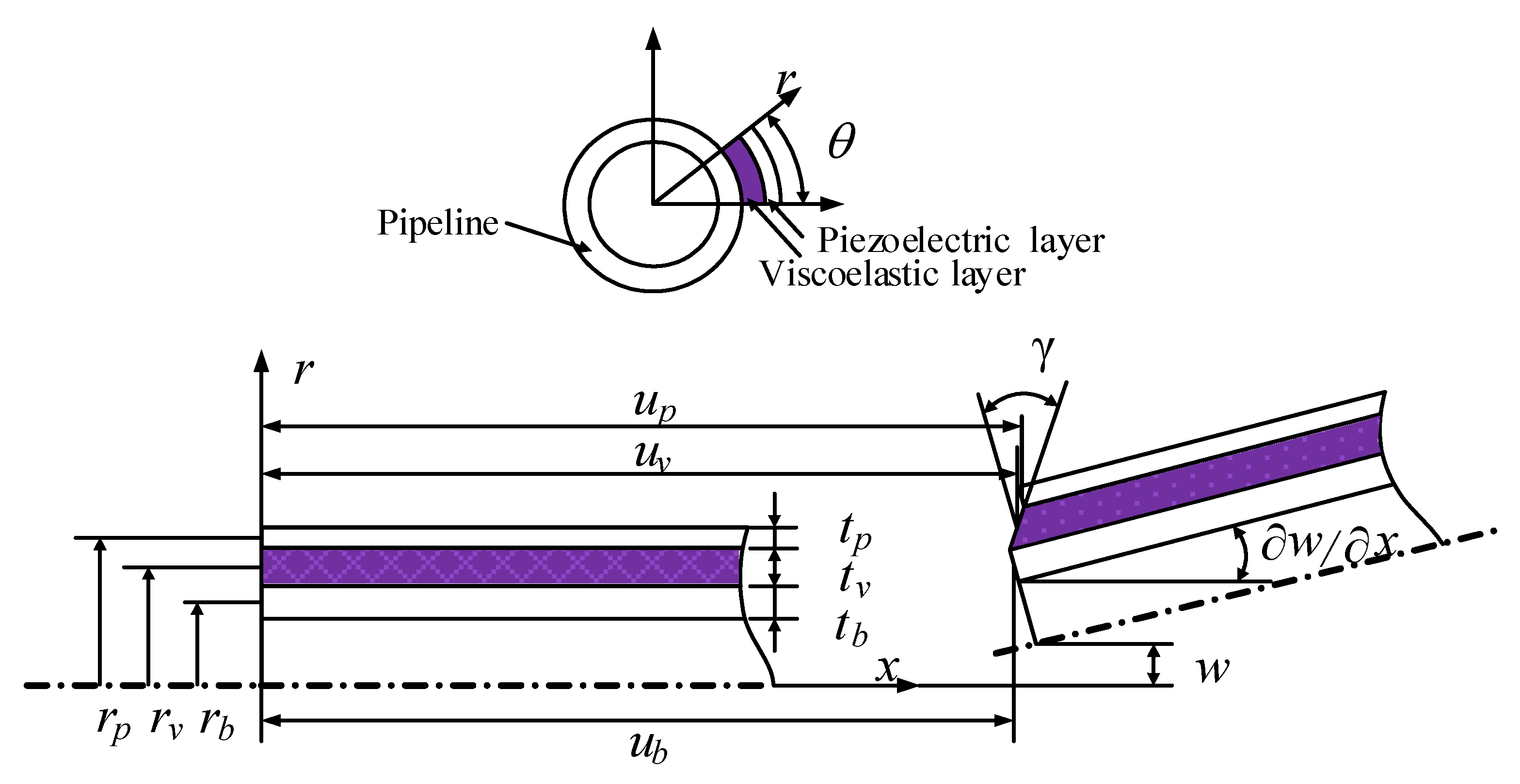
2.1. Displacement Fields
2.2. Shape Functions
2.3. Energy Expressions
2.3.1. Base Pipeline Layer
2.3.2. Viscoelastic Layer
2.3.3. Piezoelectric Layer
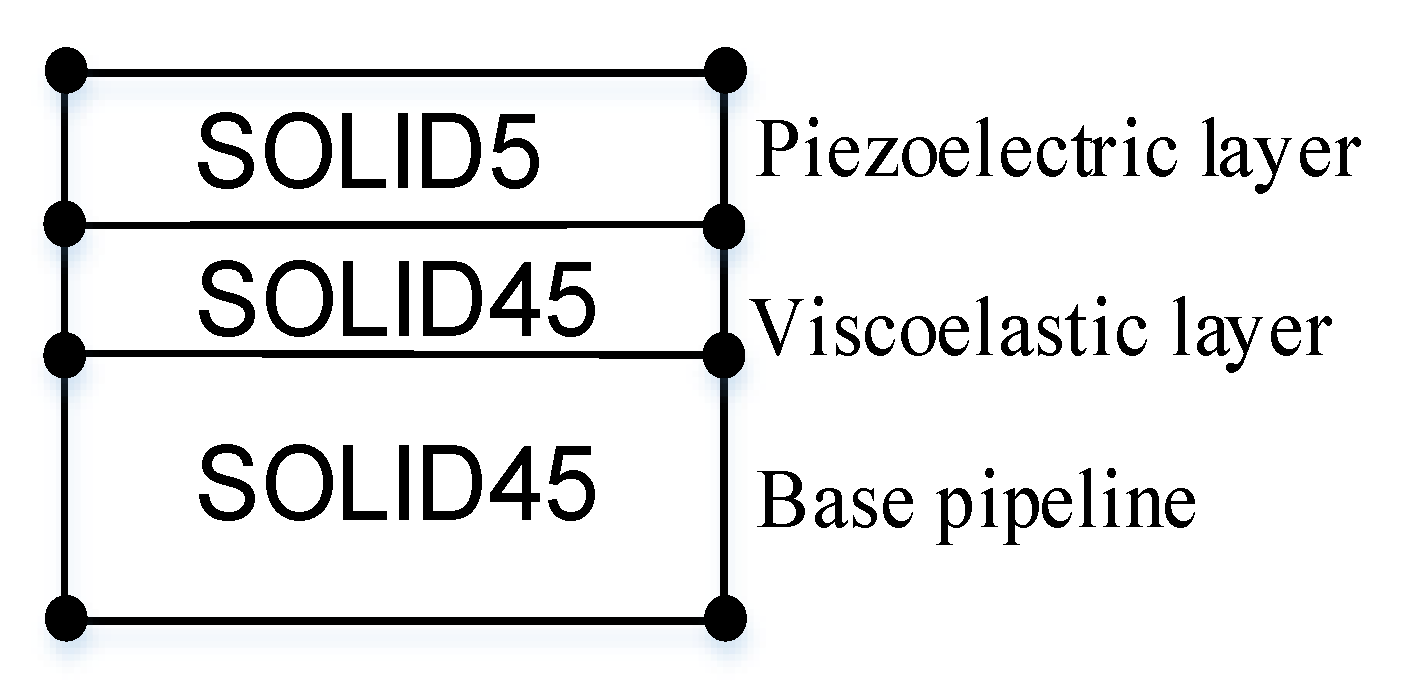
2.4. Finite Element Implementation
3. Results and Discussion
3.1. Verification of Numerical Model
3.2. Parameterization of the Proposed Model
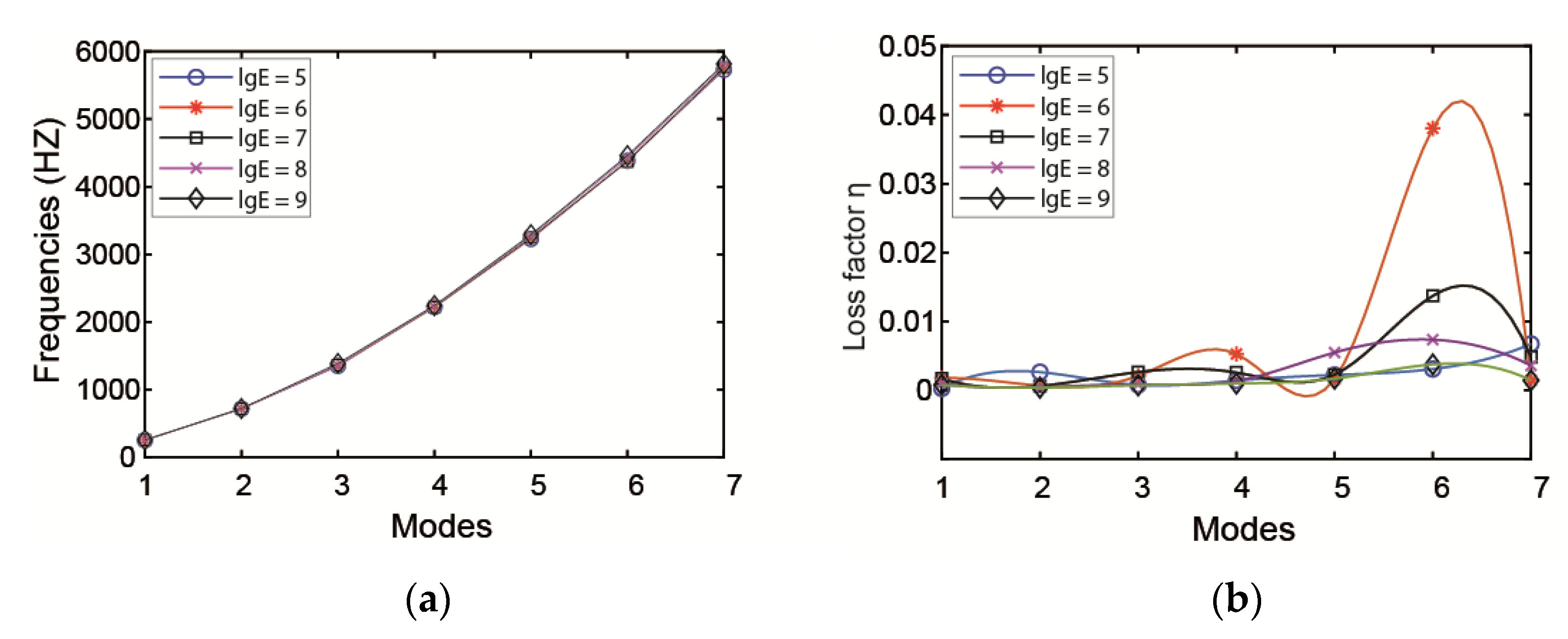
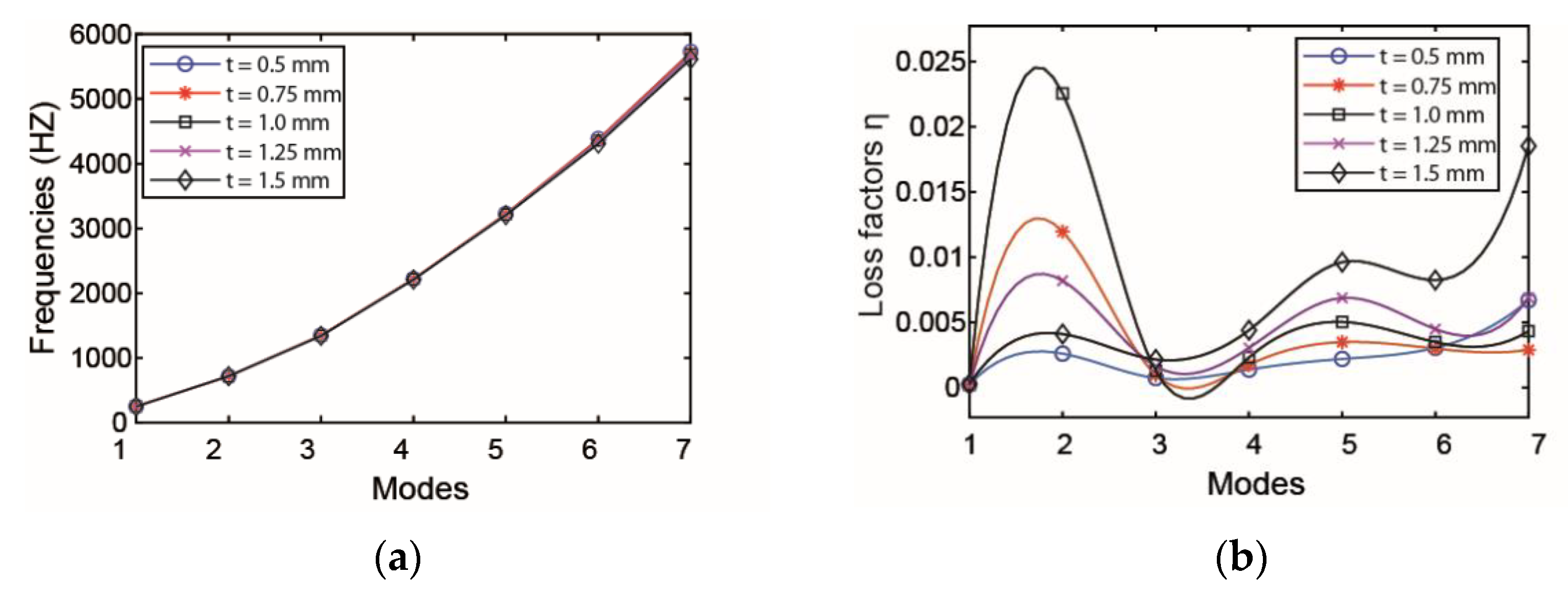
3.2.1. The Influence of Viscoelastic Layer Parameters on Pipeline Vibration
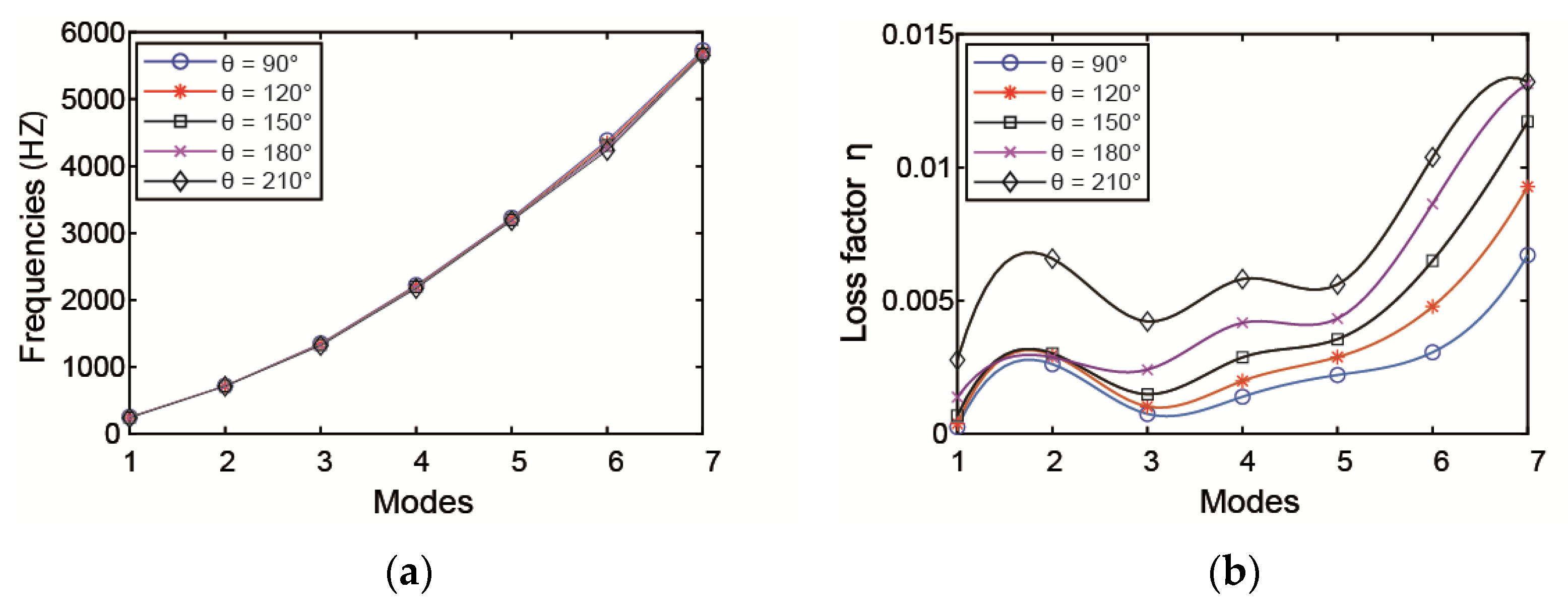
3.2.2. Influence of ACLD Laying Circle Angle
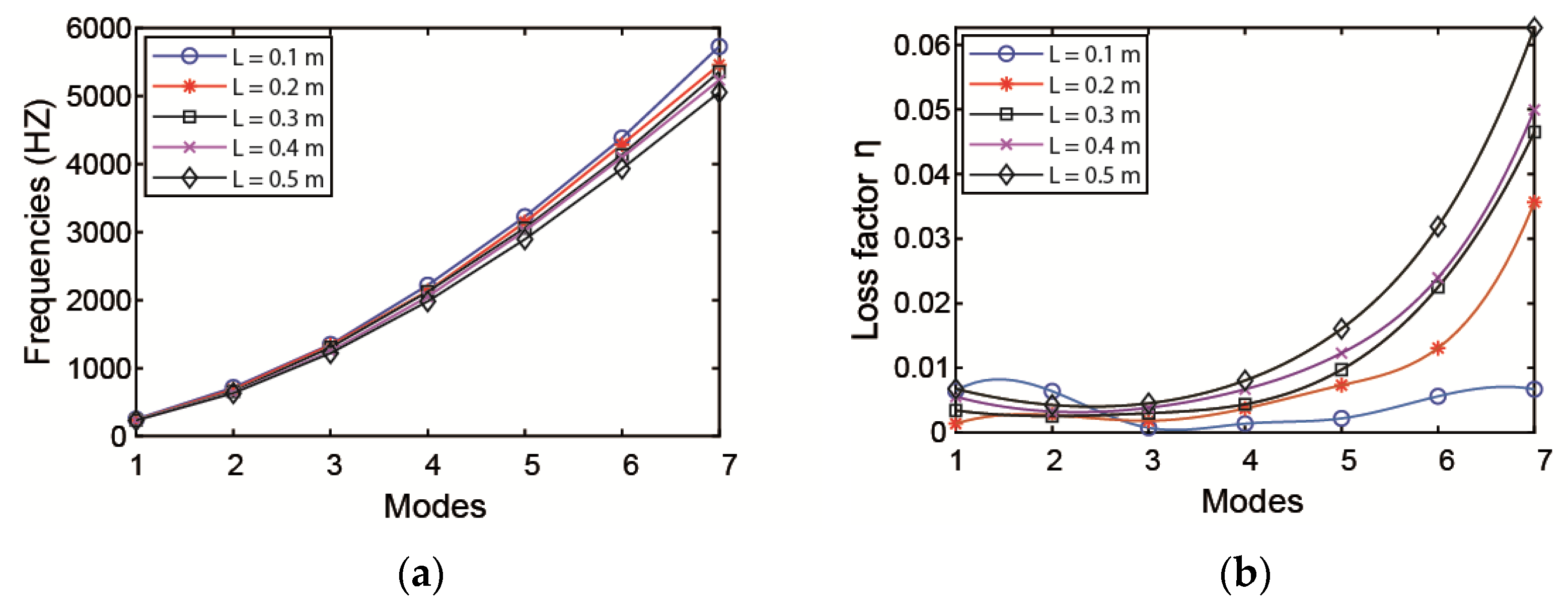
3.2.3. The Influence of the Length of ACLD
3.2.4. The Influence of Voltage
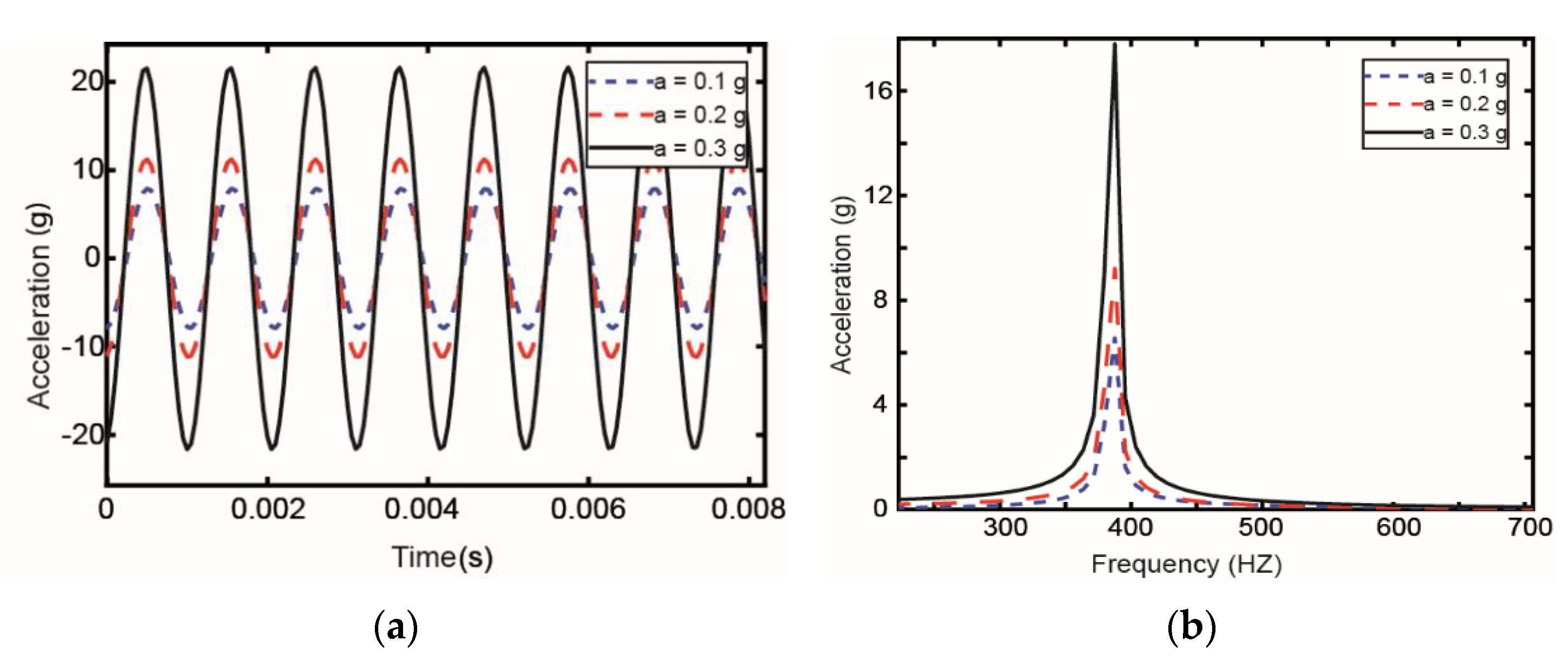
3.2.5. The Influence of Different Excitations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, H.; Lv, H.; Sun, H.; Qin, Z.; Xiong, J.; Han, Q.; Liu, J.; Wang, X. Nonlinear Vibrations of Fiber-reinforced Composite Cylindrical Shells with Bolt Loosening Boundary Conditions. J. Sound Vib. 2021, 496, 115935. [Google Scholar] [CrossRef]
- Sorokin, S.; Hoist-Jensen, O. On Power Flow Suppression in Straight Elastic Pipes by Use of Equally Spaced Eccentric Inertial Attachments. J. Vib. Acoust. 2012, 134, 041003. [Google Scholar] [CrossRef]
- Kerwin, E.M., Jr. Damping of Flexural Waves by a Constrained Viscoelastic Layer. J. Acoust. Soc. Am. 1959, 31, 952–962. [Google Scholar] [CrossRef]
- Gao, P.X.; Zhai, J.Y.; Qu, F.Z.; Han, Q.K. Vibration and damping analysis of aerospace pipeline conveying fluid with constrained layer damping treatment. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2017, 232, 1529–1541. [Google Scholar] [CrossRef]
- Vasques, C.M.A.; Mace, B.R.; Gardonio, P.; Rodrigues, J.D. Arbitrary active constrained layer damping treatments on beams: Finite element modelling and experimental validation. Comput. Struct. 2006, 84, 1384–1401. [Google Scholar] [CrossRef]
- Zhai, J.; Li, J.; Wei, D.; Gao, P.; Han, Q. Vibration Control of an Aero Pipeline System with Active Constraint Layer Damping Treatment. Appl. Sci. 2019, 9, 2094. [Google Scholar] [CrossRef]
- Kheiri, M.; Païdoussis, M.P.; Del Pozo, G.C.; Amabili, M. Dynamics of a pipe conveying fluid flexibly restrained at the ends. J. Fluids Struct. 2014, 49, 360–385. [Google Scholar] [CrossRef]
- Li, Q.S.; Yang, K.; Zhang, L. Analytical Solution for Fluid-Structure Interaction in Liquid-Filled Pipes Subjected to Impact-Induced Water H/ammer. J. Eng. Mech. 2003, 129, 1408–1417. [Google Scholar] [CrossRef]
- Gao, P.-X.; Zhai, J.-Y.; Yan, Y.-Y.; Han, Q.-K.; Qu, F.-Z.; Chen, X.-H. A model reduction approach for the vibration analysis of hydraulic pipeline system in aircraft. Aerosp. Sci. Technol. 2016, 49, 144–153. [Google Scholar] [CrossRef]
- Agnes, G.; Napolitano, K. Active constrained layer viscoelastic damping. In Proceedings of the34th AIAA/ASME/ASCE/AHS/ASC Structures Structures Dynamics, and Materials Conference, Reston, VA, USA, 19–22 April 1993; p. 1702. [Google Scholar] [CrossRef]
- Baz, A.; Ro, J.-J. Concept and performance of active constrained layer damping treatments. Sound Vib. 1994, 28, 18–21. [Google Scholar]
- Shen, I.Y. A Variational Formulation, a Work-Energy Relation and Damping Mechanisms of Active Constrained Layer Treatments. J. Vib. Acoust. 1995, 119, 192. [Google Scholar] [CrossRef]
- Lesieutre, G.A.; Lee, U. A finite element for beams having segmented active constrained layers with frequency-dependent viscoelastics. Smart Mater. Struct. 1996, 5, 615. [Google Scholar] [CrossRef]
- Liao, W.H.; Wang, K.W. A new active constrained layer configuration with enhanced boundary actions. Smart Mater. Struct. 1996, 5, 638. [Google Scholar] [CrossRef]
- Balamurugan, V.; Narayanan, S. Finite Element Formulation and Active Vibration Control Study on Beams Using Smart Constrained Layer Damping (SCLD) Treatment. J. Sound Vib. 2002, 249, 227–250. [Google Scholar] [CrossRef]
- Sonti, V.R.; Jones, J.D. Curved piezo-actuator models for vibration control of cylindrical shells. J. Acoust. Soc. Am. 1993, 93, 2352. [Google Scholar] [CrossRef]
- Guo, Y.; Li, L.; Zhang, D. Dynamic modeling and vibration analysis of rotating beams with active constrained layer damping treatment in temperature field. Compos. Struct. 2019, 226, 111217. [Google Scholar] [CrossRef]
- Cao, X.; Tanner, G.; Chronopoulos, D. Active vibration control of thin constrained composite damping plates with double piezoelectric layers. Wave Motion 2019, 92, 102423. [Google Scholar] [CrossRef]
- Zhang, D.; Zheng, L.; Li, Y. Optimal configurations of ACLD/Plate for bending vibration control using INSGA-II. INTER-NOISE NOISE-CON Congr. Conf. Proc. 2014, 249, 505–516. [Google Scholar]
- Kumar, S.; Kumar, R. Theoretical and experimental vibration analysis of rotating beams with combined ACLD and Stressed Layer Damping treatment. Appl. Acoust. 2013, 74, 675–693. [Google Scholar] [CrossRef]
- Kumar, R. Enhanced active constrained layer damping (ACLD) treatment using stand-off-layer: Robust controllers design, experimental implementation and comparison. J. Vib. Control 2012, 19, 439–460. [Google Scholar] [CrossRef]
- Koh, B.; Rustighi, E.; Waters, T.; Mace, B. Vibration control of beams and plates with hybrid active-passive constrained layer damping treatments. Proceedings of 23rd International Congress of Sound & Vibration, ICSV23, Bangkok, Thailand, 10 July 2016. [Google Scholar]
- Trindade, M.A.; Benjeddou, A. Hybrid Active-Passive Damping Treatments Using Viscoelastic and Piezoelectric Materials: Review and Assessment. J. Vib. Control 2002, 8, 699–745. [Google Scholar] [CrossRef]
- Kumar, A.; Ray, M.C. Control of smart rotating laminated composite truncated conical shell using ACLD treatment. Int. J. Mech. Sci. 2014, 89, 123–141. [Google Scholar] [CrossRef]
- Ro, J.; Baz, A. Optimum placement and control of active constrained layer damping using the modal strain energy approach. In Proceedings of the International Symposium on Smart Structures & Materials, San Diego, CA, USA, 27 July 1998; pp. 844–855. [Google Scholar]
- Kumar, N.; Singh, S.P. Vibration and damping characteristics of beams with active constrained layer treatments under parametric variations. Mater. Design 2009, 30, 4162–4174. [Google Scholar] [CrossRef]
- Tsai, T.C.; Tsau, J.H.; Chen, C.S. Vibration analysis of a beam with partially distributed internal viscous damping. Int. J. Mech. Ences 2009, 51, 907–914. [Google Scholar] [CrossRef]
- Qiu, Z.; Ling, D. Finite element modeling and robust vibration control of two-hinged plate using bonded piezoelectric sensors and actuators. Acta Mech. Solida Sin. 2014, 27, 146–161. [Google Scholar] [CrossRef]
- Daraji, A.H.; Hale, J.M. Active vibration reduction by optimally placed sensors and actuators with application to stiffened plates by beams. Smart Mater. Struct. 2014, 23, 115018. [Google Scholar] [CrossRef]
- Kapuria, S.; Yaqoob Yasin, M. Active vibration control of piezoelectric laminated beams with electroded actuators and sensors using an efficient finite element involving an electric node. Smart Mater. Struct. 2010, 19, 045019. [Google Scholar] [CrossRef]
- Zabihollah, A.; Sedagahti, R.; Ganesan, R. Active vibration suppression of smart laminated beams using layerwise theory and an optimal control strategy. Smart Mater. Struct. 2007, 16, 2190. [Google Scholar] [CrossRef]



| Quantities | Base Layer | Viscoelastic Layer | Constraining Layer |
|---|---|---|---|
| Elastic modulus (Pa) | 2.01 × 1011 | 4.5 × 105 | — |
| Density (kg/m3) | 7860 | 980 | 7400 |
| Thickness (mm) | 1 | 0.5 | 1 |
| Poisson ratio | 0.3 | 0.5 | 0.3 |
| Loss factor | — | 0.9683 | — |
| Radian | |||
| Pipeline inner diameter = 7 mm; Length = 600 mm. | |||
| Quantities | Base Layer | Viscoelastic Layer | Piezoelectric Layer |
|---|---|---|---|
| Elastic modulus (Pa) | 7.1 × 1010 | — | 3 × 109 |
| Shear modulus (Pa) | — | 5 × 107(1 + 0.7i) | — |
| Density (kg/m3) | 2700 | 1714 | 7500 |
| Thickness (mm) | 1.1 | 0.5–1.5 | 0.1 |
| The length of the beam L = 200 mm; width b = 20 mm. | |||
| Mode | 1 | 2 | 3 |
|---|---|---|---|
| Result in Reference [26] (HZ) | 20.0 | 120.0 | 330.0 |
| Result in ANSYS (HZ) | 19.2 | 120.1 | 320.1 |
| Result in MATLAB (HZ) | 19.3 | 119.8 | 330.3 |
| Coverage (%) | 65 | 80 |
|---|---|---|
| Reference [26] loss factor | 0.0363 | 0.0362 |
| Present work loss factor | 0.0364 | 0.0375 |
| Error max (%) | 2.7 | 3.5 |
| Frequency (HZ) | Loss Factor | |||||
|---|---|---|---|---|---|---|
| Mode 1 | Mode 2 | Mode 3 | Mode 1 | Mode 2 | Mode 3 | |
| Case 1 | 234.4 | 639.5 | 1252.8 | 5.34 × 10−3 | 3.11 × 10−3 | 3.05 × 10−3 |
| Case 2 | 264.6 | 692.2 | 1336.5 | 2.64 × 10−3 | 3.46 × 10−3 | 4.05 × 10−3 |
| Case 3 | 241.3 | 691.4 | 1321.8 | 1.25 × 10−2 | 4.65 × 10−3 | 1.46 × 10−2 |
| Control Voltages | Amplitude of Acceleration (g) | Droop Rate (%) |
|---|---|---|
| 0 V | 32.78 | 0 |
| 25 V | 23.12 | 29.46 |
| 50 V | 15.78 | 51.86 |
| 75 V | 15.36 | 53.14 |
| 100 V | 22.23 | 32.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Liu, X.; Rong, W.; Gao, P.; Yu, T.; Han, H.; Xu, L. Vibration and Damping Analysis of Pipeline System Based on Partially Piezoelectric Active Constrained Layer Damping Treatment. Materials 2021, 14, 1209. https://doi.org/10.3390/ma14051209
Zhang Y, Liu X, Rong W, Gao P, Yu T, Han H, Xu L. Vibration and Damping Analysis of Pipeline System Based on Partially Piezoelectric Active Constrained Layer Damping Treatment. Materials. 2021; 14(5):1209. https://doi.org/10.3390/ma14051209
Chicago/Turabian StyleZhang, Yuanlin, Xuefeng Liu, Weichong Rong, Peixin Gao, Tao Yu, Huawei Han, and Langjun Xu. 2021. "Vibration and Damping Analysis of Pipeline System Based on Partially Piezoelectric Active Constrained Layer Damping Treatment" Materials 14, no. 5: 1209. https://doi.org/10.3390/ma14051209
APA StyleZhang, Y., Liu, X., Rong, W., Gao, P., Yu, T., Han, H., & Xu, L. (2021). Vibration and Damping Analysis of Pipeline System Based on Partially Piezoelectric Active Constrained Layer Damping Treatment. Materials, 14(5), 1209. https://doi.org/10.3390/ma14051209






