Investigation by Digital Image Correlation of Mixed-Mode I and II Fracture Behavior of Polymeric IASCB Specimens with Additive Manufactured Crack-Like Notch
Abstract
1. Introduction
2. Materials and Methods
2.1. Specimen Fabrication
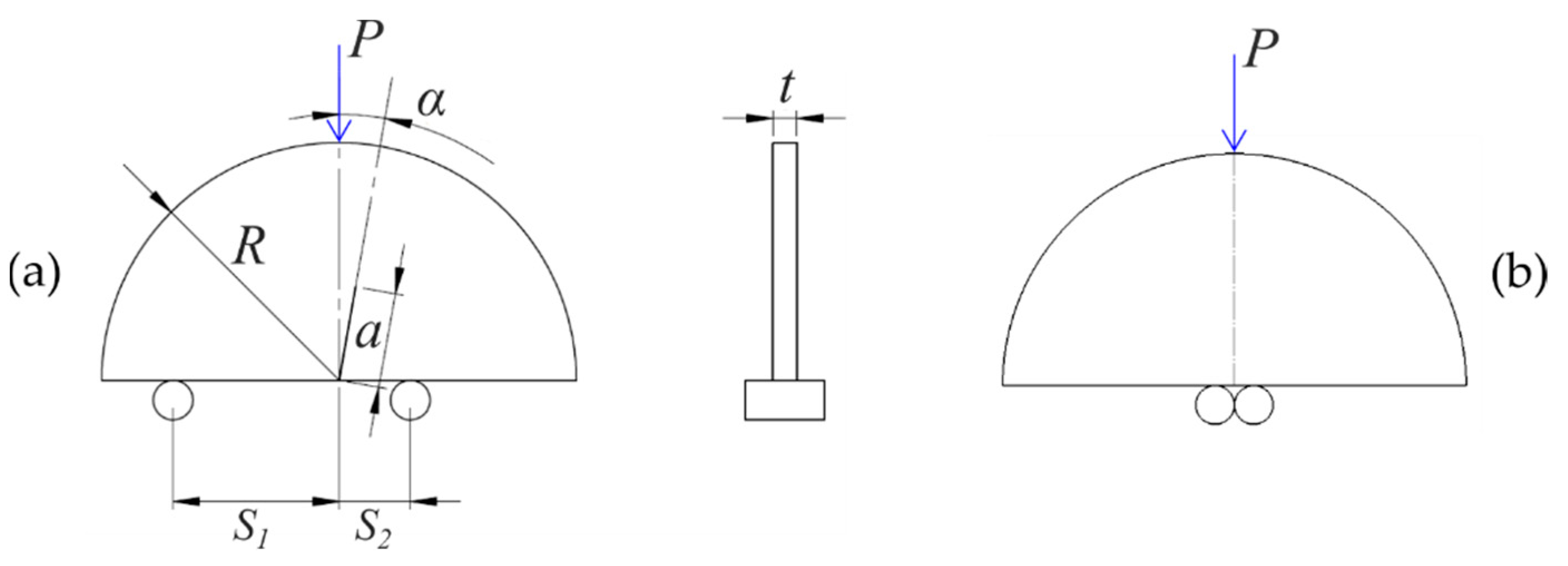
2.2. IASB Specimens
2.3. Experimental Setup
2.4. J-Integral Computation via the LDC Method
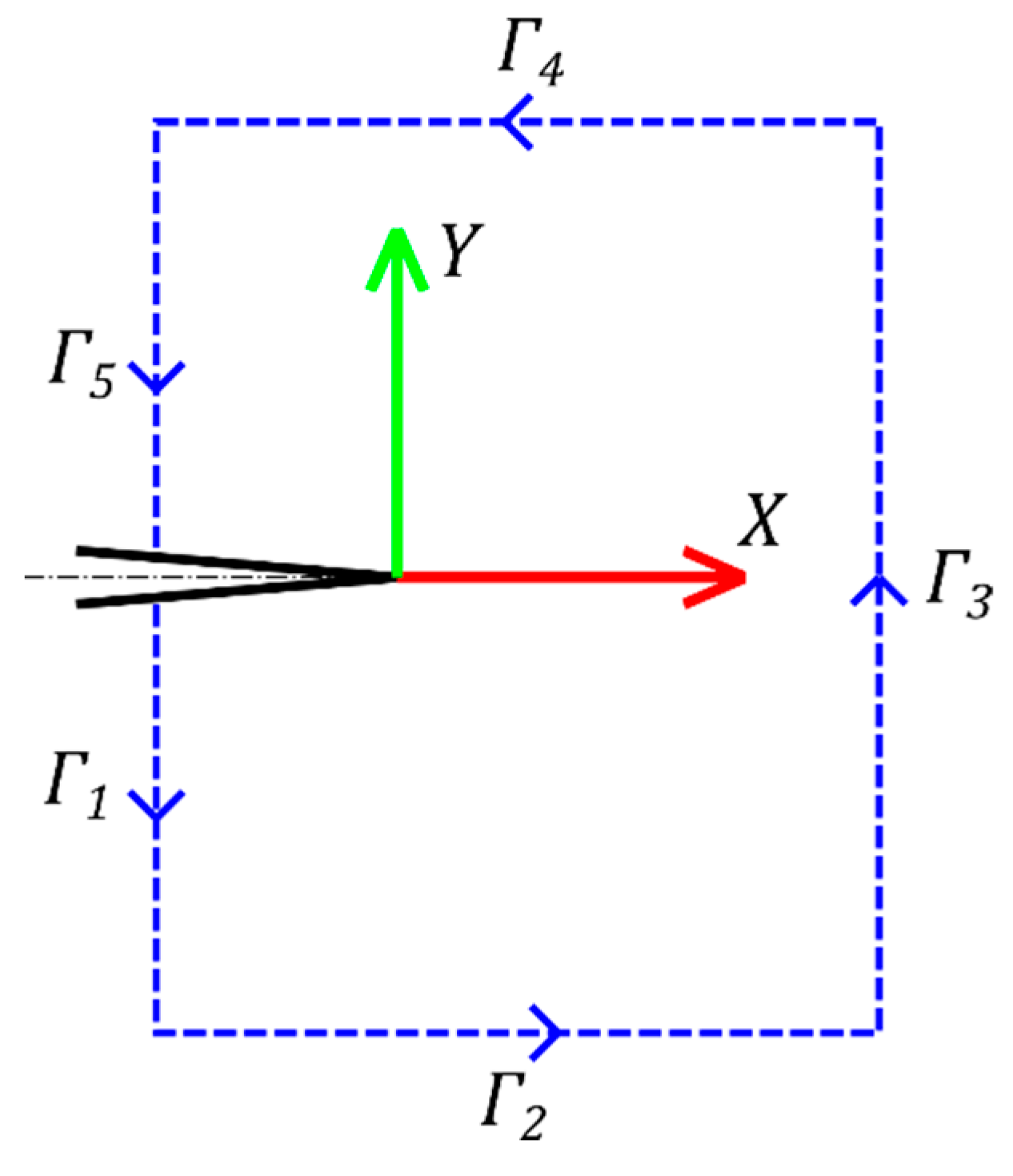
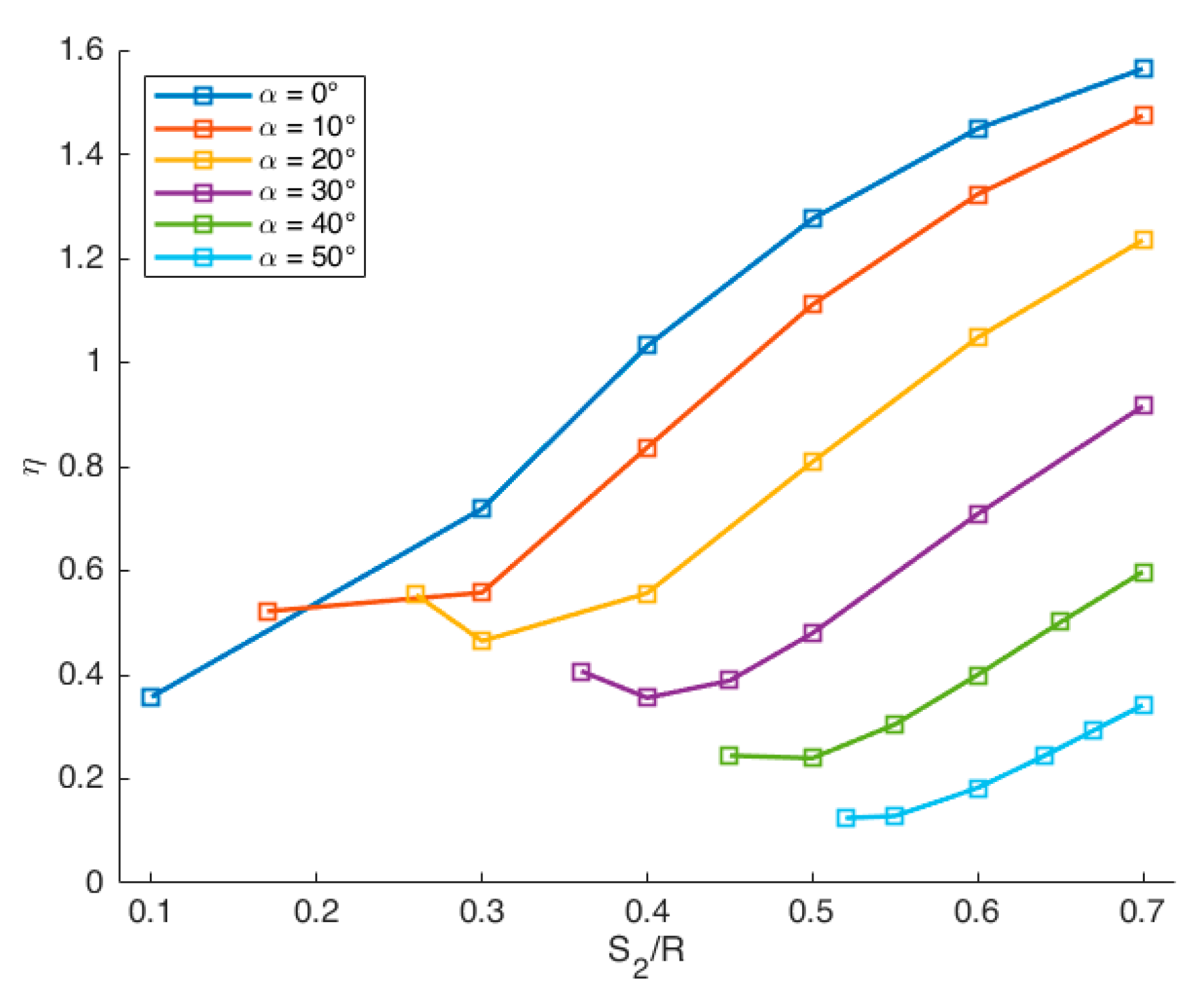
2.4.1. FEM Calculation of the J-Integral Geometry Factors
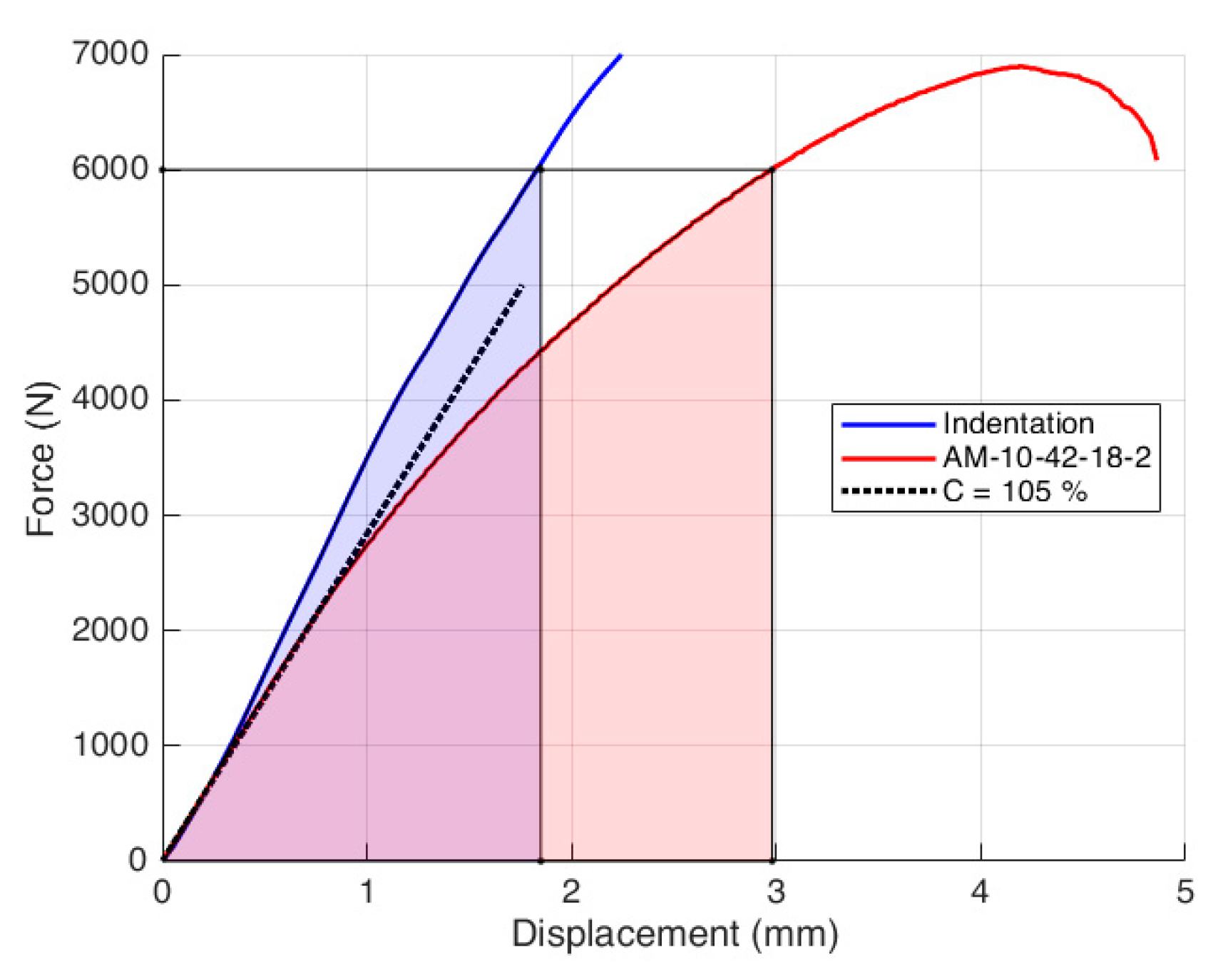
2.4.2. J-Integral Computation from the Load–Displacement Curve Results
2.5. J-Integral Computation via the DIC Method
3. Results
3.1. J-Integral Results from the LDC Method
3.2. J-Integral Computation via the DIC-Based Method
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kruth, J.; Mercelis, P.; Van Vaerenbergh, J.; Froyen, L.; Rombouts, M. Binding Mechanisms in Selective Laser Sintering and Selective Laser Melting. Rapid Prototyp. J. 2005, 11, 26–36. [Google Scholar] [CrossRef]
- Zhang, W.; Melcher, R.; Travitzky, N.; Bordia, R.K.; Greil, P. Three-Dimensional Printing of Complex-Shaped Alumina/Glass Composites. Adv. Eng. Mater. 2009, 11, 139–1043. [Google Scholar] [CrossRef]
- Brugo, T.; Palazzetti, R.; Ciric-Kostic, S.; Yan, X.T.; Minak, G.; Zucchelli, A. Fracture Mechanics of Laser Sintered Cracked Polyamide for a New Method to Induce Cracks by Additive Manufacturing. Polym. Test. 2016, 50, 301–308. [Google Scholar] [CrossRef]
- Campione, I.; Brugo, T.M.; Minak, G.; Tomić, J.J.; Bogojević, N.; Kostić, S.Ć. Investigation by Digital Image Correlation of Mixed Mode I and II Fracture Behavior of Metallic IASCB Specimens with Additive Manufactured Crack-Like Notch. Metals 2020, 10, 400. [Google Scholar] [CrossRef]
- Ameri, B.; Taheri-Behrooz, F.; Aliha, M.R.M. Fracture Loads Prediction of the Modified 3D-Printed ABS Specimens under Mixed-Mode I/II Loading. Eng. Fract. Mech. 2020, 235, 107181. [Google Scholar] [CrossRef]
- Williams, J.G.; Ewing, P.D. Fracture under complex stress—The angled crack problem. Int. J. Fract. 1972, 8, 441–446. [Google Scholar] [CrossRef]
- Papadopoulos, G.A.; Poniridis, P.I. Crack Initiation under Biaxial Loading with Higher-Order Approximation. Eng. Fract. Mech. 1989, 32, 351–360. [Google Scholar] [CrossRef]
- Silva, A.L.L.; de Jesus, A.M.P.; Xavier, J.; Correia, J.A.F.O.; Fernandes, A.A. Combined Analytical-Numerical Methodologies for the Evaluation of Mixed-Mode (I + II) Fatigue Crack Growth Rates in Structural Steels. Eng. Fract. Mech. 2017, 185, 124–138. [Google Scholar] [CrossRef]
- Oliveira, J.; Xavier, J.; Pereira, F.; Morais, J.; de Moura, M. Direct Evaluation of Mixed Mode I+II Cohesive Laws of Wood by Coupling MMB Test with DIC. Materials 2021, 14, 374. [Google Scholar] [CrossRef]
- Aliha, M.R.M.; Ayatollahi, M.R. Brittle Fracture Evaluation of a Fine Grain Cement Mortar in Combined Tensile-Shear Deformation. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 987–994. [Google Scholar] [CrossRef]
- Lim, I.L.; Johnston, I.W.; Choi, S.K.; Boland, J.N. Fracture Testing of a Soft Rock with Semi-Circular Specimens under Three-Point Bending. Part 2—Mixed-Mode. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1994, 31, 199–212. [Google Scholar] [CrossRef]
- Ayatollahi, M.R.; Aliha, M.R.M.; Saghafi, H. An Improved Semi-Circular Bend Specimen for Investigating Mixed Mode Brittle Fracture. Eng. Fract. Mech. 2011, 78, 110–123. [Google Scholar] [CrossRef]
- Darban, H.; Haghpanahi, M.; Assadi, A. Determination of Crack Tip Parameters for ASCB Specimen under Mixed Mode Loading Using Finite Element Method. Comput. Mater. Sci. 2011, 50, 1667–1674. [Google Scholar] [CrossRef]
- Saghafi, H.; Monemian, S. A New Fracture Toughness Test Covering Mixed-Mode Conditions and Positive and Negative T-Stresses. Int. J. Fract. 2010, 165, 135–138. [Google Scholar] [CrossRef]
- Saghafi, H.; Zucchelli, A.; Minak, G. Evaluating Fracture Behavior of Brittle Polymeric Materials Using an IASCB Specimen. Polym. Test. 2013, 32, 133–140. [Google Scholar] [CrossRef]
- Moore, A.J.; Tyrer, J.R. The Evaluation of Fracture Mechanics Parameters from Electronic Speckle Pattern Interferometric Fringe Patterns. Opt. Lasers Eng. 1993, 19, 325–336. [Google Scholar] [CrossRef]
- Peters, W.H.; Ranson, W.F. Digital imaging techniques in experimental stress analysis. Opt. Eng. 1982, 21, 427–431. [Google Scholar] [CrossRef]
- Doll, B.; Ozer, H.; Rivera-Perez, J.J.; Al-Qadi, I.L.; Lambros, J. Investigation of Viscoelastic Fracture Fields in Asphalt Mixtures Using Digital Image Correlation. Int. J. Fract. 2017, 205, 37–56. [Google Scholar] [CrossRef]
- Yuan, F.; Cheng, L.; Shao, X.; Dong, Z.; Zhang, L.; Wu, G.; He, X. Full-Field Measurement and Fracture and Fatigue Characterizations of Asphalt Concrete Based on the SCB Test and Stereo-DIC. Eng. Fract. Mech. 2020, 235, 107127. [Google Scholar] [CrossRef]
- ASTM D6068-96. Standard Test Method for Determining J-R Curves of Plastic Materials; ASTM International: West Conshohocken, PA, USA, 1996. [Google Scholar]
- Rice, J.R. A path independent integral and the approximate analysis of strain concentration by notches and cracks. J. Appl. Mech. 1968, 35, 379–386. [Google Scholar] [CrossRef]
- Vavrik, D.; Jandejsek, I. Experimental Evaluation of Contour J Integral and Energy Dissipated in the Fracture Process Zone. Eng. Fract. Mech. 2014, 129, 14–25. [Google Scholar] [CrossRef]
- Yamane, H.; Arikawa, S.; Yoneyama, S.; Watanabe, Y.; Asai, T.; Shiokawa, K.; Yamashita, M. J-Integral Evaluation for an Interface crack using digital image correlation. J. JSEM 2014, 14, 122–127. [Google Scholar]
- Kozłowiec, B. Numerical Methods for Estimating J Integral in Models with Regular Rectangular Meshes. Iop. Conf. Ser. Mater. Sci. Eng. 2017, 175, 012062. [Google Scholar] [CrossRef]
- Breitbarth, E.; Strohmann, T.; Besel, M.; Reh, S. Determination of Stress Intensity Factors and J Integral Based on Digital Image Correlation. Frat. Ed Integrità Strutt. 2019, 13, 12–25. [Google Scholar] [CrossRef]
- Catalanotti, G. Measurement of Resistance Curves in the Longitudinal Failure of Composites Using Digital Image Correlation. Compos. Sci. Technol. 2010, 70, 1986–1993. [Google Scholar] [CrossRef]
- Palanca, M.; Brugo, T.M.; Cristofolini, L. Use of digital image correlation to investigate the biomechanics of the vertebra. J. Mech. Med. Biol. 2015, 15, 1540004. [Google Scholar] [CrossRef]
- Shih, C.F.; Moran, B.; Nakamura, T. Energy Release Rate along a Three-Dimensional Crack Front in a Thermally Stressed Body. Int. J. Fract. 1986, 30, 79–102. [Google Scholar]
- ASTM D5045-14. Standard Test Methods for Plane-Strain Fracture Toughness and Strain Energy Release Rate of Plastic Materials; ASTM International: West Conshohocken, PA, USA, 2014. [Google Scholar]
- Gonzáles, G.L.G.; González, J.A.O.; Castro, J.T.P.; Freire, J.L.F. A J-Integral Approach Using Digital Image Correlation for Evaluating Stress Intensity Factors in Fatigue Cracks with Closure Effects. Theor. Appl. Fract. Mech. 2017, 90, 14–21. [Google Scholar] [CrossRef]
- Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]


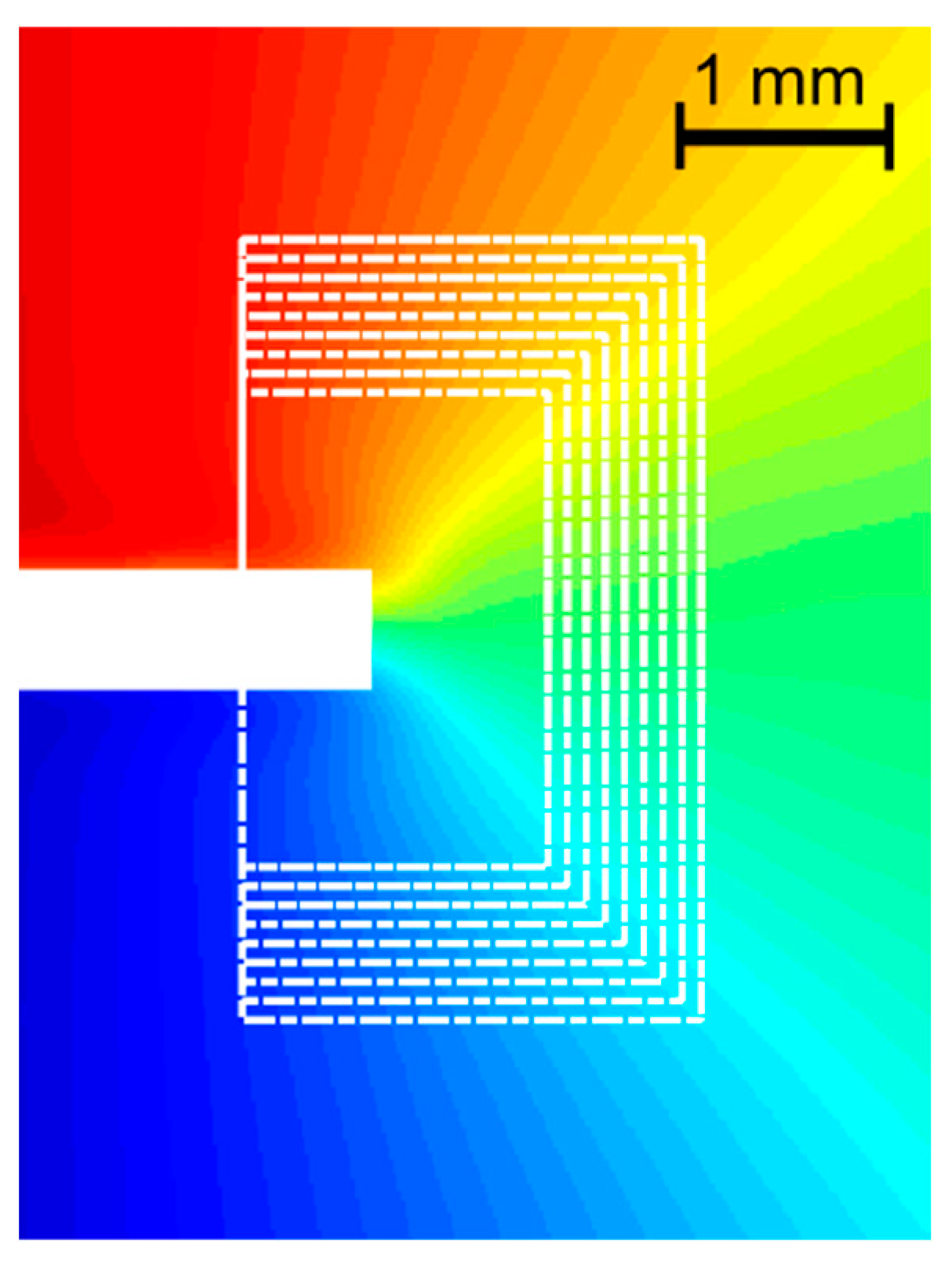
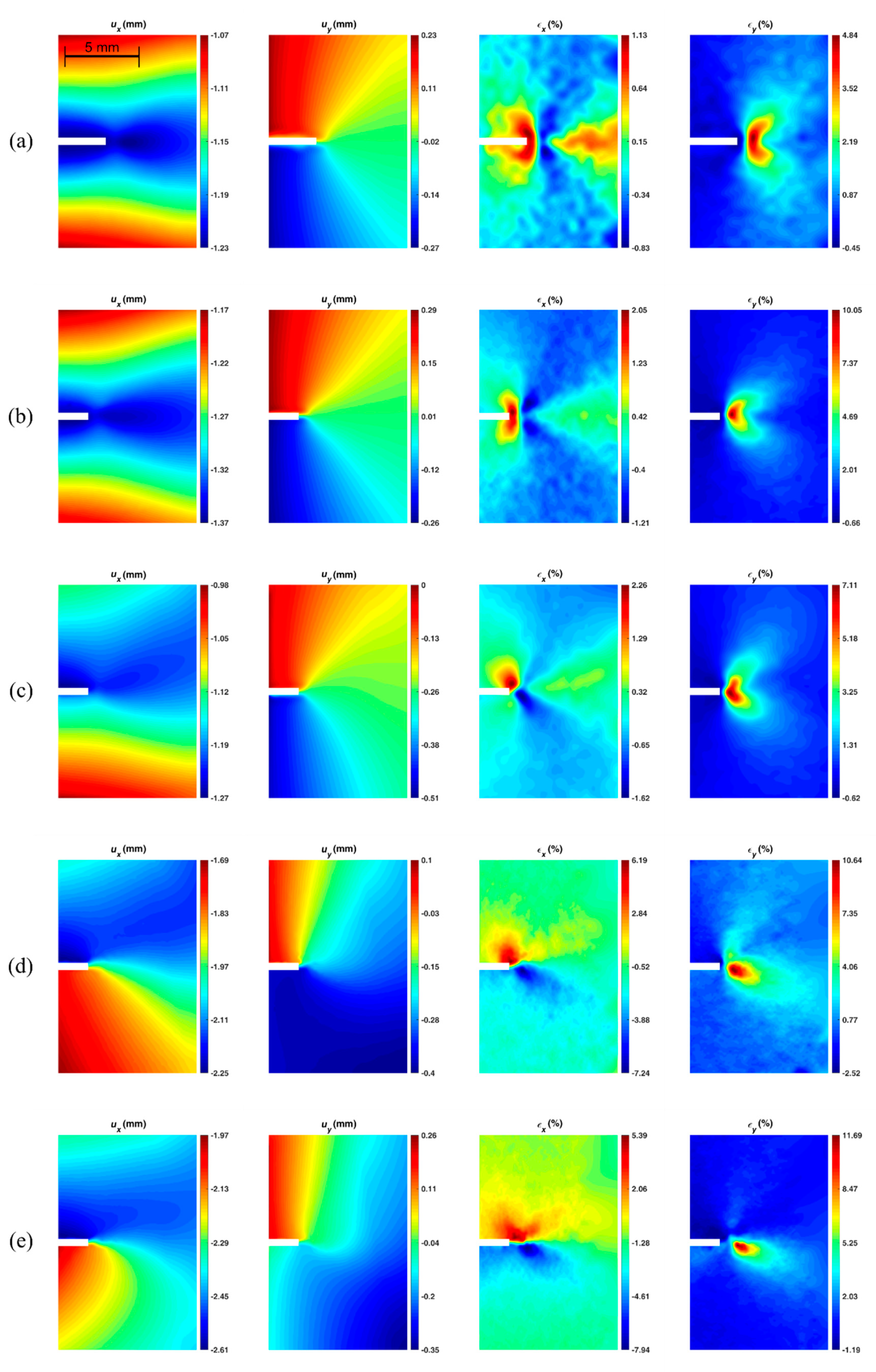
| Property | Value |
|---|---|
| Flexural Young’s modulus | 2.1 ± 0.1 GPa |
| Flexural Yield strength | 55 ± 3 MPa |
| Flexural strength | 68 ± 2 MPa |
| Type | α (°) | S1 (mm) | S2 (mm) | n | Mode | Me |
|---|---|---|---|---|---|---|
| SM | 0 | 42 | 42 | 3 | Mode I | 1 |
| AM | 0 | 42 | 42 | 3 | Mode I | 1 |
| AM | 10 | 42 | 42 | 3 | Mixed I/II | 0.77 |
| AM | 10 | 42 | 18 | 3 | Mixed I/II | 0.48 |
| AM | 10 | 42 | 10.2 | 3 | Mode II | 0.12 |
| S2/R | η | S2/R | η | S2/R | η | S2/R | η | S2/R | η | S2/R | η |
|---|---|---|---|---|---|---|---|---|---|---|---|
| α = 0° | α = 10° | α = 20° | α = 30° | α = 40° | α = 50° | ||||||
| 0.7 | 1.564 | 0.7 | 1.474 | 0.7 | 1.235 | 0.7 | 0.916 | 0.7 | 0.598 | 0.7 | 0.342 |
| 0.6 | 1.449 | 0.6 | 1.323 | 0.6 | 1.048 | 0.6 | 0.709 | 0.65 | 0.501 | 0.67 | 0.293 |
| 0.5 | 1.276 | 0.5 | 1.111 | 0.5 | 0.809 | 0.5 | 0.480 | 0.6 | 0.400 | 0.64 | 0.244 |
| 0.4 | 1.032 | 0.4 | 0.837 | 0.4 | 0.557 | 0.45 | 0.389 | 0.55 | 0.305 | 0.6 | 0.183 |
| 0.3 | 0.719 | 0.3 | 0.558 | 0.3 | 0.465 | 0.4 | 0.356 | 0.5 | 0.240 | 0.55 | 0.129 |
| 0.1 | 0.358 | 0.17 | 0.522 | 0.26 | 0.554 | 0.36 | 0.407 | 0.45 | 0.245 | 0.52 | 0.125 |
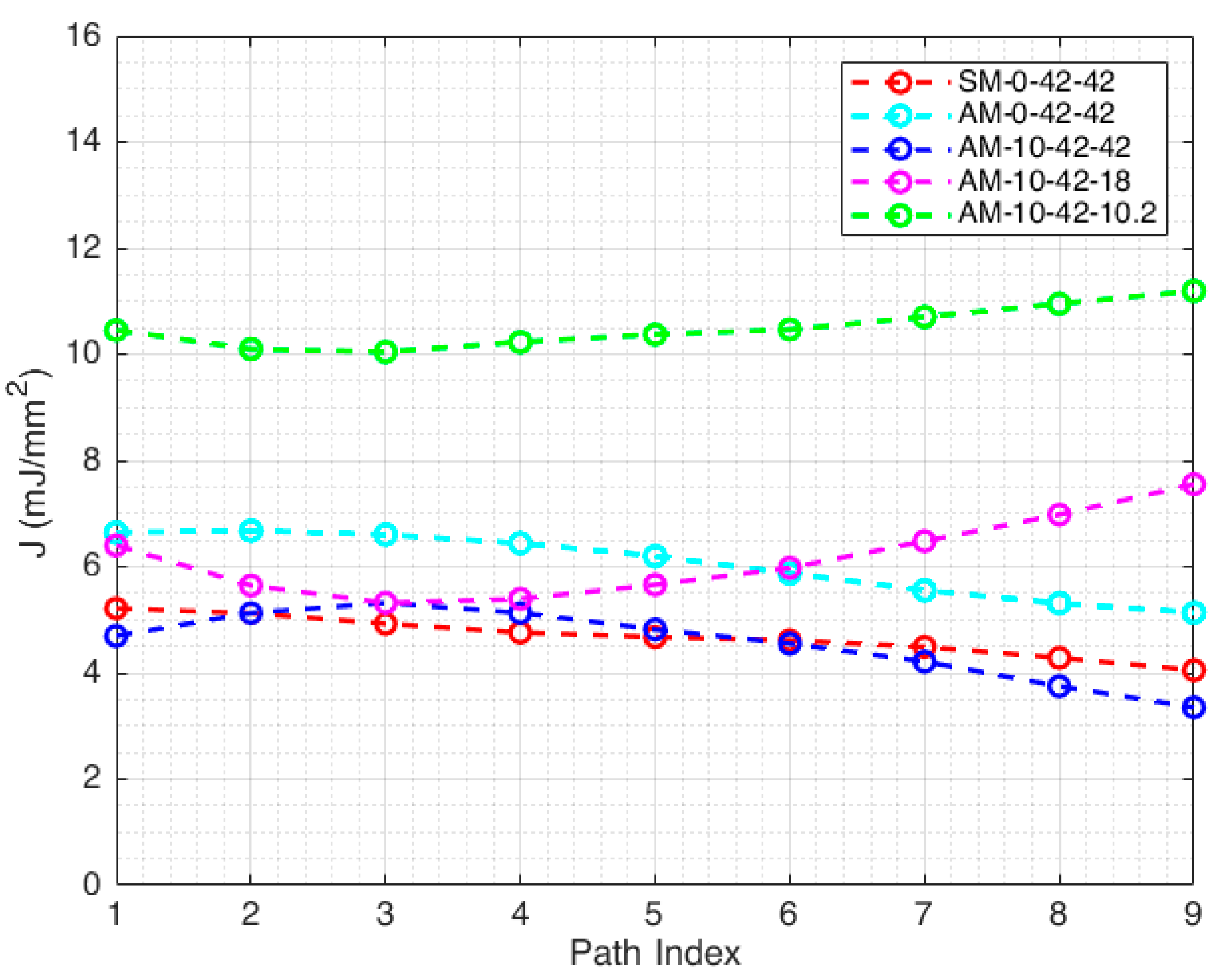
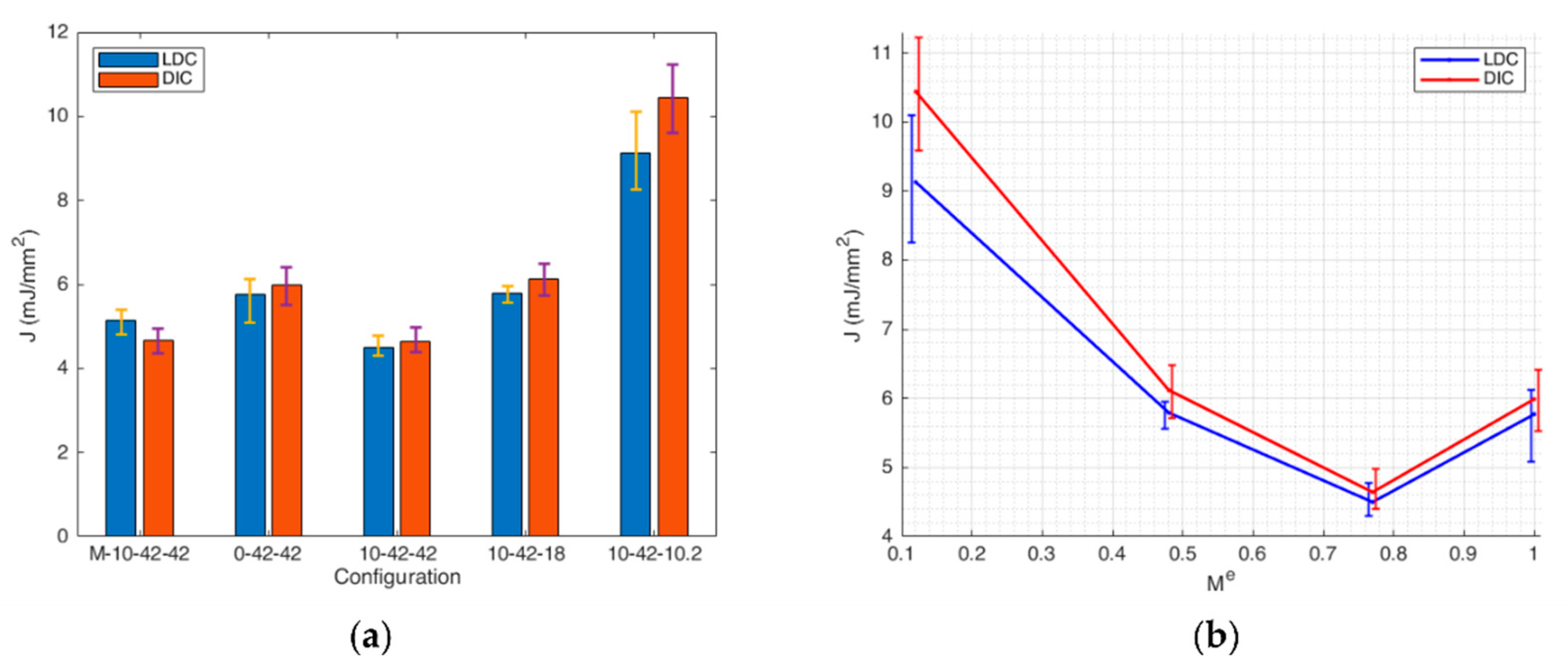
| Specimen Configuration | Me | LDC Method J (mJ/mm2) | Jmean | σ(J) | DIC Method J (mJ/mm2) | Jmean | σ(J) | LDC vs. DIC Δ% |
|---|---|---|---|---|---|---|---|---|
| SM-0-42-42-1 | 1 | 5.40 | 5.14 | 0.29 | 4.95 | 4.66 | 0.30 | −8.33 |
| SM-0-42-42-2 | 4.82 | 4.68 | −2.90 | |||||
| SM-0-42-42-3 | 5.20 | 4.36 | −16.15 | |||||
| AM-0-42-42-1 | 1 | 5.09 | 5.77 | 0.59 | 6.42 | 5.99 | 0.45 | 26.13 |
| AM-0-42-42-2 | 6.12 | 5.52 | −9.80 | |||||
| AM-0-42-42-3 | 6.10 | 6.03 | −1.15 | |||||
| AM-10-42-42-1 | 0.77 | 4.30 | 4.50 | 0.25 | 4.98 | 4.64 | 0.30 | 15.81 |
| AM-10-42-42-2 | 4.78 | 4.55 | −4.81 | |||||
| AM-10-42-42-3 | 4.42 | 4.40 | −0.45 | |||||
| AM-10-42-18-1 | 0.48 | 5.56 | 5.79 | 0.21 | 6.16 | 6.12 | 0.38 | 10.79 |
| AM-10-42-18-2 | 5.95 | 6.48 | 8.91 | |||||
| AM-10-42-18-3 | 5.87 | 5.72 | −2.56 | |||||
| AM-10-42-10.2-1 | 0.12 | 9.03 | 9.13 | 0.92 | 9.59 | 10.44 | 0.82 | 6.20 |
| AM-10-42-10.2-2 | 8.26 | 10.50 | 27.12 | |||||
| AM-10-42-10.2-3 | 10.10 | 11.23 | 11.19 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brugo, T.M.; Campione, I.; Minak, G. Investigation by Digital Image Correlation of Mixed-Mode I and II Fracture Behavior of Polymeric IASCB Specimens with Additive Manufactured Crack-Like Notch. Materials 2021, 14, 1084. https://doi.org/10.3390/ma14051084
Brugo TM, Campione I, Minak G. Investigation by Digital Image Correlation of Mixed-Mode I and II Fracture Behavior of Polymeric IASCB Specimens with Additive Manufactured Crack-Like Notch. Materials. 2021; 14(5):1084. https://doi.org/10.3390/ma14051084
Chicago/Turabian StyleBrugo, Tommaso Maria, Ivo Campione, and Giangiacomo Minak. 2021. "Investigation by Digital Image Correlation of Mixed-Mode I and II Fracture Behavior of Polymeric IASCB Specimens with Additive Manufactured Crack-Like Notch" Materials 14, no. 5: 1084. https://doi.org/10.3390/ma14051084
APA StyleBrugo, T. M., Campione, I., & Minak, G. (2021). Investigation by Digital Image Correlation of Mixed-Mode I and II Fracture Behavior of Polymeric IASCB Specimens with Additive Manufactured Crack-Like Notch. Materials, 14(5), 1084. https://doi.org/10.3390/ma14051084







