3.1. Thermodynamic Analysis
To study the types and relative contents of various constituent phases of Fe25Cr25Ni25TixAl(25−x) (x = 0; 6.25; 12.5; 18.75; 25) (Subscript represents atomic percentage) multi-principal element alloys at different temperatures, and to determine the composition of each equilibrium phase, thermodynamic analysis The software JMat-Pro performs phase diagram calculation on it. To combine the thermodynamic analysis with the order of the structure in the multi-principal element alloys, try to combine the thermodynamics with the first-principles calculations to explore a new multi-principal alloy that meets the target performance.
Among the constituent elements of the Fe
25Cr
25Ni
25Ti
xAl
(25−x) (subscript represents atomic percentage) system multi-principal element alloys, the Fe, Ni, and Ti elements are the main constituent elements of the conventional metal-based superalloy. The Ni, Ti, and Cr elements contribute to the high-temperature properties of traditional alloys. Due to the large atomic radius of the Al element, it has a great influence on the crystal structure of the alloy system. The crystal structure of the alloy can be adjusted by changing the content of the Al element to achieve the purpose of improving the properties of the alloy. In the Fe
25Cr
25Ni
25Ti
xAl
(25−x) system multi-principal element alloys, it is desirable to adjust the content of the Ti and Al elements to improve the toughness.
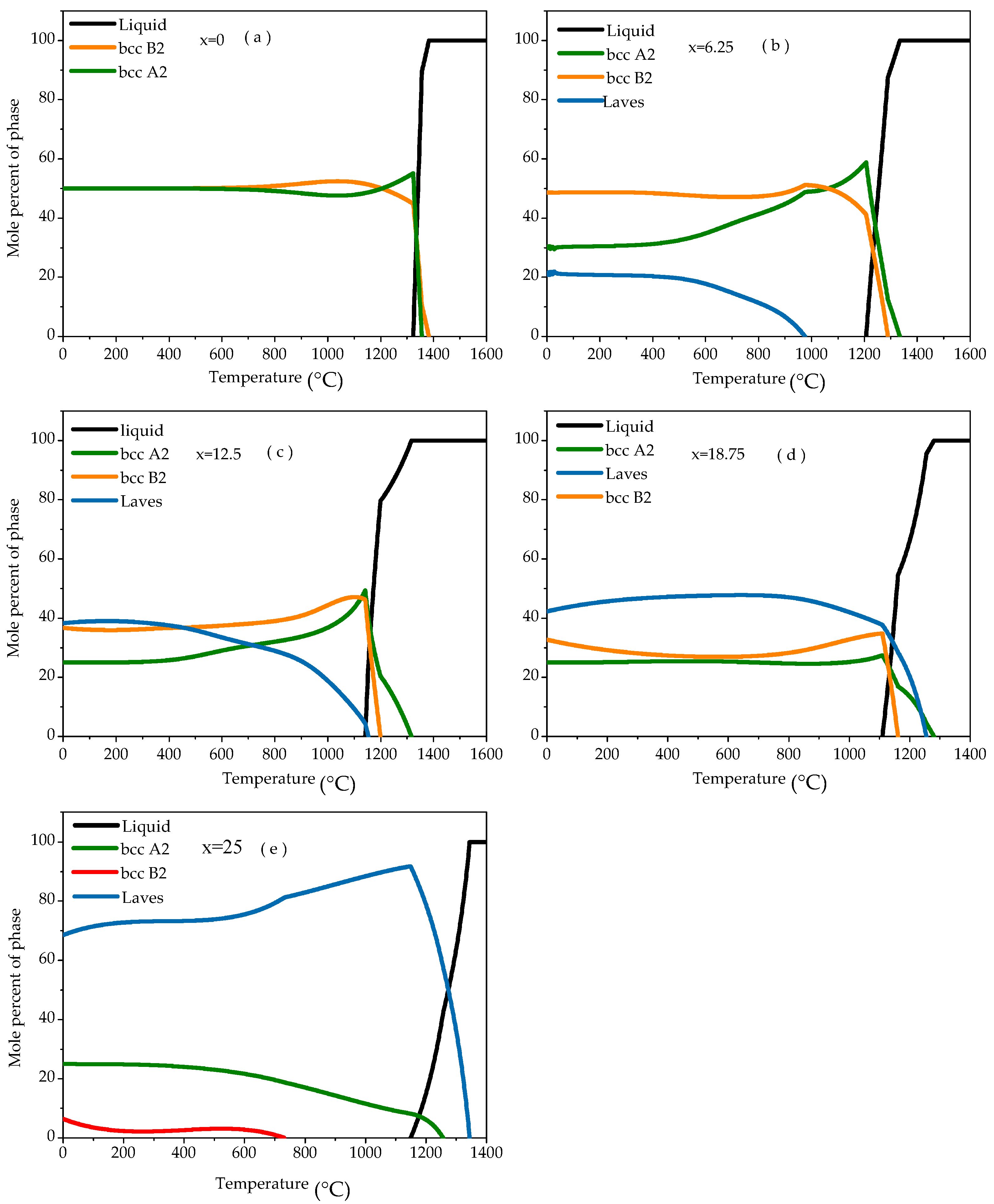
Figure 1 shows the thermodynamic calculation results for the alloy. When x = 0, the Fe
25Cr
25Ni
25Al
25 alloy phase diagram shows that the disordered BCC A2 phase and the ordered BCC B2 phase content are 50%, respectively (
Figure 1a). As the Ti content increases (x = 6.25), the Al content reduces, the content of the ordered BCC B2 phase and the disordered BCC A2 phase increased simultaneously, and the Laves phase decreased (
Figure 1b). When x = 12.5, the content of the disordered BCC A2 phase changes little, the content of the ordered BCC B2 phase continues to increase, and the Laves phase content continues to decrease (
Figure 1c). As the Ti content continued to increase (x = 18.75), the Al content continued to reduce, the content of the disordered BCC A2 phase and the ordered BCC B2 phase increases, and the Laves phase content decreases, less than 50% (
Figure 1d). When x = 25, the phase diagram of the Fe
25Cr
25Ni
25Ti
25 alloy shows that the alloy consists of a disordered BCC A2 phase, an ordered BCC B2 phase, and a Laves phase, a small BCC B2 phase content, and a Laves phase content greater than 75% (
Figure 1e). Further analysis showed that with the increase of Ti content and the decrease of Al content, the content of Al phase and B2 phase decreased gradually, the content of A2 phase decreased rapidly, and the content of Laves phase increased gradually.
Table 1 shows the mole percent of each phase of the Fe
25Cr
25Ni
25Ti
xAl
(25-x) alloy at 800 °C. It can be seen from the data in the table that as the Al content in the alloy increases, the contents of the BCC A2 phase and the BCC B2 phase gradually increase. The Laves phase content is gradually reduced.
3.2. Solidification Physical Properties
Figure 2a is the Fraction solid (at)-Temperature (°C) curve of Fe
25Cr
25Ni
25Al
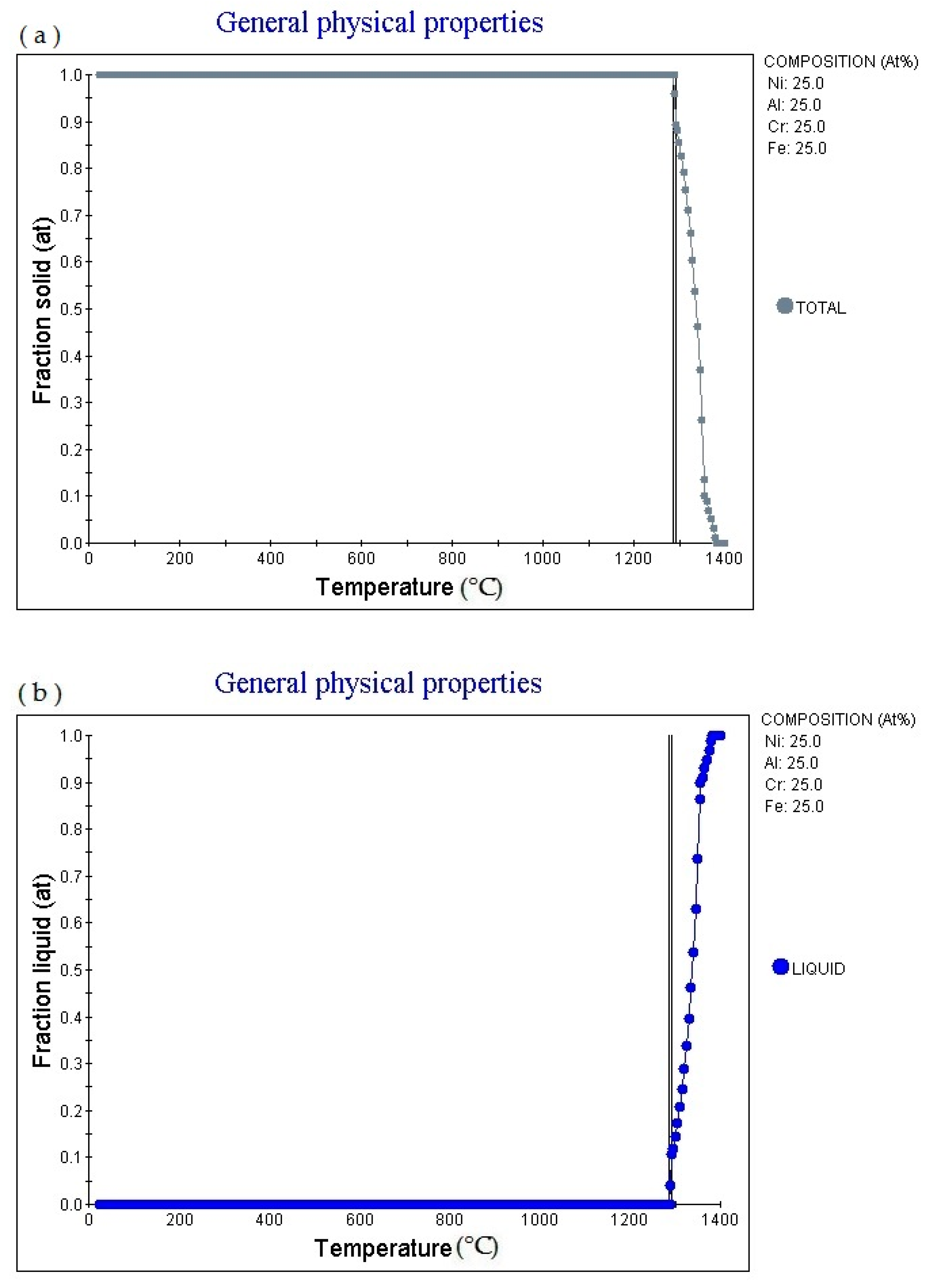
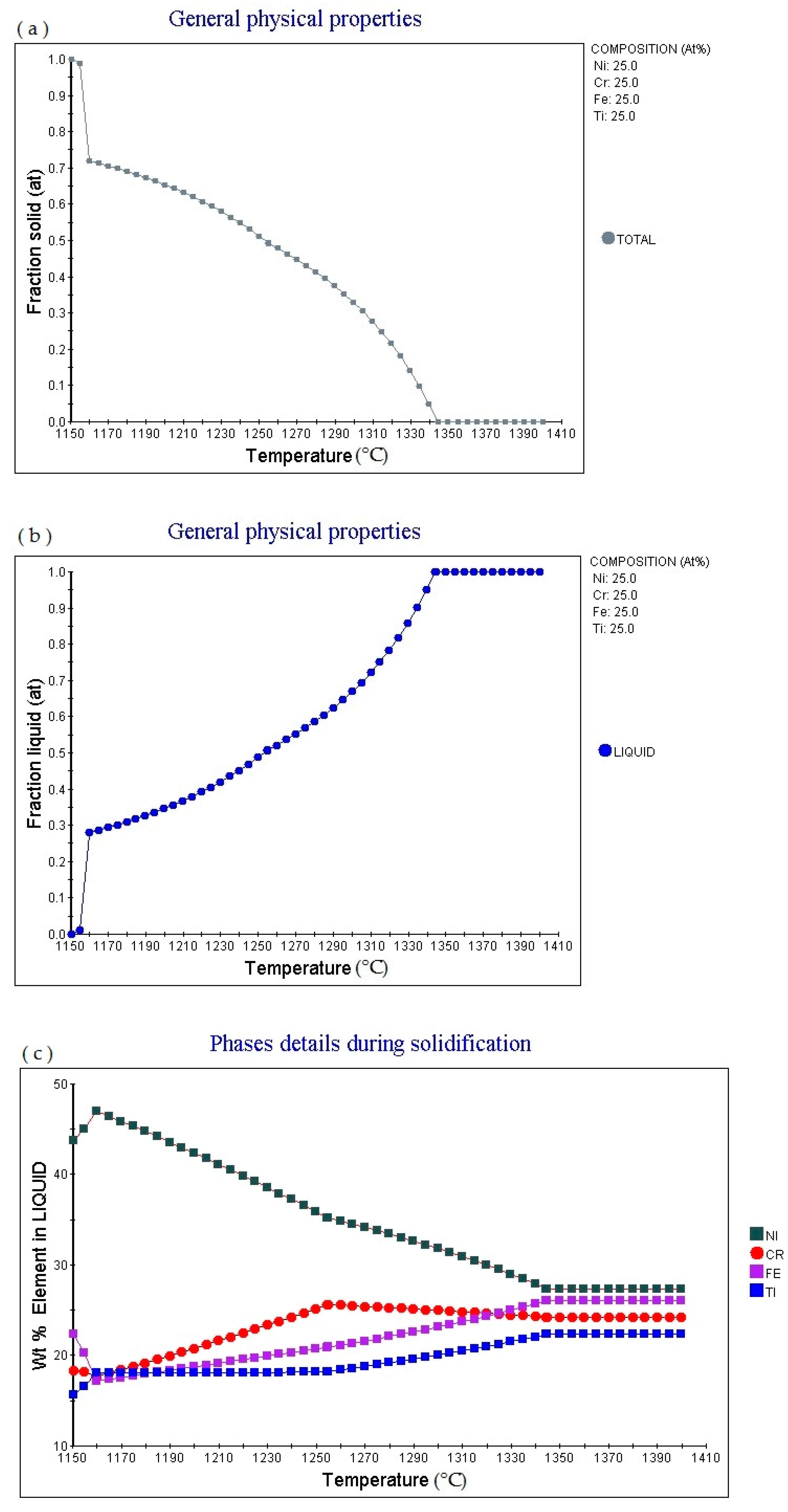
25 alloy (subscript as atomic percentage). The figure shows that as the temperature increases, the alloy gradually melts, and the melting point is 1288.53 °C: 1.0. Then as the temperature increases, the solid phase volume fraction gradually decreases. When the temperature increases to 1382.36 °C, Fraction solid (at): 0.0.
Figure 2b is the fraction liquid (at)–temperature (°C) curve of Fe
25Cr
25Ni
25Ti
18.75Al
6.25 alloy (subscript is atomic percentage). The figure shows that as the temperature increases, the volume fraction of the liquid phase in the alloy changes accordingly. The multi-principal element alloy has a fixed melting temperature, the melting temperature is 1284.85 °C, currently fraction liquid (at): 0.0. It absorbs heat during the melting process. When the temperature rises to 1356.1 °C, fraction Liquid (at): 0.9. Then as the temperature increases, the alloy gradually melts. When the temperature increases to 1382.36 °C, fraction liquid (at): 1.0.
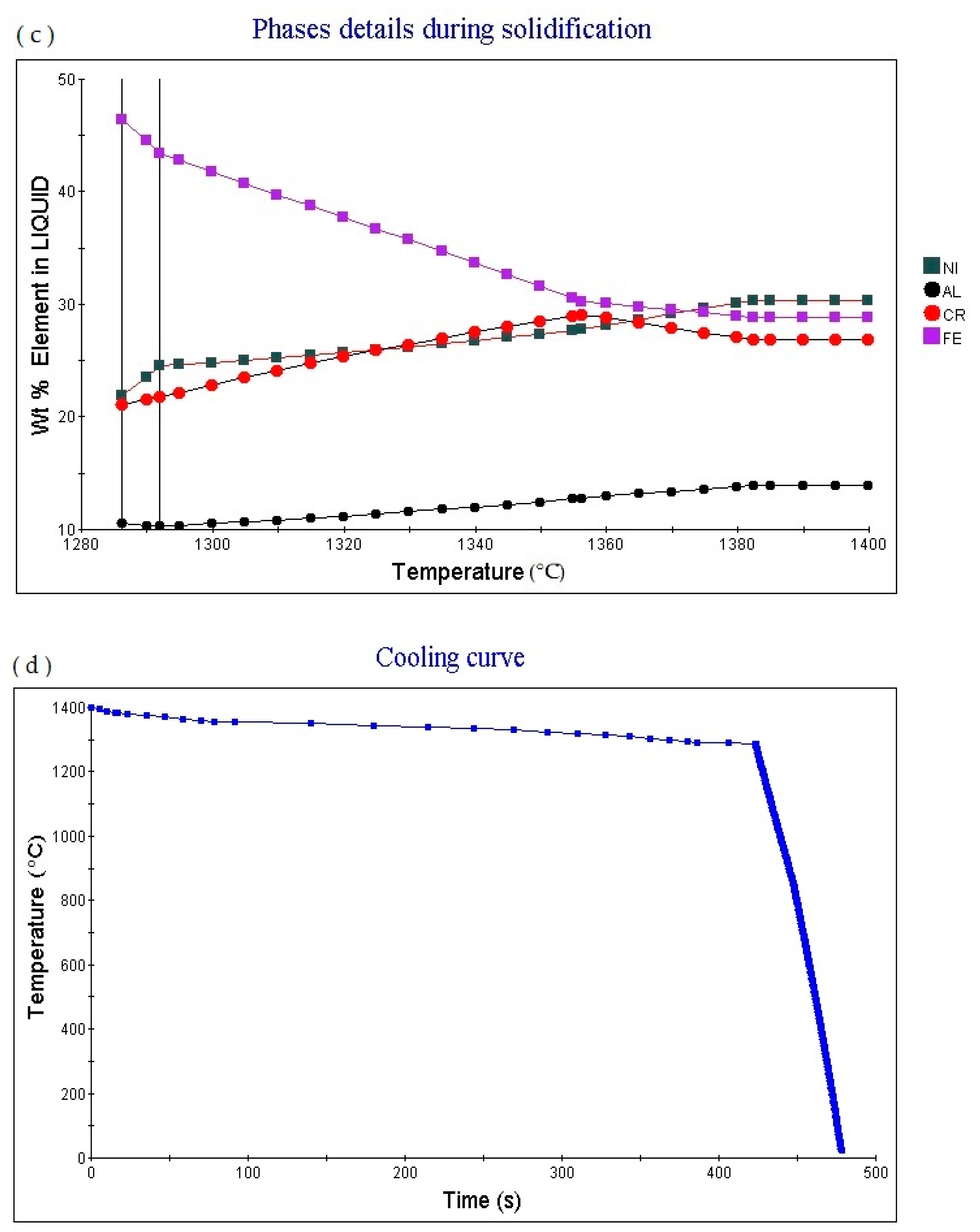
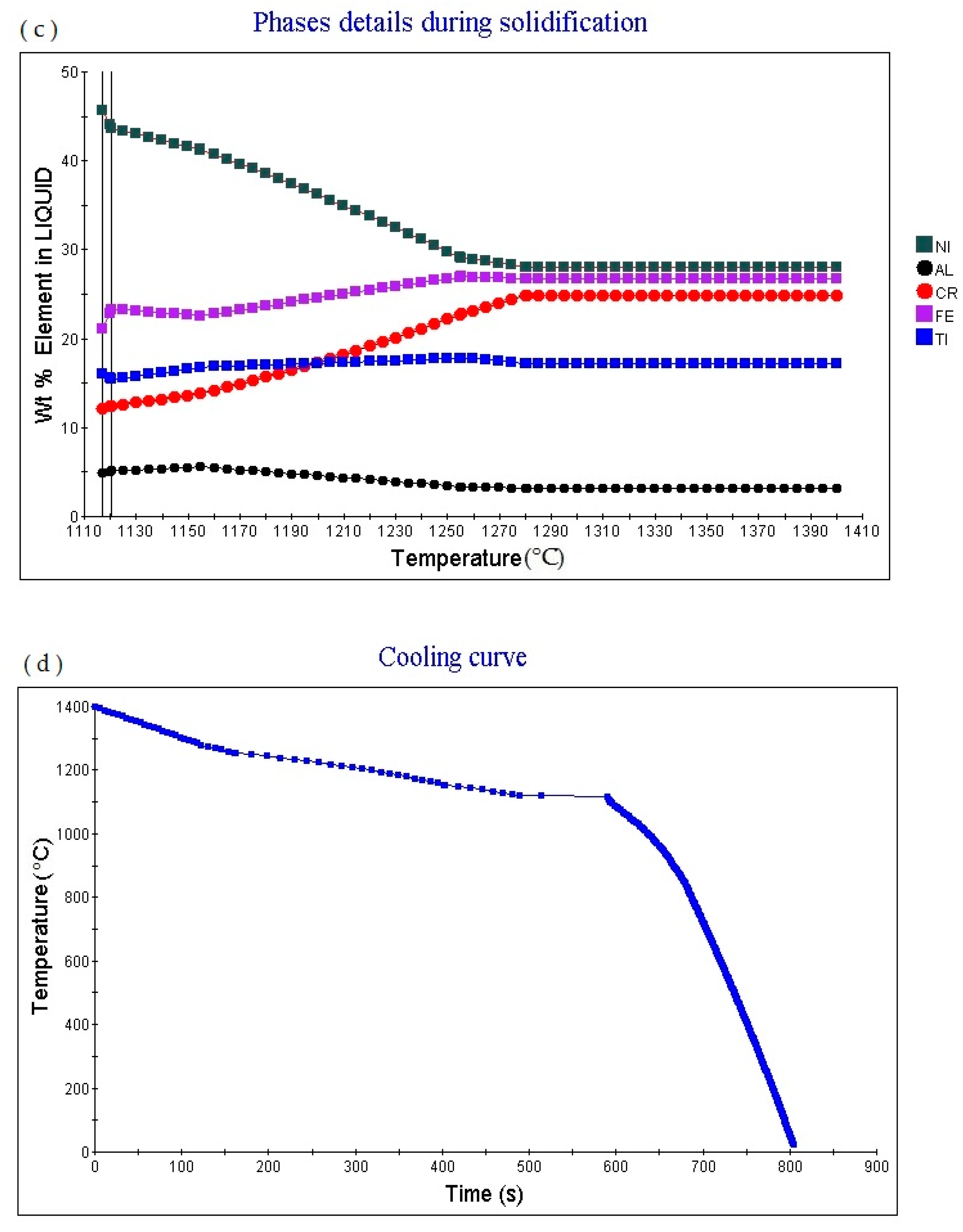
Figure 2c shows the element in liquid (wt.%)—temperature curve of the alloy. As the temperature increases, the percentage content of various elements in the alloy liquid phase will change.
Figure 2d shows the cooling curve of the alloy. The cooling rate obtained for the cooling curve is 1.0 °C/S. When the cooling time is 423.31 s and the temperature is 1288.53 °C, the cooling rate can be adjusted to obtain cooling curves with different cooling rates.
Figure 3a is the fraction solid (at)–temperature (°C) curve of Fe
25Cr
25Ni
25Ti
6.25Al
18.75 alloy (subscript is atomic percentage). The figure shows that as the temperature rises, the alloy gradually melts, and the melting point is 1140.41 °C. Fraction solid (at): 1.0. Then as the temperature increases, the solid phase volume fraction gradually decreases. When the temperature increases to 1334.85 °C, fraction solid (at): 0.0.
Figure 3b is the fraction liquid (at)–temperature (°C) curve of Fe
25Cr
25Ni
25Ti
18.75Al
6.25 alloy (subscript is atomic percentage). The figure shows that as the temperature increases, the volume fraction of the liquid phase in the alloy changes accordingly. The multi-principal element alloy has a fixed melting temperature, which is 1140.41°C, currently fraction liquid (at): 0.0. It absorbs heat during the melting process. When the temperature rises to 1146.89 °C, fraction liquid (at): 0.16. When the temperature rises to 1289.85 °C, fraction liquid (at): 0.88. Then as the temperature rises, the alloy gradually melts. When the temperature rises to 1334.85 °C, fraction liquid (at): 1.0. As the temperature rises, fraction liquid (at) remains unchanged.
Figure 3c shows the element in liquid (wt.%)—temperature curve of the alloy. As the temperature increases, the percentage content of various elements in the alloy liquid phase will change.
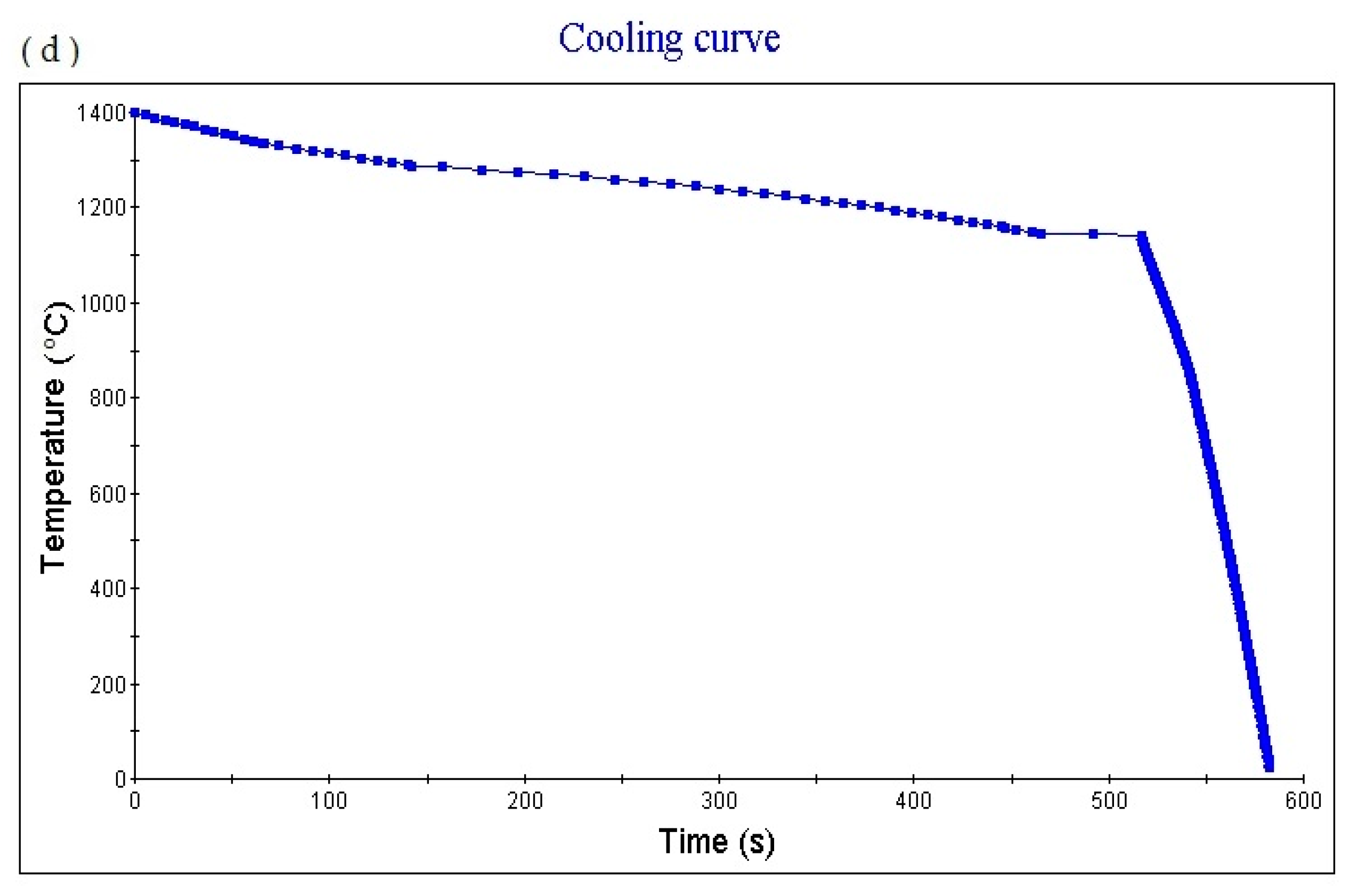
Figure 3d shows the cooling curve of the alloy. The cooling rate obtained for the cooling curve is 1.0 °C/s. when the cooling time is 516.5 s and the temperature is 1140.41 °C, the cooling rate can be adjusted to obtain cooling curves with different cooling rates.
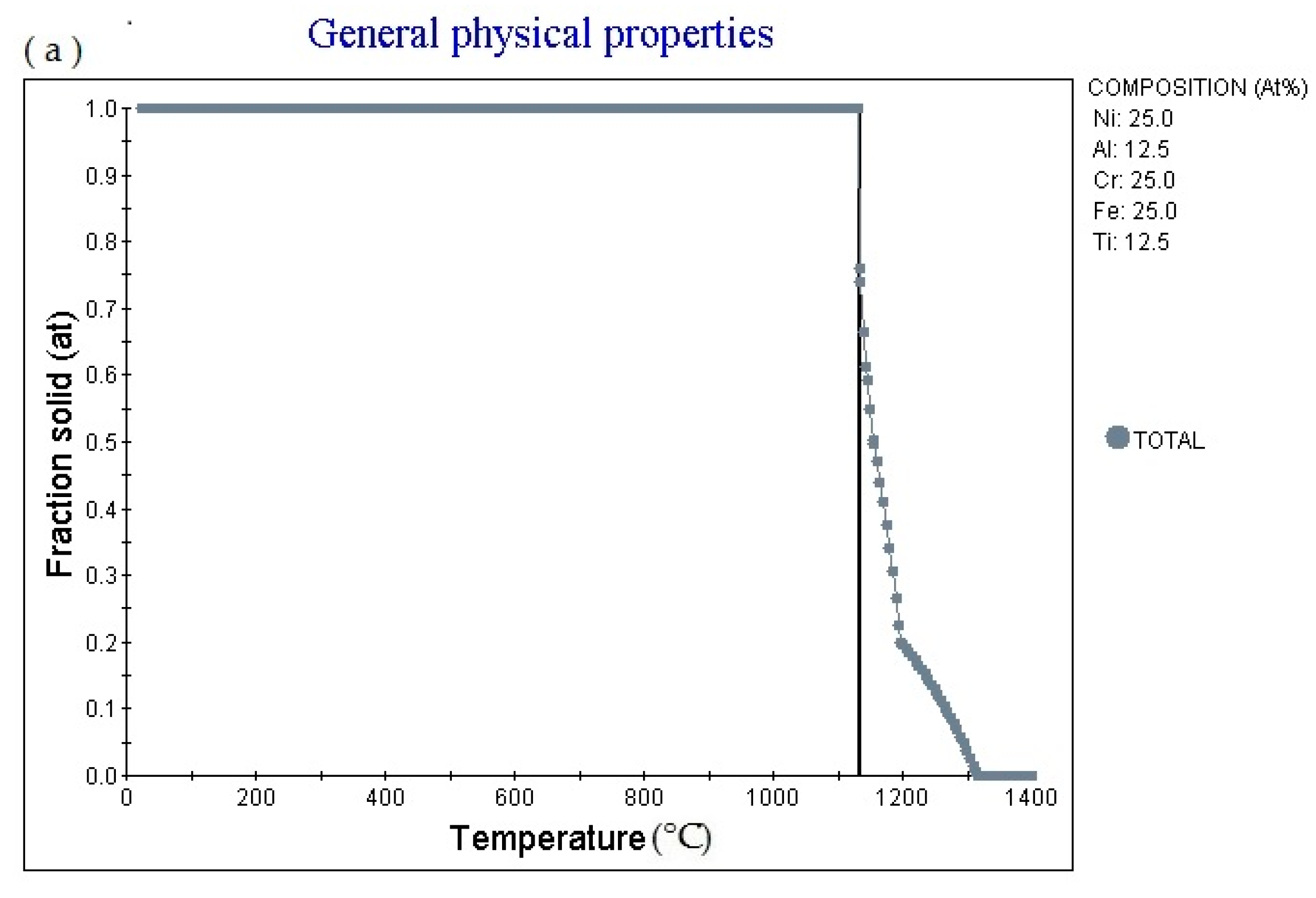
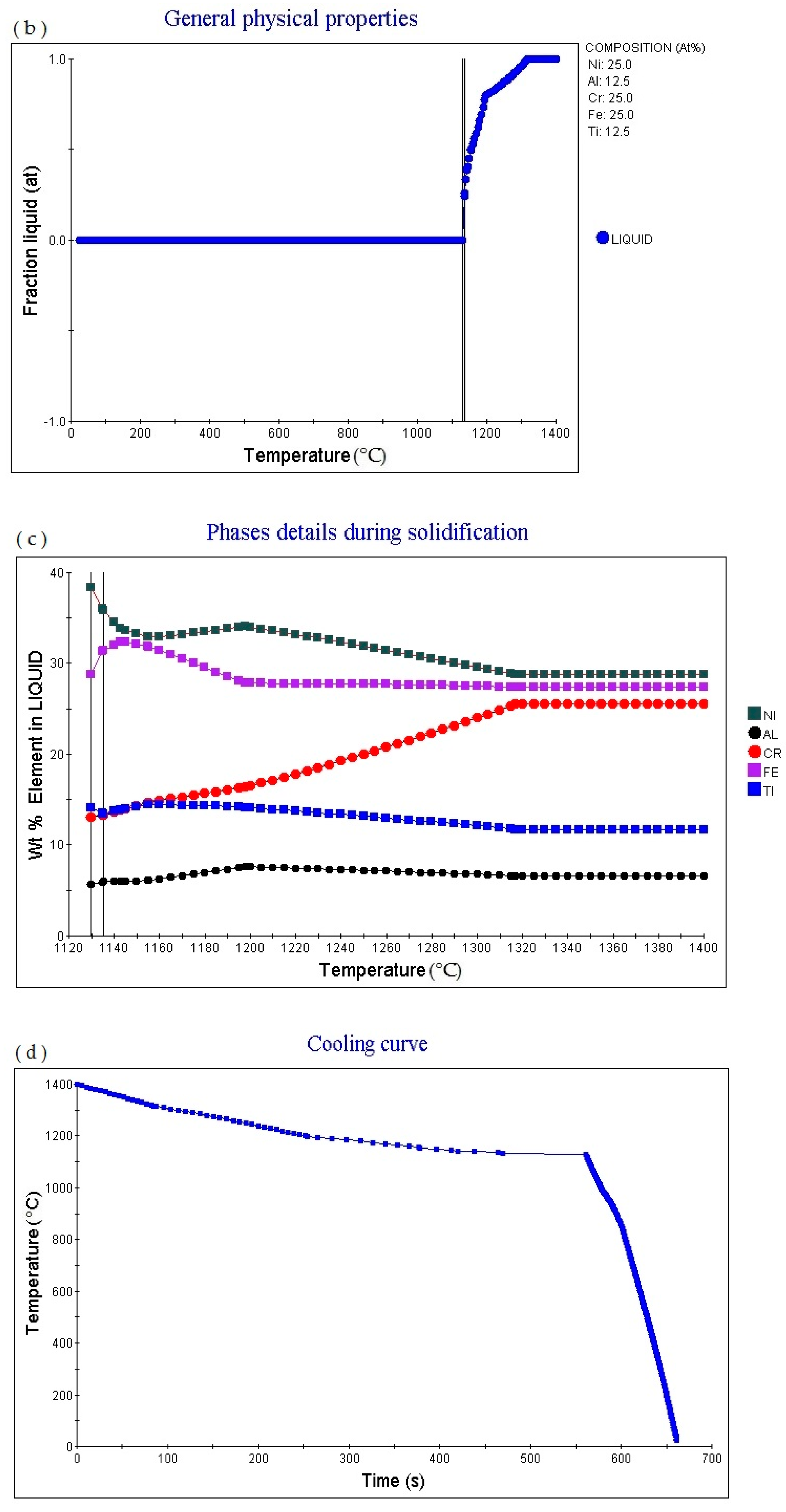
Figure 4a is the Fraction solid (at)-Temperature (°C) curve of Fe
25Cr
25Ni
25Ti
12.5Al
12.5 alloy (subscript is atomic percentage). The figure shows that as the temperature rises, the alloy gradually melts, and the melting point is 1129.91 °C, currently Fraction solid (at): 1.0. Then as the temperature increases, the solid phase volume fraction gradually decreases. When the temperature increases to 1316.71 °C, Fraction solid (at):0.0.
Figure 4b is the fraction liquid (at)–temperature (°C) curve of Fe
25Cr
25Ni
25Ti
12.5Al
12.5 alloy (subscript is atomic percentage). The figure shows that as the temperature increases, the volume fraction of the liquid phase in the alloy changes accordingly Variety. The multi-principal element alloys has a fixed melting temperature, the melting temperature is 1129.91 °C, at this time fraction liquid (at): 0.0. It absorbs heat during the melting process. When the temperature rises to 1199.85 °C, fraction liquid (at): 0.8. Then as the temperature rises, the alloy gradually melts. When the temperature rises to 1314.85 °C, fraction liquid (at): 1.0. As the temperature rises, the fraction liquid (at) remains unchanged.
Figure 4c shows the element in liquid (wt.%)—temperature curve of the alloy. As the temperature increases, the percentage content of various elements in the alloy liquid phase will change.
Figure 4d shows the cooling curve of the alloy. The cooling rate obtained for the cooling curve is 1.0 °C/s. When the cooling time is 561.03 s, the temperature is 1129.91 °C. The cooling rate can be adjusted to obtain cooling curves with different cooling rates.
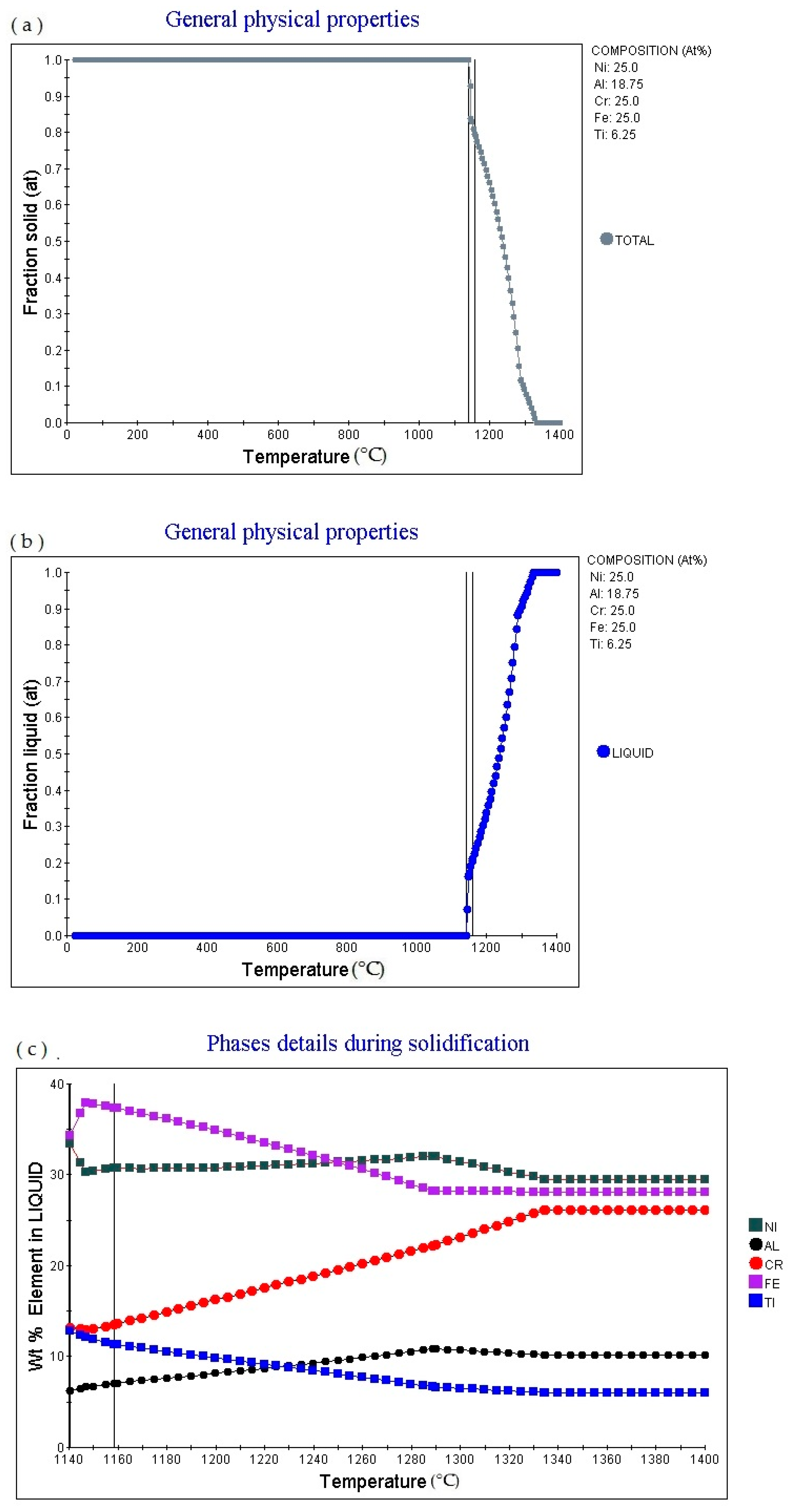
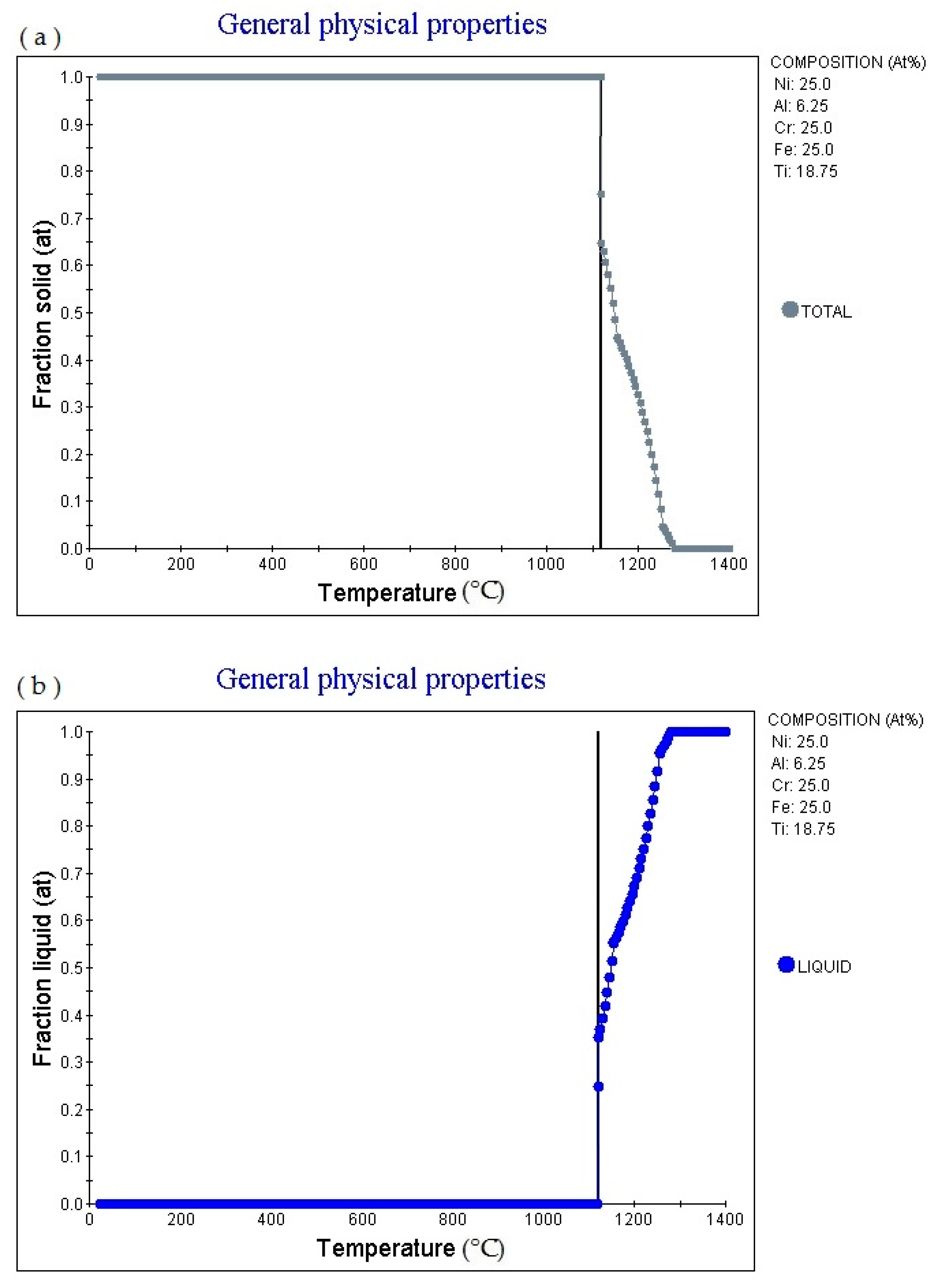
Figure 5a is the Fraction solid (at)-temperature (°C) curve of Fe
25Cr
25Ni
25Ti
18.75Al
6.25 alloy (subscript is atomic percentage). The figure shows that as the temperature rises, the alloy gradually melts, with a melting point of 1117.17 °C, currently Fraction solid (at): 1.0. Then as the temperature increases, the solid phase volume fraction gradually decreases. When the temperature increases to 1280.37 °C, Fraction solid (at): 0.0.
Figure 5b is the fraction liquid (at)–temperature (°C) curve of Fe
25Cr
25Ni
25Ti
18.75Al
6.25 (subscript is atomic percentage), which shows that as the temperature increases, the volume fraction of the liquid phase in the alloy changes accordingly. The multi-principal element alloy has a fixed melting temperature, which is 1117.17 °C, at this time fraction liquid (at): 0.0. As the temperature rises, the alloy gradually melts. When the temperature rises to 1280.37 °C, fraction liquid (at): 1.0. As the temperature rises, fraction liquid (at) remains unchanged.
Figure 5c shows the element in liquid (wt.%)—temperature curve of the alloy. As the temperature increases, the percentage content of various elements in the alloy liquid phase will change.
Figure 5d shows the cooling curve of the alloy. The cooling rate of the obtained cooling curve is 1.0 °C/S. When the cooling time is 589.38 s, the temperature is 1117.92 °C. The cooling rate can be adjusted to obtain cooling curves with different cooling rates.
Figure 6a is the Fraction solid (at)-Temperature (°C) curve of Fe
25Cr
25Ni
25Ti
25 alloy (subscript is atomic percentage). The figure shows that as the temperature increases, the alloy gradually melts. When the temperature is 1150.53 °C, Fraction solid (at): 1.0. Then as the temperature increases, the solid phase volume fraction gradually decreases. When the temperature increases to 1159.85 °C, Fraction solid (at): 0.72; when the temperature increases to 1344.85 °C, Fraction solid (at): 0.0.
Figure 6b is the fraction liquid (at)—temperature (°C) curve of Fe
25Cr
25Ni
25Ti
25 (subscript as atomic percentage). The figure shows that as the temperature increases, the volume fraction of the liquid phase in the alloy changes accordingly. The multi-principal element alloys has a fixed melting temperature, the melting temperature is 1159.85 °C, at this time fraction liquid (at): 0.0. As the temperature rises, the alloy gradually melts. When the temperature rises to 1159.85 °C, fraction liquid (at): 0.28; when the temperature rises to 1344.44 °C, fraction liquid (at): 1.0. As the temperature rises, fraction liquid (at) remains unchanged.
Figure 6c shows the element in liquid (wt.%)-temperature curve of the alloy. As the temperature increases, the percentage content of various elements in the alloy liquid phase will change.
Figure 6d shows the cooling curve of the alloy. The cooling rate of the obtained cooling curve is 1.0 °C/s. When the cooling time is 561.6 s and the temperature is 1150.53 °C, the cooling rate can be adjusted to obtain cooling curves with different cooling rates.
3.3. Enthalpy of Mixing ΔHmix, Entropy of Mixing ΔSmix and Gibbs Free Energy Calculation of Alloy
In thermodynamics, the entropy value represents the degree of chaos. The greater the degree of disorder in a system, the greater the entropy value, as shown in Formula (1) [
22]:
R: Represents the gas constant; : Represents the percentage of member i.
In multi-principal alloys, the mixing entropy plays a significant role in the formation of a solid solution, and the mixing enthalpy factor cannot be ignored. The formula for mixing enthalpy is shown in Formulas (2) and (3) [
23]:
: The atomic percentage of the i component;: The atomic percentage of the j component; binary system mixing enthalpy.
Enthalpy of mixing, also known as the heat of mixing, is one of the mixing functions, which refers to the linear relationship between the alloy’s transition temperature and the absolute value of the alloy’s mixing enthalpy. The mixing entropy and the mixing enthalpy are in a competitive position. Regardless of whether the mixing enthalpy is positive or negative, the increase of the mixing entropy will inevitably lead to a decrease in the system’s free energy, thereby improving the stability of the system. This article uses JMatPro software to predict the mixing enthalpy and mixing entropy of Fe
25Cr
25Ni
25Ti
xAl
(25−x) multi-principal element alloys, as shown in
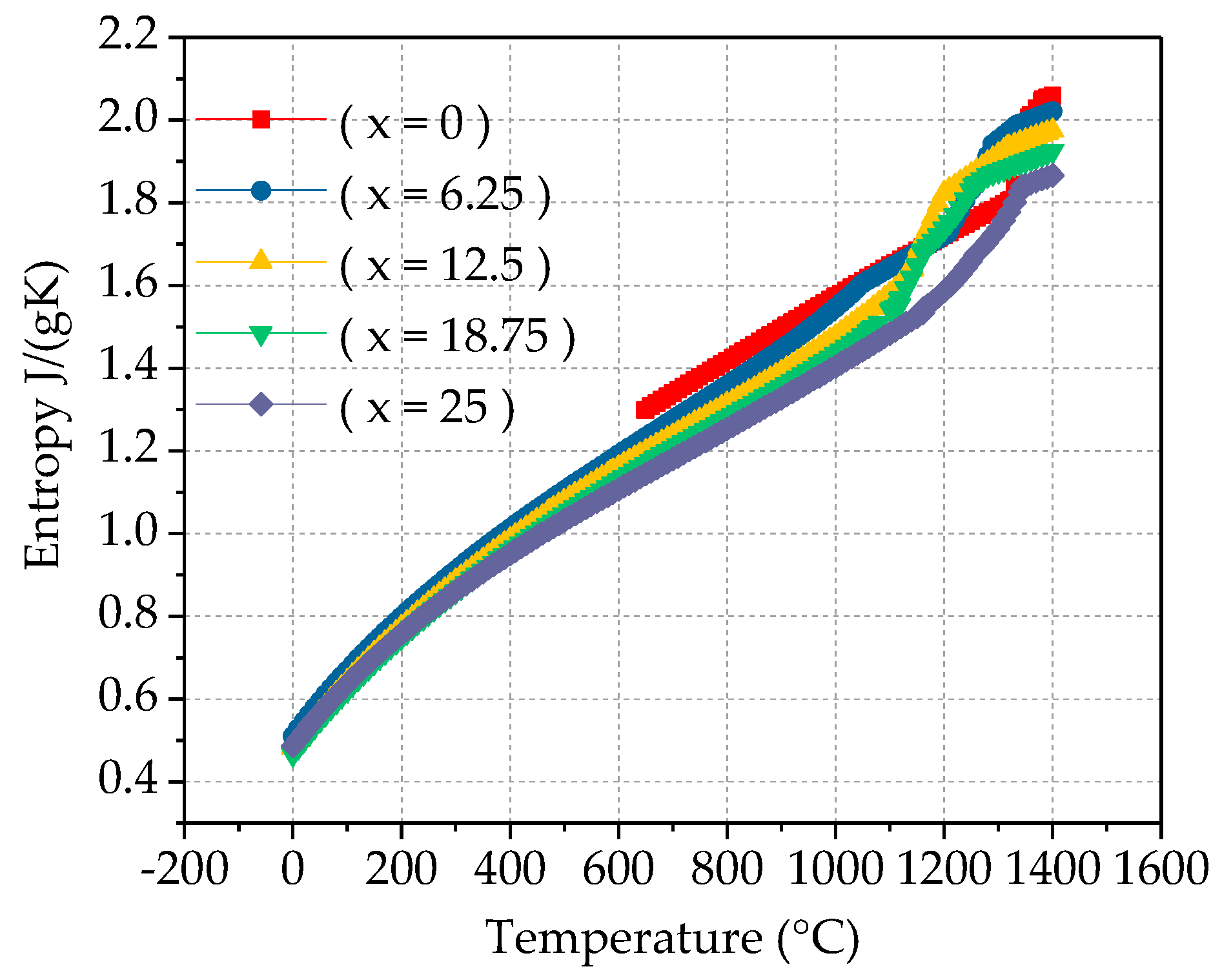
Figure 7. It can be observed from the figure that as the temperature increases, the mixing entropy and mixing enthalpy of the alloy increase, indicating that the system is more stable. The greater the absolute value of the mixing enthalpy, the higher the alloy transition temperature. The absolute value of the mixing enthalpy reflects the excess entropy value at the transition point of the alloy. By adding alloy elements or adjusting the alloy composition based on of known alloys, beneficial alloy transition temperature values can be obtained. It can be observed from
Figure 8 that as the Ti content increases, the mixing entropy of the alloy gradually increases, but the overall stability tends to be stable. The mixing enthalpy gradually decreases and tends to stabilize, as shown in
Figure 9.
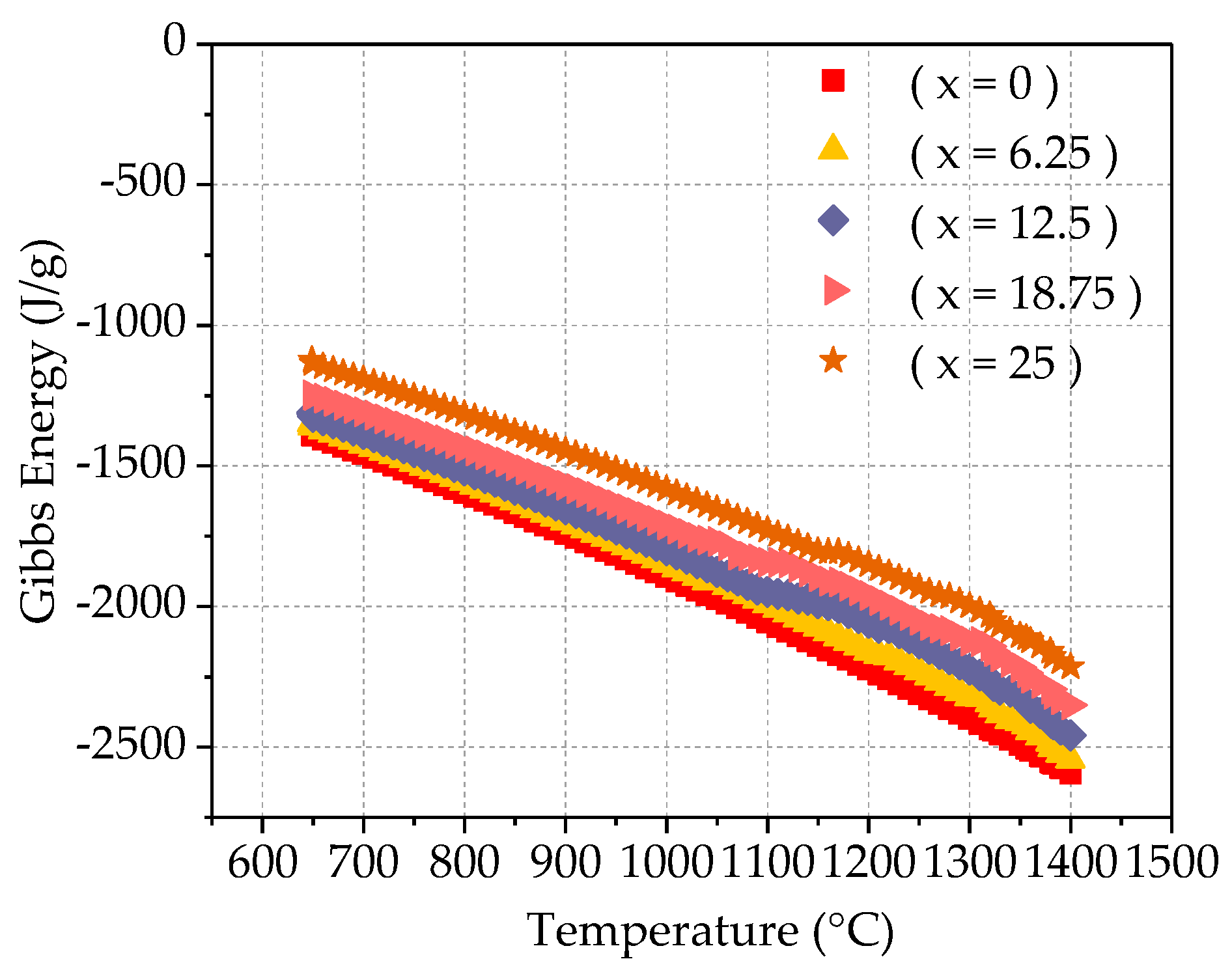
Gibbs free energy, also known as the Gibbs function, also known as free enthalpy, is an important thermodynamics parameter. It is often represented by G, and its definition is G = H − TS, Where H is enthalpy, T is temperature (absolute temperature, K), and S is entropy. Define ΔG = ΔH − TΔS (KJ/mol), G is called Gibbs free energy. Because H, T, and S are all state functions, G is the state function. The amount of Gibbs free energy change -ΔG = −(G2 − G1) ≥ W is not. It shows that the state function G is the ability of the system to do non-volume work under isothermal pressure and pressure. The reduction of G during the reaction-ΔG is the maximum non-volume work done by the system. This maximum is achieved in a reversible way. ΔG can judge the direction and mode of the reaction: −ΔG > W non-reaction proceeds spontaneously in an irreversible manner; −ΔG = W non-reaction proceeds in a reversible manner; −ΔG < W is not possible; if the reaction is carried out under isothermal pressure and pressure, no non-volume work is done, that is, W is not = 0 then ΔG < 0 proceed spontaneously; ΔG = 0 cannot proceed; ΔG > 0, the reverse reaction proceeds spontaneously. It can be seen that the direction in which the Gibbs free energy of the system decreases under isothermal pressure and pressure is the direction in which the chemical reaction that does not do non-volume work proceeds. The Gibbs free energy of any spontaneous process that does not do non-volume work under isothermal pressure and pressure will decrease. This paper uses JMatPro software to calculate the Gibbs free energy of Fe
25Cr
25Ni
25Ti
xAl
(25−x) (x = 0; 6.25; 12.5; 18.75; 25) multi-principal element alloy, as shown in
Figure 10. It can be seen from the figure that as the temperature rises high, the Gibbs free energy of the system gradually decreases, indicating that the reaction proceeds spontaneously. In the isothermal and isotactic state, as the Ti content increases, the Gibbs free energy decreases and the reaction proceeds spontaneously.
3.4. First-Principles Prediction of Alloy Stability
To quantitatively evaluate the stability and elastic properties of the phase structure of Fe
25Cr
25Ni
25TixAl
(25−x) multi-principal element alloys, the first-principle used to calculate the formation heat, bonding energy, bulk modulus, shear modulus, and Youngs’ modulus of the alloy. The modulus, Poisson’s ratio, and the nature of the anisotropy predicted. According to the phase diagram analysis described above, the composition phase of the Fe
25Cr
25Ni
25Ti
xAl
(25−x) multi-principal element alloys includes a disordered BCC1 phase, an ordered BCC2 phase, and a Laves phase. The crystal structure model of the body-centered cubic structure and the close-packed hexagonal structure is established based on the Fe supercell and the Ti supercell. The Fe crystal space group of the body-centered cubic structure is IM-3M, the lattice constant is a = b = c = 2.866 Å, and the unit cell contains two atoms, and the positions are (0 0 0) and (0.5 0.5 0.5), respectively. The disordered BCC A2 phase and the ordered BCC B2 phase established on this basis contain 16 atoms. The Ti crystal space group of the close-packed hexagonal structure is P63/mmc, and the lattice constant is a = b = 2.9506 Å, c = 4.6788 Å, α = β = 90°, γ = 120°. The atomic positions in the unit cell are (0.333, 0.667, 0.25), (0.667, 0.333, 0.75), and the established Laves phase supercell contains 12 atoms. Multi-principal element alloys have higher entropy values and greater chaos, and the parent phase is disordered. Common modeling methods include Coherent Potential Approximation (CPA) [
24] and Virtual Crystal Approximation (VCA) [
25]. Methods such as Special Quasirandom Structure (SQS), the modeling methods in this paper are all modeled by SQS [
26]. For the Fe
25Cr
25Ni
25Ti
12.5Al
12.5 alloy studied, a 2 × 2 × 2 supercell structure containing 16 atoms was used. In the modeling stage, an alloy of a certain composition was first established, and based on this, the atomic ratio adjusted to form an alloy of different compositions. For example, a Fe
25Cr
25Ni
25Ti
12.5Al
12.5 multi-principal element alloys was first established to establish a disordered BCC A2 phase, an ordered BCC B2 phase, and a Laves phase, respectively.
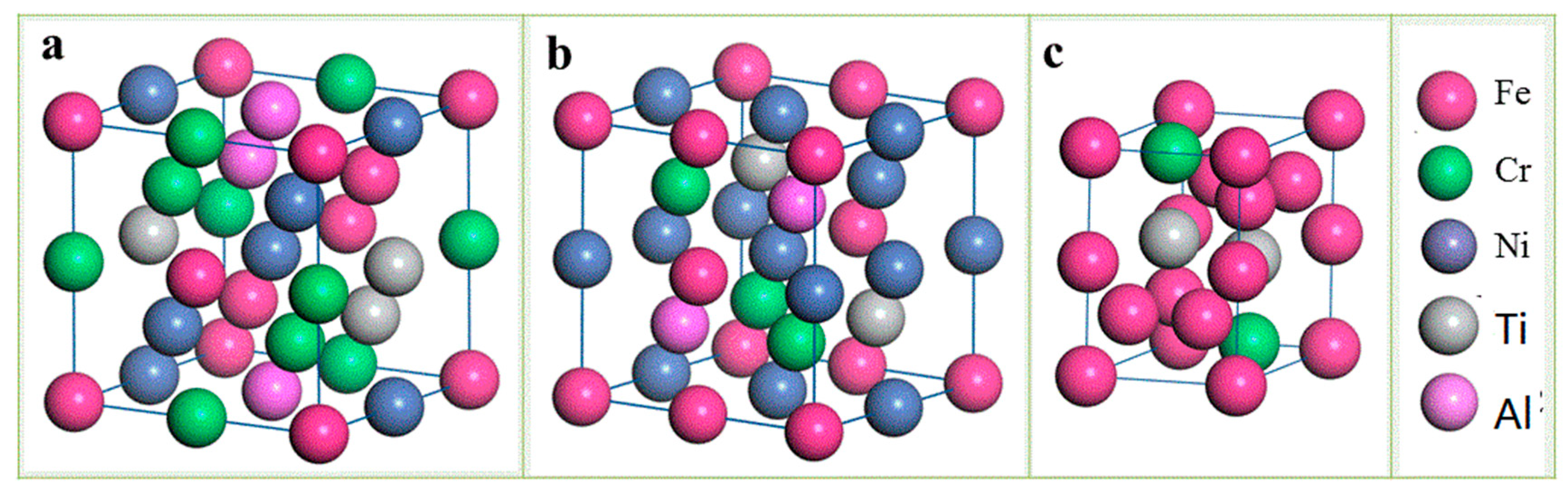
Figure 11 shows the supercell structure of the disordered BCC A2 phase, the ordered BCC B2 phase, and the fully chemically disordered Laves phase in the Fe
25Cr
25Ni
25Ti
12.5Al
12.5 alloy.
Table 2 shows the lattice parameters of the supercells calculated by the direct optimization method for the Fe
25Cr
25Ni
25Ti
12.5Al
12.5 alloy. The theoretical calculations shown in the table are in good agreement with the experimental results.
The strength and structural stability of crystals are closely related to their formation of heat and bonding energy. Heat is formed to determine which configuration is easier to form, and bonding energy is used to determine which configuration is more stable. The formation heat is defined as the difference between the energy of the compound and the corresponding composition. Usually, a negative value indicates that the substance can be stably present, and a positive value indicates that the substance is difficult to be formed. A smaller value indicates that the alloying ability is stronger. For Fe
25Cr
25Ni
25Ti
xAl
(25−x) (x = 0; 6.25; 12.5; 18.75; 25) system alloys, the expression of heat is:
is the total energy of the unit cell, ,
, , and respectively represent the heat of formation of a single atom in the solid element.
The bonding energy of a crystal is defined as the energy released by the combination of free atoms into crystals, or the energy required to decompose a crystal into a single atom, usually a negative value. Therefore, the smaller the value of the bonding energy, the more stable the crystal formed. For the Fe
25Cr
25Ni
25Ti
xAl
(25−x) alloy, the bonding energy is calculated as follows:
, , , , are isolated atomic energies of a single atom, respectively.
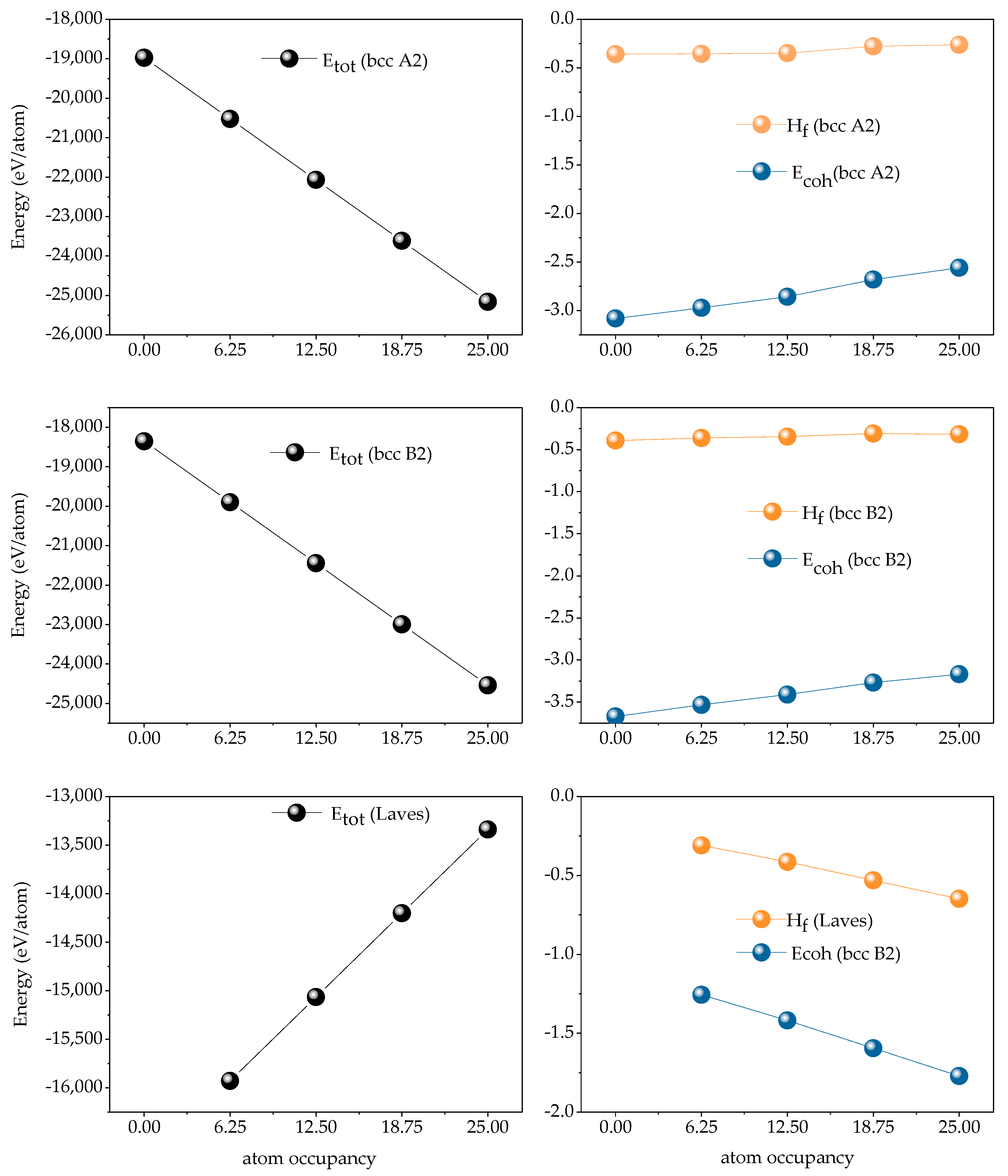
Figure 12 is the calculated total ground state energy of Fe
25Cr
25Ni
25Ti
xAl
(25-x) alloy atom assembly, forming heat and binding energy, and the result is negative, indicating that the alloy of the system is usually easy to form. From the energy point of view, the system of the alloy is stable. Further analysis, x = 0; 6.25; 12.5; 18.75; 25. With the increase of Ti content, the calculated total energy of bcc A2 phase and bcc B2 phase is getting smaller and smaller, indicating that the formation of the system is relatively stable. However, the calculated total energy for forming the Laves phase is getting larger and larger, indicating that the more difficult the Laves phase is to form, the system is not easy to stabilize. The formation heat of the bcc A2 phase gradually decreases and tends to be stable, and both are less than 0, indicating that it is easier to form. The binding energy gradually increases and tends to be stable and all are less than 0, indicating that the configuration with less Ti content is more stable. With the increase of Ti content, the formation heat and binding energy of Laves phase gradually decrease, indicating that Laves phase is easy to form in alloys with high Ti content and the configuration is more stable.
3.5. First-Principles Prediction of Alloy Elastic Properties
The elastic constant is the stiffness that characterizes the response of the crystal to the external strain ε. When a small strain is applied, the internal energy of the system has a quadratic linear relationship with the magnitude of the strain (Hooke’s law), and the elastic constant is the coefficient of the quadratic term. The expression is:
The strain tensor ε is defined as:
where ΔE represents the energy difference before and after deformation of the unit cell,
is the volume of the unit cell,
is the component of the elastic tensor, and
and
are the applied minor strains.
For a stable structure, the Born mechanical stability standard for orthorhombic crystals at zero pressure is [
27]:
According to the calculated single-crystal elastic constant
, the polycrystalline elastic properties of the material such as the bulk modulus B, the shear modulus G, the elastic modulus E, and the Poisson can be obtained by the Voigt–Reuss–Hill (VRH) approximation method [
28]. The ratios ν, Voigt, and Reuss approximate the maximum and minimum limits of polycrystalline elastic properties. The expressions are:
where
Sij is the elastic compliance of the material single crystal and
Sij is the inverse matrix of
Cij. The V and R in the subscript represent the calculation results of the Voigt and Reuss approximation models, respectively.
For a hexagonal crystal, the standard for mechanical stability is [
29]:
From the calculated single-crystal elastic constants, the polycrystalline elastic property can be approximated by Voigt–Reuss–Hill (VRH), and the expression is [
30]:
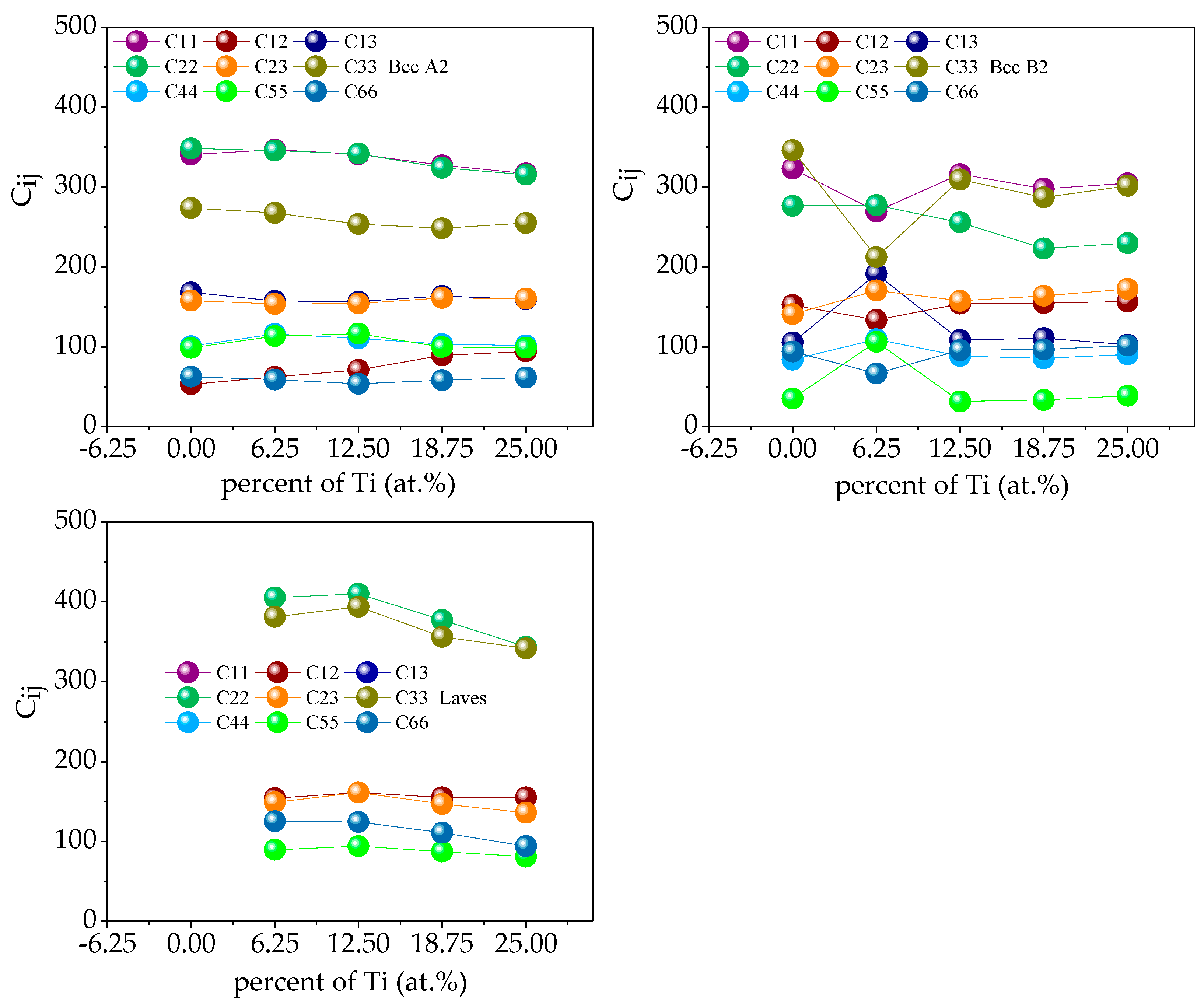
In the Fe
25Cr
25Ni
25Ti
xAl
(25-x) system multi-principal element alloys, the single-crystal elastic constants C
ij of the alloy calculated by the above formula are shown in
Figure 13. Through verification, the single-crystal elastic constants of the five alloys all meet the mechanical stability criterion, indicating that the five multi-principal element alloys structures established are mechanically stable. According to the calculated theoretical elastic constant of the single alloy crystal, the elastic properties of the alloy polycrystal obtained by the Voigt–Reuss–Hill approximation shown in
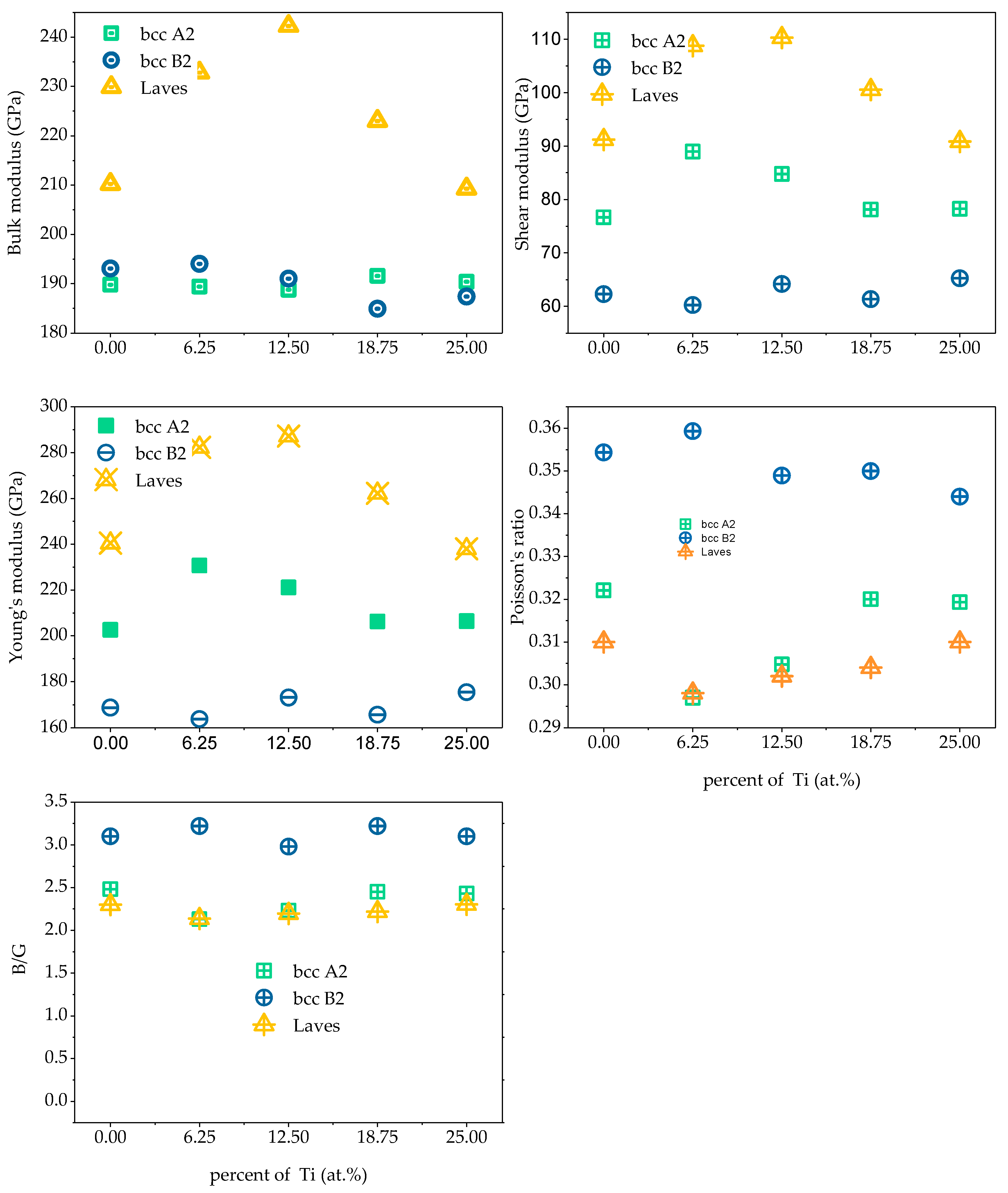
Figure 12. The bulk modulus of a crystal is the resistance of a material to uniform compression of the outside under an elastic system. Shear modulus is the ratio of shear stress to strain, which characterizes the material’s ability to resist shear strain. Young’s modulus is one of the most essential and characteristic mechanical properties of elastic materials, reflecting the softness of materials to some extent hard. Poisson’s ratio ν is commonly used to characterize the ability of a material to resist shear stress. The larger the Poisson’s ratio, the better the shape of the material. In addition to Poisson’s ratio, the ductile and brittleness of multi-principal element alloys can also be determined according to the Pugh empirical criteria [
31], specifically defined as the ratio of bulk modulus to shear modulus (B/G). When B/G < 1.75, the material exhibits brittleness; when B/G > 1.75, the material exhibits toughness, and the larger the ratio, the stronger the toughness and the better the ductility of the material.
Figure 14 shows the polycrystalline elastic properties of the five alloys. The values of shear modulus G and Young’s modulus E in the alloy are found to be BCC B2 phase < BCC A2 phase < Laves phase; illustrated in the Fe
25Cr
25Ni
25Ti
xAl
(25−x) system. Among the alloys, the Laves phase is the hardest and has the strongest resistance to shear deformation, followed by the BCC A2 phase, followed by the BCC B2 phase. When the value of bulk modulus B is x < 0.5, BCC B2 phase < BCC A2 phase < Laves phase; when x ≥ 0.5, BCC A2 phase < BCC B2 phase < Laves phase, indicating that Laves phase has the strongest volume deformation Resistance. By analyzing the Poisson’s ratio and the value of B/G, it is found that the BCC B2 phase > BCC A2 phase > Laves phase indicates that the BCC B2 phase has excellent ductility, followed by the BCC A2 phase, and the Laves phase has the worst ductility.