Lath Martensite Microstructure Modeling: A High-Resolution Crystal Plasticity Simulation Study
Abstract
1. Introduction
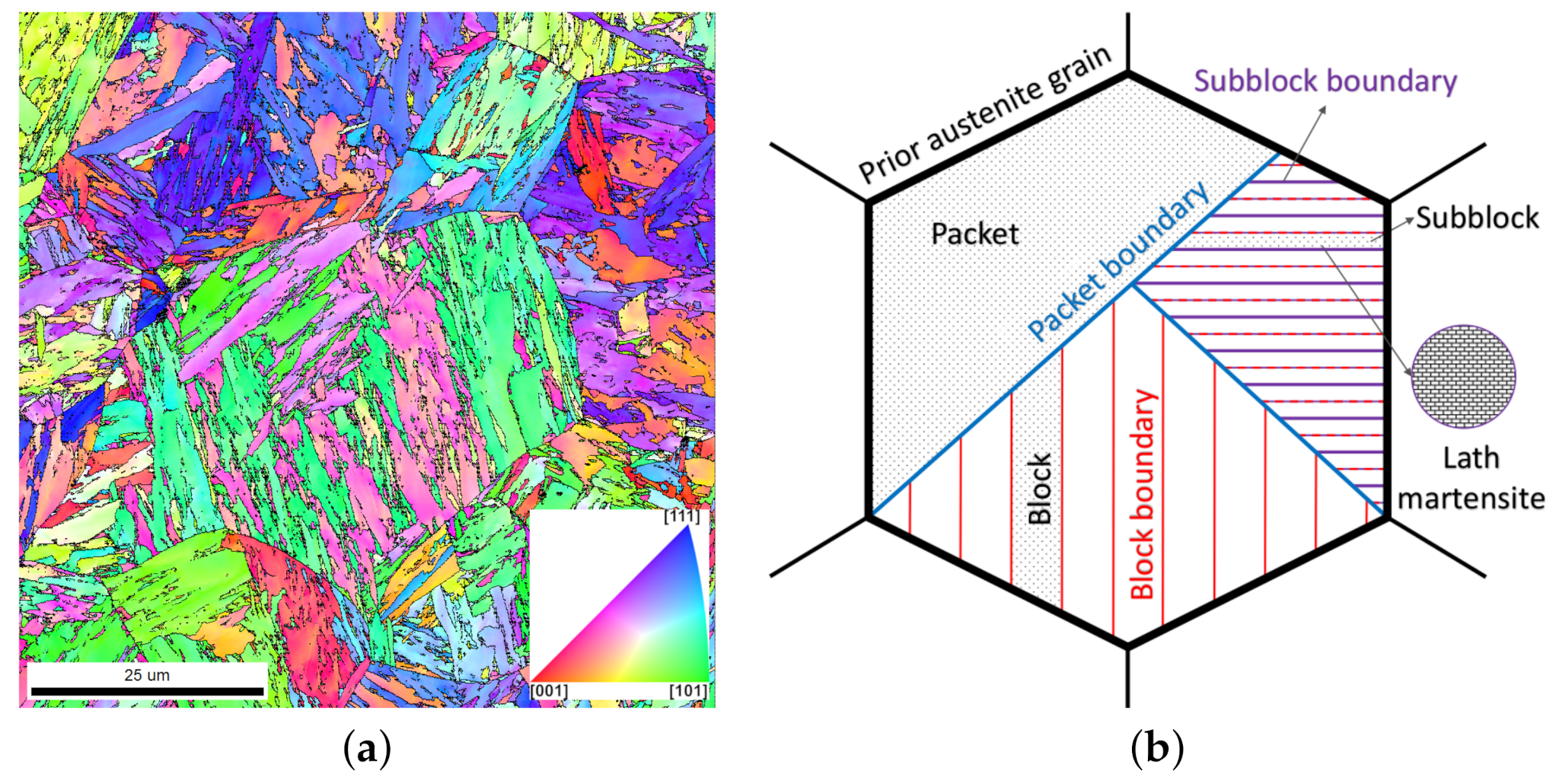
2. Generating Lath Martensitic Microstructures
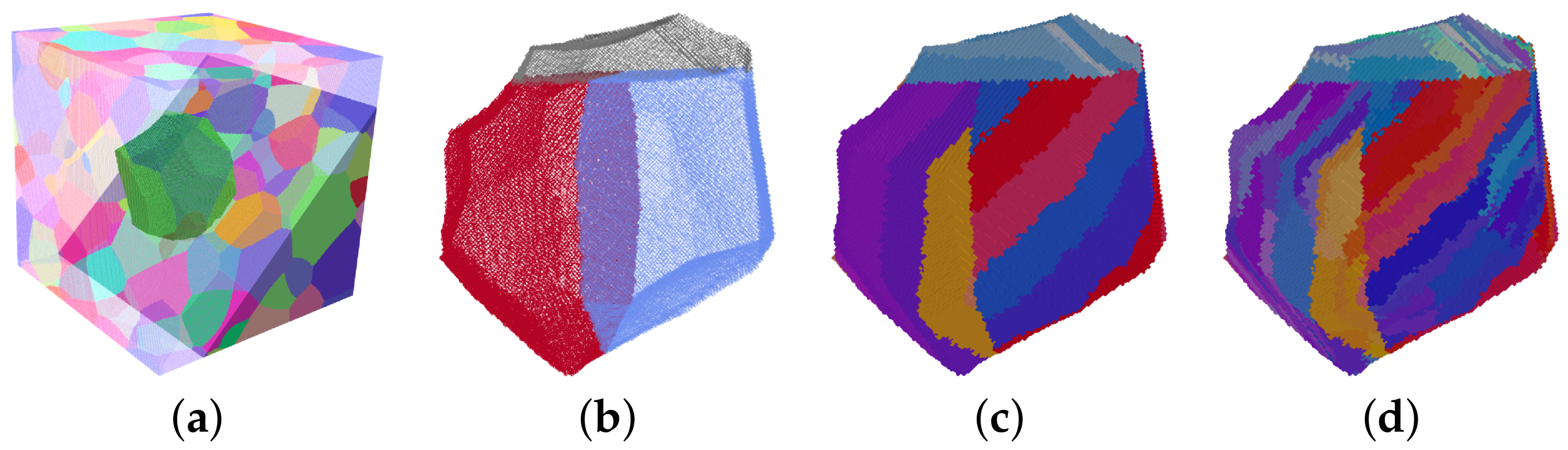
- Packet generation: The austenitic grain (Figure 3a) is subdivided by two flat boundaries into three packets with approximately the same volume. Since no rules are established on how the packets geometrically partition the prior austenite grain, the boundaries are modelled to be perpendicular to each other. The resulting T-shaped grain boundary network is randomly rotated in space (Figure 3b).
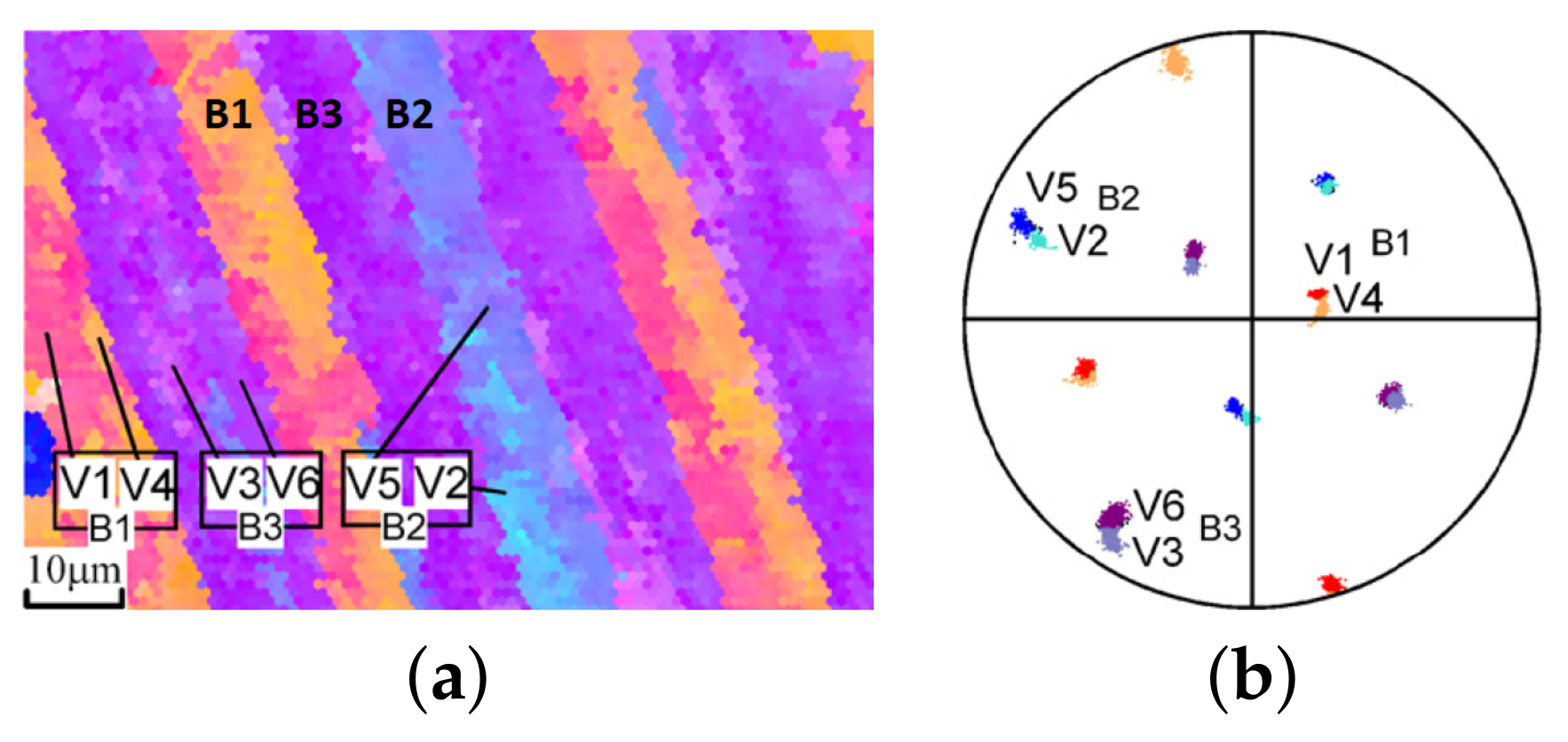
- Subblock generation: For each packet, a different habit plane is selected that is parallel to a {111} plane of the austenitic grain. The packets are then subdivided into subblocks of thickness, , parallel to the habit plane (Figure 3c). According to Morito et al. [12], subblocks in low-carbon steels appear in pairs of crystallographic orientations. For example, the 6 variants of the habit plane occur in the following pairs: V1–V4, V2–V5, and V3–V6. This variant selection is considered when assigning the crystallographic orientations. The order of the variants within a pair and the arrangement of the pairs is random, where for the former a direct repetition is disallowed.
- Lath generation: A Voronoi tessellation is performed in each subblock where each seed corresponds to one individual lath. The volume of the lath, , is inversely proportional to the number of seeds. By distorting the resulting structure of equiaxed grains, laths with an average shape of length () > width () > thickness () are achieved. The longest direction, , of the laths is aligned parallel to one of the <110> directions in the respective {111} plane, the shortest direction, , is aligned normal to the plane. Each lath gets a crystallographic orientation assigned that deviates slightly from the nominal orientation according to the KS model (Figure 3d). More precisely, a random misorientation axis is chosen and the misorientation angle scatters randomly by a value between 0 and .
- The thickness of the subblocks in the direction normal to the habit plane, . It is measured in units of length (UL) which corresponds to the side length of a voxel.
- The average volume of the lath, , controlled via the number density of seeds used in the Voronoi tessellation. It is measured in units of volume (UV) which corresponds to the volume of a voxel, i.e., UL3.
- The average aspect ratio of the lath’s dimensions, , controlled via the respective stretch factor.
- The maximum misorientation angle of the individual lath with respect to the nominal KS orientation, . It is measured in degrees ().
- The rotation of the packet geometry.
- Sequence of variants within a subblock.
- Sequence of pairs within a block.
- Misorientaton distribution of the laths within the same subblock.
3. Modeling Framework
3.1. Numerical Solution Strategy
3.2. Constitutive Model
3.3. Constitutive Parameters
4. Simulation Setup
4.1. Simulations Based on Experimental Microstructures
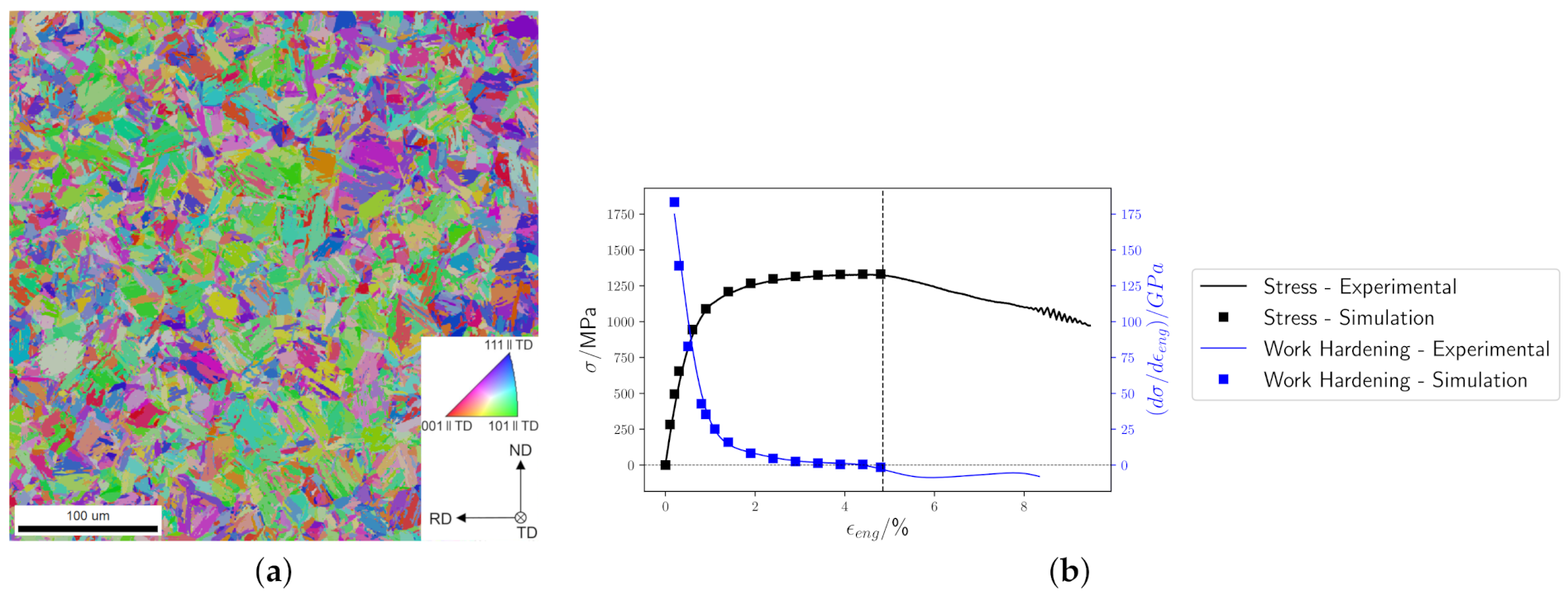
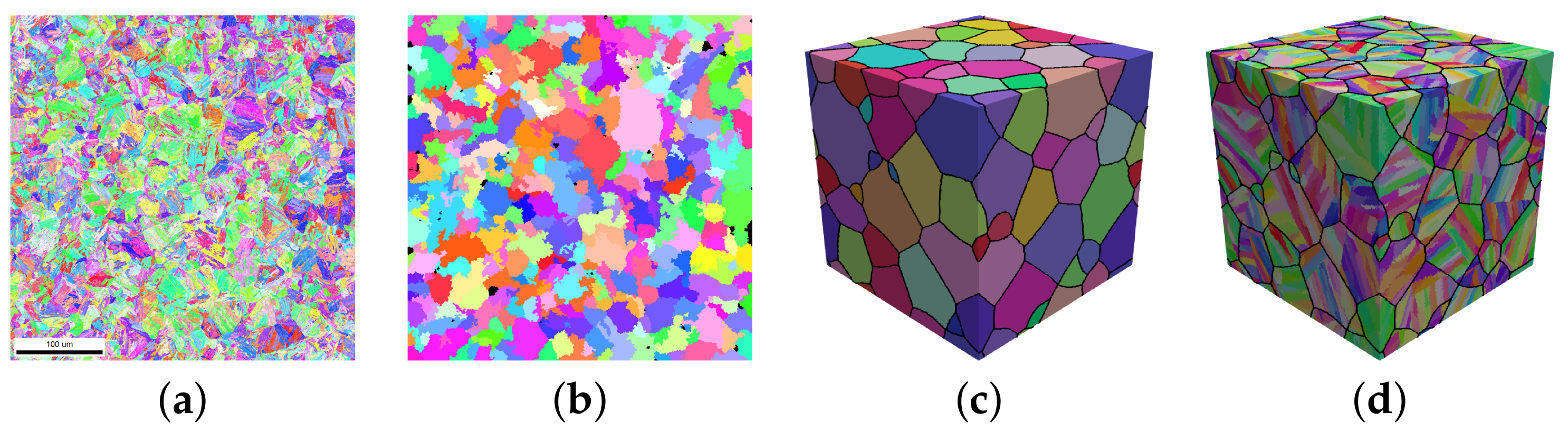
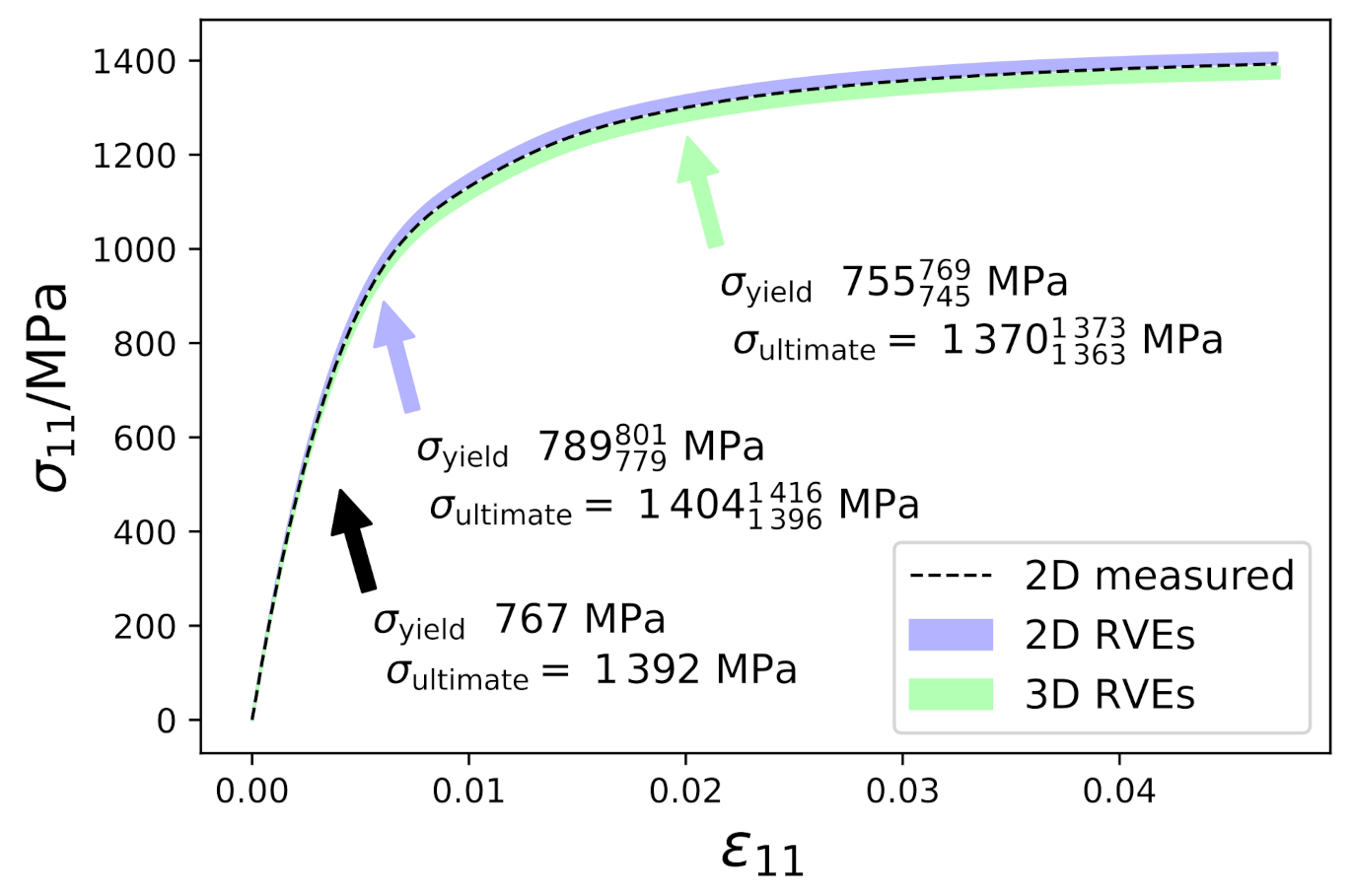
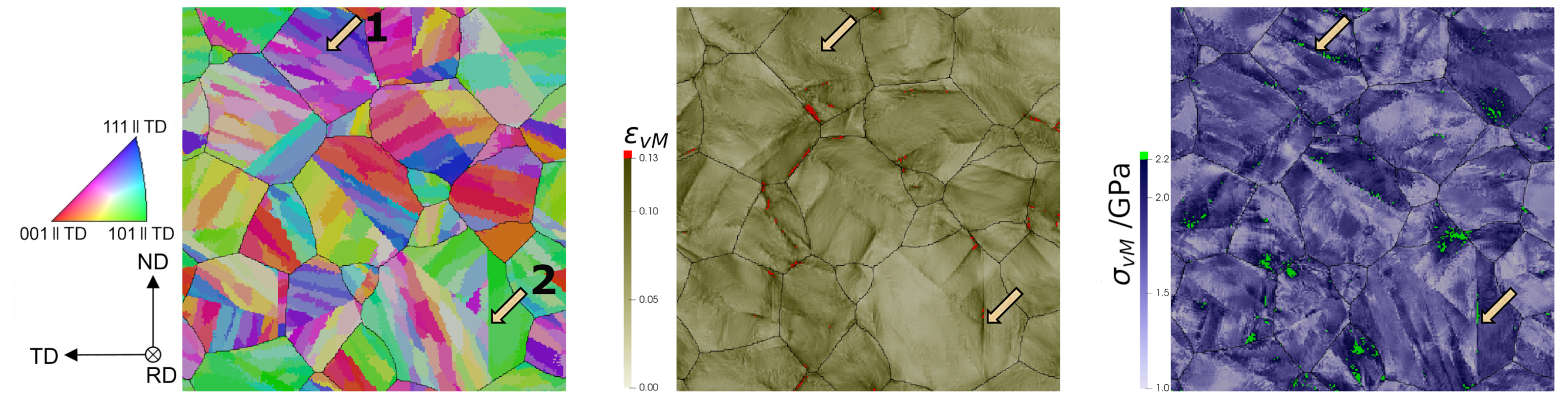
- Experimental microstructure: This is a direct 2D takeover of the measured crystallographic orientation of each of the 1143 × 1143 = 1,306,449 material points after cleaning out the retained austenite (Figure 4a). It is the same model that was used for the parameter adjustment (Section 3.3).
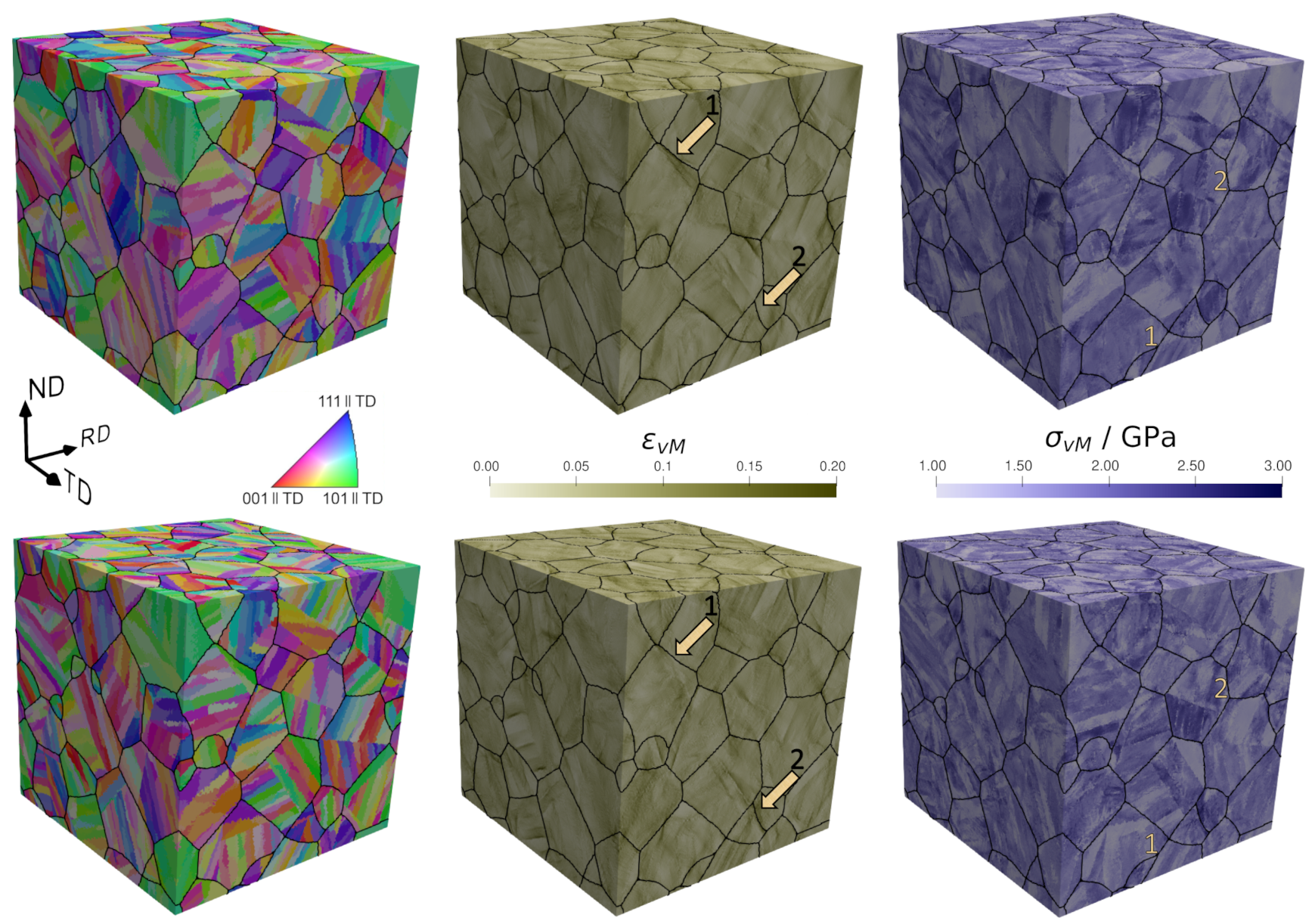
- 3D RVEs: A regular grid of 256 × 256 × 256 = 16,777,216 material points with a resolution that contains 86 equiaxed austenitic grains serves as the starting point. The values of the parameters used to create the martensitic structure from this microstructure are: UL, UV, 9:3:1, . A total of ten 3D RVEs are created using different random seeds.
- 2D RVEs: These models are created by selecting a slice from a 3D model that contains 90 austenitic grains in a 600 × 600 × 50 = 18,000,000 grid. The 3D RVE used for slicing was created using the same parameters as for the 3D models. A total of three 2D RVEs with 600 × 600 = 360,000 points are used, choosing different slices from the same 3D model.
4.2. 3D Simulations with Systematically Varied Microstructural Features
- Lath volume: The value is set to 320, 1400, and 4600 UV. Since subblocks are entirely filled with laths, a decrease in lath volume directly results in more lath per subblock and vice versa.
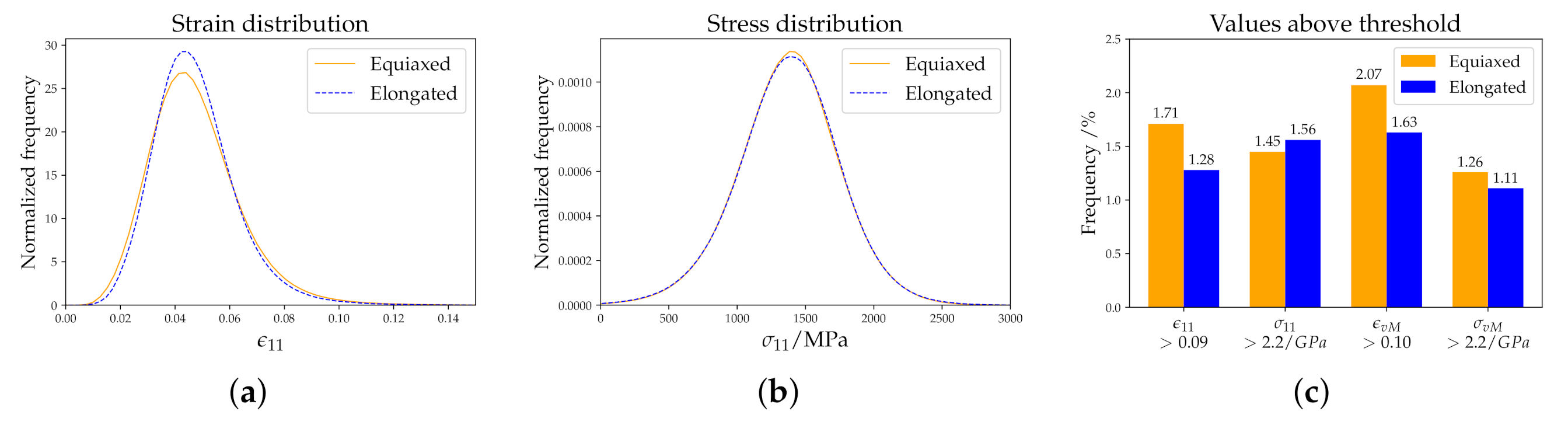
- Lath aspect ratio: Different lath shapes are created modifying , , and . Rectangular cuboid-shaped laths are created with aspect ratio 9:3:1. Plate-shaped laths are created with aspect ratio 8:8:1. Rod-shaped laths are created with aspect ratio 5:1:1. Cube-shaped laths are created with aspect ratio 1:1:1.
- Scatter: The misorientation angle is chosen as 0, 3, and 5. represents a 3D RVE made only of subblocks since all laths in a subblock will have the same orientation. Limiting is based on experimental evidence showing that the misorientation angle of a laths within a subblock does not exceed 5 .
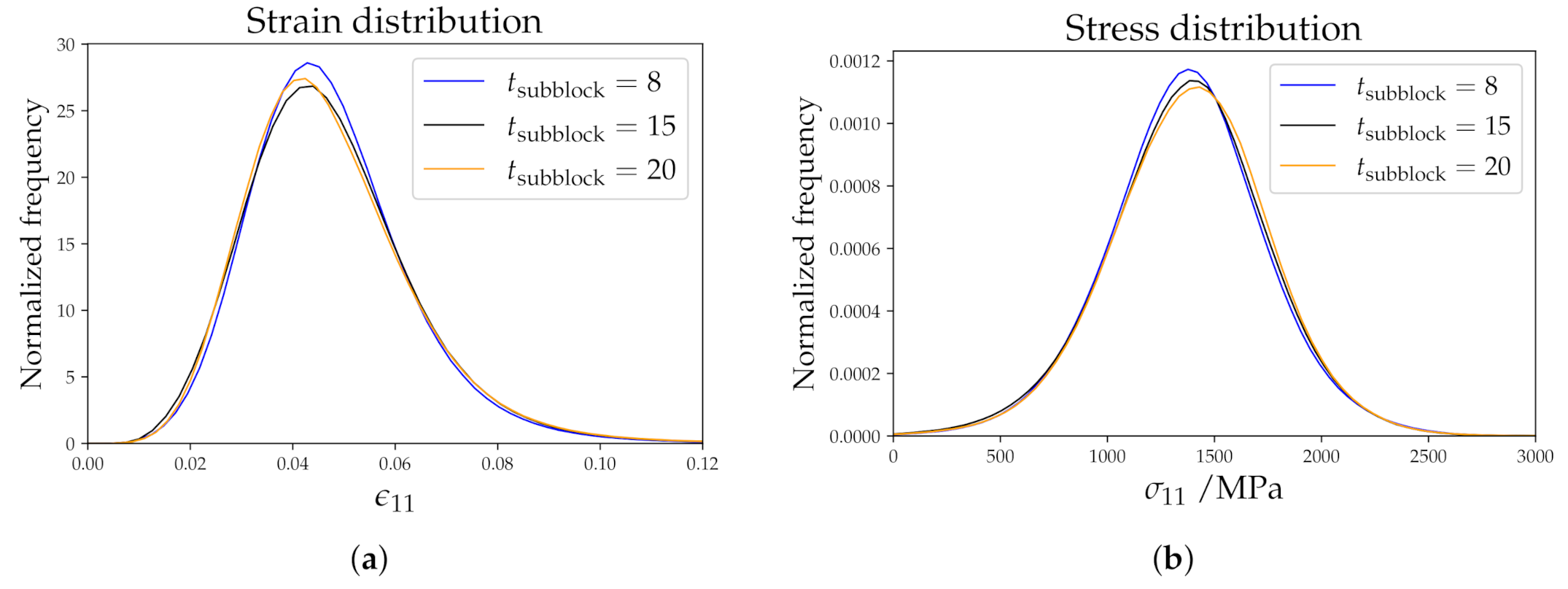
- Subblock thickness: Subblock thickness is set to 8, 15, and 20 UL.
5. Results & Discussion
5.1. Simulations Based on Experimental Microstructures
5.1.1. Average Stress–Strain Response
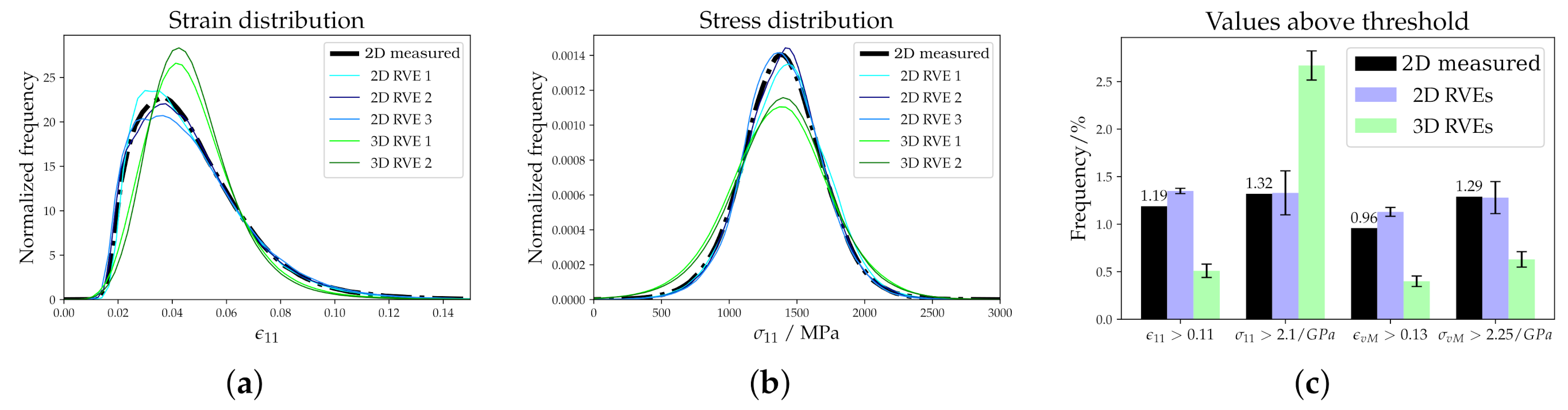
5.1.2. Correlation of Stress and Strain Fields
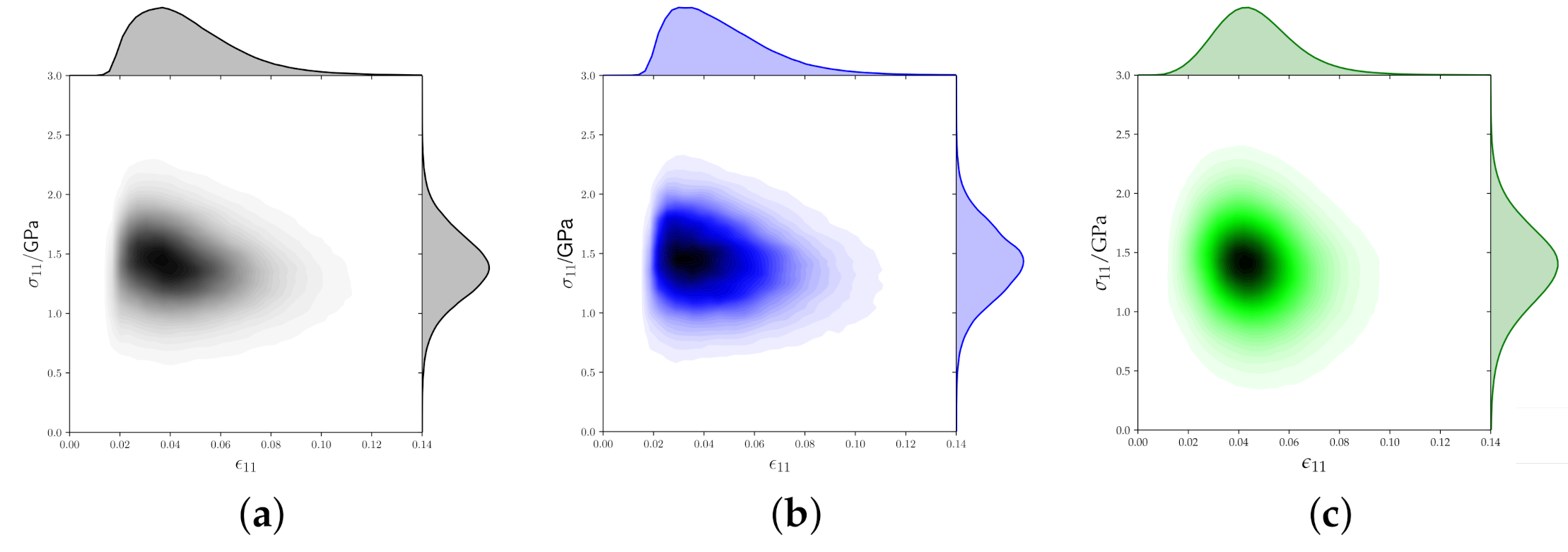
5.1.3. Micromechanics of 2D and 3D Models
5.2. 3D Simulations with Systematically Varied Microstructural Features
6. Summary and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Variant | Plane | Direction | Variant | Plane | Direction |
|---|---|---|---|---|---|
| 1 | (111) (011) | [1 0 1] [1 1 1] | 13 | (111) (011) | [0 1 1] [1 1 1] |
| 2 | [1 0 1] [1 1 1] | 14 | [0 1 1] [1 1 1] | ||
| 3 | [0 1 1] [1 1 1] | 15 | [1 0 1] [1 1 1] | ||
| 4 | [0 1 1] [1 1 1] | 16 | [1 0 1] [1 1 1] | ||
| 5 | [1 1 0] [1 1 1] | 17 | [1 1 0] [1 1 1] | ||
| 6 | [1 1 0] [1 1 1] | 18 | [1 1 0] [1 1 1] | ||
| 7 | (111) (011) | [1 0 1] [1 1 1] | 19 | (111) (011) | [1 1 0] [1 1 1] |
| 8 | [1 0 1] [1 1 1] | 20 | [1 1 0] [1 1 1] | ||
| 9 | [1 1 0] [1 1 1] | 21 | [0 1 1] [1 1 1] | ||
| 10 | [1 1 0] [1 1 1] | 22 | [0 1 1] [1 1 1] | ||
| 11 | [0 1 1] [1 1 1] | 23 | [1 0 1] [1 1 1] | ||
| 12 | [0 1 1] [1 1 1] | 24 | [1 0 1] [1 1 1] |
References
- Bhadeshia, H.; Honeycombe, R. Formation of Martensite. In Steels: Microstructure and Properties; Butterworth–Heinemann: Oxford, UK, 2017; pp. 135–177. [Google Scholar] [CrossRef]
- Olson, G.; Feinberg, Z. Kinetics of martensite transformations in steels. In Phase Transformations in Steels; Woodhead Publishing: Cambridge, UK, 2012; pp. 59–82. [Google Scholar] [CrossRef]
- Maki, T. Morphology and substructure of martensite in steels. In Phase Transformations in Steels; Woodhead Publishing: Cambridge, UK, 2012; pp. 34–58. [Google Scholar] [CrossRef]
- Krauss, G.; Marder, A.R. The morphology of martensite in iron alloys. Metall. Trans. 1971, 2, 2343–2357. [Google Scholar] [CrossRef]
- Morito, S.; Adachi, Y.; Ohba, T. Morphology and Crystallography of Sub-Blocks in Ultra-Low Carbon Lath Martensite Steel. Mater. Trans. 2009, 50, 1919–1923. [Google Scholar] [CrossRef]
- Tasan, C.C.; Diehl, M.; Yan, D.; Bechtold, M.; Roters, F.; Schemmann, L.; Zheng, C.; Peranio, N.; Ponge, D.; Koyama, M.; et al. An overview of dual-phase steels: Advances in microstructure-oriented processing and micromechanically guided design. Annu. Rev. Mater. Res. 2015, 45, 391–431. [Google Scholar] [CrossRef]
- Kurdjumow, G.; Sachs, G. Über den Mechanismus der Stahlhärtung. Z. Phys. 1930, 64, 325–343. [Google Scholar] [CrossRef]
- Nishiyama, Z. X-ray investigation of the mechanism of the transformation from face centered cubic lattice to body centered cubic. Sci. Rep. Tohoku Univ. 1934, 23, 637–664. [Google Scholar]
- Wassermann, G. Ueber den Mechanismus der α→γ-Umwandlung des Eisens. Mitt. K. Wilh. Eisenforsch. 1935, 17, 149–155. [Google Scholar]
- Greninger, A.B.; Troiano, A.R. The mechanism of Martensite formation. JOM 1949, 1, 590–598. [Google Scholar] [CrossRef]
- Yardley, V.A.; Payton, E.J. Austenite–martensite/bainite orientation relationship: Characterisation parameters and their application. Mater. Sci. Technol. 2014, 30, 1125–1130. [Google Scholar] [CrossRef]
- Morito, S.; Tanaka, H.; Konishi, R.; Furuhara, T.; Maki, T. The morphology and crystallography of lath martensite in Fe-C alloys. Acta Mater. 2003, 51, 1789–1799. [Google Scholar] [CrossRef]
- Morito, S.; Huang, X.; Furuhara, T.; Maki, T.; Hansen, N. The morphology and crystallography of lath martensite in alloy steels. Acta Mater. 2006, 54, 5323–5331. [Google Scholar] [CrossRef]
- Murata, Y. Formation Mechanism of Lath Martensite in Steels. Mater. Trans. 2018, 59, 151–164. [Google Scholar] [CrossRef]
- Wayman, C.; Bhadeshia, H. Phase transformations, nondiffusive. In Physical Metallurgy; Elsevier: Amsterdam, The Netherlands, 1996; pp. 1507–1554. [Google Scholar] [CrossRef]
- Maki, T.; Tsuzaki, K.; Tamura, I. The Morphology of Microstructure Composed of Lath Martensites in Steels. Trans. ISIJ 1980, 20, 207–214. [Google Scholar]
- Morsdorf, L.; Tasan, C.; Ponge, D.; Raabe, D. 3D structural and atomic-scale analysis of lath martensite: Effect of the transformation sequence. Acta Mater. 2015, 95, 366–377. [Google Scholar] [CrossRef]
- Morito, S.; Saito, H.; Ogawa, T.; Furuhara, T.; Maki, T. Effect of Austenite Grain Size on the Morphology and Crystallography of Lath Martensite in Low Carbon Steels. ISIJ Int. 2005, 45, 91–94. [Google Scholar] [CrossRef]
- Morito, S.; Edamatsu, Y.; Ichinotani, K.; Ohba, T.; Hayashi, T.; Adachi, Y.; Furuhara, T.; Miyamoto, G.; Takayama, N. Quantitative analysis of three-dimensional morphology of martensite packets and blocks in iron-carbon-manganese steels. J. Alloy. Compd. 2013, 577, S587–S592. [Google Scholar] [CrossRef]
- Swarr, T.; Krauss, G. The effect of structure on the deformation of as-quenched and tempered martensite in an Fe-0.2 pct C alloy. Metall. Trans. A 1976, 7, 41–48. [Google Scholar] [CrossRef]
- Furuhara, T.; Kikumoto, K.; Saito, H.; Sekine, T.; Ogawa, T.; Morito, S.; Maki, T. Phase Transformation from Fine-grained Austenite. ISIJ Int. 2008, 48, 1038–1045. [Google Scholar] [CrossRef]
- Morito, S.; Igarashi, R.; Kamiya, K.; Ohba, T.; Maki, T. Effect of Cooling Rate on Morphology and Crystallography of Lath Martensite in Fe-Ni Alloys. Mater. Sci. Forum 2010, 638–642, 1459–1463. [Google Scholar] [CrossRef]
- Li, S.; Zhu, G.; Kang, Y. Effect of substructure on mechanical properties and fracture behavior of lath martensite in 0.1C–1.1Si–1.7Mn steel. J. Alloys Compd. 2016, 675, 104–115. [Google Scholar] [CrossRef]
- Du, C.; Hoefnagels, J.; Vaes, R.; Geers, M. Block and sub-block boundary strengthening in lath martensite. Scr. Mater. 2016, 116, 117–121. [Google Scholar] [CrossRef]
- Zeghadi, A.; N’guyen, F.; Forest, S.; Gourgues, A.F.; Bouaziz, O. Ensemble averaging stress–strain fields in polycrystalline aggregates with a constrained surface microstructure—Part 1: Anisotropic elastic behaviour. Philos. Mag. 2007, 87, 1401–1424. [Google Scholar] [CrossRef]
- Zeghadi, A.; Forest, S.; Gourgues, A.F.; Bouaziz, O. Ensemble averaging stress–strain fields in polycrystalline aggregates with a constrained surface microstructure—Part 2: Crystal plasticity. Philos. Mag. 2007, 87, 1425–1446. [Google Scholar] [CrossRef]
- Du, C.; Petrov, R.; Geers, M.; Hoefnagels, J. Lath martensite plasticity enabled by apparent sliding of substructure boundaries. Mater. Des. 2019, 172, 107646. [Google Scholar] [CrossRef]
- Maresca, F.; Kouznetsova, V.G.; Geers, M.G.D. On the role of interlath retained austenite in the deformation of lath martensite. Model. Simul. Mater. Sci. Eng. 2014, 22, 045011. [Google Scholar] [CrossRef]
- Tian, C.; Ponge, D.; Christiansen, L.; Kirchlechner, C. On the mechanical heterogeneity in dual phase steel grades: Activation of slip systems and deformation of martensite in DP800. Acta Mater. 2020, 183, 274–284. [Google Scholar] [CrossRef]
- Shchyglo, O.; Du, G.; Engels, J.K.; Steinbach, I. Phase-field simulation of martensite microstructure in low-carbon steel. Acta Mater. 2019, 175, 415–425. [Google Scholar] [CrossRef]
- Briffod, F.; Shiraiwa, T.; Enoki, M. Modeling and Crystal Plasticity Simulations of Lath Martensitic Steel under Fatigue Loading. Mater. Trans. 2018, 60, 199–206. [Google Scholar] [CrossRef]
- Osipov, N. Génération et calcul de microstructures bainitiques, approche locale intragranulaire de la rupture. Ph.D. Thesis, École des Mines ParisTech, Paris, France, 2007. [Google Scholar]
- Osipov, N.; Gourgues-Lorenzon, A.F.; Marini, B.; Mounoury, V.; Nguyen, F.; Cailletaud, G. FE modelling of bainitic steels using crystal plasticity. Philos. Mag. 2008, 88, 3757–3777. [Google Scholar] [CrossRef]
- Ghassemi-Armaki, H.; Chen, P.; Bhat, S.; Sadagopan, S.; Kumar, S.; Bower, A. Microscale-calibrated modeling of the deformation response of low-carbon martensite. Acta Mater. 2013, 61, 3640–3652. [Google Scholar] [CrossRef]
- Schäfer, B.; Song, X.; Sonnweber-Ribic, P.; ul Hassan, H.; Hartmaier, A. Micromechanical Modelling of the Cyclic Deformation Behavior of Martensitic SAE 4150—A Comparison of Different Kinematic Hardening Models. Metals 2019, 9, 368. [Google Scholar] [CrossRef]
- Schäfer, B.J.; Sonnweber-Ribic, P.; ul Hassan, H.; Hartmaier, A. Micromechanical Modelling of the Influence of Strain Ratio on Fatigue Crack Initiation in a Martensitic Steel-A Comparison of Different Fatigue Indicator Parameters. Materials 2019, 12, 2852. [Google Scholar] [CrossRef]
- Roters, F.; Diehl, M.; Shanthraj, P.; Eisenlohr, P.; Reuber, C.; Wong, S.; Maiti, T.; Ebrahimi, A.; Hochrainer, T.; Fabritius, H.O.; et al. DAMASK—The Düsseldorf Advanced Material Simulation Kit for modeling multi-physics crystal plasticity, thermal, and damage phenomena from the single crystal up to the component scale. Comput. Mater. Sci. 2019, 158, 420–478. [Google Scholar] [CrossRef]
- Eisenlohr, P.; Diehl, M.; Lebensohn, R.; Roters, F. A spectral method solution to crystal elasto-viscoplasticity at finite strains. Int. J. Plast. 2013, 46, 37–53. [Google Scholar] [CrossRef]
- Shanthraj, P.; Eisenlohr, P.; Diehl, M.; Roters, F. Numerically robust spectral methods for crystal plasticity simulations of heterogeneous materials. Int. J. Plast. 2015, 66, 31–45. [Google Scholar] [CrossRef]
- Moulinec, H.; Suquet, P. A fast numerical method for computing the linear and nonlinear mechanical properties of composites. In Comptes Rendus de l’Académie des Sciences; Série II, Mécanique, Physique, Chimie, Astronomie; Academie des Sciences: Paris, France, 1994. [Google Scholar]
- Lahellec, N. Estimate of the homogenized hyperelastic behavior of periodic fiber-reinforced composites using the second-order procedure. Comptes Rendus L’Acad. Sci. Ser. IIB Mech. 2001, 329, 67–73. [Google Scholar] [CrossRef]
- Hutchinson, J.W. Bounds and self-consistent estimates for creep of polycrystalline materials. Proc. R. Soc. Lond. A Math. Phys. Sci. 1976, 348, 101–127. [Google Scholar] [CrossRef]
- Roters, F.; Eisenlohr, P.; Hantcherli, L.; Tjahjanto, D.; Bieler, T.; Raabe, D. Overview of constitutive laws, kinematics, homogenization and multiscale methods in crystal plasticity finite-element modeling: Theory, experiments, applications. Acta Mater. 2010, 58, 1152–1211. [Google Scholar] [CrossRef]
- Tasan, C.; Diehl, M.; Yan, D.; Zambaldi, C.; Shanthraj, P.; Roters, F.; Raabe, D. Integrated experimental–simulation analysis of stress and strain partitioning in multiphase alloys. Acta Mater. 2014, 81, 386–400. [Google Scholar] [CrossRef]
- EDAX. TSL OIM Analysis 7; AMETEK: Berwyn, PE, USA, 2007. [Google Scholar]
- Tasan, C.; Hoefnagels, J.; Diehl, M.; Yan, D.; Roters, F.; Raabe, D. Strain localization and damage in dual phase steels investigated by coupled in-situ deformation experiments and crystal plasticity simulations. Int. J. Plast. 2014, 63, 198–210. [Google Scholar] [CrossRef]
- Diehl, M.; Niehuesbernd, J.; Bruder, E. Quantifying the Contribution of Crystallographic Texture and Grain Morphology on the Elastic and Plastic Anisotropy of bcc Steel. Metals 2019, 9, 1252. [Google Scholar] [CrossRef]
- Cayron, C. ARPGE: A computer program to automatically reconstruct the parent grains from electron backscatter diffraction data. J. Appl. Crystallogr. 2007, 40, 1183–1188. [Google Scholar] [CrossRef]
- Groeber, M.A.; Jackson, M.A. DREAM.3D: A Digital Representation Environment for the Analysis of Microstructure in 3D. Integr. Mater. Manuf. Innov. 2014, 3, 56–72. [Google Scholar] [CrossRef]
- Bachmann, F.; Hielscher, R.; Schaeben, H. Texture Analysis with MTEX–Free and Open Source Software Toolbox. Solid State Phenom. 2010, 160, 63–68. [Google Scholar] [CrossRef]
- Diehl, M.; Shanthraj, P.; Eisenlohr, P.; Roters, F. Neighborhood influences on stress and strain partitioning in dual-phase microstructures. An investigation on synthetic polycrystals with a robust spectral-based numerical method. Meccanica 2016, 51, 429–441. [Google Scholar] [CrossRef]
- Fujita, N.; Ishikawa, N.; Roters, F.; Tasan, C.C.; Raabe, D. Experimental–numerical study on strain and stress partitioning in bainitic steels with martensite–austenite constituents. Int. J. Plast. 2018, 104, 39–53. [Google Scholar] [CrossRef]
- Diehl, M.; Wicke, M.; Shanthraj, P.; Roters, F.; Brueckner-Foit, A.; Raabe, D. Coupled Crystal Plasticity–Phase Field Fracture Simulation Study on Damage Evolution Around a Void: Pore Shape Versus Crystallographic Orientation. JOM 2017, 69, 872–878. [Google Scholar] [CrossRef]
- Reuber, C.; Eisenlohr, P.; Roters, F.; Raabe, D. Dislocation density distribution around an indent in single-crystalline nickel: Comparing nonlocal crystal plasticity finite element predictions with experiments. Acta Mater. 2014, 71, 333–348. [Google Scholar] [CrossRef]
- Maresca, F.; Kouznetsova, V.G.; Geers, M.G.D. Reduced crystal plasticity for materials with constrained slip activity. Mech. Mater. 2016, 92, 198–210. [Google Scholar] [CrossRef]


| C | Si | Mn | P | S | Cu | Al | Nb | Mo | Ni | Cr |
|---|---|---|---|---|---|---|---|---|---|---|
| ≤0.25 | ≤0.70 | ≤1.60 | ≤0.025 | ≤0.010 | ≤0.30 | ≤0.03 | ≤0.05 | ≤0.50 | ≤0.80 | ≤1.50 |
| Property | Symbol | Value | Unit |
|---|---|---|---|
| Elastic constant | 417.4 | GPa | |
| Elastic constant | 242.4 | GPa | |
| Elastic constant | 211.1 | GPa | |
| Initial resistance | 160.0 | MPa | |
| Saturation resistance | 555.0 | MPa | |
| Initial hardening rate | 90.0 | GPa | |
| Reference shear rate | 10−3 | s−1 | |
| Stress exponent | n | 20 | |
| Strain hardening exponent | a | 2.0 |
| 2D measured | 0.98 | 0.13 | −0.15 | 0.12 |
| 2D RVEs | 0.98 | 0.14 | −0.16 | 0.13 |
| 3D RVEs | 0.97 | 0.26 | −0.13 | 0.04 |
| Lath Aspect Ratio (::) | Lath Volume (/UV) | Scatter (/) | Subblock Size (/UL) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8:8:1 | 5:1:1 | 9:3:1 | 1:1:1 | 320 | 1400 | 4600 | 0 | 3 | 5 | 8 | 15 | 20 | |
| /% | 1.508 | 1.457 | 1.498 | 1.456 | 1.470 | 1.498 | 1.533 | 1.510 | 1.498 | 1.475 | 1.248 | 1.498 | 1.599 |
| /% | 1.179 | 1.271 | 1.246 | 1.121 | 1.213 | 1.246 | 1.225 | 1.225 | 1.246 | 1.261 | 1.234 | 1.246 | 1.481 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallardo-Basile, F.-J.; Naunheim, Y.; Roters, F.; Diehl, M. Lath Martensite Microstructure Modeling: A High-Resolution Crystal Plasticity Simulation Study. Materials 2021, 14, 691. https://doi.org/10.3390/ma14030691
Gallardo-Basile F-J, Naunheim Y, Roters F, Diehl M. Lath Martensite Microstructure Modeling: A High-Resolution Crystal Plasticity Simulation Study. Materials. 2021; 14(3):691. https://doi.org/10.3390/ma14030691
Chicago/Turabian StyleGallardo-Basile, Francisco-José, Yannick Naunheim, Franz Roters, and Martin Diehl. 2021. "Lath Martensite Microstructure Modeling: A High-Resolution Crystal Plasticity Simulation Study" Materials 14, no. 3: 691. https://doi.org/10.3390/ma14030691
APA StyleGallardo-Basile, F.-J., Naunheim, Y., Roters, F., & Diehl, M. (2021). Lath Martensite Microstructure Modeling: A High-Resolution Crystal Plasticity Simulation Study. Materials, 14(3), 691. https://doi.org/10.3390/ma14030691







