Optimization of Resistance Spot Welding with Inserted Strips via FEM and Response Surface Methodology
Abstract
:1. Introduction
2. Finite Element Modeling
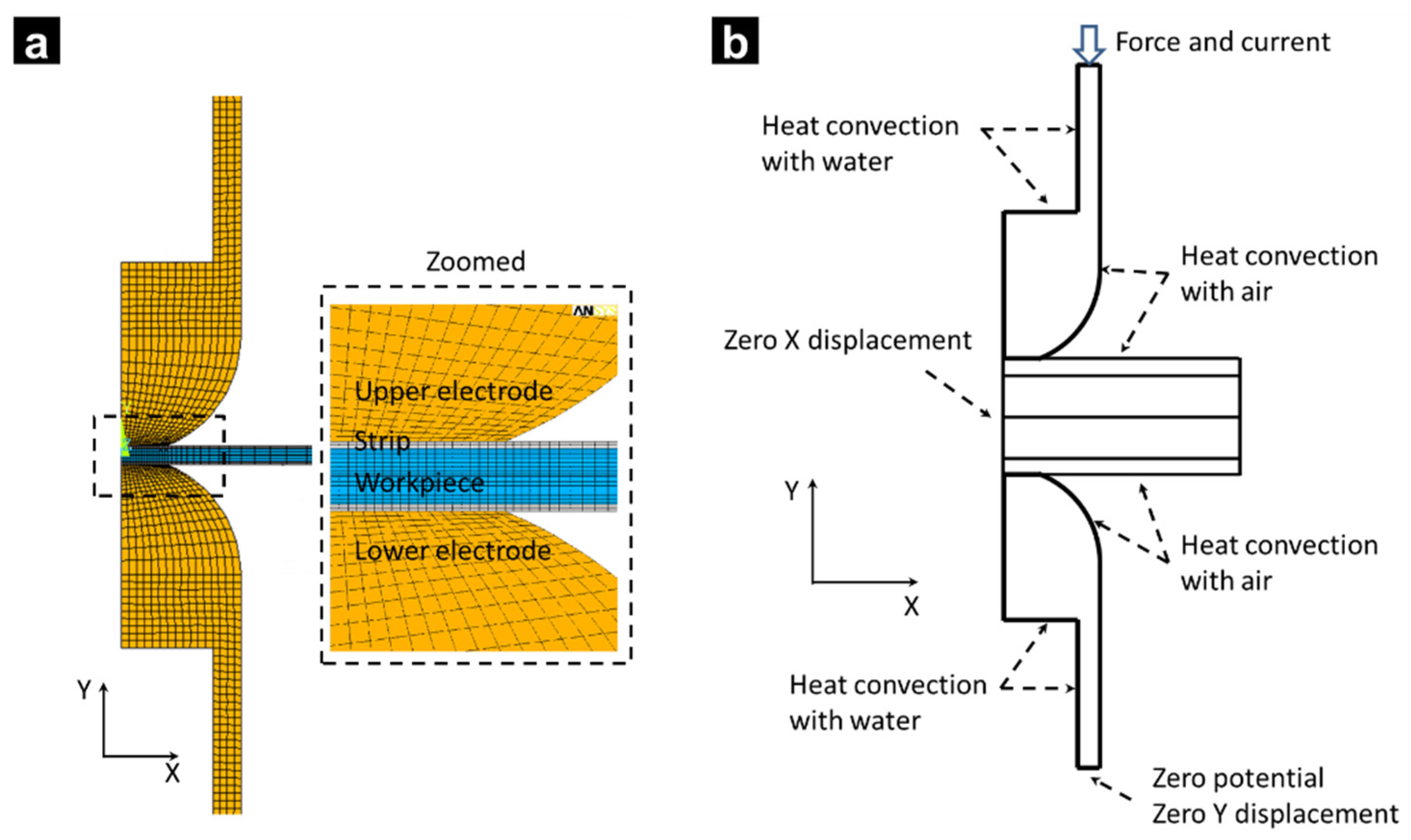
2.1. Model Construction
2.1.1. Geometrical Model
2.1.2. Boundary Condition
2.1.3. Material Properties and Welding Parameters
2.1.4. Contact Resistance Model
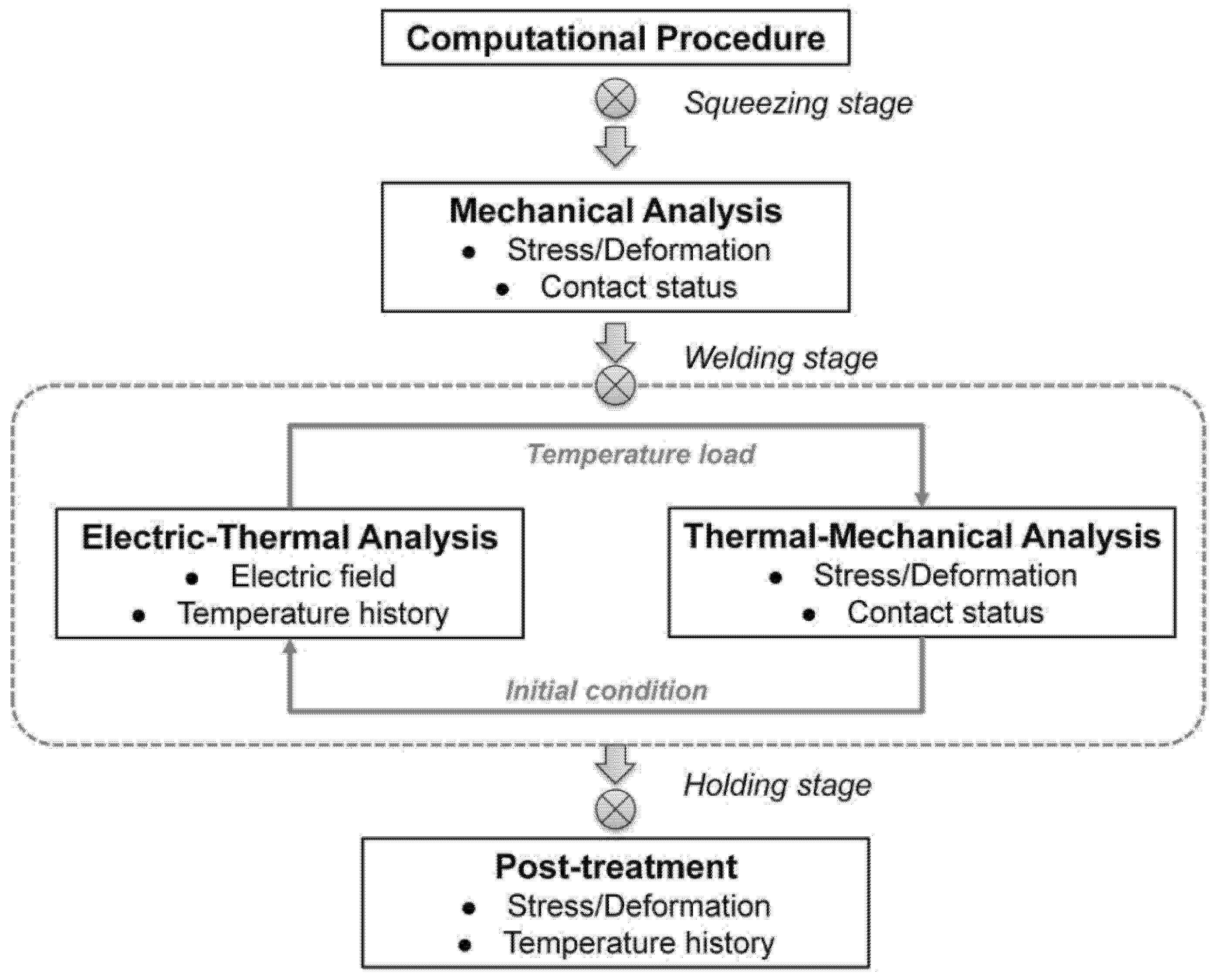
2.1.5. Computational Procedure
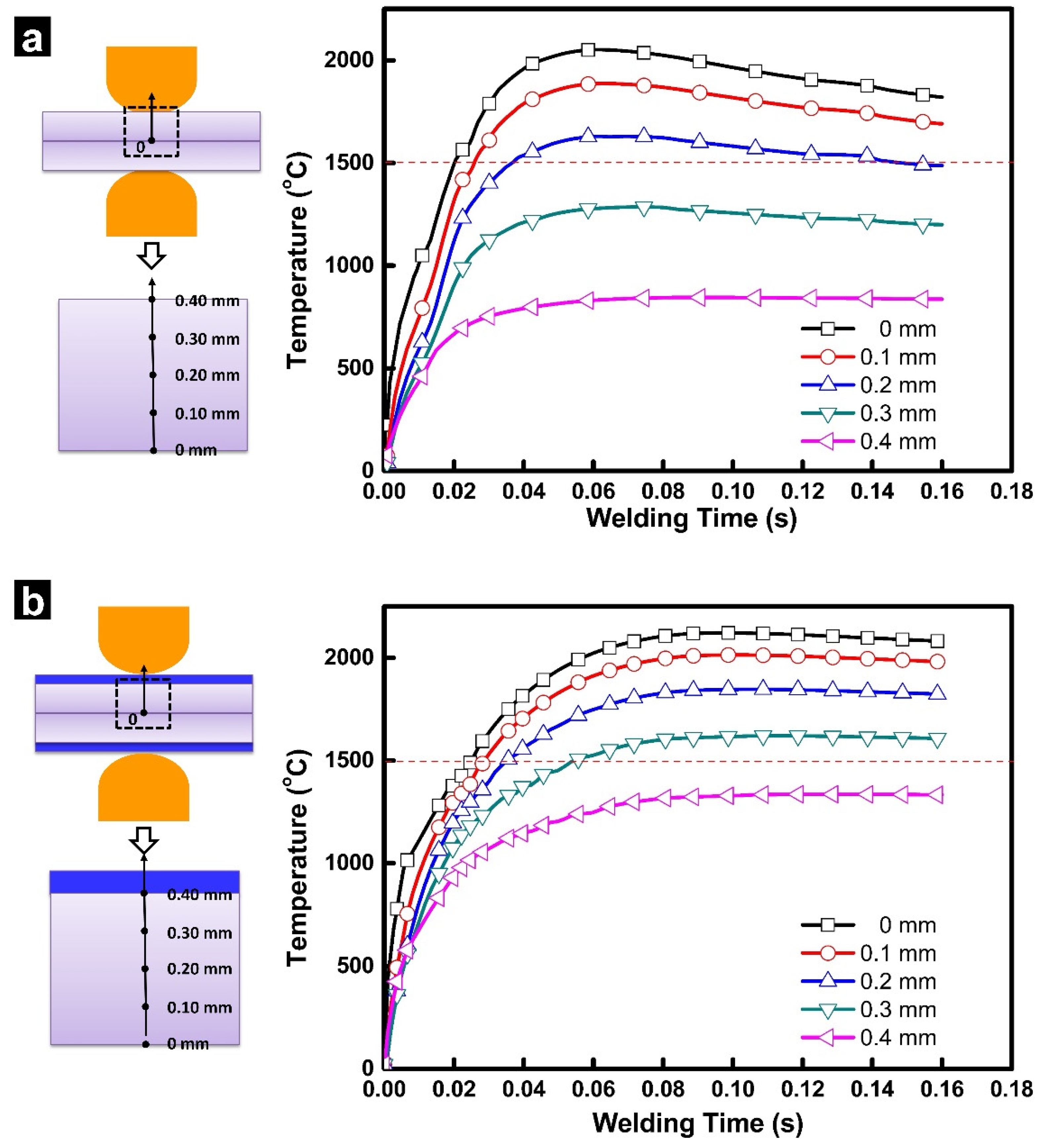
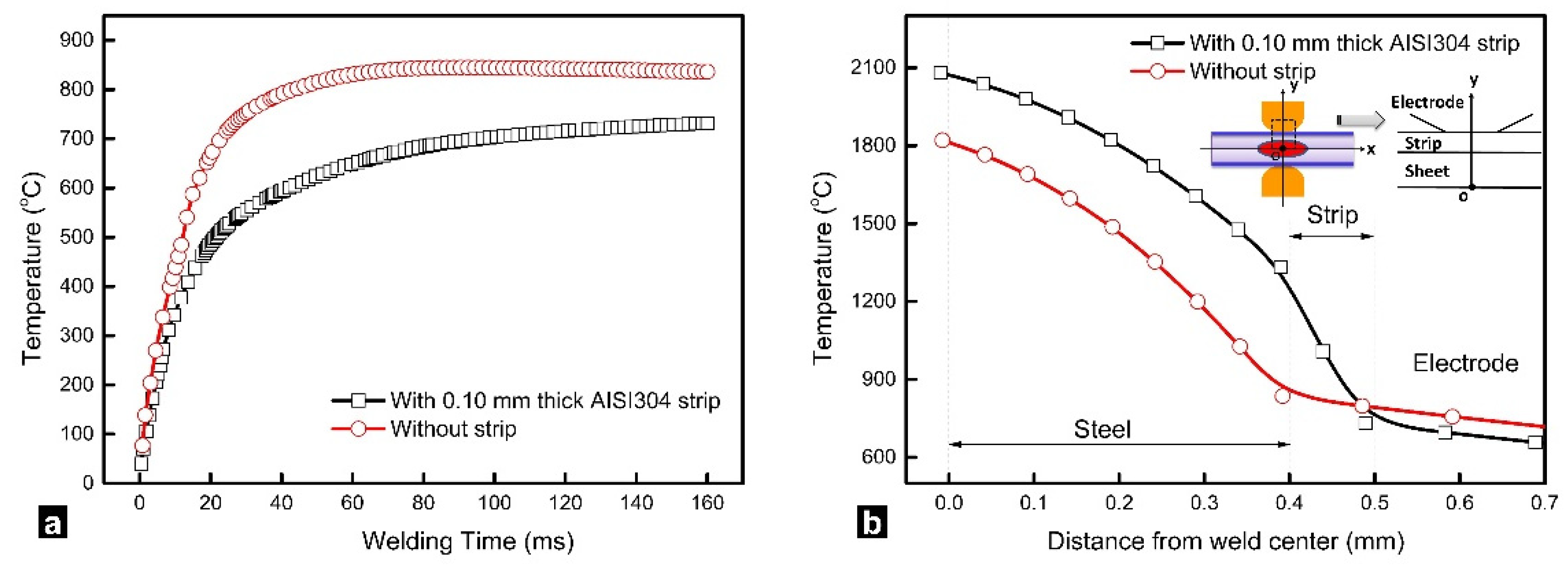
2.2. Temperature History
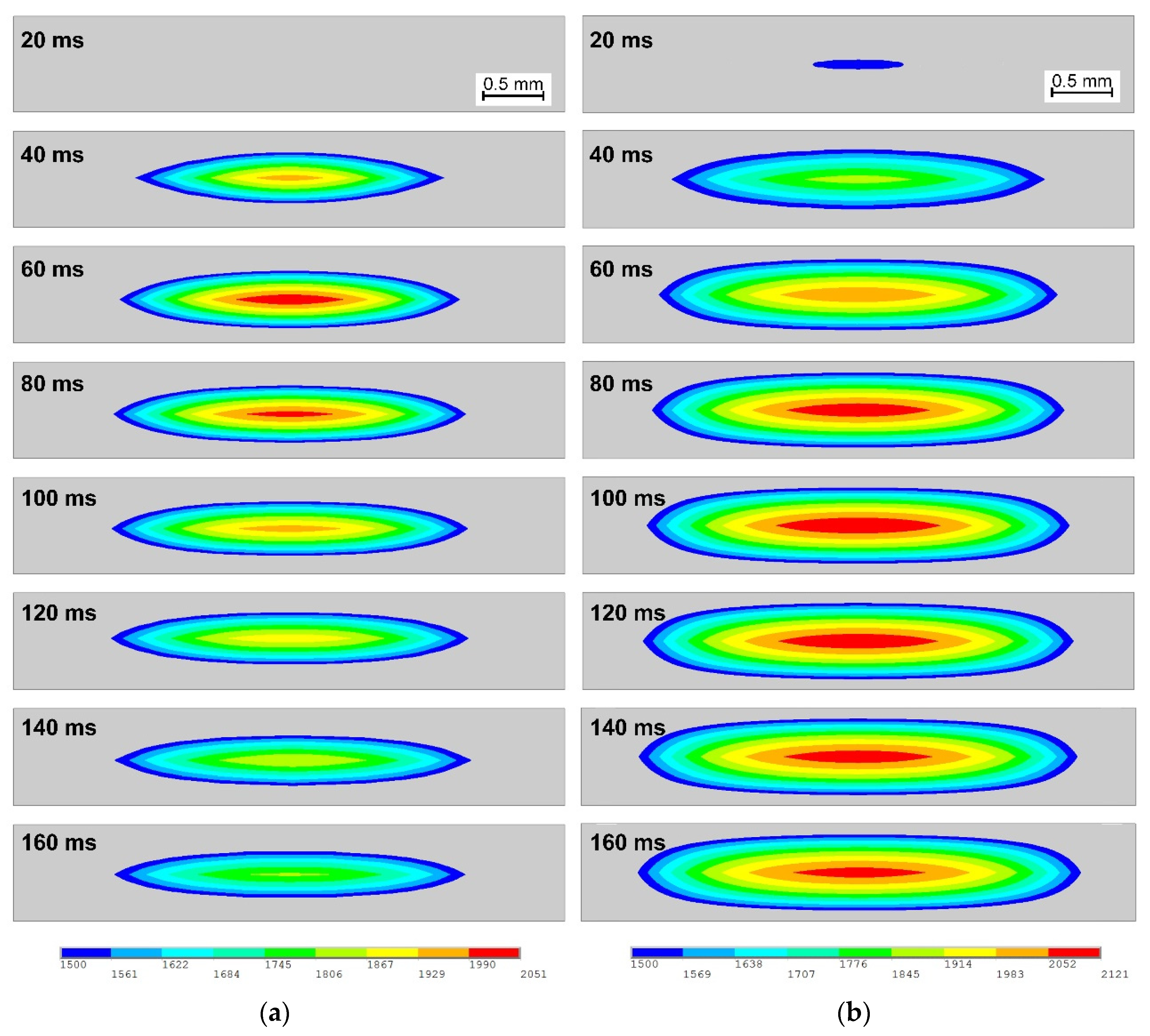
2.3. Weld Formation Process
2.4. Electrode Surface Temperature
2.5. Validation of Simulated Results
3. Results and Discussions
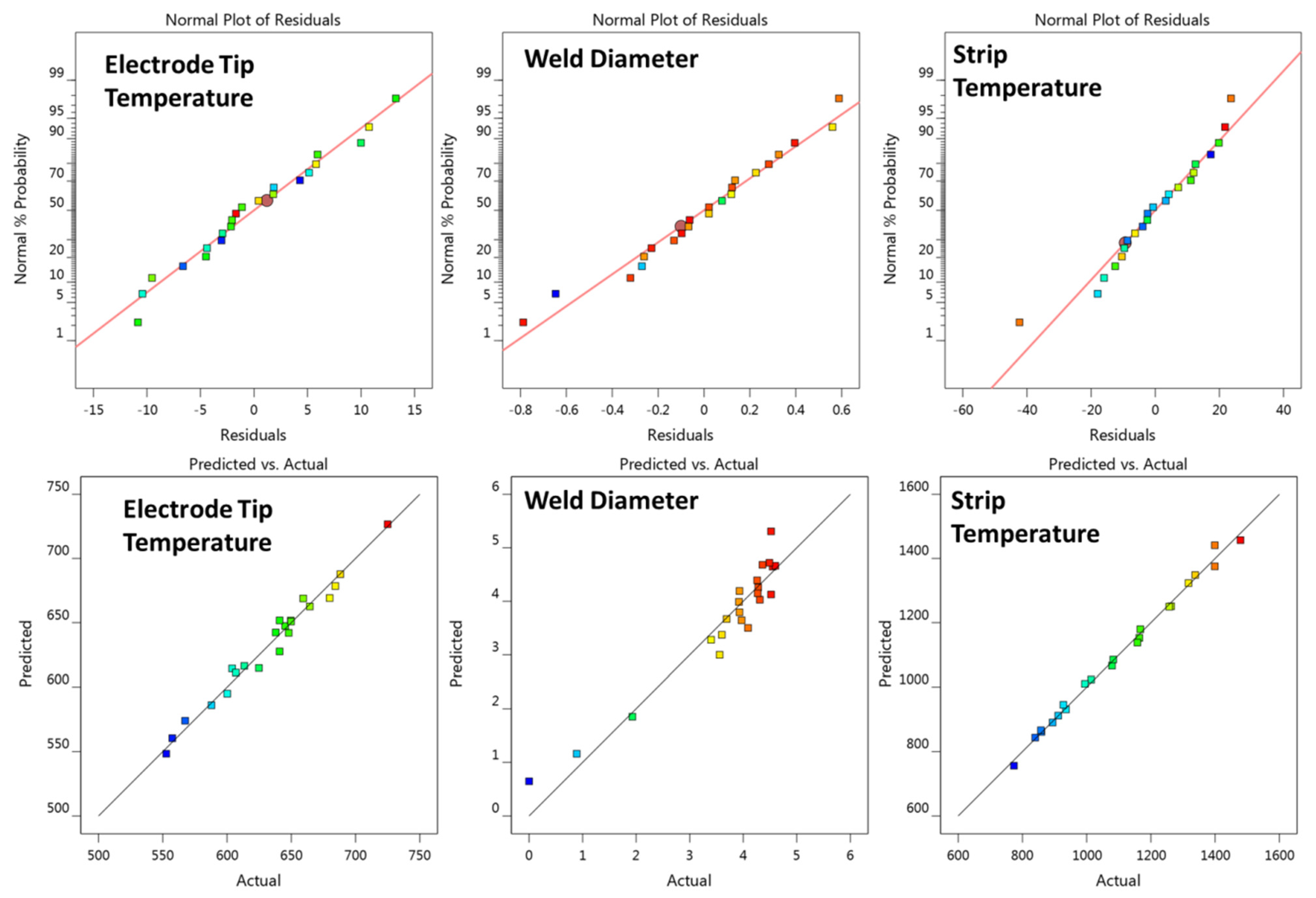
3.1. Development of Regression Model
3.1.1. Second-Order Regression Equation
3.1.2. Design of Experiment
3.1.3. Regression Models
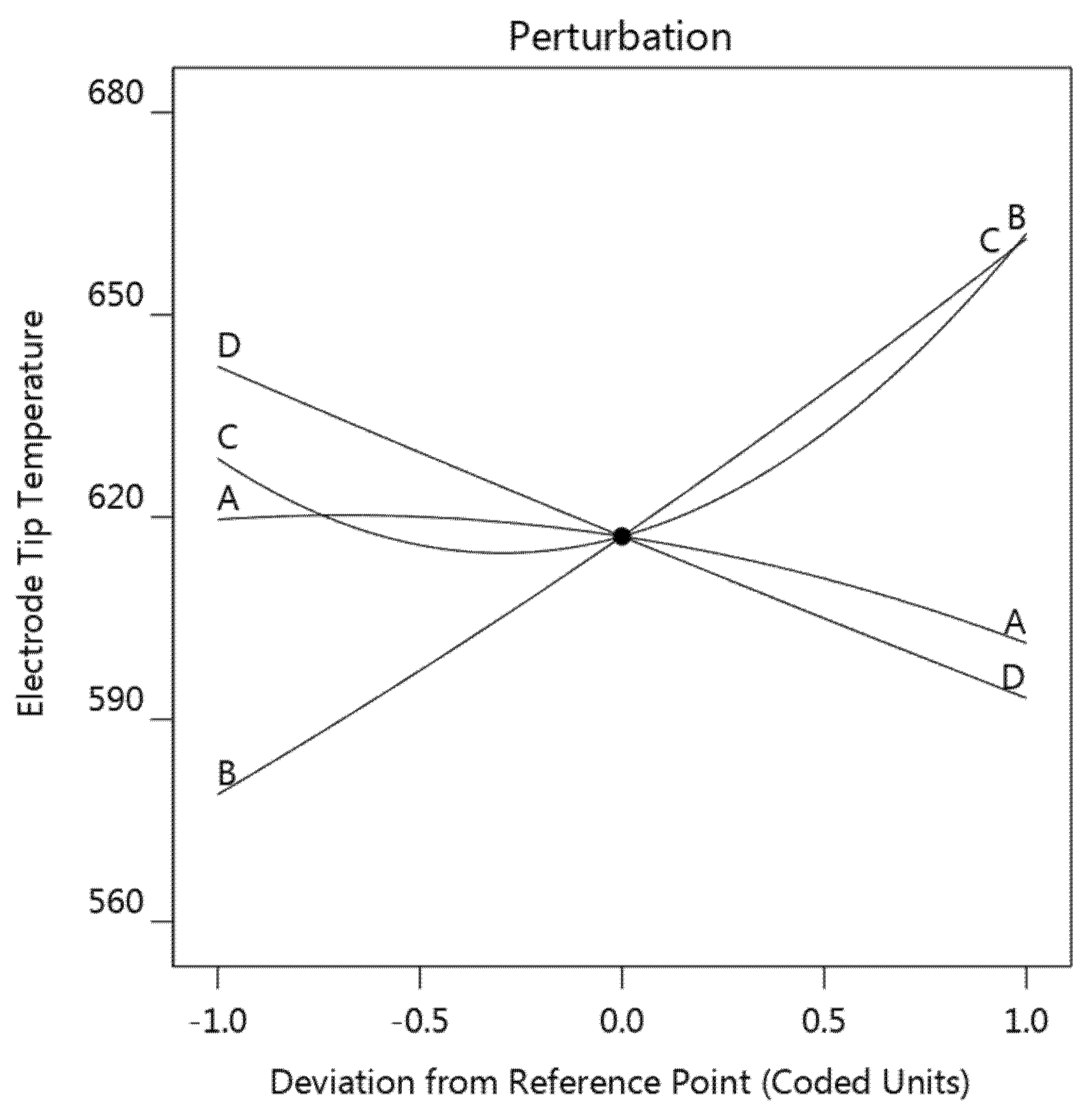
3.2. Effect of Process Parameters on the Responses
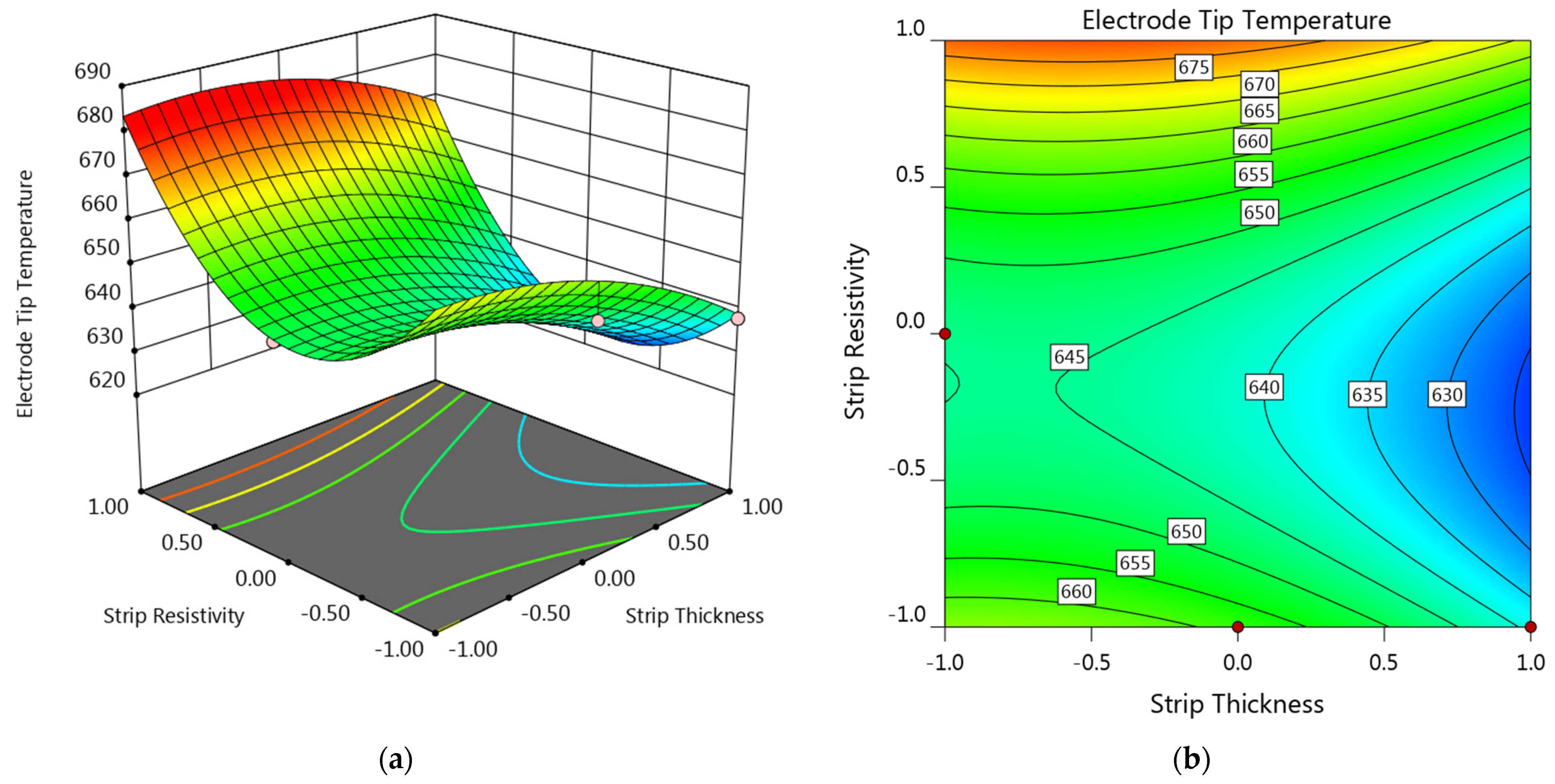
3.2.1. Electrode Tip Temperature
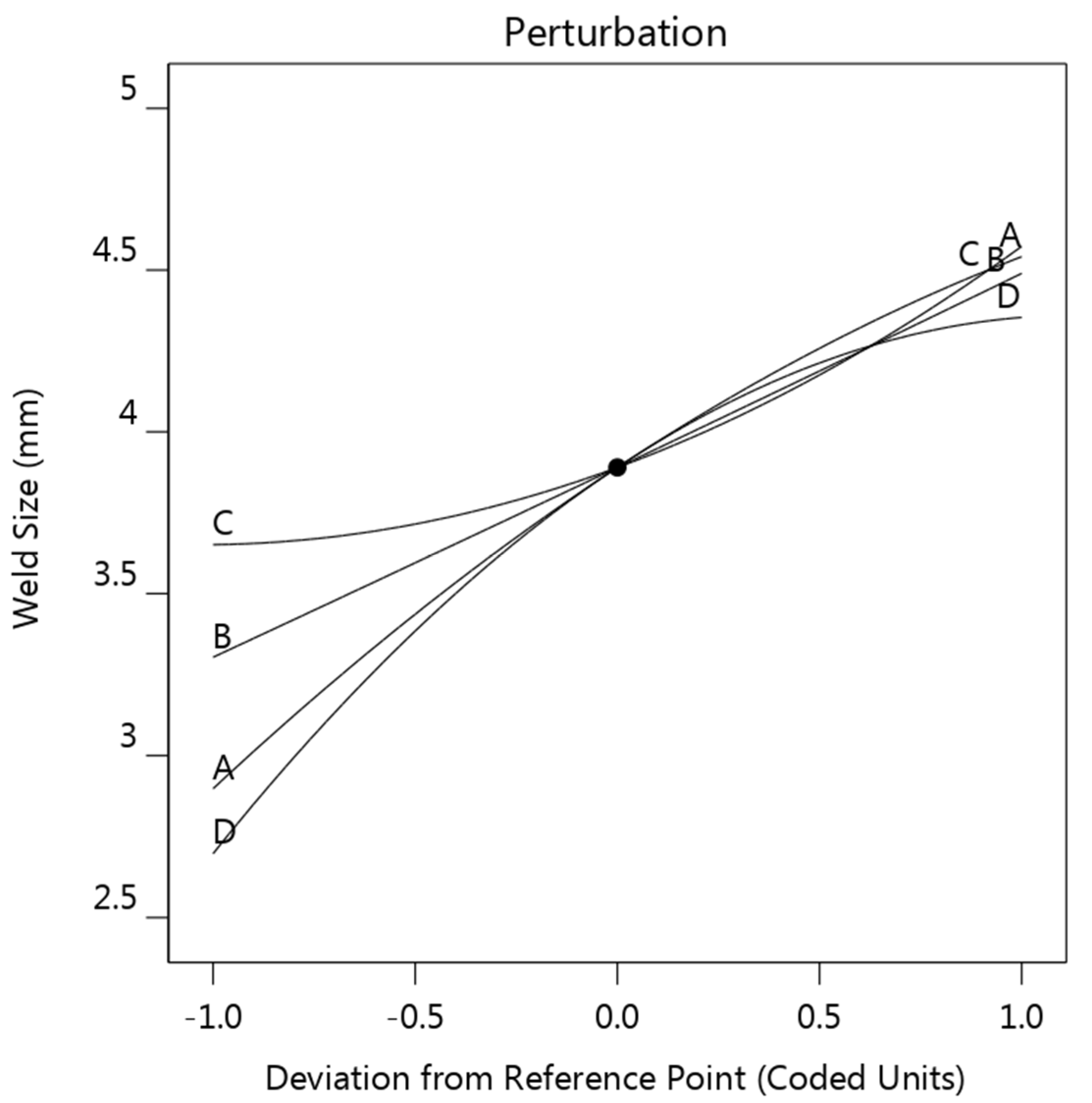
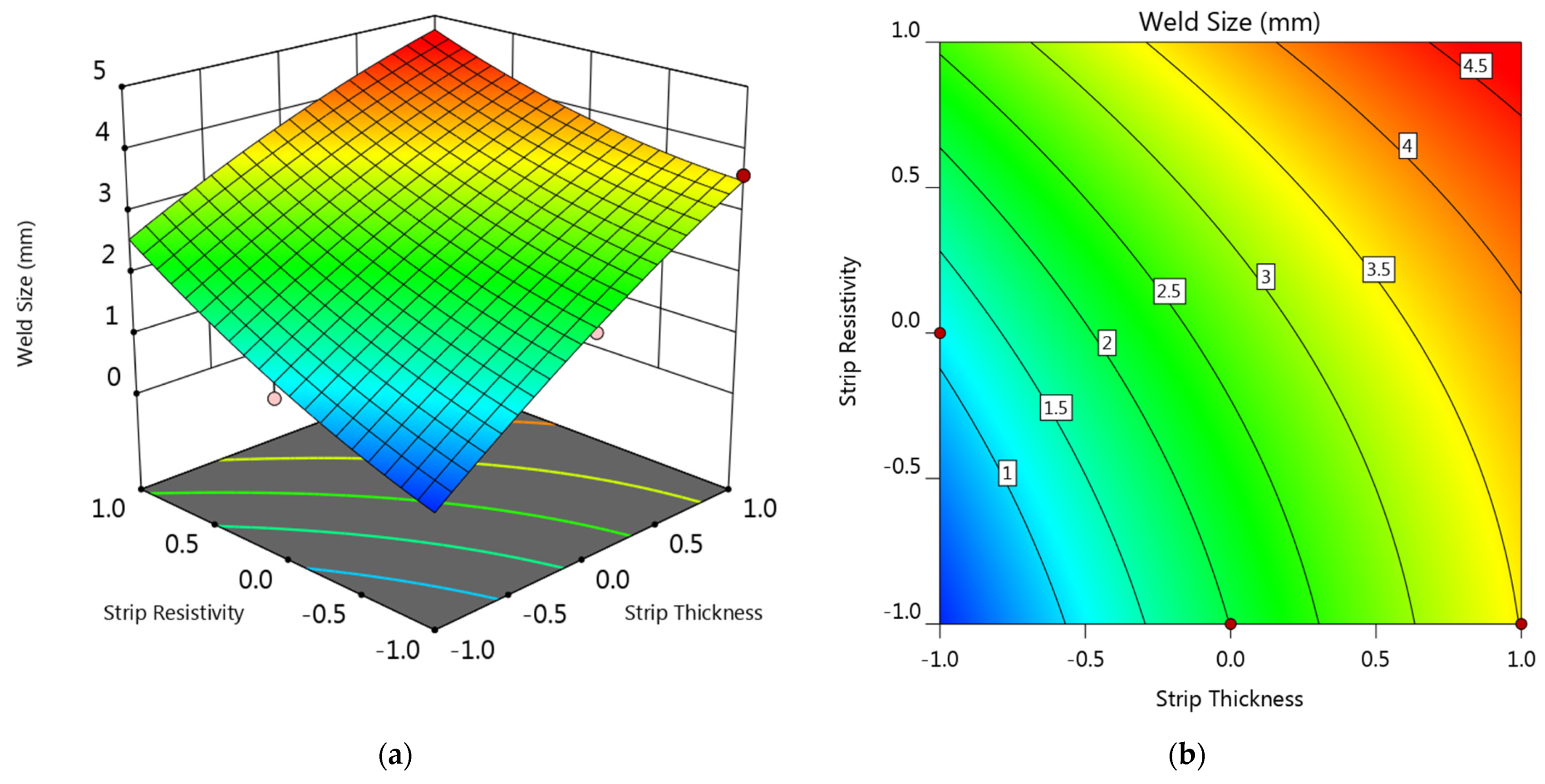
3.2.2. Weld Diameter
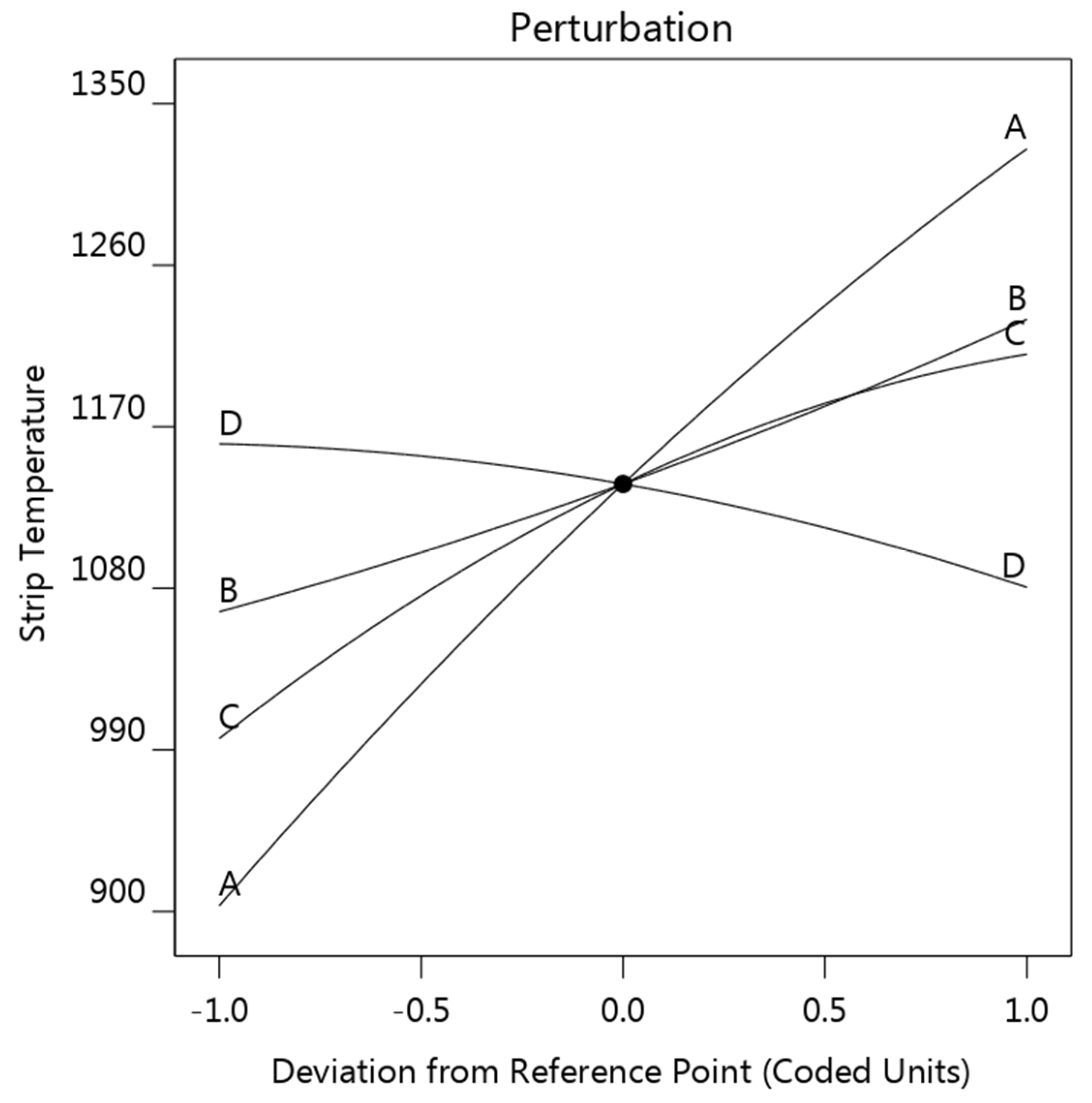
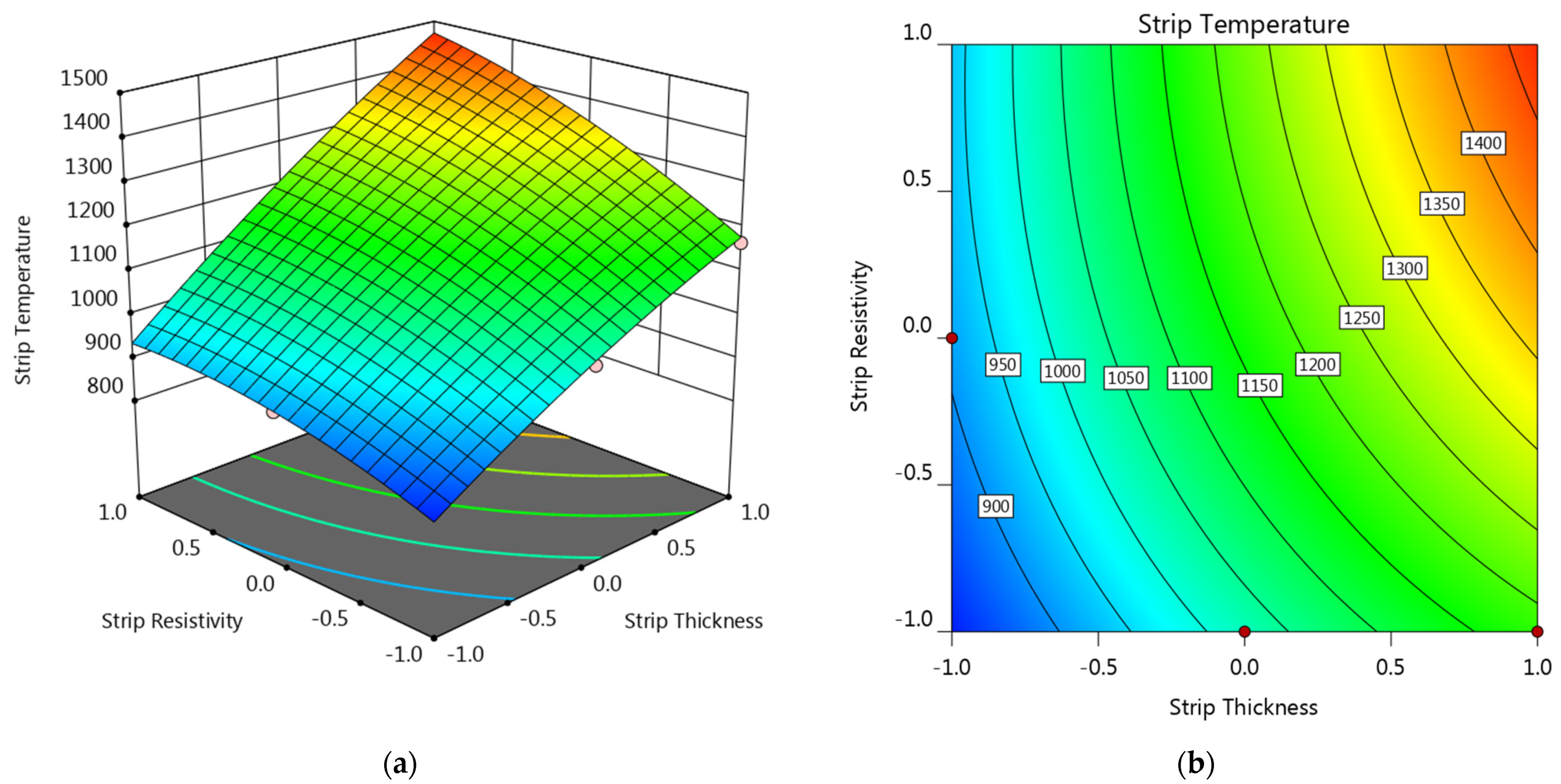
3.2.3. Strip Temperature
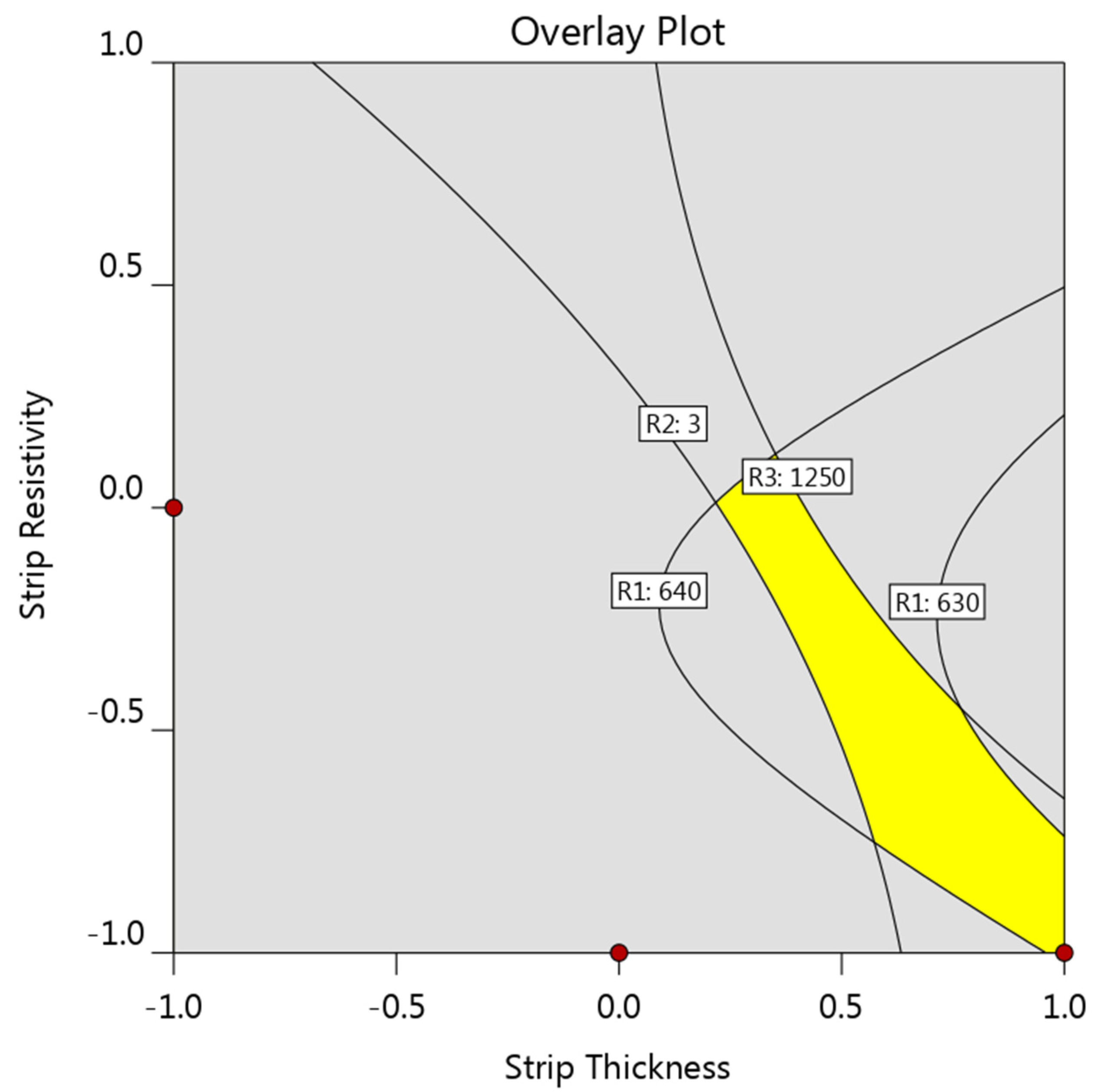
3.3. Determination of the Process Window for a Preferable Strip
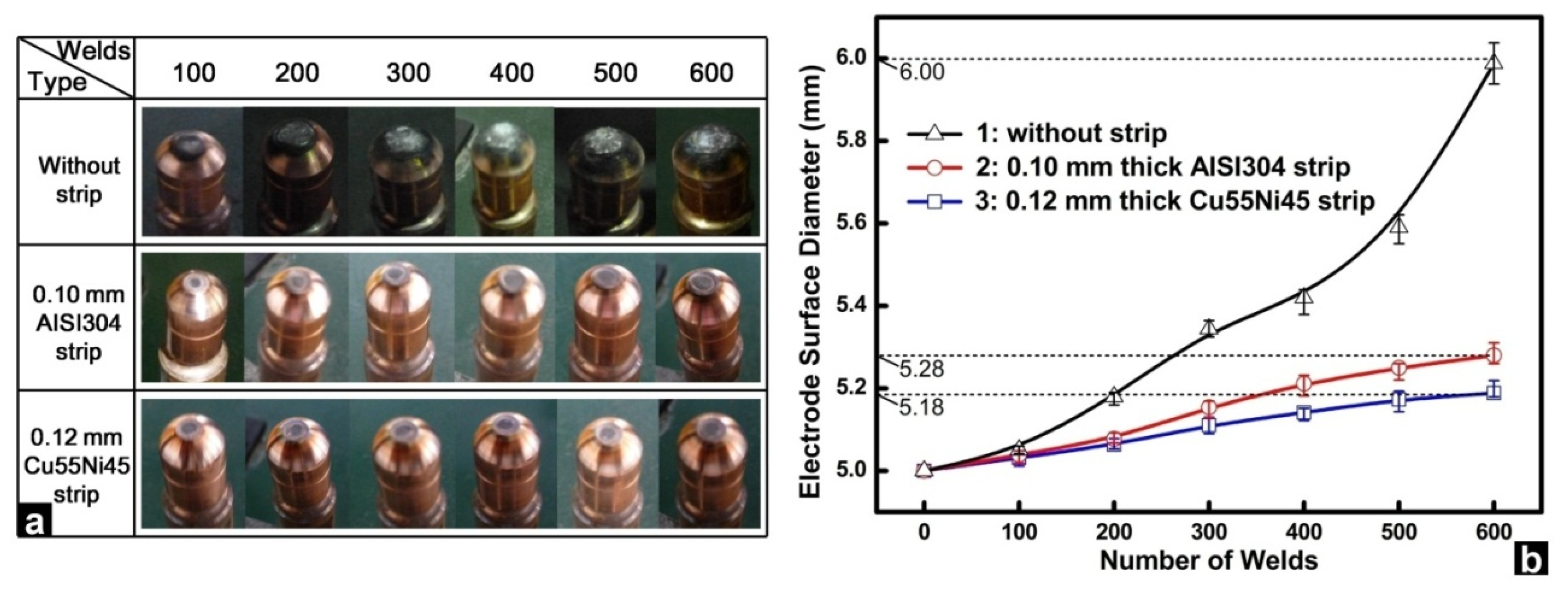
3.4. Experiment Validation
4. Conclusions
- (1)
- The inserted strips would lead to earlier weld initiation of weld and bigger final weld size in both diameter and thickness, and meanwhile lower electrode surface temperature.
- (2)
- Strip thickness showed a negative effect on the electrode tip temperature, while the increase of strip resistivity led to a first-down-then-up electrode tip temperature. Both the strip thickness and the resistivity showed a positive effect on the weld diameter and the maximum strip temperature.
- (3)
- A graphical optimization suggested a Cu55Ni45 strip with thickness of 0.12 mm for a 0.4 mm steel sheet.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Temperature (°C) | Young’s Modulus (GPa) | Electrical Resistivity (Ω·m × 10−7) | Specific Heat (J·kg−1·K−1) | Thermal Expansion Coefficient (K−1 × 10−5) |
|---|---|---|---|---|
| 21 | 124 | 0.264 | 397.75 | 1.66 |
| 93 | 105 | 0.300 | 401.93 | 1.67 |
| 204 | 93 | 0.399 | 418.68 | 1.71 |
| 316 | 83 | 0.505 | 431.24 | 1.75 |
| 427 | 55 | 0.619 | 439.61 | 1.78 |
| 538 | 39 | 0.699 | 452.17 | 1.84 |
| 649 | 25 | 0.800 | 464.73 | 1.85 |
| 732 | - | - | 477.30 | - |
| 760 | 16 | 0.898 | - | 1.89 |
| 774 | - | - | - | - |
| 799 | - | - | - | - |
| 871 | 14 | 0.948 | - | 1.93 |
| 982 | 7 | 0.998 | - | - |
| Temperature (°C) | Yield Strength (MPa) | Electrical Resistivity (Ω·m × 10 −7) | Specific Heat (J·kg−1·K−1) | Thermal Expansion Coefficient (K−1 × 10−5) |
|---|---|---|---|---|
| 21 | 188 | 1.42 | 443.8 | 1.1 |
| 93 | 178 | 1.86 | 452.2 | 1.15 |
| 204 | - | 2.67 | 510.8 | 1.22 |
| 316 | 140 | 3.76 | 564 | 1.3 |
| 427 | 122 | 4.95 | 611.3 | 1.35 |
| 538 | - | 6.48 | 661.5 | 1.4 |
| 649 | 75.8 | 8.18 | 762 | 1.46 |
| 732 | - | - | 1004.8 | - |
| 760 | 13.8 | 10.1 | 2386.5 | 1.4 |
| 774 | - | 11.2 | 1189.1 | 1.35 |
| 799 | - | 11.8 | - | 1.35 |
| 871 | 188 | 1.42 | 443.8 | 1.1 |
| 1093 | 178 | 1.86 | 452.2 | 1.15 |
| Temperature (°C) | Young’s Modulus (GPa) | Electrical Resistivity (Ω·m × 10−7) | Specific Heat (J·kg−1·K−1) | Thermal Expansion Coefficient (K−1 × 10−5) |
|---|---|---|---|---|
| 21 | 200 | 7.2 | 412 | 1.4 |
| 93 | - | 7.7 | 445 | - |
| 204 | - | 8.5 | 502 | - |
| 316 | - | 9.3 | 551 | - |
| 427 | - | 10.1 | 622 | - |
| 538 | 147 | 10.7 | 858 | 1.8 |
| 649 | - | 11.3 | 876 | - |
| 760 | - | 11.9 | 889 | - |
| 871 | 100 | 12.4 | 657 | 1.83 |
| 982 | - | 13.5 | 643 | - |
| 1093 | 50 | 15.0 | 690 | 1.86 |
| 1204 | - | 16.4 | 711 | - |
| 1755 | 15 | - | - | 1.9 |
| Source | Sum of Squares | df | Mean Square | F Value | Prob > F | |
|---|---|---|---|---|---|---|
| Model | 39,900.97 | 7 | 5700.139 | 106.679 | <0.0001 | significant |
| A-A | 1021.73 | 1 | 1021.726 | 19.122 | 0.0006 | |
| B-B | 24,934.92 | 1 | 24,934.923 | 466.660 | <0.0001 | |
| C-C | 3595.16 | 1 | 3595.162 | 67.284 | <0.0001 | |
| D-D | 7773.95 | 1 | 7773.949 | 145.490 | <0.0001 | |
| AB | 719.82 | 1 | 719.820 | 13.472 | 0.0025 | |
| A2 | 194.26 | 1 | 194.260 | 3.636 | 0.0773 | |
| C2 | 3645.55 | 1 | 3645.548 | 68.227 | <0.0001 | |
| Residual | 748.06 | 14 | 53.433 | |||
| Cor Total | 40649.03 | 21 | ||||
| R-Squared = 0.9816 | Adj R-Squared = 0.9724 | |||||
| Pred R-Squared = 0.9551 | Adeq Precision = 40.2028 | |||||
| Source | Sum of Squares | df | Mean Square | F Value | Prob > F | |
|---|---|---|---|---|---|---|
| Model | 28.02 | 7 | 4.003 | 22.612 | <0.0001 | significant |
| A-A | 7.33 | 1 | 7.326 | 41.386 | <0.0001 | |
| B-B | 3.29 | 1 | 3.294 | 18.609 | 0.0007 | |
| C-C | 2.08 | 1 | 2.082 | 11.759 | 0.0041 | |
| D-D | 7.57 | 1 | 7.573 | 42.781 | <0.0001 | |
| AD | 4.00 | 1 | 4.003 | 22.613 | 0.0003 | |
| CD | 1.25 | 1 | 1.250 | 7.060 | 0.0188 | |
| D2 | 2.65 | 1 | 2.653 | 14.987 | 0.0017 | |
| Residual | 2.48 | 14 | 0.177 | |||
| Cor Total | 30.50 | 21 | ||||
| R-Squared = 0.9187 | Adj R-Squared = 0.8781 | |||||
| Pred R-Squared = 0.7943 | Adeq Precision = 18.3722 | |||||
| Source | Sum of Squares | df | Mean Square | F Value | Prob > F | |
|---|---|---|---|---|---|---|
| Model | 926,739.32 | 7 | 132,391.332 | 253.237 | <0.0001 | significant |
| A-A | 633,080.32 | 1 | 633,080.315 | 1210.953 | <0.0001 | |
| B-B | 91,660.70 | 1 | 91,660.700 | 175.328 | <0.0001 | |
| C-C | 153,993.21 | 1 | 153,993.206 | 294.557 | <0.0001 | |
| D-D | 18,474.23 | 1 | 18,474.231 | 35.337 | <0.0001 | |
| AC | 8660.82 | 1 | 8660.821 | 16.566 | 0.0011 | |
| A2 | 2394.08 | 1 | 2394.079 | 4.579 | 0.0505 | |
| C2 | 4758.75 | 1 | 4758.748 | 9.103 | 0.0092 | |
| Residual | 7319.13 | 14 | 522.795 | |||
| Cor Total | 934,058.45 | 21 | ||||
| R-Squared = 0.9922 | Adj R-Squared = 0.9882 | |||||
| Pred R-Squared = 0.9809 | Adeq Precision = 49.7324 | |||||
References
- Singh, H.; Coates, G. Advanced High-Strength Steel Lightweighting: Minimum Thickness Study and AHSS Application Guidelines. Technical Presentation. Great Designs in Steel Symposium 2014, Michigan, USA, May 2014, American Iron and Steel Institute. Available online: www.autosteel.org (accessed on 1 December 2021).
- Williams, N.T.; Parker, J.D. Review of resistance spot welding of steel sheets Part 2 Factors influencing electrode life. Int. Mater. Rev. 2004, 49, 77–108. [Google Scholar] [CrossRef]
- Zhao, Y.Y.; Zhang, Y.S.; Lai, X.M.; Wang, P.-C. Resistance Spot Welding of Ultra-Thin Automotive Steel. J. Manuf. Sci. Eng. 2013, 135, 021012. [Google Scholar] [CrossRef]
- Zhao, Y.Y.; Zhang, Y.S.; Lai, X.M.; Wang, P.-C. Effect of Inserted Strips on Electrode Degradation in Resistance Spot Welding. Weld. J. 2014, 93, 411s–420s. [Google Scholar]
- Trommer, G. Resistance Spot Welding Using Continuous Tape. Weld. J. 2009, 88, 20s–22s. [Google Scholar]
- Satonaka, S.; Iwanmoto, C.; Qiu, R.F.; Fujioka, T. Trends and new applications of spot welding for aluminium alloy sheets. Weld. Int. 2006, 20, 858–864. [Google Scholar] [CrossRef]
- Patel, C.R.; Patel, D.A. Effect of process parameters on the strength of aluminium alloy a5052 sheets joint welded by resistance spot welding with cover plates. Int. J. Eng. Res. Appl. 2012, 2, 1081–1087. [Google Scholar]
- Qiu, R.F.; Satonaka, S.; Iwamoto, C. Mechanical properties and microstructures of magnesium alloy AZ31B joint fabricated by resistance spot welding with cover plates. Sci. Technol. Weld. Join. 2009, 14, 691–697. [Google Scholar] [CrossRef]
- Shi, H.; Qiu, R.; Zhu, J.; Zhang, K.; Yu, H.; Ding, G. Effects of welding parameters on the characteristics of magnesium alloy joint welded by resistance spot welding with cover plates. Mater. Des. 2010, 31, 4853–4857. [Google Scholar] [CrossRef]
- Zhang, Y.; Luo, Z.; Li, Y.; Liu, Z.; Huang, Z. Microstructure characterization and tensile properties of Mg/Al dissimilar joints manufactured by thermo-compensated resistance spot welding with Zn interlayer. Mater. Des. 2015, 75, 166–173. [Google Scholar] [CrossRef]
- Satonaka, S.; Iwamoto, C.; Murakami, G.I.; Matsumoto, Y. Resistance spot welding of magnesium alloy sheets with cover plates. Weld. World 2012, 56, 44–50. [Google Scholar] [CrossRef]
- Abdo, A.; Harraz, M.; Reisgen, U.; Schleser, M.; Schiebahn, A. Resistance spot welding of aluminum alloy 5182 to zinc coated dp600 steel using process tape technique. Int. J. Adv. Sci. Res. Dev. 2013, 1, 2212–2216. [Google Scholar]
- Qiu, R.F.; Iwamoto, C.; Satonaka, S. Interfacial microstructure and strength of steel/aluminum alloy joints welded by resistance spot welding with cover plate. J. Mater. Process. Technol. 2009, 209, 4186–4193. [Google Scholar] [CrossRef]
- Qiu, R.F.; Satonaka, S.; Iwamoto, C. Effect of interfacial reaction layer continuity on the tensile strength of resistance spot welded joints between aluminum alloy and steels. Mater. Des. 2009, 30, 3686–3689. [Google Scholar] [CrossRef]
- Min, D.; Yong, Z.; Jie, L. Dissimilar spot welding joints of AZ31-443 ferritic stainless steel with cover plate. Int. J. Adv. Manuf. Tech. 2016, 85, 1539–1545. [Google Scholar] [CrossRef]
- Khan, M.F.; Dwivedi, D.K.; Sharma, S. Development of response surface model for tensile shear strength of weld-bonds of aluminium alloy 6061 T651. Mater. Des. 2012, 34, 673–678. [Google Scholar] [CrossRef]
- Balta, B.; Arici, A.A.; Yilmaz, A. Optimization of process parameters for friction weld steel tube to forging joints. Mater. Des. 2016, 103, 209–222. [Google Scholar] [CrossRef]
- Zhao, Y.Y.; Zhang, Y.S.; Hu, W.; Lai, X.M. Optimization of laser welding thin-gage galvanized steel via response surface methodology. Opt. Lasers Eng. 2012, 50, 1267–1273. [Google Scholar] [CrossRef]
- Sohail, Y.; Parag, B.; Nemeshwaree, B.; Giorgio, R. Optimizing organophosphorus fire resistant finish for cotton fabric using box-behnken design. Int. J. Environ. Res. 2016, 10, 313–320. [Google Scholar]
- Sohail, Y.; Massimo, C.; Nemeshwaree, B.; Perwuelz, A.; Giraud, S.; Rovero, G.; Guan, J.P.; Chen, G.Q. Process optimization of eco-friendly flame retardant finish for cotton fabric: A response surface methodology approach. Surf. Rev. Lett. 2017, 24, 17750114. [Google Scholar]
- Shen, J.; Zhang, Y.S.; Lai, X.M.; Wang, P.C. Modeling of Resistance Spot Welding of Multiple Stacks of Steel Sheets. Mater. Des. 2010, 32, 550–560. [Google Scholar] [CrossRef]
- Wan, X.D.; Wang, Y.X.; Zhang, P. Modeling the effect of welding current on resistance spot welding of DP600 steel. J. Mater. Process. Technol. 2014, 214, 2723–2729. [Google Scholar] [CrossRef]
- Li, M.V.; Dong, P.; Kimchi, M. A Contact Resistance Model for Resistance Spot Welding Process: Theory and Implementation.High Productivity Joining Processes. Proceedings of ICAWT’97 International Conference on Advances in Welding Technology, Columbus, Ohio, 17–19 September 1997; pp. 357–369. [Google Scholar]
- Kohlrausch, F. Ueber das Problem eines elektrisch erwarmten leiters. Ann. Der Phys. 1900, 306, 312–325. [Google Scholar] [CrossRef]
- Chang, B.H.; Li, M.V.; Zhou, Y. Comparative study of small scale and ‘large scale’ resistance spot welding. Sci. Technol. Weld. Join. 2001, 6, 273–280. [Google Scholar] [CrossRef]
- Chang, B.H.; Zhou, Y. Numerical study on the effect of electrode force in small-scale resistance spot welding. J. Mater. Process. Technol. 2003, 139, 635–641. [Google Scholar] [CrossRef]
- Zhao, Y.Y.; Zhang, Y.S.; Wang, P.C. Weld Formation Characteristics in Resistance Spot Welding of Ultra-Thin Steel. Weld. J. 2017, 96, 71s–82s. [Google Scholar]
- Eisazadeh, H.; Hamedi, M.; Halvaee, A. New parametric study of nugget size in resistance spot welding process using finite element method. Mater. Des. 2010, 31, 149–157. [Google Scholar] [CrossRef]
- Li, W. Modeling and on-line estimation of electrode wear in resistance spot welding. ASME J. Manuf. Sci. Eng. 2005, 127, 709–717. [Google Scholar] [CrossRef]


| Welding Parameters | Value |
|---|---|
| Electrode diameter (mm) | 5 |
| Electrode force (kN) | 1.8 |
| Welding current (kA) | 5.7 |
| Squeeze time (ms) | 200 |
| Weld time (ms) | 160 |
| Hold time (ms) | 100 |
| Notation | Factor | Level | ||
|---|---|---|---|---|
| −1 | 0 | 1 | ||
| A | Strip thickness (mm) | 0.05 | 0.1 | 0.15 |
| B | Weld current (kA) | 5.0 | 5.5 | 6.0 |
| C | Strip resistivity (μΩ·m) | 0.3 | 0.55 | 0.8 |
| D | Sheet thickness (mm) | 0.4 | 0.6 | 0.8 |
| No. | Factors | Tip Temperature (°C) | Weld Diameter (mm) | Strip Temperature (°C) | |||
|---|---|---|---|---|---|---|---|
| A | B | C | D | ||||
| 1 | 0 | 1 | 1 | 1 | 684.3 | 4.55 | 1263 |
| 2 | −1 | 0 | 0 | −1 | 645.3 | 0.89 | 911.5 |
| 3 | −1 | 0 | 1 | 0 | 659.3 | 3.93 | 935.5 |
| 4 | 1 | 0 | 1 | 0 | 640.9 | 4.52 | 1399 |
| 5 | 1 | 1 | 0 | 1 | 604 | 4.6 | 1338 |
| 6 | 1 | −1 | −1 | 0 | 587.9 | 3.92 | 1079 |
| 7 | −1 | 0 | −1 | 1 | 606.9 | 3.93 | 773.5 |
| 8 | 1 | 0 | −1 | −1 | 637.9 | 3.6 | 1167 |
| 9 | −1 | −1 | 0 | −1 | 600.2 | 0 | 839.8 |
| 10 | 0 | 1 | 1 | −1 | 725 | 4.31 | 1317 |
| 11 | −1 | −1 | 1 | 0 | 613.5 | 3.4 | 859 |
| 12 | 1 | 1 | 0 | −1 | 664.4 | 4.49 | 1479 |
| 13 | 0 | −1 | 1 | −1 | 648 | 3.56 | 1164 |
| 14 | −1 | 1 | 0 | 1 | 649.6 | 4.36 | 927.6 |
| 15 | 0 | 1 | −1 | 0 | 679.9 | 4.28 | 1083 |
| 16 | 1 | −1 | 0 | 0 | 567.4 | 4.26 | 1257 |
| 17 | 0 | 0 | −1 | −1 | 649.8 | 1.93 | 1014 |
| 18 | 0 | −1 | −1 | 1 | 557.4 | 3.69 | 857.7 |
| 19 | 0 | −1 | 0 | 1 | 552.7 | 3.97 | 994.6 |
| 20 | −1 | 1 | −1 | 0 | 688.2 | 4.09 | 894 |
| 21 | 1 | 0 | 1 | 1 | 640.9 | 4.52 | 1399 |
| 22 | 0 | 0 | 0 | 0 | 624.8 | 4.27 | 1158 |
| Response | R-Squared | Adj R-Squared | F-Value | p-Value | Response Equation |
|---|---|---|---|---|---|
| Electrode Tip Temperature (°C) | 0.9816 | 0.9724 | 106.679 | <0.0001 | |
| Weld Diameter (mm) | 0.9187 | 0.8781 | 22.612 | <0.0001 | |
| Strip Temperature (°C) | 0.9922 | 0.9882 | 253.237 | <0.0001 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Wang, W.; Wei, X. Optimization of Resistance Spot Welding with Inserted Strips via FEM and Response Surface Methodology. Materials 2021, 14, 7489. https://doi.org/10.3390/ma14237489
Zhao Y, Wang W, Wei X. Optimization of Resistance Spot Welding with Inserted Strips via FEM and Response Surface Methodology. Materials. 2021; 14(23):7489. https://doi.org/10.3390/ma14237489
Chicago/Turabian StyleZhao, Yangyang, Wurong Wang, and Xicheng Wei. 2021. "Optimization of Resistance Spot Welding with Inserted Strips via FEM and Response Surface Methodology" Materials 14, no. 23: 7489. https://doi.org/10.3390/ma14237489
APA StyleZhao, Y., Wang, W., & Wei, X. (2021). Optimization of Resistance Spot Welding with Inserted Strips via FEM and Response Surface Methodology. Materials, 14(23), 7489. https://doi.org/10.3390/ma14237489





