Principles of Stress-Strength Modelling of the Highly Thermally Loaded Materials—The Influence of an Effect of Strength Differential on the Material Effort
Abstract
:1. Introduction
2. The Material Effort Description by the Energy Approach
- Beltrami (1885):
- Huber (1904):
- Mises (1914) and Hencky (1924):
- Schleicher (1926):
- Burzyński (1928):
- Zawadzki (1956):
- Pęcherski (2011):
2.1. The Huber Material Effort
2.2. An Extended Burzyński Material Effort
3. Huber–Mises–Hencky and Burzyński Equivalent Stress
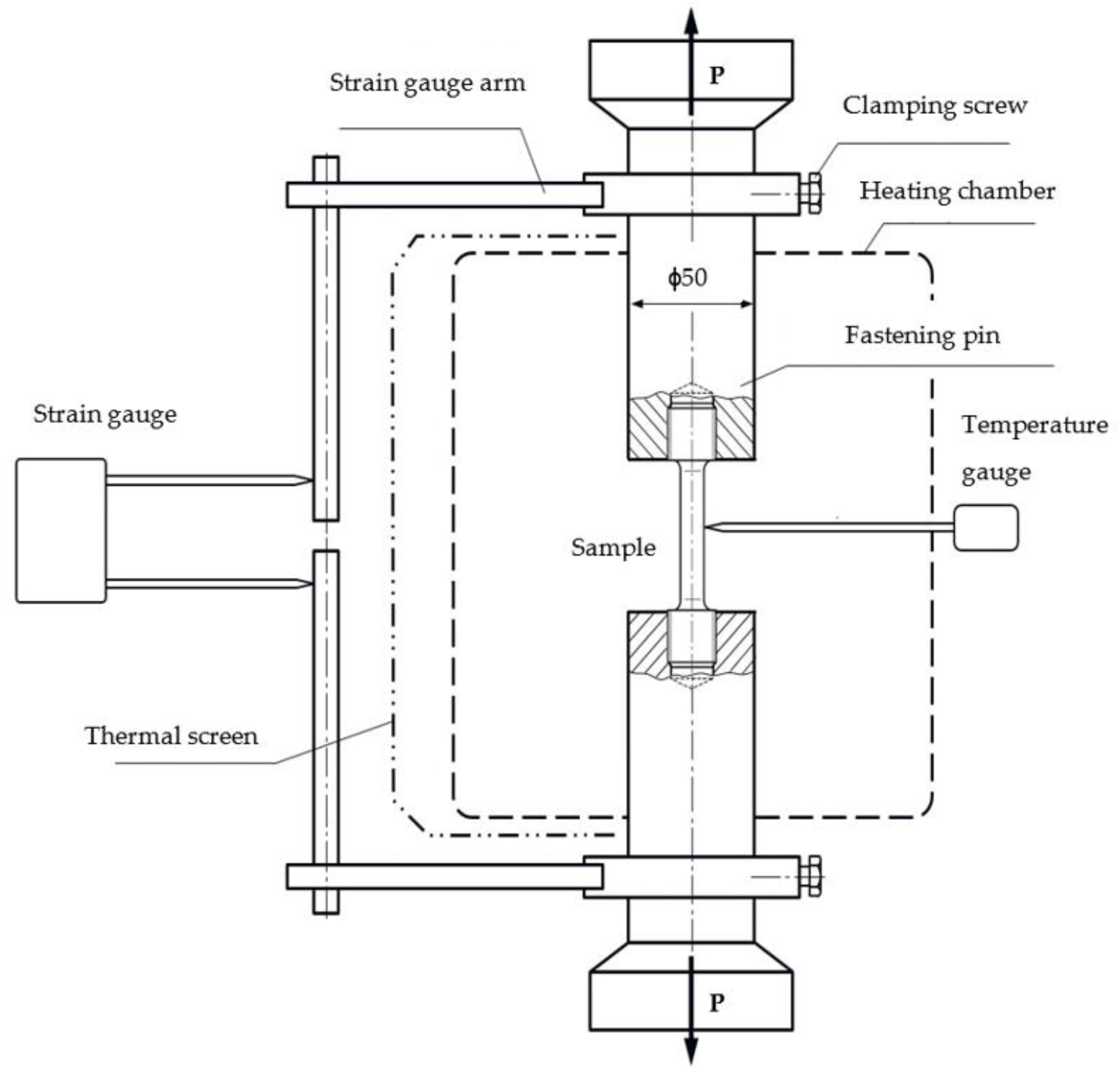
4. Experimental Procedure
- (a)
- Screw-in the sample inside the fastening pins.
- (b)
- Put the fastening pins inside the mount of the testing machine.
- (c)
- Assure that the tensile force gauge shows zero.
- (d)
- Close the heating chamber.
- (e)
- Insert the temperature gauge into the heating chamber.
- (f)
- Attach the thermal screen.
- (g)
- Set the desired temperature (with variation equal to ±5 °C).
- (h)
- Preload the sample with a force no higher than 200 N, check the position of the strain gauge arm, and attach the strain gauge.
- (i)
- After 10 min of heating at a constant temperature, the load starts to grow at a maximum rate of 200 N/mm2 min.
- (j)
- Once well inside the plastic stage, deformation rate is steadily increased up to 0.1 min−1 until rupture.
- (k)
- The last step involves switching off heating, and performing data post-processing to evaluate yield strength .
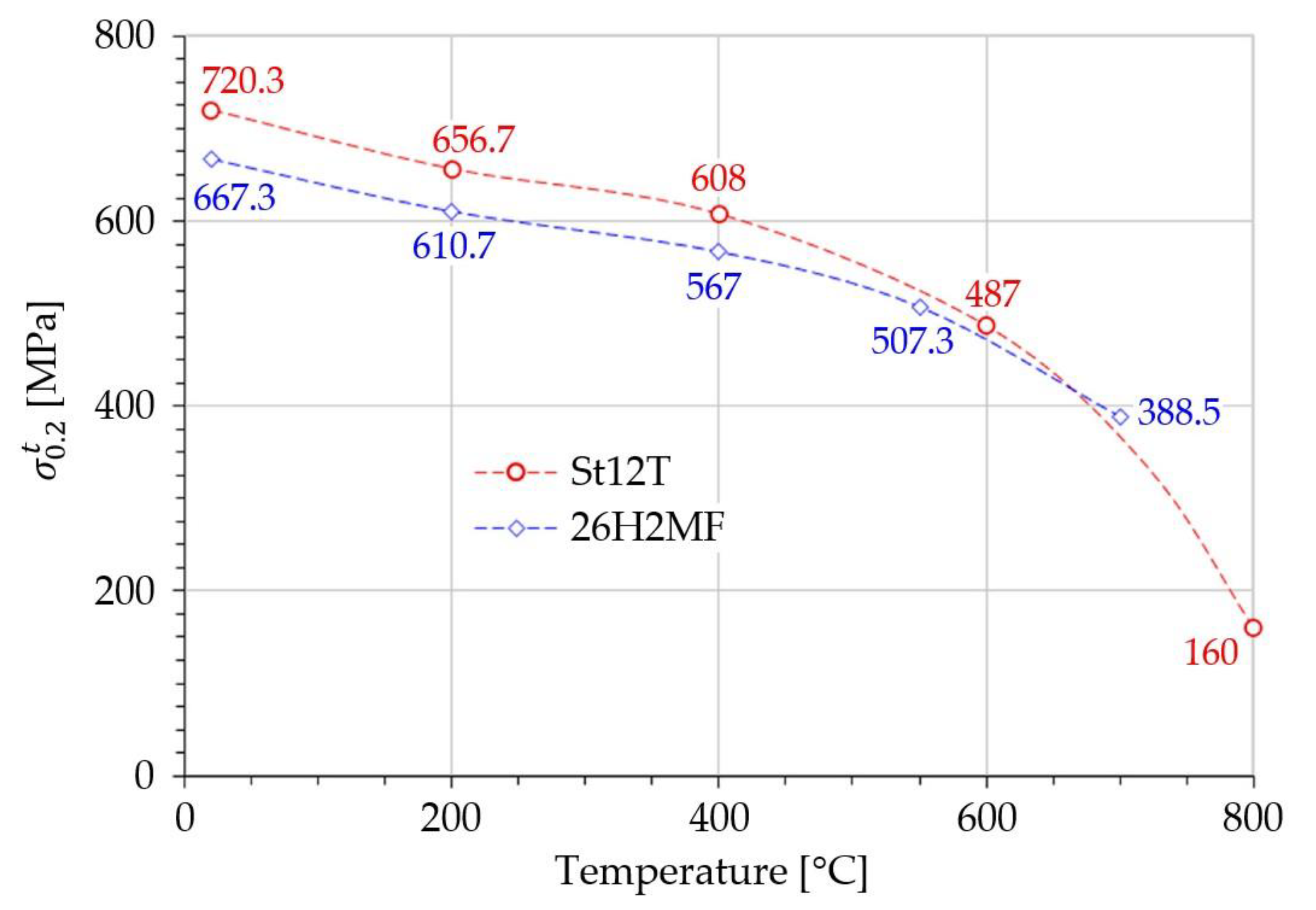
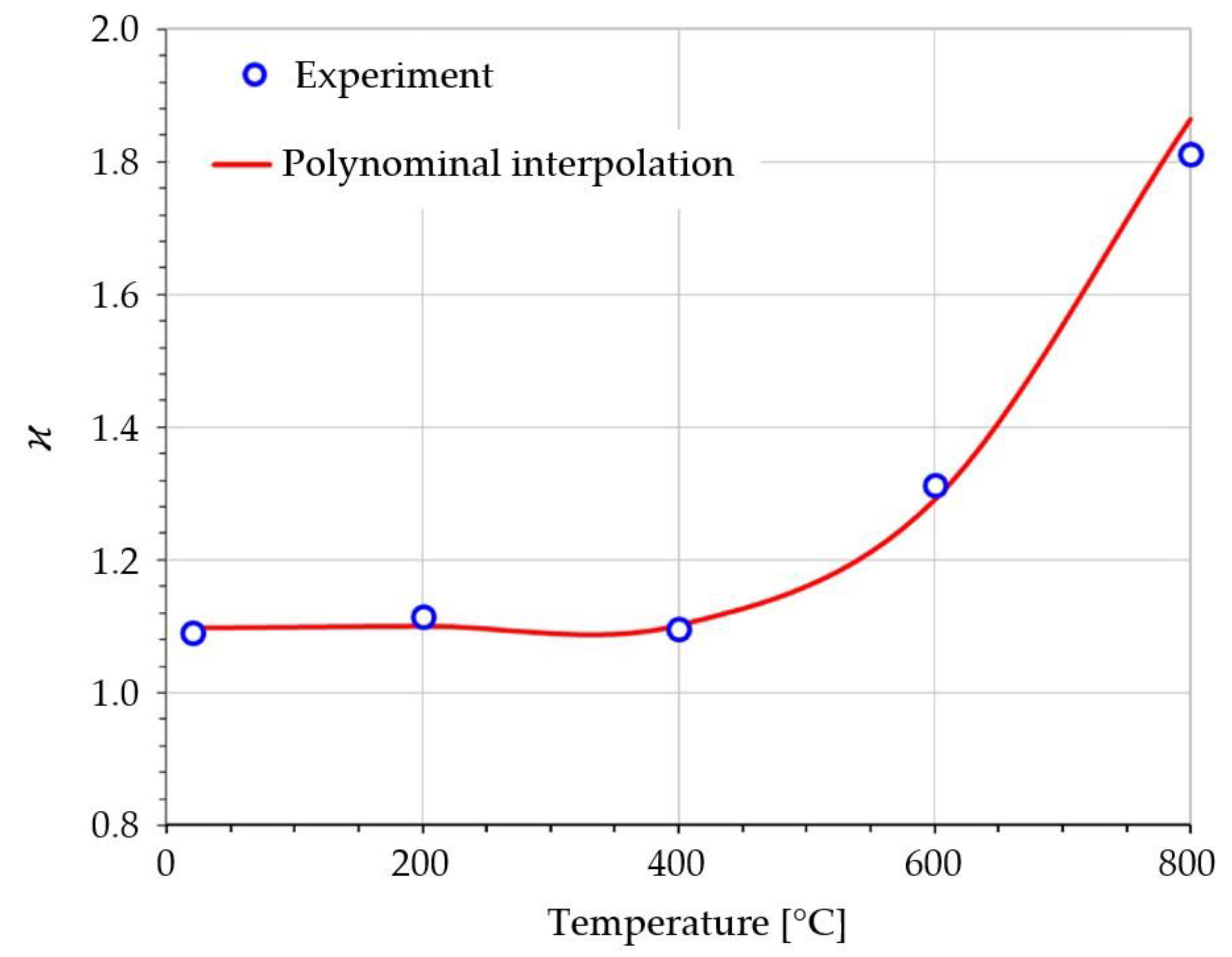
5. Limit Properties of the St12T Steel
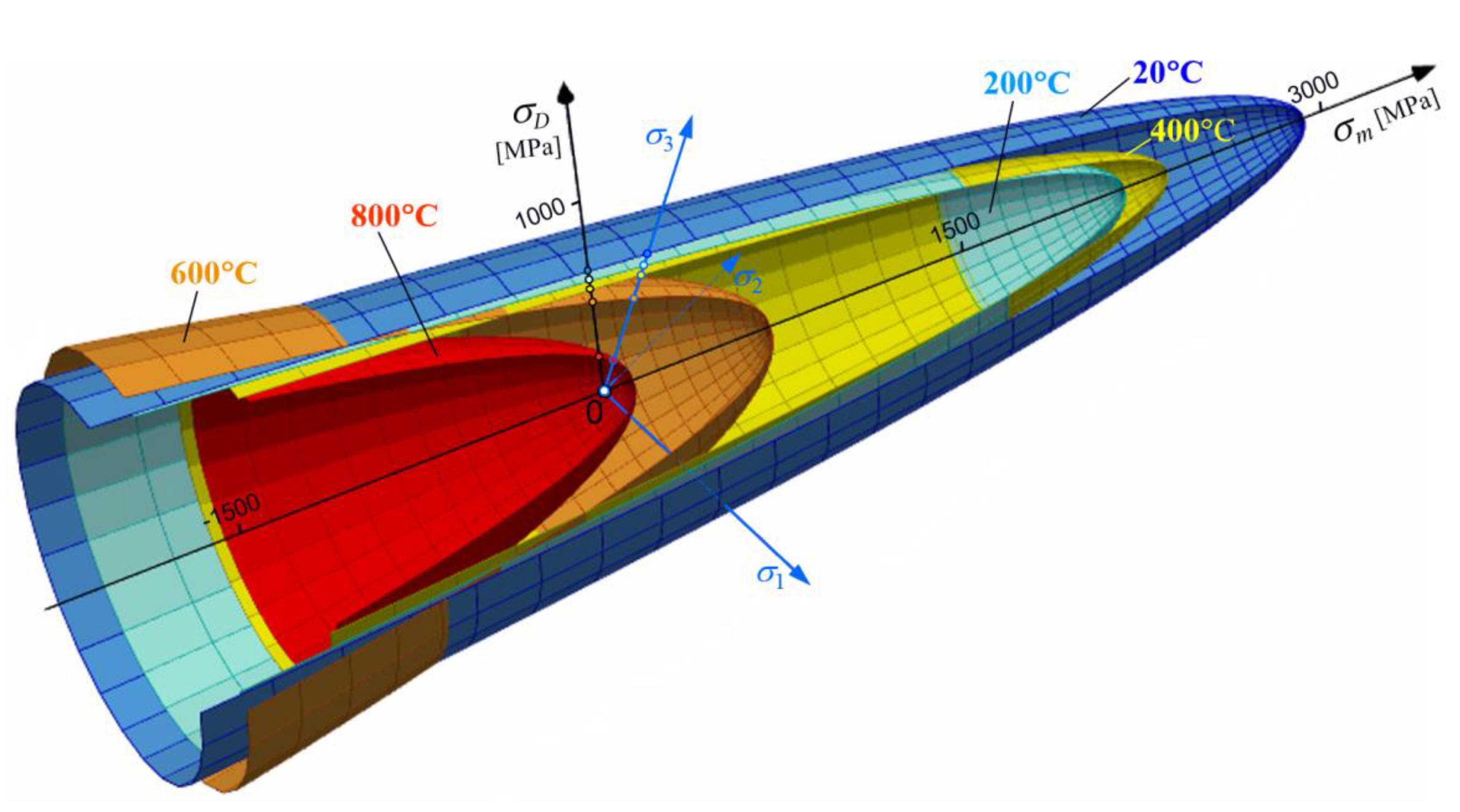
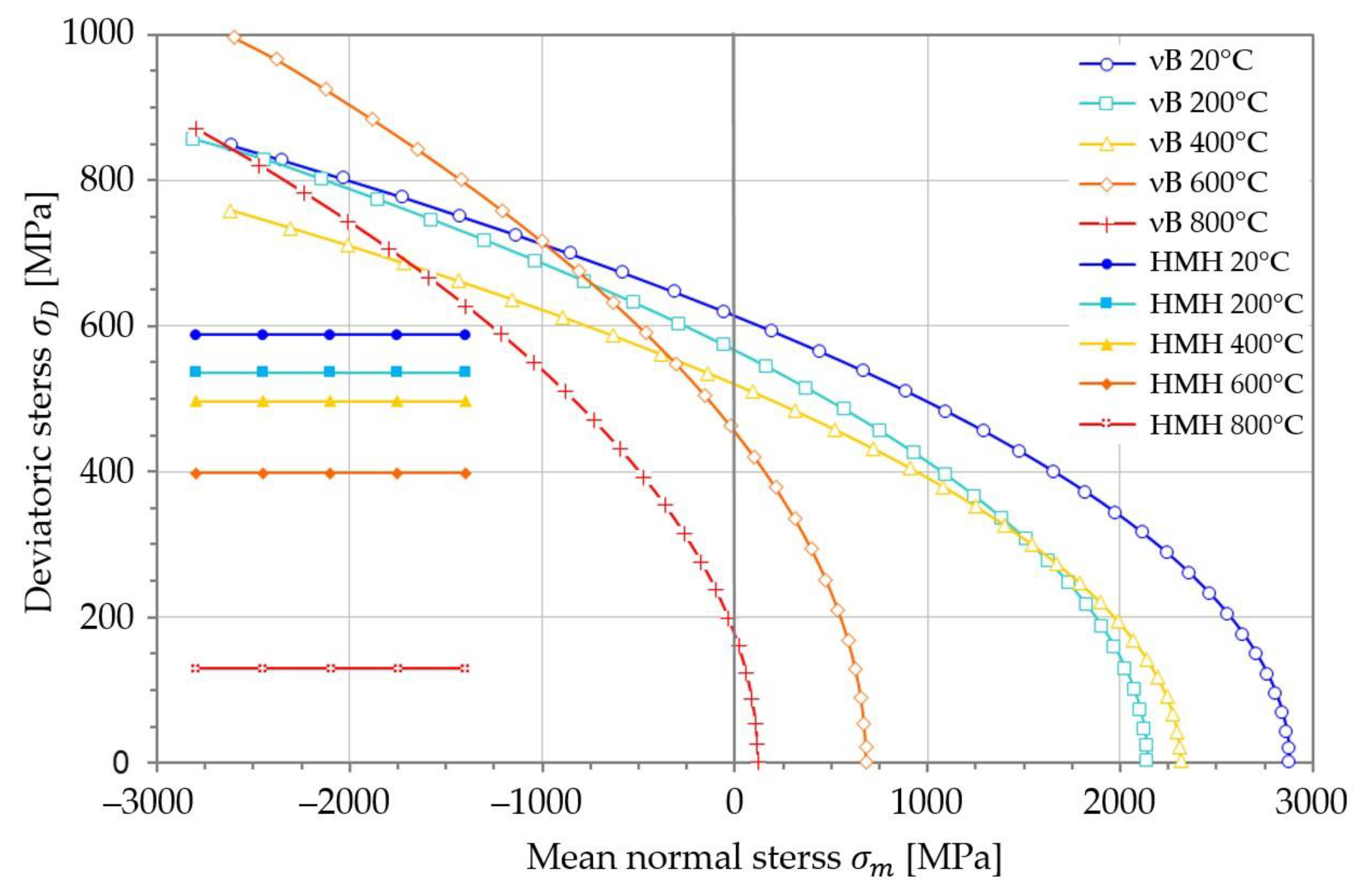
6. Thermal Shifts of Burzyński Plastic Regions
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lecomte-Beckers, J.; Carton, M.; Schubert, F.; Ennis, P. Materials for Advanced Power Engineering. In Proceedings of the 7th Liège Conference; Forschungszentrum Jülich: Jülich, Germany, 2002; pp. 25–30. [Google Scholar]
- Altenbach, H.; Bolchoun, A.; Kolupae, V. Phenomenological Yield and Failure Criteria. In Plasticity of Pressure-Sensitive Materials; Altenbach, H., Ochsner, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2014; ISBN 978-3-642-40945-5. [Google Scholar]
- Park, N.; Stoughton, T.B.; Yoon, J.W. A Criterion for General Description of Anisotropic Hardening Considering Strength Differential Effect with Non-Associated Flow Rule. Int. J. Plast. 2019, 121, 76–100. [Google Scholar] [CrossRef]
- Lenkovs’kyi, T.M.; Kun’, P.S.; Dudda, B.; Kharchenko, E.V. Conditions of Self-Similarity of Edge Transverse Shear Cracks in a Square Plate. Mater. Sci. 2018, 54, 361–367. [Google Scholar] [CrossRef]
- Taler, J.; Duda, P. Solving Direct and Inverse Heat Conduction Problems; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 978-3-540-33470-5. [Google Scholar]
- Burzyński, W. Studjum Nad Hipotezami Wytężenia; Akademja Nauk Technicznych: Lwów, Poland, 1928. [Google Scholar]
- Burzyński, W. Theoretical Foundations of the Hypotheses of Material Effort. Czas. Tech. 1929, 47, 1–41. [Google Scholar]
- Banaś, K.; Badur, J. Influence of Strength Differential Effect on Material Effort of a Turbine Guide Vane Based on Thermoelastoplastic Analysis. J. Therm. Stresses 2017, 40, 1368–1385. [Google Scholar] [CrossRef]
- Huber, M. Specific Work of Strain as a Measure of Material Effort. Proc. Lwów Polytech. Soc. 1904, 22, 49–50. [Google Scholar]
- Pęcherski, R. Burzyński Yield Condition Vis-A-Vis the Related Studies Reported in the Literature. Eng. Trans. 2008, 56, 383–391. [Google Scholar]
- Frąś, T.; Kowalewski, Z.; Pęcherski, R.; Rusinek, A. Applications of Burzyński Failure Criteria—I. Isotropic Materials with Asymmetry of Elastic Range. Eng. Trans. 2010, 58, 3–13. [Google Scholar]
- Pęcherski, R.; Frąś, T. Applications of the Burzyński Hypothesis of Material Effort for Isotropic Solids. Mech. Control 2010, 29, 45–50. [Google Scholar]
- Badur, J.; Bryk, M.; Ziółkowski, P.; Slawinski, D.; Ziółkowski, P.J.; Kornet, S.; Stajnke, M. On a Comparison of Huber-Mises-Hencky with Burzynski-Pecherski Equivalent Stresses for Glass Body during Nonstationary Thermal Load. AIP Conf. Proc. 2017, 1822. [Google Scholar] [CrossRef] [Green Version]
- Banaszkiewicz, M.; Dudda, W. Applicability of Notch Stress-Strain Correction Methods to Low-Cycle Fatigue Life Prediction of Turbine Rotors Subjected to Thermomechanical Loads. Acta Mech. Autom. 2018, 12, 179–185. [Google Scholar] [CrossRef] [Green Version]
- Dudda, W.; Ziółkowski, P.J.; Badur, J. Validation Plastic Model with Hardening of St12t. AIP Conf. Proc. 2019, 2077, 20016. [Google Scholar]
- Banaszkiewicz, M.; Dudda, W.; Badur, J. The Effect of Strength Differential on Material Effort and Lifetime of Steam Turbine Rotors Under Thermo-Mechanical Load. Eng. Trans. 2019, 67, 167–184. [Google Scholar] [CrossRef]
- Skrzypek, J.; Ganczarski, A. Mechanics of Modern Materials—Models, Anizotropy, Limit Surfaces Composite Ma-Terials, Dissipative Processes; Cracow University of Technology: Kraków, Poland, 2013. [Google Scholar]
- Cai, L.; He, Y.; Wang, S.; Li, Y.; Li, F. Thermal-Fluid-Solid Coupling Analysis on the Temperature and Thermal Stress Field of a Nickel-Base Superalloy Turbine Blade. Materials 2021, 14, 3315. [Google Scholar] [CrossRef]
- Yao, J.; Xin, B.; Gong, Y.; Cheng, G. Effect of Initial Temperature on the Microstructure and Properties of Stellite-6/Inconel 718 Functional Gradient Materials Formed by Laser Metal Deposition. Materials 2021, 14, 3609. [Google Scholar] [CrossRef] [PubMed]
- Bolaina, C.; Teloxa, J.; Varela, C.; Sierra, F.Z. Thermomechanical Stress Distributions in a Gas Turbine Blade Under the Effect of Cooling Flow Variations. J. Turbomach. 2013, 135. [Google Scholar] [CrossRef]
- Beghini, M.; Bertini, L.; Santus, C.; Monelli, B.D.; Scrinzi, E.; Pieroni, N.; Giovannetti, I. High Temperature Fatigue Testing of Gas Turbine Blades. Procedia Struct. Integr. 2017, 7, 206–213. [Google Scholar] [CrossRef]
- Orłowski, K.; Ochrymiuk, T.; Sandak, J.; Sandak, A. Estimation of Fracture Toughness and Shear Yield Stress of Orthotropic Materials in Cutting with Rotating Tools. Eng. Fract. Mech. 2017, 178, 433–444. [Google Scholar] [CrossRef]
- Chuchala, D.; Sandak, J.; Orłowski, K.; Muzinski, T.; Lackowski, M.; Ochrymiuk, T. Effect of the Drying Method of Pine and Beech Wood on Fracture Toughness and Shear Yield Stress. Materials 2020, 13, 4692. [Google Scholar] [CrossRef]
- Yu, M.-H. Unified Strength Theory and Its Applications; Springer: Berlin/Heidelberg, Germany, 2004; ISBN 978-3-642-62368-4. [Google Scholar]
- Zyczkowski, M. Discontinuous Bifurcations in the Case of the Burzyński-Torre Yield Condition. Acta Mech. 1999, 132, 19–35. [Google Scholar] [CrossRef]
- Pęcherski, R.; Szeptyński, P.; Nowak, M. An Extension of Burzyński Hypothesis of Material Effort Accounting for the Third Invariant of Stress Tensor. Arch. Metall. Mater. 2011, 56, 503–508. [Google Scholar] [CrossRef] [Green Version]
- Nowak, Z.; Nowak, M.; Pęcherski, R.; Potoczek, M.; Śliwa, R.E. Mechanical Properties Of The Ceramic Open-Cell Foams Of Variable Cell Sizes. Arch. Metall. Mater. 2015, 60, 1957–1964. [Google Scholar] [CrossRef] [Green Version]
- Dudda, W. Mechanical Characteristics of 26H2MF and St12T Steels under Compression at Elevated Temperatures. Strength Mater. 2020, 52, 325–328. [Google Scholar] [CrossRef]
- Dudda, W. Influence of High Temperatures on the Mechanical Characteristics of 26H2MF and ST12T STEELS. Mater. Sci. 2019, 55, 435–439. [Google Scholar] [CrossRef]
- Dudda, W.; Kraszewski, B. A Theoretical Validation of Burzyński Hypothesis for a Stress-Strain Analysis of Heat-Resistant Steel. Case Stud. Therm. Eng. 2021, 23, 100806. [Google Scholar] [CrossRef]
- Dudda, W.; Ziółkowski, P.J.; Badur, J. On Burzyński Stress during Thermomechanical Loading of the Turbine Blade. In Proceedings of the 14th International Scientific and Technical Conference: Thermal Power Plants Operation-Modernisations-Renovations, Słok, Poland, 22–24 May 2019. [Google Scholar]
- Badur, J.; Bryk, M. Accelerated Start-up of the Steam Turbine by Means of Controlled Cooling Steam Injection. Energy 2019, 173, 1242–1255. [Google Scholar] [CrossRef]
- Froissart, M.; Ziółkowski, P.; Dudda, W.; Badur, J. Heat Exchange Enhancement of Jet Impingement Cooling with the Novel Humped-Cone Heat Sink. Case Stud. Therm. Eng. 2021, 28, 101445. [Google Scholar] [CrossRef]

| Temperature | E(T) [GPa] | Rm(T) [MPa] | ||
|---|---|---|---|---|
| 20 °C | 217.9 | 720.3 | 786.0 | 874.3 |
| 200 °C | 206.9 | 656.7 | 731.7 | 804.3 |
| 400 °C | 193.1 | 608.0 | 666.3 | 728.5 |
| 600 °C | 141.8 | 487.0 | 639.3 | 570.5 |
| 800 °C | 81.3 | 160.0 | 290.0 | 190 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ochrymiuk, T.; Dudda, W.; Froissart, M.; Badur, J. Principles of Stress-Strength Modelling of the Highly Thermally Loaded Materials—The Influence of an Effect of Strength Differential on the Material Effort. Materials 2021, 14, 7449. https://doi.org/10.3390/ma14237449
Ochrymiuk T, Dudda W, Froissart M, Badur J. Principles of Stress-Strength Modelling of the Highly Thermally Loaded Materials—The Influence of an Effect of Strength Differential on the Material Effort. Materials. 2021; 14(23):7449. https://doi.org/10.3390/ma14237449
Chicago/Turabian StyleOchrymiuk, Tomasz, Waldemar Dudda, Marcin Froissart, and Janusz Badur. 2021. "Principles of Stress-Strength Modelling of the Highly Thermally Loaded Materials—The Influence of an Effect of Strength Differential on the Material Effort" Materials 14, no. 23: 7449. https://doi.org/10.3390/ma14237449
APA StyleOchrymiuk, T., Dudda, W., Froissart, M., & Badur, J. (2021). Principles of Stress-Strength Modelling of the Highly Thermally Loaded Materials—The Influence of an Effect of Strength Differential on the Material Effort. Materials, 14(23), 7449. https://doi.org/10.3390/ma14237449







