Accuracy in Cement Hydration Investigations: Combined X-ray Microtomography and Powder Diffraction Analyses
Abstract
1. Introduction
2. Materials and Methods
2.1. Portland Cement
2.2. Paste Preparation
2.3. Thermogravimetric Analysis
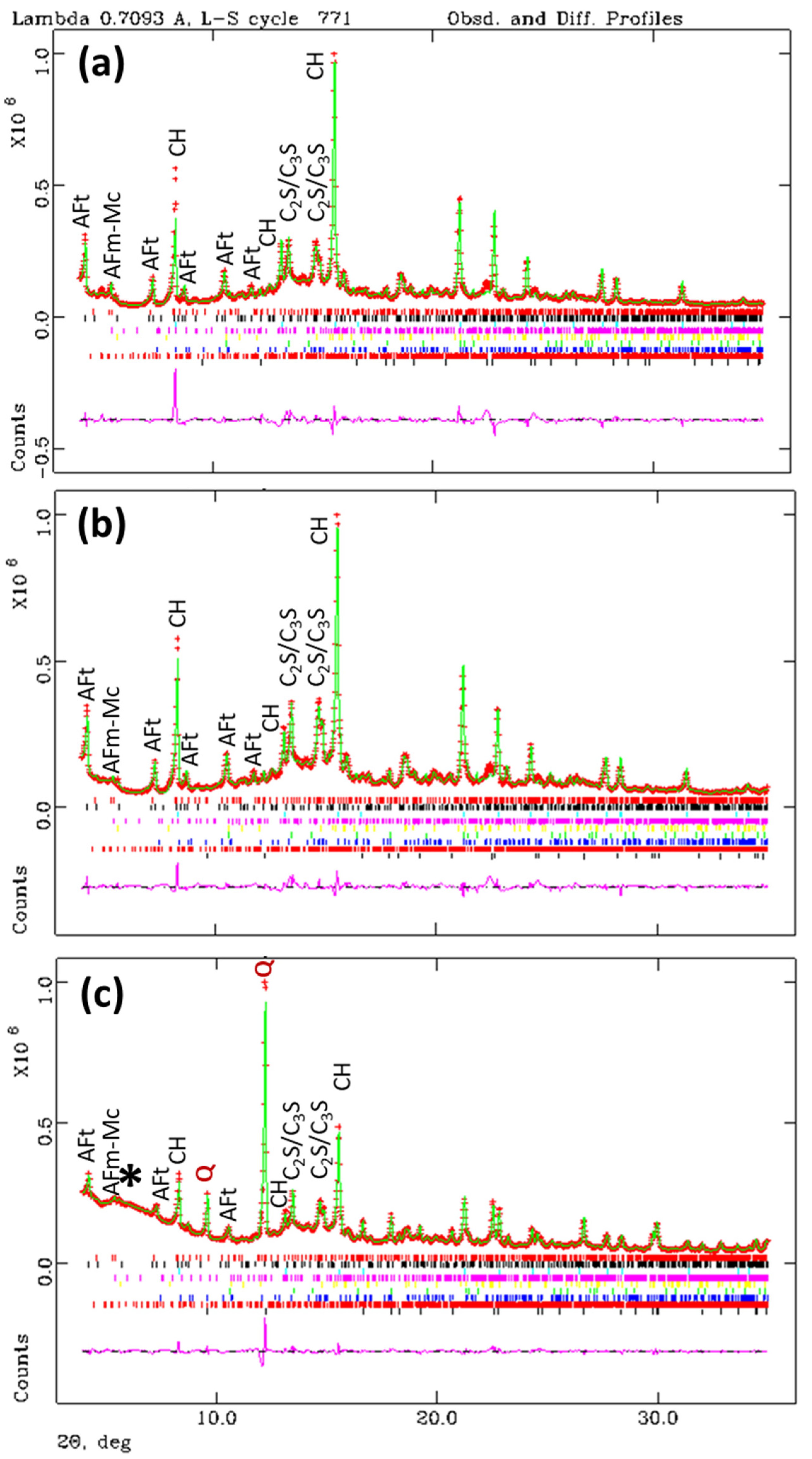
2.4. Laboratory X-ray Powder Diffraction (LXRPD) and Data Analysis
2.5. Laboratory X-ray Computed Microtomography (μCT) and Data Processing and Analysis
3. Results
3.1. Thermal Analysis
3.2. Laboratory X-ray Powder Diffraction Study
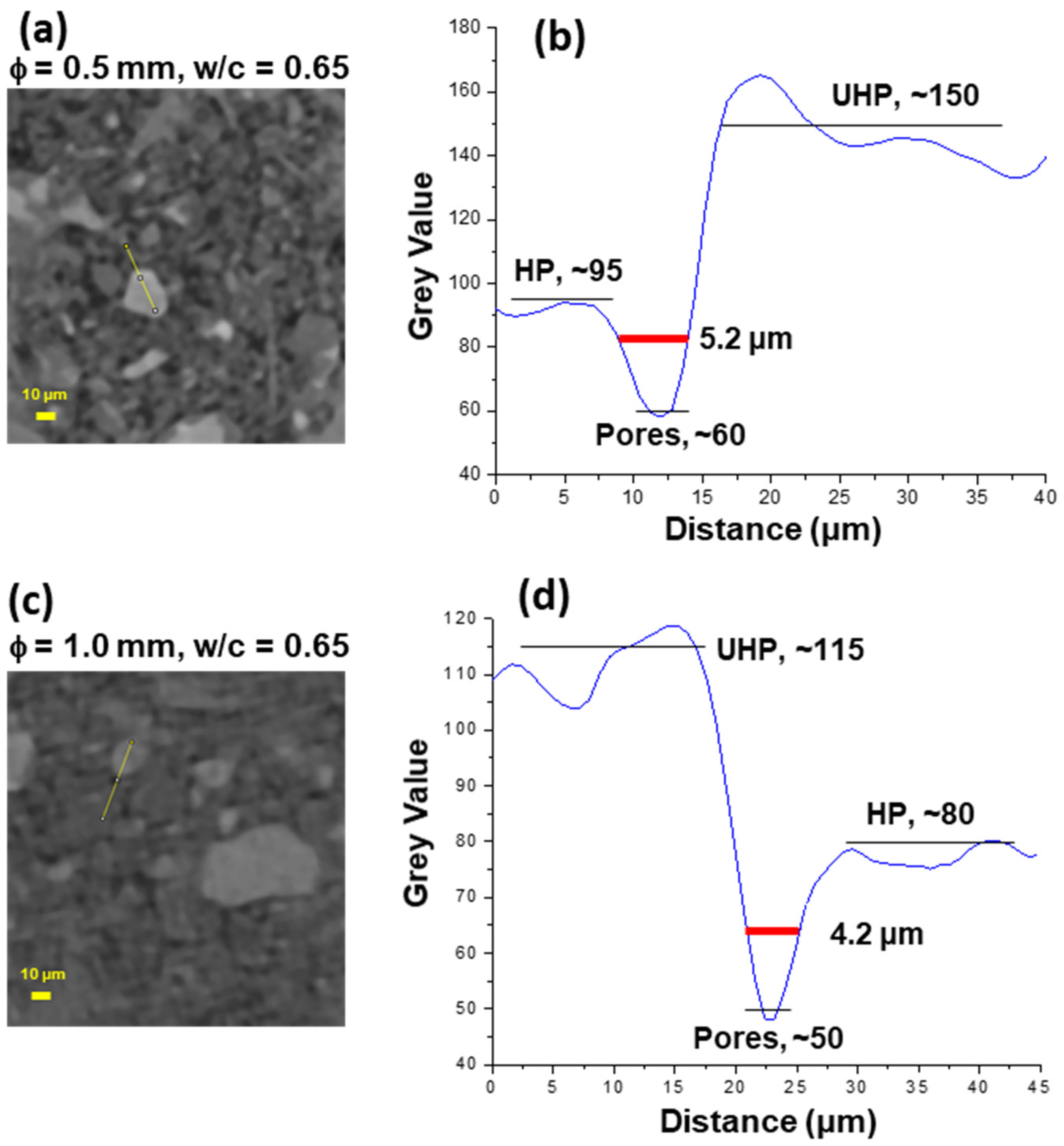
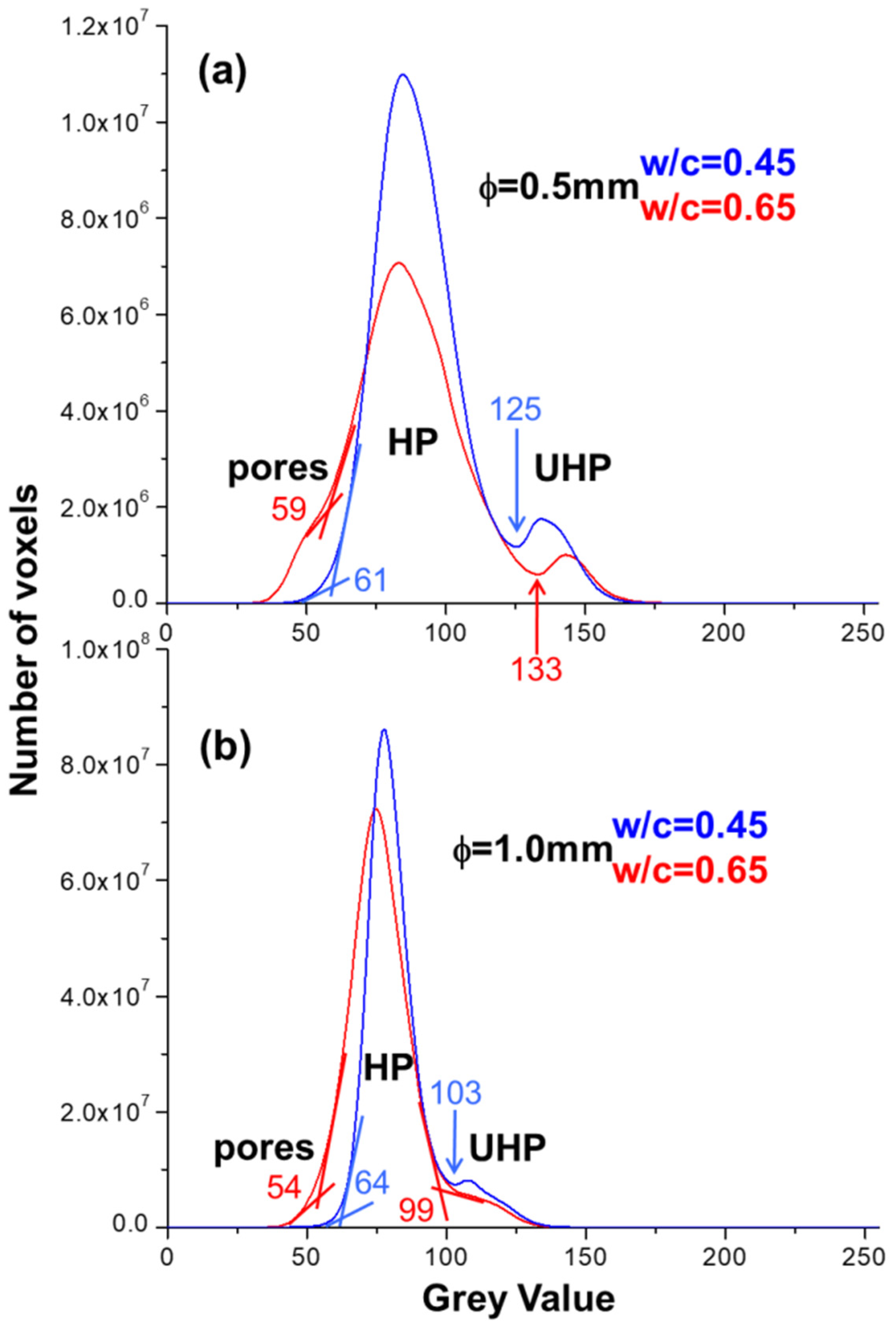
3.3. Laboratory X-ray Computed Microtomographic Study
4. Discussion
4.1. Comparison Involving the Thermal Analyses
4.1.1. Thermal Analysis and Nominal Compositions
4.1.2. Thermal Analysis and Rietveld Quantitative Phase Analysis (RQPA) of the Pastes from the Cylinders
4.2. Comparison of RQPA Results Obtained in Different Conditions for the Same Pastes
4.2.1. Considerations about the Width of the Capillaries for Cement Paste Analysis
4.2.2. Comparison of the RQPA Results or the Same Pastes in Different Capillary Sizes
4.3. Comparison of the RQPA and μCT Results for the Pastes within the Same Capillaries
5. Conclusions
- A methodology for obtaining μCT and LXRPD datasets for a cement paste within a capillary is reported. The resulting data have the necessary quality to be quantitatively analysed by global thresholding segmentation and Rietveld approaches.
- For establishing this methodology, the combined X-ray tomographic and diffraction study was complemented with results from pastes casted in moulds. The thermal analysis results and the amorphous contents derived from RQPA, by using the internal standard methodology, gave the necessary information to ascertain whether the results were accurate, or not.
- It is concluded that the values obtained by segmentation of laboratory μCT data are accurate, within ~2 vol%, but only if free water is added to the hydrated product component. This result holds for the employed μCT main experimental conditions: 0.80 μm voxel size and ~2 μm of true spatial resolution.
- To minimise the consequences of unavoidable experimental variations, relatively thick capillaries are recommended. The diameters should be close to 1.0 mm.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Scrivener, K.L.; Snellings, R.; Lothenbach, B. A Practical Guide to Microstructural Analysis of Cementitious Materials; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Juenger, M.C.; Snellings, R.; Bernal, S.A. Supplementary cementitious materials: New sources, characterization, and performance insights. Cem. Concr. Res. 2019, 122, 257–273. [Google Scholar] [CrossRef]
- Liu, J.; Yu, C.; Shu, X.; Ran, Q.; Yang, Y. Recent advance of chemical admixtures in concrete. Cem. Concr. Res. 2019, 124. [Google Scholar] [CrossRef]
- Taylor, H.F.W. Cement Chemistry, 2nd ed.; Academic Press: New York, NY, USA, 1997; Volume 20, p. 335. [Google Scholar]
- Avet, F.; Snellings, R.; Diaz, A.A.; Ben Haha, M.; Scrivener, K. Development of a new rapid, relevant and reliable (R3) test method to evaluate the pozzolanic reactivity of calcined kaolinitic clays. Cem. Concr. Res. 2016, 85, 1–11. [Google Scholar] [CrossRef]
- Walkley, B.; Provis, J. Solid-state nuclear magnetic resonance spectroscopy of cements. Mater. Today Adv. 2019, 1, 100007. [Google Scholar] [CrossRef]
- Kunther, W.; Dai, Z.; Skibsted, J. Thermodynamic modeling of hydrated white Portland cement–metakaolin–limestone blends utilizing hydration kinetics from 29Si MAS NMR spectroscopy. Cem. Concr. Res. 2016, 86, 29–41. [Google Scholar] [CrossRef]
- Wang, L.; Guo, F.; Lin, Y.; Yang, H.; Tang, S. Comparison between the effects of phosphorous slag and fly ash on the C-S-H structure, long-term hydration heat and volume deformation of cement-based materials. Constr. Build. Mater. 2020, 250, 118807. [Google Scholar] [CrossRef]
- Wang, L.; Jin, M.; Zhou, S.; Tang, S.; Lu, X. Investigation of microstructure of C-S-H and micro-mechanics of cement pastes under NH4NO3 dissolution by 29Si MAS NMR and microhardness. Measurement 2021, 185, 110019. [Google Scholar] [CrossRef]
- Muller, A.; Scrivener, K.; Skibsted, J.; Gajewicz, A.; McDonald, P. Influence of silica fume on the microstructure of cement pastes: New insights from 1H NMR relaxometry. Cem. Concr. Res. 2015, 74, 116–125. [Google Scholar] [CrossRef]
- Nagel, S.M.; Strangfeld, C.; Kruschwitz, S. Application of 1H proton NMR relaxometry to building materials—A review. J. Magn. Reson. Open 2021, 6–7, 100012. [Google Scholar] [CrossRef]
- de la Torre, Á.G.; Cabeza, A.; Calvente, A.; Bruque, S.; Aranda, M.A.G. Full Phase Analysis of Portland Clinker by Penetrating Synchrotron Powder Diffraction. Anal. Chem. 2000, 73, 151–156. [Google Scholar] [CrossRef]
- Aranda, M.A.G.; de la Torre, Á.G.; Leon-Reina, L. Rietveld Quantitative Phase Analysis of OPC Clinkers, Cements and Hydration Products. Rev. Miner. Geochem. 2012, 74, 169–209. [Google Scholar] [CrossRef]
- Jansen, D.; Stabler, C.; Goetz-Neunhoeffer, F.; Dittrich, S.; Neubauer, J. Does Ordinary Portland Cement contain amorphous phase? A quantitative study using an external standard method. Powder Diffr. 2011, 26, 31–38. [Google Scholar] [CrossRef]
- Leon-Reina, L.; de la Torre, A.G.; Porras-Vázquez, J.M.; Cruz, M.; Ordonez, L.M.; Alcobé, X.; Gispert-Guirado, F.; Larrañaga-Varga, A.; Paul, M.; Fuellmann, T.; et al. Round robin on Rietveld quantitative phase analysis of Portland cements. J. Appl. Crystallogr. 2009, 42, 906–916. [Google Scholar] [CrossRef]
- Le Saout, G.; Kocaba, V.; Scrivener, K. Application of the Rietveld method to the analysis of anhydrous cement. Cem. Concr. Res. 2011, 41, 133–148. [Google Scholar] [CrossRef]
- De La Torre, A.G.; Bruque, S.; Aranda, M.A.G. Rietveld quantitative amorphous content analysis. J. Appl. Crystallogr. 2001, 34, 196–202. [Google Scholar] [CrossRef]
- Jansen, D.; Goetz-Neunhoeffer, F.; Stabler, C.; Neubauer, J. A remastered external standard method applied to the quantification of early OPC hydration. Cem. Concr. Res. 2011, 41, 602–608. [Google Scholar] [CrossRef]
- Withers, P.J.; Bouman, C.; Carmignato, S.; Cnudde, V.; Grimaldi, D.; Hagen, C.K.; Maire, E.; Manley, M.; Du Plessis, A.; Stock, S.R. X-ray computed tomography. Nat. Rev. Methods Prim. 2021, 1, 18. [Google Scholar] [CrossRef]
- da Silva, Í.B. X-ray Computed Microtomography technique applied for cementitious materials: A review. Micron 2018, 107, 1–8. [Google Scholar] [CrossRef]
- du Plessis, A.; Boshoff, W.P. A review of X-ray computed tomography of concrete and asphalt construction materials. Constr. Build. Mater. 2019, 199, 637–651. [Google Scholar] [CrossRef]
- Brisard, S.; Serdar, M.; Monteiro, P.J. Multiscale X-ray tomography of cementitious materials: A review. Cem. Concr. Res. 2019, 128, 105824. [Google Scholar] [CrossRef]
- Kong, W.; Wei, Y.; Wang, S.; Chen, J.; Wang, Y. Research progress on cement-based materials by X-ray computed tomography. Int. J. Pavement Res. Technol. 2020, 13, 366–375. [Google Scholar] [CrossRef]
- Sugiyama, T.; Promentilla, M.A.B. Advancing Concrete Durability Research through X-ray Computed Tomography. J. Adv. Concr. Technol. 2021, 19, 730–755. [Google Scholar] [CrossRef]
- De La Torre, A.G.; Aranda, M.A. Accuracy in Rietveld quantitative phase analysis of Portland cements. J. Appl. Crystallogr. 2003, 36, 1169–1176. [Google Scholar] [CrossRef]
- Stutzman, P. Powder diffraction analysis of hydraulic cements: ASTM Rietveld round-robin results on precision. Powder Diffr. 2005, 20, 97–100. [Google Scholar] [CrossRef][Green Version]
- García-Maté, M.; Álvarez-Pinazo, G.; León-Reina, L.; De la Torre, A.; Aranda, M. Rietveld quantitative phase analyses of SRM 2686a: A standard Portland clinker. Cem. Concr. Res. 2018, 115, 361–366. [Google Scholar] [CrossRef]
- Scrivener, K.L.; Füllmann, T.; Gallucci, E.; Walenta, G.; Bermejo, E. Quantitative study of Portland cement hydration by X-ray diffraction/Rietveld analysis and independent methods. Cem. Concr. Res. 2004, 34, 1541–1547. [Google Scholar] [CrossRef]
- O’Donnell, J.H.; Von Dreele, R.B.; Chan, M.K.Y.; Toby, B.H. A scripting interface for GSAS-II. J. Appl. Crystallogr. 2018, 51, 1244–1250. [Google Scholar] [CrossRef]
- Madsen, I.C.; Scarlett, N.V.Y.; Cranswick, L.M.D.; Lwin, T. Outcomes of the International Union of Crystallography Commission on Powder Diffraction Round Robin on Quantitative Phase Analysis: Samples 1a to 1h. J. Appl. Crystallogr. 2001, 34, 409–426. [Google Scholar] [CrossRef]
- Scarlett, N.V.Y.; Madsen, I.C.; Cranswick, L.M.D.; Lwin, T.; Groleau, E.; Stephenson, G.; Aylmore, M.; Agron-Olshinaa, N. Outcomes of the International Union of Crystallography Commission on Powder Diffraction Round Robin on Quantitative Phase Analysis: Samples 2, 3, 4, synthetic bauxite, natural granodiorite and pharmaceuticals. J. Appl. Crystallogr. 2002, 35, 383–400. [Google Scholar] [CrossRef]
- Naber, C.; Stegmeyer, S.; Jansen, D.; Goetz-Neunhoeffer, F.; Neubauer, J. The PONKCS method applied for time resolved XRD quantification of supplementary cementitious material reactivity in hydrating mixtures with ordinary Portland cement. Constr. Build. Mater. 2019, 214, 449–457. [Google Scholar] [CrossRef]
- Mejdi, M.; Wilson, W.; Saillio, M.; Chaussadent, T.; Divet, L.; Tagnit-Hamou, A. Quantifying glass powder reaction in blended-cement pastes with the Rietveld-PONKCS method. Cem. Concr. Res. 2020, 130, 105999. [Google Scholar] [CrossRef]
- Deboodt, T.; Ideker, J.H.; Isgor, O.B.; Wildenschild, D. Quantification of synthesized hydration products using synchrotron microtomography and spectral analysis. Constr. Build. Mater. 2017, 157, 476–488. [Google Scholar] [CrossRef]
- Deboodt, T.; Wildenschild, D.; Ideker, J.H.; Isgor, O.B. Comparison of thresholding techniques for quantifying portland cement hydrates using synchrotron microtomography. Constr. Build. Mater. 2020, 266, 121109. [Google Scholar] [CrossRef]
- Bernal, I.M.; Shirani, S.; Cuesta, A.; Santacruz, I.; Aranda, M.A. Phase and microstructure evolutions in LC3 binders by multi-technique approach including synchrotron microtomography. Constr. Build. Mater. 2021, 300, 124054. [Google Scholar] [CrossRef]
- De Weerdt, K.; Ben Haha, M.; Le Saout, G.; Kjellsen, K.; Justnes, H.; Lothenbach, B. Hydration mechanisms of ternary Portland cements containing limestone powder and fly ash. Cem. Concr. Res. 2011, 41, 279–291. [Google Scholar] [CrossRef]
- John, V.M.; Quattrone, M.; Abrao, P.C.R.A.; Cardoso, F.A. Rethinking cement standards: Opportunities for a better future. Cem. Concr. Res. 2019, 124, 105832. [Google Scholar] [CrossRef]
- Von Dreele, R.B.; Larson, A.C. General Structure Analysis System (GSAS). Alamos Natl. Lab. Rep. LAUR. 2004, 96, 748. [Google Scholar]
- Thompson, P.; Cox, D.E.; Hastings, J.B. Rietveld refinement of Debye–Scherrer synchrotron X-ray data from Al2O3. J. Appl. Crystallogr. 1987, 20, 79–83. [Google Scholar] [CrossRef]
- Finger, L.W.; Cox, D.E.; Jephcoat, A.P. A correction for powder diffraction peak asymmetry due to axial divergence. J. Appl. Crystallogr. 1994, 27, 892–900. [Google Scholar] [CrossRef]
- De la Torre, Á.G.; Santacruz, I.; León-Reina, L.; Cuesta, A.; Aranda, M.A. Diffraction and crystallography applied to anhy-drous cements. In Cementitious Materials; Walter de Gruyter GmbH: Berlin, Germany, 2017; pp. 3–30. [Google Scholar] [CrossRef]
- De La Torre, A.; Santacruz, I.; León-Reina, L.; Cuesta, A.; Aranda, M.A. Diffraction and crystallography applied to hydrating cements. In Cementitious Materials; Pöllmann, H., Ed.; De Gruyter: Berlin, Germany, 2017; pp. 31–60. [Google Scholar]
- He, K.; Sun, J.; Tang, X. Guided image filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef] [PubMed]
- Milanfar, P. A Tour of Modern Image Filtering: New Insights and Methods, both Practical and Theoretical. IEEE Signal. Process. Mag. 2012, 30, 106–128. [Google Scholar] [CrossRef]
- Schindelin, J.; Arganda-Carreras, I.; Frise, E.; Kaynig, V.; Longair, M.; Pietzsch, T.; Preibisch, S.; Rueden, C.; Saalfeld, S.; Schmid, B.; et al. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [PubMed]
- Lothenbach, B.; Durdzinski, P.; De Weerdt, K. Thermogravimetric analysis. In A Practical Guide to Microstructural Analysis of Cementitious Materials; Scrivener, K., Snellings, R., Lothenbach, B., Eds.; CRC Press: Boca Raton, FL, USA, 2016; pp. 177–211. [Google Scholar]
- Eik, M.; Antonova, A.; Puttonen, J. Phase contrast tomography to study near-field effects of polypropylene fibres on hardened cement paste. Cem. Concr. Compos. 2020, 114, 103800. [Google Scholar] [CrossRef]
- Shirani, S.; Cuesta, A.; Morales-Cantero, A.; De la Torre, A.G.; Olbinado, M.P.; Aranda, M.A. Influence of curing temperature on belite cement hydration: A comparative study with Portland cement. Cem. Concr. Res. 2021, 147, 106499. [Google Scholar] [CrossRef]
- Soin, A.V.; Catalan, L.J.; Kinrade, S.D. A combined QXRD/TG method to quantify the phase composition of hydrated Portland cements. Cem. Concr. Res. 2013, 48, 17–24. [Google Scholar] [CrossRef]
- Lothenbach, B.; Le Saout, G.; Gallucci, E.; Scrivener, K. Influence of limestone on the hydration of Portland cements. Cem. Concr. Res. 2008, 38, 848–860. [Google Scholar] [CrossRef]
- Schöler, A.; Lothenbach, B.; Winnefeld, F.; Zajac, M. Hydration of quaternary Portland cement blends containing blast-furnace slag, siliceous fly ash and limestone powder. Cem. Concr. Compos. 2015, 55, 374–382. [Google Scholar] [CrossRef]
- Gallucci, E.; Scrivener, K.; Groso, A.; Stampanoni, M.; Margaritondo, G. 3D experimental investigation of the microstructure of cement pastes using synchrotron X-ray microtomography (μCT). Cem. Concr. Res. 2007, 37, 360–368. [Google Scholar] [CrossRef]
- Parisatto, M.; Dalconi, M.C.; Valentini, L.; Artioli, G.; Rack, A.; Tucoulou, R.; Cruciani, G.; Ferrari, G. Examining microstructural evolution of Portland cements by in-situ synchrotron micro-tomography. J. Mater. Sci. 2014, 50, 1805–1817. [Google Scholar] [CrossRef]
- Allen, A.J.; Thomas, J.J.; Jennings, H.M. Composition and density of nanoscale calcium–silicate–hydrate in cement. Nat. Mater. 2007, 6, 311–316. [Google Scholar] [CrossRef]
- Cuesta, A.; De La Torre, Á.G.; Santacruz, I.; Diaz, A.; Trtik, P.; Holler, M.; Lothenbach, B.; Aranda, M.A.G. Quantitative disentanglement of nanocrystalline phases in cement pastes by synchrotron ptychographic X-ray tomography. IUCrJ 2019, 6, 473–491. [Google Scholar] [CrossRef] [PubMed]




| t0 a | t = 50 d b ϕ = 0.50 mm | t = 50 d b ϕ = 1.00 mm | t = 50 d Cylinder | ρ (g/cm3) | |
|---|---|---|---|---|---|
| C3S | 44.2 | 7.5 | 4.2 | 4.3 | 3.15 |
| C2S | 8.2 | 5.6 | 5.4 | 6.0 | 3.30 |
| C4AF | 8.3 | 3.4 | 2.4 | 2.5 | 3.73 |
| C3A | 3.6 | 1.9 | 0.9 | 1.0 | 3.05 |
| H0.5 | 0.9 | -- | -- | -- | 2.71 |
| 2.8 | 4.7 | 2.1 | 2.8 | 2.71 | |
| CH | -- | 8.3 | 11.6 | 10.8 | 2.23 |
| AFt | -- | 6.5 | 11.2 | 10.8 | 1.78 |
| AFm-Mc | -- | 0.3 | 0.5 | 0.6 | 2.22 |
| ACn (mainly C-S-H gel) | -- | 47.0 | 47.0 | 47.0 | -- |
| FW | 31.0 | 14.3 | 14.3 | 14.3 | 1.00 |
| t0 a | t = 50 d b ϕ = 0.50 mm | t = 50 d b ϕ = 1.00 mm | t = 50 d Cylinder | |
|---|---|---|---|---|
| C3S | 38.8 | 3.6 | 2.4 | 3.1 |
| C2S | 7.2 | 5.2 | 4.5 | 4.3 |
| C4AF | 7.3 | 1.6 | 1.3 | 1.4 |
| C3A | 3.2 | 0.9 | 0.6 | 0.8 |
| H0.5 | 0.8 | -- | -- | -- |
| 2.2 | 2.0 | 1.9 | 5.5 | |
| CH | -- | 11.1 | 12.4 | 10.0 |
| AFt | -- | 10.2 | 11.1 | 9.8 |
| AFm-Mc | -- | 0.6 | 1.1 | 0.8 |
| ACn (mainly C-S-H gel) | -- | 39.3 | 39.3 | 39.3 |
| FW | 39.4 | 25.0 | 25.0 | 25.0 |
| Pore (vol%) | HP (vol%) | UHP (vol%) | rHP (vol%) | rUHP (vol%) | |
|---|---|---|---|---|---|
| ϕ = 0.5 mm, w/c = 0.45 | 1.5 | 89.1 | 9.5 | 90.4 | 9.6 |
| Thresholds | 0–61 | 62–124 | 125–255 | ||
| ϕ = 0.5 mm, w/c = 0.65 | 8.3 | 85.8 | 5.6 | 93.9 | 6.1 |
| Thresholds | 0–59 | 60–132 | 133–255 | ||
| ϕ = 1.0 mm, w/c = 0.45 | 1.5 | 89.6 | 8.9 | 91.0 | 9.0 |
| Thresholds | 0–64 | 65–102 | 103–255 | ||
| ϕ = 1.0 mm, w/c = 0.65 | 2.4 | 90.2 | 7.4 | 92.4 | 7.6 |
| Thresholds | 0–54 | 55–98 | 99–255 |
| RQPA | μCT | |||
|---|---|---|---|---|
| HP (vol%) | UHP (vol%) | rHP (vol%) | rUHP (vol%) | |
| ϕ = 0.5 mm, w/c = 0.45 | 89.1 | 10.9 | 90.4 | 9.6 |
| ϕ = 1.0 mm, w/c = 0.45 | 92.7 | 7.3 | 91.0 | 9.0 |
| ϕ = 0.5 mm, w/c = 0.65 | 94.2 | 5.8 | 93.9 | 6.1 |
| ϕ = 1.0 mm, w/c = 0.65 | 95.5 | 4.5 | 92.4 | 7.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salcedo, I.R.; Cuesta, A.; Shirani, S.; León-Reina, L.; Aranda, M.A.G. Accuracy in Cement Hydration Investigations: Combined X-ray Microtomography and Powder Diffraction Analyses. Materials 2021, 14, 6953. https://doi.org/10.3390/ma14226953
Salcedo IR, Cuesta A, Shirani S, León-Reina L, Aranda MAG. Accuracy in Cement Hydration Investigations: Combined X-ray Microtomography and Powder Diffraction Analyses. Materials. 2021; 14(22):6953. https://doi.org/10.3390/ma14226953
Chicago/Turabian StyleSalcedo, Inés R., Ana Cuesta, Shiva Shirani, Laura León-Reina, and Miguel A. G. Aranda. 2021. "Accuracy in Cement Hydration Investigations: Combined X-ray Microtomography and Powder Diffraction Analyses" Materials 14, no. 22: 6953. https://doi.org/10.3390/ma14226953
APA StyleSalcedo, I. R., Cuesta, A., Shirani, S., León-Reina, L., & Aranda, M. A. G. (2021). Accuracy in Cement Hydration Investigations: Combined X-ray Microtomography and Powder Diffraction Analyses. Materials, 14(22), 6953. https://doi.org/10.3390/ma14226953







