Experimental Study on the Permeation and Migration Rules of Pressurized Water in Textile-Reinforced Concrete (TRC)
Abstract
:1. Introduction
2. Experiments and Results
2.1. Proportions of Concrete Mix
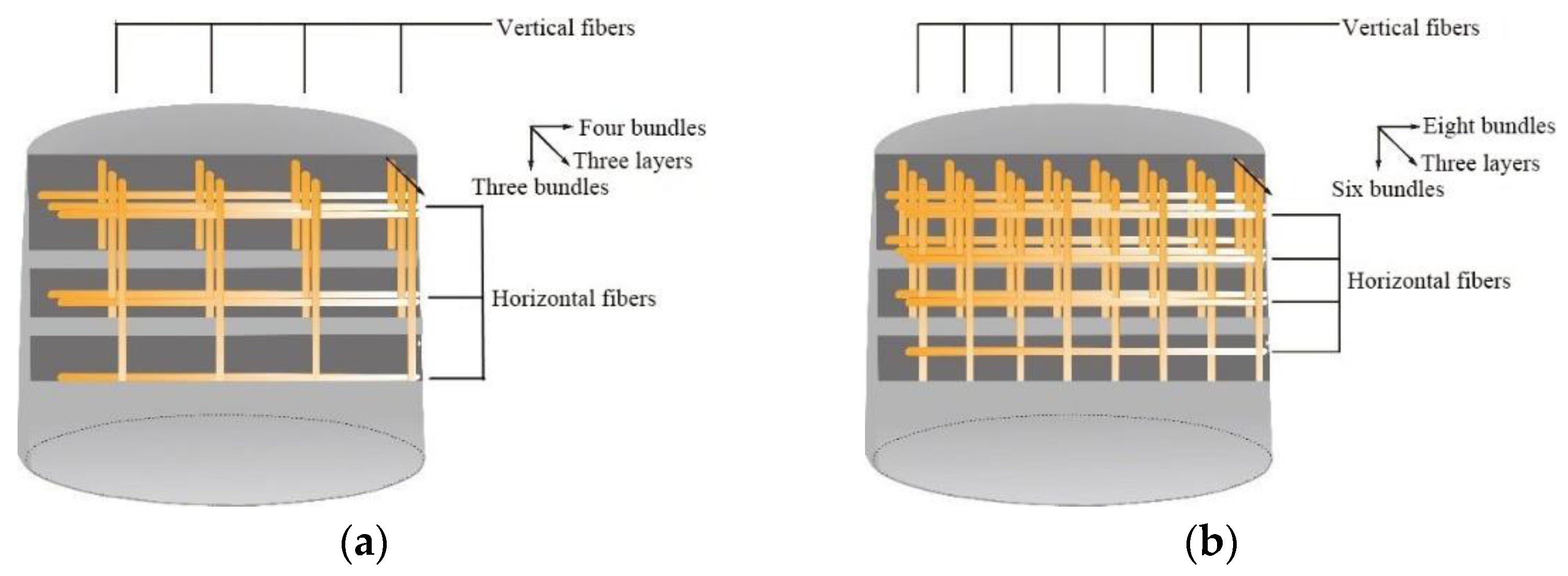
2.2. Preparation of Textile
2.3. Specimen Grouping
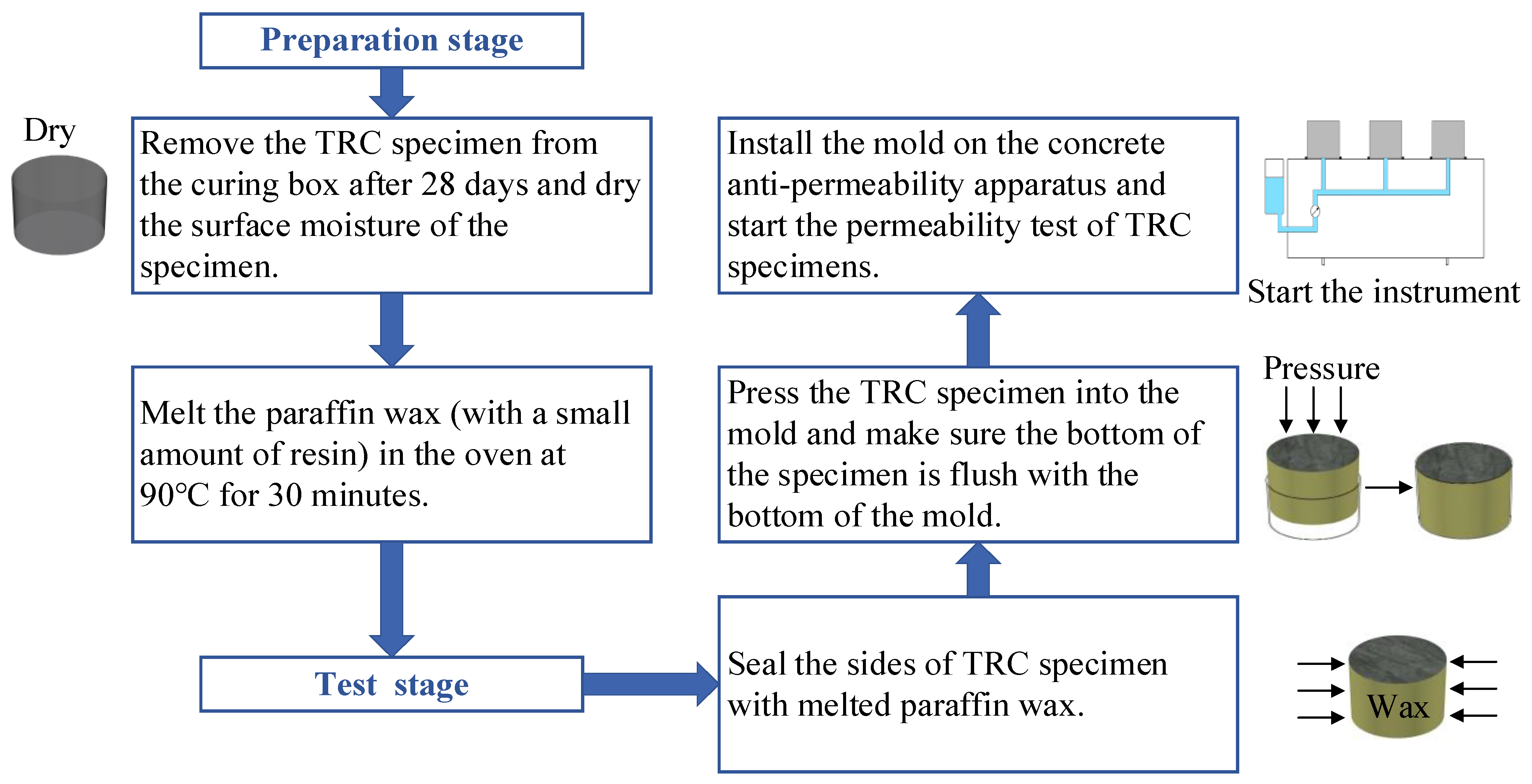
2.4. Specimen Preparation
2.5. TRC Permeability Test
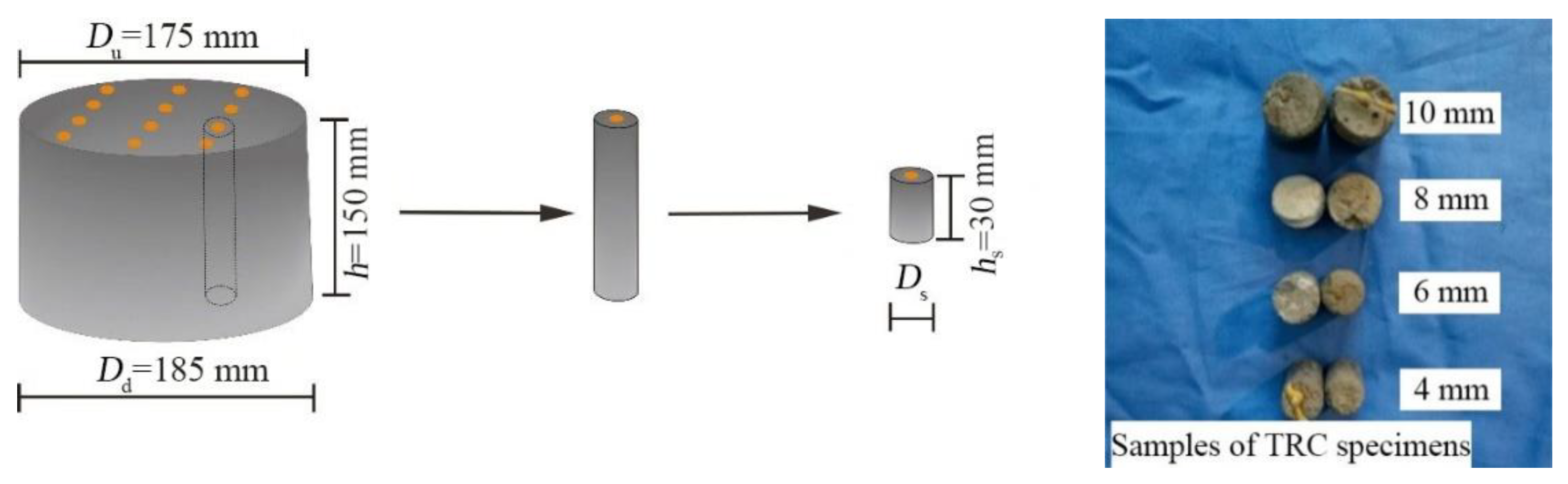
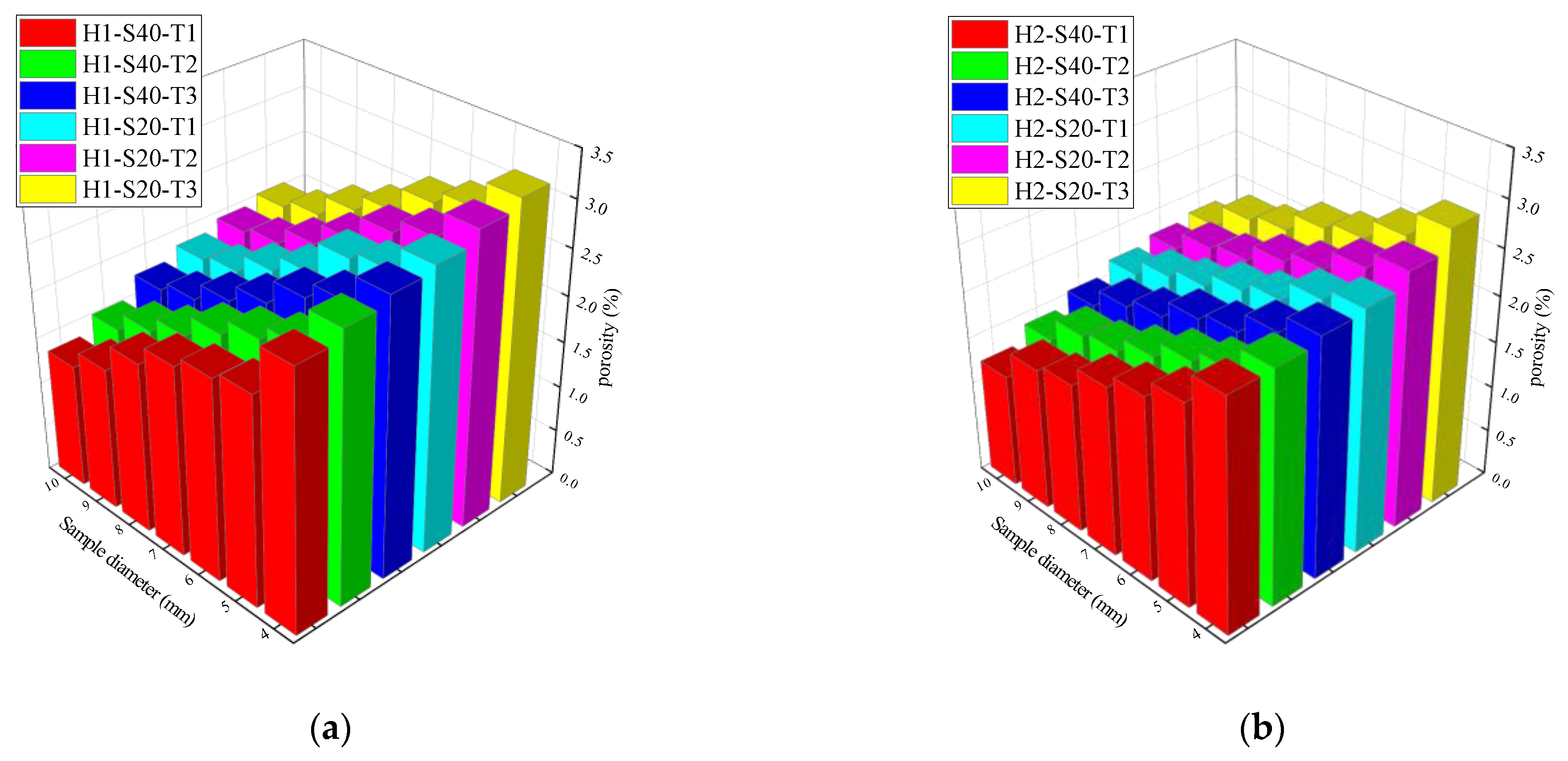
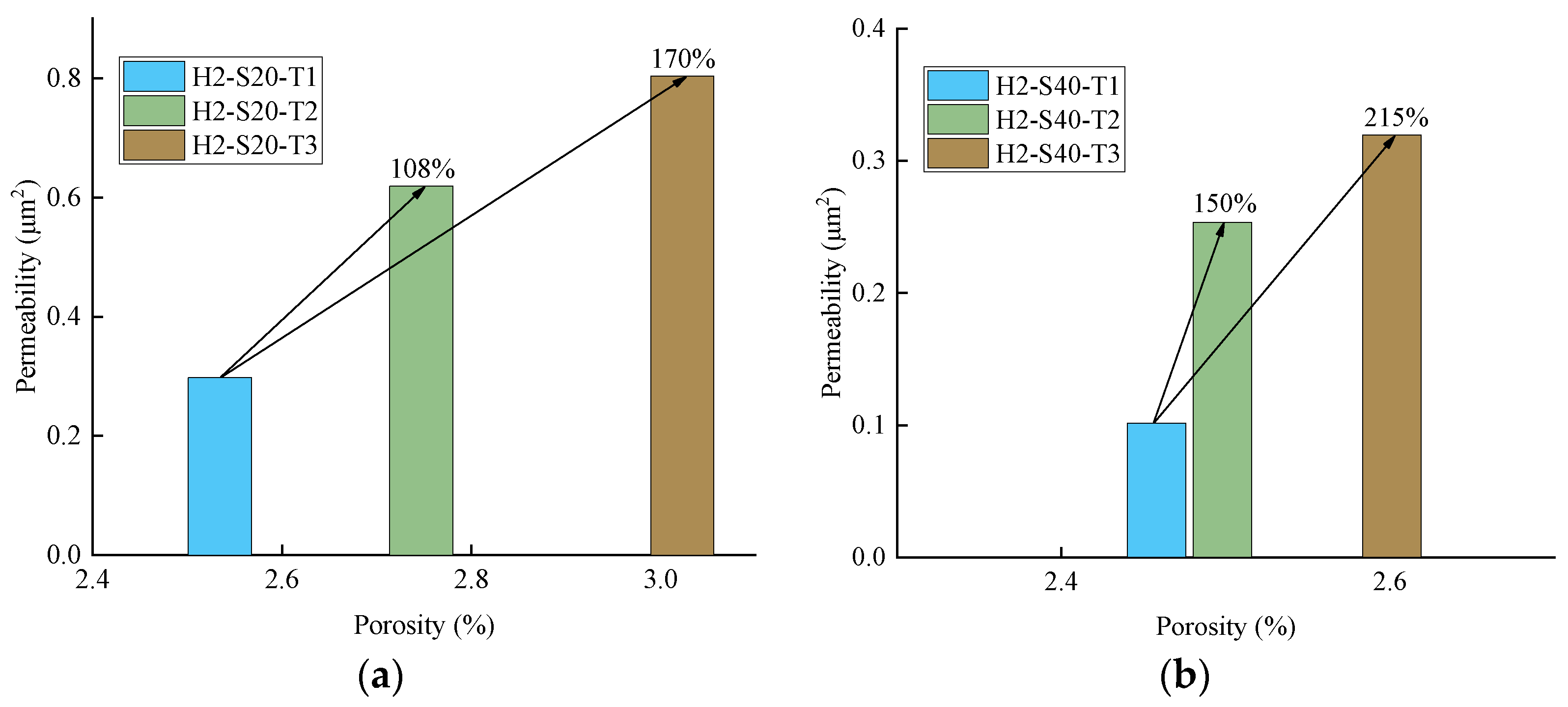
2.6. Porosity Analysis
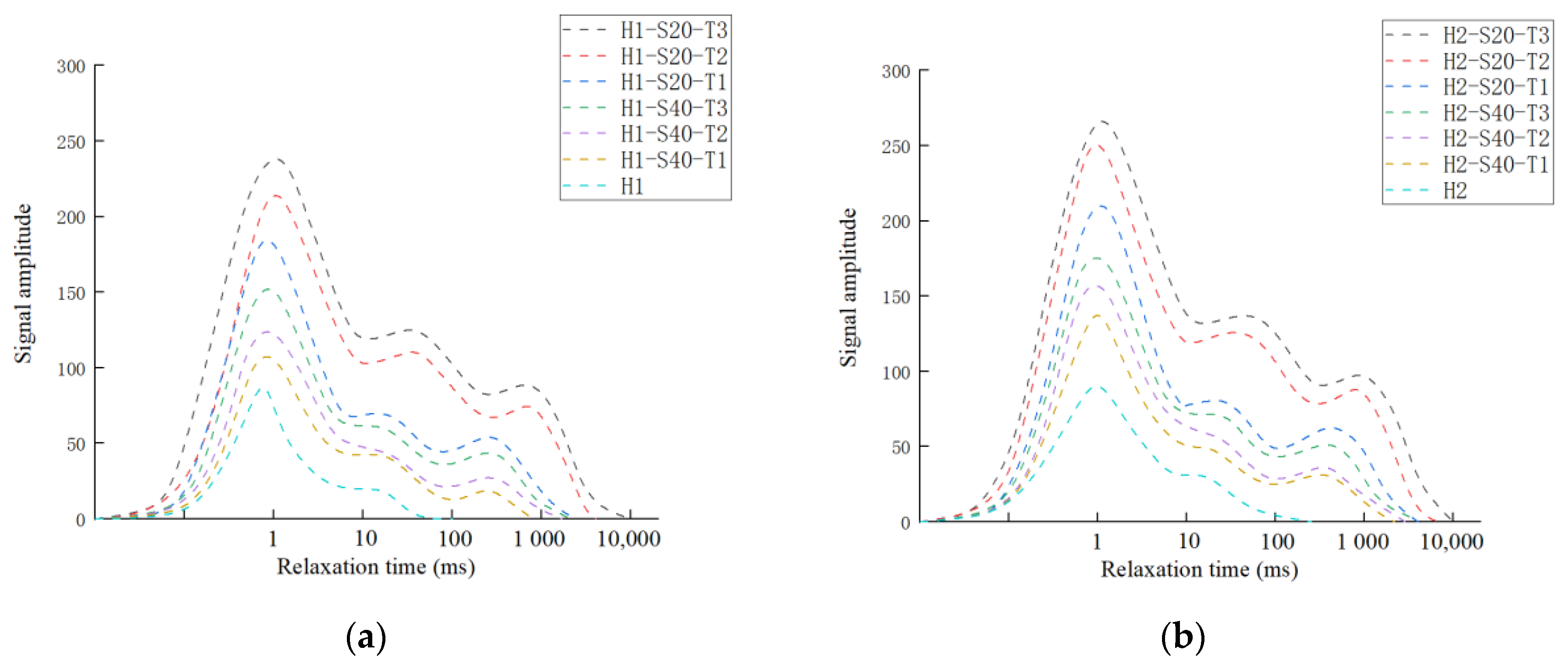
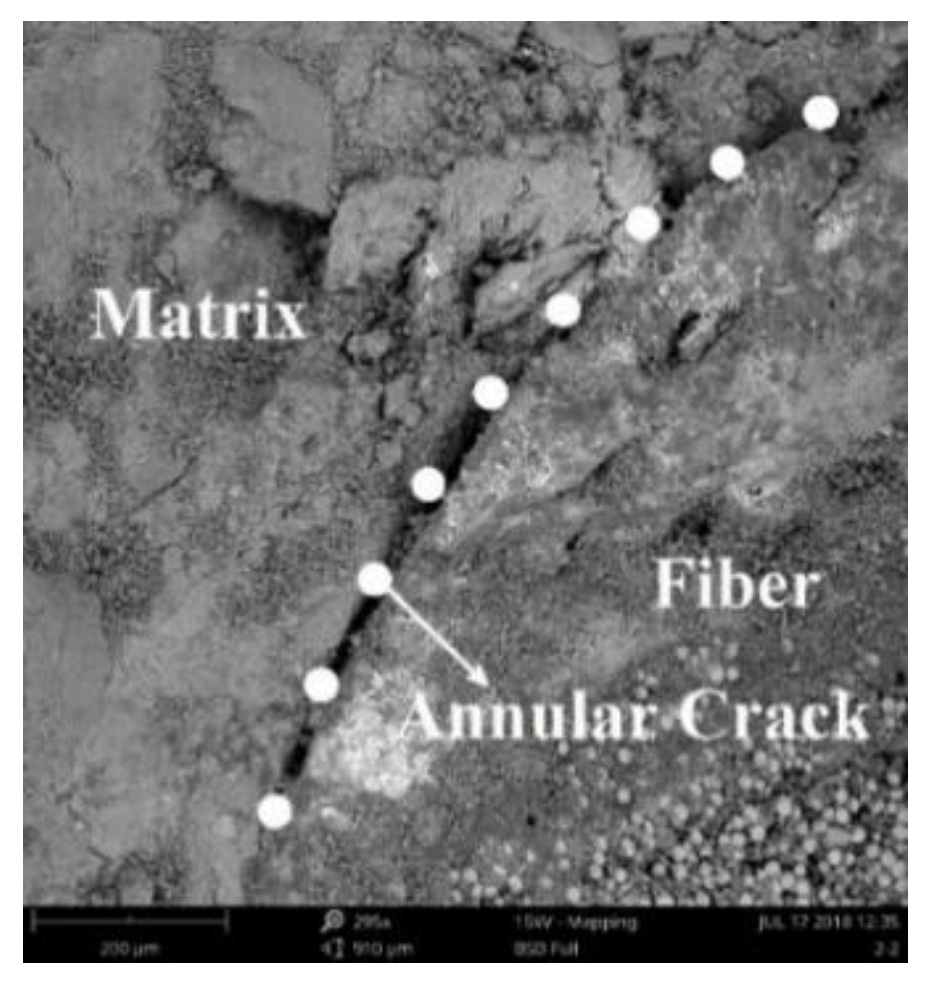
2.7. Microscopic Test Results
3. Theoretical Analysis
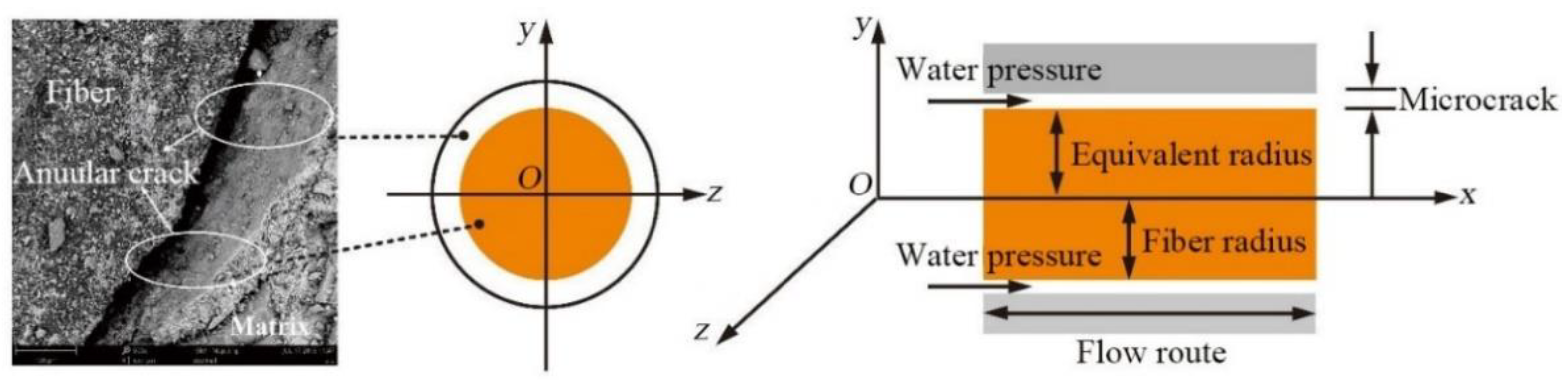
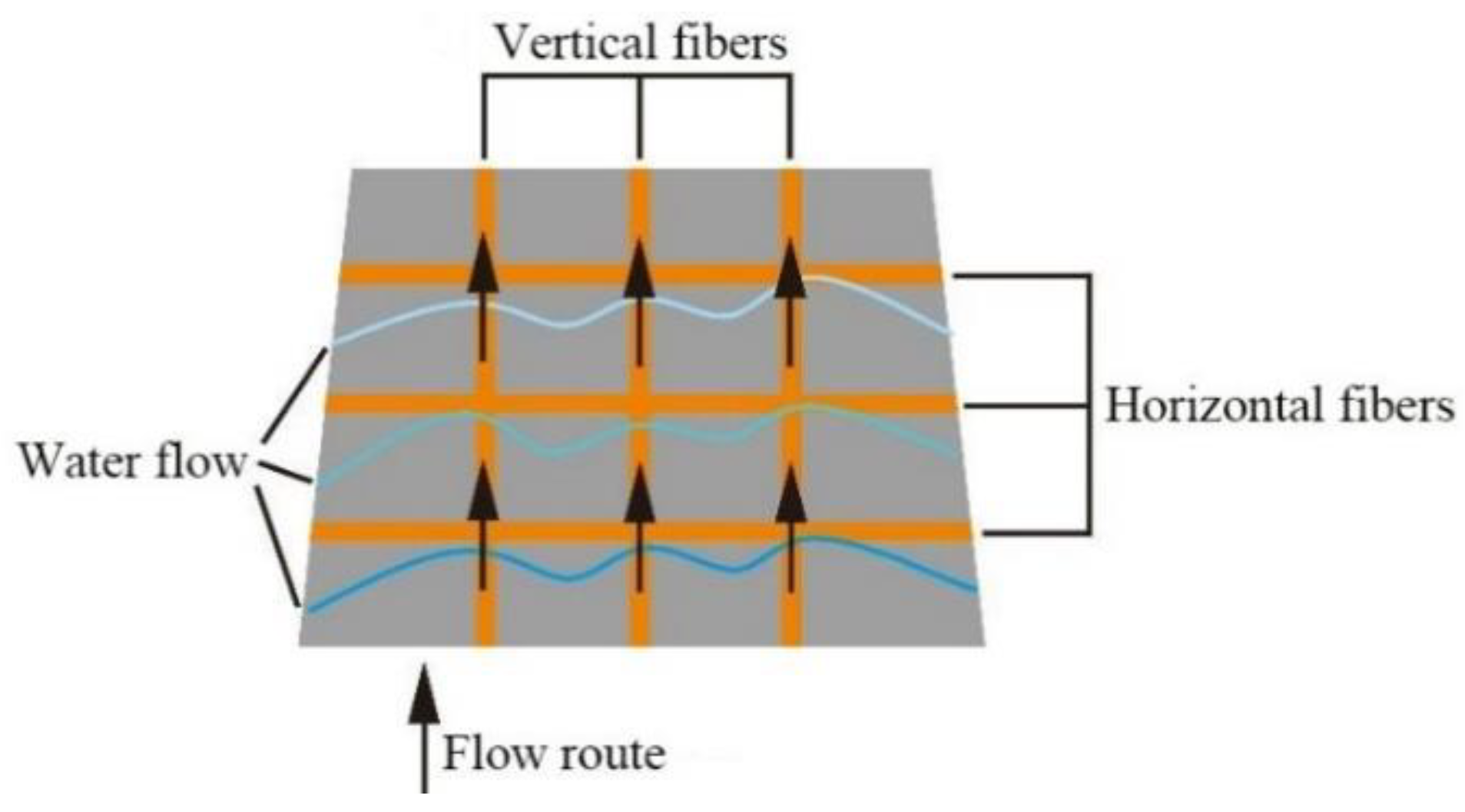
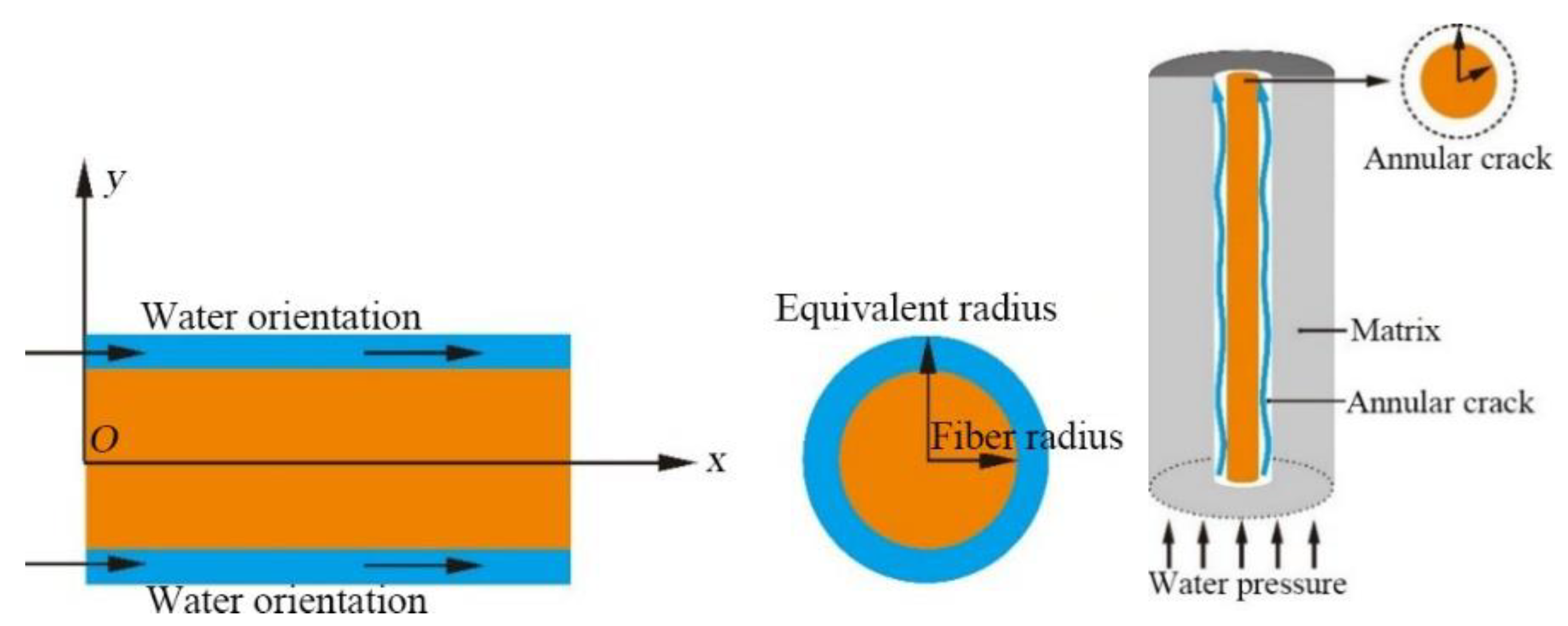
3.1. Mathematical Model of the Concentric Circular Slit Flow
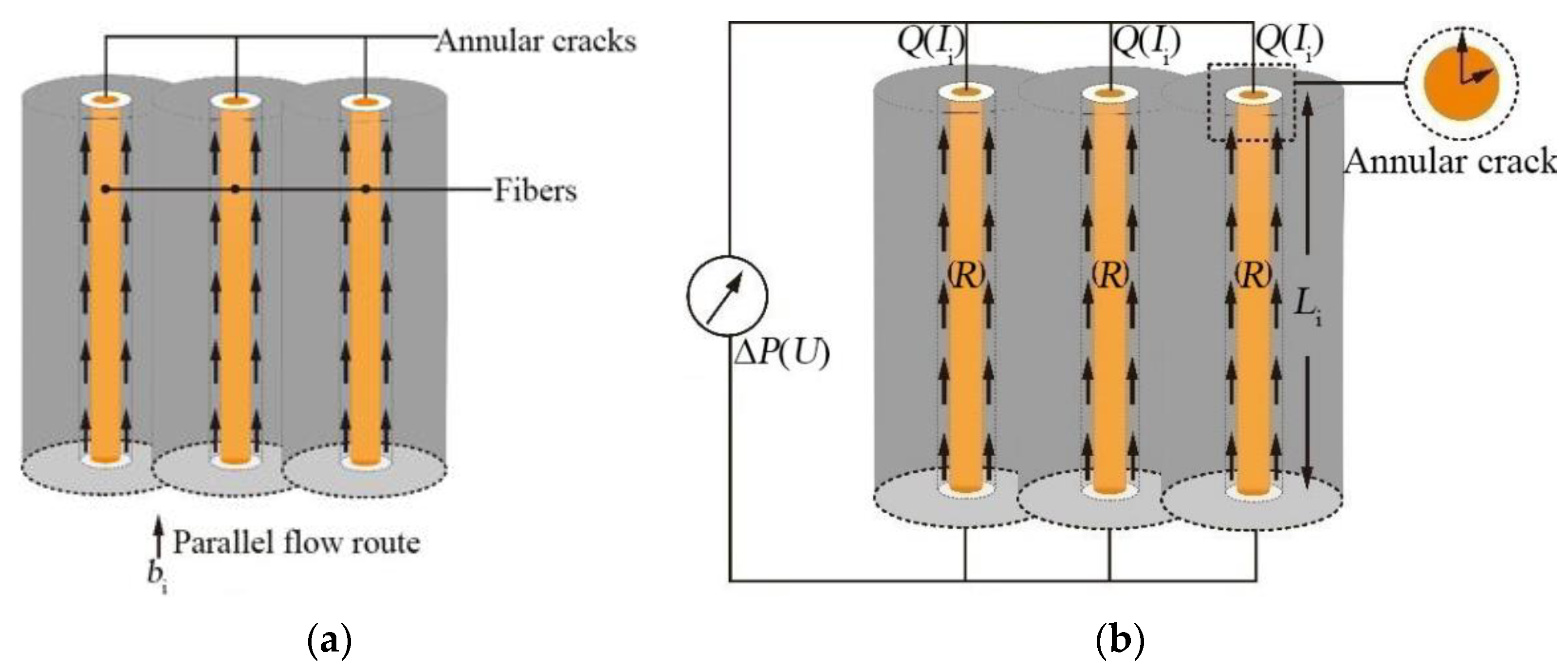
3.2. TRC Penetration Model
3.2.1. Introduction of the Model
3.2.2. Model Establishment
3.3. TRC Penetration Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Metha, P.K. Concrete Microstructure, Properties, and Materials; McGraw-Hill Education: New York, NY, USA, 2014. [Google Scholar]
- Wang, K.J.; Jansen, D.C. Permeability study of cracked concrete. Cem. Concr. Res. 1997, 27, 381–393. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Li, H.; Abdelhady, A.; Yang, J.; Wang, H. Effects of specimen shape and size on the permeability and mechanical properties of porous concrete. Constr. Build. Mater. 2021, 266, 121074. [Google Scholar] [CrossRef]
- Wang, L.; He, T.; Zhou, Y.; Tang, S.; Tan, J.; Liu, Z.; Su, J. The influence of fiber type and length on the cracking resistance, durability and pore structure of face slab concrete. Constr. Build. Mater. 2021, 282, 122706. [Google Scholar] [CrossRef]
- Li, H.; Xu, S.L. Development and Optimization of Cementitious Matrices for Textile Reinforced Concrete. J. Hydroelectr. Eng. 2006, 25, 72–76. [Google Scholar]
- Hegger, J.; Will, N.; Bruckermann, O.; Voss, S. Load–bearing behaviour and simulation of textile reinforced concrete. Mater. Struct. 2006, 39, 765–776. [Google Scholar] [CrossRef]
- Butler, M.; Mechtcherine, V.; Hempel, S. Experimental investigations on the durability of fibre–matrix inter-faces in textile-reinforced concrete. Cem. Concr. Compos. 2009, 31, 221–231. [Google Scholar] [CrossRef]
- Wang, W.; Shi, P.; Deng, L.; Chu, H.; Kong, X. Residual Strength Evaluation of Corroded Textile-Reinforced Concrete by the Deep Learning-Based Method. Materials 2020, 13, 3226. [Google Scholar] [CrossRef]
- Yin, S.P.; Yu, Y.L.; Xi, Y.P. Flexural performance of TRC-strengthened RC beam under chloride environment. Anti-Corros. Methods Mater. 2018, 65, 444–450. [Google Scholar]
- Li, H. Analysis and Experimental Study on Textile Reinforced Concrete Elements; Dalian University of Technology: Dalian, China, 2005. [Google Scholar]
- Alva, P.; Arnon, B.; Barzin, M. Textile Reinforced Concrete. Taylor & Francis Group; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Viktor, M. Novel cement-based composites for the strengthening and repair of concrete structures. Constr. Build. Mater. 2013, 41, 365–373. [Google Scholar]
- Li, Y.; Yin, S.; Dai, J.; Liu, M. Numerical investigation on the influences of different factors on the seismic performance of TRC-strengthened RC columns. J. Build. Eng. 2020, 30, 101245. [Google Scholar] [CrossRef]
- Yin, S.P.; Xu, S.L. An Experimental Study on Improved Mechanical Behavior of Textile-Reinforced Concrete. Adv. Mater. Res. 2010, 168–170, 1850–1853. [Google Scholar] [CrossRef]
- Truong, B.T.; Bui, T.T.; Limam, A.; Larbi, A.S.; Le Nguyen, K.; Michel, M. Experimental investigations of reinforced concrete beams repaired/reinforced by TRC composites. Compos. Struct. 2017, 168, 826–839. [Google Scholar] [CrossRef]
- Ahmad, S.; Azad, A.K. An exploratory study on correlating the permeability of concrete with its porosity and tortuosity. Adv. Cem. Res. 2013, 25, 288–294. [Google Scholar] [CrossRef]
- Banthia, N.; Biparva, A.; Mindess, S. Permeability of concrete under stress. Cem. Concr. Res. 2005, 35, 1651–1655. [Google Scholar] [CrossRef]
- Yin, S.; Xu, S.; Lv, H. Flexural Behavior of Reinforced Concrete Beams with TRC Tension Zone Cover. J. Mater. Civ. Eng. 2014, 26, 320–330. [Google Scholar] [CrossRef]
- Hai, N.T.; Hong, V.X.; Amir, S.L. Experimental study of the effect of simultaneous mechanical and high-temperature loadings on the behaviour of textile-reinforced concrete (TRC). Constr. Build. Mater. 2016, 125, 253–270. [Google Scholar]
- Pourasee, A.; Peled, A.; Weiss, J. Fluid transport in cracked fabric-reinforced-cement-based composites. J. Mater. Civ. Eng. 2011, 23, 1227–1238. [Google Scholar] [CrossRef]
- Yin, S.-P.; Li, S.-C.; Su, X.; Hu, X.-Q. Study of the mechanical properties of TRC-strengthened eccentric columns exposed to dry and wet cycles in a chloride salt erosion environment. Eng. Struct. 2020, 204, 110014. [Google Scholar]
- Sheng, J.; Yin, S.-P.; Wang, F. Experimental study on the fatigue behaviour of RC beams strengthened with TRC after sustained load corrosion. Constr. Build. Mater. 2017, 131, 713–720. [Google Scholar]
- Dolatabadi, M.K.; Janetzko, S.; Gries, T.; Kang, B.G.; Sander, A. Permeability of AR-glass fibers roving embedded in cementitious matrix. Mater. Struct. 2011, 44, 245–251. [Google Scholar] [CrossRef]
- Mechtcherine, V.; Lieboldt, M. Permeation of water and gases through cracked textile reinforced concrete. Cem. Concr. Compos. 2011, 33, 725–734. [Google Scholar] [CrossRef]
- Lieboldt, M.; Mechtcherine, V. Transport of Liquids and Gases through Textile Reinforced Concrete. In Proceedings of the International Conference on Material Science, Aachen, Germany, 6–8 September 2010. [Google Scholar]
- Lieboldt, M.; Mechtcherine, V.; Barhum, R. Transport of water and gases in crack-free and cracked textile reinforced concrete. In Concrete Repair; CRC Press: Boca Raton, FL, USA, 2008; pp. 111–112. [Google Scholar]
- Paul, A. Chemical durability of glasses; a thermodynamic approach. J. Mater. Sci. 1977, 12, 2246–2268. [Google Scholar] [CrossRef]
- Majumdar, A.J.; West, J.M.; Larner, L.J. Properties of glass fibres in cement environment. J. Mater. Sci. 1977, 12, 927–936. [Google Scholar] [CrossRef]
- Larner, L.; Speakman, K.; Majumdar, A. Chemical interactions between glass fibres and cement. J. Non-Cryst. Solids 1976, 20, 43–74. [Google Scholar] [CrossRef]
- Xu, S.L.; Kruger, M.; Reinhardt, H.W.; Ozbolt, J.K. Bond characteristics of carbon, alkali resistant glass, and aramid textiles in mortar. J. Mater. Civ. Eng. 2005, 16, 356–364. [Google Scholar] [CrossRef]
- Wang, B.; Yuan, K.; Lu, X.; Zhao, J. Calculation method of cracking load and deflection of textile reinforced self-stressing concrete. Constr. Build. Mater. 2021, 304, 124622. [Google Scholar] [CrossRef]
- Andrea, B.; Alexandra, S.; Ioan, A. NMR relaxation of molecules confined inside the cement paste pores under partially saturated conditions. Cem. Concr. Res. 2016, 89, 56–62. [Google Scholar]
- Burduhos, N.D.D.; Vizureanu, P.; Ardelean, I.; Sandu, A.V.; Corbu, O.C.; Matei, E. Revealing the Influence of Microparticles on Geo-polymers’ Synthesis and Porosity. Materials 2020, 13, 3211. [Google Scholar] [CrossRef] [PubMed]
- Deng, K.J. The Theory and Application of Nuclear Magnetic Resonance Logging; China University of Petroleum Press: Shandong, China, 2010. [Google Scholar]
- Hu, M.L. Fluid Mechanics; Wuhan University of Technology Press: Wuhan, China, 2013. [Google Scholar]
- Tao, Y.; Liu, W.Q. An equivalent seepage resistance model with seepage-stress coupling for fractured rock mass. Rock Soil Mech. 2012, 33, 2041–2047. [Google Scholar]




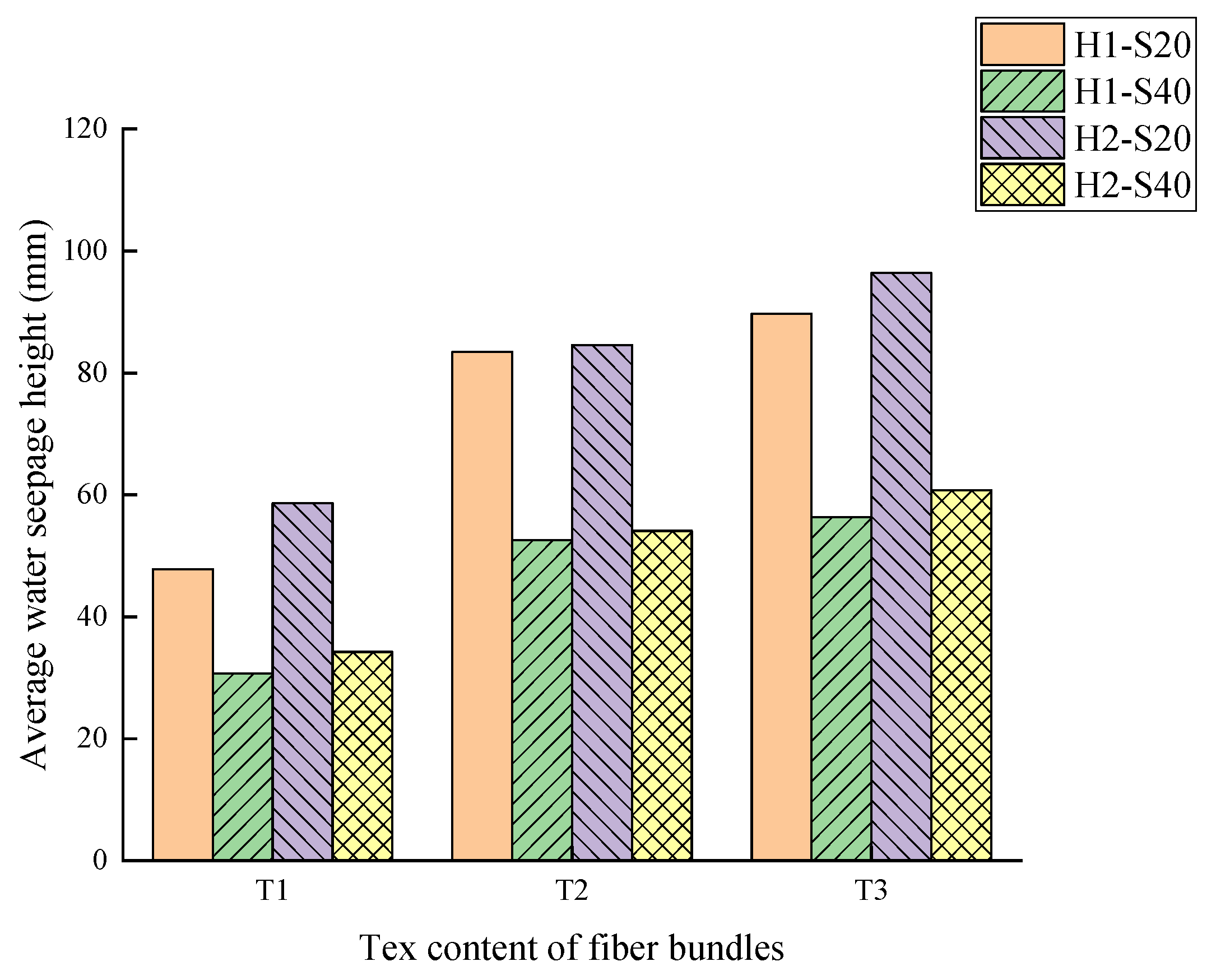




| Water Cement Ratio | Water | Cement | Sand | Stone |
|---|---|---|---|---|
| 0.45 | 185 | 411 | 545 | 1158 |
| 0.55 | 185 | 337 | 633 | 1125 |
| Tensile Strength (MPa) | Elastic Modulus (GPa) | Density (g/m3) | Sectional Area (mm2) |
|---|---|---|---|
| 1600 | 72 | 2700 | 0.975 |
| Tex Content | 9.2 k | 18.4 k | 27.6 k |
|---|---|---|---|
| Equivalent radius | 0.557 mm | 0.788 mm | 0.965 mm |
| Specimen Number | Water-Cement Ratio | Grid Size | Tex Content | Number |
|---|---|---|---|---|
| H1-S20-T1 | 0.45 | 20 mm × 20 mm | 9.2 k × 9.2 k | 12 |
| H1-S20-T2 | 0.45 | 20 mm × 20 mm | 18.4 k × 18.4 k | 12 |
| H1-S20-T3 | 0.45 | 20 mm × 20 mm | 27.6 k × 27.6 k | 12 |
| H1-S40-T1 | 0.45 | 40 mm × 40 mm | 9.2 k × 9.2 k | 12 |
| H1-S40-T2 | 0.45 | 40 mm × 40 mm | 18.4 k × 18.4 k | 12 |
| H1-S40-T3 | 0.45 | 40 mm × 40 mm | 27.6 k × 27.6 k | 12 |
| H2-S20-T1 | 0.55 | 20 mm × 20 mm | 9.2 k × 9.2 k | 12 |
| H2-S20-T2 | 0.55 | 20 mm × 20 mm | 18.4 k × 18.4 k | 12 |
| H2-S20-T3 | 0.55 | 20 mm × 20 mm | 27.6 k × 27.6 k | 12 |
| H2-S40-T1 | 0.55 | 40 mm × 40 mm | 9.2 k × 9.2 k | 12 |
| H2-S40-T2 | 0.55 | 40 mm × 40 mm | 18.4 k × 18.4 k | 12 |
| H2-S40-T3 | 0.55 | 40 mm × 40 mm | 27.6 k × 27.6 k | 12 |
| Specimen Number | Average Water Seepage Height (mm) | Relative Permeability Coefficient (mm/h) |
|---|---|---|
| H1-S2-T1 | 30.67 | 7.35 × 10−6 |
| H1-S2-T2 | 52.56 | 2.16 × 10−5 |
| H1-S2-T3 | 56.32 | 2.48 × 10−5 |
| H1-S4-T1 | 47.78 | 1.78 × 10−5 |
| H1-S4-T2 | 83.45 | 5.44 × 10−5 |
| H1-S4-T3 | 89.69 | 6.28 × 10−5 |
| H2-S2-T1 | 34.23 | 9.15 × 10−6 |
| H2-S2-T2 | 54.11 | 2.29 × 10−5 |
| H2-S2-T3 | 60.73 | 2.88 × 10−5 |
| H2-S4-T1 | 58.62 | 2.68 × 10−5 |
| H2-S4-T2 | 84.57 | 5.59 × 10−5 |
| H2-S4-T3 | 96.37 | 7.26 × 10−5 |
| Specimen Number | Experimental Values (μm2) | Theoretical Values (μm2) | Errors (%) |
|---|---|---|---|
| H1-S20-T1 | 0.19762 | 0.20428 | 3.370 |
| H1-S20-T2 | 0.60281 | 0.60031 | 0.415 |
| H1-S20-T3 | 0.69633 | 0.67764 | 2.684 |
| H1-S40-T1 | 0.08142 | 0.0967 | 18.767 |
| H1-S40-T2 | 0.23913 | 0.24012 | 0.414 |
| H1-S40-T3 | 0.27457 | 0.27106 | 1.278 |
| H2-S20-T1 | 0.29746 | 0.28374 | 4.612 |
| H2-S20-T2 | 0.6191 | 0.59667 | 3.623 |
| H2-S20-T3 | 0.80392 | 0.80789 | 0.494 |
| H2-S40-T1 | 0.10142 | 0.11338 | 11.793 |
| H2-S40-T2 | 0.25345 | 0.25867 | 2.060 |
| H2-S40-T3 | 0.31925 | 0.32316 | 1.225 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Liu, J.; Wang, Q. Experimental Study on the Permeation and Migration Rules of Pressurized Water in Textile-Reinforced Concrete (TRC). Materials 2021, 14, 6512. https://doi.org/10.3390/ma14216512
Wang B, Liu J, Wang Q. Experimental Study on the Permeation and Migration Rules of Pressurized Water in Textile-Reinforced Concrete (TRC). Materials. 2021; 14(21):6512. https://doi.org/10.3390/ma14216512
Chicago/Turabian StyleWang, Boxin, Jiaqi Liu, and Qing Wang. 2021. "Experimental Study on the Permeation and Migration Rules of Pressurized Water in Textile-Reinforced Concrete (TRC)" Materials 14, no. 21: 6512. https://doi.org/10.3390/ma14216512
APA StyleWang, B., Liu, J., & Wang, Q. (2021). Experimental Study on the Permeation and Migration Rules of Pressurized Water in Textile-Reinforced Concrete (TRC). Materials, 14(21), 6512. https://doi.org/10.3390/ma14216512








