Application of Positron Annihilation Spectroscopy in Accelerator-Based Irradiation Experiments
Abstract
1. Introduction
2. Methodology
2.1. Positron Stopping in Solids—Interaction Volume
2.1.1. Radioisotope Positron Sources
2.1.2. Slow Positron Beam Experiments
2.2. Techniques of Positron Annihilation Spectroscopy
2.2.1. Positron Annihilation Lifetime Spectroscopy (PALS)
2.2.2. Doppler Broadening Spectroscopy
2.3. Positron Trapping at Defects
2.4. Positron Diffusion in Solids
3. Application of PAS Techniques in Accelerator-Based Irradiation Experiments
3.1. Self-Ion Irradiation
3.2. Hydrogen (Proton) Implantation
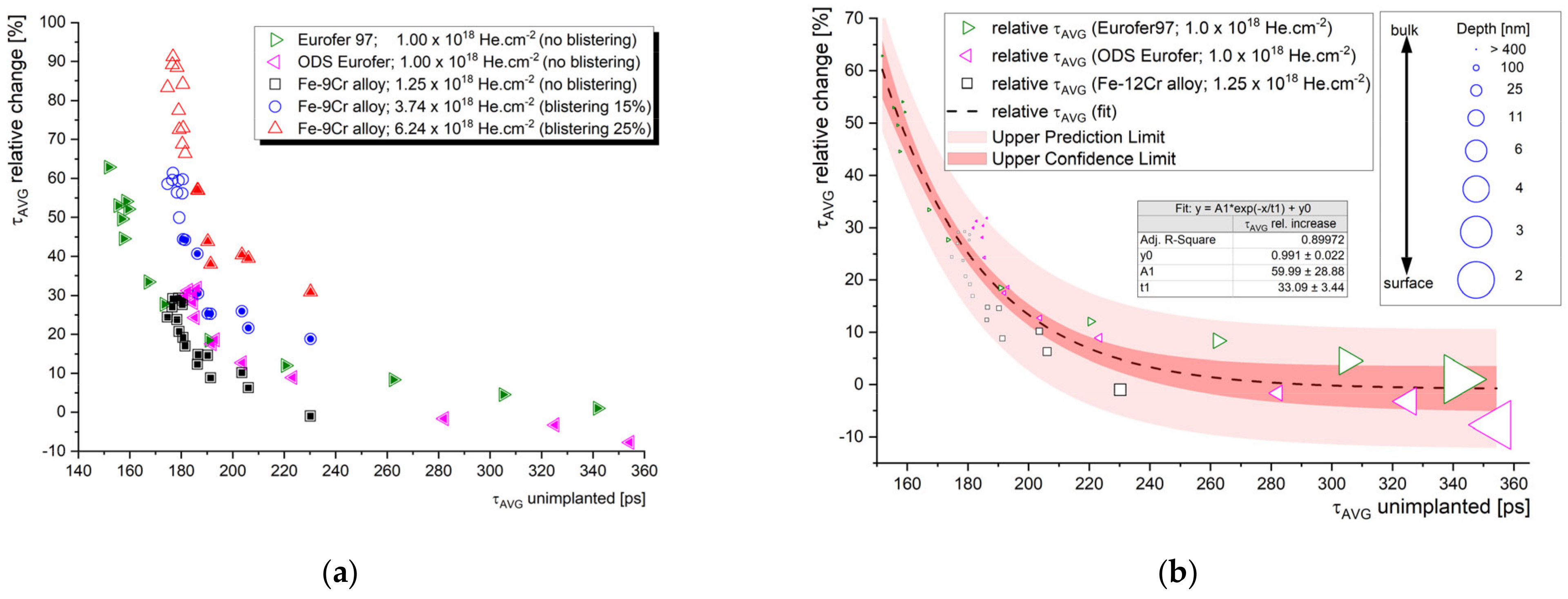
3.3. Helium (Alpha) Irradiation
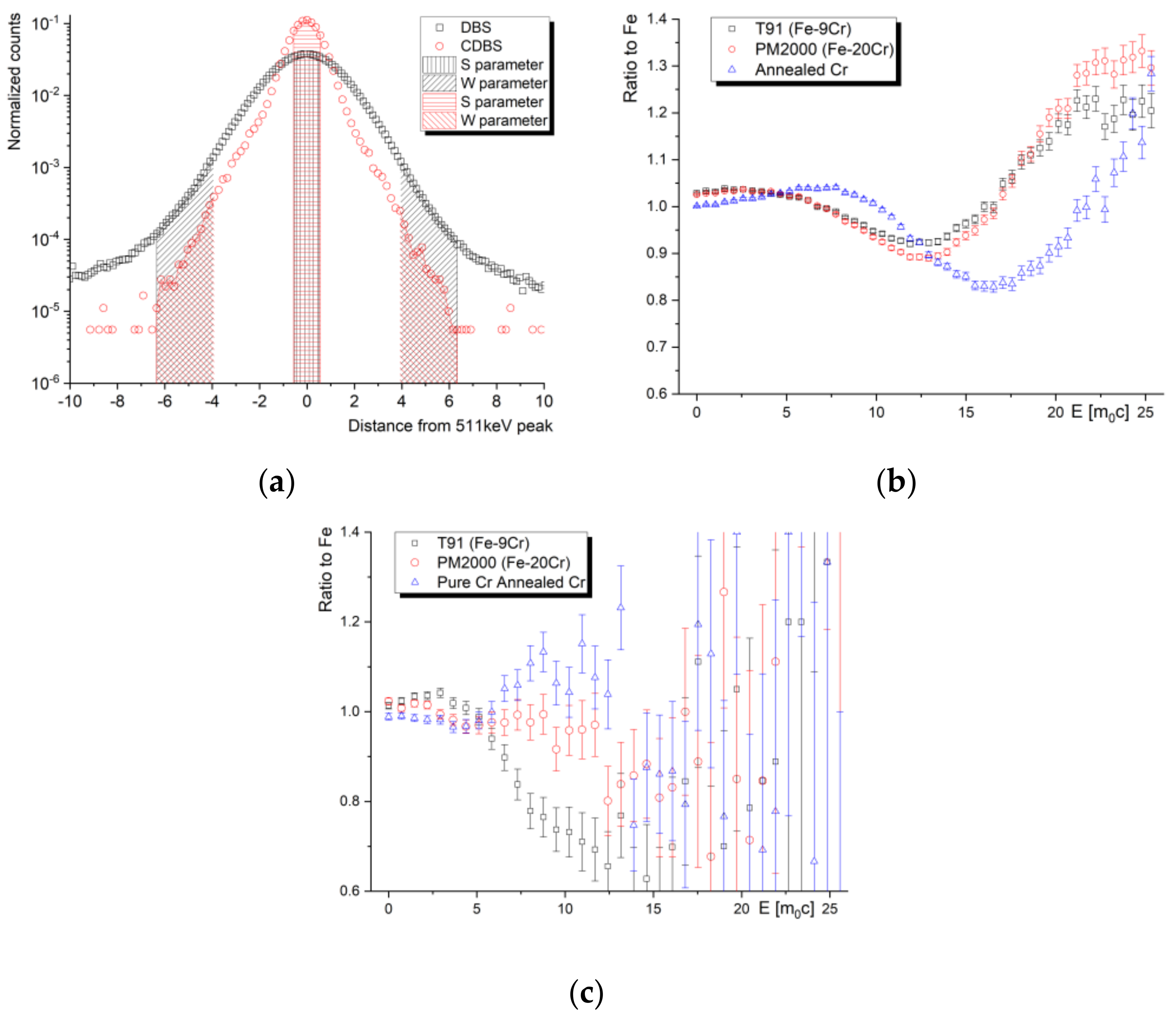
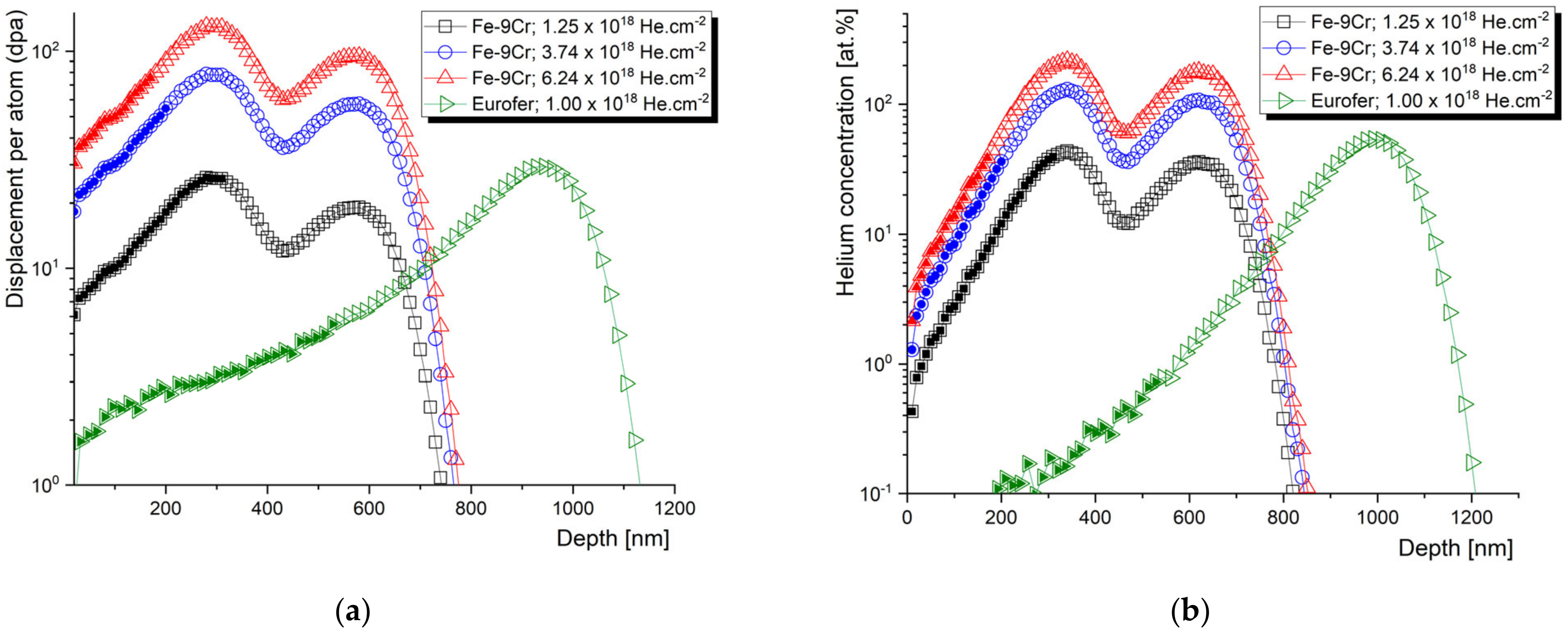
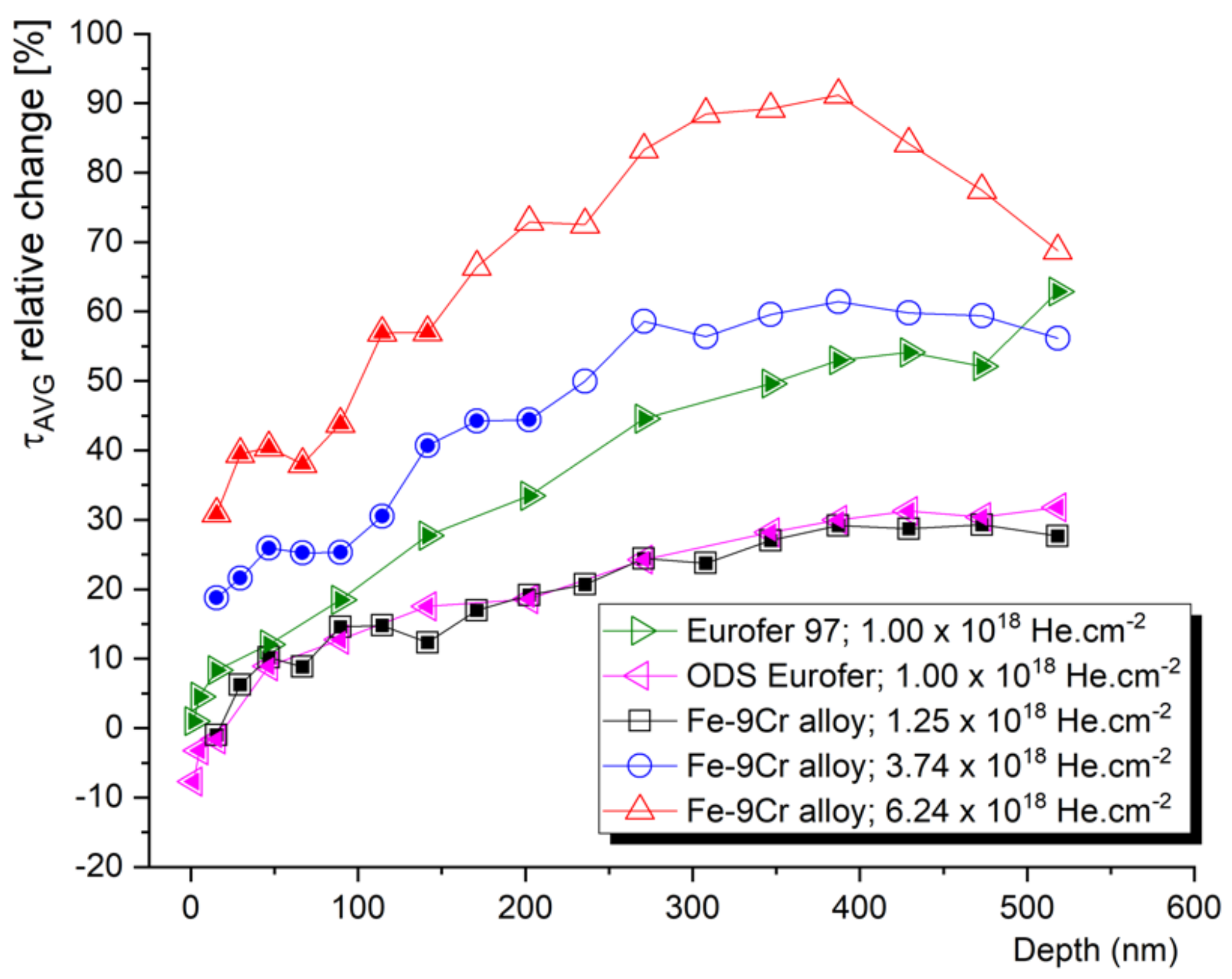
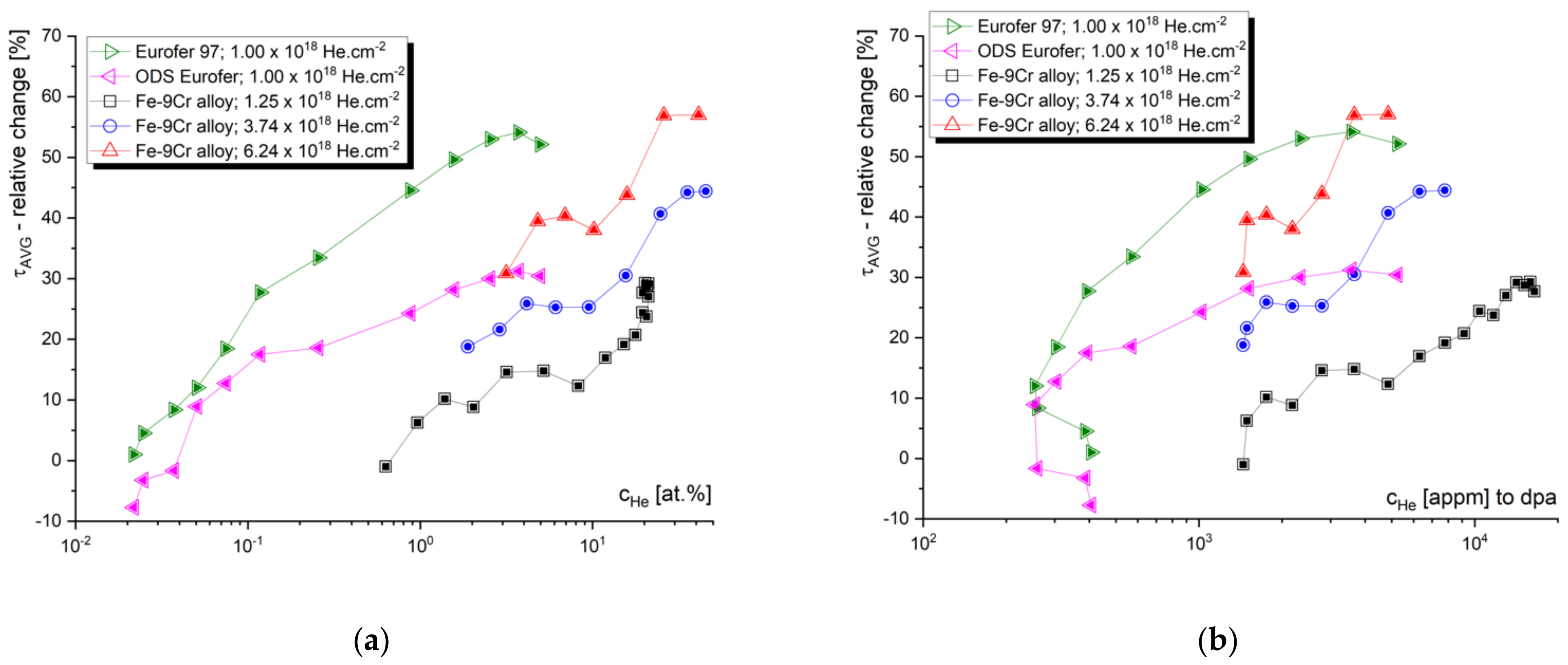
3.4. Synergistic Effects of Helium and Hydrogen on Self-Ion-Induced Damage in Steels
4. Summary
Funding
Conflicts of Interest
References
- Was, G.S. Fundamentals of Radiation Materials Science: Metals and Alloys, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar] [CrossRef]
- Hoffelner, W. Materials for Nuclear Plants: From Safe Design to Residual Life Assessments; Springer-Verlag London Limited: London, UK, 2013. [Google Scholar] [CrossRef]
- Phythian, W.J.; English, C.A. Microstructural evolution in reactor pressure vessel steels. J. Nucl. Mater. 1993, 205, 162–177. [Google Scholar] [CrossRef]
- Hautojärvi, P.; Vehanen, A. Introduction to Positron Annihilation. In Positrons in Solids; Hautojärvi, P., Ed.; Springer: Berlin/Heidelberg, Germany, 1979; pp. 1–23. [Google Scholar] [CrossRef]
- Slugen, V.; Kögel, G.; Sperr, P.; Triftshäuser, W. Positron annihilation studies of neutron irradiated and thermally treated reactor pressure vessel steels. J. Nucl. Mater. 2002, 302, 89–95. [Google Scholar] [CrossRef]
- Davies, L.M. A comparison of Western and Eastern nuclear reactor pressure vessel steels. Int. J. Press. Vessel. Pip. 1999, 76, 163–208. [Google Scholar] [CrossRef]
- Was, G.S.; Petti, D.; Ukai, S.; Zinkle, S. Materials for future nuclear energy systems. J. Nucl. Mater. 2019, 527, 151837. [Google Scholar] [CrossRef]
- Debelle, A.; Barthe, M.F.; Sauvage, T.; Belamhawal, R.; Chelgoum, A.; Desgardin, P.; Labrim, H. Helium behaviour and vacancy defect distribution in helium implanted tungsten. J. Nucl. Mater. 2007, 362, 181–188. [Google Scholar] [CrossRef]
- Lhuillier, P.E.; Belhabib, T.; Desgardin, P.; Courtois, B.; Sauvage, T.; Barthe, M.F.; Thomann, A.L.; Brault, P.; Tessier, Y. Helium retention and early stages of helium-vacancy complexes formation in low energy helium-implanted tungsten. J. Nucl. Mater. 2013, 433, 305–313. [Google Scholar] [CrossRef]
- Slugen, V.; Kuriplach, J.; Ballo, P.; Domonkos, P.; Kögel, G.; Sperr, P.; Egger, W.; Triftshäuser, W.; Domankova, V.M.; Kovac, P.; et al. Positron annihilation Investigations of defects in copper alloys selected for nuclear fusion technology. Fusion Eng. Des. 2004, 70, 141–153. [Google Scholar] [CrossRef]
- Richter, A.; Anwand, W.; Chen, C.L.; Böttger, R. Evaluation of defect formation in helium irradiated Y2O3 doped W-Ti alloys by positron annihilation and nanoindentation. J. Nucl. Mater. 2017, 494, 294–302. [Google Scholar] [CrossRef]
- Labrim, H.; Barthe, M.F.; Desgardin, P.; Sauvage, T.; Blondiaux, G.; Corbel, C.; Piron, J.P. Vacancy defects induced in sintered polished UO 2 disks by helium implantation. Appl. Surf. Sci. 2006, 252, 3256–3261. [Google Scholar] [CrossRef]
- Roudil, D.; Barthe, M.F.; Jégou, C.; Gavazzi, A.; Vella, F. Investigation of defects in actinide-doped UO2 by positron annihilation spectroscopy. J. Nucl. Mater. 2012, 420, 63–68. [Google Scholar] [CrossRef]
- Labrim, H.; Barthe, M.F.; Desgardin, P.; Sauvage, T.; Corbel, C.; Blondiaux, G.; Piron, J.P. Thermal evolution of the vacancy defects distribution in 1 MeV helium implanted sintered UO2. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2007, 261, 883–887. [Google Scholar] [CrossRef]
- Xu, Q.; Fukumoto, K.; Ishi, Y.; Kuriyama, Y.; Uesugi, T.; Sato, K.; Mori, Y.; Yoshiie, T. Irradiation damage from low-dose high-energy protons on mechanical properties and positron annihilation lifetimes of Fe-9Cr alloy. J. Nucl. Mater. 2016, 468, 260–263. [Google Scholar] [CrossRef]
- Parente, P.; Leguey, T.; de Castro, V.; Gigl, T.; Reiner, M.; Hugenschmidt, C.; Pareja, R. Characterization of ion-irradiated ODS Fe-Cr alloys by doppler broadening spectroscopy using a positron beam. J. Nucl. Mater. 2015, 464, 140–146. [Google Scholar] [CrossRef]
- Fluss, M.J.; Hosemann, P.; Marian, J. Charged-Particle Irradiation for Neutron Radiation Damage Studies. Charact. Mater. 2012, 1–17. [Google Scholar] [CrossRef]
- Krsjak, V.; Dai, Y. Microstructural probing of ferritic/martensitic steels using internal transmutation-based positron source. J. Nucl. Mater. 2015, 465, 311–315. [Google Scholar] [CrossRef]
- Dai, Y.; Brun, R.; Gao, W.; Geissmann, K.; Hahl, S.; Hou, H.; Huang, Y.; Linder, H.P.; Long, B.; Spahr, A.; et al. The fourth SINQ Target Irradiation Program, STIP-IV. J. Nucl. Mater. 2012, 431, 2–9. [Google Scholar] [CrossRef]
- Čižek, J.; Bečvář, F.; Procházka, I. Three-detector setup for positron-lifetime spectroscopy of solids containing 60Co radionuclide. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2000, 450, 325–337. [Google Scholar] [CrossRef]
- Petriska, M.; Slugen, V.; Sabelova, V.; Sojak, S.; Veternikova, J. QtCDB2 software for coincidence Doppler broadening measurement system. J. Phys. Conf. Ser. 2013, 443, 012086. [Google Scholar] [CrossRef]
- Saro, M.; Kršjak, V.; Petriska, M.; Slugeň, V. Sodium-22 source contribution determination in positron annihilation measurements using GEANT4. In Proceedings of the Applied Physics of Condensed Matter (APCOM 2019), Strbske Pleso, Slovakia, 29 July 2019. [Google Scholar] [CrossRef]
- Stephanovich, V.A.; Dryzek, J. The exact solution of the diffusion trapping model of defect profiling with variable energy positrons. Phys. Lett. A 2013, 377, 3038–3047. [Google Scholar] [CrossRef][Green Version]
- Logan, J.V.; Short, M.P.; Webster, P.T.; Morath, C.P. More accurate parameterization of positron implantation depth profiles for the sensitivity range of positron-based characterization techniques. J. Appl. Phys. 2020, 128, 045105. [Google Scholar] [CrossRef]
- Dryzek, J.; Singleton, D. Implantation profile and linear absorption coefficients for positrons injected in solids from radioactive sources 22Na and 68Ge {minus 45 degree rule} 68Ga. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2006, 252, 197–204. [Google Scholar] [CrossRef]
- Čížek, J.; Janeček, M.; Vlasák, T.; Smola, B.; Melikhova, O.; Islamgaliev, R.K.; Dobatkin, S.V. The development of vacancies during severe plastic deformation. Mater. Trans. 2019, 60, 1533–1542. [Google Scholar] [CrossRef]
- Dubov, L.Y.; Akmalova, Y.A.; Stepanov, S.V.; Funtikov, Y.V.; Shtotsky, Y.V. Evaluation of positron implantation profiles in various materials for22Na source. Acta Phys. Pol. A 2017, 132, 1482–1485. [Google Scholar] [CrossRef]
- Dressler, R.; Ayranov, M.; Bemmerer, D.; Bunka, M.; Dai, Y.; Lederer, C.; Fallis, J.; Murphy, A.S.; Pignatari, M.; Schumann, D.; et al. Mn samples for nuclear astrophysics: The needs, the possibilities and the sources. J. Phys. G Nucl. Part. Phys. 2012, 39, 105201. [Google Scholar] [CrossRef]
- Dryzek, J.; Horodek, P. GEANT4 simulation of slow positron beam implantation profiles. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2008, 266, 4000–4009. [Google Scholar] [CrossRef]
- Saro, M.; Kršjak, V.; Lauko, R.; Slugeň, V. Application of Na-22 positron source to the investigation of ion-implanted iron samples. In Proceedings of the 18th International Conference on Positron Annihilation (ICPA-18), Orlando, FL, USA, 19–24 August 2018. [Google Scholar] [CrossRef]
- Everaerts, J.; Salvati, E.; Korsunsky, A.M. Nanoscale Depth Profiling of Residual Stresses Due to Fine Surface Finishing. Adv. Mater. Interfaces 2019, 6, 1900947. [Google Scholar] [CrossRef]
- Horodek, P.; Dryzek, J. GEANT4 simulation of implantation profiles for positrons injected in solids Na and 68Ge/68Ga. Nukleonika 2010, 55, 21–23. [Google Scholar]
- Hugenschmidt, C.; Piochacz, C. NEPOMUC: Neutron induced positron source Munich. J. Large-Scale Res. Facil. JLSRF 2015, 1, 22. [Google Scholar] [CrossRef]
- Schultz, P.J.; Lynn, K.G. Interaction of positron beams with surfaces, thin films, and interfaces. Rev. Mod. Phys. 1988, 60, 701. [Google Scholar] [CrossRef]
- Weisstein, W.E. Gaussian Function from MathWorld-A Wolfram Web Resource; CRC Press: Boca Raton, FL, USA, 1999; Available online: https://mathworld.wolfram.com/GaussianFunction.html (accessed on 17 October 2021).
- Čížek, J. Characterization of lattice defects in metallic materials by positron annihilation spectroscopy: A review. J. Mater. Sci. Technol. 2018, 34, 577–598. [Google Scholar] [CrossRef]
- Krsjak, V.; Kuriplach, J.; Shen, T.; Sabelova, V.; Sato, K.; Dai, Y. Helium behavior in ferritic/martensitic steels irradiated in spallation target. J. Nucl. Mater. 2015, 456, 382–388. [Google Scholar] [CrossRef]
- Bečvář, F.; Čížek, J.; Procházka, I. Performance of a high-resolution digital positron-lifetime spectrometer. Acta Phys. Pol. A 2008, 1279–1284. [Google Scholar] [CrossRef]
- Farrell, K.; Maziasz, P.J.; Lee, E.H.; Mansur, L.K. Modification of radiation damage microstructure by helium. Radiat. Eff. 1983, 78, 277–295. [Google Scholar] [CrossRef]
- Eldrup, M.; Jensen, K.O. Positron Trapping Rates into Cavities in Al: Temperature and Size Effects. Phys. Status Solidi 1987, 102, 145–152. [Google Scholar] [CrossRef]
- Van Veen, A.; Schut, H.; de Vries, J.; Hakvoort, R.A.; Ijpma, M.R. Analysis of positron profiling data by means of VEPFIT. In Proceedings of the 4th International Workshop on: Slow-Positron Beam Techniques for Solids and Surfaces, London, ON, Canada, 3–6 July 1990; pp. 171–198. [Google Scholar] [CrossRef]
- Krsjak, V.; Hruska, P.; Degmova, J.; Sojak, S.; Noga, P.; Shen, T.; Sabelova, V.; Egger, W.; Slugen, V. A new approach to near-surface positron annihilation analysis of ion irradiated ferritic alloys. Nanoscale Adv. 2021. [Google Scholar] [CrossRef]
- Ziegler, J.F.; Ziegler, M.D.; Biersack, J.P. SRIM-The stopping and range of ions in matter (2010). Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2010, 268, 1818–1823. [Google Scholar] [CrossRef]
- Kaganov, M.I.; Lifshitz, I.M.; Tanatarov, L.V. Relaxation between electrons and the crystalline lattice. Sov. Phys. JETP 1957, 4, 173–178. [Google Scholar]
- Wang, Z.; Jin, Y.; Hou, M.; Jin, G. Modeling of damage creation in metallic materials under swift heavy ion irradiations. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2000, 169, 98–105. [Google Scholar] [CrossRef]
- Rutherford, A.M.; Duffy, D.M. Modelling swift heavy ion irradiation in iron. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2009, 267. [Google Scholar] [CrossRef]
- Abhaya, S.; Rajaraman, R.; Sarguna, R.M.; Parida, P.K.; David, C.; Amarendra, G. Defect microstructure in high temperature Ni+ implanted FeCrCoNi-a positron beam study. J. Alloys Compd. 2019, 806, 780–787. [Google Scholar] [CrossRef]
- Agarwal, S.; Liedke, M.O.; Jones, A.C.L.; Reed, E.; Kohnert, A.A.; Uberuaga, B.P.; Wang, Y.Q.; Cooper, J.; Kaoumi, D.; Li, N.; et al. A new mechanism for void-cascade interaction from nondestructive depth-resolved atomic-scale measurements of ion irradiation-induced defects in Fe. Sci. Adv. 2020, 6, eaba8437. [Google Scholar] [CrossRef]
- He, C.W.; Barthe, M.F.; Desgardin, P.; Akhmadaliev, S.; Behar, M.; Jomard, F. Positron studies of interaction between yttrium atoms and vacancies in bcc iron with relevance for ODS nanoparticles formation. J. Nucl. Mater. 2014, 455, 398–401. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, Z.; Cui, M.; Li, B.; Gao, X.; Sun, J.; Yao, C.; Wei, K.; Shen, T.; Pang, L.; et al. Temperature dependent surface modification of T91 steel under 3.25 MeV Fe-ion implantation. Appl. Surf. Sci. 2015, 326, 1–6. [Google Scholar] [CrossRef]
- Zhu, H.; Wang, Z.; Gao, X.; Cui, M.; Li, B.; Sun, J.; Yao, C.; Wei, K.; Shen, T.; Pang, L.; et al. Positron annihilation Doppler broadening spectroscopy study on Fe-ion irradiated NHS steel. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2015, 344, 5–10. [Google Scholar] [CrossRef]
- Pecko, S.; Heintze, C.; Bergner, F.; Anwand, W.; Slugeň, V. Fe2+ ion irradiated JRQ steel investigated by nanoindentation and slow-positron Doppler broadening spectroscopy. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2018, 415, 1–8. [Google Scholar] [CrossRef]
- Echenique, P.M.; Flores, F.; Ritchie, R.H. Dynamic screening: Capture and loss processes of protons moving in solids. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 1988, 33, 91–97. [Google Scholar] [CrossRef]
- Astrelin, V.T.; Burdakov, A.V.; Bykov, P.V.; Ivanov, I.A.; Ivanov, A.A.; Jongen, Y.; Konstantinov, S.G.; Kudryavtsev, A.M.; Kuklin, K.N.; Mekler, K.I.; et al. Blistering of the selected materials irradiated by intense 200 keV proton beam. J. Nucl. Mater. 2010, 396, 43–48. [Google Scholar] [CrossRef]
- Troev, T.; Markovski, A.; Peneva, S.; Yoshiie, T. Positron lifetime calculations of defects in chromium containing hydrogen or helium. J. Nucl. Mater. 2006, 359, 93–101. [Google Scholar] [CrossRef]
- Shivachev, B.L.; Troev, T.; Yoshiie, T. Positron lifetime computations of defects in nickel containing hydrogen or helium. J. Nucl. Mater. 2002, 306, 105–111. [Google Scholar] [CrossRef]
- Troev, T.; Popov, E.; Staikov, P.; Nankov, N. Positron lifetime studies of defects in alpha-Fe containing helium. Phys. Status Solidi C 2009, 6, 2373–2375. [Google Scholar] [CrossRef]
- Horodek, P.; Kulik, M. Application of positron beam for the long range effect studies in proton implanted iron. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2019, 443, 84–89. [Google Scholar] [CrossRef]
- Zhang, W.; Shen, Z.; Tang, R.; Jin, S.; Song, Y.; Long, Y.; Wei, Y.; Zhou, X.; Chen, C.; Guo, L. Proton-irradiation induced defects in modified 310S steels characterized with positron annihilation spectroscopy and transmission electron microscopy. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2018, 427, 1–8. [Google Scholar] [CrossRef]
- Pecko, S.; Sojak, S.; Slugeň, V. Comparative study of irradiated and hydrogen implantation damaged German RPV steels from PAS point of view. Appl. Surf. Sci. 2014, 312, 172–175. [Google Scholar] [CrossRef]
- Liu, X.; Wang, R.; Jiang, J.; Wu, Y.; Zhang, C.; Ren, A.; Xu, C.; Qian, W. Slow positron beam and nanoindentation study of irradiation-related defects in reactor vessel steels. J. Nucl. Mater. 2014, 451, 249–254. [Google Scholar] [CrossRef]
- Zhao, D.; Li, S.; Wang, X.; Wang, Y.; Liu, F.; Cao, X. Proton irradiation induced defects in T92 steels: An investigation by TEM and positron annihilation spectroscopy. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2019, 442, 59–66. [Google Scholar] [CrossRef]
- Ma, Y.; Ran, G.; Chen, N.; Lei, P.; Shen, Q. Investigation of mechanical properties and proton irradiation behaviors of SA-738 Gr.B steel used as reactor containment. Nucl. Mater. Energy 2016, 8, 18–22. [Google Scholar] [CrossRef]
- Sato, K.; Ikemura, K.; Krsjak, V.; Vieh, C.; Brun, R.; Xu, Q.; Yoshiie, T.; Dai, Y. Defect structures of F82H irradiated at SINQ using positron annihilation spectroscopy. J. Nucl. Mater. 2016, 468, 281–284. [Google Scholar] [CrossRef]
- Sato, K.; Xu, Q.; Yoshiie, T.; Dai, Y.; Kikuchi, K. Positron annihilation lifetime measurements of austenitic stainless and ferritic/martensitic steels irradiated in the SINQ target irradiation program. J. Nucl. Mater. 2012, 431, 52–56. [Google Scholar] [CrossRef]
- Das, S. Recent advances in characterising irradiation damage in tungsten for fusion power. SN Appl. Sci. 2019, 1, 1–20. [Google Scholar] [CrossRef]
- Dai, Y.; Odette, G.R.; Yamamoto, T. The Effects of Helium in Irradiated Structural Alloys; Elsevier Inc.: Amsterdam, The Netherlands, 2012. [Google Scholar] [CrossRef]
- Garner, F.A.; Oliver, B.M.; Greenwood, L.R.; James, M.R.; Ferguson, P.D.; Maloy, S.A.; Sommer, W.F. Determination of helium and hydrogen yield from measurements on pure metals and alloys irradiated by mixed high energy proton and spallation neutron spectra in LANSCE. J. Nucl. Mater. 2001, 296, 66–82. [Google Scholar] [CrossRef]
- Krsjak, V.; Degmova, J.; Sojak, S.; Slugen, V. Effects of displacement damage and helium production rates on the nucleation and growth of helium bubbles–Positron annihilation spectroscopy aspects. J. Nucl. Mater. 2018, 499, 38–46. [Google Scholar] [CrossRef]
- Sabelova, V.; Krsjak, V.; Kuriplach, J.; Petriska, M.; Slugen, V.; Veternikova, J. Simeg, Characterization of helium implanted Fe-Cr alloys by means of positron annihilation methods. J. Nucl. Mater. 2014, 450, 54–58. [Google Scholar] [CrossRef]
- Sabelova, V.; Krsjak, V.; Kuriplach, J.; Dai, Y.; Slugen, V. Coincidence Doppler broadening study of Eurofer 97 irradiated in spallation environment. J. Nucl. Mater. 2015, 458, 350–354. [Google Scholar] [CrossRef]
- Sharma, S.K.; Saini, S.; Srivastava, A.P.; Pujari, P.K. Identification of chemical surrounding and type of vacancy defects in the damaged region of ion irradiated Ni–Cr alloy. Materialia 2021, 15, 100999. [Google Scholar] [CrossRef]
- Zhu, T.; Jin, S.; Zhang, P.; Song, L.; Lian, X.; Fan, P.; Zhang, Q.; Yuan, D.; Wu, H.; Yu, R.; et al. Characterization of helium-vacancy complexes in He-ions implanted Fe9Cr by using positron annihilation spectroscopy. J. Nucl. Mater. 2018, 505, 69–72. [Google Scholar] [CrossRef]
- Degmová, J.; Kršjak, V.; Shen, T.; Veterniková, J.Š.; Gatciová, A.; Sojak, S.; Hruška, P. Near-surface investigation of positron diffusion length in helium-implanted Fe9Cr and its ODS variant. Appl. Surf. Sci. 2021, 538, 148004. [Google Scholar] [CrossRef]
- Carvalho, I.; Schut, H.; Fedorov, A.; Luzginova, N.; Desgardin, P.; Sietsma, J. Helium implanted RAFM steels studied by positron beam Doppler Broadening and Thermal Desorption Spectroscopy. J. Phys. Conf. Ser. 2013, 443, 12034. [Google Scholar] [CrossRef]
- Xin, Y.; Ju, X.; Qiu, J.; Guo, L.; Chen, J.; Yang, Z.; Zhang, P.; Cao, X.; Wang, B. Vacancy-type defects and hardness of helium implanted CLAM steel studied by positron-annihilation spectroscopy and nano-indentation technique. Fusion Eng. Des. 2012, 87, 432–436. [Google Scholar] [CrossRef]
- Song, L.; Wang, B.; Zhu, T.; Gong, Y.; Xu, Q.; Guo, L.; Jin, S.; Zhang, P.; Song, Y.; Cao, X. Evolution of defects with isochronal annealing in helium-irradiated 316L studied by slow positron beam. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 2020, 467, 80–85. [Google Scholar] [CrossRef]
- Lu, E.; Cao, X.; Jin, S.; Zhang, P.; Zhang, C.; Yang, J.; Wu, Y.; Guo, L.; Wang, B. Investigation of vacancy-type defects in helium irradiated FeCrNi alloy by slow positron beam. J. Nucl. Mater. 2015, 458, 240–244. [Google Scholar] [CrossRef]
- Xin, Y.; Ju, X.; Qiu, J.; Guo, L.; Li, T.; Luo, F.; Zhang, P.; Cao, X.; Wang, B. Vacancy-type defect production in CLAM steel after the co-implantation of He and H ion beams studied by positron-annihilation spectroscopy. J. Nucl. Mater. 2013, 432, 120–126. [Google Scholar] [CrossRef]
- Kögler, R.; Anwand, W.; Richter, A.; Butterling, M.; Ou, X.; Wagner, A.; Chen, C.L. Nanocavity formation and hardness increase by dual ion beam irradiation of oxide dispersion strengthened FeCrAl alloy. J. Nucl. Mater. 2012, 427, 133–139. [Google Scholar] [CrossRef]
- Jin, P.; Shen, T.; Cui, M.; Zhu, Y.; Li, B.; Zhang, T.; Li, J.; Jin, S.; Lu, E.; Cao, X.; et al. Study on vacancy-type defects in SIMP steel induced by separate and sequential H and He ion implantation. J. Nucl. Mater. 2019, 520, 131–139. [Google Scholar] [CrossRef]
- Zhu, T.; Wang, B.; Song, L.; Liu, X.; Song, Y.; Liu, Y.; Zhang, P.; Cao, X.; Xu, Q. Sensitivity of positrons at hydrogen storage sites in FeCr alloy containing vacancy and helium atom. Int. J. Hydrogen Energy 2020, 45, 15571–15577. [Google Scholar] [CrossRef]
- Shi, J.J.; Yang, W.; Zhu, Z.J.; Liu, X.B.; Jiang, J.; Wang, R.S.; Wu, Y.C. Slow positron beam study of highly irradiated RPV steel under proton and ion impact. Radiat. Phys. Chem. 2019, 156, 199–204. [Google Scholar] [CrossRef]
- Jiang, J.; Wu, Y.C.; Liu, X.B.; Wang, R.S.; Nagai, Y.; Inoue, K.; Shimizu, Y.; Toyama, T. Microstructural evolution of RPV steels under proton and ion irradiation studied by positron annihilation spectroscopy. J. Nucl. Mater. 2015, 458, 326–334. [Google Scholar] [CrossRef]
- Ramachandran, R.; Julie, S.; Rajaraman, R.; Govindaraj, R.; David, C.; Amarendra, G. High-temperature radiation damage studies of Reduced Activation Ferritic/Martensitic (RAFM) steel at fusion relevant He/dpa ratio using positron beam based Doppler broadening spectroscopy. J. Nucl. Mater. 2021, 544, 18–22. [Google Scholar] [CrossRef]
- Ramachandran, R.; David, C.; Magudapathy, P.; Rajaraman, R.; Govindaraj, R.; Amarendra, G. Study of defect complexes and their evolution with temperature in hydrogen and helium irradiated RAFM steel using positron annihilation spectroscopy. Fusion Eng. Des. 2019, 142, 55–62. [Google Scholar] [CrossRef]
- Li, L.; Jin, S.; Zhang, P.; Wang, D.; Cao, X.; Guo, L.; Xu, Q.; Li, J.; Zhang, T.; Li, L.; et al. Effect of interaction between H and He on micro-defects in Fe9Cr alloy investigated by slow positron beam. J. Nucl. Mater. 2019, 526, 151748. [Google Scholar] [CrossRef]
- Šćepanović, M.; de Castro, V.; García-Cortés, I.; Sánchez, F.J.; Gigl, T.; Hugenschmidt, C.; Leguey, T. Characterisation of open volume defects in Fe–Cr and ODS Fe–Cr alloys after He+ and Fe+ ion irradiations. J. Nucl. Mater. 2020, 538, 152230. [Google Scholar] [CrossRef]
- García-Cortés, I.; Leguey, T.; Sánchez, F.J.; Maira, A.; Moroño, A.; Muñoz, P.; Scepanovic, M.; Marco, J.F. Study of damage in binary Fe 85 Cr 15 alloys irradiated by ions and the effect of an external magnetic field during irradiation. J. Nucl. Mater. 2019, 517, 138–147. [Google Scholar] [CrossRef]
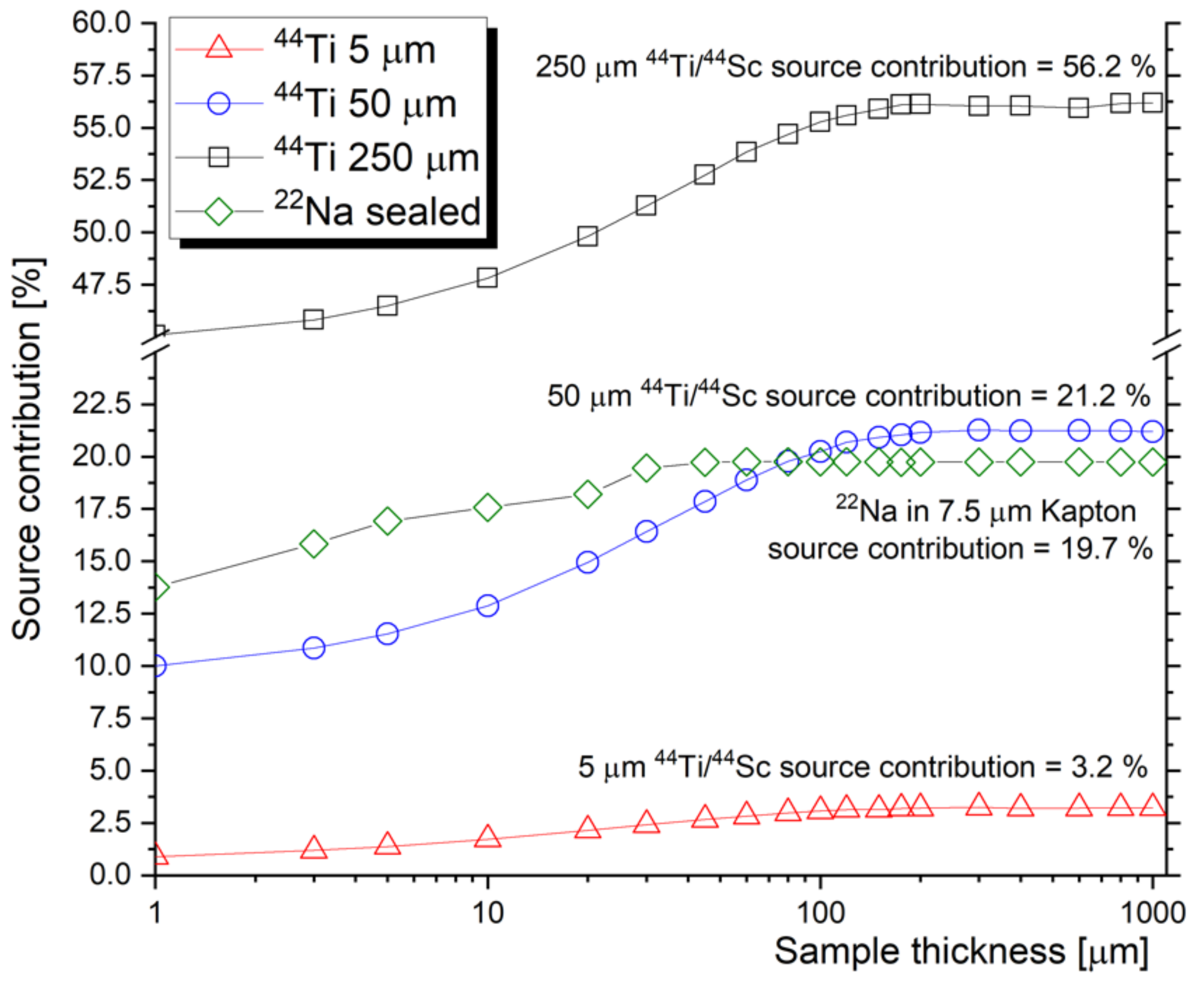
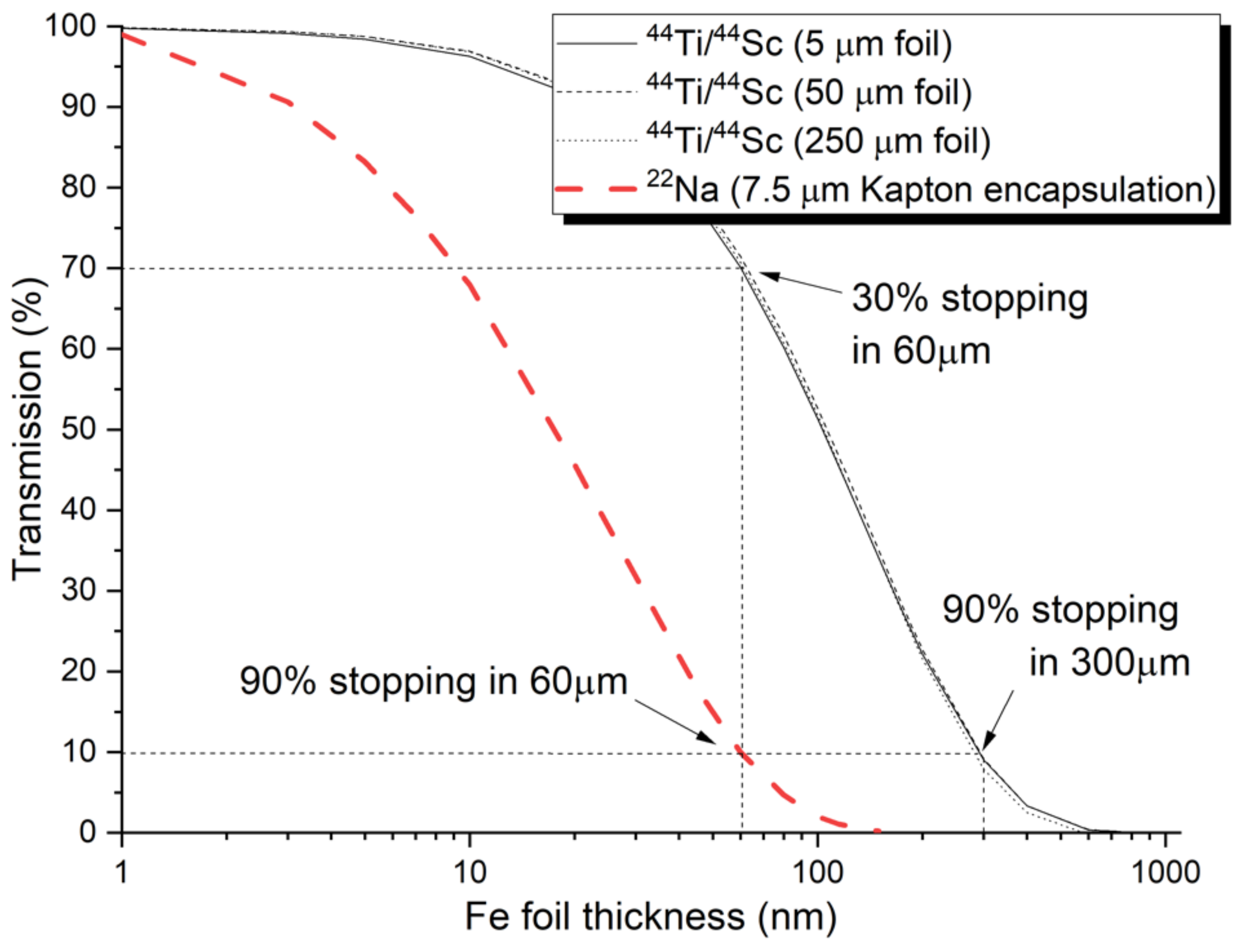

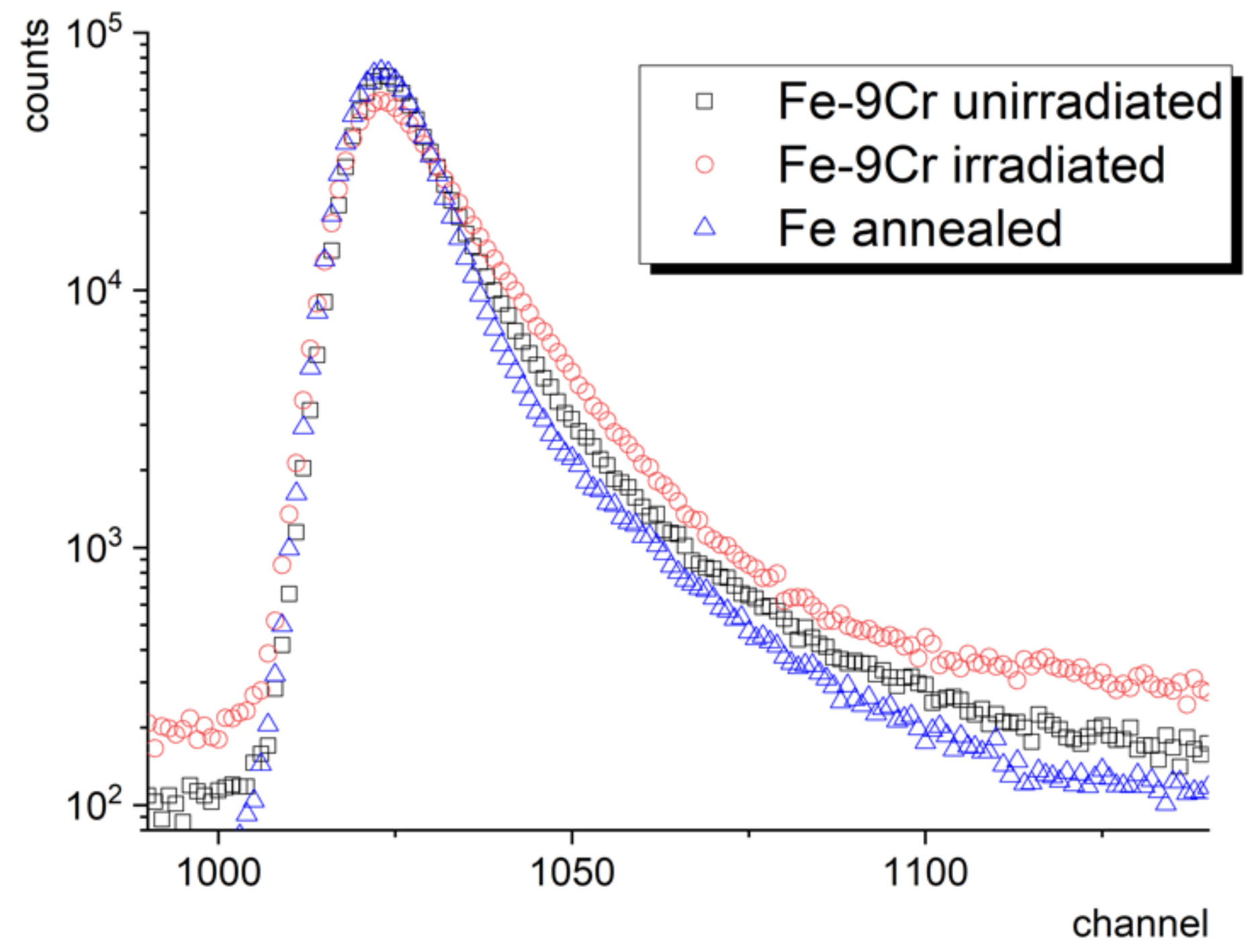
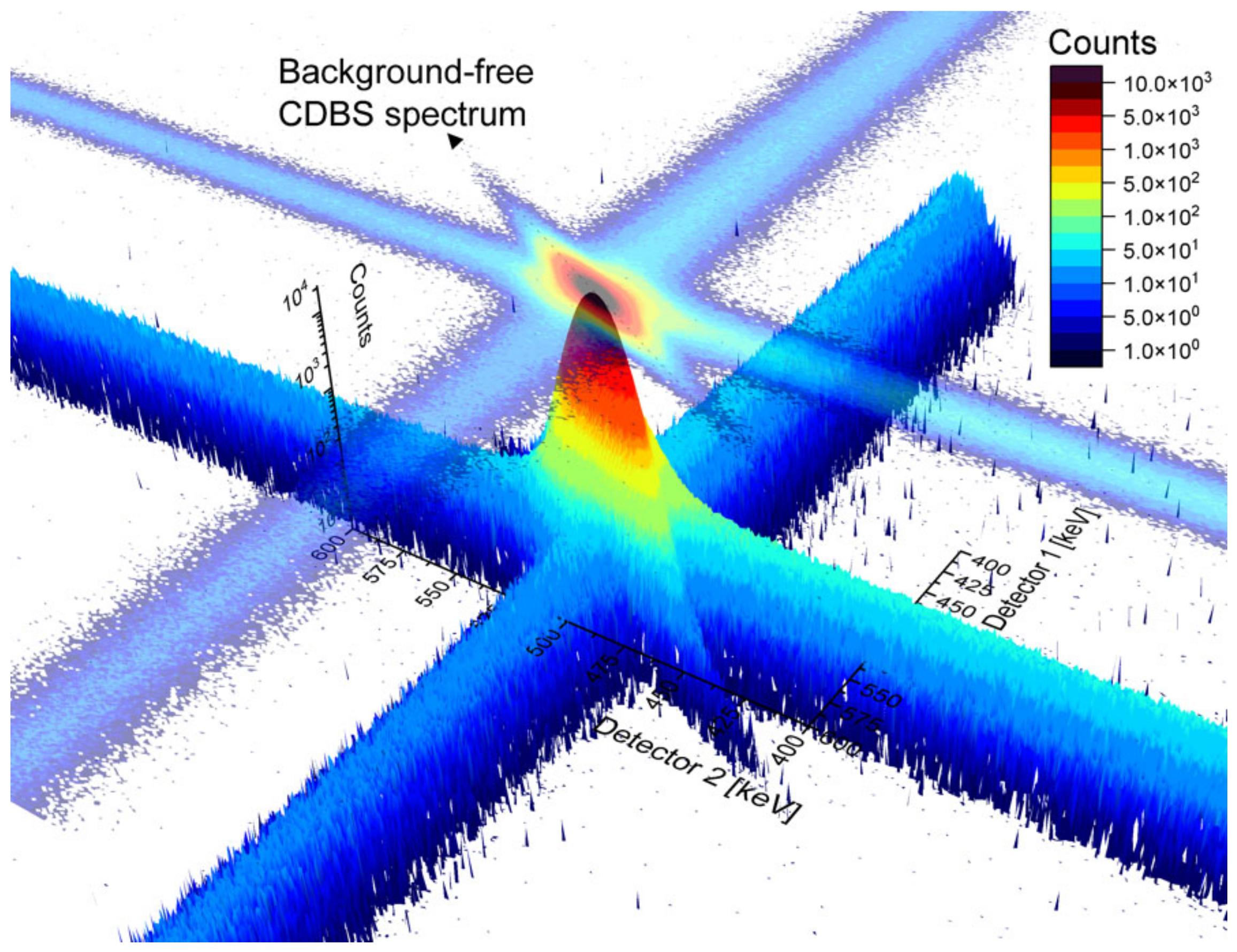
| Material | Ion (E) | T [°C] | Fluence(s) [cm−2] | Techniques | Ref. |
|---|---|---|---|---|---|
| FeCrCoNi (HEA) | Ni+ (1.5 MeV) | 500 | 5 × 1016 | DBS (SPB 0.25–21.5 keV) + VEPFIT analysis; GIXRD; EBSD | [47] |
| Fe film | Fe+ (2 MeV) | RT | 5.65 × 1014 | DBS (SPB 0.05–16 keV) + VEPFIT analysis; LT (SPB 0.5–16 keV) | [48] |
| BCC Fe | Y+ (1.2 MeV) | RT | 1.0 × 1014 2.0 × 1015 3.0 × 1015 | DBS (SPB 0.5–25 keV) + VEPFIT analysis, SIMS | [49] |
| Fe–9%Cr (T91 steel) | Fe+ (3.25 MeV) | RT; 300; 450 | 1.7 × 1016 | DBS (SPB 0.5–20 keV) + VEPFIT analysis; nanoindentation | [50] |
| High Si Fe–11Cr | Fe+ (3.25 MeV) | RT, 450 | 4.3 × 1015; 1.7 × 1016 | DBS (SPB 0.18–20.18 keV) + VEPFIT analysis | [51] |
| RPV steel (JRQ) | Fe2+ (5 MeV) | 300 | 2.66 × 1013 - 2.66 × 1015 | DBS (SPB 30 eV–36 keV); Nanoindentation | [52] |
| Material | Ion (E) | T [°C] | Fluence(s) [cm−2] | Techniques | Ref. |
|---|---|---|---|---|---|
| Fe–9Cr alloy | H+ (11 MeV); H+ (150 MeV), incl. H (1100 appm/dpa) and He (120 appm/dpa) | RT (150 MeV); 300 (11 MeV) | 4.5 × 1015 (150 MeV); 6.0 × 1016 (11 MeV); | PALS (22Na); Tensile | [15] |
| Polycrystalline Fe | H+ (73 keV; 173 keV; multi-energy 50–173 keV) | RT | 3 × 1015; 1 × 1016; 3 × 1016; | DBS (SPB 0.1–36 keV) + VEPFIT analysis; Elastic Recoil Detection (ERD) | [58] |
| Modified 310S steel | H+ (50 keV); | 290 | 4.0 × 1016; 1.2 × 1017; | DBS (SPB ~ 0.2–20 keV); TEM | [59] |
| German RPV weld metals | H+ (100 keV) | <100 | 6.2 × 1017; 5.1 × 1018; 2.0 × 1019; | PALS (22Na) | [60] |
| Chinese RPV steel (A508-3) | H+ (240 keV) | <100 | 2.5 × 1016; 5.5 × 1016; 1.1 × 1017; 2.5 × 1017; | DBS (SPB 0.25–26 keV); Nanoindentation | [61] |
| Fe–9%Cr steel (T92) | H+ (250 keV) | RT | 0.01 dpa; 0.05 dpa; 0.2 dpa | DBS (SPB 1–25 keV); TEM; Nanoindentation | [62] |
| SA-738Gr.B steel (AP1000 reactor containment steel) | H+ (400 keV) | 150 | 1.07 × 1017; 2.68 × 1017; 5.37 × 1017; | PALS (22Na);TEM | [63] |
| Material | Ion (E) | T [°C] | Fluence(s) [cm−2] | Techniques | Ref. |
|---|---|---|---|---|---|
| Fe–12%Cr alloy | He (250 keV) | <80 | 1.25 × 1018 | LT (SPB 1 to 18 keV) DBS (SPB 0.5 to 38 keV) | [70] |
| Ni–40% Cr alloy | He (65 keV) | - | 3 × 1016; 2 × 1017; 7 × 10 17 | DBS (SPB 0.2–20 keV) + VEPFIT analysis; Theoretical calculations | [72] |
| Fe–9%Cr alloy | He (100 keV) | 250; 350; 450; 600 | 5 × 1016 | PALS (22Na); DBS (SPB ~0.1 to ~20 keV); CDBS (SPB 8 keV) | [73] |
| Fe–9%Cr–1%W steel (Eurofer97) + its ODS variant | He (500 keV) | RT | 1 × 1018 | DBS (SPB 0.5 to 36 keV) | [74] |
| Fe–9%Cr–1%W steel (Eurofer97) | He (3 keV) | 100; 250 | 3 × 1019 (100 °C) 1–2 × 1019 (250 °C) | DBS (SPB 0.1 to 25 keV); TDS | [75] |
| Fe–9%Cr steel (CLAM) | He (140 keV) | RT–600 | 1 × 1016 | DBS (SPB ~0.1 to ~21 keV) + VEPFIT analysis; Nanoindentation | [76] |
| 316L stainless steels | He (50 keV) | RT (post-irr. anneal. 100–1000) | 1 × 1016 | DBS (SPB 0.18 to 20 keV) | [77] |
| FeCrNi alloy 316L stainless steels | He (140 keV) | RT; 300 | 1 × 1016 (RT); 5 × 1016 (RT; 300 °C) | DBS (SPB 0.18 to 20 keV) | [78] |
| Material | Ion (E) | T [°C] | Fluence(s) [cm−2] | Techniques | Ref. |
|---|---|---|---|---|---|
| Fe–9%Cr steel (CLAM) | H (80 keV,); He (140 keV) | RT | H: 5 × 1015–5 × 1016 He: 1 × 1015–1 × 1016 | DBS (SPB 0.1–20 keV) + VEPFIT analysis | [79] |
| ODS FeCrAl (PM2000) | Fe (2.5 MeV) He (350 keV) | RT, 300 | 2.74 × 1015/He 2.94 × 1016/Fe | LT (22Na) DBS, CDBS (SPB 30 eV–35 keV) + VEPFIT analysis Nanoindentation | [80] |
| Fe–9%Cr steel (SIMP) | H (80 keV, 260 keV); He (130 keV; 500 keV) | RT | H: 2.78 × 1015–1 × 1018 He: 7.14 × 1015–1.8 × 1016 | DBS (SPB 0.18–20 keV) TEM | [81] |
| Fe–9%Cr steel | H (80 keV,); He (140 keV) | RT | H: 5 × 1016 He: 1 × 1016 | LT (22Na); DBS (SPB 0.18–20 keV) + theoretical calculations | [82] |
| RPV steel (A508-3) | Fe (3 MeV) H (240 keV) | 100 | H: 2.5 × 1016–1.13 × 1018 Fe: 4.55 × 1013–2.06 × 1015 | DBS (SPB 0.5–26 keV) | [83] |
| RPV steel (A508-3) | Fe (3 MeV) H (110 + 240 keV) | 100 | 0.05–1.0 dpa; | DBS (SPB 0.5–26 keV) LT (SPB 14 keV); APT; TEM; Nanoindentation | [84] |
| Fe–9%Cr steel (INRAFM) | Fe (1.1 MeV) He (50 + 90 + 130 keV) | 200, 400, 500 | Fe (70 dpa) He (700 appm) | DBS (SPB 0.2–22 keV) + VEPFIT analysis | [85] |
| Fe–9%Cr steel (INRAFM) | H (80 keV) He (130 keV) | RT; Post-irradiation annealing up to 700 | H (1500 appm); He (450 appm) | DBS (SPB 0.25–22 keV) incl. VEPFIT analysis | [86] |
| Fe9Cr alloy | Ni (1 MeV); H (50 keV); He (80 keV) | RT (Ni); RT (Ni + H); RT (Ni) + 450 (H); RT (Ni) +450 (H) 450 (He) | Fe: 3.4 × 1013 H: 1 × 1016 He: 2 × 1015 | DBS (SPB 0.18 keV–20.18 keV) | [87] |
| Fe14Cr alloy; Fe14Cr ODS | Fe (1 MeV); He (50 keV); | RT (Fe) 400–450 (He) | Fe: 6.5 × 1015 He: 6.5 × 1015; 1 × 1016 | DBS (SPB ~0.1 keV–30 keV) CDBS (SPB 7 keV; 18 keV) | [88] |
| Fe15Cr alloy | He (45 keV) Fe (1 MeV) | RT | He: 4.0 × 1016 Fe: 8.24 × 1015; 1.12 × 1016 | DBS, CDBS (SPB ~0.2 keV–30 keV) | [89] |
| Fe12Cr ODS12Cr ODS14Cr ODS14CrWTi | Fe (10 MeV); Fe (4 MeV)/ He (1.6 MeV)/ H (500 keV) | RT (Single beam); 600 (Triple beam) | Fe: 5 × 1015; Fe: 1.49 × 1016/He 1.4 × 1015/H 3.55 × 1015 | DBS (SPB 1–30 keV) CDBS (SPB 30 keV) | [16] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krsjak, V.; Degmova, J.; Noga, P.; Petriska, M.; Sojak, S.; Saro, M.; Neuhold, I.; Slugen, V. Application of Positron Annihilation Spectroscopy in Accelerator-Based Irradiation Experiments. Materials 2021, 14, 6238. https://doi.org/10.3390/ma14216238
Krsjak V, Degmova J, Noga P, Petriska M, Sojak S, Saro M, Neuhold I, Slugen V. Application of Positron Annihilation Spectroscopy in Accelerator-Based Irradiation Experiments. Materials. 2021; 14(21):6238. https://doi.org/10.3390/ma14216238
Chicago/Turabian StyleKrsjak, Vladimir, Jarmila Degmova, Pavol Noga, Martin Petriska, Stanislav Sojak, Matus Saro, Igor Neuhold, and Vladimir Slugen. 2021. "Application of Positron Annihilation Spectroscopy in Accelerator-Based Irradiation Experiments" Materials 14, no. 21: 6238. https://doi.org/10.3390/ma14216238
APA StyleKrsjak, V., Degmova, J., Noga, P., Petriska, M., Sojak, S., Saro, M., Neuhold, I., & Slugen, V. (2021). Application of Positron Annihilation Spectroscopy in Accelerator-Based Irradiation Experiments. Materials, 14(21), 6238. https://doi.org/10.3390/ma14216238







