Growing Interface with Phase Separation and Spontaneous Convection during Hydrodynamically Stable Displacement
Abstract
1. Introduction
2. Materials and Methods
2.1. Solutions
2.2. Displacement
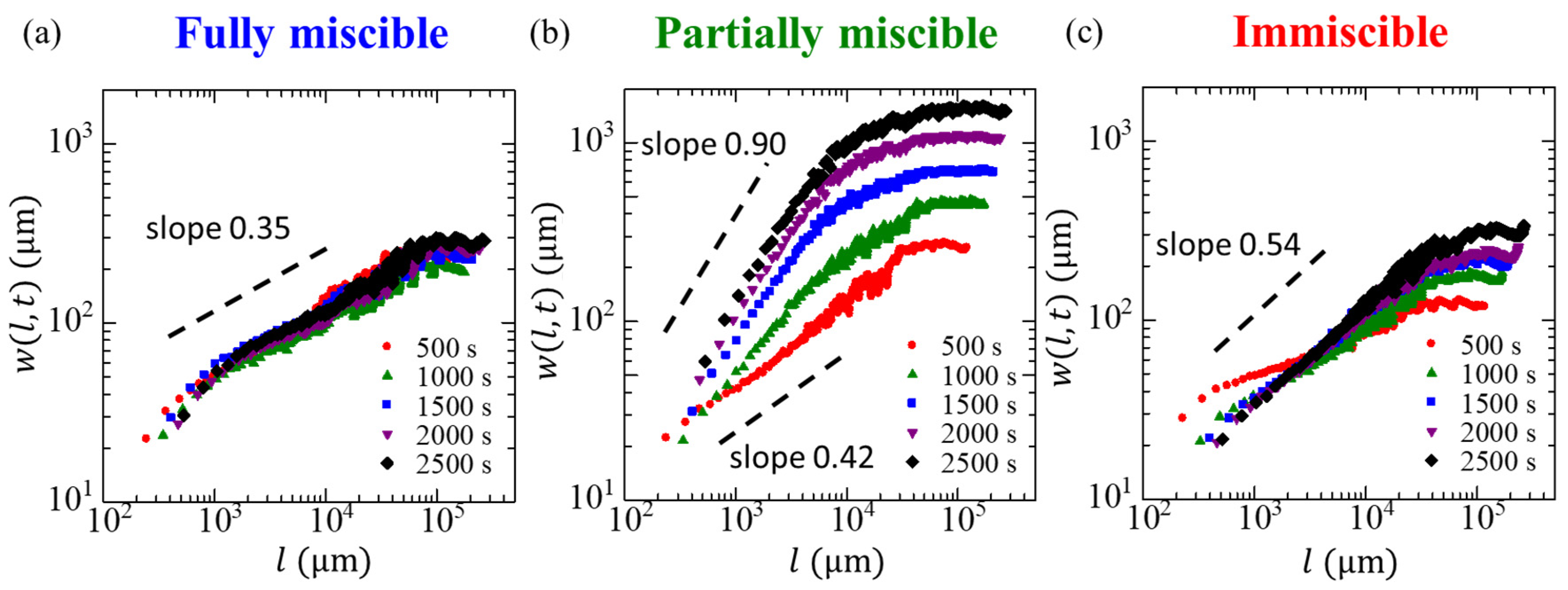
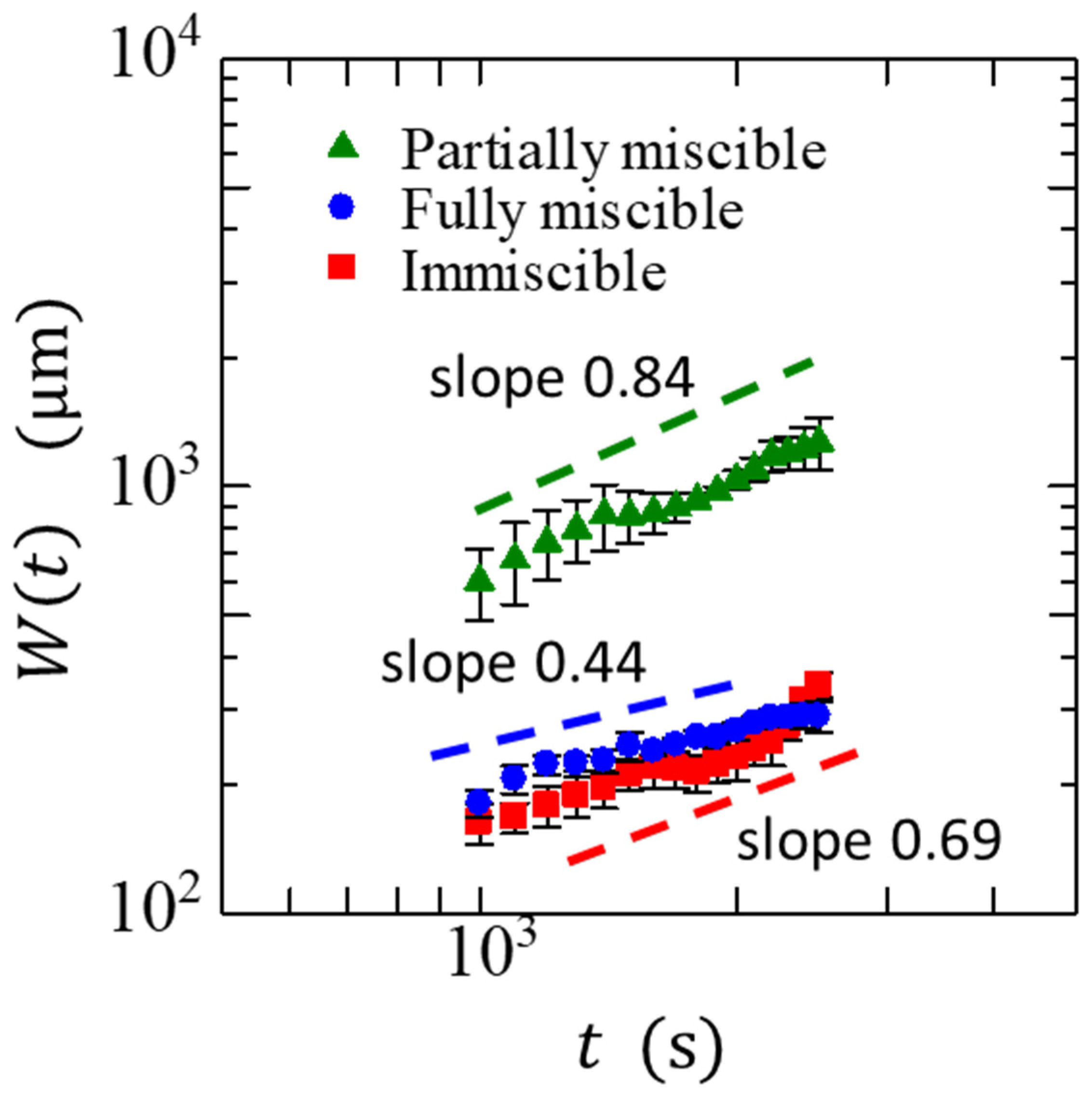
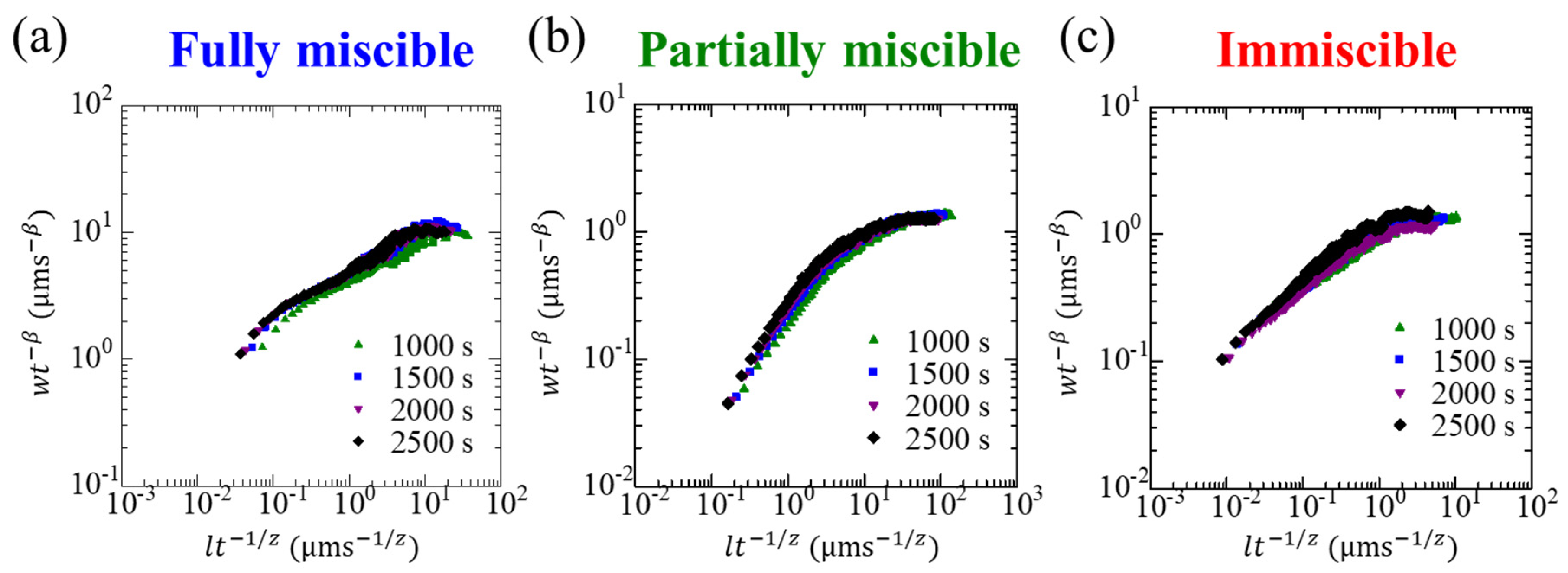
2.3. Family–Vicsek Scaling
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saffman, P.G.; Taylor, G. The Penetration of a Fluid into a Porous Medium or Hele-Shaw Cell Containing a More Viscous Liquid. Proc. R. Soc. A 1958, 245, 312–329. [Google Scholar] [CrossRef]
- Engelberts, W.F.; Klinkenberg, L.J. Laboratory experiments on the displacement of oil by water from packs of granular material. In Proceedings of the 3rd World Petroleum Congress, The Hague, The Netherlands, 28 May–6 June 1951; pp. 544–554. [Google Scholar]
- Homsy, G.M. Viscous Fingering in Porous Media. Annu. Rev. Fluid Mech. 1987, 19, 271–311. [Google Scholar] [CrossRef]
- Li, Z.; Leshansky, A.M.; Pismen, L.M.; Tabeling, P. Step-emulsification in a microfluidic device. Lab Chip 2015, 15, 1023–1031. [Google Scholar] [CrossRef]
- Schuszter, G.; Brau, F.; De Wit, A. Flow-driven control of calcium carbonate precipitation patterns in a confined geometry. Phys. Chem. Chem. Phys. 2016, 18, 25592–25600. [Google Scholar] [CrossRef]
- Griffiths, W.D.; Ainsworth, M.J. Instability of the Liquid Metal–Pattern Interface in the Lost Foam Casting of Aluminum Alloys. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2016, 47, 3137–3149. [Google Scholar] [CrossRef]
- Orr, F.M.J.; Taber, J.J. Use of Carbon Dioxide in Enhanced Oil Recovery. Science 1984, 224, 563–569. [Google Scholar] [CrossRef]
- Lake, L.W.; Johns, R.T.; Rossen, W.R.; Pope, G.A. Fundamentals of Enhanced Oil Recovery; Society of Petroleum Engineers: Richardson, TX, USA, 2014; ISBN 978-1-61399-328-6. [Google Scholar]
- McCloud, K.V.; Maher, J.V. Experimental perturbations to Saffman-Taylor flow. Phys. Rep. 1995, 260, 139–185. [Google Scholar] [CrossRef]
- Nagatsu, Y. Viscous Fingering Phenomena with Chemical Reactions. Curr. Phys. Chem. 2015, 5, 52–63. [Google Scholar] [CrossRef]
- De Wit, A. Chemo-hydrodynamic patterns in porous media. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2016, 374, 20150419. [Google Scholar] [CrossRef]
- De Wit, A. Chemo-Hydrodynamic Patterns and Instabilities. Annu. Rev. Fluid Mech. 2020, 52, 531–555. [Google Scholar] [CrossRef]
- Suzuki, R.X.; Nagatsu, Y.; Mishra, M.; Ban, T. Fingering pattern induced by spinodal decomposition in hydrodynamically stable displacement in a partially miscible system. Phys. Rev. Fluids 2019, 4, 104005. [Google Scholar] [CrossRef]
- Suzuki, R.X.; Nagatsu, Y.; Mishra, M.; Ban, T. Phase separation effects on a partially miscible viscous fingering dynamics. J. Fluid Mech. 2020, 898, A11. [Google Scholar] [CrossRef]
- Suzuki, R.X.; Takeda, R.; Nagatsu, Y.; Mishra, M.; Ban, T. Fluid Morphologies Governed by the Competition of Viscous Dissipation and Phase Separation in a Radial Hele-Shaw Flow. Coatings 2020, 10, 960. [Google Scholar] [CrossRef]
- Suzuki, R.X.; Tada, H.; Hirano, S.; Ban, T.; Mishra, M.; Takeda, R.; Nagatsu, Y. Anomalous patterns of Saffman-Taylor fingering instability during a metastable phase separation. Phys. Chem. Chem. Phys. 2021, 23, 10926–10935. [Google Scholar] [CrossRef]
- Ban, T.; Aoyama, A.; Matsumoto, T. Self-generated Motion of Droplets Induced by Korteweg Force. Chem. Lett. 2010, 39, 1294–1296. [Google Scholar] [CrossRef]
- Ban, T.; Yamada, T.; Aoyama, A.; Takagi, Y.; Okano, Y. Composition-dependent shape changes of self-propelled droplets in a phase-separating system. Soft Matter 2012, 8, 3908. [Google Scholar] [CrossRef]
- Korteweg, D.J. Sur la forme que prennent les équations du mouvement des fluides si l’on tient compte des forces capillaires cauśees par des variations de densité. Arch. Néerl. Sci. Exactes Nat. 1901, 6, 1–24. [Google Scholar]
- Molin, D.; Mauri, R. Enhanced heat transport during phase separation of liquid binary mixtures. Phys. Fluids 2007, 19, 074102. [Google Scholar] [CrossRef]
- Barabási, A.-L.; Stanley, H.E. Fractal Concepts in Surface Growth; Cambridge University Press: Cambridge, UK, 2002; ISBN 9780511599798. [Google Scholar]
- Kardar, M.; Parisi, G.; Zhang, Y.C. Dynamic scaling of growing interfaces. Phys. Rev. Lett. 1986, 56, 889–892. [Google Scholar] [CrossRef]
- Family, F.; Vicsek, T. Scaling of the active zone in the Eden process on percolation networks and the ballistic deposition model. J. Phys. A Math. Gen. 1985, 18, L75–L81. [Google Scholar] [CrossRef]
- Myllys, M.; Maunuksela, J.; Alava, M.; Ala-Nissila, T.; Merikoski, J.; Timonen, J. Kinetic roughening in slow combustion of paper. Phys. Rev. E 2001, 64, 036101. [Google Scholar] [CrossRef]
- Wakita, J.; Itoh, H.; Matsuyama, T.; Matsushita, M. Self-Affinity for the growing interface of bacterial colonies. J. Phys. Soc. Jpn. 1997, 66, 67–72. [Google Scholar] [CrossRef]
- Takeuchi, K.A.; Sano, M. Universal fluctuations of growing interfaces: Evidence in turbulent liquid crystals. Phys. Rev. Lett. 2010, 104, 230601. [Google Scholar] [CrossRef]
- Broyles, B.S.; Shalliker, R.A.; Cherrak, D.E.; Guiochon, G. Visualization of viscous fingering in chromatographic columns. J. Chromatogr. A 1998, 822, 173–187. [Google Scholar] [CrossRef]
- Nordbotten, J.M.; Celia, M.A.; Bachu, S. Injection and storage of CO2 in deep saline aquifers: Analytical solution for CO2 plume evolution during injection. Transp. Porous Media 2005, 58, 339–360. [Google Scholar] [CrossRef]
- Snyder, S.M.; Cole, K.D.; Sziag, D.C. Phase Compositions, Viscosities, and Densities for Aqueous Two-Phase Systems Composed of Polyethylene Glycol and Various Salts at 25 °C. J. Chem. Eng. Data 1992, 37, 268–274. [Google Scholar] [CrossRef]
- Hernández-Machado, A.; Soriano, J.; Lacasta, A.M.; Rodríguez, M.A.; Ramírez-Plscina, L.; Ortín, J. Interface roughening in Hele-Shaw flows with quenched disorder: Experimental and theoretical results. Europhys. Lett. 2001, 55, 194–200. [Google Scholar] [CrossRef][Green Version]
- Dubé, M.; Rost, M.; Elder, K.R.; Alava, M.; Majaniemi, S.; Ala-Nissila, T. Liquid conservation and nonlocal interface dynamics in imbibition. Phys. Rev. Lett. 1999, 83, 1628–1631. [Google Scholar] [CrossRef]
- Laurila, T.; Pradas, M.; Hernández-Machado, A.; Ala-Nissila, T. Influence of disorder strength on phase-field models of interfacial growth. Phys. Rev. E—Stat. Nonlinear Soft Matter Phys. 2008, 78, 031603. [Google Scholar] [CrossRef]
- Horvath, V.K.; Family, F.; Vicsek, T. Dynamic scaling of the interface in two-phase viscous flows in porous media. J. Phys. A Math. Gen. 1991, 24, 24–29. [Google Scholar] [CrossRef]
- He, S.; Kahanda, G.L.M.K.S.; Wong, P. Roughness of wetting fluid invasion fronts in porous media. Phys. Rev. Lett. 1992, 69, 3731–3734. [Google Scholar] [CrossRef] [PubMed]
- Soriano, J.; Mercier, A.; Planet, R.; Hernández-Machado, A.; Rodríguez, M.A.; Ortín, J. Anomalous roughening of viscous fluid fronts in spontaneous imbibition. Phys. Rev. Lett. 2005, 95, 104501. [Google Scholar] [CrossRef] [PubMed]
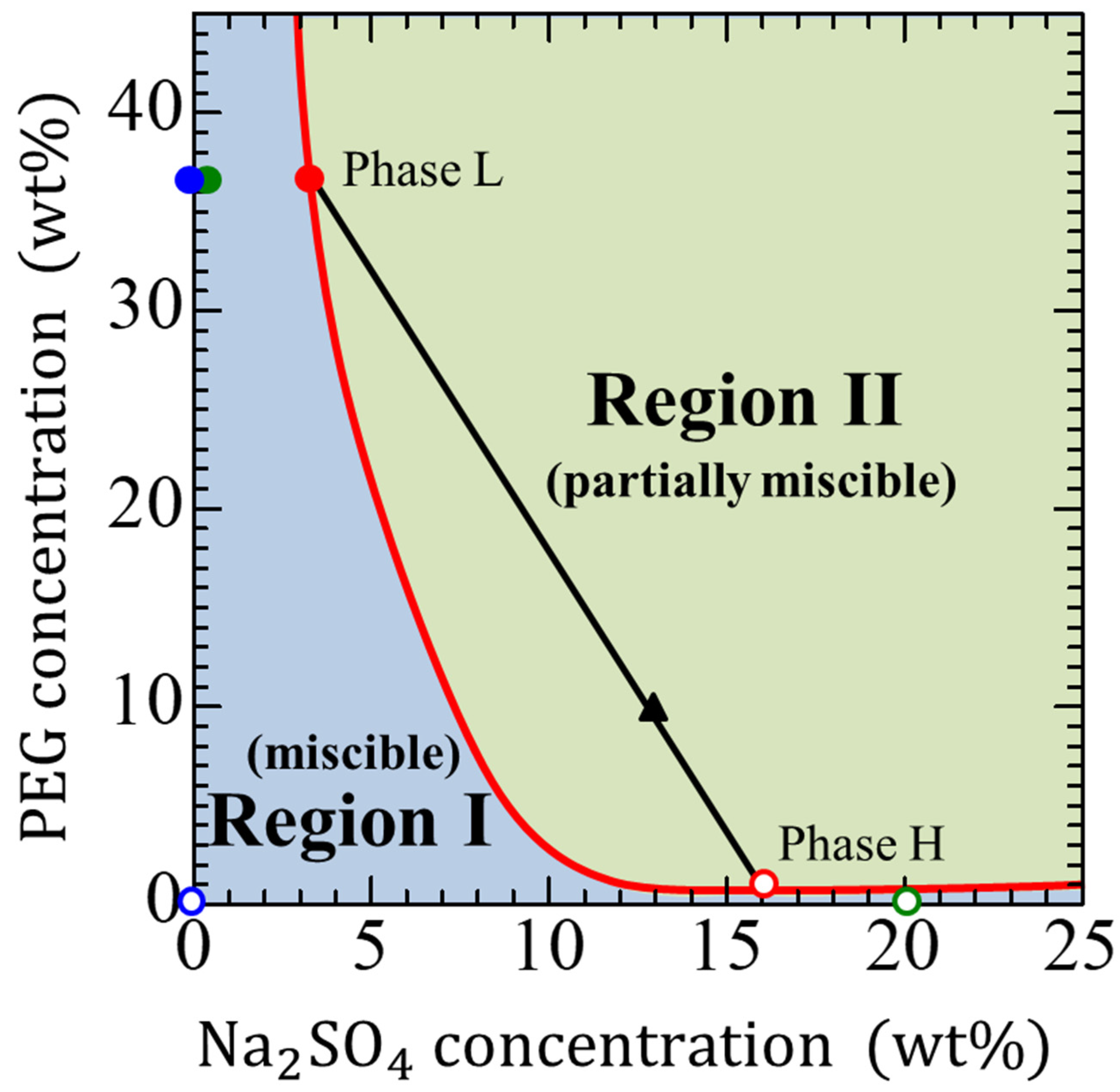
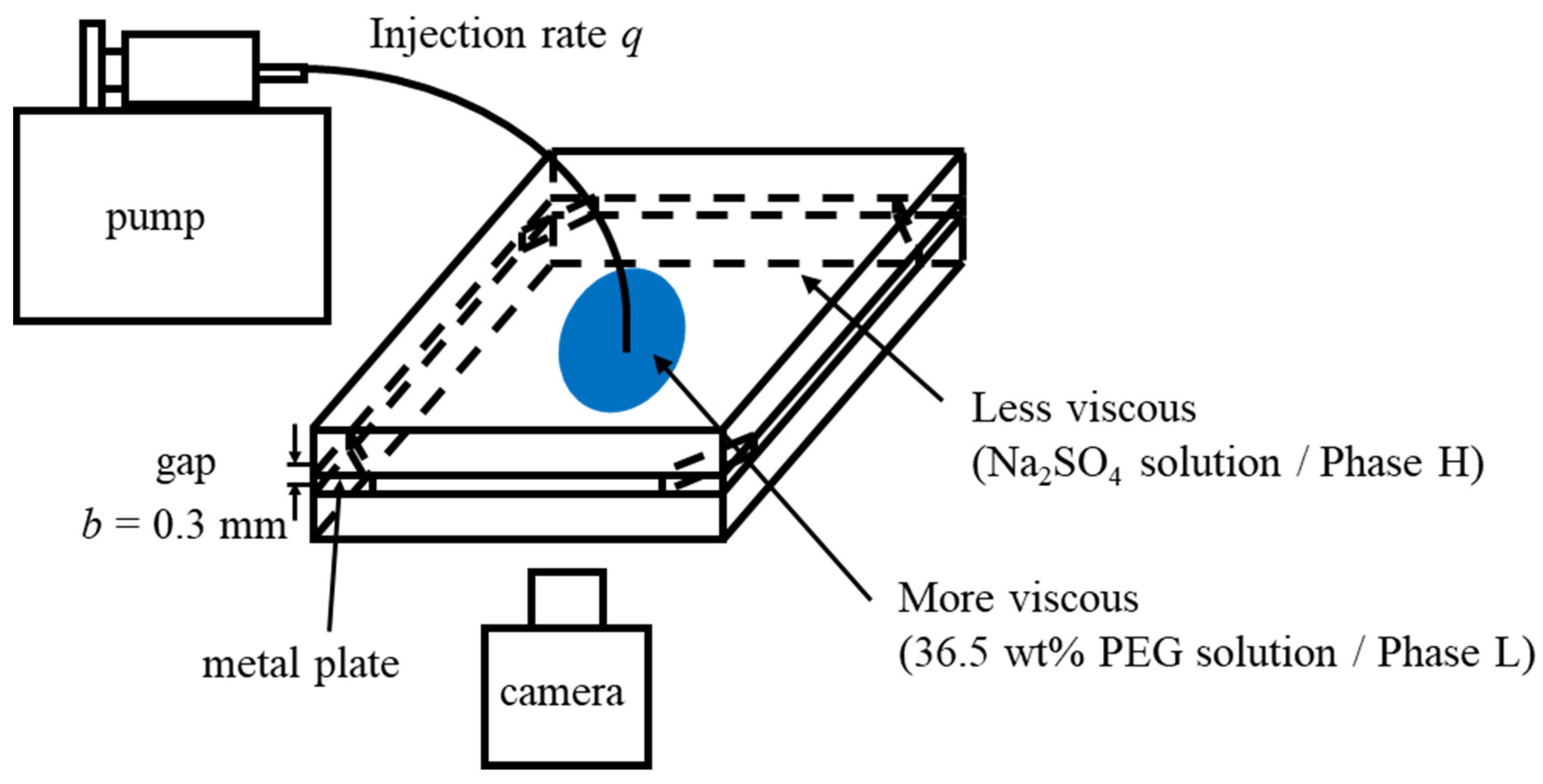
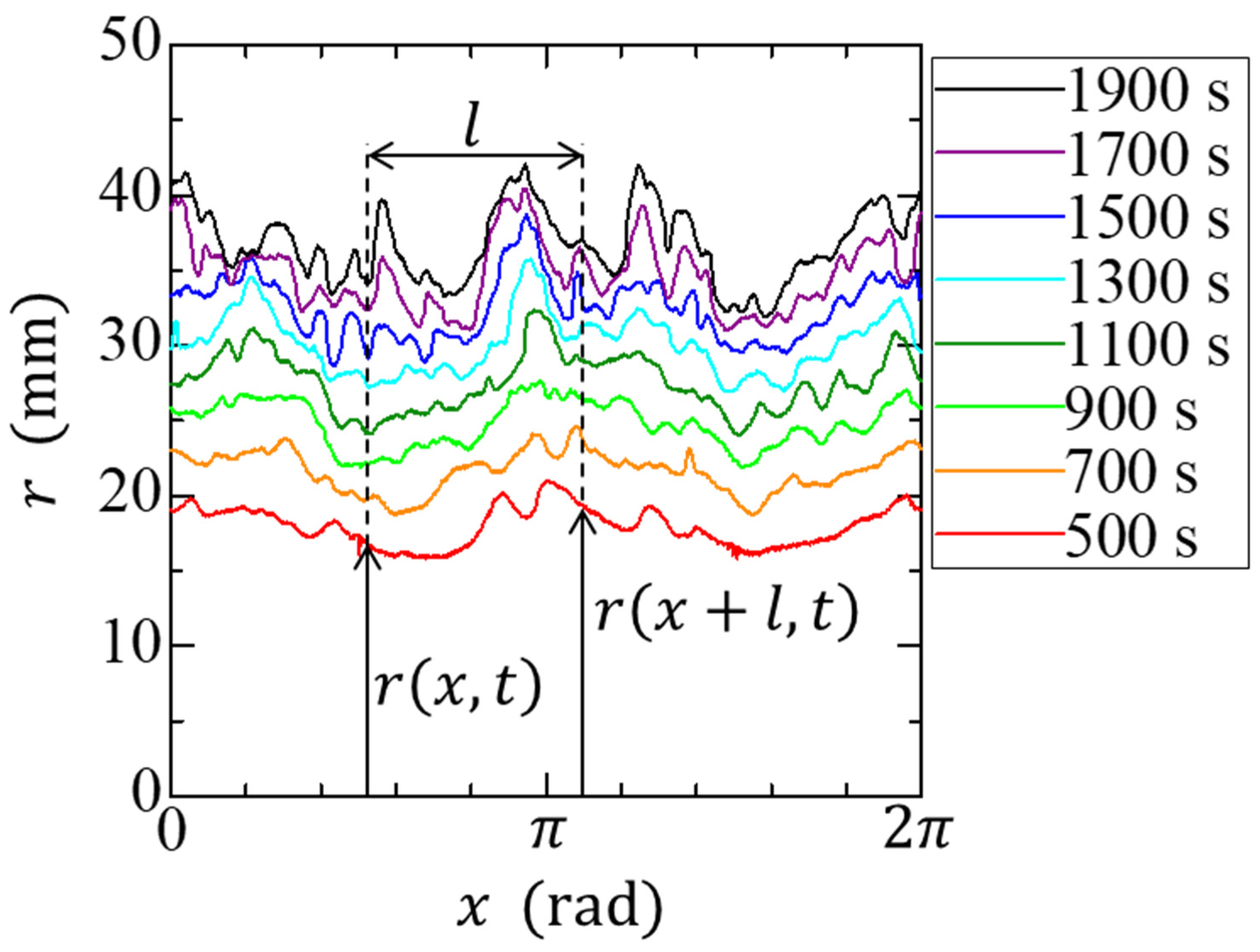
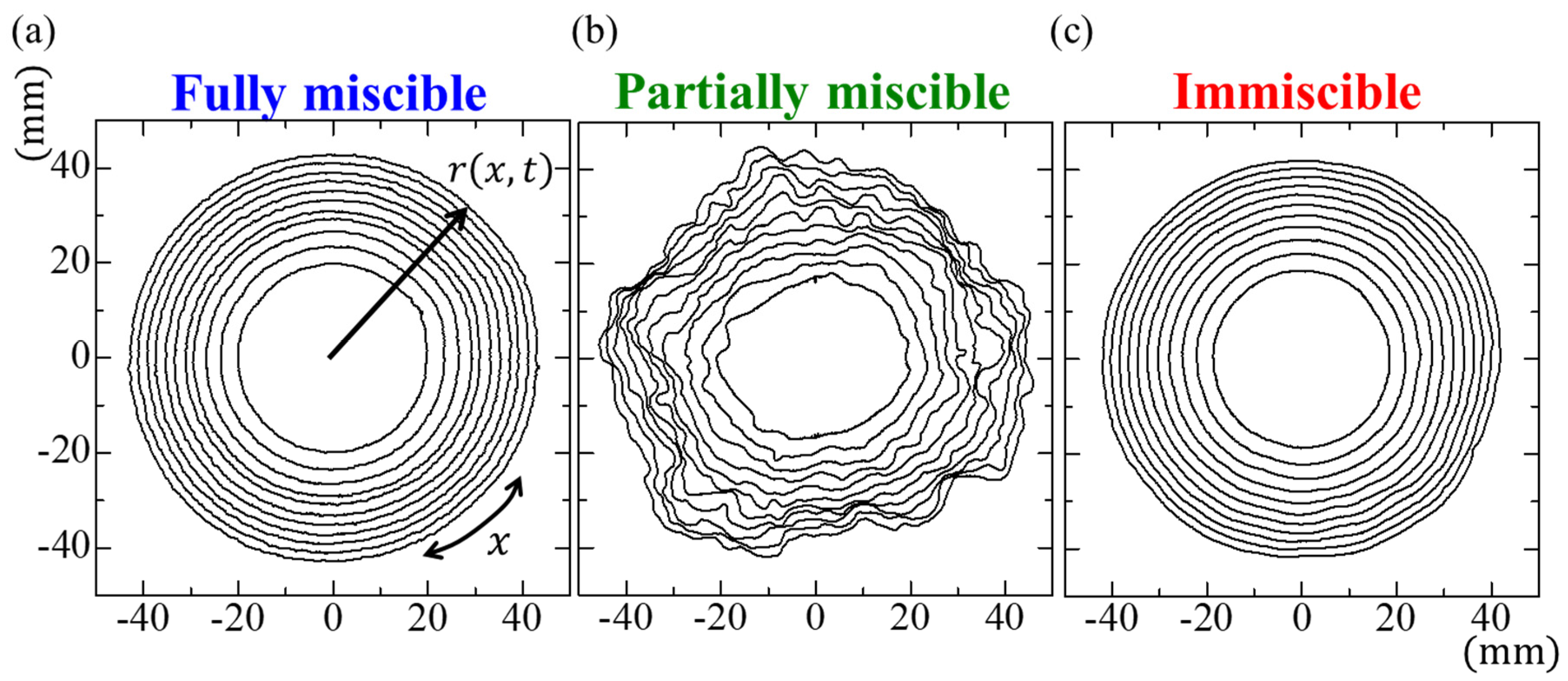
| System | Displacing More Viscous Liquid (Density, Viscosity) | Displaced Less Viscous Liquid (Density, Viscosity) |
|---|---|---|
| Fully miscible | 36.5 wt% PEG solution (1.07 g/cm3, 112 mPa·s) | 0 wt% Na2SO4 solution (0.997 g/cm3, 0.972 mPa·s) |
| Partially miscible | 36.5 wt% PEG solution (1.07 g/cm3, 112 mPa·s) | 20 wt% Na2SO4 solution (1.19 g/cm3, 2.08 mPa·s) |
| Immiscible | Phase L (1.08 g/cm3, 125 mPa·s) | Phase H (1.16 g/cm3, 1.76 mPa·s) |
| Fully Miscible | Partially Miscible | Immiscible | |
|---|---|---|---|
| 0.35 ± 0.02 | 0.86 ± 0.03 | 0.49 ± 0.02 | |
| 0.44 ± 0.12 | 0.84 ± 0.17 | 0.69 ± 0.05 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ban, T.; Tanaka, R.; Suzuki, R.X.; Nagatsu, Y. Growing Interface with Phase Separation and Spontaneous Convection during Hydrodynamically Stable Displacement. Materials 2021, 14, 6089. https://doi.org/10.3390/ma14206089
Ban T, Tanaka R, Suzuki RX, Nagatsu Y. Growing Interface with Phase Separation and Spontaneous Convection during Hydrodynamically Stable Displacement. Materials. 2021; 14(20):6089. https://doi.org/10.3390/ma14206089
Chicago/Turabian StyleBan, Takahiko, Ryohei Tanaka, Ryuta X. Suzuki, and Yuichiro Nagatsu. 2021. "Growing Interface with Phase Separation and Spontaneous Convection during Hydrodynamically Stable Displacement" Materials 14, no. 20: 6089. https://doi.org/10.3390/ma14206089
APA StyleBan, T., Tanaka, R., Suzuki, R. X., & Nagatsu, Y. (2021). Growing Interface with Phase Separation and Spontaneous Convection during Hydrodynamically Stable Displacement. Materials, 14(20), 6089. https://doi.org/10.3390/ma14206089







