Residual Stress Distribution Design for Gear Surfaces Based on Genetic Algorithm Optimization
Abstract
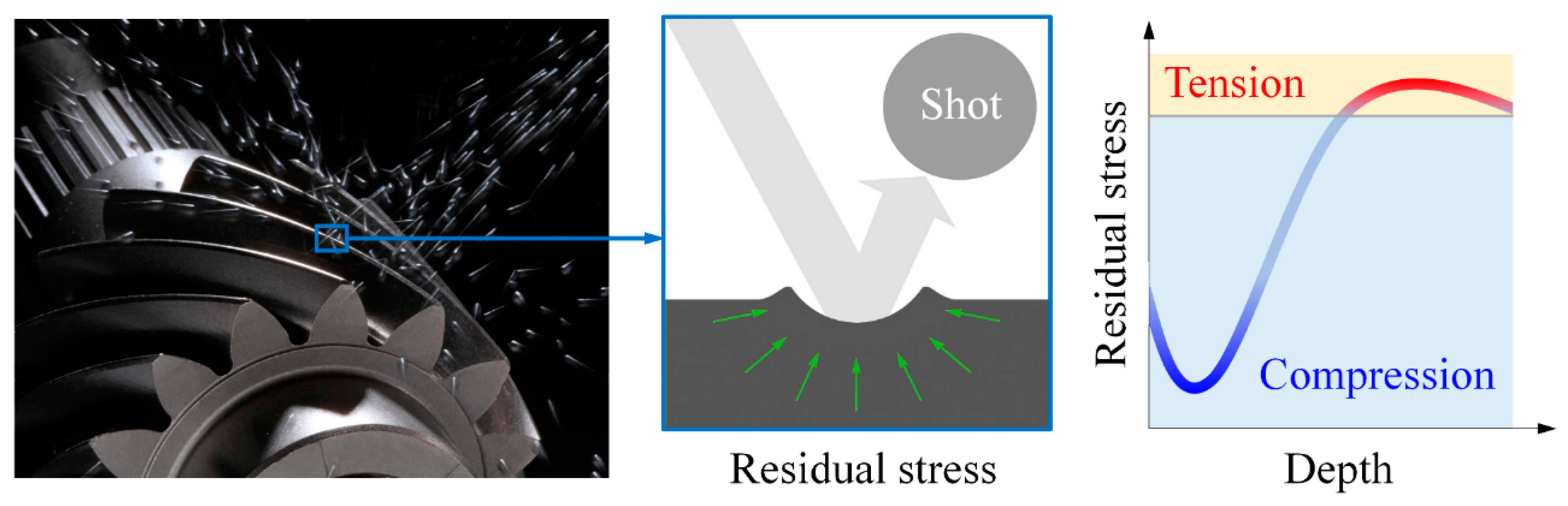
1. Introduction
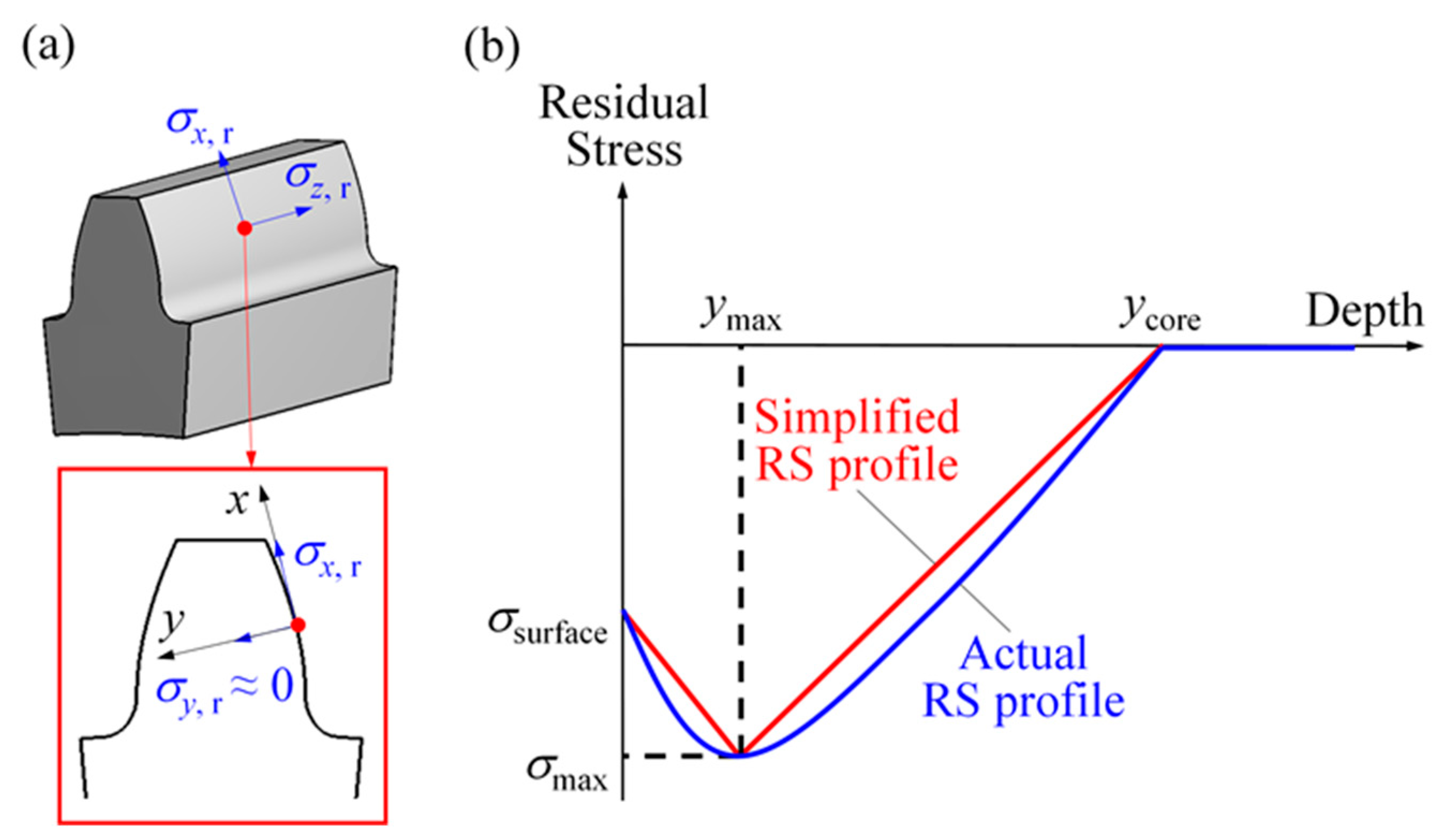
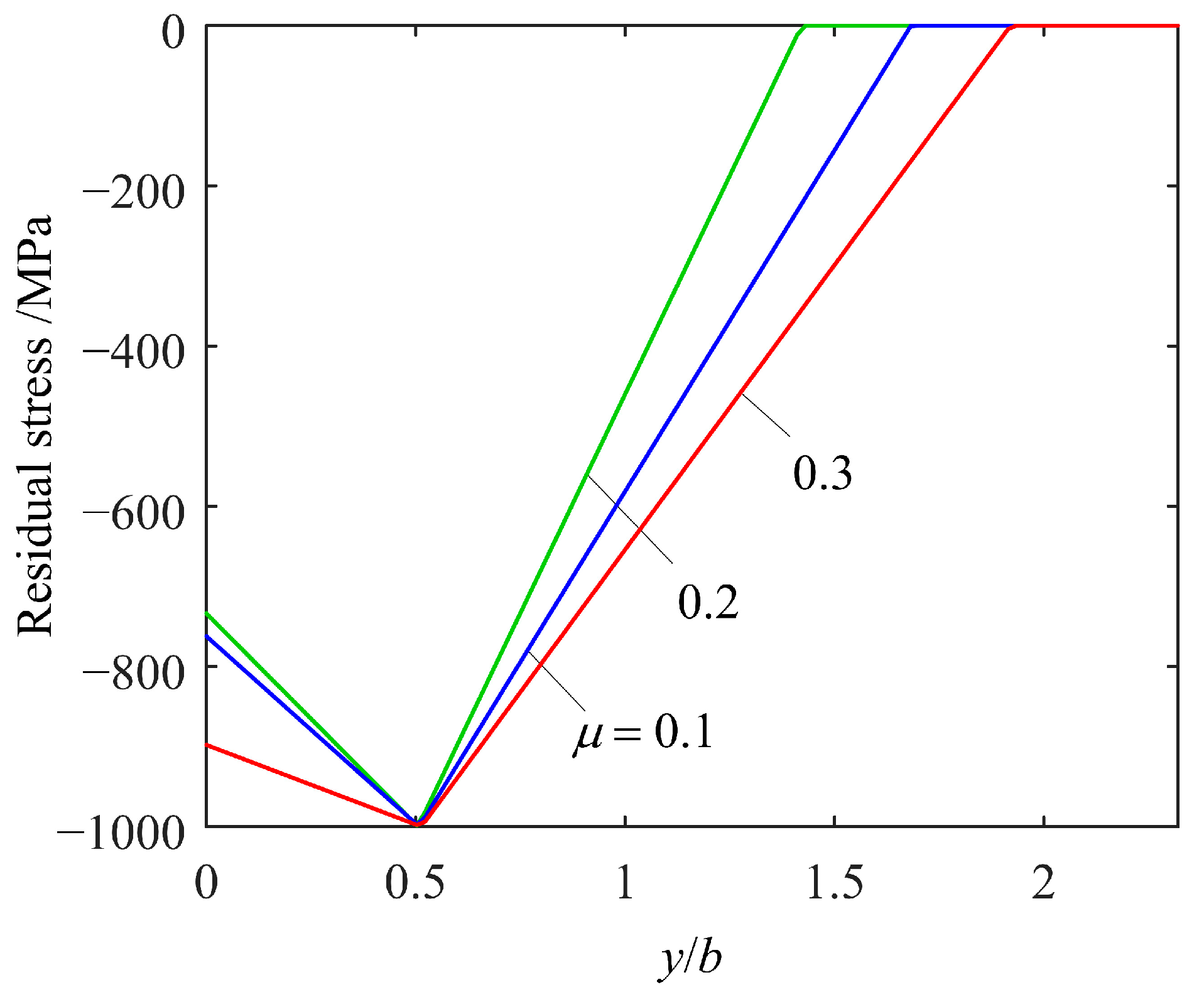
2. Residual Stress Distribution
- (1)
- σsurface—the RS at the surface;
- (2)
- σmax—the peak RS;
- (3)
- ymax—the depth of σmax;
- (4)
- ycore—the depth where RS vanishes.
3. Gear Contact Model
4. Fatemi–Socie Multiaxial Fatigue Criterion
5. Optimization Scheme
- (1)
- The generation number reaches the prescribed upper limit Gmax;
- (2)
- The relative change in the highest fitness over Gs generations is less than the function tolerance value e.
6. Results and Discussion
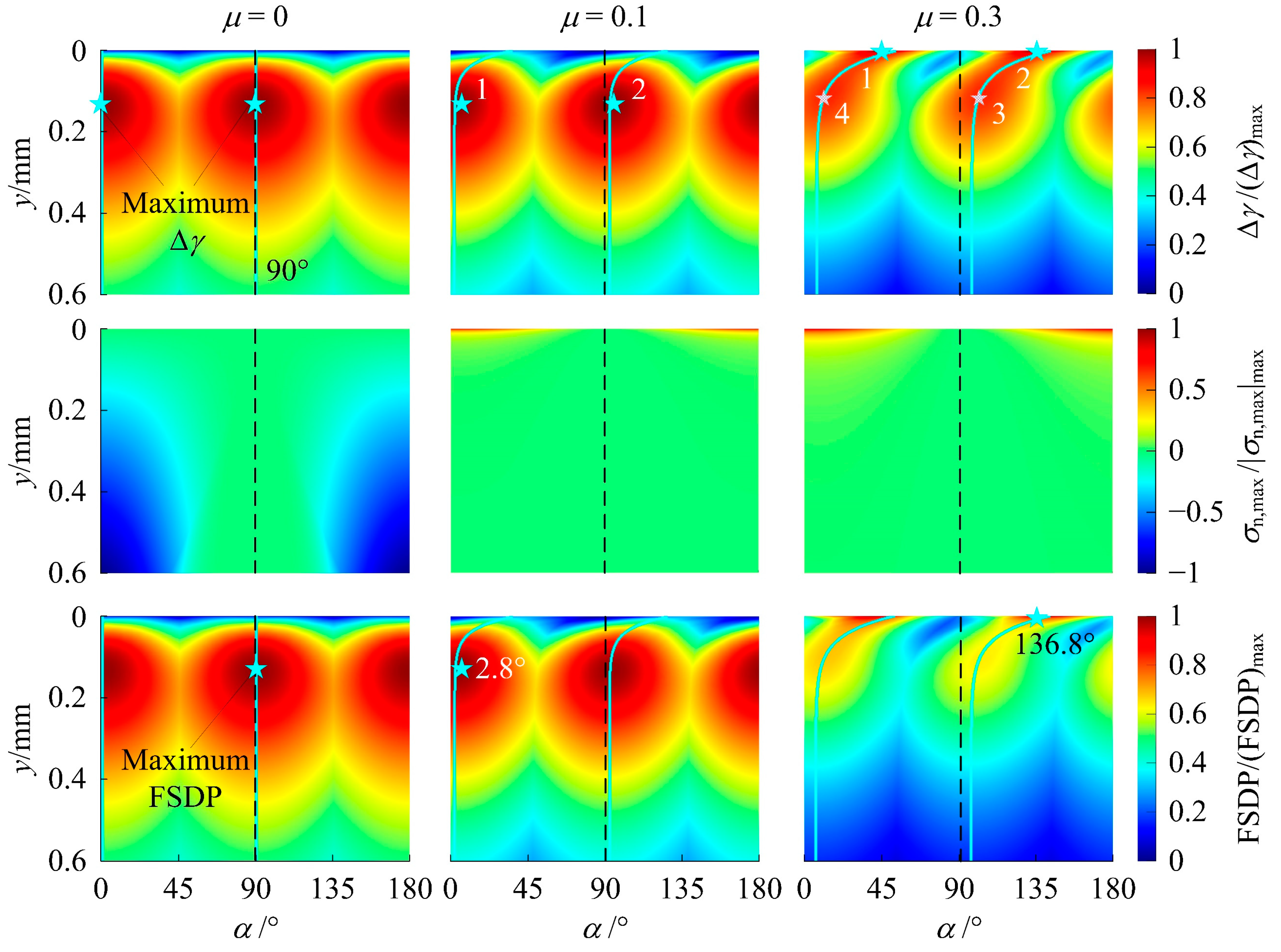
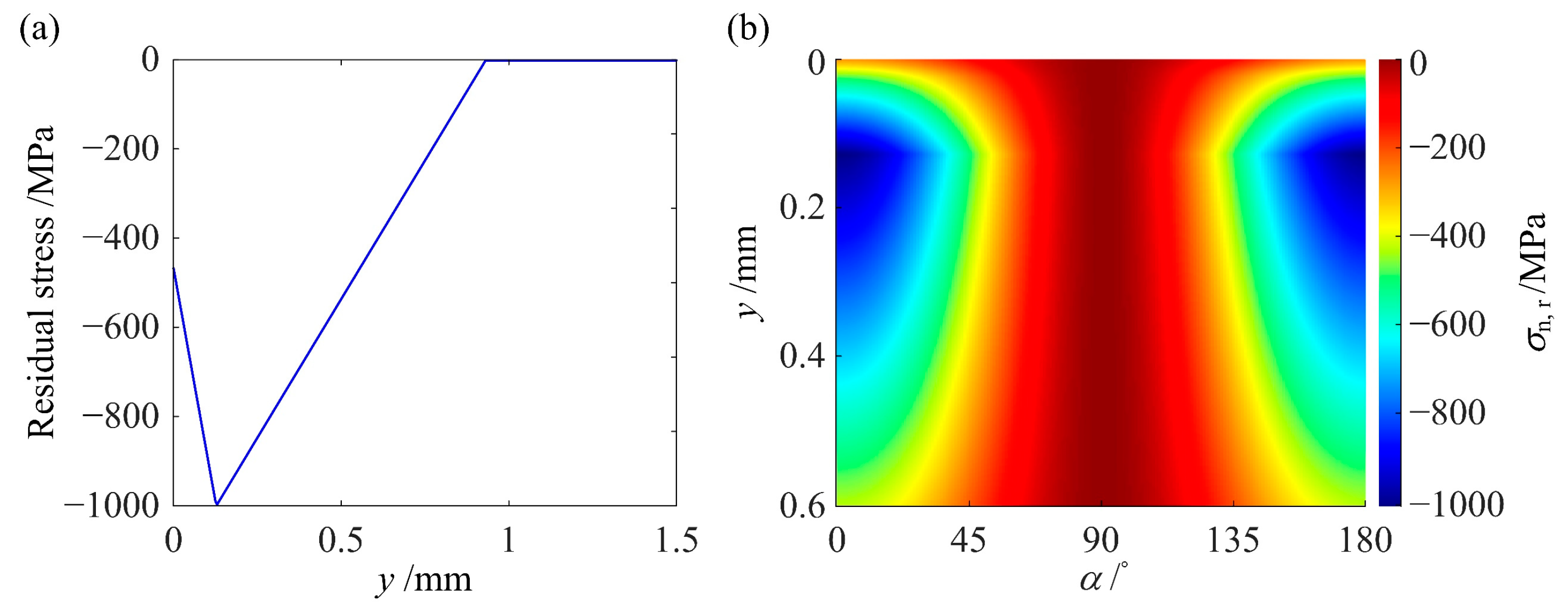
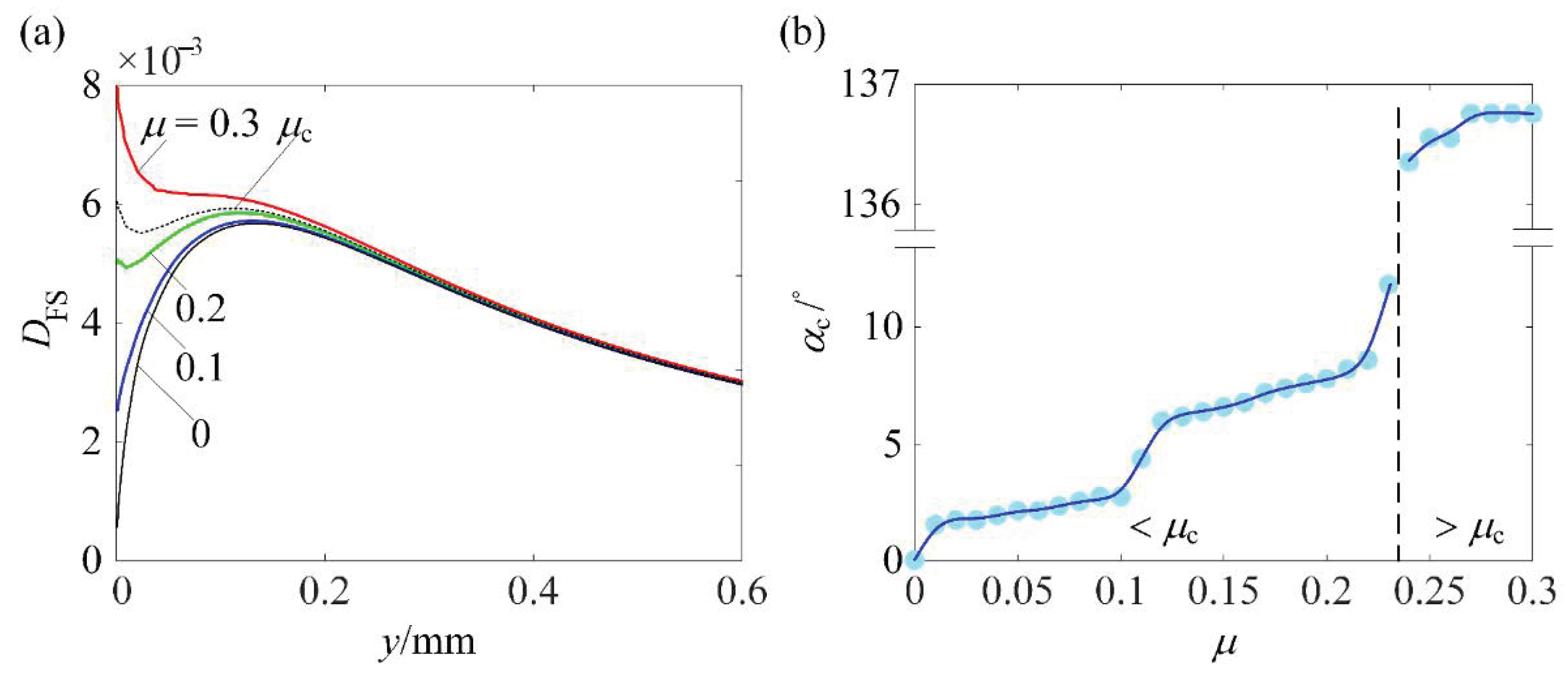
6.1. Mechanism for RS to Increase (Nf)min
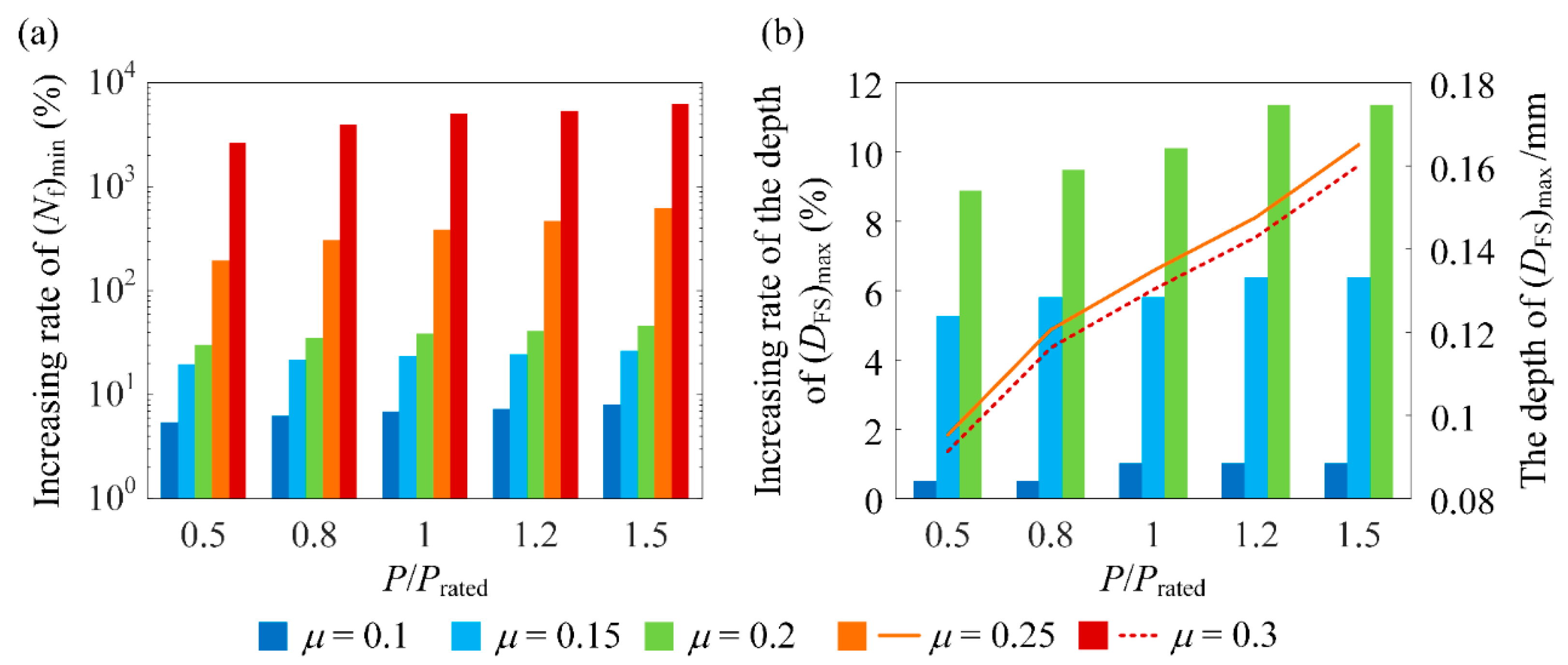
6.2. Increase in (Nf)min Induced by the Optimum RS Distribution
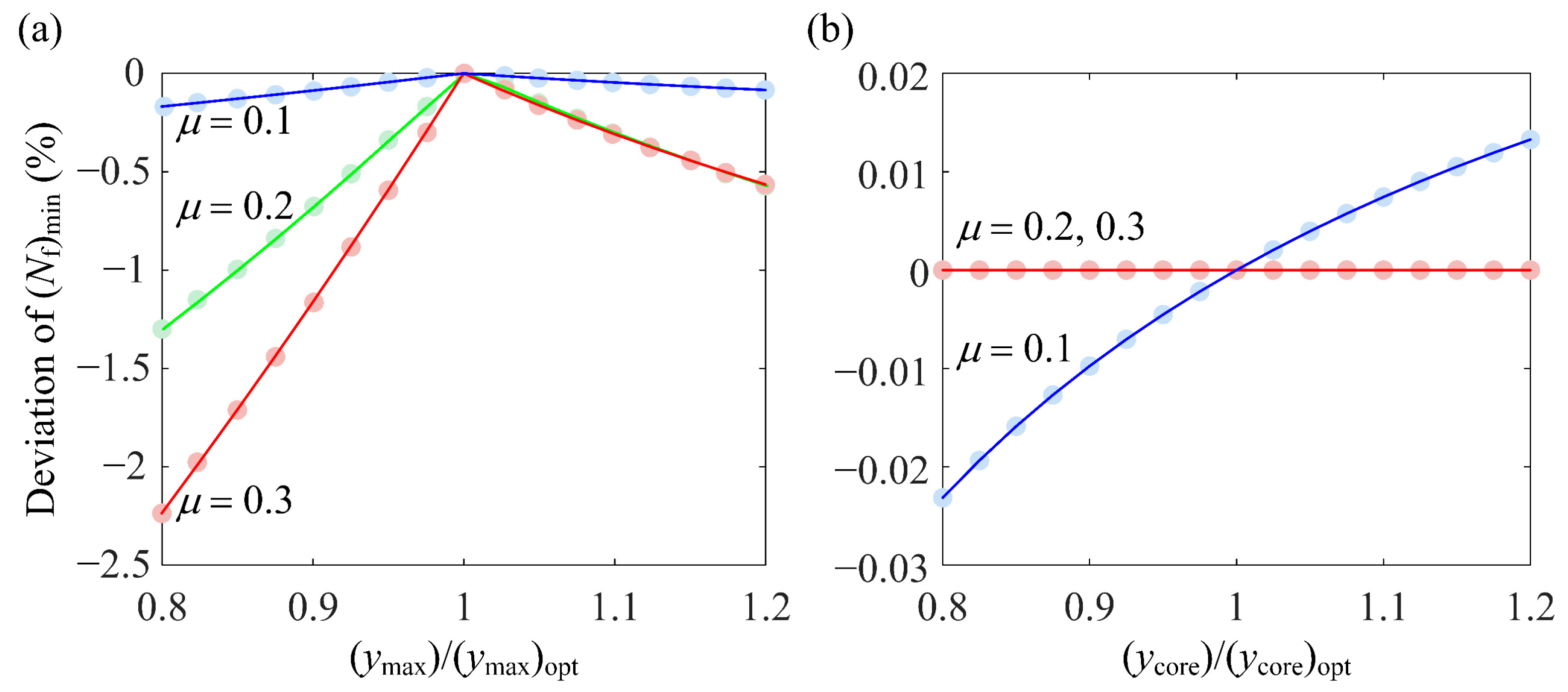
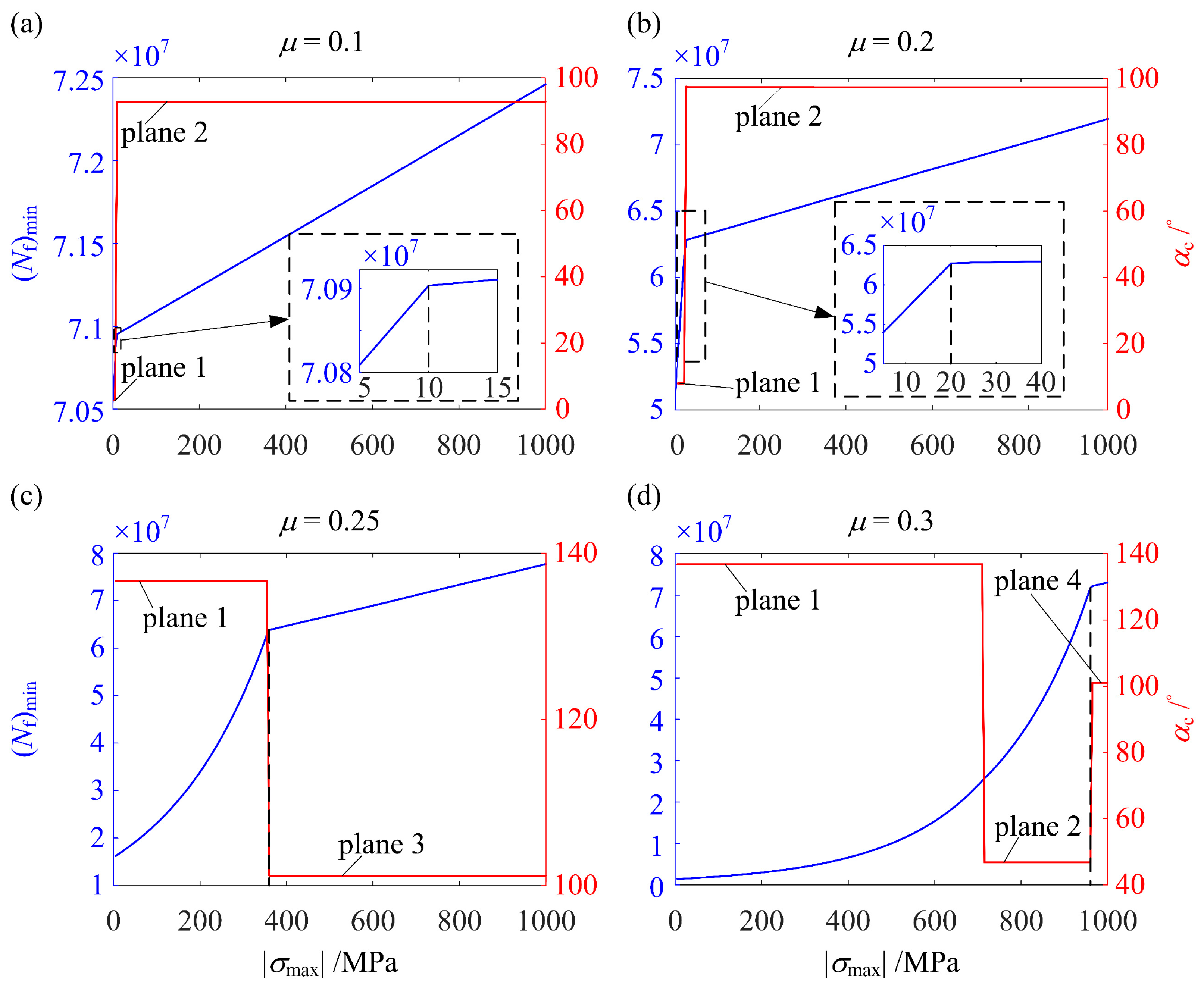
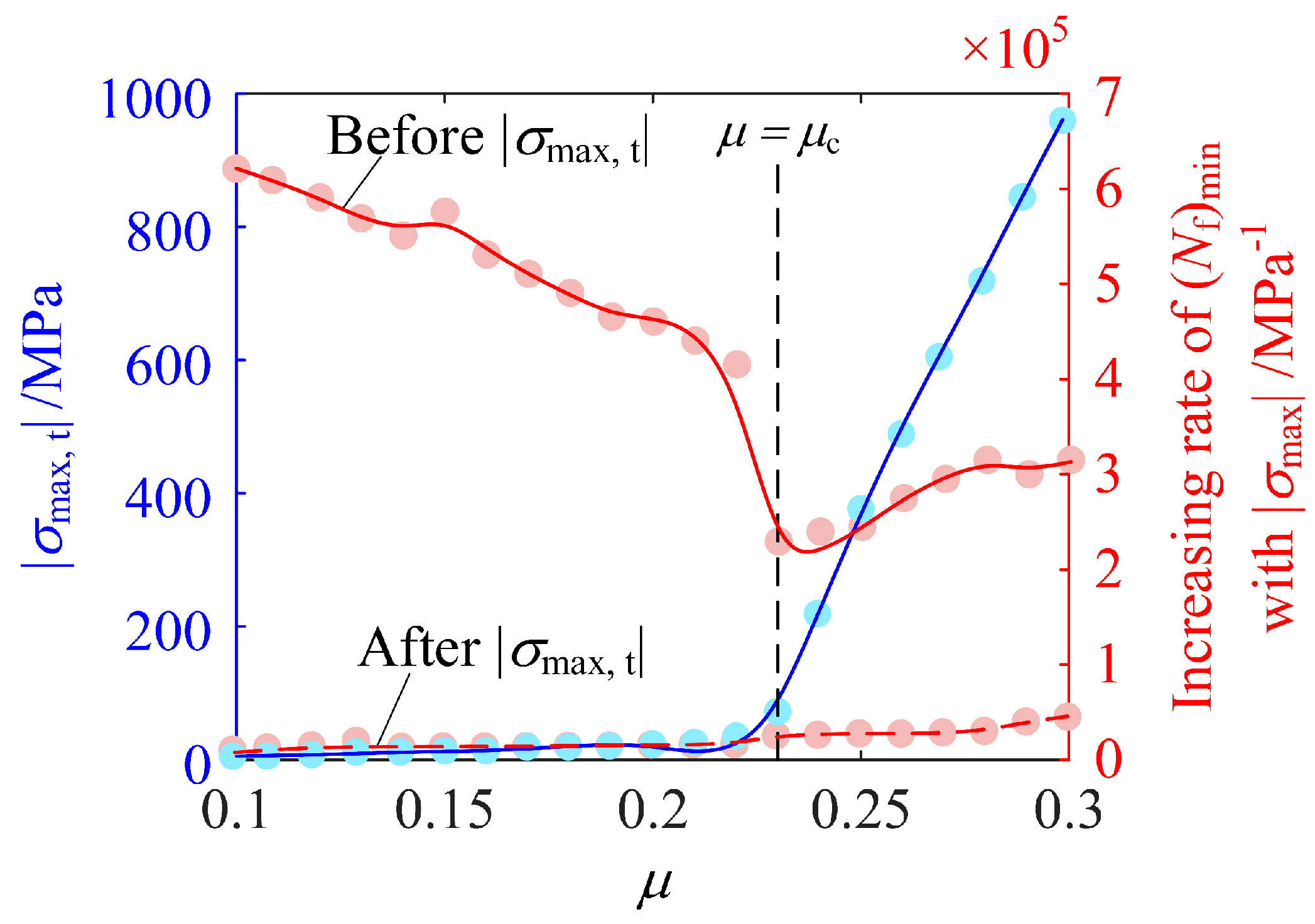
6.3. Effect on (Nf)min When the RS Distribution Deviates from the Optimum
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| critical plane | The plane that has the maximum shear strain range over a loading cycle |
| FSDP | Fatemi–Socie damage parameter |
| RS | Residual stress |
| DFS | The maximum FSDP on all the critical planes of a material point |
| (DFS)max | The maximum DFS of all material points |
| Nf | Fatigue initiation life of a material point |
| (Nf)min | Minimum fatigue initiation life of all material points or fatigue initiation life of the gear surface |
| α | Plane orientation |
| αc | The orientation of the critical plane corresponding to DFS |
| Δγ | The maximum shear strain range on a plane over a loading cycle |
| σn,max | Maximum normal stress on a plane over a cycle |
| σsurface | RS at the surface |
| σmax | Peak RS |
| ymax | Depth of σmax |
| ycore | Depth where RS vanishes |
| σmax,t | The transition value for σmax |
| Subscripts | |
| opt | Values associated with the optimum RS distribution |
| 1, 2, 3, … | Values associated with plane 1, 2, 3, … |
Appendix A
References
- Jiang, G.; He, H.; Yan, J.; Xie, P. Multiscale convolutional neural networks for fault diagnosis of wind turbine gearbox. IEEE Trans. Ind. Electron. 2018, 66, 3196–3207. [Google Scholar] [CrossRef]
- Liu, J. A dynamic modelling method of a rotor-roller bearing-housing system with a localized fault including the additional excitation zone. J. Sound Vib. 2020, 469, 115144. [Google Scholar] [CrossRef]
- Mechanism of Gear Tooth Failures; American Gear Manufacturing Association: Alexandria, VA, USA, 2004.
- Kundu, P.; Darpe, A.K.; Kulkarni, M.S. An ensemble decision tree methodology for remaining useful life prediction of spur gears under natural pitting progression. Struct. Health Monit. 2020, 19, 854–872. [Google Scholar] [CrossRef]
- Doğan, O.; Karpat, F. Crack detection for spur gears with asymmetric teeth based on the dynamic transmission error. Mech. Mach. Theory 2019, 133, 417–431. [Google Scholar] [CrossRef]
- Luo, Y.; Baddour, N.; Liang, M. Dynamical modeling and experimental validation for tooth pitting and spalling in spur gears. Mech. Syst. Signal Process. 2019, 119, 155–181. [Google Scholar] [CrossRef]
- Sharif, K.; Evans, H.; Snidle, R. Modelling of elastohydrodynamic lubrication and fatigue of rough surfaces: The effect of lambda ratio. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2012, 226, 1039–1050. [Google Scholar] [CrossRef]
- Li, S.; Kahraman, A. A micro-pitting model for spur gear contacts. Int. J. Fatigue 2014, 59, 224–233. [Google Scholar] [CrossRef]
- Paulson, N.R.; Sadeghi, F.; Habchi, W. A coupled finite element EHL and continuum damage mechanics model for rolling contact fatigue. Tribol. Int. 2017, 107, 173–183. [Google Scholar] [CrossRef]
- Wang, W.; Liu, H.; Zhu, C.; Jinyuan, T.; Jiang, C. Evaluation of contact fatigue risk of a carburized gear considering of mechanical properties. Friction 2019. [Google Scholar] [CrossRef]
- Wang, W.; Liu, H.; Zhu, C.; Sun, Z. Evaluation of contact fatigue life of a wind turbine carburized gear considering gradients of mechanical properties. Int. J. Damage Mech. 2019, 28, 1170–1190. [Google Scholar] [CrossRef]
- Golmohammadi, Z.; Sadeghi, F. A Coupled Multibody Finite Element Model for Investigating Effects of Surface Defects on Rolling Contact Fatigue. J. Tribol. 2019, 141. [Google Scholar] [CrossRef]
- Jebahi, M.; Gakwaya, A.; Lévesque, J.; Mechri, O.; Ba, K. Robust methodology to simulate real shot peening process using discrete-continuum coupling method. Int. J. Mech. Sci. 2016, 107, 21–33. [Google Scholar] [CrossRef]
- Liu, H.; Liu, H.; Zhu, C.; He, H.; Wei, P. Evaluation of Contact Fatigue Life of a Wind Turbine Gear Pair Considering Residual Stress. J. Tribol. 2018, 140, 041102. [Google Scholar] [CrossRef]
- Paladugu, M.; Hyde, R.S. Influence of microstructure on retained austenite and residual stress changes under rolling contact fatigue in mixed lubrication conditions. Wear 2018, 406–407, 84–91. [Google Scholar] [CrossRef]
- Wang, W.; Liu, H.; Zhu, C.; Du, X.; Tang, J. Effect of the residual stress on contact fatigue of a wind turbine carburized gear with multiaxial fatigue criteria. Int. J. Mech. Sci. 2019, 151, 263–273. [Google Scholar] [CrossRef]
- Xu, X.; Lai, J.; Lohmann, C.; Tenberge, P.; Weibring, M.; Dong, P. A model to predict initiation and propagation of micro-pitting on tooth flanks of spur gears. Int. J. Fatigue 2019, 122, 106–115. [Google Scholar] [CrossRef]
- Ooi, G.T.C.; Roy, S.; Sundararajan, S. Investigating the effect of retained austenite and residual stress on rolling contact fatigue of carburized steel with XFEM and experimental approaches. Mater. Sci. Eng. A 2018, 732, 311–319. [Google Scholar] [CrossRef]
- Guan, J.; Wang, L.; Mao, Y.; Shi, X.; Ma, X.; Hu, B. A continuum damage mechanics based approach to damage evolution of M50 bearing steel considering residual stress induced by shot peening. Tribol. Int. 2018, 126, 218–228. [Google Scholar] [CrossRef]
- Zhang, Y.; Qu, S.; Lu, F.; Lai, F.; Ji, V.; Liu, H.; Li, X. Microstructures and rolling contact fatigue behaviors of 17Cr2Ni2MoVNb steel under combined ultrasonic surface rolling and shot peening. Int. J. Fatigue 2020, 141, 105867. [Google Scholar] [CrossRef]
- Walvekar, A.A.; Sadeghi, F. Rolling contact fatigue of case carburized steels. Int. J. Fatigue 2017, 95, 264–281. [Google Scholar] [CrossRef]
- Morris, D.; Sadeghi, F.; Chen, Y.C.; Wang, C.; Wang, B. Effect of residual stresses on microstructural evolution due to rolling contact fatigue. J. Tribol. 2018, 140, 061402. [Google Scholar] [CrossRef]
- Johnson, K.L. Contact Mechanics; Cambridge University Press: Cambridge, UK, 1985; ISBN 9781139171731. [Google Scholar]
- Pham, T.Q.; Khun, N.W.; Butler, D.L. New approach to estimate coverage parameter in 3D FEM shot peening simulation. Surf. Eng. 2017, 33, 687–695. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, W.; Zhang, S.; Zhao, Z. Modeling of Finite-Length Line Contact Problem with Consideration of Two Free-End Surfaces. J. Tribol. 2016, 138, 1–10. [Google Scholar] [CrossRef]
- Geitner, M.; Zornek, B.; Tobie, T.; Stahl, K. Investigations on the pitting load capacity of internal spur and helical gears. Forsch. im Ingenieurwesen/Eng. Res. 2019, 83, 553–561. [Google Scholar] [CrossRef]
- Wang, Q.; Zhao, B.; Fu, Y.; Kong, X.; Ma, H. An improved time-varying mesh stiffness model for helical gear pairs considering axial mesh force component. Mech. Syst. Signal Process. 2018, 106, 413–429. [Google Scholar] [CrossRef]
- Hills, D.A.; Nowell, D.S.A. Elastic Contacts, 1st ed.; Butterworth-Heinemann: Oxford, UK, 1993. [Google Scholar]
- Fatemi, A.; Socie, D.F. A critical plane approach to multiaxial fatigue damage including out-of-phase loading. Fatigue Fract. Eng. Mater. Struct. 1988, 11, 149–165. [Google Scholar] [CrossRef]
- Basan, R.; Marohnić, T. Multiaxial fatigue life calculation model for components in rolling-sliding line contact with application to gears. Fatigue Fract. Eng. Mater. Struct. 2019, 42, 1478–1493. [Google Scholar] [CrossRef]
- Shamsaei, N.; Fatemi, A. Effect of hardness on multiaxial fatigue behaviour and some simple approximations for steels. Fatigue Fract. Eng. Mater. Struct. 2009, 32, 631–646. [Google Scholar] [CrossRef]
- Tong, Z.; Xin, J.; Tong, S.; Yang, Z.; Zhao, J.; Mao, J. Internal flow structure, fault detection, and performance optimization of centrifugal pumps. J. Zhejiang Univ. A 2020, 21, 85–117. [Google Scholar] [CrossRef]
- Chen, Y.; Tong, Z.; Zheng, Y.; Samuelson, H.; Norford, L. Transfer learning with deep neural networks for model predictive control of HVAC and natural ventilation in smart buildings. J. Clean. Prod. 2020, 254, 119866. [Google Scholar] [CrossRef]
- Zhang, D.; Tong, Z.; Li, Y. The role of cash holding towards cleaner production in China’s manufacturing sectors: A financial constraint perspective. J. Clean. Prod. 2020, 245, 118875. [Google Scholar] [CrossRef]
- Bonori, G.; Barbieri, M.; Pellicano, F. Optimum profile modifications of spur gears by means of genetic algorithms. J. Sound Vib. 2008, 313, 603–616. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, G.; Li, X.; Ren, Y. Global optimization of reliability design for large ball mill gear transmission based on the Kriging model and genetic algorithm. Mech. Mach. Theory 2013, 69, 321–336. [Google Scholar] [CrossRef]
- Zhang, J.; Qin, X.; Xie, C.; Chen, H.; Jin, L. Optimization design on dynamic load sharing performance for an in-wheel motor speed reducer based on genetic algorithm. Mech. Mach. Theory 2018, 122, 132–147. [Google Scholar] [CrossRef]
- Wang, S.; Li, Y.; Yao, M.; Wang, R. Compressive residual stress introduced by shot peening. J. Mater. Process. Technol. 1998, 73, 64–73. [Google Scholar] [CrossRef]
- James, M.N.; Hughes, D.J.; Chen, Z.; Lombard, H.; Hattingh, D.G.; Asquith, D.; Yates, J.R.; Webster, P.J. Residual stresses and fatigue performance. Eng. Fail. Anal. 2007, 14, 384–395. [Google Scholar] [CrossRef]
- Chen, M.; Jiang, C.; Xu, Z.; Zhan, K.; Ji, V. Experimental study on macro- and microstress state, microstructural evolution of austenitic and ferritic steel processed by shot peening. Surf. Coat. Technol. 2019, 359, 511–519. [Google Scholar] [CrossRef]
- Vantadori, S.; Zanichelli, A. Fretting-fatigue analysis of shot-peened aluminium and titanium test specimens. Fatigue Fract. Eng. Mater. Struct. 2020. [Google Scholar] [CrossRef]
- Lin, Q.; Liu, H.; Zhu, C.; Chen, D.; Zhou, S. Effects of different shot peening parameters on residual stress, surface roughness and cell size. Surf. Coat. Technol. 2020, 398, 126054. [Google Scholar] [CrossRef]
- Mirjalili, S. Genetic algorithm. Stud. Comput. Intell. 2019, 780, 43–55. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Goodier, J.N. Theory of Elasticity; McGraw-Hill: New York, NY, USA, 1951. [Google Scholar]
- Farrahi, G.H.; Lebrijn, J.L.; Couratin, D. Effect of shot peening on resdiual stress and fatigue life of a spring steel. Fatigue Fract. Eng. Mater. Struct. 1995, 18, 211–220. [Google Scholar] [CrossRef]
- Cao, Y.J.; Sun, J.Q.; Ma, F.; Chen, Y.Y.; Cheng, X.Z.; Gao, X.; Xie, K. Effect of the microstructure and residual stress on tribological behavior of induction hardened GCr15 steel. Tribol. Int. 2017, 115, 108–115. [Google Scholar] [CrossRef]
- Yang, D.; Xiao, X.; Liu, Y.; Sun, J. Peripheral milling-induced residual stress and its effect on tensile-tensile fatigue life of aeronautic titanium alloy Ti-6Al-4V. Aeronaut. J. 2019, 123, 212–229. [Google Scholar] [CrossRef]
- Peyrac, C.; Flavenot, J. Optimisation of carburising and shot peening, in order to improve both bending and contact fatigue behaviour for gear applications. In Proceedings of the ICSP-9, Paris, France, 6–9 September 2005. [Google Scholar]
- Terrin, A.; Meneghetti, G. A comparison of rolling contact fatigue behaviour of 17NiCrMo6-4 case-hardened disc specimens and gears. Fatigue Fract. Eng. Mater. Struct. 2018, 41, 2321–2337. [Google Scholar] [CrossRef]
- Zammit, A. Shot Peening of Austempered Ductile Iron. In Advanced Surface Engineering Research; IntechOpen: Rijeka, Croatia, 2018. [Google Scholar]




| Parameter | Pinion | Gear |
|---|---|---|
| Normal module mn/mm | 5.645 | |
| Pressure angle α/◦ | 15 | |
| Helix angle β/◦ | 22.3 | |
| Contact ratio εα | 1.746 | |
| Face width L/mm | 54 | |
| Tooth number | z1 = 37 | z2 = 48 |
| Radius at the pitch point/mm | R1 = 27.029 | R2 = 35.065 |
| Rated output torque Trated/(N·m) | 3000 | |
| Rotating speed n/(r/min) | 500 | |
| Material | AISI 8620RH | |
| Young’s modulus/GPa | E1 = E2 = 210 | |
| Poisson’s ratio ν | ν1 = ν2 = 0.3 | |
| Yield strength Y/MPa | 1300 | |
| Population size, N | 200 |
| Maximum generation number, Gmax | 500 |
| Maximum stall generation number, Gs | 20 |
| Function tolerance, e | 10−6 |
| Crossover fraction, Pc | 0.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Jiang, Y.; Tong, Z.; Tong, S. Residual Stress Distribution Design for Gear Surfaces Based on Genetic Algorithm Optimization. Materials 2021, 14, 366. https://doi.org/10.3390/ma14020366
Chen Z, Jiang Y, Tong Z, Tong S. Residual Stress Distribution Design for Gear Surfaces Based on Genetic Algorithm Optimization. Materials. 2021; 14(2):366. https://doi.org/10.3390/ma14020366
Chicago/Turabian StyleChen, Zhou, Yibo Jiang, Zheming Tong, and Shuiguang Tong. 2021. "Residual Stress Distribution Design for Gear Surfaces Based on Genetic Algorithm Optimization" Materials 14, no. 2: 366. https://doi.org/10.3390/ma14020366
APA StyleChen, Z., Jiang, Y., Tong, Z., & Tong, S. (2021). Residual Stress Distribution Design for Gear Surfaces Based on Genetic Algorithm Optimization. Materials, 14(2), 366. https://doi.org/10.3390/ma14020366





