A New Shear Strength Criterion for Rock Masses with Non-Persistent Discontinuities Considering the Nonlinear Progressive Failure Process
Abstract
1. Introduction
2. The Establishment of the New Shear Strength Criterion
2.1. Data Collection
2.2. The New Shear Strength Criterion
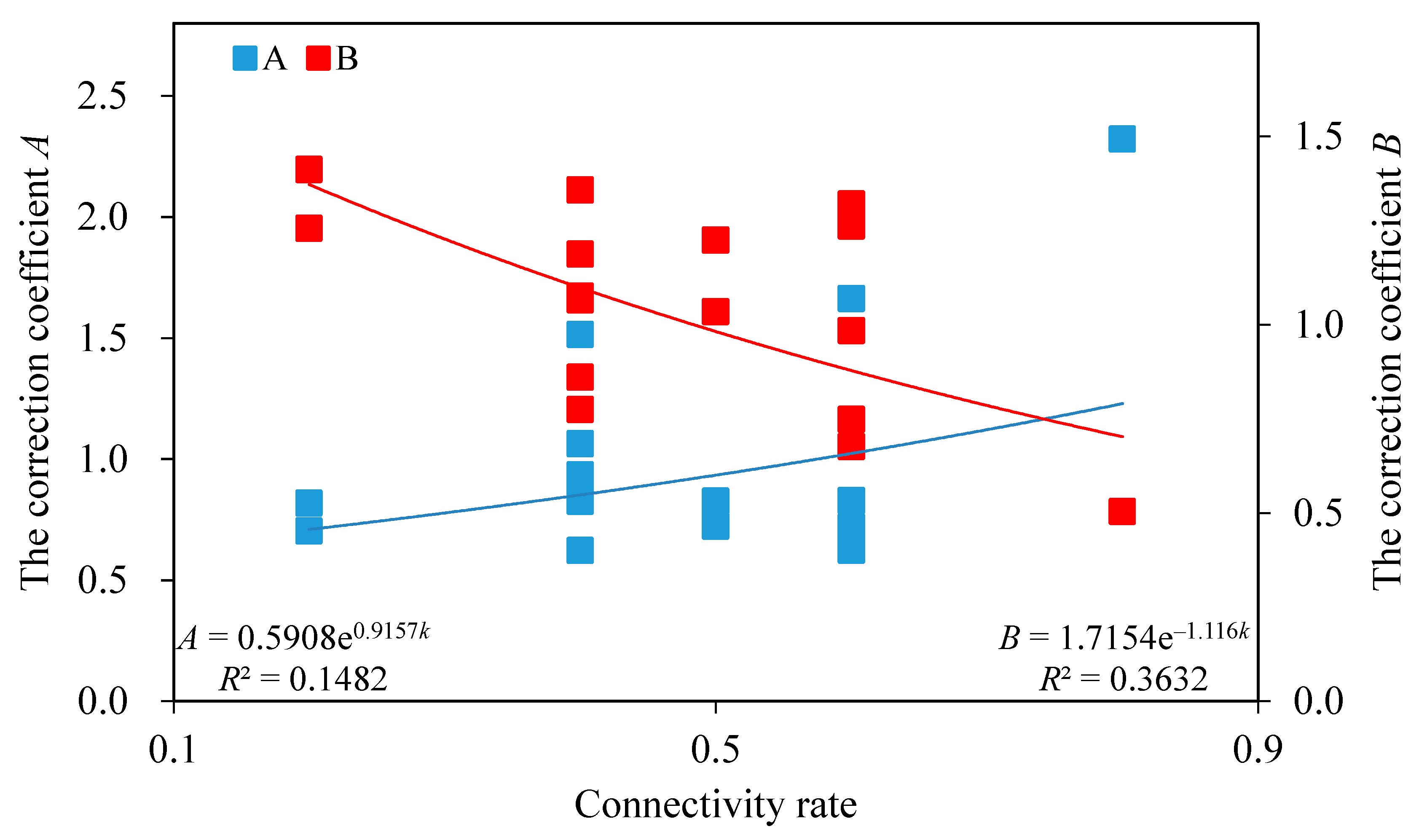
2.3. The Fitting Curve of Correction Coefficients Based on Test Results
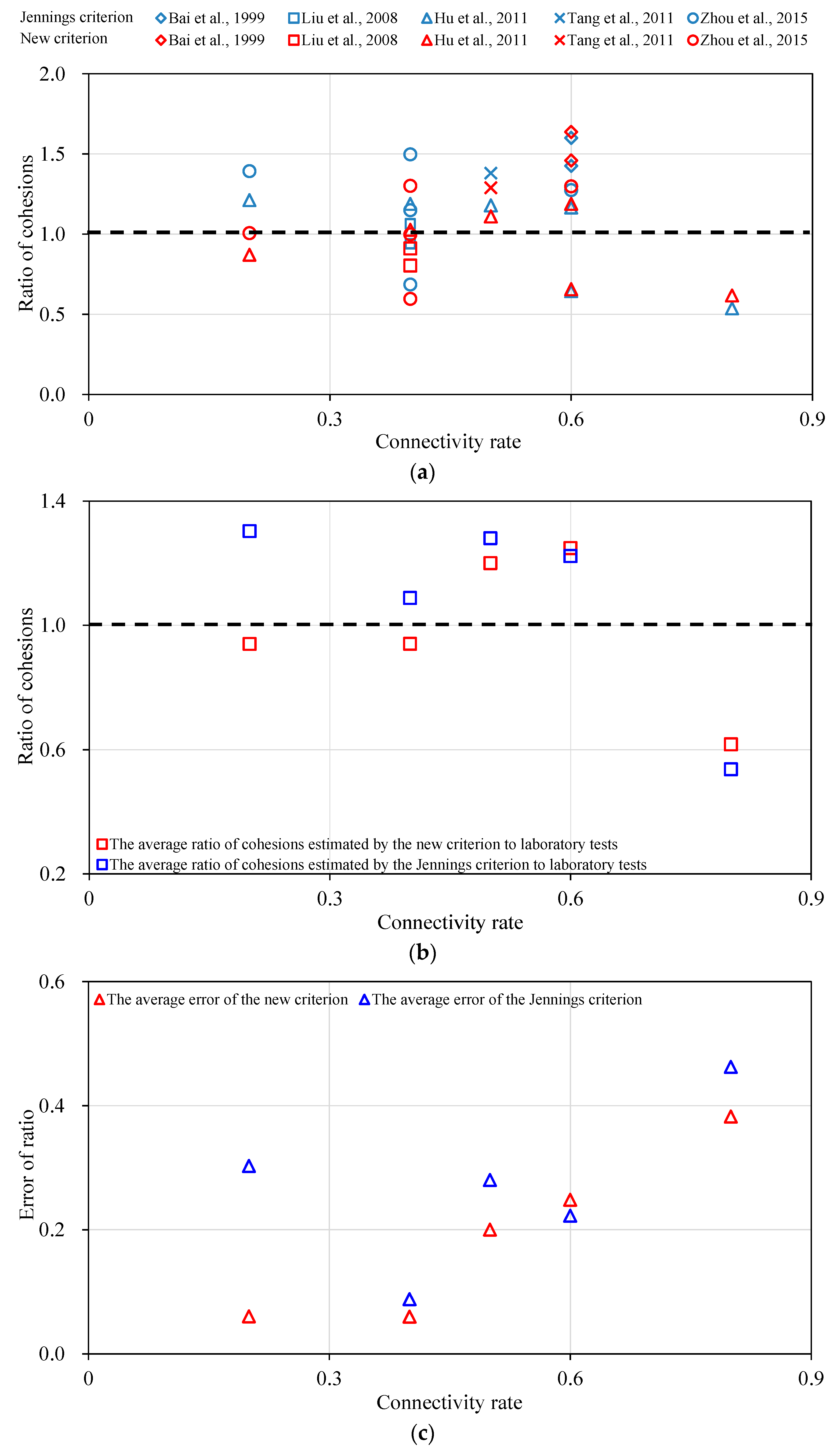
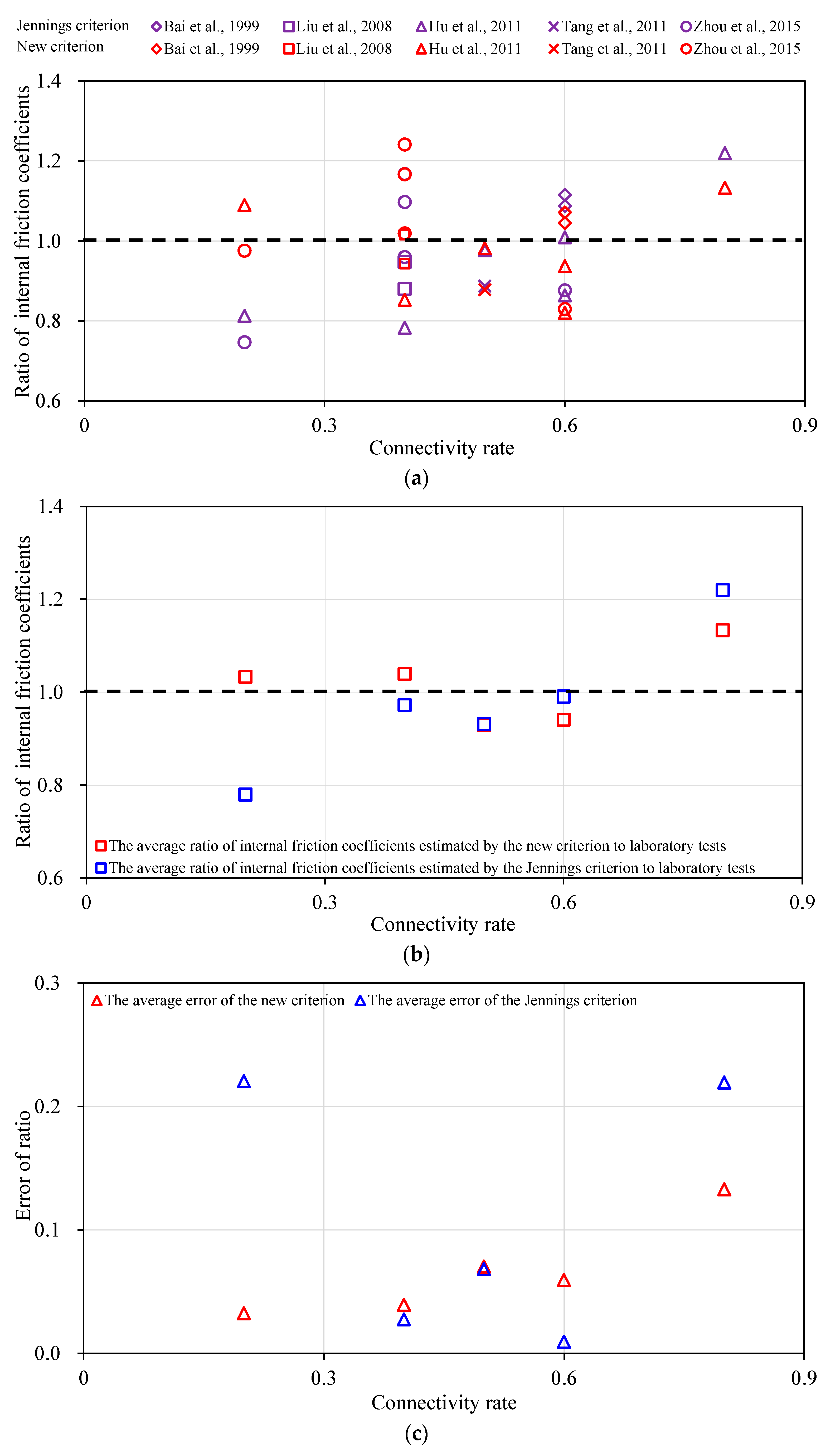
3. The Reliability of the New Shear Strength Criterion
4. Discussion
4.1. The Nonlinear Features of the Rock Bridge Strength during Progressive Failure
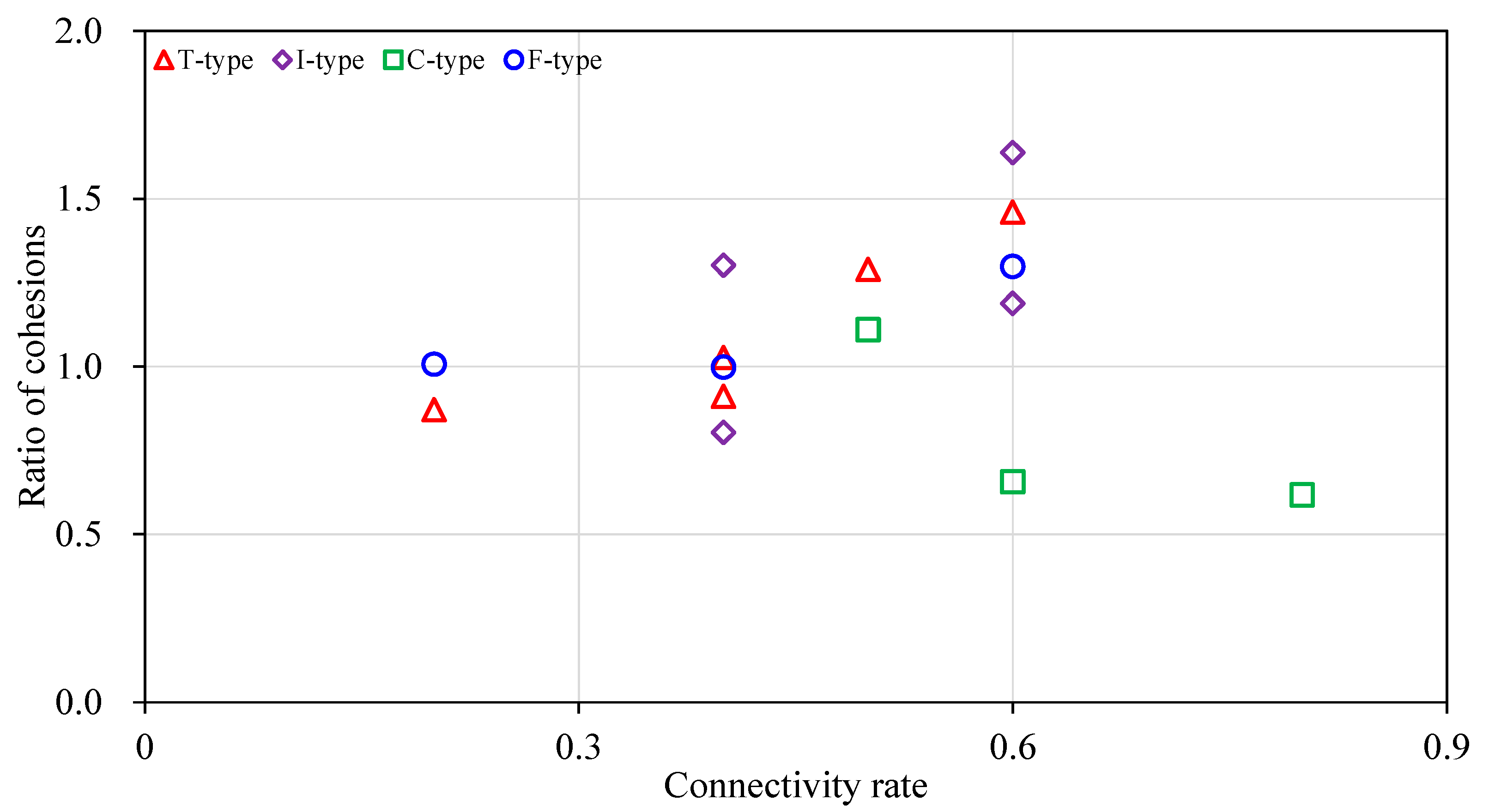
4.2. The Influence of Sample Types
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Goodman, R.E.; Taylor, R.L.; Brekke, T.A. A model for the mechanics of jointed rock. J. Soil Mech. Found. Div. 1968, 94, 637–659. [Google Scholar]
- Barton, N. A model study of rock-joint deformation. Int. J. Rock Mech. Min. Sci. 1972, 9, 579–602. [Google Scholar] [CrossRef]
- Hoek, E. Strength of jointed rock masses. Geotechnique 1983, 33, 187–223. [Google Scholar] [CrossRef]
- Barton, N. Review of a new shear-strength criterion for rock joints. Eng. Geol. 1973, 7, 287–332. [Google Scholar] [CrossRef]
- Jing, L.; Stephansson, O.; Nordlund, E. Study of rock joints under cyclic loading conditions. Rock Mech. Rock Eng. 1993, 26, 215–232. [Google Scholar] [CrossRef]
- Homand, F.; Belem, T.; Souley, M. Friction and degradation of rock joint surfaces under shear loads. Int. J. Numer. Anal. Methods Geomech. 2001, 25, 973–999. [Google Scholar] [CrossRef]
- Qi, S.W.; Wu, F.Q.; Zhou, Y.D.; Song, Y.H.; Gong, M.F. Influence of deep seated discontinuities on the left slope of Jinping I Hydropower Station and its stability analysis. Bull. Eng. Geol. Environ. 2010, 69, 333–342. [Google Scholar] [CrossRef]
- Saroglou, C.; Qi, S.W.; Guo, S.F.; Wu, F.Q. ARMR, a new classification system for the rating of anisotropic rock masses. Bull. Eng. Geol. Environ. 2019, 78, 3611–3626. [Google Scholar] [CrossRef]
- Newmark, N.M. Effects of earthquakes on dams and embankments. Geotechnique 1965, 15, 139–160. [Google Scholar] [CrossRef]
- Jibson, R.W. Methods for assessing the stability of slopes during earthquakes-A retrospective. Eng. Geol. 2011, 122, 43–50. [Google Scholar] [CrossRef]
- Lajtai, E.Z. Strength of discontinuous rocks in direct shear. Geotechnique 1969, 19, 218–233. [Google Scholar] [CrossRef]
- Jennings, J.E. A mathematical theory for the calculation of the stability of open cast mines. In Proceedings of the Symposium on the Theoretical Background to the Planning of Open Pit Mines, Johannesburg, South Africa, 1 January 1970; pp. 87–102. [Google Scholar]
- Savilabti, T.; Nordlund, E.; Stepanssion, O. Shear box testing and modelling of joint bridges. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstract. In Proceedings of the International Symposium on Rock Joints, Loen, Norway, 4–6 June 1990; pp. 295–300. [Google Scholar]
- Xu, J.N.; Zhu, W.S. The strength of colinear cracks failure under shearing—Compressive stress. Chin. J. Rock Mech. Eng. 1995, 14, 306–311. (In Chinese) [Google Scholar]
- Bai, S.W.; Ren, W.Z.; Feng, D.X.; Zhou, S.H. Research on the strength behaviour of rock containing coplanar close intermittent joints by direct shear test. Rock Soil Mech. 1999, 20, 10–15. (In Chinese) [Google Scholar]
- Chen, H.K.; Tang, H.M. Method for calculating strength parameters of structural planes controlling the rock block stability. J. Eng. Geol. 2008, 16, 37–41. (In Chinese) [Google Scholar]
- Liu, S.G.; Liu, H.N.; Wang, S.J.; Hu, B.; Zhang, X.P. Direct shear tests and PFC2d numerical simulation of intermittent joints. Chin. J. Rock Mech. Eng. 2008, 27, 1828–1836. (In Chinese) [Google Scholar]
- Hu, B.; Yang, Z.R.; Liu, S.G.; Wang, S.J.; Liu, H.N. Direct shear strength behavior of rock mass containing coplanar close intermittent joints. J. Eng. Geol. 2008, 16, 327–331. (In Chinese) [Google Scholar]
- Hu, B.; Zhang, N.; Wang, S.J.; Chen, J.S. Model test and strength analysis research on intermittent joint rock mass. Chin. J. Undergr. Space Eng. 2011, 7, 657–665. (In Chinese) [Google Scholar]
- Hu, B.; Wang, S.J.; Liu, X.L. Direct shear strength model of rock mass with coplanar intermittent joints. J. Jiangsu Univ. 2012, 33, 601–605. (In Chinese) [Google Scholar]
- Zhou, H.; Meng, F.Z.; Zhang, C.Q.; Lu, J.J.; Xu, R.C. Experimental study on effect of joints with different locations and sizes on rock failure. Chin. J. Rock Mech. Eng. 2015, 34, 3018–3028. (In Chinese) [Google Scholar]
- Liu, Y.M.; Xia, C.C.; Li, H.Z. Development in joints research and its application to rock mass containing discontinuous joints. Chin. J. Undergr. Space Eng. 2007, 3, 682–687. (In Chinese) [Google Scholar]
- Liu, Y.M.; Liu, J.; Xia, C.C. Research on strength behavior of rock mass containing discontinuous joints by direct shear test under different joint surface morphologies. Rock Soil Mech. 2014, 35, 1269–1274. (In Chinese) [Google Scholar]
- Xia, C.C.; Xiao, W.M.; Ding, Z.Z. Modification of Jennings strength criterion for intermittent joints considering rock bridge weakening and joint surface undulating angle. Chin. J. Rock Mech. Eng. 2010, 29, 485–492. (In Chinese) [Google Scholar]
- Tang, Z.C.; Xia, C.C.; Ding, Z.Z. Analysis of shear deformation law for intermittent jointed rock mass. Rock Soil Mech. 2011, 32, 2353–2358. (In Chinese) [Google Scholar]
- Tang, Z.C.; Xia, C.C.; Liu, Y.M. Modified Jennings shear strength criterion based on mechanical weakening model of rock bridges. Chin. J. Geotech. Eng. 2012, 34, 2093–2099. (In Chinese) [Google Scholar]
- Gehle, C.; Kutter, H.K. Breakage and shear behavior of intermittent rock joints. Int. J. Rock Mech. Min. Sci. 2003, 40, 687–700. [Google Scholar] [CrossRef]
- Gerolymatou, E.; Triantafyllidis, T. Shearing of materials with intermittent joints. Rock Mech. Rock Eng. 2016, 49, 2689–2700. [Google Scholar] [CrossRef]
- Martin, C. Seventeenth Canadian geotechnical colloquium: The effect of cohesion loss and stress path on brittle rock strength. Can. Geotech. J. 1997, 34, 698–725. [Google Scholar] [CrossRef]
- Hajiabdolmajid, V.; Kaiser, P.; Martin, C. Modelling brittle failure of rock. Int. J. Rock Mech. Min. Sci. 2002, 39, 731–774. [Google Scholar] [CrossRef]
- Wong, R.H.C.; Wang, S.W. Experimental and numerical study on the effect of material property, normal stress and the position of joint on the progressive failure under direct shear. NARMS-TAC2002. In Proceedings of the Mining and Tunneling Innovation and Opportunity, Toronto, ON, Canada, 7–10 July 2002; pp. 1009–1016. [Google Scholar]
- Guo, S.; Qi, S. Numerical study on progressive failure of hard rock samples with an unfilled undulate joint. Eng. Geol. 2015, 193, 173–182. [Google Scholar] [CrossRef]
- Guo, S.F.; Qi, S.W.; Zhan, Z.F.; Zheng, B.W. Plastic-strain-dependent strength model to simulate the cracking process of brittle rocks with an existing non-persistent joint. Eng. Geol. 2017, 231, 114–125. [Google Scholar] [CrossRef]
- Huang, X.L.; Qi, S.W.; Zheng, B.W.; Guo, S.F.; Liang, N.; Zhan, Z.F. Progressive failure characteristics of brittle rock under high-strain-rate compression using the bonded particle model. Materials 2020, 13, 3943. [Google Scholar] [CrossRef] [PubMed]
- Brace, W.F. An extension of the Griffith theory of fracture to rocks. J. Geophys. Res. 1960, 65, 3477–3480. [Google Scholar] [CrossRef]
- Horii, H.; Nemat-Nasser, S. Brittle failure in compression: Splitting, faulting and brittle-ductile transition. Philos. Trans. R. Soc. Lond. Ser. A 1986, 319, 337–374. [Google Scholar]
- Cai, M.; Kaiser, P.K.; Tasaka, Y.; Maejima, T.; Morioka, H.; Minami, M. Generalized crack initiation and crack damage stress thresholds of brittle rock masses near underground excavations. Int. J. Rock Mech. Min. Sci. 2004, 41, 833–847. [Google Scholar] [CrossRef]
- Guo, S.F.; Qi, S.W.; Zhan, Z.F.; Ma, L.N.; Getahun, E.; Zhang, S.S. Numerical study on the progressive failure of heterogeneous geomaterials under varied confining stresses. Eng. Geol. 2020, 269, 10556. [Google Scholar] [CrossRef]

| Sample Type | Connectivity Rate | Quality Ratio of Materials | Cohesion of the Rock Bridge (MPa) | Angle of the Internal Friction of the Rock Bridge (°) | Cohesion of the Discontinuity (MPa) | Angle of the Internal Friction of the Discontinuity (°) | Reference |
|---|---|---|---|---|---|---|---|
| T-type I-type | 0.6 | Sand: Gypsum: Water = 3:3:2 | 4.23 | 26.55 | 0 | 35.2 | [15] |
| T-type I-type | 0.4 | Cement: Sand: Water = 5:5:2 | 5.2 | 56.31 | 0.19 | 39.69 | [17] |
| T-type I-type C-type | 0.2, 0.4, 0.5, 0.6, 0.8 | Cement: Sand: Water = 5:5:2 | 4.7 | 59.24 | 0.63 | 37.95 | [19] |
| T-type | 0.5 | Cement: Sand: Water = 2:3:1 | 3.93 | 39.5 | 0 | 32.3 | [25] |
| F-type I-type B-type | 0.2, 0.4, 0.6 | Quartz sand: Cement = 1:1 | 8.3 | 37.16 | 1.63 | 32.8 | [21] |
| Sample Type | Connectivity Rate | Shear Rate | Cohesion (MPa) | Coefficient of the Internal Friction | Reference |
|---|---|---|---|---|---|
| T-type | 0.6 | 0.003 mm/s | 1.186 | 0.559 | [15] |
| I-type | 1.057 | 0.573 | |||
| T-type | 0.4 | 0.005 mm/s | 3 | 1.4 | [17] |
| I-type | 3.4 | 1.3 | |||
| T-type | 0.2 | 0.005 mm/s | 3.205 | 1.836 | [19] |
| T-type | 0.4 | 2.585 | 1.664 | ||
| I-type | 0.6 | 1.9367 | 1.13 | ||
| C-type | 0.5 | 2.259 | 1.238 | ||
| C-type | 0.6 | 3.504 | 1.29 | ||
| C-type | 0.8 | 2.687 | 0.759 | ||
| T-type | 0.5 | 0.005 mm/s | 1.423 | 0.821 | [25] |
| F-type | 0.2 | 1 kN/s | 5 | 0.985 | [21] |
| F-type | 0.4 | 4.9 | 0.743 | ||
| F-type | 0.6 | 3.37 | 0.787 | ||
| I-type | 0.4 | 3.76 | 0.649 | ||
| B-type | 0.4 | 8.2 | 0.61 |
| Sample Type | Connectivity Rate | A | B | Reference |
|---|---|---|---|---|
| T-type | 0.6 | 0.701 | 0.677 | [15] |
| I-type | 0.6 | 0.625 | 0.749 | |
| T-type | 0.4 | 0.937 | 1.187 | [17] |
| I-type | 0.4 | 1.065 | 1.076 | |
| T-type | 0.2 | 0.819 | 1.256 | [19] |
| T-type | 0.4 | 0.827 | 1.358 | |
| I-type | 0.6 | 0.829 | 0.985 | |
| C-type | 0.5 | 0.827 | 1.035 | |
| C-type | 0.6 | 1.663 | 1.262 | |
| C-type | 0.8 | 2.322 | 0.504 | |
| T-type | 0.5 | 0.724 | 1.225 | [25] |
| F-type | 0.2 | 0.704 | 1.412 | [21] |
| F-type | 0.4 | 0.853 | 1.066 | |
| F-type | 0.6 | 0.720 | 1.321 | |
| I-type | 0.4 | 0.624 | 0.861 | |
| B-type | 0.4 | 1.516 | 0.775 |
| Sample Type | Connectivity Rate | Test Result of the Cohesion c (MPa) | Estimated Cohesion by the Jennings Criterion c1 (MPa) | Ratio of c1 to c Rc1 | Estimated Cohesion by the New Criterion c2 (MPa) | Ratio of c2 to c Rc2 | Reference |
|---|---|---|---|---|---|---|---|
| T-type | 0.6 | 1.186 | 1.692 | 1.427 | 1.7316 | 1.46 | [15] |
| I-type | 0.6 | 1.057 | 1.692 | 1.601 | 1.7316 | 1.6382 | |
| T-type | 0.4 | 3.000 | 3.196 | 1.065 | 2.7347 | 0.9116 | [17] |
| I-type | 0.4 | 3.400 | 3.196 | 0.940 | 2.7347 | 0.8043 | |
| T-type | 0.2 | 3.205 | 3.886 | 1.212 | 2.7939 | 0.8717 | [19] |
| T-type | 0.4 | 2.585 | 3.072 | 1.188 | 2.6551 | 1.0271 | |
| I-type | 0.6 | 1.9367 | 2.258 | 1.166 | 2.302 | 1.1886 | |
| C-type | 0.5 | 2.259 | 2.665 | 1.180 | 2.5096 | 1.1109 | |
| C-type | 0.6 | 3.504 | 2.258 | 0.644 | 2.302 | 0.657 | |
| C-type | 0.8 | 2.687 | 1.444 | 0.537 | 1.6594 | 0.6175 | |
| T-type | 0.5 | 1.423 | 1.965 | 1.381 | 1.835 | 1.2896 | [25] |
| F-type | 0.2 | 5.000 | 6.966 | 1.393 | 5.0373 | 1.0075 | [21] |
| F-type | 0.4 | 4.900 | 5.632 | 1.149 | 4.8957 | 0.9991 | |
| F-type | 0.6 | 3.370 | 4.298 | 1.275 | 4.3757 | 1.2984 | |
| I-type | 0.4 | 3.760 | 5.632 | 1.498 | 4.8957 | 1.302 | |
| B-type | 0.4 | 8.200 | 5.632 | 0.687 | 4.8957 | 0.597 |
| Sample Type | Connectivity Rate | Test Result of the Internal Friction Coefficient tanφ | Estimated Internal Friction Coefficient by the Jennings Criterion tanφ1 | Ratio of tanφ1 to tanφ Rf1 | Estimated Internal Friction Coefficient by the New Criterion tanφ2 | Ratio of tanφ2 to tanφ Rf2 | Reference |
|---|---|---|---|---|---|---|---|
| T-type | 0.6 | 0.559 | 0.623 | 1.1154 | 0.5988 | 1.0711 | [15] |
| I-type | 0.6 | 0.573 | 0.623 | 1.0876 | 0.5988 | 1.045 | |
| T-type | 0.4 | 1.400 | 1.232 | 0.88 | 1.3199 | 0.9428 | [17] |
| I-type | 0.4 | 1.300 | 1.232 | 0.9477 | 1.3199 | 1.0153 | |
| T-type | 0.2 | 1.836 | 1.491 | 0.8123 | 2.0005 | 1.0896 | [19] |
| T-type | 0.4 | 1.664 | 1.303 | 0.7829 | 1.4186 | 0.8525 | |
| I-type | 0.6 | 1.130 | 1.140 | 1.0088 | 1.0581 | 0.9364 | |
| C-type | 0.5 | 1.238 | 1.208 | 0.9762 | 1.2148 | 0.9812 | |
| C-type | 0.6 | 1.290 | 1.114 | 0.8637 | 1.0581 | 0.8202 | |
| C-type | 0.8 | 0.759 | 0.926 | 1.2195 | 0.86 | 1.133 | |
| T-type | 0.5 | 0.821 | 0.728 | 0.887 | 0.7208 | 0.8779 | [25] |
| F-type | 0.2 | 0.985 | 0.735 | 0.7464 | 0.961 | 0.9756 | [21] |
| F-type | 0.4 | 0.743 | 0.713 | 0.9594 | 0.757 | 1.0188 | |
| F-type | 0.6 | 0.787 | 0.690 | 0.8763 | 0.6529 | 0.8296 | |
| I-type | 0.4 | 0.649 | 0.713 | 1.0972 | 0.757 | 1.1664 | |
| B-type | 0.4 | 0.610 | 0.713 | 1.1673 | 0.757 | 1.241 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, B.; Qi, S.; Guo, S.; Huang, X.; Liang, N.; Zou, Y.; Luo, G. A New Shear Strength Criterion for Rock Masses with Non-Persistent Discontinuities Considering the Nonlinear Progressive Failure Process. Materials 2020, 13, 4694. https://doi.org/10.3390/ma13214694
Zheng B, Qi S, Guo S, Huang X, Liang N, Zou Y, Luo G. A New Shear Strength Criterion for Rock Masses with Non-Persistent Discontinuities Considering the Nonlinear Progressive Failure Process. Materials. 2020; 13(21):4694. https://doi.org/10.3390/ma13214694
Chicago/Turabian StyleZheng, Bowen, Shengwen Qi, Songfeng Guo, Xiaolin Huang, Ning Liang, Yu Zou, and Guangming Luo. 2020. "A New Shear Strength Criterion for Rock Masses with Non-Persistent Discontinuities Considering the Nonlinear Progressive Failure Process" Materials 13, no. 21: 4694. https://doi.org/10.3390/ma13214694
APA StyleZheng, B., Qi, S., Guo, S., Huang, X., Liang, N., Zou, Y., & Luo, G. (2020). A New Shear Strength Criterion for Rock Masses with Non-Persistent Discontinuities Considering the Nonlinear Progressive Failure Process. Materials, 13(21), 4694. https://doi.org/10.3390/ma13214694




