Multigene Expression Programming Based Forecasting the Hardened Properties of Sustainable Bagasse Ash Concrete
Abstract
:1. Introduction
2. Modeling Techniques and Database
2.1. Multigene Expression Programming
2.2. Modeling Database
2.3. Cross-Validation with k-Fold Algorithm
2.4. Models Evaluation by Statistical Measures
3. Mix Proportions for Bagasse Ash Concrete (BAC)
4. Results and Discussion
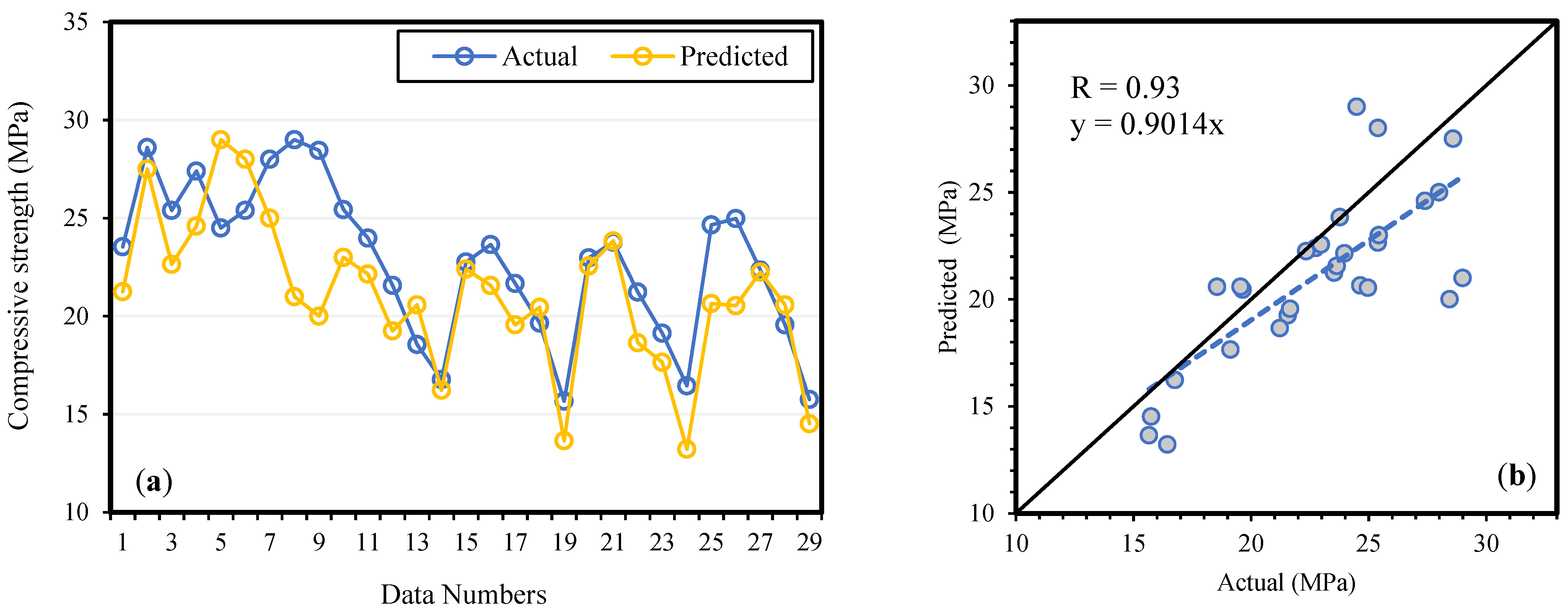
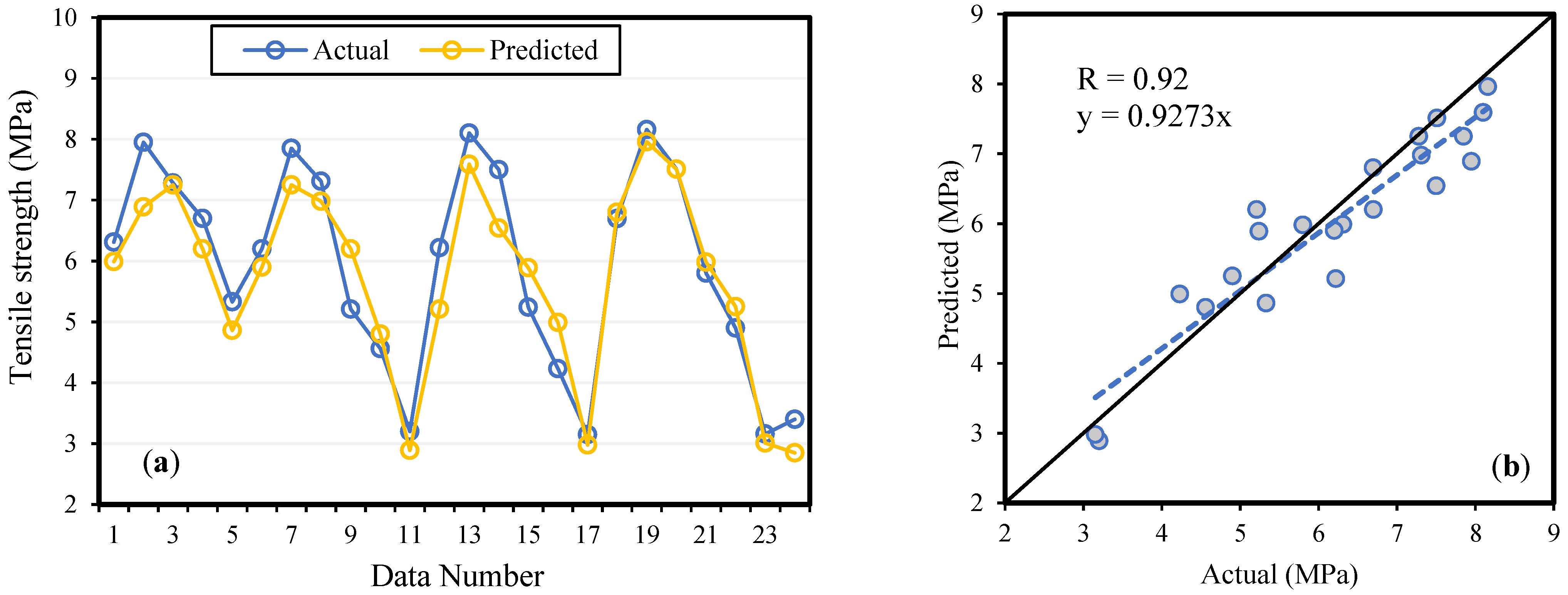
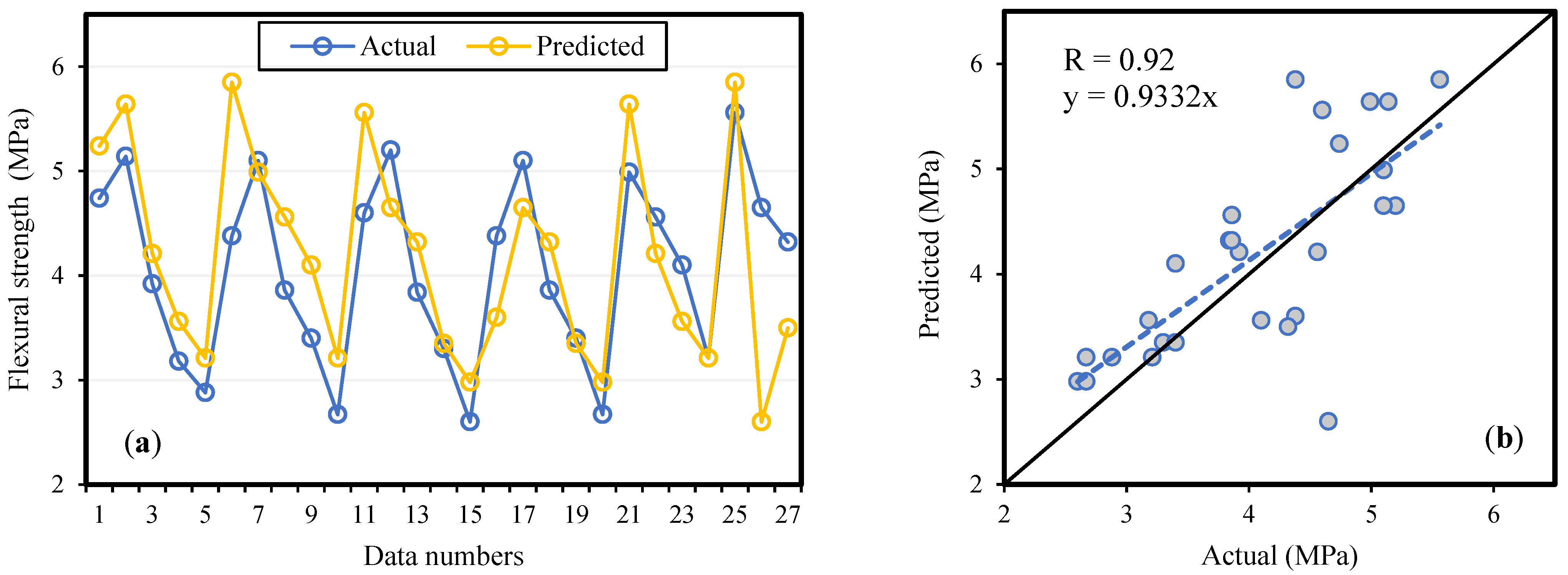
4.1. Mechanical Properties of BAC
4.2. Formulation of BAC Mechanical Properties
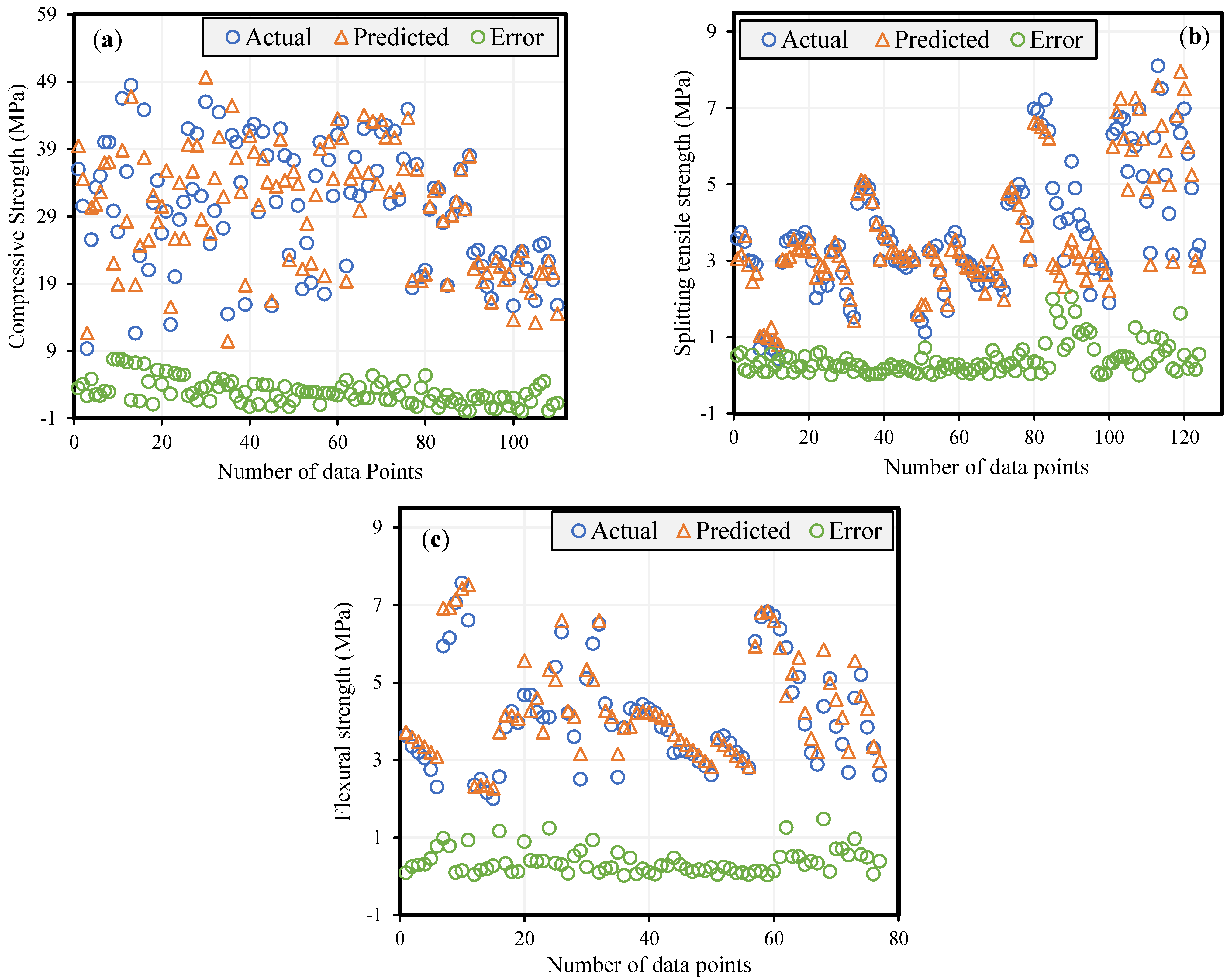
4.3. Models Validation by Experimental Data
4.4. Statistical Analysis and Generalizability of the Models
4.5. 10-Fold Cross-Validation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Du, H.; Dai Pang, S. Value-added utilization of marine clay as cement replacement for sustainable concrete production. J. Clean. Prod. 2018, 198, 867–873. [Google Scholar] [CrossRef]
- He, Z.; Zhu, X.; Wang, J.; Mu, M.; Wang, Y. Comparison of CO2 emissions from OPC and recycled cement production. Constr. Build. Mater. 2019, 211, 965–973. [Google Scholar] [CrossRef]
- Mao, L.X.; Hu, Z.; Xia, J.; Feng, G.L.; Azim, I.; Yang, J.; Liu, Q.F. Multi-phase modelling of electrochemical rehabilitation for ASR and chloride affected concrete composites. Compos. Struct. 2019, 207, 176–189. [Google Scholar] [CrossRef]
- Iqbal, M.F.; Javed, M.F.; Rauf, M.; Azim, I.; Ashraf, M.; Yang, J.; Liu, Q.F. Sustainable utilization of foundry waste: Forecasting mechanical properties of foundry sand based concrete using multi-expression programming. Sci. Total Environ. 2021, 780, 146524. [Google Scholar] [CrossRef] [PubMed]
- Iqbal, M.F.; Liu, Q.F.; Azim, I.; Zhu, X.; Yang, J.; Javed, M.F.; Rauf, M. Prediction of mechanical properties of green concrete incorporating waste foundry sand based on gene expression programming. J. Hazard. Mater. 2020, 384, 121322. [Google Scholar] [CrossRef] [PubMed]
- Frontera, P.; Malara, A.; Mistretta, M. Recent Trends in Sustainability Assessment of “Green Concrete”. In Smart Innovation, Systems and Technologies; New Metropolitan Perspectives; Bevilacqua, C., Calabrò, F., Della Spina, L., Eds.; Springer Nature: Cham, Switzerland, 2020; Volume 178, pp. 1402–1412. [Google Scholar]
- Pippo, W.A.; Luengo, C.A. Sugarcane energy use: Accounting of feedstock energy considering current agro-industrial trends and their feasibility. Int. J. Energy Environ. Eng. 2013, 4, 10. [Google Scholar] [CrossRef] [Green Version]
- Cordeiro, G.C.; Toledo Filho, R.D.; Fairbairn, E.M.; Tavares, L.M.; Oliveira, C.H. Influence of mechanical grinding on the pozzolanic activity of residual sugarcane bagasse ash. In Proceedings of the International RILEM Conference on the Use of Recycled Materials in Building and Structures, Barcelona, Spain, 8–11 November 2004; pp. 731–740. [Google Scholar]
- Pedersen, K.H.; Jensen, A.D.; Skjøth-Rasmussen, M.S.; Dam-Johansen, K. A review of the interference of carbon containing fly ash with air entrainment in concrete. Prog. Energy Combust. Sci. 2008, 34, 135–154. [Google Scholar] [CrossRef]
- Chusilp, N.; Jaturapitakkul, C.; Kiattikomol, K. Utilization of bagasse ash as a pozzolanic material in concrete. Constr. Build. Mater. 2009, 23, 3352–3358. [Google Scholar] [CrossRef]
- Hasan, N.M.S.; Sobuz, H.R.; Tamanna, N.; Slah, M. Properties of concrete by using bagasse ash and recycle aggregate. Concr. Res. Lett. 2014, 5, 768–785. [Google Scholar]
- Jagadesh, P.; Ramachandramurthy, A.; Murugesan, R. Evaluation of mechanical properties of Sugar Cane Bagasse Ash concrete. Constr. Build. Mater. 2018, 176, 608–617. [Google Scholar] [CrossRef]
- Bahurudeen, A.; Santhanam, M. Performance evaluation of sugarcane bagasse ash-based cement for durable concrete. In Proceedings of the 4th International Conference on the Durability of Concrete Structures, Purdue University, West Lafayette, IN, USA, 24–26 July 2014. [Google Scholar]
- Bahurudeen, A.; Wani, K.; Basit, M.A.; Santhanam, M. Assesment of pozzolanic performance of sugarcane bagasse ash. J. Mater. Civ. Eng. 2016, 28, 04015095. [Google Scholar] [CrossRef]
- Rerkpiboon, A.; Tangchirapat, W.; Jaturapitakkul, C. Strength, chloride resistance, and expansion of concretes containing ground bagasse ash. Constr. Build. Mater. 2015, 101, 983–989. [Google Scholar] [CrossRef]
- Khan, M.I. Predicting properties of high performance concrete containing composite cementitious materials using artificial neural networks. Autom. Constr. 2012, 22, 516–524. [Google Scholar] [CrossRef]
- Dantas, A.T.A.; Leite, M.B.; de Jesus Nagahama, K. Prediction of compressive strength of concrete containing construction and demolition waste using artificial neural networks. Constr. Build. Mater. 2013, 38, 717–722. [Google Scholar] [CrossRef]
- Golafshani, E.M.; Behnood, A.; Arashpour, M. Predicting the compressive strength of normal and High-Performance Concretes using ANN and ANFIS hybridized with Grey Wolf Optimizer. Constr. Build. Mater. 2020, 232, 117266. [Google Scholar] [CrossRef]
- Parichatprecha, R.; Nimityongskul, P. Analysis of durability of high performance concrete using artificial neural networks. Constr. Build. Mater. 2009, 23, 910–917. [Google Scholar] [CrossRef]
- Farooq, F.; Nasir Amin, M.; Khan, K.; Rehan Sadiq, M.; Javed, M.F.; Aslam, F.; Alyousef, R. A Comparative Study of Random Forest and Genetic Engineering Programming for the Prediction of Compressive Strength of High Strength Concrete (HSC). Appl. Sci. 2020, 10, 7330. [Google Scholar] [CrossRef]
- Zhang, J.; Li, D.; Wang, Y. Toward intelligent construction: Prediction of mechanical properties of manufactured-sand concrete using tree-based models. J. Clean. Prod. 2020, 258, 120665. [Google Scholar] [CrossRef]
- Sun, Y.; Li, G.; Zhang, J.; Qian, D. Prediction of the strength of rubberized concrete by an evolved random forest model. Adv. Civ. Eng. 2019, 2019. [Google Scholar] [CrossRef] [Green Version]
- Chou, J.S.; Chiu, C.K.; Farfoura, M.; Al-Taharwa, I. Optimizing the prediction accuracy of concrete compressive strength based on a comparison of data-mining techniques. J. Comput. Civ. Eng. 2011, 25, 242–253. [Google Scholar] [CrossRef]
- Deng, F.; He, Y.; Zhou, S.; Yu, Y.; Cheng, H.; Wu, X. Compressive strength prediction of recycled concrete based on deep learning. Constr. Build. Mater 2018, 175, 562–569. [Google Scholar] [CrossRef]
- Alexiadis, A. Deep Multiphysics and Particle–Neuron Duality: A Computational Framework Coupling (Discrete) Multiphysics and Deep Learning. Appl. Sci. 2019, 9, 5369. [Google Scholar] [CrossRef] [Green Version]
- Ashteyat, A.; Obaidat, Y.T.; Murad, Y.Z.; Haddad, R. Compressive strength prediction of lightweight short columns at elevated temperature using gene expression programing and artificial neural network. J. Civ. Eng. Manag. 2020, 26, 189–199. [Google Scholar] [CrossRef]
- Behnood, A.; Golafshani, E.M. Predicting the compressive strength of silica fume concrete using hybrid artificial neural network with multi-objective grey wolves. J. Clean. Prod. 2018, 202, 54–64. [Google Scholar] [CrossRef]
- Sadrmomtazi, A.; Sobhani, J.; Mirgozar, M. Modeling compressive strength of EPS lightweight concrete using regression, neural network and ANFIS. Constr. Build. Mater. 2013, 42, 205–216. [Google Scholar] [CrossRef]
- Öztaş, A.; Pala, M.; Özbay, E.; Kanca, E.; Caglar, N.; Bhatti, M.A. Predicting the compressive strength and slump of high strength concrete using neural network. Constr. Build. Mater. 2006, 20, 769–775. [Google Scholar] [CrossRef]
- Nguyen, T.; Kashani, A.; Ngo, T.; Bordas, S. Deep neural network with high-order neuron for the prediction of foamed concrete strength. Comput.-Aided Civ. Infrastruct. Eng. 2019, 34, 316–332. [Google Scholar] [CrossRef]
- Getahun, M.A.; Shitote, S.M.; Gariy, Z.C.A. Artificial neural network based modelling approach for strength prediction of concrete incorporating agricultural and construction wastes. Constr. Build. Mater. 2018, 190, 517–525. [Google Scholar] [CrossRef]
- Oltean, M.; Groşan, C. Evolving evolutionary algorithms using multi expression programming. In Advances in Artificial Life. ECAL 2003. Lecture Notes in Computer Science; Banzhaf, W., Ziegler, J., Christaller, T., Dittrich, P., Kim, J.T., Eds.; Springer: BBerlin/Heidelberg, Germany, 2003; Volume 2801, pp. 651–658. [Google Scholar] [CrossRef]
- Shah, M.; Alaloul, W.; Alqahtani, A.; Aldrees, A.; Musarat, M.; Javed, M. Predictive Modeling Approach for Surface Water Quality: Development and Comparison of Machine Learning Models. Sustainability 2021, 13, 7515. [Google Scholar] [CrossRef]
- Javed, M.F.; Farooq, F.; Memon, S.A.; Akbar, A.; Khan, M.A.; Aslam, F.; Alyousef, R.; Alabduljabbar, H.; Rehman, S.K.U. New prediction model for the ultimate axial capacity of concrete-filled steel tubes: An evolutionary approach. Crystals 2020, 10, 741. [Google Scholar] [CrossRef]
- Aslam, F.; Farooq, F.; Amin, M.N.; Khan, K.; Waheed, A.; Akbar, A.; Alabdulijabbar, H. Applications of Gene Expression Programming for Estimating Compressive Strength of High-Strength Concrete. Adv. Civ. Eng. 2020, 2020. [Google Scholar] [CrossRef]
- Shah, M.I.; Memon, S.A.; Khan Niazi, M.S.; Amin, M.N.; Aslam, F.; Javed, M.F. Machine Learning-Based Modeling with Optimization Algorithm for Predicting Mechanical Properties of Sustainable Concrete. Adv. Civ. Eng. 2021, 2021. [Google Scholar] [CrossRef]
- Oltean, M.; Grosan, C. A comparison of several linear genetic programming techniques. Complex Syst. 2003, 14, 285–314. [Google Scholar]
- Shah, M.I.; Amin, M.N.; Khan, K.; Niazi, M.S.K.; Aslam, F.; Alyousef, R.; Mosavi, A. Performance Evaluation of Soft Computing for Modeling the Strength Properties of Waste Substitute Green Concrete. Sustainability 2021, 5, 2867. [Google Scholar] [CrossRef]
- Arabshahi, A.; Gharaei-Moghaddam, N.; Tavakkolizadeh, M. Development of applicable design models for concrete columns confined with aramid fiber reinforced polymer using Multi-Expression Programming. Structures 2020, 23, 225–244. [Google Scholar] [CrossRef]
- Oltean, M.; Dumitrescu, D. Multi Expression Programming; Technical report, UBB-01-2002; Babeş-Bolyai University: Cluj-Napoca, Romania, 2002. [Google Scholar]
- Gandomi, A.H.; Faramarzifar, A.; Rezaee, P.G.; Asghari, A.; Talatahari, S. New design equations for elastic modulus of concrete using multi expression programming. J. Civ. Eng. Manag. 2015, 21, 761–774. [Google Scholar] [CrossRef] [Green Version]
- Sharifi, S.; Abrishami, S.; Gandomi, A.H. Consolidation assessment using Multi Expression Programming. Appl. Soft Comput. 2020, 86, 105842. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, B.; Wang, L.; Zhu, F. Predicting cement compressive strength using double-layer multi-expression Programming. In Proceedings of the 2012 Fourth International Conference on Computational and Information Sciences, Chongqing, China, 17–19 August 2012; pp. 94–97. [Google Scholar]
- Alavi, A.H.; Mollahasani, A.; Gandomi, A.H.; Bazaz, J.B. Formulation of secant and reloading soil deformation moduli using multi expression programming. Eng. Comput. 2012, 29, 173–197. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Gandomi, A.H.; Alavi, A.H.; Vesalimahmood, M. Modeling of compressive strength of HPC mixes using a combined algorithm of genetic programming and orthogonal least squares. Struct. Eng. Mech. 2010, 36, 225–241. [Google Scholar] [CrossRef]
- Srinivasan, R.; Sathiya, K. Experimental study on bagasse ash in concrete. Int. J. Serv. Learn. Eng. 2010, 5, 60–66. [Google Scholar] [CrossRef] [Green Version]
- Patel, J.A.; Raijiwala, D. Experimental study on use of sugar cane bagasse ash in concrete by partially replacement with cement. Int. J. Innov. Res. Sci. Eng. Technol. 2015, 4, 2228–2232. [Google Scholar]
- Neeraja, D.; Jagan, S.; Kumar, S.; Mohan, P.G. Experimental Study on Strength Properties of Concrete by Partial Replacement of Cement with Sugarcane Bagasse Ash. Nat. Environ. Pollut. Technol. 2014, 13, 629. [Google Scholar]
- Ganesan, K.; Rajagopal, K.; Thangavel, K. Evaluation of bagasse ash as supplementary cementitious material. Cem. Concr. Compos. 2007, 29, 515–524. [Google Scholar] [CrossRef]
- Subramani, T.; Prabhakaran, M. Experimental study on bagasse ash in concrete. Int. J. Appl. Innov. Eng. Manag. 2015, 4, 163–172. [Google Scholar]
- Rukzon, S.; Chindaprasirt, P. Utilization of bagasse ash in high-strength concrete. Mater. Des. 2012, 34, 45–50. [Google Scholar] [CrossRef]
- Cordeiro, G.C.; Toledo Filho, R.D.; Tavares, L.M.; Fairbairn, E.D.M.R. Ultrafine grinding of sugar cane bagasse ash for application as pozzolanic admixture in concrete. Cem. Concr. Res. 2009, 39, 110–115. [Google Scholar] [CrossRef]
- Kumar, T.S.; Balaji, K.; Rajasekhar, K. Assessment of Sorptivity and Water Absorption of Concrete with Partial Replacement of Cement by Sugarcane Bagasse Ash (SCBA) and Silica Fume. Int. J. Appl. Eng. Res. 2016, 11, 5747–5752. [Google Scholar]
- Amin, N.-U. Use of bagasse ash in concrete and its impact on the strength and chloride resistivity. J. Mater. Civ. Eng. 2011, 23, 717–720. [Google Scholar] [CrossRef]
- Hailu, B.; Dinku, A. Application of sugarcane bagasse ash as a partial cement replacement material. Zede J. 2012, 29, 1–12. [Google Scholar]
- Mangi, S.A.; Jamaluddin, N.; Ibrahim, M.W.; Abdullah, A.H.; Awal, A.S.M.A.; Sohu, S.; Ali, N. Utilization of sugarcane bagasse ash in concrete as partial replacement of cement. IOP Conf. Ser. Mater. Sci. Eng. 2017, 271, 1–8. [Google Scholar] [CrossRef]
- Dhengare, S.W.; Raut, S.P.; Bandwal, N.V.; Khangan, A. Investigation into utilization of sugarcane bagasse ash as supplementary cementitious material in concrete. Int. J. 2015, 3, 109. [Google Scholar]
- Hussein, A.A.E.; Shafiq, N.; Nuruddin, M.F.; Memon, F.A. Compressive strength and microstructure of sugar cane bagasse ash concrete. Res. J. Appl. Sci. Eng. Technol. 2014, 7, 2569–2577. [Google Scholar] [CrossRef]
- Reddy, M.V.S.; Ashalatha, K.; Madhuri, M.; Sumalatha, P. Utilization of sugarcane bagasse ash (SCBA) in concrete by partial replacement of cement. IOSR J. Mech. Civ. Eng. 2015, 12, 12–16. [Google Scholar]
- Ganesan, K.; Rajagopal, K.; Thangavel, K. Evaluation of bagasse ash as corrosion resisting admixture for carbon steel in concrete. Anti-Corros. Methods Mater. 2007, 54, 230–236. [Google Scholar] [CrossRef]
- Yashwanth, M.K.; Raghavendra, A.; Kumar, B.N. An experimental study on alternative cementitious materials: Bagasse ash as partial replacement for cement in structural lightweight concrete. Indian Concr. J. 2017, 91, 51–58. [Google Scholar]
- Shafiq, N.; Hussein, A.A.E.; Nuruddin, M.F.; Al Mattarneh, H. Effects of sugarcane bagasse ash on the properties of concrete. Proc. Inst. Civ. Eng. -Eng. Sustain. 2016, 171, 123–132. [Google Scholar] [CrossRef]
- Priya, K.L.; Ragupathy, R. Effect of sugarcane bagasse ash on strength properties of concrete. Int. J. Res. Eng. Technol. 2016, 5, 159–164. [Google Scholar]
- Praveenkumar, S.; Sankarasubramanian, G. Mechanical and durability properties of bagasse ash-blended high-performance concrete. SN Appl. Sci. 2019, 1, 166469. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.; Ji, T.; Gao, S.J.; Yang, Z.; Wu, N. Characteristics and applications of sugar cane bagasse ash waste in cementitious materials. Materials 2019, 12, 39. [Google Scholar] [CrossRef] [Green Version]
- Arenas-Piedrahita, J.C.; Montes-García, P.; Mendoza-Rangel, J.M.; Calvo, H.L.; Valdez-Tamez, P.L.; Martínez-Reyes, J. Mechanical and durability properties of mortars prepared with untreated sugarcane bagasse ash and untreated fly ash. Constr. Build. Mater. 2016, 105, 69–81. [Google Scholar] [CrossRef]
- Cordeiro, G.C.; Toledo Filho, R.D.; Tavares, L.M.; Fairbairn, E.M.R. Experimental characterization of binary and ternary blended-cement concretes containing ultrafine residual rice husk and sugar cane bagasse ashes. Constr. Build. Mater. 2012, 29, 641–646. [Google Scholar] [CrossRef]
- Elwell, D.J.; Fu, G. Compression Testing of Concrete: Cylinders vs. Cubes; New York State Department of Transportation: New York, NY, USA, 1995.
- Shah, M.I.; Javed, M.F.; Abunama, T. Proposed formulation of surface water quality and modelling using gene expression, machine learning, and regression techniques. Environ. Sci. Pollut. Res. 2021, 11, 13202–13220. [Google Scholar] [CrossRef]
- Raju, K.S.; Murty, M.R.; Rao, M.V.; Satapathy, S.C. Support Vector Machine with k-fold cross validation model for software fault prediction. Int. J. Pure Appl. Math. 2018, 118, 321–334. [Google Scholar]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. Ijcai 1995, 14, 1137–1145, Montreal, QC, Canada. [Google Scholar]
- Azim, I.; Yang, J.; Javed, M.F.; Iqbal, M.F.; Mahmood, Z.; Wang, F.; Liu, Q.F. Prediction model for compressive arch action capacity of RC frame structures under column removal scenario using gene expression programming. Structures 2020, 25, 212–228. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H.; Mirzahosseini, M.R.; Nejad, F.M. Nonlinear genetic-based models for prediction of flow number of asphalt mixtures. J. Mater. Civ. Eng. 2011, 23, 248–263. [Google Scholar] [CrossRef]
- Despotovic, M.; Nedic, V.; Despotovic, D.; Cvetanovic, S. Evaluation of empirical models for predicting monthly mean horizontal diffuse solar radiation. Renew. Sustain. Energy Rev. 2016, 56, 246–260. [Google Scholar] [CrossRef]
- Akram, T.; Memon, S.A.; Obaid, H. Production of low cost self-compacting concrete using bagasse ash. Constr. Build. Mater. 2009, 2, 703–712. [Google Scholar] [CrossRef]
- Jagadesh, P.; Ramachandramurthy, A.; Murugesan, R.; Sarayu, K. Micro-Analytical studies on sugar cane bagasse ash. Sadhana 2015, 40, 1629–1638. [Google Scholar] [CrossRef] [Green Version]
- Souza, L.M.S.D.; Fairbairn, E.D.M.R.; Toledo Filho, R.D.; Cordeiro, G.C. Influence of initial CaO/SiO2 ratio on the hydration of rice husk ash-Ca (OH)2 and sugar cane bagasse ash-Ca(OH)2 pastes. Química Nova 2014, 37, 1600–1605. [Google Scholar]
- Frank, I.E.; Todeschini, R. The Data Analysis Handbook; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Golbraikh, A.; Tropsha, A. Beware of q2! J. Mol. Graph. Model. 2002, 20, 269–276. [Google Scholar] [CrossRef]
- Roy, P.P.; Roy, K. On some aspects of variable selection for partial least squares regression models. QSAR Comb. Sci. 2008, 27, 302–313. [Google Scholar] [CrossRef]
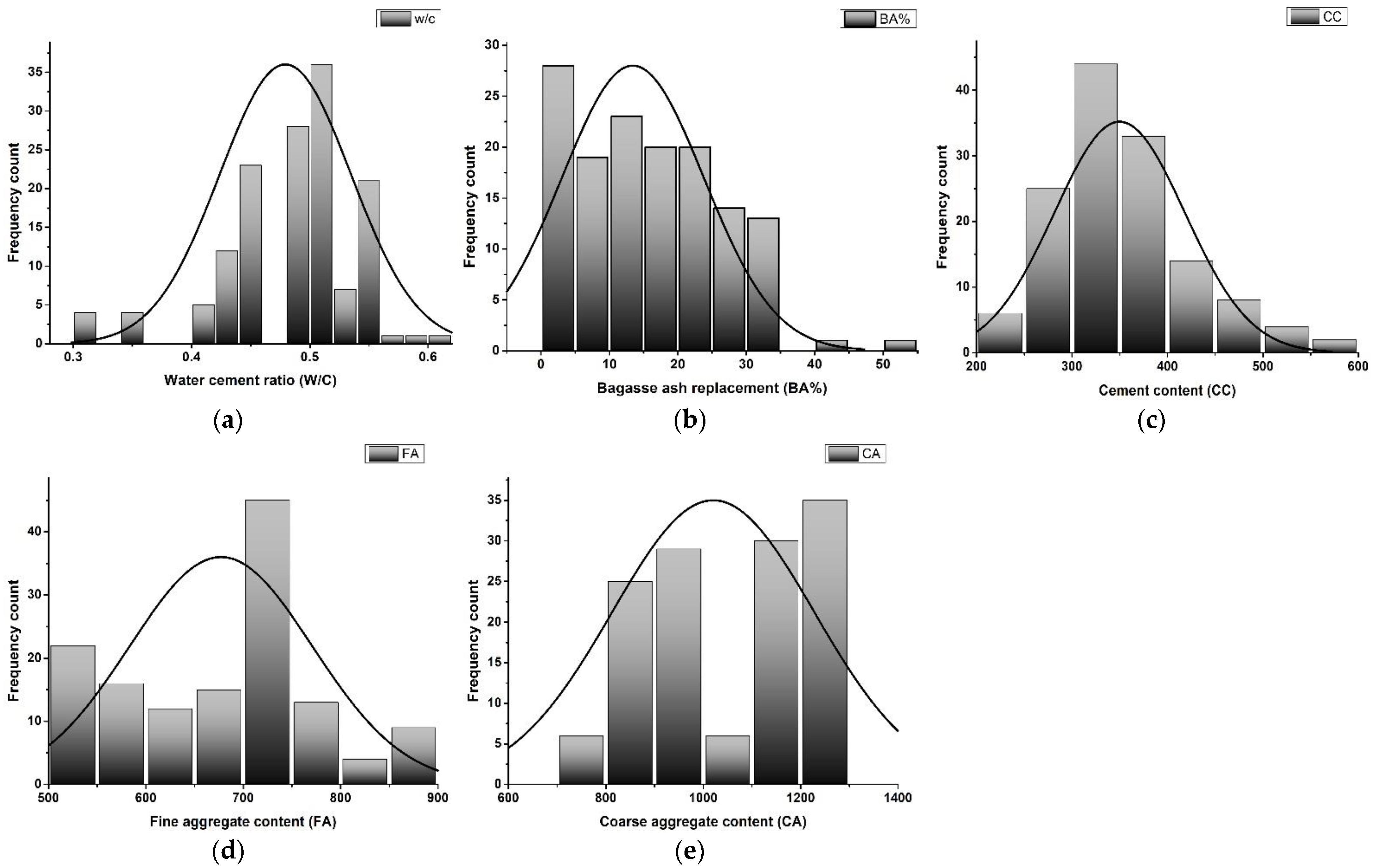

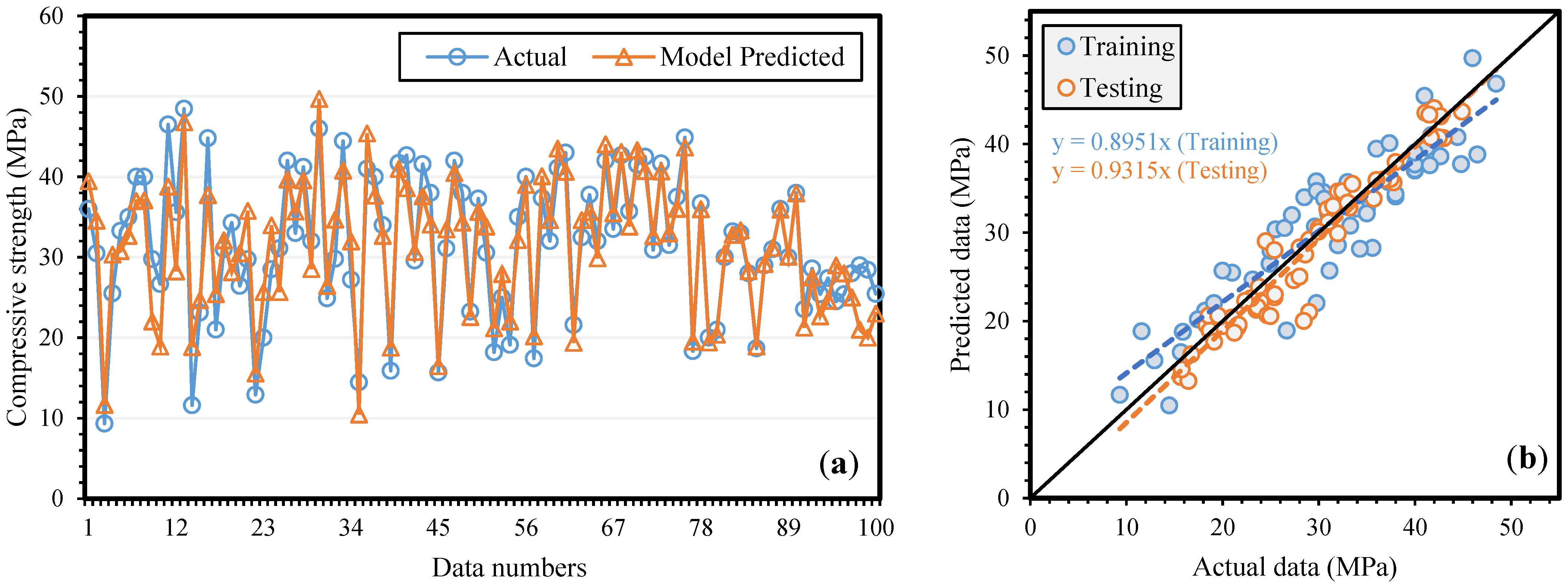
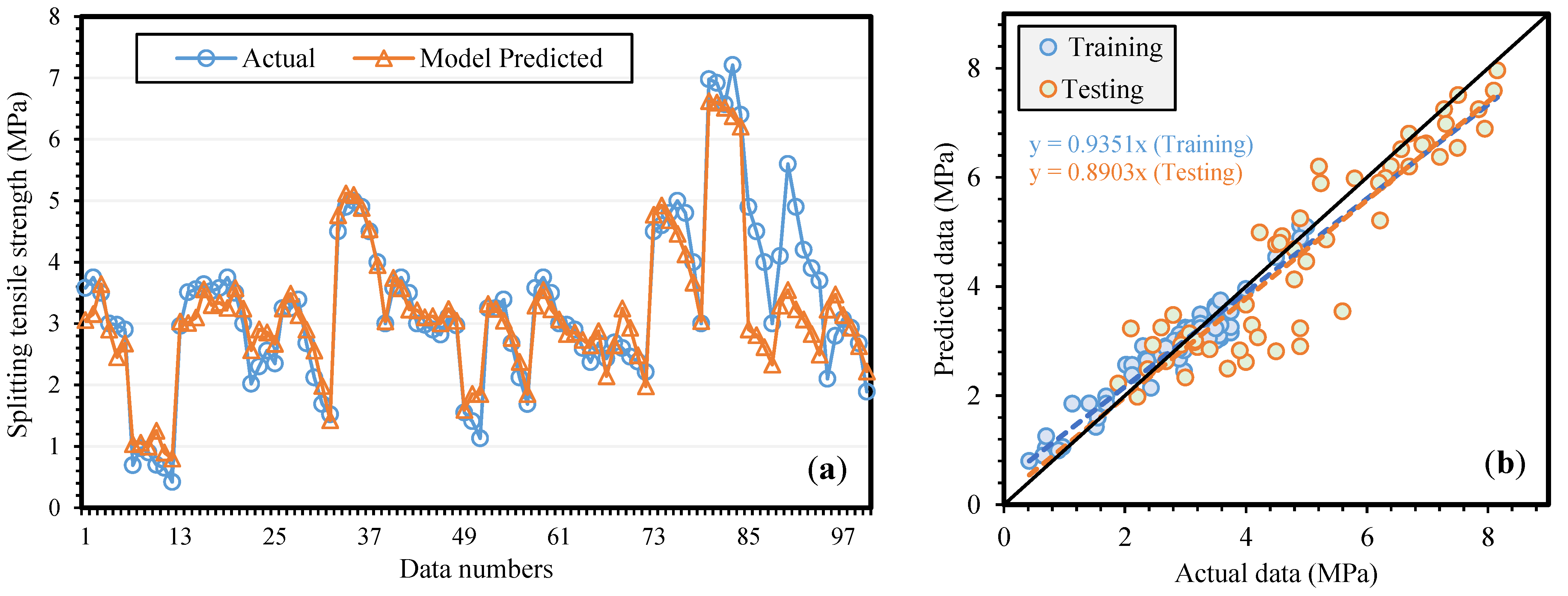
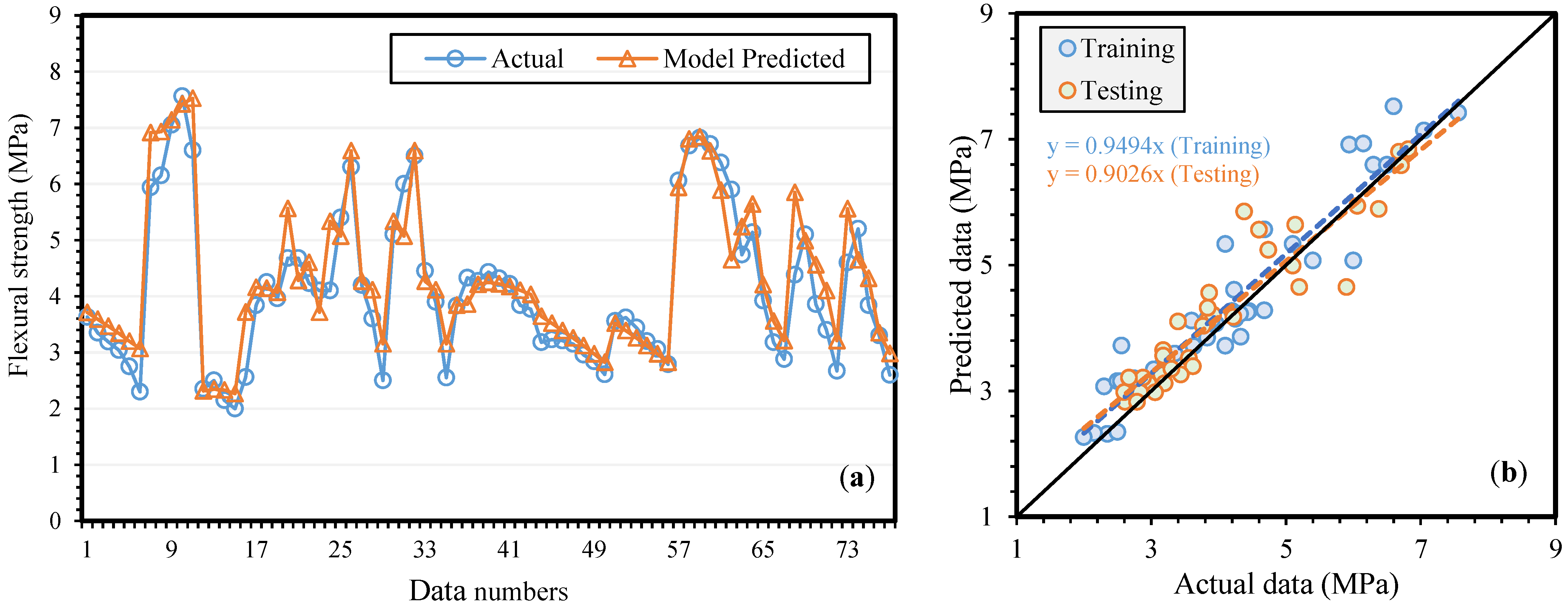

| Setting Parameters | Optimum Value |
|---|---|
| Subpopulation | 50 |
| length of code | 40 |
| Subpopulation size | 250 |
| Number of generations | 1000 |
| Mutation probability | 0.01 |
| Crossover probability | 0.9 |
| Mathematical operators | +, −, ×, ÷ |
| Variables | 0.5 |
| Tournament size | 4 |
| Operators | 0.5 |
| Parameter | Unit | Range | Min | Max | Mean | SD |
|---|---|---|---|---|---|---|
| W/C | - | 0.3 | 0.3 | 0.6 | 0.47 | 0.074 |
| CC | Kg/m3 | 444 | 112 | 555 | 336.5 | 98.5 |
| BA% | % | 50 | 0 | 50 | 13.41 | 10.46 |
| FA | Kg/m3 | 614 | 239 | 853 | 603.5 | 232.1 |
| CA | Kg/m3 | 772 | 477 | 1249 | 884.6 | 392.3 |
| Mix | Cement Kg/m3 | CA Kg/m3 | BA Kg/m3 | W/C | FA Kg/m3 | Water Kg/m3 | Density (Kg/m3) | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Cement | CA | FA | BA | |||||||
| NC | 366 | 1013.5 | 0 | 0.5 | 742.3 | 183 | 3150 | 2510 | 1680 | 2450 |
| 10BA | 329.4 | 1013.5 | 36.6 | 0.5 | 742.3 | 183 | ||||
| 20BA | 292.8 | 1013.5 | 73.2 | 0.5 | 742.3 | 183 | ||||
| 30BA | 256.2 | 1013.5 | 109.8 | 0.5 | 742.3 | 183 | ||||
| 40BA | 219.6 | 1013.5 | 146.4 | 0.5 | 742.3 | 183 | ||||
| Models | Data | R | RMSE | RSE | NSE | MAE | RRMSE | ρ | OF |
|---|---|---|---|---|---|---|---|---|---|
| Training | 0.91 | 3.47 | 0.16 | 0.87 | 2.96 | 0.04 | 0.020 | ||
| Testing | 0.94 | 2.98 | 0.12 | 0.89 | 2.98 | 0.09 | 0.046 | 0.036 | |
| Validation | 0.93 | 2.87 | 0.15 | 0.89 | 1.67 | 0.04 | 0.020 | ||
| Training | 0.90 | 2.43 | 0.23 | 0.85 | 3.67 | 0.09 | 0.047 | ||
| Testing | 0.92 | 2.65 | 0.26 | 0.91 | 3.69 | 0.12 | 0.062 | 0.031 | |
| Validation | 0.92 | 3.25 | 0.31 | 0.90 | 3.98 | 0.10 | 0.052 | ||
| Training | 0.91 | 3.92 | 0.29 | 0.86 | 1.87 | 0.13 | 0.068 | 0.052 | |
| Testing | 0.91 | 3.34 | 0.28 | 0.87 | 1.45 | 0.15 | 0.078 | ||
| Validation | 0.93 | 3.67 | 0.19 | 0.86 | 2.87 | 0.16 | 0.079 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amin, M.N.; Khan, K.; Aslam, F.; Shah, M.I.; Javed, M.F.; Musarat, M.A.; Usanova, K. Multigene Expression Programming Based Forecasting the Hardened Properties of Sustainable Bagasse Ash Concrete. Materials 2021, 14, 5659. https://doi.org/10.3390/ma14195659
Amin MN, Khan K, Aslam F, Shah MI, Javed MF, Musarat MA, Usanova K. Multigene Expression Programming Based Forecasting the Hardened Properties of Sustainable Bagasse Ash Concrete. Materials. 2021; 14(19):5659. https://doi.org/10.3390/ma14195659
Chicago/Turabian StyleAmin, Muhammad Nasir, Kaffayatullah Khan, Fahid Aslam, Muhammad Izhar Shah, Muhammad Faisal Javed, Muhammad Ali Musarat, and Kseniia Usanova. 2021. "Multigene Expression Programming Based Forecasting the Hardened Properties of Sustainable Bagasse Ash Concrete" Materials 14, no. 19: 5659. https://doi.org/10.3390/ma14195659
APA StyleAmin, M. N., Khan, K., Aslam, F., Shah, M. I., Javed, M. F., Musarat, M. A., & Usanova, K. (2021). Multigene Expression Programming Based Forecasting the Hardened Properties of Sustainable Bagasse Ash Concrete. Materials, 14(19), 5659. https://doi.org/10.3390/ma14195659








