Electrical Resistivity of Cu and Au at High Pressure above 5 GPa: Implications for the Constant Electrical Resistivity Theory along the Melting Curve of the Simple Metals
Abstract
:1. Introduction
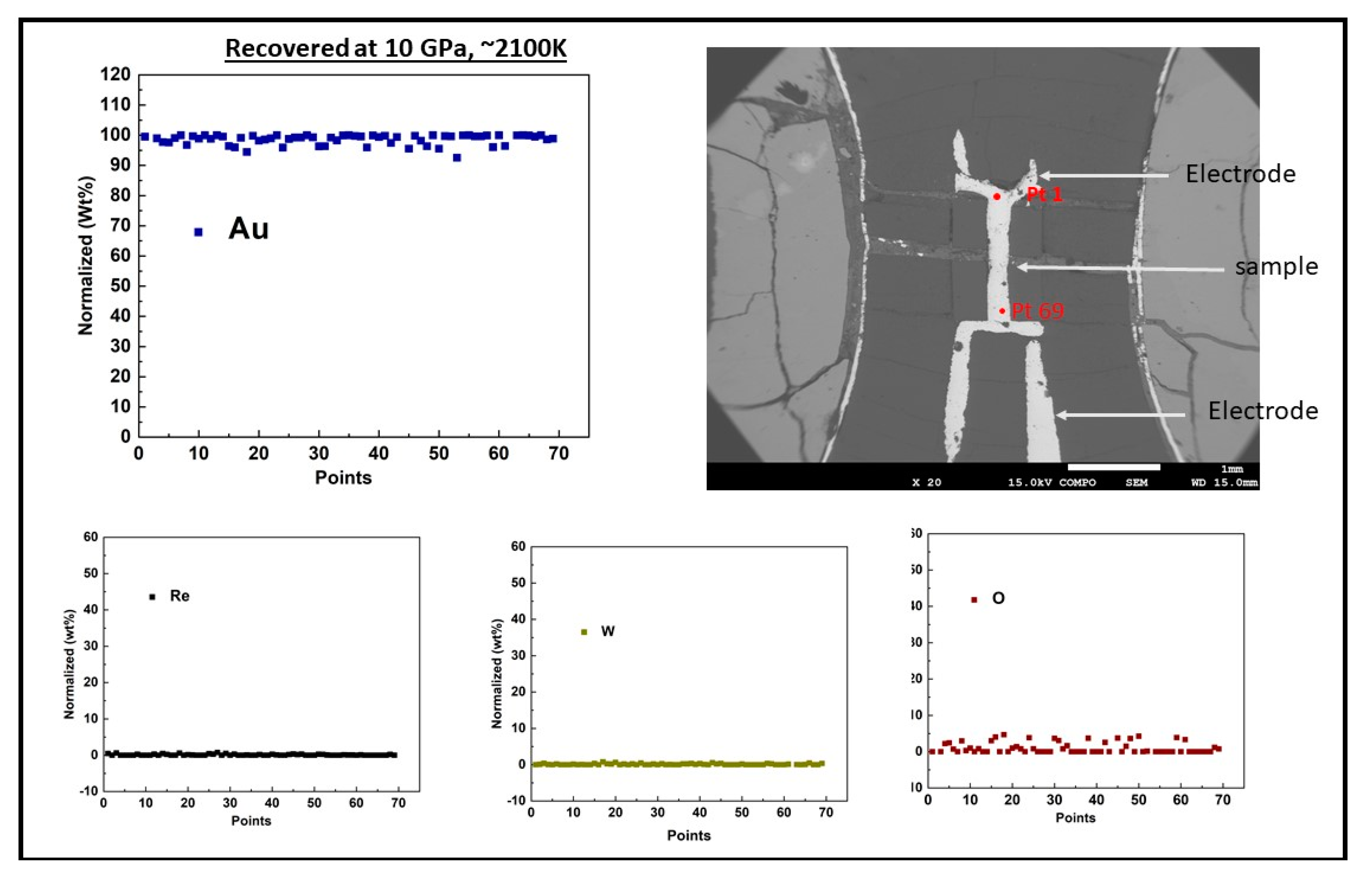
2. Experimental Details
3. Results
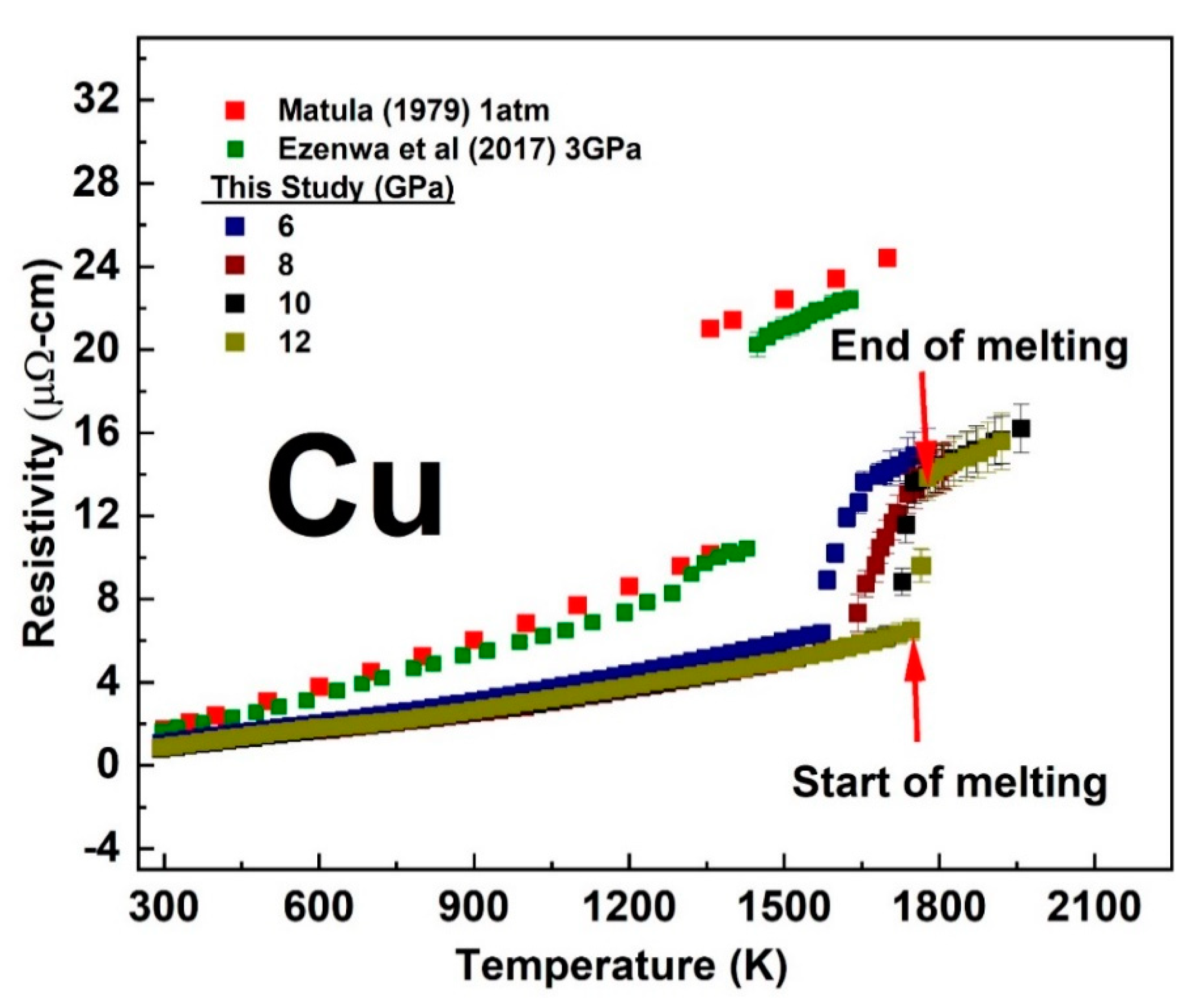
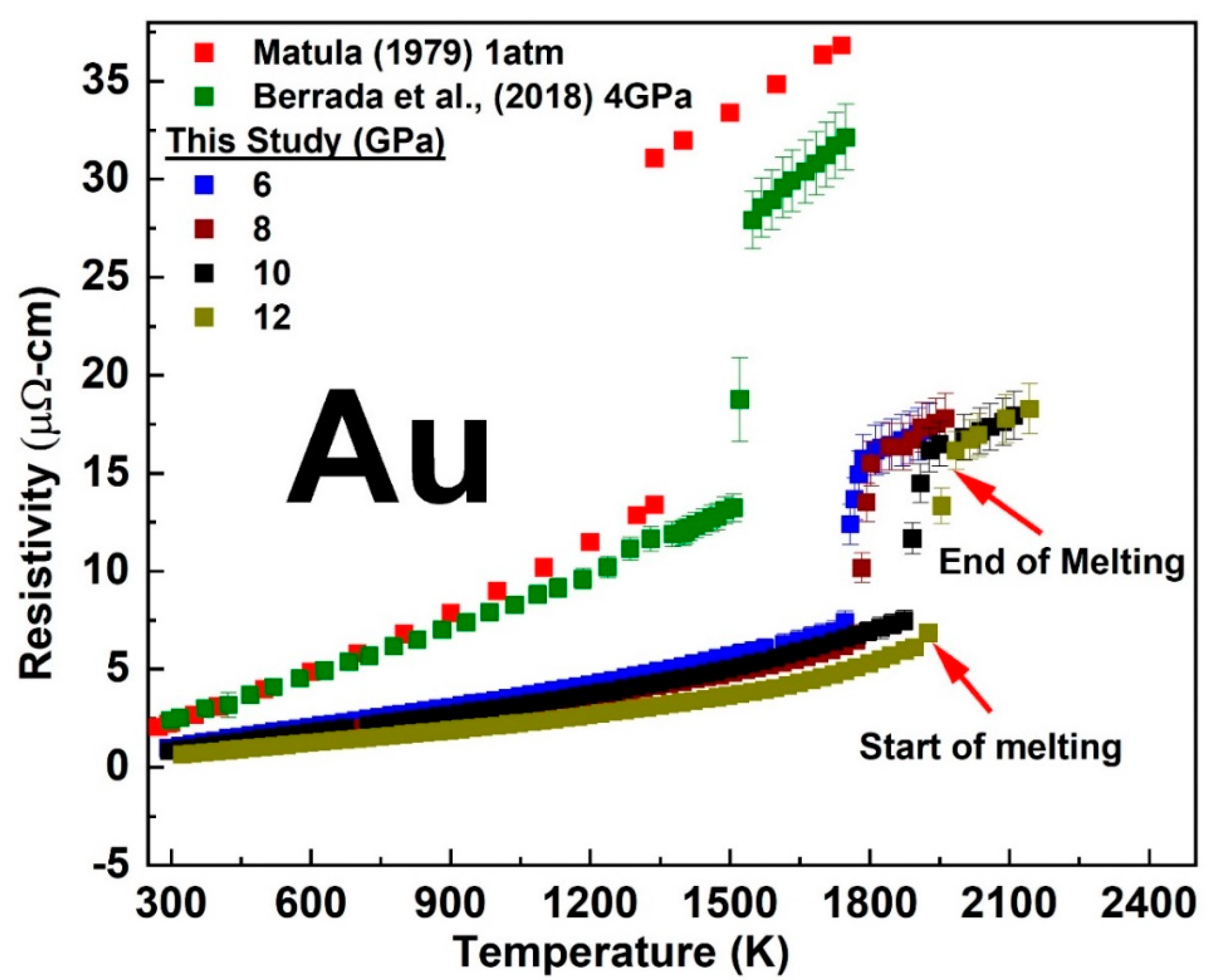
3.1. Temperature-Dependent Electrical Resistivity of Cu and Au at a Fixed Pressure
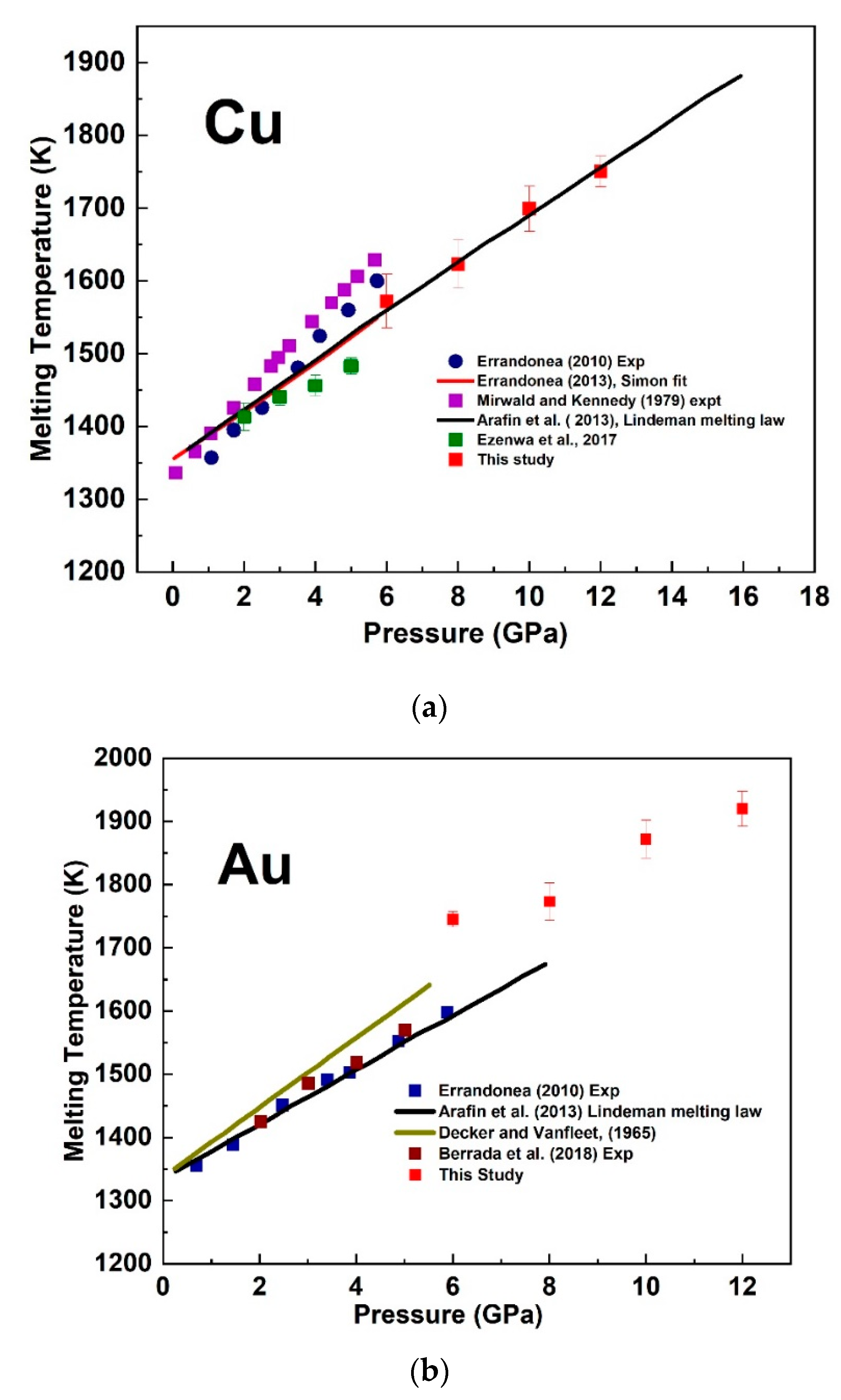
3.2. The Melting Curve of Cu and Au
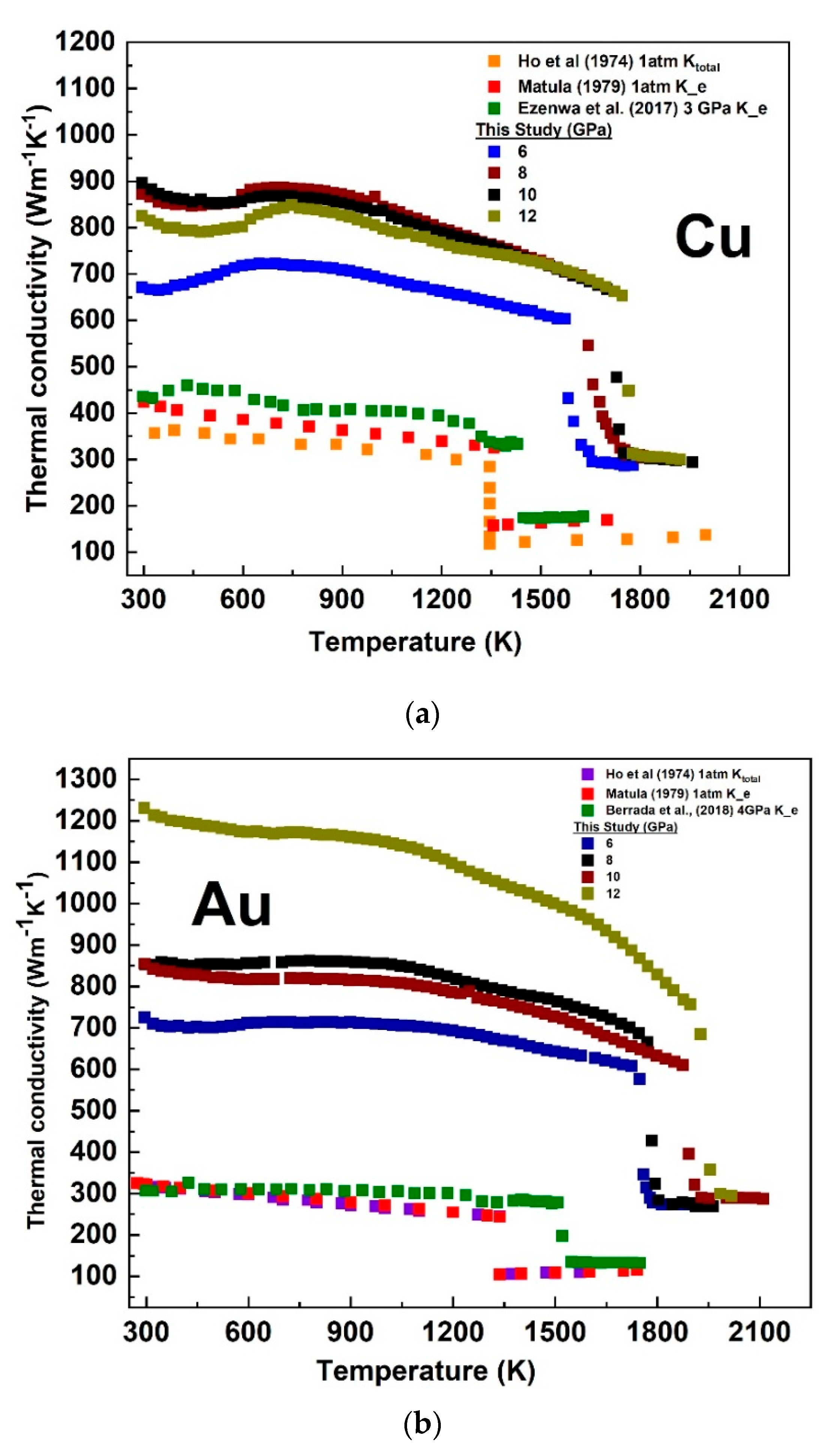
3.3. Temperature-Dependent Electronic Thermal Conductivity of Cu and Au at a Fixed Pressure
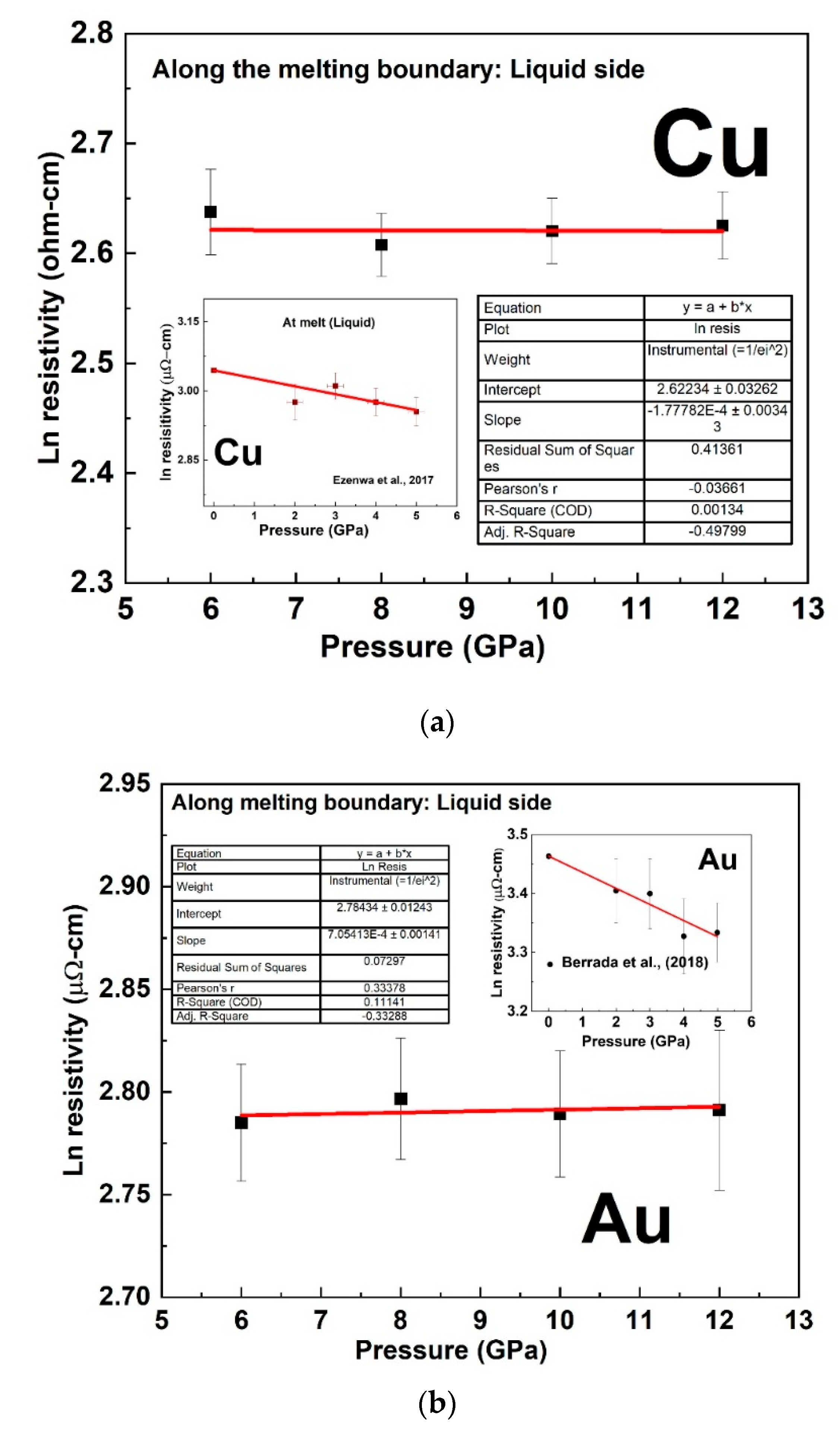
4. Discussions on the Constant Resistivity along the Melting Curve of Cu and Au
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, J.; Fei, Y. Experimental constraints on core composition. Treatise Geochem. 2003, 2, 568. [Google Scholar]
- Shoenberg, D. The Fermi surfaces of copper, silver. and gold. I. the de Haas-van Alphen effect. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Sci. 1962, 255, 85–133. [Google Scholar]
- Baym, G. Direct calculation of electronic properties of metals from neutron scattering data. Phys. Rev. 1964, 135, A1691. [Google Scholar] [CrossRef]
- Miller, J.C. Optical properties of liquid metals at high temperatures. Philos. Mag. 1969, 20, 1115–1132. [Google Scholar] [CrossRef]
- Ezenwa, I.C.; Secco, R.A. Fe melting transition: Electrical resistivity, thermal conductivity, and heat flow at the inner core boundaries of mercury and ganymede. Crystals 2019, 9, 359. [Google Scholar] [CrossRef] [Green Version]
- Ziman, J.M. Electrons and Phonons: The Theory of Transport Phenomena in Solids; Oxford University Press: Oxford, UK, 1960. [Google Scholar]
- Evans, R.; Greenwood, D.A.; Lloyd, P. Calculations of the transport properties of liquid transition metals. Phys. Lett. A 1971, 35, 57–58. [Google Scholar] [CrossRef]
- Mott, N.F. The electrical resistivity of liquid transition metals. Philos. Mag. 1972, 26, 1249–1261. [Google Scholar] [CrossRef]
- Stacey, F.D.; Anderson, O.L. Electrical and thermal conductivities of Fe–Ni–Si alloy under core conditions. Phys. Earth Planet. Inter. 2001, 124, 153–162. [Google Scholar] [CrossRef]
- Stacey, F.D.; Loper, D.E. A revised estimate of the conductivity of iron alloy at high pressure and implications for the core energy balance. Phys. Earth Planet. Inter. 2007, 161, 13–18. [Google Scholar] [CrossRef]
- Ezenwa, I.C.; Secco, R.A.; Yong, W.; Pozzo, M.; Alfè, D. Electrical resistivity of solid and liquid Cu up to 5 GPa: Decrease along the melting boundary. J. Phys. Chem. Solids 2017, 110, 386–393. [Google Scholar] [CrossRef]
- Littleton, J.A.; Secco, R.A.; Yong, W. Decreasing electrical resistivity of silver along the melting boundary up to 5 GPa. High Press. Res. 2018, 38, 99–106. [Google Scholar] [CrossRef]
- Berrada, M.; Secco, R.A.; Yong, W. Decreasing electrical resistivity of gold along the melting boundary up to 5 GPa. High Press. Res. 2018, 38, 367–376. [Google Scholar] [CrossRef]
- McMahan, A.K.; Albers, R.C. Insulating nickel at a pressure of 34 TPa. Phys. Rev. Lett. 1982, 49, 1198. [Google Scholar] [CrossRef]
- McMahan, A.K. Pressure effects on the electronic structure of 4f and 5f materials. J. Less Common Met. 1989, 149, 1–11. [Google Scholar] [CrossRef]
- Ross, M.; Boehler, R.; Errandonea, D. Melting of transition metals at high pressure and the influence of liquid frustration: The late metals Cu, Ni, and Fe. Phys. Rev. B 2007, 76, 184117. [Google Scholar] [CrossRef]
- Rahm, M.; Cammi, R.; Ashcroft, N.W.; Hoffmann, R. Squeezing all elements in the periodic table: Electron configuration and electronegativity of the atoms under compression. J. Am. Chem. Soc. 2019, 141, 10253–10271. [Google Scholar] [CrossRef]
- Ezenwa, I.C.; Yoshino, T. Martian core heat flux: Electrical resistivity and thermal conductivity of liquid Fe at martian core PT conditions. Icarus 2021, 360, 114367. [Google Scholar] [CrossRef]
- Ezenwa, I.C.; Yoshino, T. Technique, cell assembly, and measurement of T-dependent electrical resistivity of liquid Fe devoid of contamination at P.; T conditions. Rev. Sci. Instrum. 2020, 91, 023903. [Google Scholar] [CrossRef] [PubMed]
- Ezenwa, I.C.; Secco, R.A. Constant electrical resistivity of Zn along the melting boundary up to 5 GPa. High Press. Res. 2017, 37, 319–333. [Google Scholar] [CrossRef]
- Matula, R.A. Electrical resistivity of copper, gold, palladium, and silver. J. Phys. Chem. Ref. Data 1979, 8, 1147–1298. [Google Scholar] [CrossRef] [Green Version]
- Ohta, K.; Kuwayama, Y.; Hirose, K.; Shimizu, K.; Ohishi, Y. Experimental determination of the electrical resistivity of iron at Earth’s core conditions. Nature 2016, 534, 95–98. [Google Scholar] [CrossRef]
- Kor, K.S.D.; Tripathi, N. Temperature and pressure dependence of effective Debye temperature in associated liquids based on quasi crystalline model. J. Phys. Soc. Jpn. 1974, 36, 552–554. [Google Scholar] [CrossRef]
- Bloch, F. Zum elektrischen Widerstandsgesetz bei tiefen Temperaturen. Z. Für Phys. 1930, 59, 208–214. [Google Scholar] [CrossRef]
- Bid, A.; Bora, A.; Raychaudhuri, A.K. Temperature dependence of the resistance of metallic nanowires of diameter⩾ 15 nm: Applicability of Bloch-Grüneisen theorem. Phys. Rev. B 2006, 74, 035426. [Google Scholar] [CrossRef] [Green Version]
- Hoc, N.Q.; Tinh, B.D.; Hien, N.D. Influence of temperature and pressure on the electrical resistivity of gold and copper up to 1350 K and 100 GPa. Mater. Res. Bull. 2020, 128, 110874. [Google Scholar] [CrossRef]
- Basu, A.; Field, M.R.; McCulloch, D.G.; Boehler, R. New measurement of melting and thermal conductivity of iron close to outer core conditions. Geosci. Front. 2020, 11, 565–568. [Google Scholar] [CrossRef]
- Mirwald, P.W.; Kennedy, G.C. The melting curve of gold, silver, and copper to 60-Kbar pressure: A reinvestigation. J. Geophys. Res. Solid Earth 1979, 84, 6750–6756. [Google Scholar] [CrossRef]
- Errandonea, D. The melting curve of ten metals up to 12 GPa and 1600 K. J. Appl. Phys. 2010, 108, 033517. [Google Scholar] [CrossRef]
- Errandonea, D. High-pressure melting curves of the transition metals Cu, Ni, Pd, and Pt. Phys. Rev. B 2013, 87, 054108. [Google Scholar] [CrossRef]
- Arafin, S.; Singh, R.N.; George, A.K. Melting of metals under pressure. Phys. B Condens. Matter 2013, 419, 40–44. [Google Scholar] [CrossRef]
- Decker, D.L.; Vanfleet, H.B. Melting and high-temperature electrical resistance of gold under pressure. Phys. Rev. 1965, 138, A129. [Google Scholar] [CrossRef]
- Konôpková, Z.; McWilliams, R.S.; Gómez-Pérez, N.; Goncharov, A.F. Direct measurement of thermal conductivity in solid iron at planetary core conditions. Nature 2016, 534, 99–101. [Google Scholar] [CrossRef] [PubMed]
- Saha, P.; Mazumder, A.; Mukherjee, G.D. Thermal conductivity of dense hcp iron: Direct measurements using laser heated diamond anvil cell. Geosci. Front. 2020, 11, 1755–1761. [Google Scholar] [CrossRef]
- Klemens, P.G.; Williams, R.K. Thermal conductivity of metals and alloys. Int. Met. Rev. 1986, 31, 197–215. [Google Scholar] [CrossRef]
- Secco, R.A. Thermal conductivity and Seebeck coefficient of Fe and Fe-Si alloys: Implications for variable Lorenz number. Phys. Earth Planet. Inter. 2017, 265, 23–34. [Google Scholar] [CrossRef]
- Deng, L.; Seagle, C.; Fei, Y.; Shahar, A. High pressure and temperature electrical resistivity of iron and implications for planetary cores. Geophys. Res. Lett. 2013, 40, 33–37. [Google Scholar] [CrossRef]
- Ezenwa, I.C.; Secco, R.A. Invariant electrical resistivity of Co along the melting boundary. Earth Planet. Sci. Lett. 2017, 474, 120–127. [Google Scholar] [CrossRef]
- Ezenwa, I.C.; Secco, R.A. Electronic transition in solid Nb at high pressure and temperature. J. Appl. Phys. 2017, 121, 225903. [Google Scholar] [CrossRef]
- Ezenwa, I.C.; Yoshino, T. Electrical resistivity of solid and liquid Pt: Insight into electrical resistivity of ε-Fe. Earth Planet. Sci. Lett. 2020, 544, 116380. [Google Scholar] [CrossRef]
- Pommier, A.; Leinenweber, K.; Pirotte, H.; Yu, T.; Wang, Y. In situ electrical resistivity and viscosity measurements of iron alloys under pressure using synchrotron X-ray radiography. High Press. Res. 2021, 41, 1–13. [Google Scholar] [CrossRef]
- Zhang, Y.; Hou, M.; Liu, G.; Zhang, C.; Prakapenka, V.B.; Greenberg, E.; Fei, Y.; Cohen, R.E.; Lin, J.F. Reconciliation of experiments and theory on transport properties of iron and the geodynamo. Phys. Rev. Lett. 2020, 125, 078501. [Google Scholar] [CrossRef] [PubMed]
- Ho, C.Y.; Powell, R.W.; Liley, P.E. Thermal Conductivity of the Elements: A Comprehensive Review; Defense Technical Information Center: Fort Belvoir, VA, USA, 1974. [Google Scholar]
- Tonkov, E.Y.; Ponyatovsky, E.G. Phase Transformations of Elements Under High Pressure; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Templeton, I.M. The effect of hydrostatic pressure on the Fermi surfaces of copper, silver and gold. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1966, 292, 413–423. [Google Scholar]
- Ashcroft, N.W.; Lekner, J. Structure and resistivity of liquid metals. Phys. Rev. 1966, 145, 83. [Google Scholar] [CrossRef]
- Faber, T.E. Introduction to the Theory of Liquid Metals; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Zallen, R. The effect of pressure on optical properties of the noble metals. In Optical Properties and Electronic Structure of Metals and Alloys: Proceedings of the International Colloquium; North-Holland Publishing Company: Amsterdam, The Netherlands, 1966; p. 164. [Google Scholar]
- McWilliams, R.S.; Konôpková, Z.; Goncharov, A.F. A flash heating method for measuring thermal conductivity at high pressure and temperature: Application to Pt. Phys. Earth Planet. Inter. 2015, 247, 17–26. [Google Scholar] [CrossRef] [Green Version]
- Gomi, H.; Yoshino, T. Resistivity, Seebeck coefficient, and thermal conductivity of platinum at high pressure and temperature. Phys. Rev. B 2019, 100, 214302. [Google Scholar] [CrossRef] [Green Version]



| Cu | ||
|---|---|---|
| Pressure (GPa) | “A” (µΩ·cm) | “n” |
| 6 | 4.476 | 2.165 |
| 8 | 3.414 | 2.239 |
| 10 | 3.487 | 2.229 |
| 12 | 3.857 | 2.164 |
| Au | ||
|---|---|---|
| Pressure (GPa) | “A” (µΩ·cm) | “n” |
| 6 | 1.941 | 2.154 |
| 8 | 1.423 | 2.228 |
| 10 | 1.594 | 2.189 |
| 12 | 1.057 | 2.229 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ezenwa, I.C.; Yoshino, T. Electrical Resistivity of Cu and Au at High Pressure above 5 GPa: Implications for the Constant Electrical Resistivity Theory along the Melting Curve of the Simple Metals. Materials 2021, 14, 5476. https://doi.org/10.3390/ma14195476
Ezenwa IC, Yoshino T. Electrical Resistivity of Cu and Au at High Pressure above 5 GPa: Implications for the Constant Electrical Resistivity Theory along the Melting Curve of the Simple Metals. Materials. 2021; 14(19):5476. https://doi.org/10.3390/ma14195476
Chicago/Turabian StyleEzenwa, Innocent C., and Takashi Yoshino. 2021. "Electrical Resistivity of Cu and Au at High Pressure above 5 GPa: Implications for the Constant Electrical Resistivity Theory along the Melting Curve of the Simple Metals" Materials 14, no. 19: 5476. https://doi.org/10.3390/ma14195476
APA StyleEzenwa, I. C., & Yoshino, T. (2021). Electrical Resistivity of Cu and Au at High Pressure above 5 GPa: Implications for the Constant Electrical Resistivity Theory along the Melting Curve of the Simple Metals. Materials, 14(19), 5476. https://doi.org/10.3390/ma14195476






