An Experimental and Theoretical Determination of Oscillatory Shear-Induced Crystallization Processes in Viscoelastic Photonic Crystal Media
Abstract
1. Introduction
2. Materials and Methods
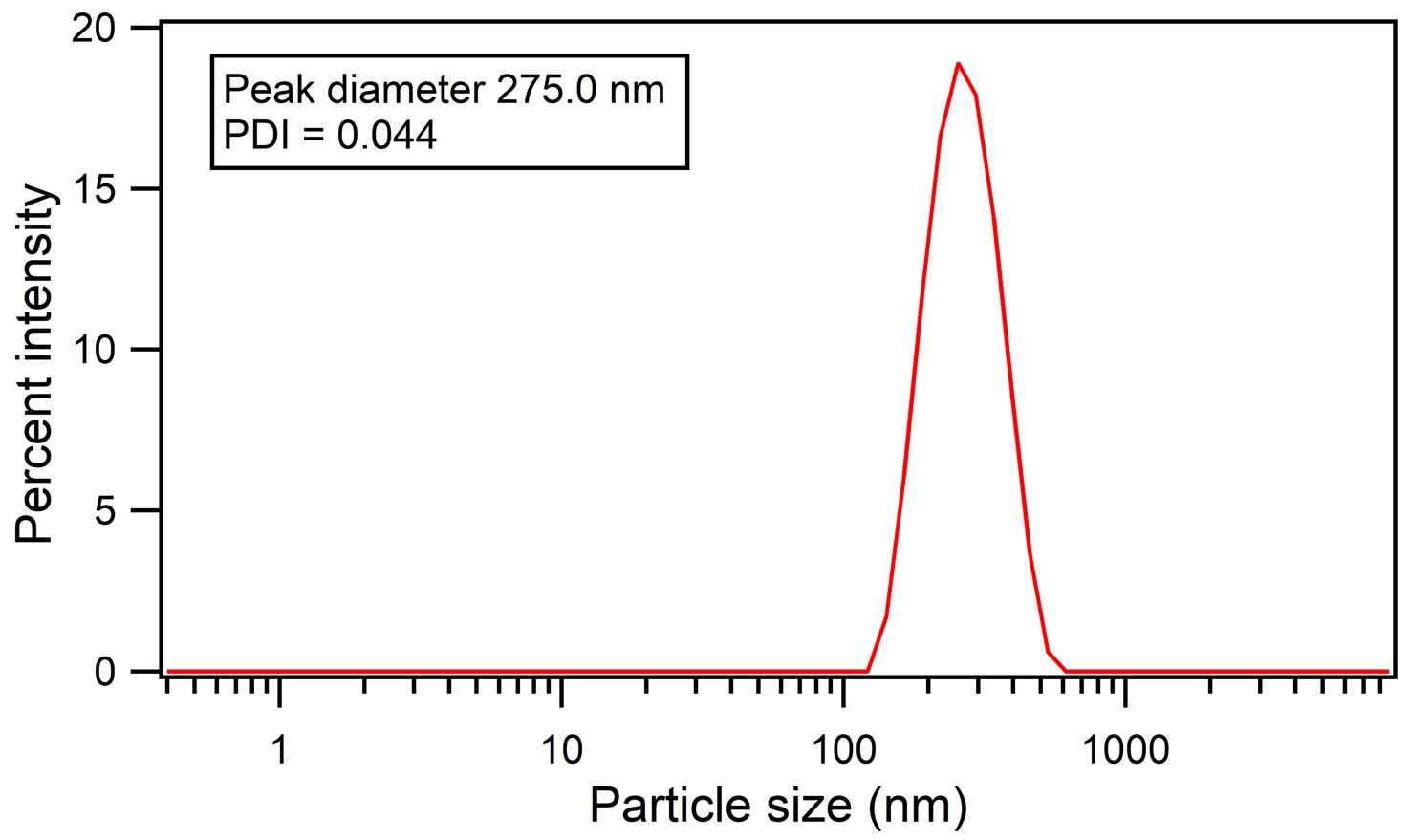
2.1. Samples
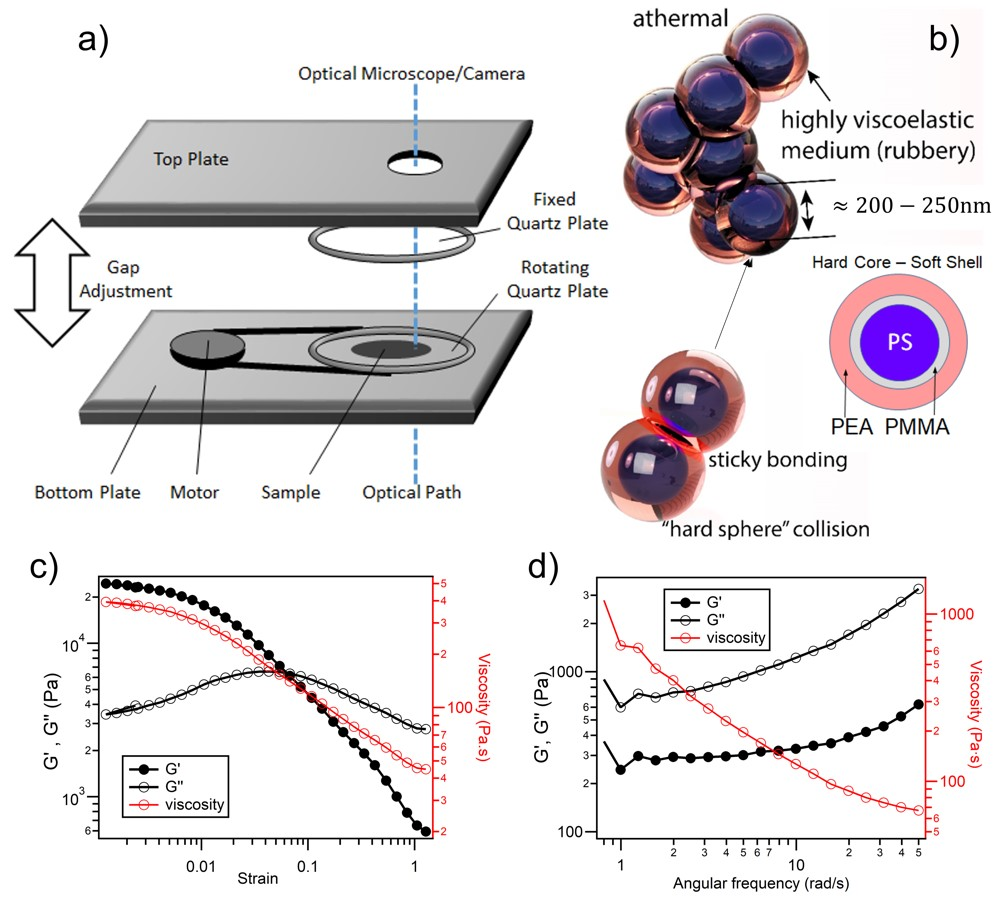
2.2. Shear Cell Assembly
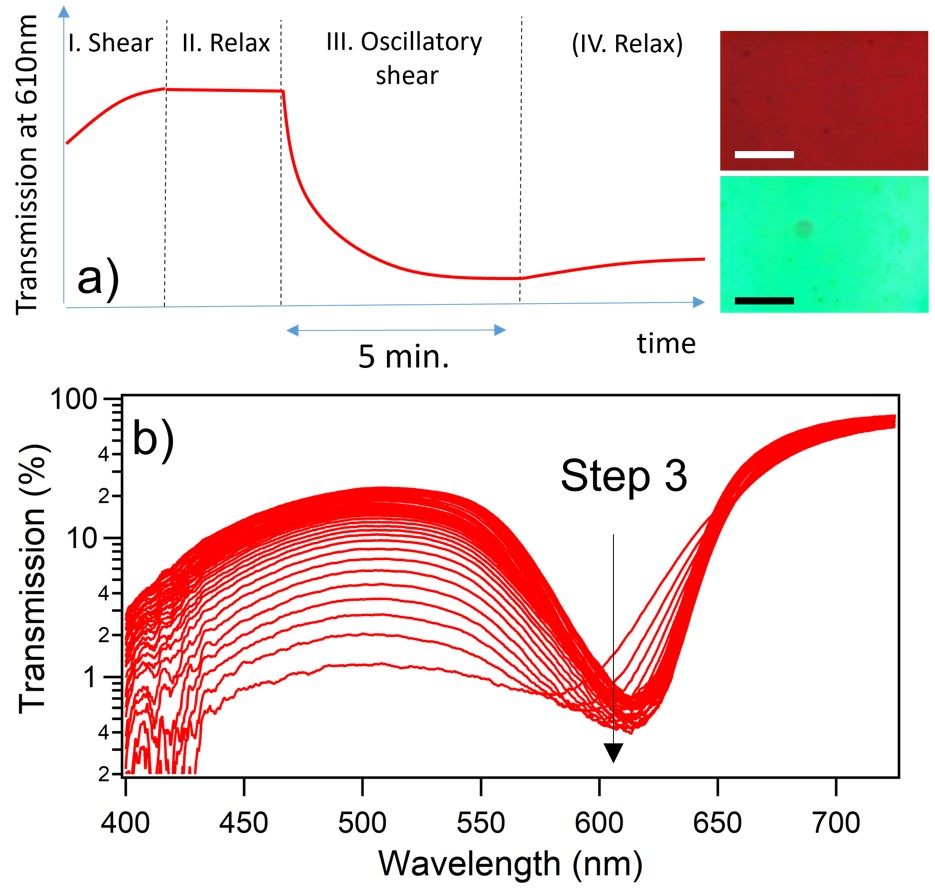
2.3. Microscopy/Spectroscopy
3. Results
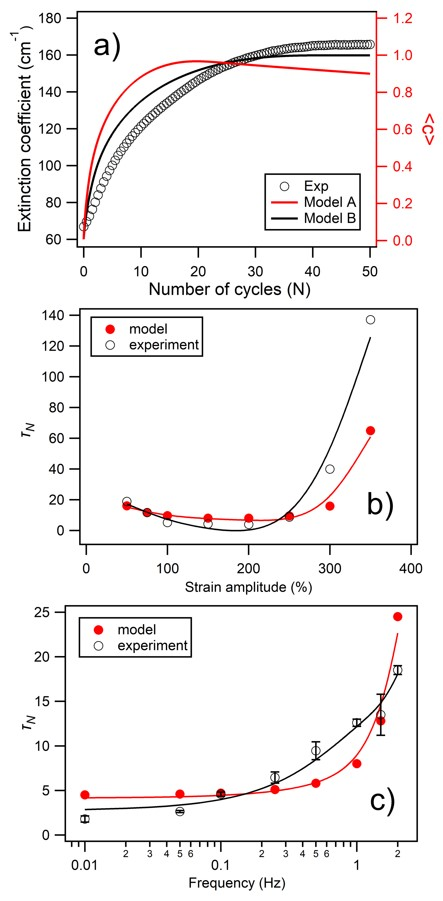
3.1. Experimental Results
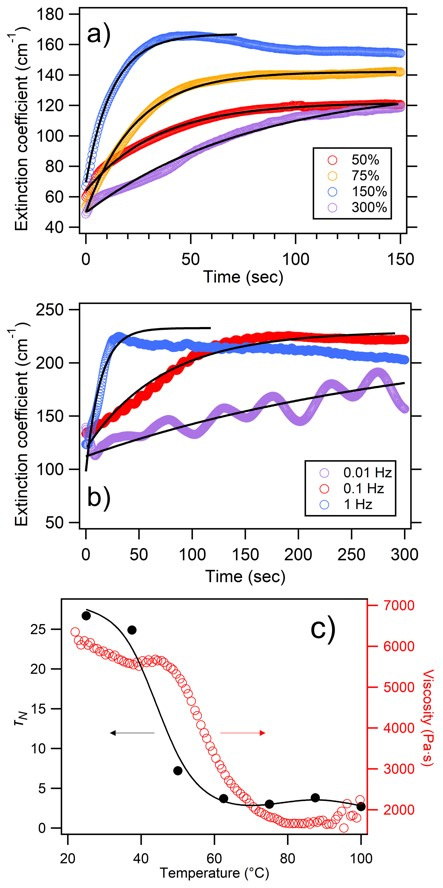
3.1.1. Strain Amplitude () Dependence
3.1.2. Oscillation Frequency (f) Dependence
3.1.3. Temperature Dependence
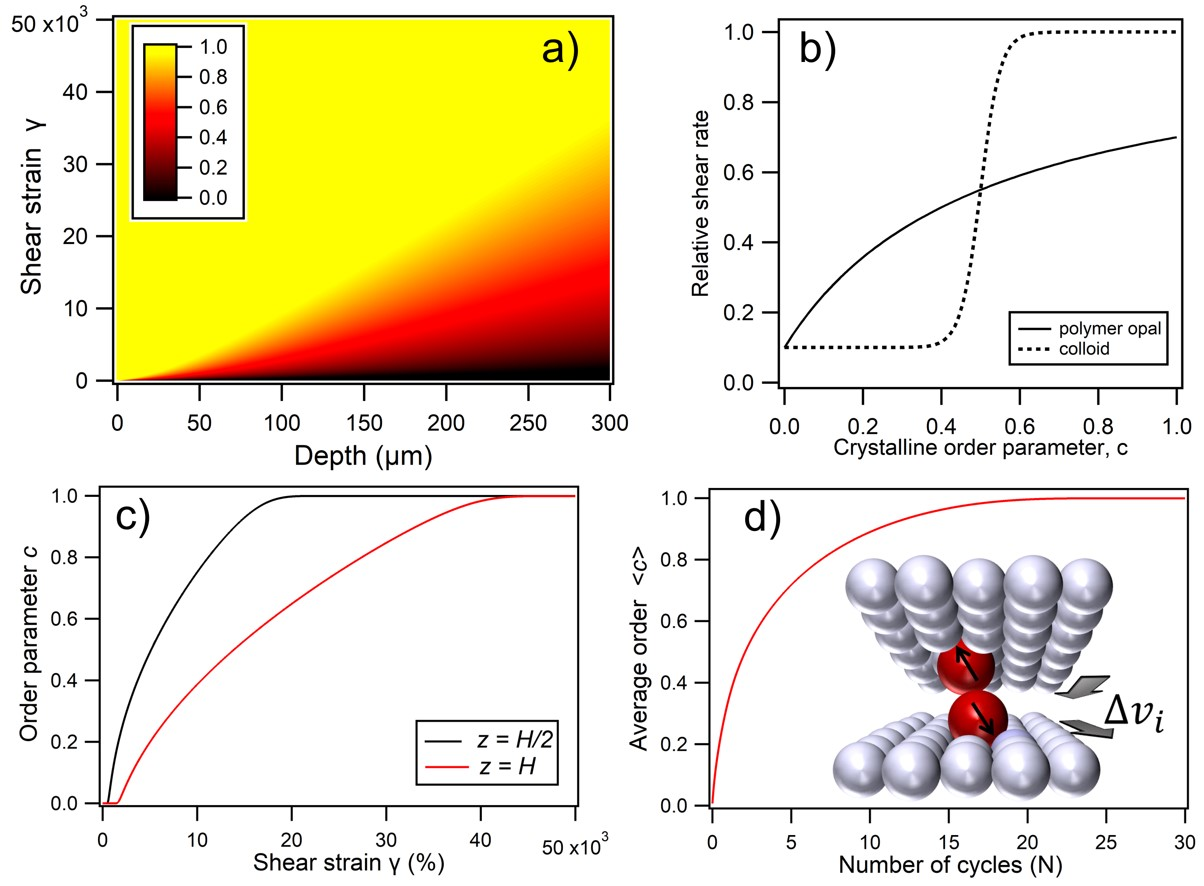
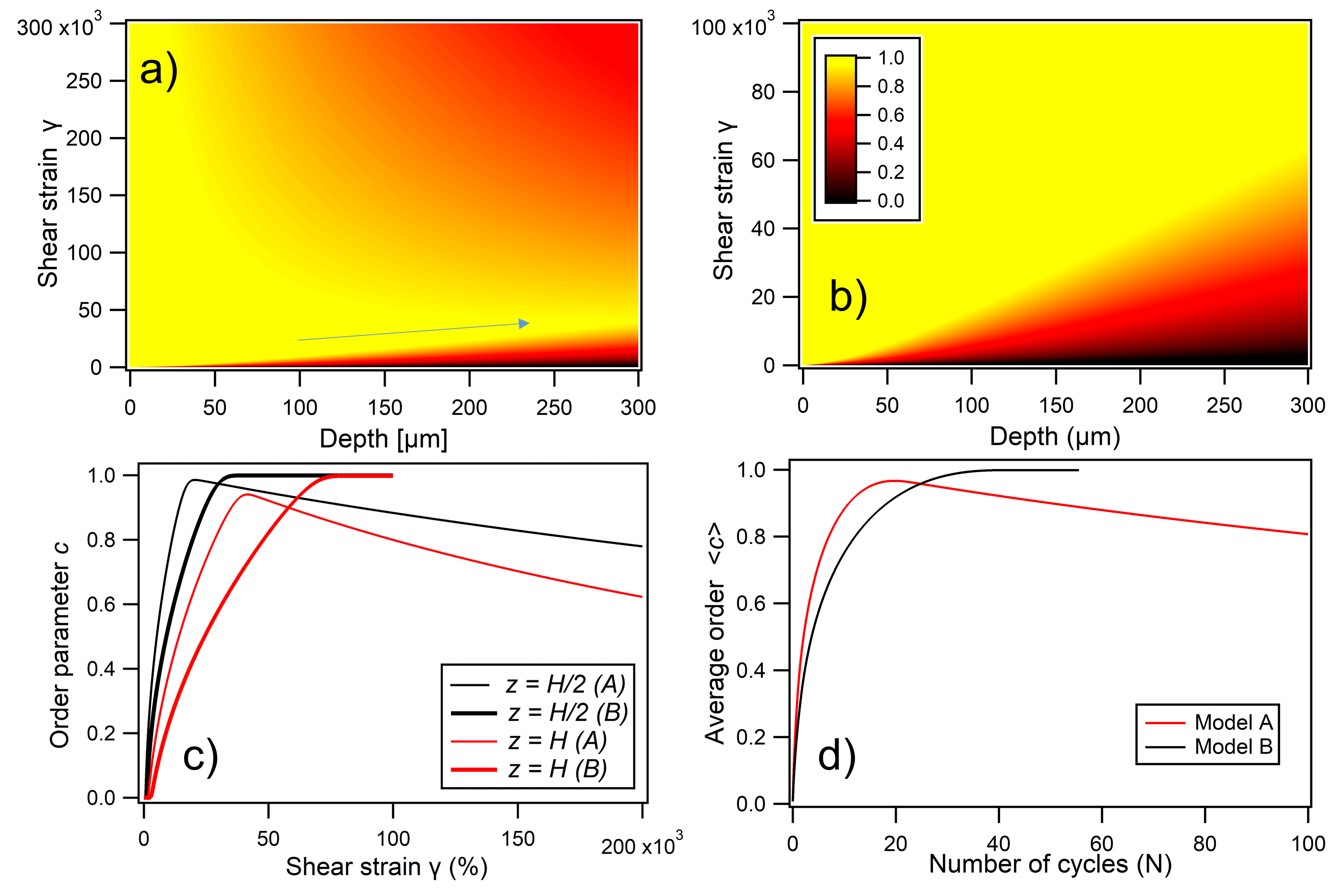
3.2. Theory and Simulation
3.2.1. Intuitive Model
3.2.2. Frequency and Amplitude Dependence
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Sanders, J.V. Colour of Precious Opal. Nature 1964, 204, 1151–1153. [Google Scholar] [CrossRef]
- Vukusic, P.; Sambles, J.; Lawrence, C. Structural Colour-Colour mixing in wing scales of a butterfly. Nature 2000, 404, 457. [Google Scholar] [CrossRef] [PubMed]
- Vignolini, S.; Rudall, P.; Rowland, A.; Reed, A.; Moyroud, E.; Faden, R.; Baumberg, J.; Glover, B.; Steiner, U. Pointillist structural color in Pollia fruit. Proc. Natl. Acad. Sci. USA 2012, 109, 15712–15715. [Google Scholar] [CrossRef]
- Kolle, M.; Salgard-Cunha, P.; Scherer, M.; Huang, F.; Vukusic, P.; Mahajan, S.; Baumberg, J.; Steiner, U. Mimicking the colourful wing scale structure of the Papilio blumei butterfly. Nat. Nanotechnol. 2010, 5, 511–515. [Google Scholar] [CrossRef] [PubMed]
- Braun, P. Materials Science Colour without Colourants. Nature 2011, 472, 423–424. [Google Scholar] [CrossRef] [PubMed]
- Astratov, V.N.; Adawi, A.M.; Fricker, S.; Skolnick, M.S.; Whittaker, D.M.; Pusey, P.N. Interplay of order and disorder in the optical properties of opal photonic crystals. Phys. Rev. B 2002, 66, 165215. [Google Scholar] [CrossRef]
- Boroditsky, M.; Krauss, T.F.; Coccioli, R.; Vrijen, R.; Bhat, R.; Yablonovitch, E. Light extraction from optically pumped light-emitting diode by thin-slab photonic crystals. Appl. Phys. Lett. 1999, 75, 1036–1038. [Google Scholar] [CrossRef]
- Yablonovitch, E. Photonic Band-Gap Structures. J. Opt. Soc. Am. B-Opt. Phys. 1993, 10, 283–295. [Google Scholar] [CrossRef]
- Norris, D.; Vlasov, Y. Chemical approaches to three-dimensional semiconductor photonic crystals. Adv. Mater. 2001, 13, 371–376. [Google Scholar] [CrossRef]
- Vlasov, Y.; Bo, X.; Sturm, J.; Norris, D. On-chip natural assembly of silicon photonic bandgap crystals. Nature 2001, 414, 289–293. [Google Scholar] [CrossRef]
- De La Rue, R. Photonic crystals: Microassembly in 3D. Nat. Mater. 2003, 2, 74–76. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, E.; O’Dwyer, C. Artificial opal photonic crystals and inverse opal structures-fundamentals and applications from optics to energy storage. J. Mater. Chem. C 2015, 3, 6109–6143. [Google Scholar] [CrossRef]
- Colvin, V.L. From opals to optics: Colloidal photonic crystals. Mrs Bull. 2001, 26, 637–641. [Google Scholar] [CrossRef]
- Neterebskaia, V.O.; Goncharenko, A.O.; Morozova, S.M.; Kolchanov, D.S.; Vinogradov, A.V. Inkjet Printing Humidity Sensing Pattern Based on Self-Organizing Polystyrene Spheres. Nanomaterials 2020, 10, 1538. [Google Scholar] [CrossRef] [PubMed]
- Ye, Y.H.; LeBlanc, F.; Hache, A.; Truong, V.V. Self-assembling three-dimensional colloidal photonic crystal structure with high crystalline quality. Appl. Phys. Lett. 2001, 78, 52–54. [Google Scholar] [CrossRef]
- Finlayson, C.E.; Spahn, P.; Snoswell, D.R.E.; Yates, G.; Kontogeorgos, A.; Haines, A.I.; Hellmann, G.P.; Baumberg, J.J. 3D Bulk Ordering in Macroscopic Solid Opaline Films by Edge-Induced Rotational Shearing. Adv. Mater. 2011, 23, 1540–1544. [Google Scholar] [CrossRef]
- Zhao, Q.; Finlayson, C.; Snoswell, D.; Haines, A.; Schafer, C.; Spahn, P.; Hellmann, G.; Petukhov, A.; Herrmann, L.; Burdet, P.; et al. Large-scale ordering of nanoparticles using viscoelastic shear processing. Nat. Commun. 2016, 7, 1–10. [Google Scholar] [CrossRef]
- Imai, Y.; Finlayson, C.E.; Goldberg-Oppenheimer, P.; Zhao, Q.B.; Spahn, P.; Snoswell, D.R.E.; Haines, A.I.; Hellmann, G.P.; Baumberg, J.J. Electrically conductive polymeric photonic crystals. Soft Matter 2012, 8, 6280–6290. [Google Scholar] [CrossRef]
- Finlayson, C.E.; Goddard, C.; Papachristodoulou, E.; Snoswell, D.R.E.; Kontogeorgos, A.; Spahn, P.; Hellmann, G.P.; Hess, O.; Baumberg, J.J. Ordering in stretch-tunable polymeric opal fibers. Opt. Express 2011, 19, 3144–3154. [Google Scholar] [CrossRef]
- Finlayson, C.E.; Baumberg, J.J. Polymer opals as novel photonic materials. Polym. Int. 2013, 62, 1403–1407. [Google Scholar] [CrossRef]
- Sussman, J.; Snoswell, D.; Kontogeorgos, A.; Baumberg, J.; Spahn, P. Thermochromic polymer opals. Appl. Phys. Lett. 2009, 95, 173116. [Google Scholar] [CrossRef]
- Schafer, C.; Gallei, M.; Zahn, J.; Engelhardt, J.; Hellmann, G.; Rehahn, M. Reversible Light-, Thermo-, and Mechano-Responsive Elastomeric Polymer Opal Films. Chem. Mater. 2013, 25, 2309–2318. [Google Scholar] [CrossRef]
- Pursiainen, O.; Baumberg, J.; Winkler, H.; Viel, B.; Spahn, P.; Ruhl, T. Nanoparticle-tuned structural color from polymer opals. Opt. Express 2007, 15, 9553–9561. [Google Scholar] [CrossRef]
- Snoswell, D.R.E.; Baumberg, J.J. Stretching the Imagination. Textiles 2009, 4, 8–10. [Google Scholar]
- Zhao, Q.; Finlayson, C.; Schaefer, C.; Spahn, P.; Gallei, M.; Herrmann, L.; Petukhov, A.; Baumberg, J. Nanoassembly of Polydisperse Photonic Crystals Based on Binary and Ternary Polymer Opal Alloys. Adv. Opt. Mater. 2016, 4, 1494–1500. [Google Scholar] [CrossRef]
- Phan, S.E.; Russel, W.B.; Zhu, J.X.; Chaikin, P.M. Effects of polydispersity on hard sphere crystals. J. Chem. Phys. 1998, 108, 9789–9795. [Google Scholar] [CrossRef]
- Li, H.T.; Wu, P.; Zhao, G.W.; Guo, J.; Wang, C.C. Fabrication of industrial-level polymer photonic crystal films at ambient temperature Based on uniform core/shell colloidal particles. J. Colloid Interface Sci. 2021, 584, 145–153. [Google Scholar] [CrossRef]
- Gallei, M. Functional Polymer Opals and Porous Materials by Shear-Induced Assembly of Tailor-Made Particles. Macromol. Rapid Commun. 2018, 39, 16. [Google Scholar] [CrossRef] [PubMed]
- Pursiainen, O.; Baumberg, J.; Winkler, H.; Viel, B.; Spahn, P.; Ruhl, T. Shear-induced organization in flexible polymer opals. Adv. Mater. 2008, 20, 1484–1487. [Google Scholar] [CrossRef]
- Rosetta, G.; An, T.; Zhao, Q.B.; Baumberg, J.J.; Tomes, J.J.; Gunn, M.D.; Finlayson, C.E. Chromaticity of structural color in polymer thin film photonic crystals. Opt. Express 2020, 28, 36219–36228. [Google Scholar] [CrossRef]
- Kontogeorgos, A.; Snoswell, D.R.E.; Finlayson, C.E.; Baumberg, J.J.; Spahn, P.; Hellmann, G.P. Inducing Symmetry Breaking in Nanostructures: Anisotropic Stretch-Tuning Photonic Crystals. Phys. Rev. Lett. 2010, 105, 233909. [Google Scholar] [CrossRef]
- Snoswell, D.R.E.; Finlayson, C.E.; Zhao, Q.; Baumberg, J.J. Real-time measurements of crystallization processes in viscoelastic polymeric photonic crystals. Phys. Rev. E 2015, 92, 052315. [Google Scholar] [CrossRef] [PubMed]
- Zhu, J.X.; Li, M.; Rogers, R.; Meyer, W.; Ottewill, R.H.; Russell, W.B.; Chaikin, P.M. Crystallization of hard-sphere colloids in microgravity. Nature 1997, 387, 883–885. [Google Scholar] [CrossRef]
- Asher, S.; Weissman, J.; Tikhonov, A.; Coalson, R.; Kesavamoorthy, R. Diffraction in crystalline colloidal-array photonic crystals. Phys. Rev. E 2004, 69, 066619. [Google Scholar] [CrossRef]
- Jiang, P.; Bertone, J.F.; Hwang, K.S.; Colvin, V.L. Single-crystal colloidal multilayers of controlled thickness. Chem. Mater. 1999, 11, 2132–2140. [Google Scholar] [CrossRef]
- Haw, M.; Poon, W.; Pusey, P. Direct observation of oscillatory-shear-induced order in colloidal suspensions. Phys. Rev. E 1998, 57, 6859–6864. [Google Scholar] [CrossRef]
- Panine, P.; Narayanan, T.; Vermant, J.; Mewis, J. Structure and rheology during shear-induced crystallization of a latex suspension. Phys. Rev. E 2002, 66, 022401. [Google Scholar] [CrossRef]
- Wu, Y.; Derks, D.; van Blaaderen, A.; Imhof, A. Melting and crystallization of colloidal hard-sphere suspensions under shear. Proc. Natl. Acad. Sci. USA 2009, 106, 10564–10569. [Google Scholar] [CrossRef] [PubMed]
- Lander, B.; Seifert, U.; Speck, T. Crystallization in a sheared colloidal suspension. J. Chem. Phys. 2013, 138, 224907. [Google Scholar] [CrossRef]
- Ackerson, B.J. Shear Induced Order and Shear Processing of Model Hard-Sphere Suspensions. J. Rheol. 1990, 34, 553–590. [Google Scholar] [CrossRef]
- Liu, J.; Weitz, D.A.; Ackerson, B.J. Coherent Crystallography of Shear-Aligned Crystals of Hard-Sphere Colloids. Phys. Rev. E 1993, 48, 1106–1114. [Google Scholar] [CrossRef]
- Ackerson, B.; Pusey, P. Shear-Induced Order in Suspensions of Hard-Spheres. Phys. Rev. Lett. 1988, 61, 1033–1036. [Google Scholar] [CrossRef] [PubMed]
- Gevorkian, A.; Morozova, S.M.; Kheiri, S.; Khuu, N.; Chen, H.Y.; Young, E.; Yan, N.; Kumacheva, E. Actuation of Three-Dimensional-Printed Nanocolloidal Hydrogel with Structural Anisotropy. Adv. Funct. Mater. 2021, 31, 2010743. [Google Scholar] [CrossRef]
- Haywood, A.D.; Davis, V.A. Effects of liquid crystalline and shear alignment on the optical properties of cellulose nanocrystal films. Cellulose 2017, 24, 705–716. [Google Scholar] [CrossRef]
- Wong, H.S.; Mackley, M.; Butler, S.; Baumberg, J.; Snoswell, D.; Finlayson, C.E.; Zhao, Q.B. The rheology and processing of “edge sheared” colloidal polymer opals. J. Rheol. 2014, 58, 397–409. [Google Scholar] [CrossRef]
- Snoswell, D.; Kontogeorgos, A.; Baumberg, J.; Lord, T.; Mackley, M.; Spahn, P.; Hellmann, G. Shear ordering in polymer photonic crystals. Phys. Rev. E 2010, 81, 020401. [Google Scholar] [CrossRef]
- Miller, C.C. Stokes-Einstein law for Diffusion in Solution. Proc. Roy. Soc. A 1924, 106, 724. [Google Scholar]
- Markmann, V.; Dartsch, M.; Valerio, J.; Frenzel, L.; Lokteva, I.; Walther, M.; Westermeier, F.; Grubel, G.; Lehmkuhler, F. Shear-induced ordering in liquid microjets seen by x-ray cross correlation analysis. Struct. Dyn. 2020, 7, 054901. [Google Scholar] [CrossRef]
- Priebe, M.; Kalbfleisch, S.; Tolkiehn, M.; Koster, S.; Abel, B.; Davies, R.J.; Salditt, T. Orientation of biomolecular assemblies in a microfluidic jet. New J. Phys. 2010, 12, 043056. [Google Scholar] [CrossRef][Green Version]
- Trebbin, M.; Steinhauser, D.; Perlich, J.; Buffet, A.; Roth, S.V.; Zimmermann, W.; Thiele, J.; Forster, S. Anisotropic particles align perpendicular to the flow direction in narrow microchannels. Proc. Natl. Acad. Sci. USA 2013, 110, 6706–6711. [Google Scholar] [CrossRef]
- Frenkel, D. Order Through Disorder-Entropy Strikes Back. Phys. World 1993, 6, 24–25. [Google Scholar] [CrossRef]
- Castelli, A.; de Graaf, J.; Marras, S.; Brescia, R.; Goldoni, L.; Manna, L.; Arciniegas, M.P. Understanding and tailoring ligand interactions in the self-assembly of branched colloidal nanocrystals into planar superlattices. Nat. Commun. 2018, 9, 9. [Google Scholar] [CrossRef] [PubMed]
- Kalsin, A.M.; Fialkowski, M.; Paszewski, M.; Smoukov, S.K.; Bishop, K.J.M.; Grzybowski, B.A. Electrostatic self-assembly of binary nanoparticle crystals with a diamond-like lattice. Science 2006, 312, 420–424. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q. Oscillatory Shearing in Polymer Opals. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2015. [Google Scholar]
- Ruhl, T.; Spahn, P.; Hellmann, G.P. Artificial opals prepared by melt compression. Polymer 2003, 44, 7625–7634. [Google Scholar] [CrossRef]
- Viel, B.; Ruhl, T.; Hellmann, G. Reversible deformation of opal elastomers. Chem. Mater. 2007, 19, 5673–5679. [Google Scholar] [CrossRef]
- Schafer, C.; Smolin, D.; Hellmann, G.; Gallei, M. Fully Reversible Shape Transition of Soft Spheres in Elastomeric Polymer Opal Films. Langmuir 2013, 29, 11275–11283. [Google Scholar] [CrossRef]
- Spahn, P.; Finlayson, C.E.; Etah, W.M.; Snoswell, D.R.E.; Baumberg, J.J.; Hellmann, G.P. Modification of the refractive-index contrast in polymer opal films. J. Mater. Chem. 2011, 21, 8893–8897. [Google Scholar] [CrossRef]
- Available online: http://www.linkam.co.uk/css450-specifications (accessed on 24 August 2021).
- Ossi, P. Disordered Materials; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Catherall, A.; Melrose, J.; Ball, R. Shear thickening and order-disorder effects in concentrated colloids at high shear rates. J. Rheol. 2000, 44, 1–25. [Google Scholar] [CrossRef]
- Finlayson, C.; Baumberg, J. Generating Bulk-Scale Ordered Optical Materials Using Shear-Assembly in Viscoelastic Media. Materials 2017, 10, 688. [Google Scholar] [CrossRef] [PubMed]
- Senjanovic, I.; Vladimir, N. Physical insight into Timoshenko beam theory and its modification with extension. Struct. Eng. Mech. 2013, 48, 519–545. [Google Scholar] [CrossRef]
- Shereda, L.T.; Larson, R.G.; Solomon, M.J. Local stress control of spatiotemporal ordering of colloidal crystals in complex flows. Phys. Rev. Lett. 2008, 101, 038301. [Google Scholar] [CrossRef] [PubMed]
- Shereda, L.; Larson, R.; Solomon, M. Boundary-Driven Colloidal Crystallization in Simple Shear Flow. Phys. Rev. Lett. 2010, 105, 228302. [Google Scholar] [CrossRef] [PubMed]
| Step | Mode of Shear | Gap (μm) | Strain | Shear Rate (s−1) | Frequency (Hz) | Time (s) |
|---|---|---|---|---|---|---|
| 1 (Randomize) | continuous | 300 | - | 2 | - | 10 |
| 2 (Relaxation) | relaxation | 300 | - | - | - | 10 |
| 3 (Crystallization) | oscillatory | 300 | 25–350% | 0.01–140 | 0.01–10 | 300 |
| Fixed f, T | Fixed σ, T | Fixed f, σ | |||||
|---|---|---|---|---|---|---|---|
| (cm−1) | (Hz) | (s) | (°C) | ||||
| 50 | 18.9 (±0.3) | 121.4 | 0.01 | 178.7 | 1.8 (±0.4) | 25 | 26.7 (±1.0) |
| 75 | 11.6 (±0.1) | 142.0 | 0.05 | 52.5 | 2.6 (±0.1) | 37.5 | 24.9 (±1.1) |
| 100 | 5.2 (±0.2) | 184.4 | 0.1 | 45.8 | 4.6 (±0.2) | 50 | 7.2 (±0.2) |
| 150 | 4.3 (±0.1) | 168.1 | 0.25 | 25.8 | 6.5 (±0.6) | 62.5 | 3.7 (±0.1) |
| 200 | 4.0 (±0.1) | 139.8 | 0.5 | 18.9 | 9.5 (±1.0) | 75 | 3.0 (±0.1) |
| 250 | 8.7 (±0.2) | 133.5 | 1.0 | 12.6 | 12.6 (±0.4) | 87.5 | 3.8 (±0.3) |
| 300 | 39.9 (±0.9) | 113.8 | 1.5 | 9.0 | 13.5 (±2.3) | 100 | 2.7 (±0.1) |
| 350 | 137.1 (±8.9) | 56.2 | 2.5 | 7.4 | 18.5 (±0.5) | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Finlayson, C.E.; Rosetta, G.; Baumberg, J.J. An Experimental and Theoretical Determination of Oscillatory Shear-Induced Crystallization Processes in Viscoelastic Photonic Crystal Media. Materials 2021, 14, 5298. https://doi.org/10.3390/ma14185298
Finlayson CE, Rosetta G, Baumberg JJ. An Experimental and Theoretical Determination of Oscillatory Shear-Induced Crystallization Processes in Viscoelastic Photonic Crystal Media. Materials. 2021; 14(18):5298. https://doi.org/10.3390/ma14185298
Chicago/Turabian StyleFinlayson, Chris E., Giselle Rosetta, and Jeremy J. Baumberg. 2021. "An Experimental and Theoretical Determination of Oscillatory Shear-Induced Crystallization Processes in Viscoelastic Photonic Crystal Media" Materials 14, no. 18: 5298. https://doi.org/10.3390/ma14185298
APA StyleFinlayson, C. E., Rosetta, G., & Baumberg, J. J. (2021). An Experimental and Theoretical Determination of Oscillatory Shear-Induced Crystallization Processes in Viscoelastic Photonic Crystal Media. Materials, 14(18), 5298. https://doi.org/10.3390/ma14185298







