Multiscale Analysis of Mechanical Properties of 3D Orthogonal Woven Composites with Randomly Distributed Voids
Abstract
:1. Introduction
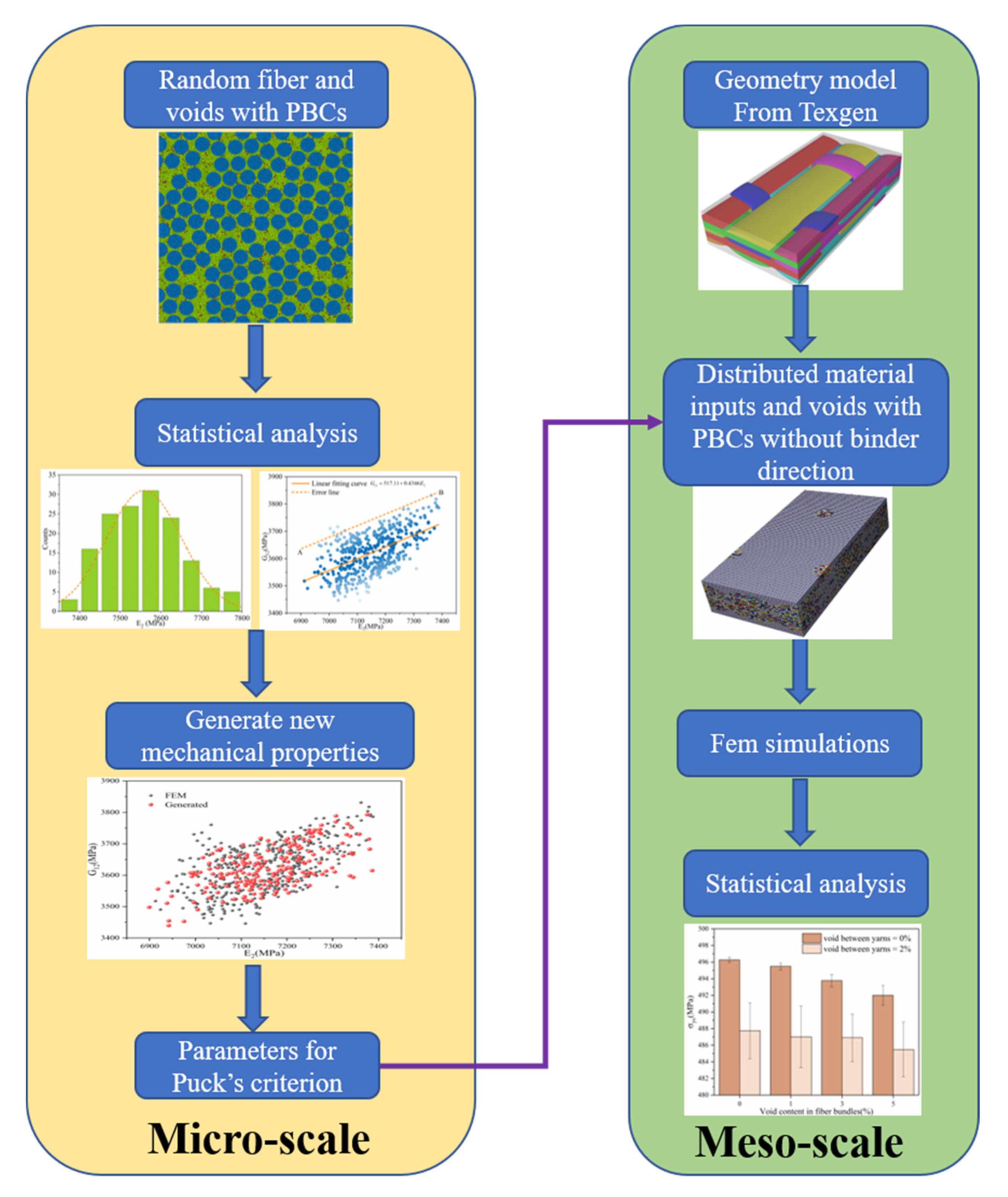
2. Multiscale Models and Methods
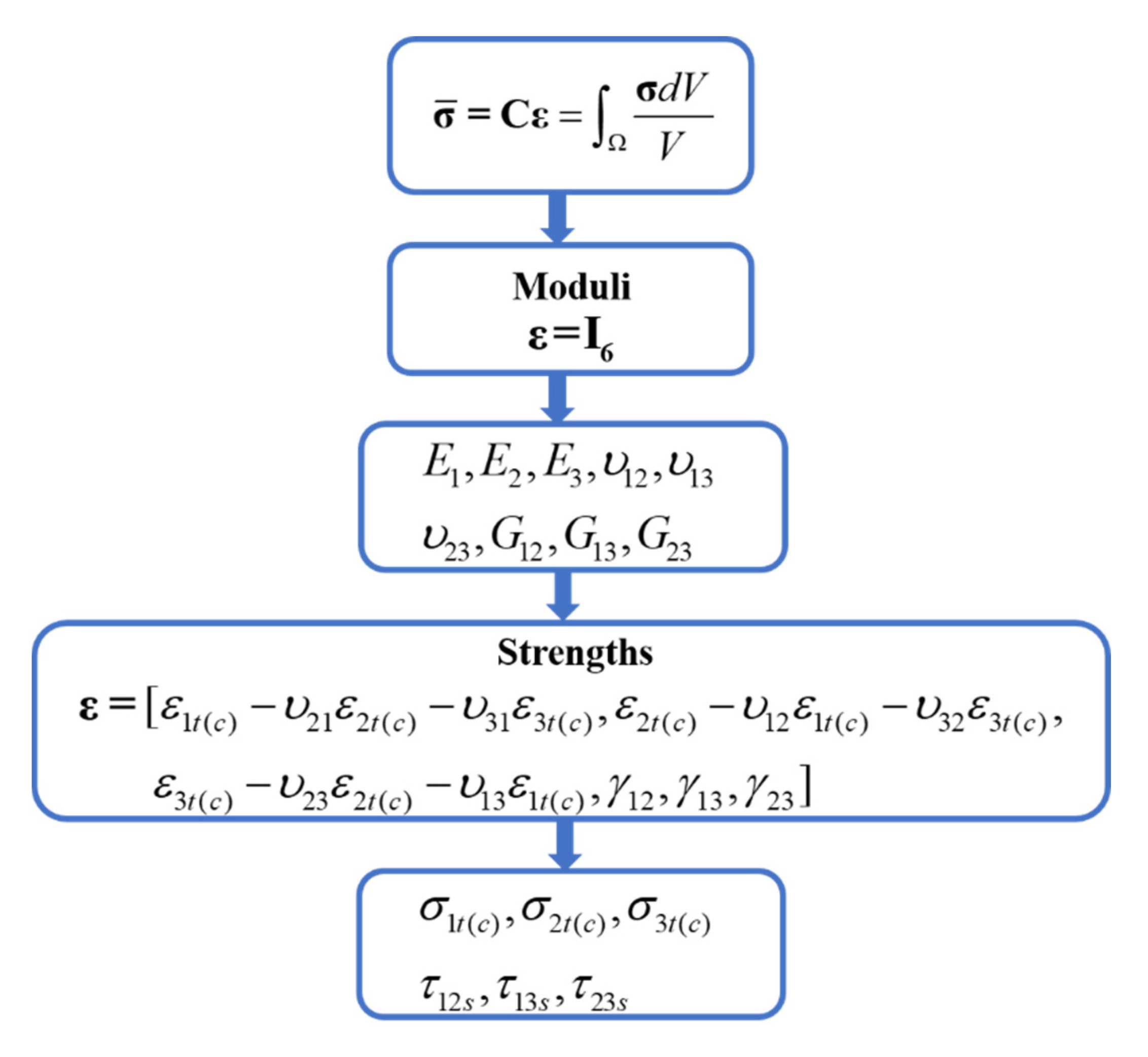
2.1. Microscale Model for UD Composites
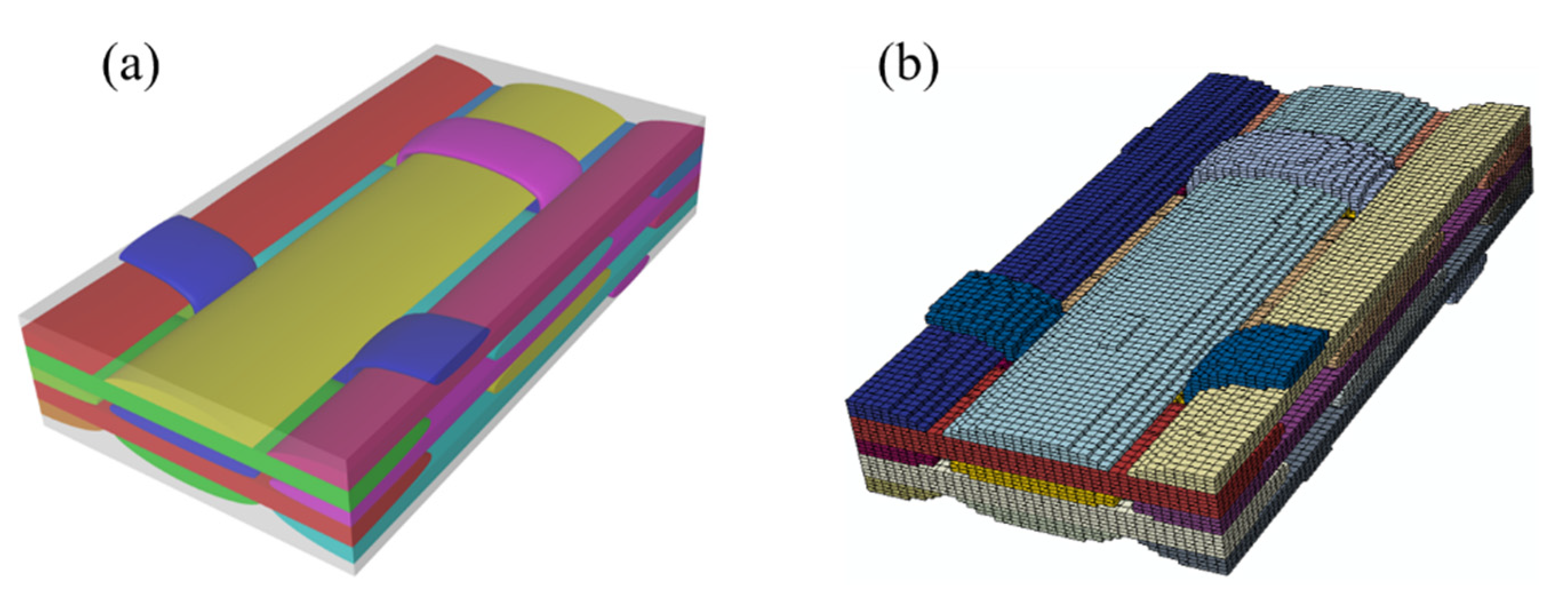
2.2. Mesoscale Model for 3DOWCs
2.3. Periodic Boundary Conditions
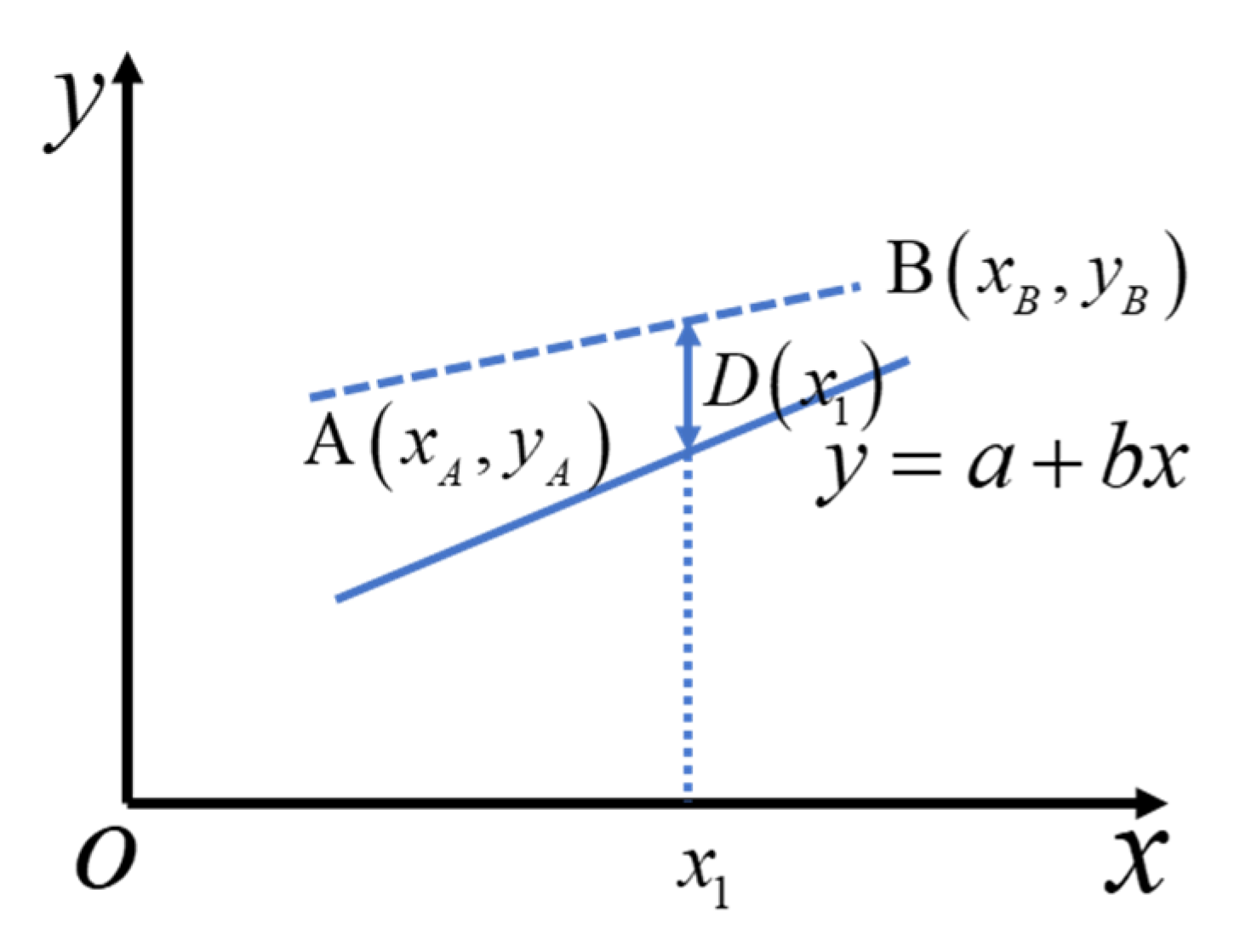
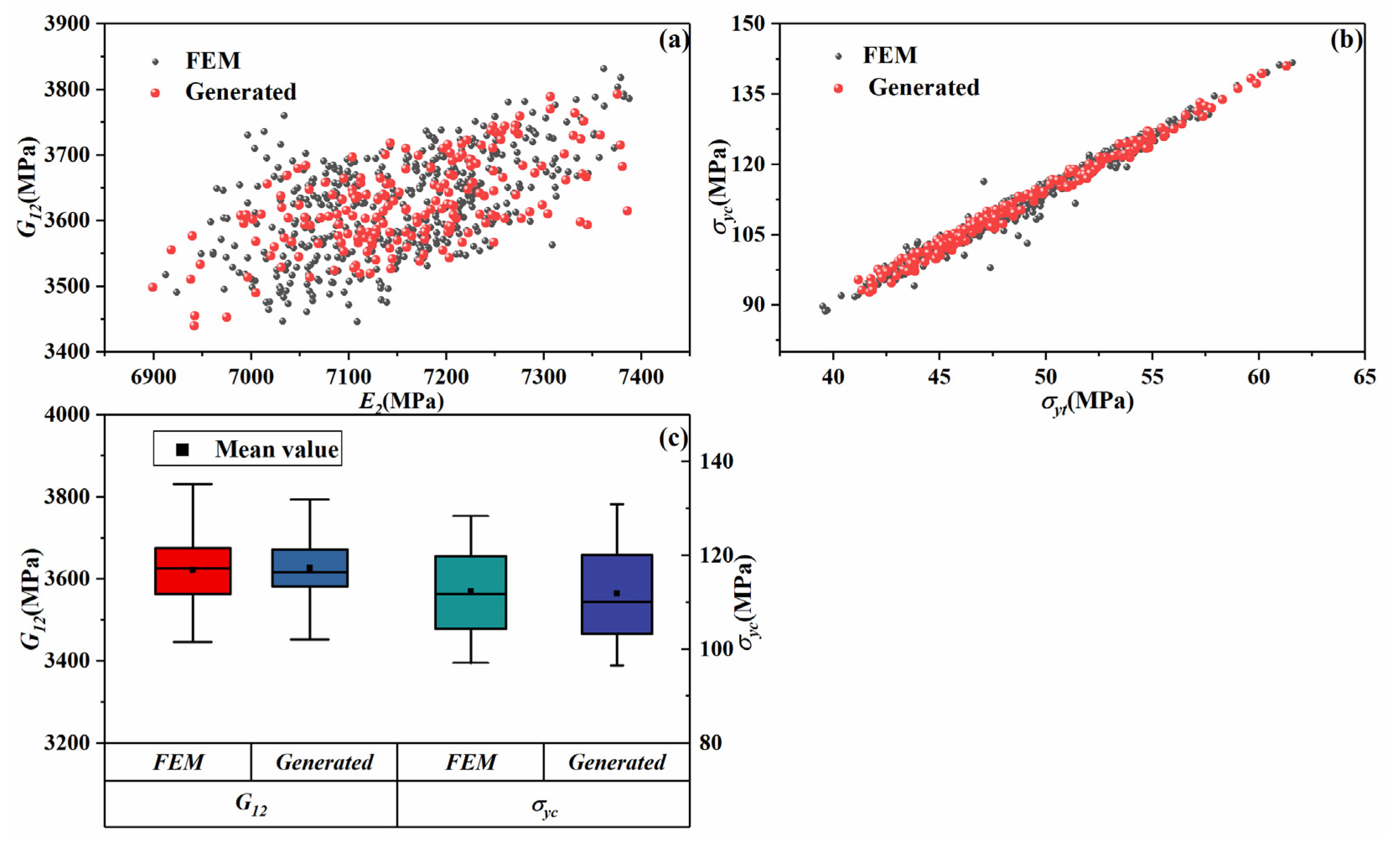
2.4. Distance Function for Generating Mechanical Properties of Microscale Model
3. Failure Criteria and Constitutive Models
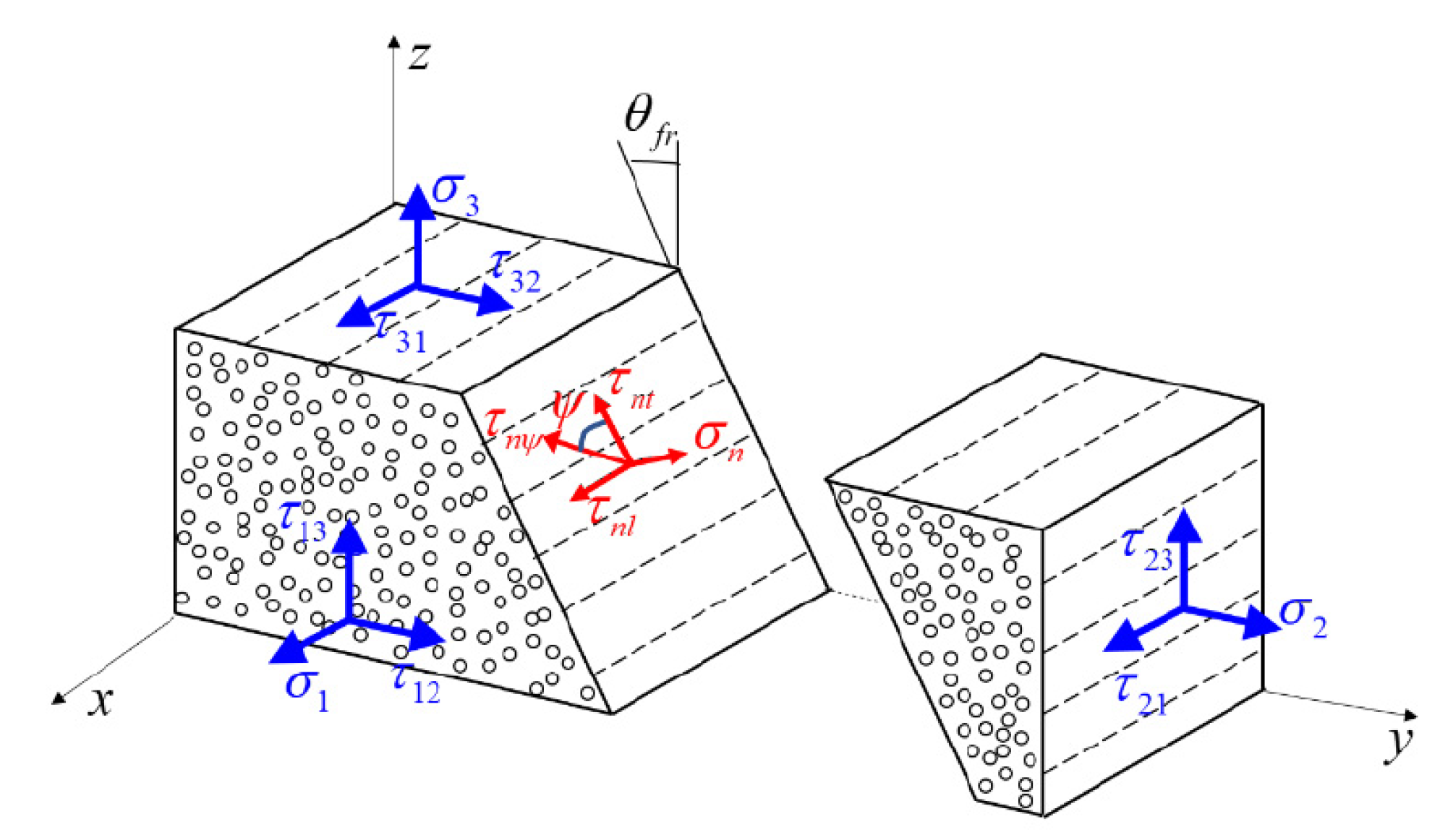
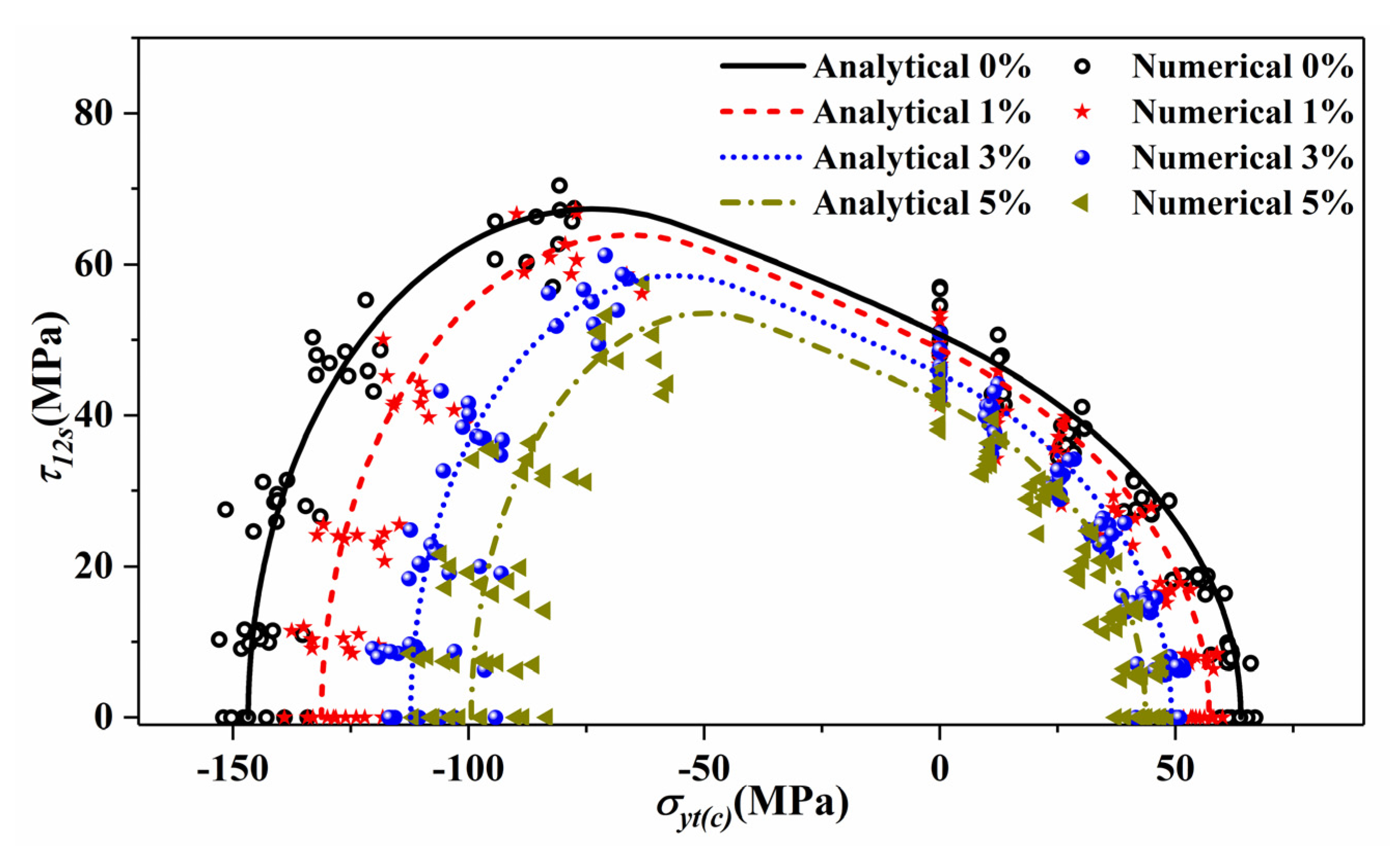
3.1. Failure Initiation Criteria
3.2. Damage Constitutive Model
4. Results and Discussion
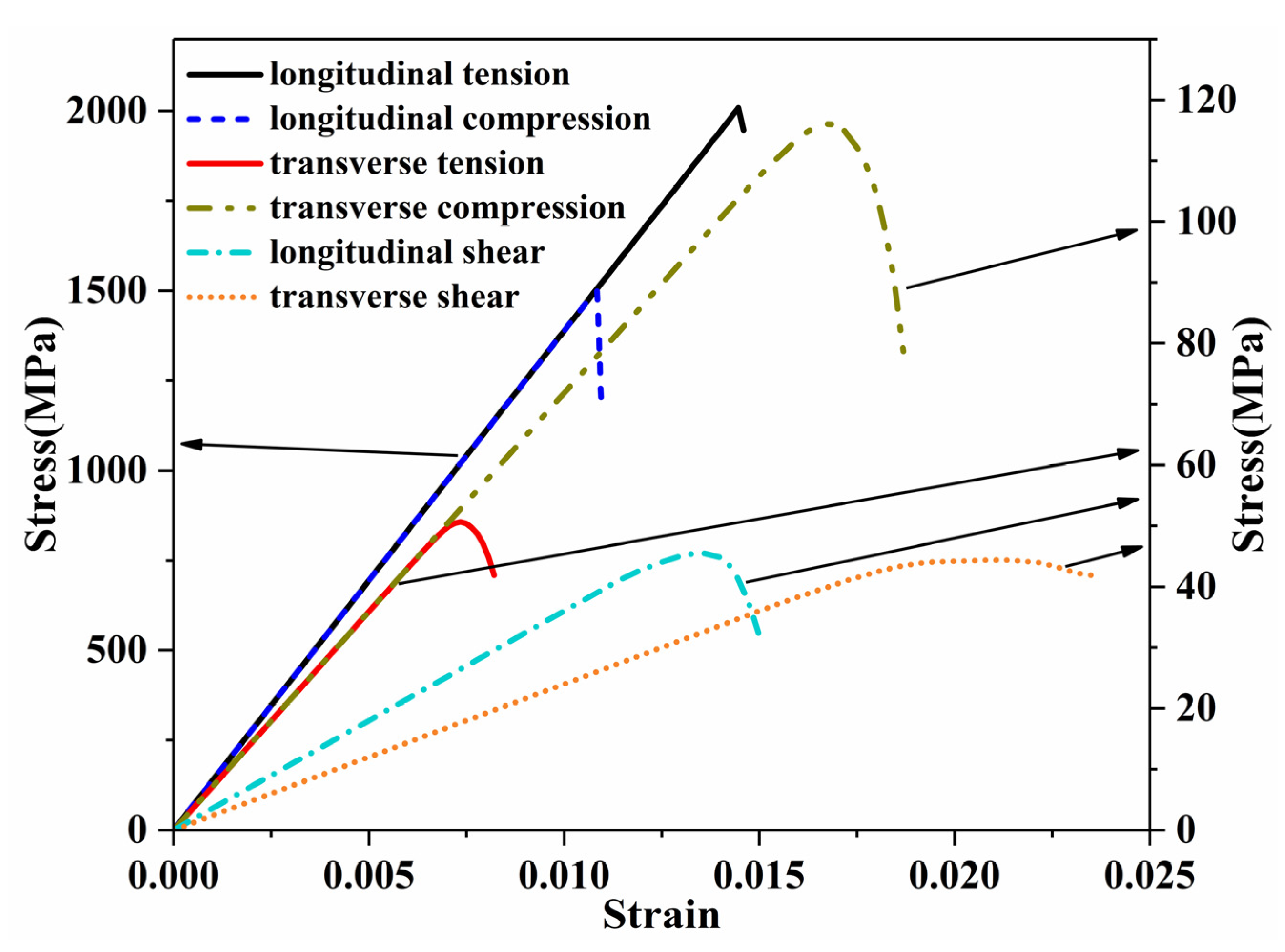
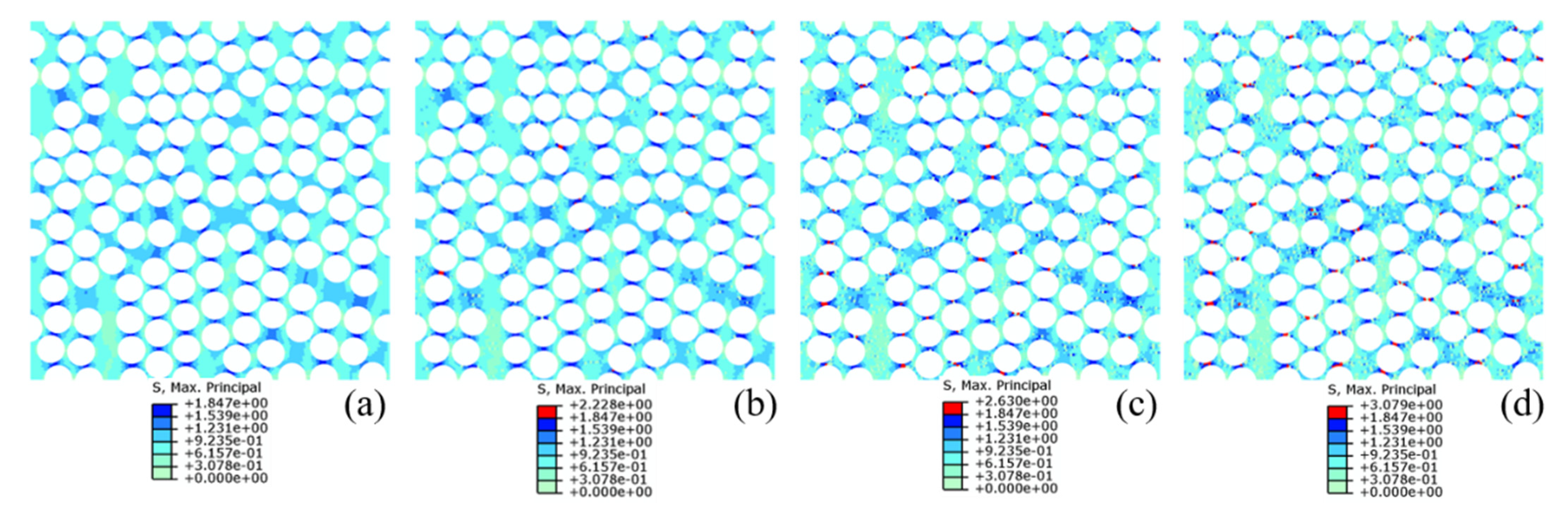
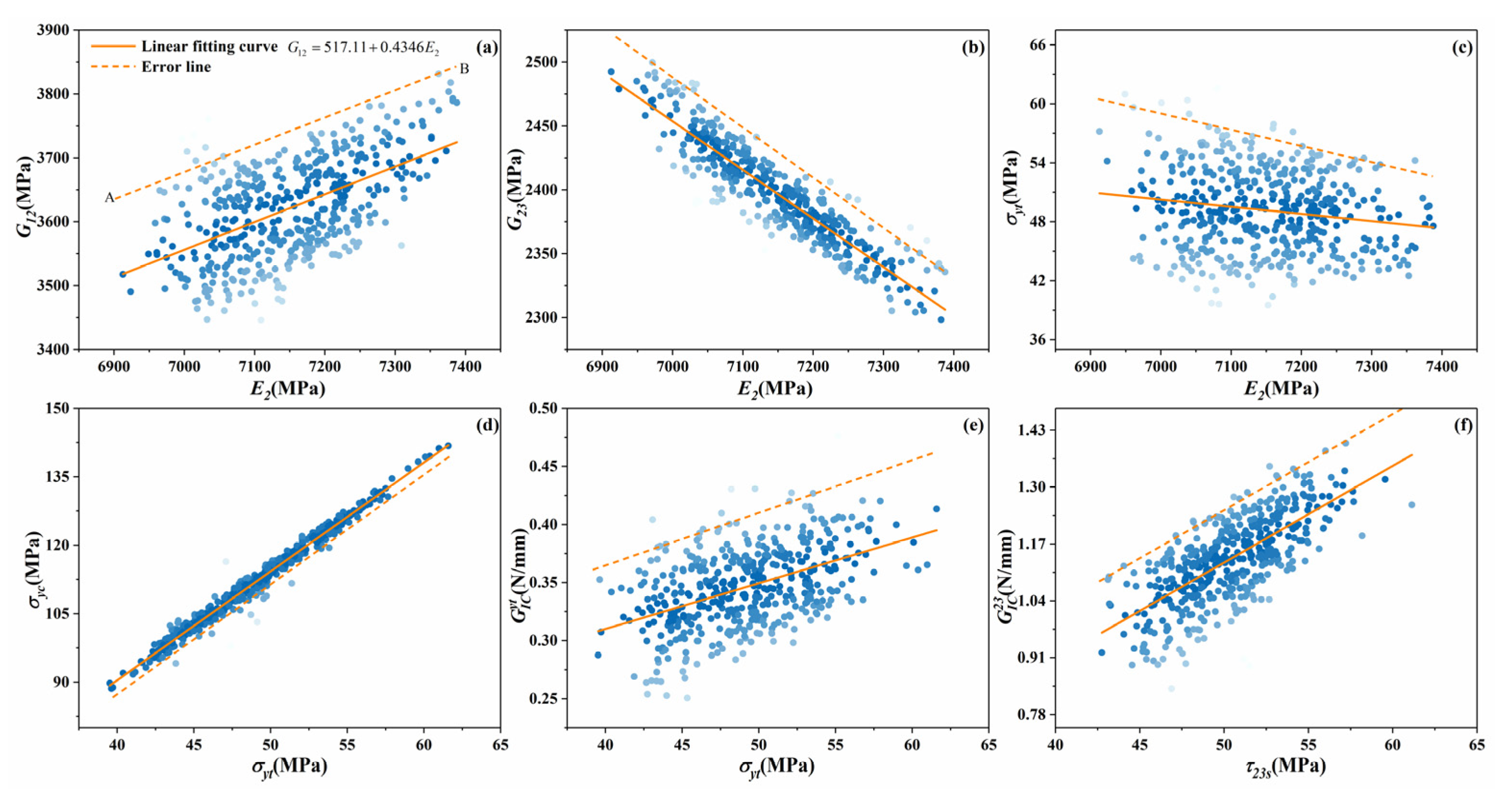
4.1. Microscale Model
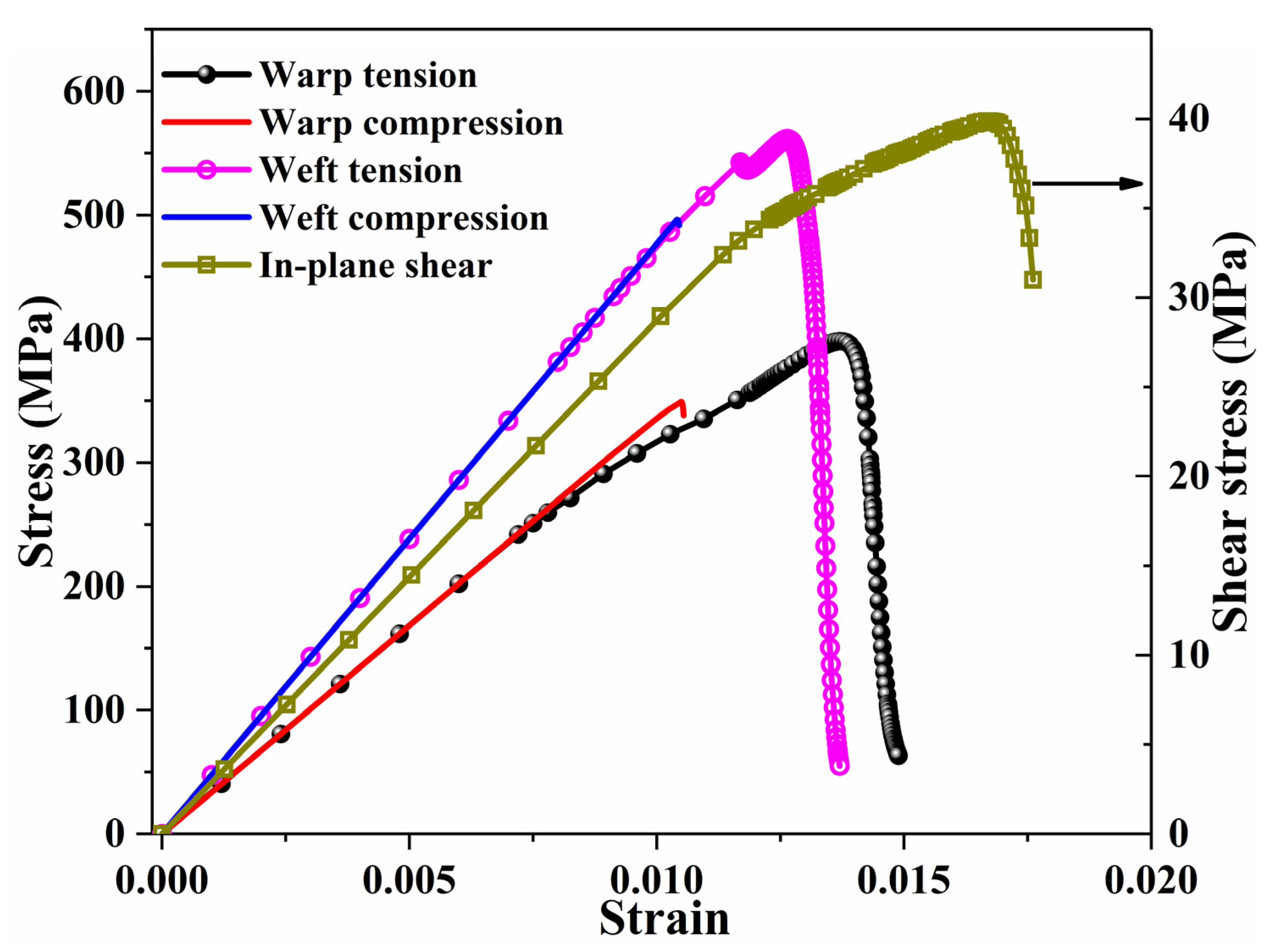
4.2. Mesoscale Model
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Void | Mean | Std | Void | Mean | Std | Void | Mean | Std | |||
|---|---|---|---|---|---|---|---|---|---|---|---|
| (MPa) | 0 | 138,553.96 | 5.304 | (MPa) | 0 | 2022.16 | 0.251 | (N/mm) | 0 | 15.16 | 5.8 × 10−4 |
| 1% | 138,513.33 | 5.4 | 1% | 2005.18 | 2.664 | 1% | 15.1 | 0.0236 | |||
| 3% | 138,433.2 | 5.583 | 3% | 2002.2 | 0.158 | 3% | 14.99 | 0.02594 | |||
| 5% | 138,353.58 | 5.736 | 5% | 2001.07 | 0.243 | 5% | 14.9 | 0.02473 | |||
| (MPa) | 0 | 7558.85 | 92.336 | (MPa) | 0 | 1503.3 | 0.18 | (N/mm) | 0 | 8.256 | 2.81 × 10−4 |
| 1% | 7423.79 | 95.367 | 1% | 1502.14 | 0.365 | 1% | 8.245 | 0.00364 | |||
| 3% | 7149.63 | 96.21 | 3% | 1500.29 | 1.807 | 3% | 8.238 | 0.00876 | |||
| 5% | 6852.07 | 109.8 | 5% | 1497.43 | 2.274 | 5% | 8.235 | 0.01295 | |||
| 0 | 0.318 | 4.038 × 10−4 | (MPa) | 0 | 64.07 | 2.053 | (N/mm) | 0 | 0.426 | 0.0358 | |
| 1% | 0.3172 | 4.007 × 10−4 | 1% | 57.41 | 4.512 | 1% | 0.394 | 0.0352 | |||
| 3% | 0.3156 | 4.019 × 10−4 | 3% | 49.17 | 4.142 | 3% | 0.346 | 0.0344 | |||
| 5% | 0.3139 | 4.454 × 10−4 | 5% | 43.69 | 3.505 | 5% | 0.315 | 0.032 | |||
| 0 | 0.4755 | 0.00602 | (MPa) | 0 | 147.2 | 5.299 | (N/mm) | 0 | 2.236 | 0.1241 | |
| 1% | 0.4728 | 0.00619 | 1% | 131.78 | 11.065 | 1% | 1.809 | 0.1482 | |||
| 3% | 0.4664 | 0.00709 | 3% | 112.3 | 10.002 | 3% | 1.777 | 0.141 | |||
| 5% | 0.4597 | 0.00871 | 5% | 99.53 | 8.314 | 5% | 1.585 | 0.1409 | |||
| (MPa) | 0 | 3876.98 | 73.309 | (MPa) | 0 | 50.91 | 2.637 | (N/mm) | 0 | 0.581 | 0.0548 |
| 1% | 3790.19 | 76.972 | 1% | 48.92 | 2.695 | 1% | 0.554 | 0.0549 | |||
| 3% | 3621.21 | 75.79 | 3% | 45.54 | 2.705 | 3% | 0.52 | 0.0493 | |||
| 5% | 3445.74 | 77.938 | 5% | 41.9 | 2.389 | 5% | 0.479 | 0.0475 | |||
| (MPa) | 0 | 2528.02 | 38.013 | (MPa) | 0 | 60.06 | 4.352 | (N/mm) | 0 | 1.381 | 0.1438 |
| 1% | 2486.08 | 38.284 | 1% | 55.17 | 4.032 | 1% | 1.253 | 0.1214 | |||
| 3% | 2396.78 | 40.006 | 3% | 50.35 | 3.117 | 3% | 1.135 | 0.099 | |||
| 5% | 2306.22 | 47.622 | 5% | 46.08 | 3.126 | 5% | 1.026 | 0.0956 |
References
- Fuchs, E.R.H.; Field, F.R.; Roth, R.; Kirchain, R. Strategic materials selection in the automobile body: Economic opportunities for polymer composite design. Compos. Sci. Technol. 2008, 68, 1989–2002. [Google Scholar] [CrossRef]
- Huang, T.; Wang, Y.; Wang, G. Review of the Mechanical Properties of a 3D Woven Composite and Its Applications. Polym. -Plast. Technol. Eng. 2018, 57, 740–756. [Google Scholar] [CrossRef]
- Su, Z.; Huang, F.; Liu, Q. Development of low cost out-of-autoclave Molding Technology for Advanced Composite Materials. Hi-Tech. Fiber Appl. 2021, 46, 18–27. [Google Scholar]
- Almeida, S.; Neto, Z.D.S.N. Effect of void content on the strength of composite laminates. Compos. Struct. 1994, 28, 139–148. [Google Scholar] [CrossRef]
- Zhang, A.; Lu, H.; Zhang, D. Research on the mechanical properties prediction of carbon/epoxy composite laminates with different void contents. Polym. Compos. 2016, 37, 14–20. [Google Scholar] [CrossRef]
- Di Landro, L.; Montalto, A.; Bettini, P.; Guerra, S.; Montagnoli, F.; Rigamonti, M. Detection of Voids in Carbon/Epoxy Laminates and Their Influence on Mechanical Properties. Polym. Polym. Compos. 2017, 25, 371–380. [Google Scholar] [CrossRef]
- Tao, W.; Zhu, P.; Xu, C.; Liu, Z. Uncertainty quantification of mechanical properties for three-dimensional orthogonal woven composites. Part II: Multiscale simulation. Compos. Struct. 2020, 235, 111764. [Google Scholar] [CrossRef]
- Šejnoha, M.; Zeman, J. Micromechanical modeling of random or imperfect composites. WIT Trans. Built Environ. 2006, 85. [Google Scholar] [CrossRef] [Green Version]
- Šejnoha, M.; Zeman, J. Micromechanical modeling of imperfect textile composites. Int. J. Eng. Sci. 2008, 46, 513–526. [Google Scholar] [CrossRef]
- Puck, A.; Kopp, J.; Knops, M. Guidelines for the determination of the parameters in Puck’s action plane strength criterion. Compos. Sci. Technol. 2002, 62, 371–378. [Google Scholar] [CrossRef]
- Potter, K.; Khan, B.; Wisnom, M.; Bell, T.; Stevens, J. Variability, fibre waviness and misalignment in the determination of the properties of composite materials and structures. Compos. Part A Appl. Sci. Manuf. 2008, 39, 1343–1354. [Google Scholar] [CrossRef]
- Mesogitis, T.S.; Skordos, A.A.; Long, A.C. Uncertainty in the manufacturing of fibrous thermosetting composites: A review. Compos. Part A Appl. Sci. Manuf. 2014, 57, 67–75. [Google Scholar] [CrossRef] [Green Version]
- Gao, X.; Yuan, L.; Fu, Y.; Yao, X.; Yang, H. Prediction of mechanical properties on 3D braided composites with void defects. Compos. Part B Eng. 2020, 197, 108164. [Google Scholar] [CrossRef]
- Shi, D.; Teng, X.; Jing, X.; Lyu, S.; Yang, X. A multi-scale stochastic model for damage analysis and performance dispersion study of a 2.5D fiber-reinforced ceramic matrix composites. Compos. Struct. 2020, 248, 112549. [Google Scholar] [CrossRef]
- Wang, X.F.; Wang, X.W.; Zhou, G.; Zhou, C. Multi-scale Analyses of 3D Woven Composite Based On Periodicity Boundary Conditions. J. Compos. Mater. 2007, 41, 1773–1788. [Google Scholar] [CrossRef]
- Zhou, Y.; Lu, Z.; Yang, Z. Progressive damage analysis and strength prediction of 2D plain weave composites. Compos. Part B Eng. 2013, 47, 220–229. [Google Scholar] [CrossRef]
- Vajari, D.A.; González, C.; Llorca, J.; Legarth, B.N. A numerical study of the influence of microvoids in the transverse mechanical response of unidirectional composites. Compos. Sci. Technol. 2014, 97, 46–54. [Google Scholar] [CrossRef] [Green Version]
- Vajari, D.A. A micromechanical study of porous composites under longitudinal shear and transverse normal loading. Compos. Struct. 2015, 125, 266–276. [Google Scholar] [CrossRef]
- Wang, M.; Zhang, P.; Fei, Q.; Guo, F. Computational evaluation of the effects of void on the transverse tensile strengths of unidirectional composites considering thermal residual stress. Compos. Struct. 2019, 227. [Google Scholar] [CrossRef]
- Paiboon, J.; Griffiths, D.; Huang, J.; Fenton, G.A. Numerical analysis of effective elastic properties of geomaterials containing voids using 3D random fields and finite elements. Int. J. Solids Struct. 2013, 50, 3233–3241. [Google Scholar] [CrossRef] [Green Version]
- Griffiths, D.V.; Paiboon, J.; Huang, J.; Fenton, G.A. Homogenization of geomaterials containing voids by random fields and finite elements. Int. J. Solids Struct. 2012, 49, 2006–2014. [Google Scholar] [CrossRef] [Green Version]
- Suo, Y.; Wang, B.; Jia, P.; Gong, Y. The effect of fabrication defects on the mechanical behaviors of metal matrix composites. Mater. Today Commun. 2020, 25, 101663. [Google Scholar] [CrossRef]
- Tao, W.; Zhu, P.; Xu, C.; Liu, Z. Uncertainty quantification of mechanical properties for three-dimensional orthogonal woven composites. Part I: Stochastic reinforcement geometry reconstruction. Compos. Struct. 2020, 235, 111763. [Google Scholar] [CrossRef]
- Zhou, L.C.; Chen, M.W.; Liu, C.; Wu, H.A. A multi-scale stochastic fracture model for characterizing the tensile behavior of 2D woven composites. Compos. Struct. 2018, 204, 536–547. [Google Scholar] [CrossRef]
- Rafiee, R.; Torabi, M.A. Stochastic prediction of burst pressure in composite pressure vessels. Compos. Struct. 2018, 185, 573–583. [Google Scholar] [CrossRef]
- Guo, J.; Wen, W.; Zhang, H.; Cui, H.; Song, J. Representative cell modeling strategy of 2.5D woven composites considering the randomness of weft cross-section for mechanical properties prediction. Eng. Fract. Mech. 2020, 237, 107255. [Google Scholar] [CrossRef]
- Dong, C. Effects of Process-Induced Voids on the Properties of Fibre Reinforced Composites. J. Mater. Sci. Technol. 2016, 32, 597–604. [Google Scholar] [CrossRef] [Green Version]
- Jiang, H.; Ren, Y.; Liu, Z.; Zhang, S. Microscale finite element analysis for predicting effects of air voids on mechanical properties of single fiber bundle in composites. J. Mater. Sci. 2018, 54, 1363–1381. [Google Scholar] [CrossRef]
- Carrera, E.; Petrolo, M.; Nagaraj, M.; Delicata, M. Evaluation of the influence of voids on 3D representative volume elements of fiber-reinforced polymer composites using CUF micromechanics. Compos. Struct. 2020, 254, 112833. [Google Scholar] [CrossRef]
- Hyde, A.; He, J.; Cui, X.; Lua, J.; Liu, L. Effects of microvoids on strength of unidirectional fiber-reinforced composite materials. Compos. Part B Eng. 2020, 187, 107844. [Google Scholar] [CrossRef]
- Dong, J.; Huo, N. A two-scale method for predicting the mechanical properties of 3D braided composites with internal defects. Compos. Struct. 2016, 152, 1–10. [Google Scholar] [CrossRef]
- Huang, T.; Gong, Y. A multiscale analysis for predicting the elastic properties of 3D woven composites containing void defects. Compos. Struct. 2018, 185, 401–410. [Google Scholar] [CrossRef]
- Lin, H.; Brown, L.P.; Long, A.C. Modelling and Simulating Textile Structures Using TexGen. Adv. Mater. Res. 2011, 331, 44–47. [Google Scholar] [CrossRef]
- Liu, Y.; Straumit, I.; Vasiukov, D.; Lomov, S.V.; Panier, S. Prediction of linear and non-linear behavior of 3D woven composite using mesoscopic voxel models reconstructed from X-ray micro-tomography. Compos. Struct. 2017, 179, 568–579. [Google Scholar] [CrossRef]
- Barbero, E.J. Finite Element Analysis of Composite Materials Using Ansys®; Chapman and Hall/CRC: Boca Raton, FL, USA, 2013. [Google Scholar]
- Li, S.; Warrior, N.; Zou, Z.; Almaskari, F. A unit cell for FE analysis of materials with the microstructure of a staggered pattern. Compos. Part A Appl. Sci. Manuf. 2011, 42, 801–811. [Google Scholar] [CrossRef]
- Lubliner, J.; Oliver, J.; Oller, S.; Onate, E. A plastic-damage model for concrete. Int. J. Solids Struct. 1989, 25, 299–326. [Google Scholar] [CrossRef]
- Lee, J.; Fenves, G.L. Plastic-Damage Model for Cyclic Loading of Concrete Structures. J. Eng. Mech. 1998, 124, 892–900. [Google Scholar] [CrossRef]
- Puck, A.; Schürmann, H. Failure analysis of frp laminates by means of physically based phenomenological models. Compos. Sci. Technol. 1998, 58, 1045–1067. [Google Scholar] [CrossRef]
- Gu, J.; Chen, P. Extension of Puck’s inter fibre fracture (IFF) criteria for UD composites. Compos. Sci. Technol. 2018, 162, 79–85. [Google Scholar] [CrossRef] [Green Version]
- Deuschle, H.M.; Puck, A. Application of the Puck failure theory for fibre-reinforced composites under three-dimensional stress: Comparison with experimental results. J. Compos. Mater. 2013, 47, 827–846. [Google Scholar] [CrossRef]
- Knops, M. Analysis of Failure in Fiber Polymer Laminates: The Theory of Alfred Puck; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar] [CrossRef]
- Deuschle, H.M.; Kröplin, B.-H. Finite element implementation of Puck’s failure theory for fibre-reinforced composites under three-dimensional stress. J. Compos. Mater. 2012, 46, 2485–2513. [Google Scholar] [CrossRef]
- Schirmaier, F.J.; Weiland, J.; Kärger, L.; Henning, F. A new efficient and reliable algorithm to determine the fracture angle for Puck’s 3D matrix failure criterion for UD composites. Compos. Sci. Technol. 2014, 100, 19–25. [Google Scholar] [CrossRef]
- Thomson, D.M.; Cui, H.; Erice, B.; Hoffmann, J.; Wiegand, J.; Petrinic, N. Experimental and numerical study of strain-rate effects on the IFF fracture angle using a new efficient implementation of Puck’s criterion. Compos. Struct. 2017, 181, 325–335. [Google Scholar] [CrossRef]
- Tuo, H.; Lu, Z.; Ma, X.; Zhang, C.; Chen, S. An experimental and numerical investigation on low-velocity impact damage and compression-after-impact behavior of composite laminates. Compos. Part B Eng. 2019, 167, 329–341. [Google Scholar] [CrossRef]
- Duvaut, G.; Lions, J.L.; John, C.W.; Cowin, S.C. Inequalities in Mechanics and Physics. J. Appl. Mech. 1977, 44, 364. [Google Scholar] [CrossRef]
- Cox, B.N.; Dadkhah, M.S.; Inman, R.V.; Morris, W.L.; Zupon, J. Mechanisms of compressive failure in 3D composites. Acta Metall. Mater. 1992, 40, 3285–3298. [Google Scholar] [CrossRef]
- Cox, B.N.; Dadkhah, M.S.; Morris, W.K.; Flintoff, J.G. Failure mechanisms of 3D woven composites in tension, compression, and bending. Acta Metall. Materialia. 1994, 42, 3967–3984. [Google Scholar] [CrossRef]





| Fiber | 231 | 12.97 | 0.3 | 11.28 | 4.45 | 3350 | 2500 |
| Matrix | 3.5 | 0.35 | 103.4 | 241 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, Y.; Huang, T.; Zhang, X.; Suo, Y.; Jia, P.; Zhao, S. Multiscale Analysis of Mechanical Properties of 3D Orthogonal Woven Composites with Randomly Distributed Voids. Materials 2021, 14, 5247. https://doi.org/10.3390/ma14185247
Gong Y, Huang T, Zhang X, Suo Y, Jia P, Zhao S. Multiscale Analysis of Mechanical Properties of 3D Orthogonal Woven Composites with Randomly Distributed Voids. Materials. 2021; 14(18):5247. https://doi.org/10.3390/ma14185247
Chicago/Turabian StyleGong, Yaohua, Tao Huang, Xun’an Zhang, Yongyong Suo, Purong Jia, and Shuyi Zhao. 2021. "Multiscale Analysis of Mechanical Properties of 3D Orthogonal Woven Composites with Randomly Distributed Voids" Materials 14, no. 18: 5247. https://doi.org/10.3390/ma14185247
APA StyleGong, Y., Huang, T., Zhang, X., Suo, Y., Jia, P., & Zhao, S. (2021). Multiscale Analysis of Mechanical Properties of 3D Orthogonal Woven Composites with Randomly Distributed Voids. Materials, 14(18), 5247. https://doi.org/10.3390/ma14185247






