Effect of the Construction of Carbon Fiber Plate Insert to Midsole on Running Performance
Abstract
:1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Experimental Footwear
2.3. Methodology
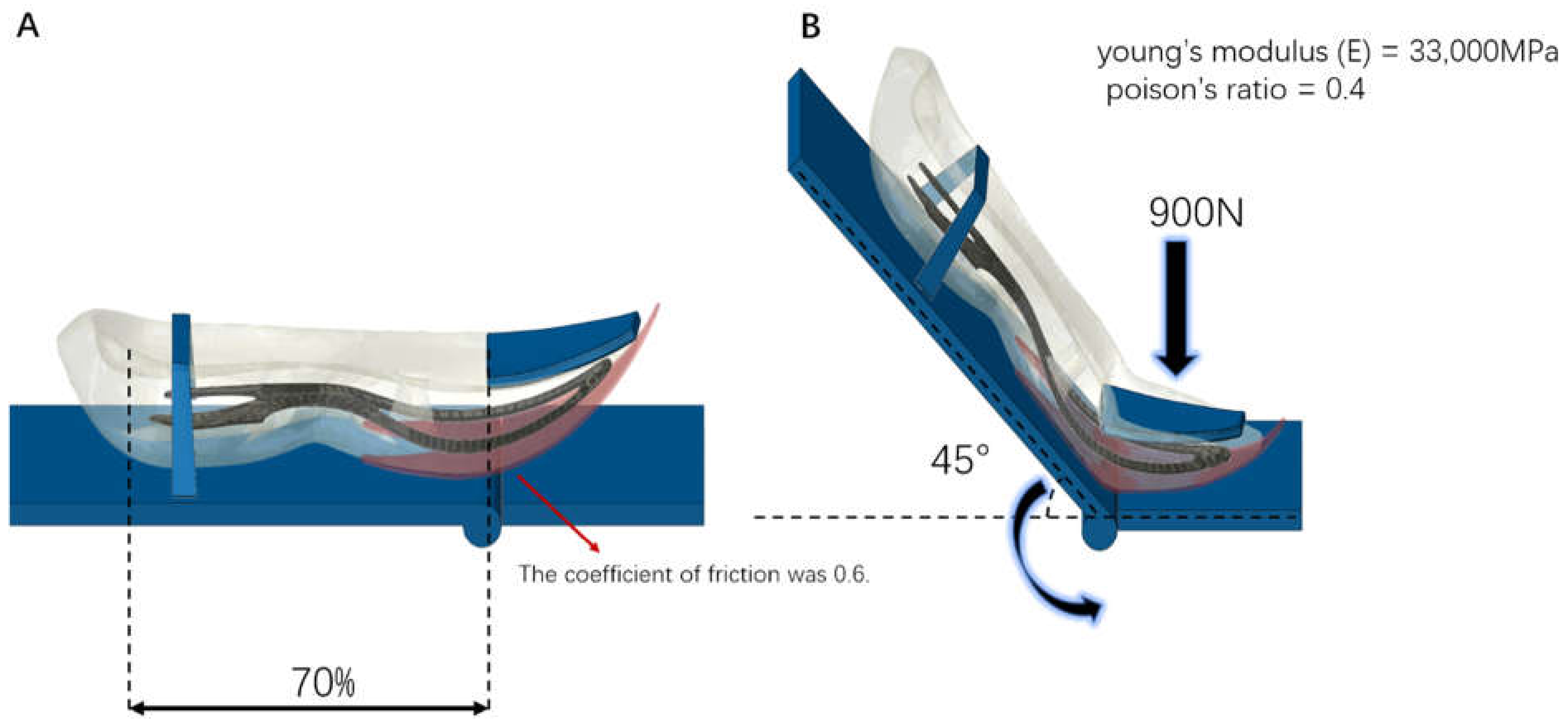
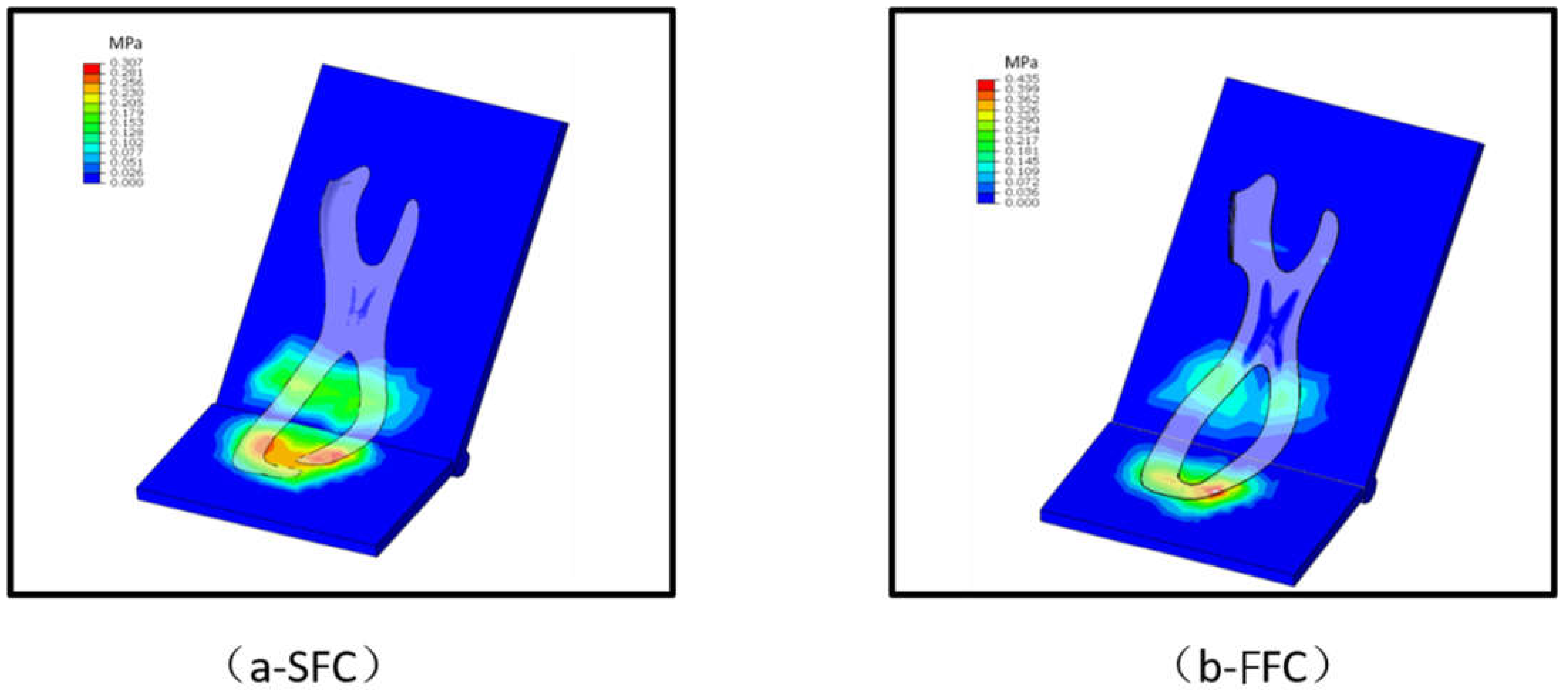
2.3.1. Finite Element Simulation
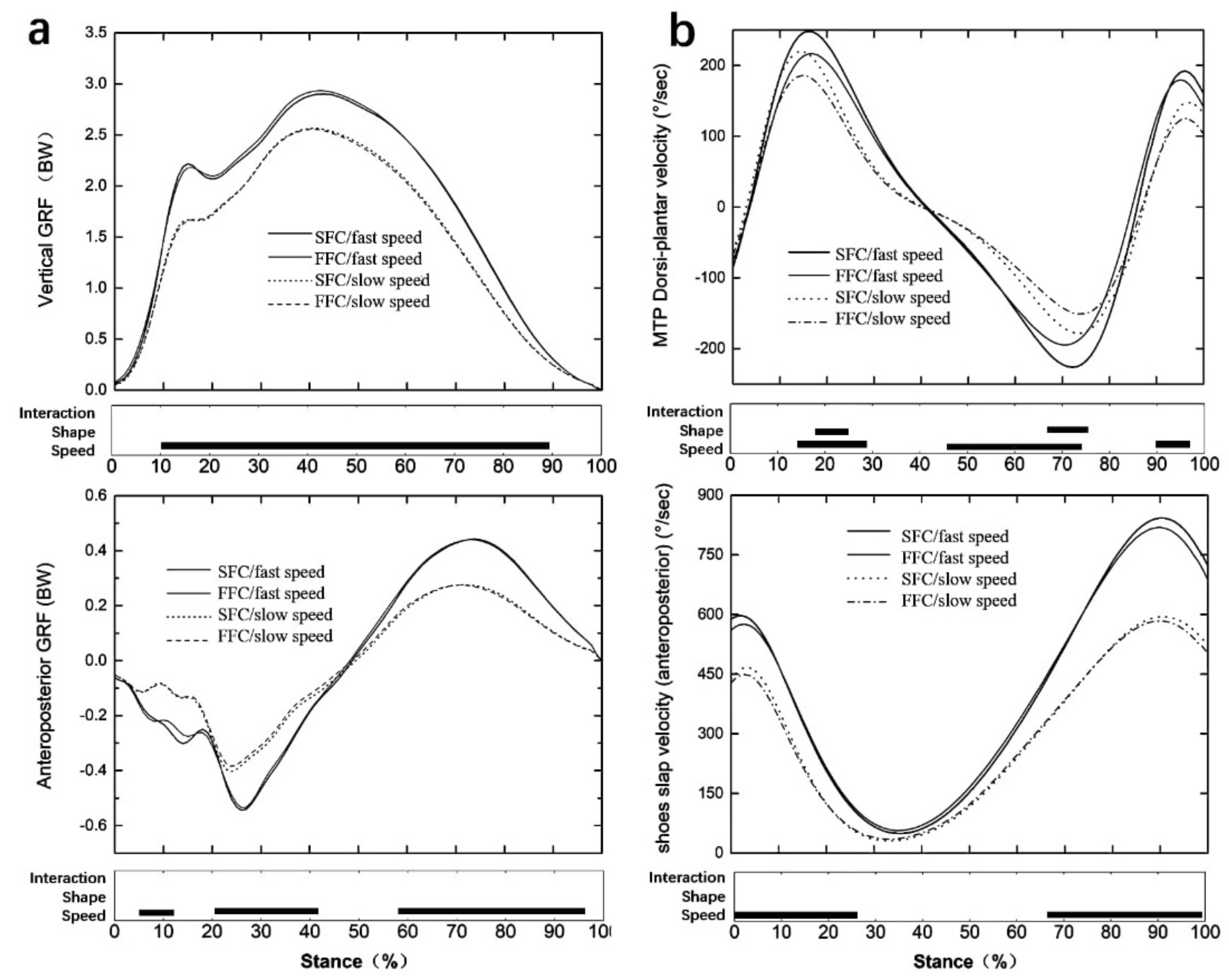
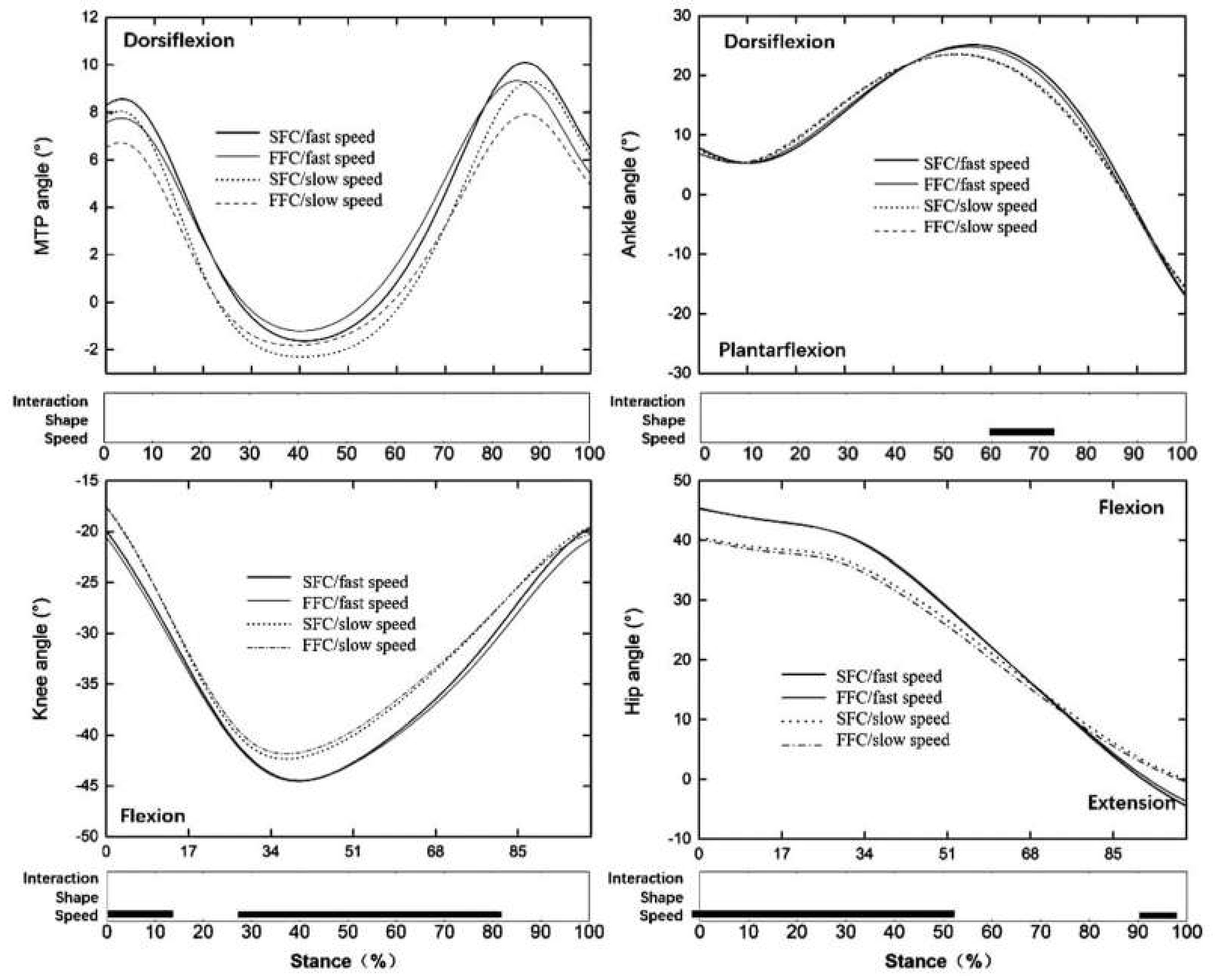
2.3.2. Biomechanical Data Collection
2.4. Statistical Analysis
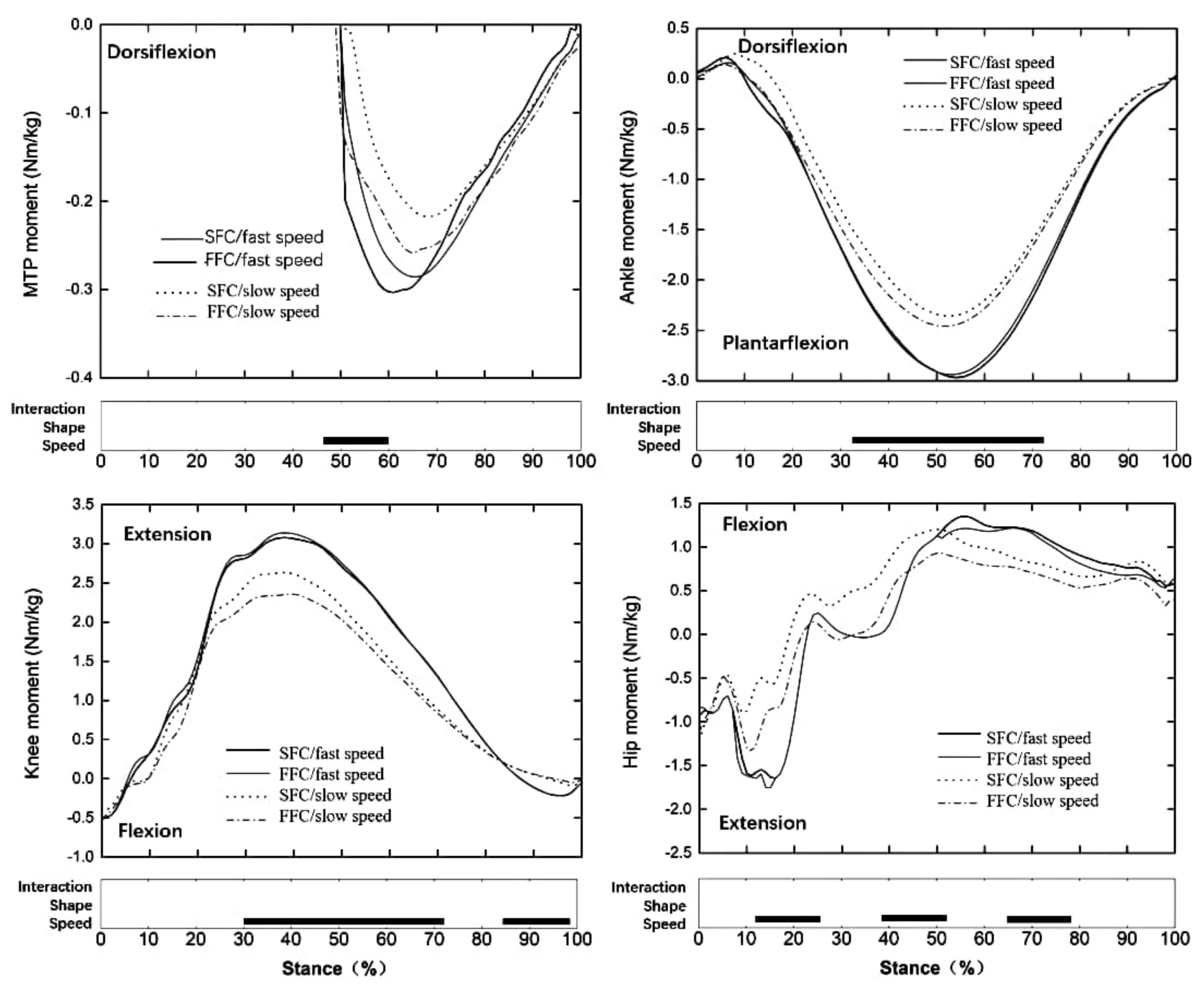
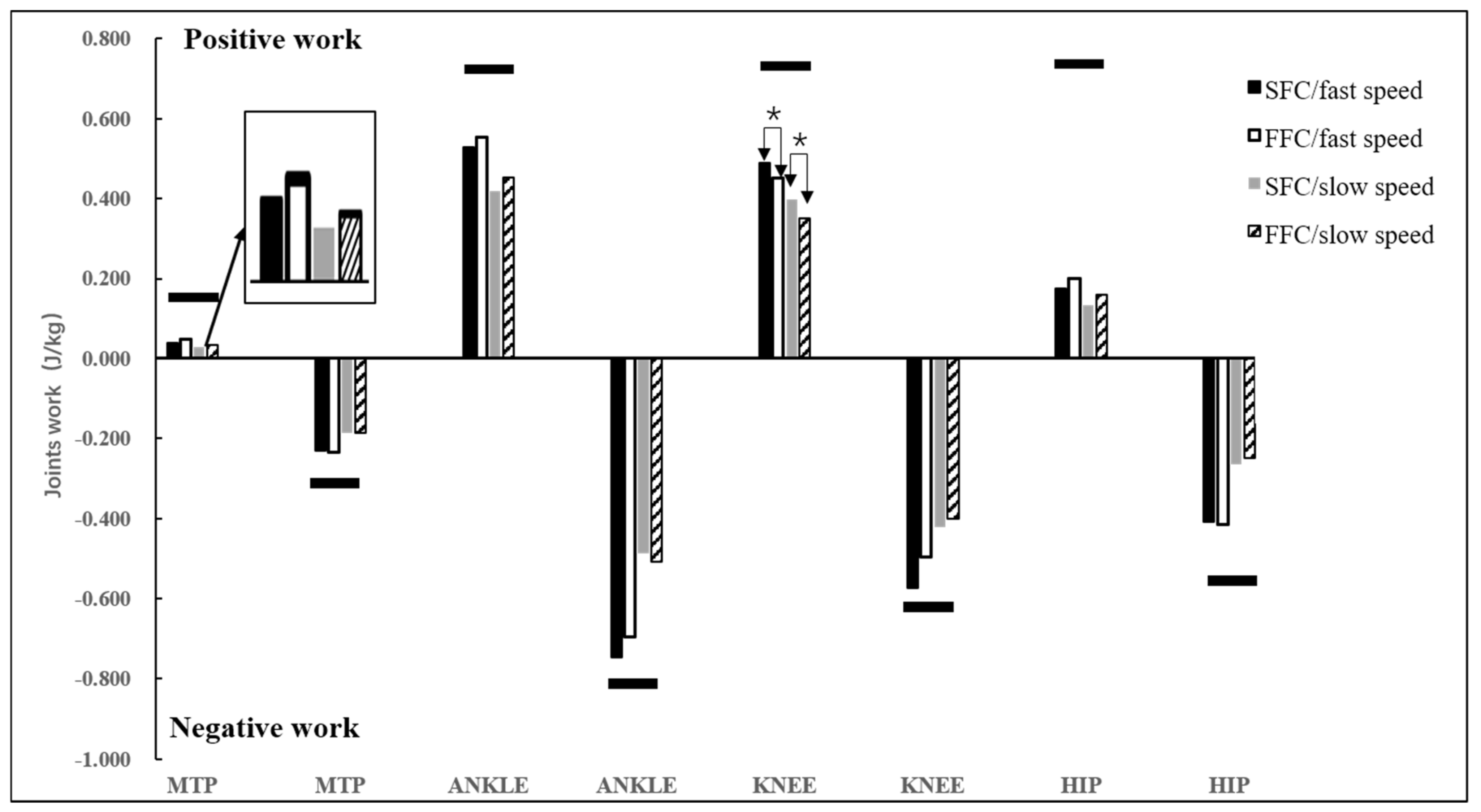
3. Results
4. Discussion
Limitations and Future Directions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Willwacher, S.; König, M.; Braunstein, B.; Goldmann, J.P.; Brüggemann, G.P. The gearing function of running shoe longitudinal bending stiffness. Gait Posture 2014, 40, 386–390. [Google Scholar] [CrossRef] [PubMed]
- Toon, D. Design and Analysis of Sprint Footwear to Investigate the Effects of Longitudinal Bending Stiffness on Sprinting Performance. Ph.D. Thesis, Loughborough University, Loughborough, UK, 2008. [Google Scholar]
- Kersting, U.; Brüggemann, G.-P. Midsole material-related force control during heel-toe running. Res. Sports Med. 2006, 14, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Hébert-Losier, K.; Finlayson, S.J.; Driller, M.W.; Dubois, B.; Beaven, C.M. Metabolic and performance responses of male runners wearing 3 types of footwear: Nike vaporfly 4%, saucony endorphin racing flats, and their own shoes. J. Sport Health Sci. 2020, in press. [Google Scholar] [CrossRef] [PubMed]
- Burns, G.T.; Tam, N. Is it the shoes? A simple proposal for regulating footwear in road running. Br. J. Sports Med. 2020, 54, 439–440. [Google Scholar] [CrossRef]
- Heidenfelder, J.; Odenwald, S.; Milani, T. Mechanical properties of different midsole materials in running shoes. J. Biomech. 2006, 39, S550. [Google Scholar] [CrossRef]
- Nigg, B.M.; Cigoja, S.; Nigg, S.R. Effects of running shoe construction on performance in long-distance running. Footwear Sci. 2020, 12, 133–138. [Google Scholar] [CrossRef]
- Nigg, B.M.; Cigoja, S.; Nigg, S.R. Teeter-totter effect: A new mechanism to understand shoe-related improvements in long-distance running. Br. J. Sports Med. 2021, 55, 462–463. [Google Scholar] [CrossRef] [PubMed]
- Gregory, R.W.; Axtell, R.S.; Robertson, M.I.; Lunn, W.R. The Effects of a Carbon Fiber Shoe Insole on Athletic Performance in Collegiate Athletes. J. Sports Sci. 2018, 6, 219–230. [Google Scholar]
- Hoogkamer, W.; Kipp, S.; Frank, J.H.; Farina, E.M.; Luo, G.; Kram, R. A comparison of the energetic cost of running in marathon racing shoes. Sports Med. 2018, 48, 1009–1019. [Google Scholar] [CrossRef] [Green Version]
- Smith, G.E.; Lake, M.L.; Lees, A. Metatarsophalangeal joint function during sprinting: A comparison of barefoot and sprint spike shod foot conditions. J. Appl. Biomech. 2014, 30, 206–212. [Google Scholar] [CrossRef] [Green Version]
- Smith, G.; Lake, M.; Sterzing, T.; Milani, T. The influence of sprint spike bending stiffness on sprinting performance and metatarsophalangeal joint function. Footwear Sci. 2016, 8, 109–118. [Google Scholar] [CrossRef] [Green Version]
- Roy, J.P.; Stefanyshyn, D.J. Shoe midsole longitudinal bending stiffness and running economy, joint energy, and EMG. Med. Sci. Sports Exerc. 2006, 38, 562–569. [Google Scholar] [CrossRef] [Green Version]
- Hunter, I.; McLeod, A.; Valentine, D.; Low, T.; Ward, J.; Hager, R. Running economy, mechanics, and marathon racing shoes. J. Sports Sci. 2019, 37, 2367–2373. [Google Scholar] [CrossRef]
- Oh, K.; Park, S. The bending stiffness of shoes is beneficial to running energetics if it does not disturb the natural MTP joint flexion. J. Biomech. 2017, 53, 127–135. [Google Scholar] [CrossRef]
- Barnes, K.R.; Kilding, A.E. A Randomized Crossover Study Investigating the Running Economy of Highly-Trained Male and Female Distance Runners in Marathon Racing Shoes versus Track Spikes. Sports Med. 2019, 49, 331–342. [Google Scholar] [CrossRef]
- Willwacher, S.; König, M.; Potthast, W.; Brüggemann, G.-P. Does Specific Footwear Facilitate Energy Storage and return at the metatarsophalangeal joint in running. J. Appl. Biomech. 2013, 29, 583–592. [Google Scholar] [CrossRef] [Green Version]
- Healey, L.; Hoogkamer, W. Longitudinal bending stiffness does not affect running economy in Nike Vaporfly shoes. SportRxiv 2021. [Google Scholar] [CrossRef]
- Hoogkamer, W.; Kipp, S.; Kram, R.J.S.M. The Biomechanics of Competitive Male Runners in Three Marathon Racing Shoes: A Randomized Crossover Study. Sports Med. 2018, 49, 133–143. [Google Scholar] [CrossRef]
- Allen, D.G.; Kurihara, S. The effects of muscle length on intracellular calcium transients in mammalian cardiac muscle. J. Physiol. 1982, 327, 79–94. [Google Scholar] [CrossRef]
- Pontzer, H. Effective limb length and the scaling of locomotor cost in terrestrial animals. J. Exp. Biol. 2007, 210, 1752–1761. [Google Scholar] [CrossRef] [Green Version]
- Hoogkamer, W.; Kipp, S.; Frank, J.H.; Farina, E.M.; Luo, G.; Kram, R. Correction to A Comparison of the Energetic Cost of Running in Marathon Racing Shoes. Sports Med. 2017, 48, 1521–1522. [Google Scholar] [CrossRef] [Green Version]
- Tung, K.D.; Franz, J.R.; Kram, R. A test of the metabolic cost of cushioning hypothesis during unshod and shod running. Sci. Sports Exerc. 2014, 46, 324–329. [Google Scholar] [CrossRef]
- Farina, E.M.; Haight, D.; Luo, G. Creating footwear for performance running. Footwear Sci. 2019, 11 (Suppl. 1), S134–S135. [Google Scholar] [CrossRef]
- Hasegawa, H.; Yamauchi, T.; Kraemer, W.J. Foot strike patterns of runners at the 15-km point during an elite-level half marathon. J. Strength Cond. Res. 2007, 21, 888–893. [Google Scholar] [PubMed]
- Larson, P.; Higgins, E.; Kaminski, J.; Decker, T.; Preble, J.; Lyons, D.; McIntyre, K.; Normile, A. Foot strike patterns of recreational and sub-elite runners in a long-distance road race. J. Sports 2011, 29, 1665–1673. [Google Scholar] [CrossRef] [PubMed]
- Kasmer, M.E.; Liu, X.C.; Roberts, K.G.; Valadao, J.M. Foot-strike pattern and performance in a marathon. Int. J. Sports Physiol. Perform. 2013, 8, 286–292. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Erdemir, A.; Saucerman, J.; Lemmon, D.; Loppnow, B.; Turso, B.; Ulbrecht, J.S.; Cavanagh, P.R. Local plantar pressure relief in therapeutic footwear: Design guidelines from finite element models. J. Biomech. 2005, 38, 1798–1806. [Google Scholar] [CrossRef] [PubMed]
- Arum, T. Finite element modeling of the human foot and footwear. In Proceedings of the ABAQUS Users’ Conference, Boston, MA, USA, 23–25 May 2006. [Google Scholar]
- Fekete, G.; Biro, I.; Csizmadia, B. Mechanical model for estimating wear in tibiofemoral connection in total knee replacements. Biomech. Hung. 2017, 10, 55–63. [Google Scholar] [CrossRef]
- Bíró, I.; Csizmadia, B.M.; Fekete, G. Numerical sensitivity analysis on anatomical landmarks with regard to the human knee joint. Acta Polytech. Hung. 2016, 13, 7–26. [Google Scholar]
- Standard Test Method for Flexibility of Running Shoes (Withdrawn 2002). ASTM F911-85. 1994.
- Cappozzo, A.; Catani, F.; Della Croce, U.; Leardini, A. Position and orientation in space of bones during movement: Anatomical frame definition and determination. Clin. Biomech. 1995, 10, 171–178. [Google Scholar] [CrossRef]
- Manal, K.; McClay, I.; Stanhope, S.; Richards, J.; Galinat, B. Comparison of surface mounted markers and attachment methods in estimating tibial rotations during walking: An in vivo study. Gait Posture 2000, 11, 38–45. [Google Scholar] [CrossRef]
- Heiderscheit, B.C.; Hamill, J.; van Emmerik, R.E.A. Variability of Stride characteristics and joint coordination among individuals with unilateral patellofemoral pain. J. Appl. Biomech. 2002, 18, 110–121. [Google Scholar] [CrossRef]
- Isherwood, J.; Rimmer, E.; Fu, F.; Xie, Z.; Sterzing, T. Biomechanical and perceptual cushioning sensitivity based on mechanical running shoe properties. Footwear Sci. 2021, 13, 221–231. [Google Scholar] [CrossRef]
- Isherwood, J.; Hughes, L.; Qian, J.-Y.; Sterzing, T. Article, Biomechanical effects of the continuous loop running in comparison to discontinuous runway running on locomotion and running shoe characterization. Footwear Sci. 2020, 12, 39–54. [Google Scholar] [CrossRef]
- Hennig, E.M.; Milani, T.L.; Lafortune, M.A. Use of ground reaction force parameters in predicting peak tibial accelerations in running. J. Appl. Biomech. 1993, 9, 306–314. [Google Scholar] [CrossRef] [Green Version]
- Pataky, T.C.; Vanrenterghem, J.; Robinson, M.A. Zero- vs. one-dimensional, parametric vs. non-parametric, and confidence interval vs. hypothesis testing procedures in one-dimensional biomechanical trajectory analysis. J. Biomech. 2015, 48, 1277–1285. [Google Scholar] [CrossRef] [Green Version]
- Besson, T.; Morio, C.; Millet, G.Y.; Rossi, J. Influence of shoe drop on running kinematics and kinetics in female runners. Eur. J Sports Sci. 2019, 19, 1320–1327. [Google Scholar] [CrossRef] [PubMed]
- Stefanyshyn, D.J.; Nigg, B.M. Mechanical energy contribution of the metatarsophalangeal joint to running and sprinting. J. Biomech. 1997, 30, 11–12. [Google Scholar] [CrossRef]
- Belli, K. Moment and Power of Lower Limb Joints in Running. Int. J. Sports Med. 2002, 23, 136–141. [Google Scholar] [CrossRef] [PubMed]
- Raichlen, D.A.; Armstrong, H.; Lieberman, D.E. Calcaneus length determines running economy: Implications for endurance running performance in modern humans and Neandertals. J. Hum. Evol. 2011, 60, 299–308. [Google Scholar] [CrossRef]
- Cigoja, S.; Firminger, C.R.; Asmussen, M.J.; Fletcher, J.R.; Edwards, W.B.; Nigg, B.M. Does increased midsole bending stiffness of sport shoes redistribute lower limb joint work during running? J. Sci. Med. Sport 2019, 22, 1272–1277. [Google Scholar] [CrossRef]
- Fletcher, J.R.; MacIntosh, B.R. Running economy from a muscle energetics Perspective. Front. Physiol. 2017, 8, 433. [Google Scholar] [CrossRef] [PubMed]
- Manuela, B.; Jaime, L.; Di, S.; Jenny, S.; Yih-Kuen, J. Serunstudy: Development of running profiles using a mixed methods analysis. PLoS ONE 2018, 13, e0200389. [Google Scholar]
- Videbæk, S.; Bueno, A.M.; Nielsen, R.O.; Rasmussen, S. Incidence of running-related injuries per 1000h of running in different types of runners: A systematic review and meta-analysis. Sports Med. 2015, 45, 1017–1026. [Google Scholar] [CrossRef] [Green Version]
- Gu, Y.D.; Li, J.S.; Lake, M.J.; Zeng, Y.J.; Ren, X.J.; Li, Z.Y. Image-based midsole insert design and the material effects on heel plantar pressure distribution during simulated walking loads. Comput. Methods Biomech. Biomed. Engin. 2011, 14, 747–753. [Google Scholar] [CrossRef] [PubMed]
- Dempster, J.; Dutheil, F.; Ugbolue, U.C. The Prevalence of Lower Extremity Injuries in Running and Associated Risk Factors: A Systematic Review. Phys. Act. Health 2021, 5, 133–145. [Google Scholar] [CrossRef]
- Zhou, H.; Chen, C.; Xu, D.; Ugbolue, U.C.; Baker, J.S.; Gu, Y. Biomechanical Characteristics between Bionic Shoes and Normal Shoes during the Drop-Landing Phase: A Pilot Study. Int. J. Environ. Res. Public Health. 2021, 18, 3223. [Google Scholar] [CrossRef]

| Measurement Method | Variable | Experimental Shoe Condition | |
|---|---|---|---|
| SFC | FFC | ||
| Weight(g) | 184.17 | 187.92 | |
| Forefoot flexion | Peak torque (Nm) | 16.50 | 15.44 |
| Stiffness (Nm/deg) | 0.370 | 0.369 | |
| Energy return (%) | 33.97 | 34.66 | |
| FE simulation | Peak torque (Nm) | 13.54 | 13.68 |
| Stiffness (Nm/deg) | 0.301 | 0.304 | |
| Energy return (%) | 64.08 | 64.82 | |
| Variables | SFC(F) | SFC(S) | FFC(F) | SFC(S) | Main Effect (Construction) | Main Effect (Speed) | Interaction Effect | Effect Size (ηp2) F | Effect Size (ηp2) s |
|---|---|---|---|---|---|---|---|---|---|
| ground contact time (ms) | 185.13 ± 20.13 | 231.42 ± 11.44 | 184.69 ± 22.80 | 227.63 ± 16.48 | p = 0.636 | p = 0.000 | p = 0.147 | 0.034 | 0.094 |
| breaking phase time (ms) | 92.552 ± 0.01 | 117.88 ± 0.00 | 91.495 ± 0.020 | 113.696 ± 0.006 | p = 0.964 | P = 0.009 | p = 0.557 | 0.234 | 0.121 |
| proplusion phase time(ms) | 92.583 ± 1.547 | 114.532 ± 2.30 | 93.196 ± 2.182 | 115.012 ± 2.304 | p = 0.487 | p = 0.004 | p = 0.219 | 0.052 | 0.059 |
| mpj plantarflexion velocity (sagittal) (°/sec) | 255.33 ± 29.04 | 201.55 ± 32.69 | 212.60 ± 39.14 | 171.64 ± 34.26 | p = 0.015 | p = 0.001 | p = 0.216 | 0.341 | 0.287 |
| MTP neagitve work(J/kg) | 0.052 ± 0.006 | 0.049 ± 0.008 | 0.042 ± 0.007 | 0.040 ± 0.002 | p = 0.123 | p = 0.553 | p = 0.339 | 0.176 | 0.073 |
| MTP dorsiflexion angle at toe-off (°) | 7.29 ± 2.54 | 6.81 ± 2.16 | 5.76 ± 2.14 | 5.35 ± 2.09 | p = 0.478 | p = 0.248 | p = 0.363 | 0.173 | 0.131 |
| MTP range of motion(sagittal) (°) | 13.46 ± 1.50 | 12.82 ± 2.04 | 12.09 ± 1.84 | 11.24 ± 2.27 | p = 0.135 | p = 0.092 | p = 0.107 | 0.254 | 0.191 |
| mpj dorsiflexion angle (sagittal) at pp (°) | 7.63 ± 3.03 | 4.61 ± 2.69 | 6.81 ± 2.80 | 3.88 ± 2.33 | p = 0.453 | p = 0.002 | p = 0.410 | 0.179 | 0.142 |
| mpj dorsiflexion angle (sagittal) maximum (°) | 11.81 ± 3.11 | 10.92 ± 2.89 | 10.85 ± 2.70 | 9.59 ± 2.13 | p = 0.297 | p = 0.296 | p = 0.123 | 0.116 | 0.114 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, F.; Levadnyi, I.; Wang, J.; Xie, Z.; Fekete, G.; Cai, Y.; Gu, Y. Effect of the Construction of Carbon Fiber Plate Insert to Midsole on Running Performance. Materials 2021, 14, 5156. https://doi.org/10.3390/ma14185156
Fu F, Levadnyi I, Wang J, Xie Z, Fekete G, Cai Y, Gu Y. Effect of the Construction of Carbon Fiber Plate Insert to Midsole on Running Performance. Materials. 2021; 14(18):5156. https://doi.org/10.3390/ma14185156
Chicago/Turabian StyleFu, Fengqin, Ievgen Levadnyi, Jiayu Wang, Zhihao Xie, Gusztáv Fekete, Yuhui Cai, and Yaodong Gu. 2021. "Effect of the Construction of Carbon Fiber Plate Insert to Midsole on Running Performance" Materials 14, no. 18: 5156. https://doi.org/10.3390/ma14185156
APA StyleFu, F., Levadnyi, I., Wang, J., Xie, Z., Fekete, G., Cai, Y., & Gu, Y. (2021). Effect of the Construction of Carbon Fiber Plate Insert to Midsole on Running Performance. Materials, 14(18), 5156. https://doi.org/10.3390/ma14185156







