A Study to Derive Equivalent Mechanical Properties of Porous Materials with Orthotropic Elasticity
Abstract
:1. Introduction
2. Prior Research and Background Theory
2.1. Study on Equivalent Properties Derivation
2.2. Orthotropic Elasticity
3. Deriving Equivalent Properties Using Simulation
3.1. Computer Software
3.2. Equivalence Derivation Process
3.3. Determination of Unit Cell Model and Its Shape
3.4. Simulation Procedure
3.5. Simulation Results
4. Verification and Results through Experiments
4.1. Experimental Equipment and Methods
4.2. Shape of Test Specimen
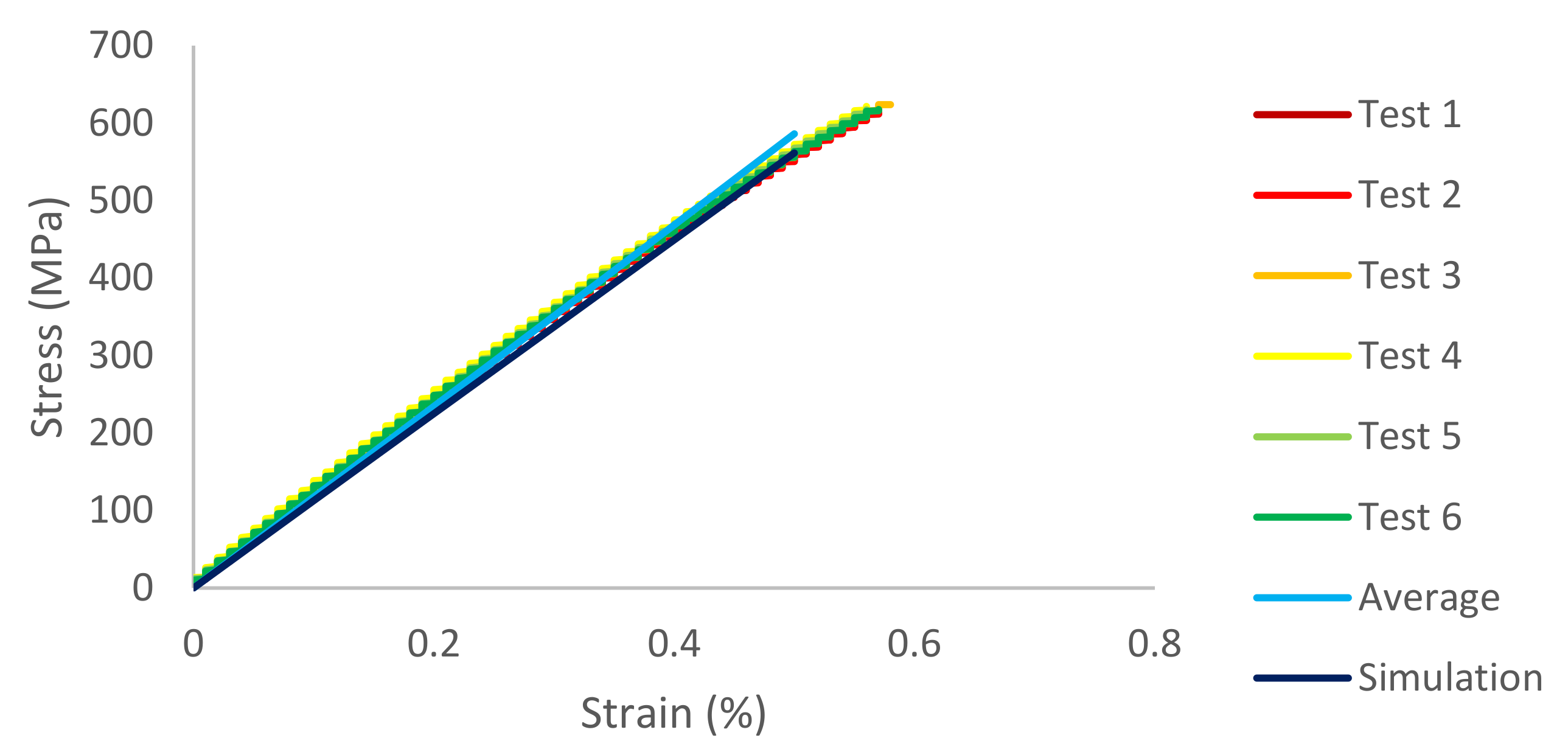
4.3. Measurement Results
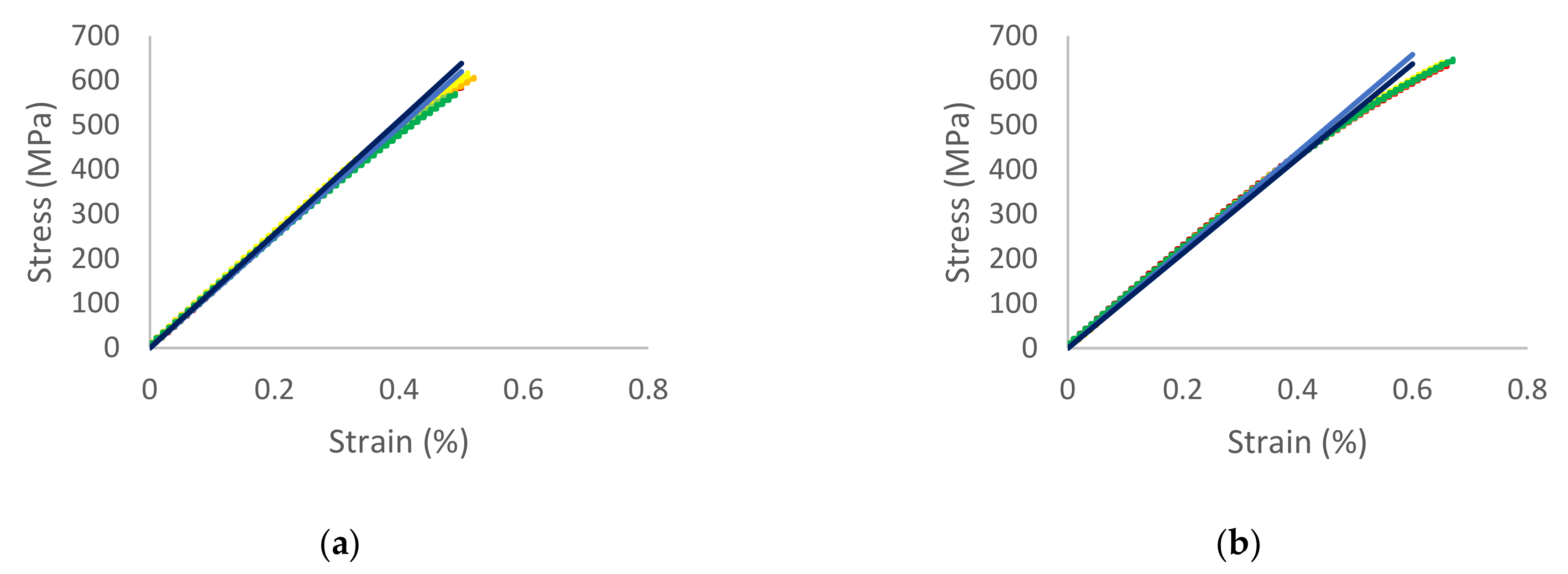
4.4. Comparison and Verification
5. Discussion
6. Conclusions
- In the case of a finite element method using porous or composite material, it is inefficient to perform the analysis using material modeling. The equivalent properties of a material were estimated by applying the representative volume element method.
- Working from the assumption that the pores are horizontally/vertically asymmetrical, an elastic modulus matrix of an orthogonal anisotropic material was constructed. The equivalent elastic modulus and equivalent Poisson’s ratio of a representative volumetric element were calculated using the equivalent strain and equivalent stress.
- Based on the element volume and element stress values derived from the finite element method program, the representative stress value and elastic modulus matrix were calculated using Python. In addition, the equivalent material properties were derived using the calculated elastic modulus matrix.
- A thin-plate specimen made of STS304 was etched in a specific pattern to simulate pores. The elastic modulus and Poisson’s ratio were measured using UTM and verified through comparison with simulation results.
- This research can be applied to many industries such as medicine and dentistry, which treat porous materials such as bacterial biofilm, bones, teeth, and porous tantalum. As porosity of certain materials can influence the retention and formation of bacterial biofilm, this research is very powerful for analysis for materials with porosity.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Katsoulidis, A.P.; Antypov, D.; Whitehead, G.F.S.; Carrington, E.J.; Adams, D.J.; Berry, N.G.; Darling, G.R.; Dyer, M.S.; Rosseinsky, M.J. Chemical control of structure and guest uptake by a conformationally mobile porous material. Nature 2019, 565, 213–217. [Google Scholar] [CrossRef] [PubMed]
- Slater, A.G.; Cooper, A.I. Porous materials function-led design of new porous materials. Science 2015, 348, 8075. [Google Scholar] [CrossRef] [PubMed]
- Nomura, T.; Okinaka, N.; Akiyama, T. Impregnation of porous material with phase change material for thermal energy storage. Mater. Chem. Phys. 2009, 115, 846–850. [Google Scholar] [CrossRef]
- Trunh, L.; Lee, D. Welding of Thin Tab and Battery Case for Lithium-ion Battery Cylindrical Cell Using Nanosecond Pulsed Fiber Laser. J. Weld. Jt. 2020, 28, 389–394. [Google Scholar] [CrossRef]
- Mour, M.; Das, D.; Winkler, T.; Hoenig, E.; Mielke, G.; Morlock, M.M.; Schilling, A.F. Advances in Porous Biomaterials for Dental and Orthopaedic Applications. Materials 2010, 3, 2947–2974. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Bao, C.; Wismeijer, D.; Wu, G. The physicochemical/biological properties of porous tantalum and the potential surface modification techniques to improve its clinical application in dental implantology. Mater. Sci. Eng. C 2015, 49, 323–329. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Chang, K.; Muzaffer, S. Fatigue Analysis of the Effects of Incomplete Penetration Defects on Fatigue Crack Initiation Points in Butt-Welded Members. J. Weld. Jt. 2020, 38, 543–550. [Google Scholar]
- Wu, C.; Kim, J. Review on Mitigation of Welding-Induced Distortion Based on FEM Analysis. J. Weld. Jt. 2020, 38, 56–66. [Google Scholar] [CrossRef] [Green Version]
- Babu, K.P.; Mohite, P.M.; Upadhyah, C.S. Development of an RVE and its stiffness predictions based on mathematical homogenization theory for short fibre composites. Int. J. Solids Struct. 2018, 130–131, 80–114. [Google Scholar] [CrossRef]
- Breuer, K.; Stommel, M. RVE modelling of short fiber reinforced thermoplastics with discrete fiber orientation and fiber length distribution. SN Appl. Sci. 2020, 2, 91. [Google Scholar] [CrossRef] [Green Version]
- Bargmann, S.; Klusemann, B.; Markmann, J.; Schnabel, J.E.; Schneider, K.; Soyarslan, C.; Wilmers, J. Generation of 3D representative volume elements for heterogeneous materials: A review. Prog. Mater. Sci. 2018, 96, 322–384. [Google Scholar] [CrossRef]
- Pan, Y.; Iorga, L.; Pelegri, A.A. Generation of 3D representative volume elements for heterogeneous materials: A review. Compsites Sci. Technol. 2008, 68, 2792–2798. [Google Scholar] [CrossRef]
- Pyo, C. A Study for Estimation of Equivalent Mechanical Properties of Materials with Porosity Part I. Isotropic Elasticity in Plane Stress. Korean Soc. Mech. Technol. 2021, 23, 347–353. [Google Scholar]
- Pyo, C. A Study for Estimation of Equivalent Mechanical Properties of Materials with Porosity Part II. Orthotropic Elasticity in Plane Stress. Korean Soc. Mech. Technol. 2021, 21, 412–419. [Google Scholar]
- Schmitz, A.; Horst, P. A finite element unit-cell method for homogenized mechanical properties of heterogeneous plates. Compos. Part A Appl. Sci. Manuf. 2014, 61, 23–32. [Google Scholar] [CrossRef]
- Zheng, Q.; Fan, H. Equivalent continuum method of plane-stress dominated plate-lattice materials. Thin-Walled Struct. 2021, 164, 107865. [Google Scholar] [CrossRef]
- Daniel, I.M.; Ishai, O. Engineering Mechanics of Composite Materials; Oxford University Press: New York, NY, USA, 2006; pp. 63–92. [Google Scholar]
- Pyo, C.; Kim, J.; Kim, J. Estimation of Heat Source Model’s Parameters for GMAW with Non-linear Global Optimization—Part I: Application of Multi-island Genetic Algorithm. Metals 2020, 10, 885. [Google Scholar] [CrossRef]
- Deng, D.; Murakawa, H. Numerical simulation of temperature field and residual stress in multi-pass welds in stainless steel pipe and comparison with experimental measurements. Comput. Mater. Sci. 2006, 37, 269–277. [Google Scholar] [CrossRef]
- Sixun, T.; Haipeng, G.; Hao, L.; Lei, Q. The FEM Model Driven Method of the Static Performance Calculation for Gas Joumal Bearing by Python. In Proceedings of the 2018 IEEE International Conference on Mechatronics and Automation, Changchun, China, 5–8 August 2018; pp. 18–22. [Google Scholar]
- Stafslien, S.; Bahr, J.; Feser, J.; Weisz, J.; Chisholm, B.; Ready, T.; Boudjou, P. Combinatorial Materials Research Applied to the Development of New Surface Coatings I: A Multiwell Plate Screening Method for the High-Throughput Assessment of Bacterial Biofilm Retention on Surfaces. J. Comb. Chem. 2006, 8, 156–162. [Google Scholar] [CrossRef] [PubMed]
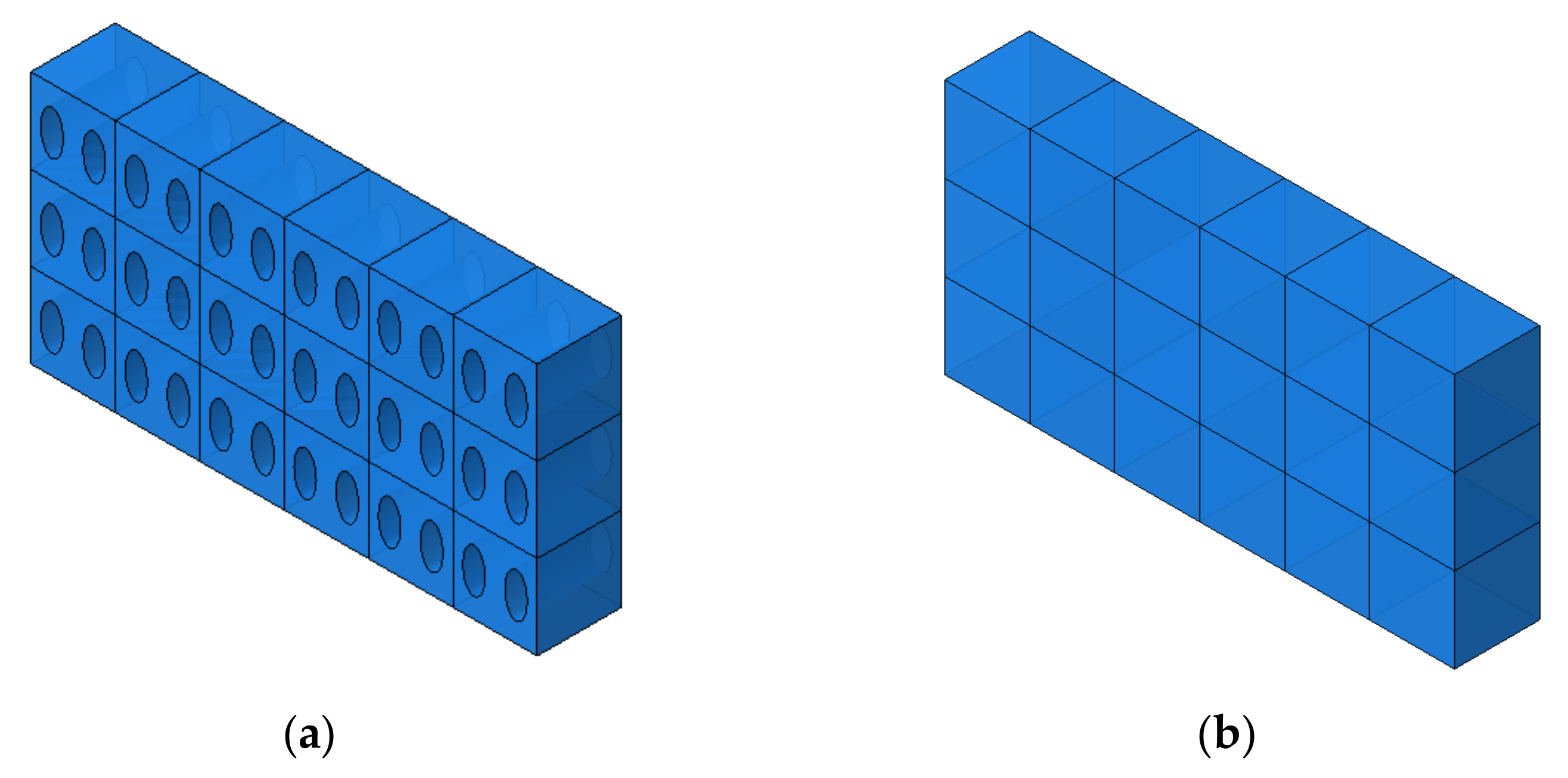

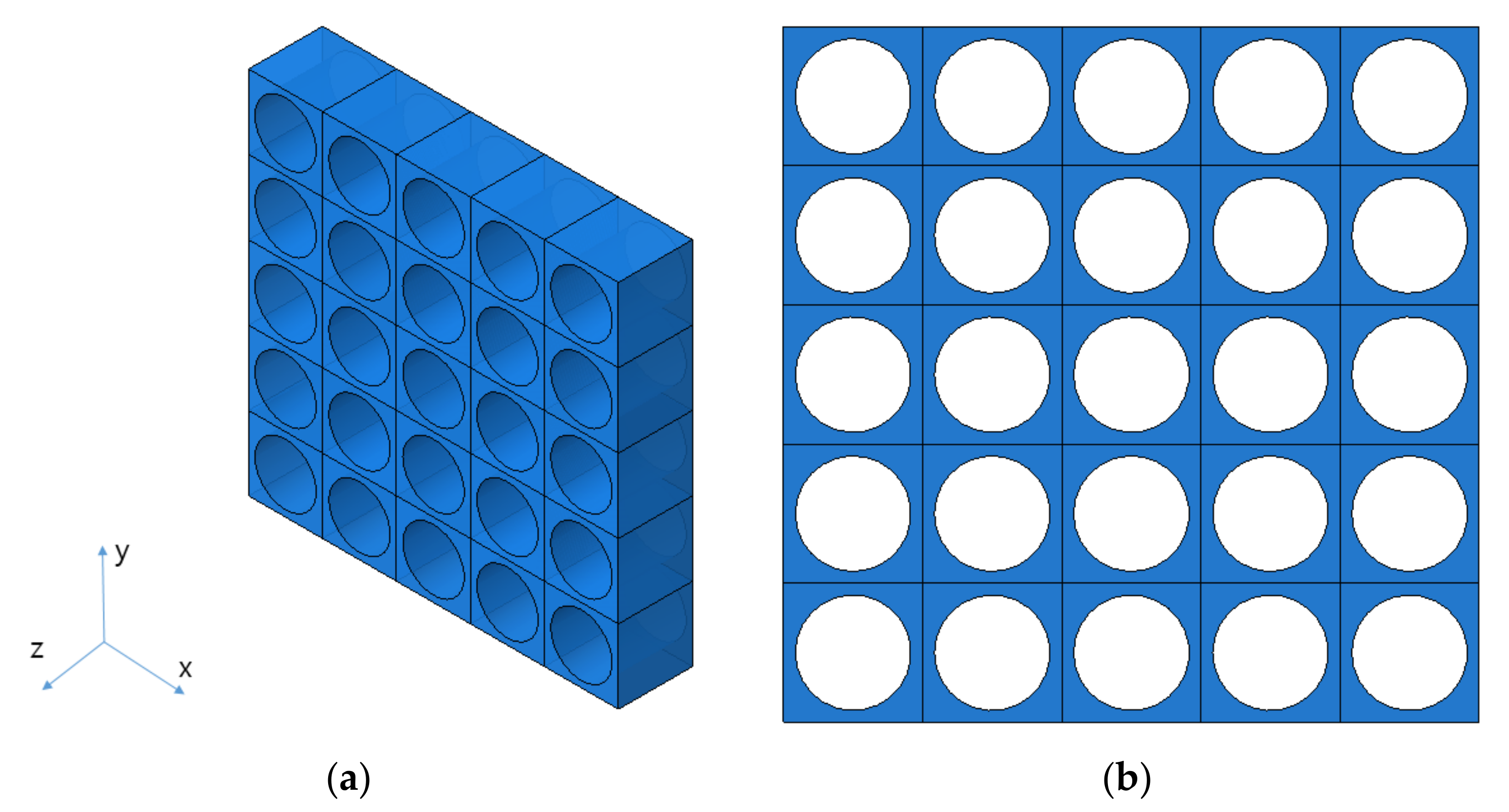
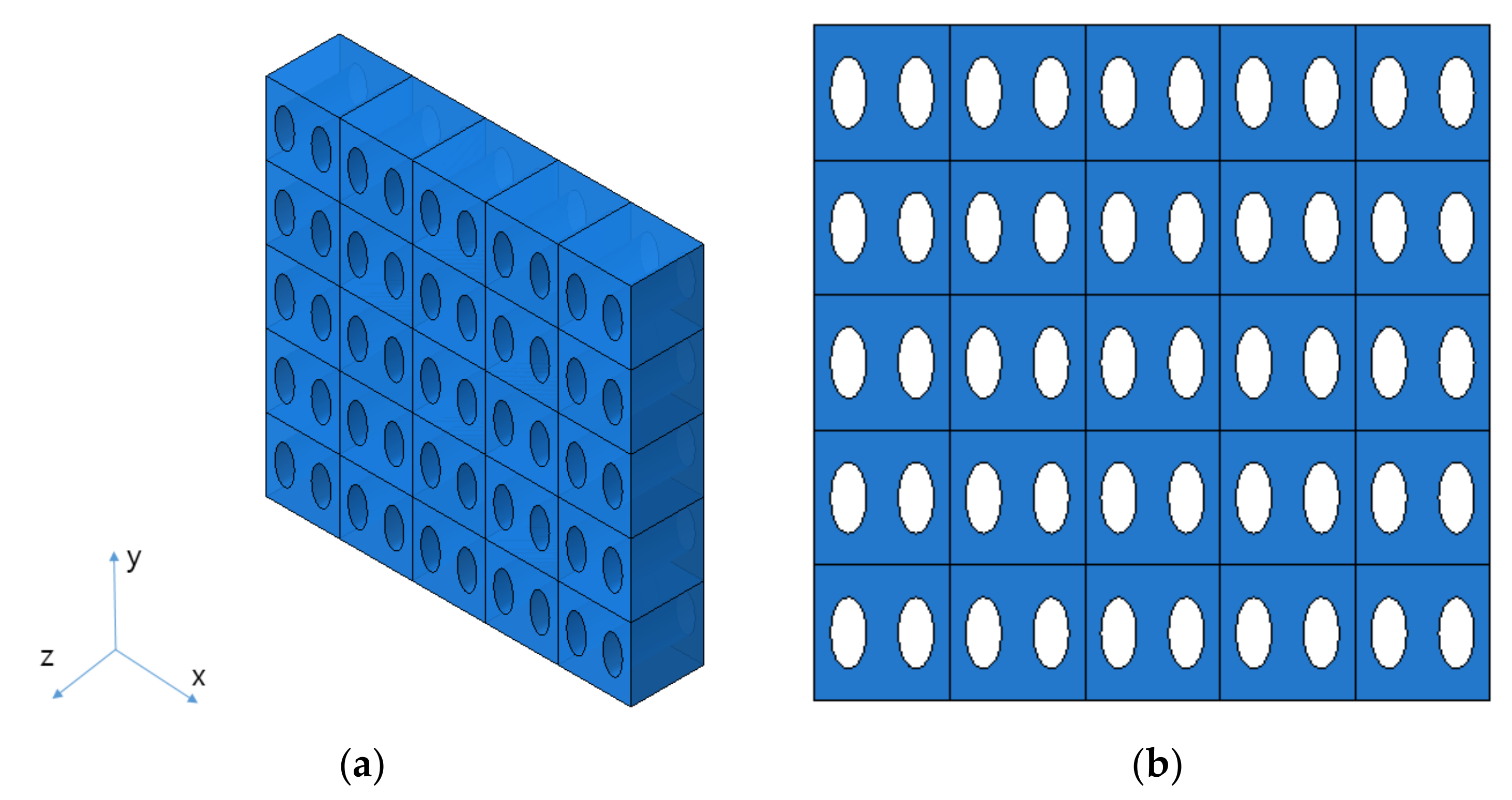
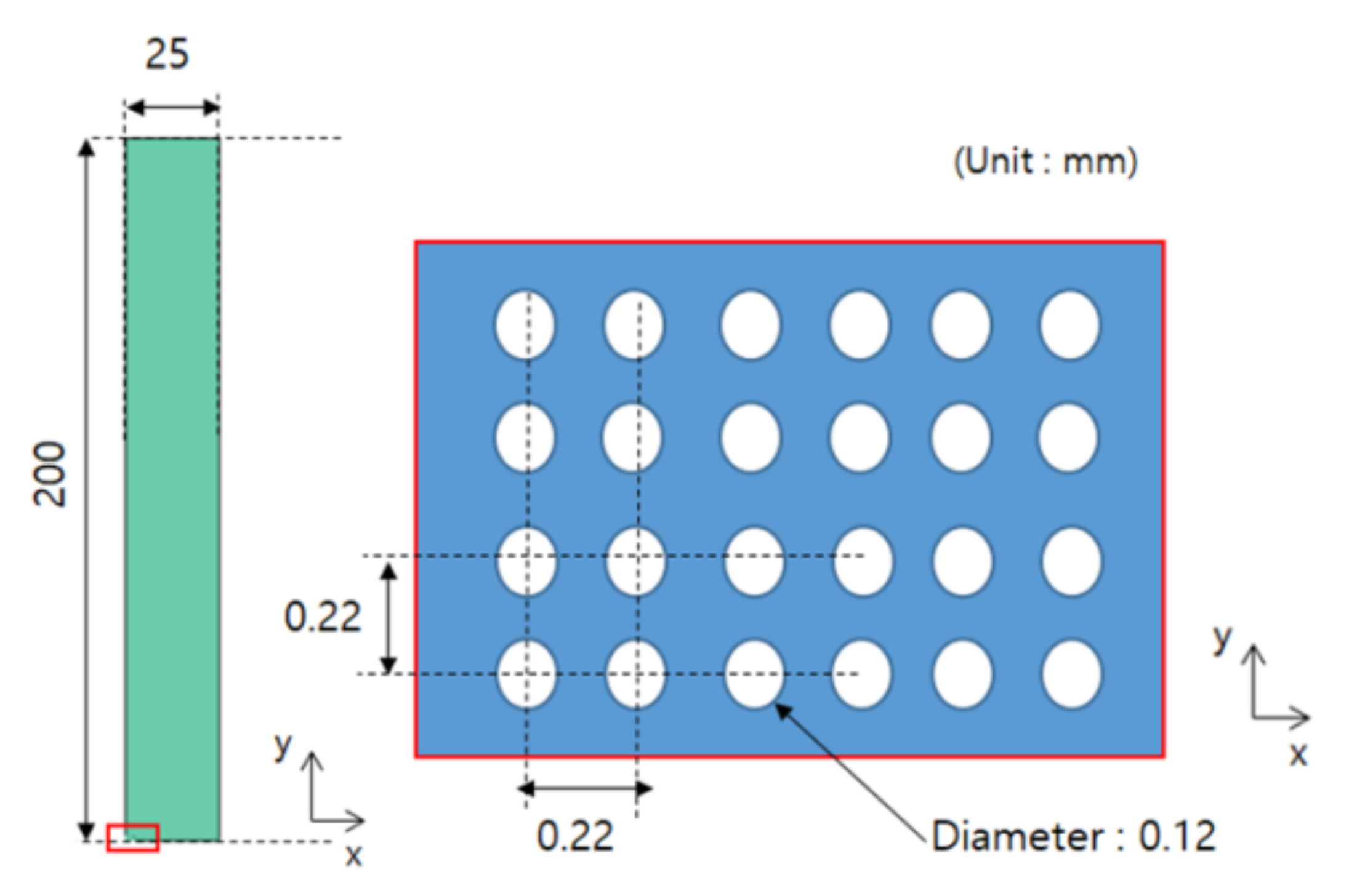
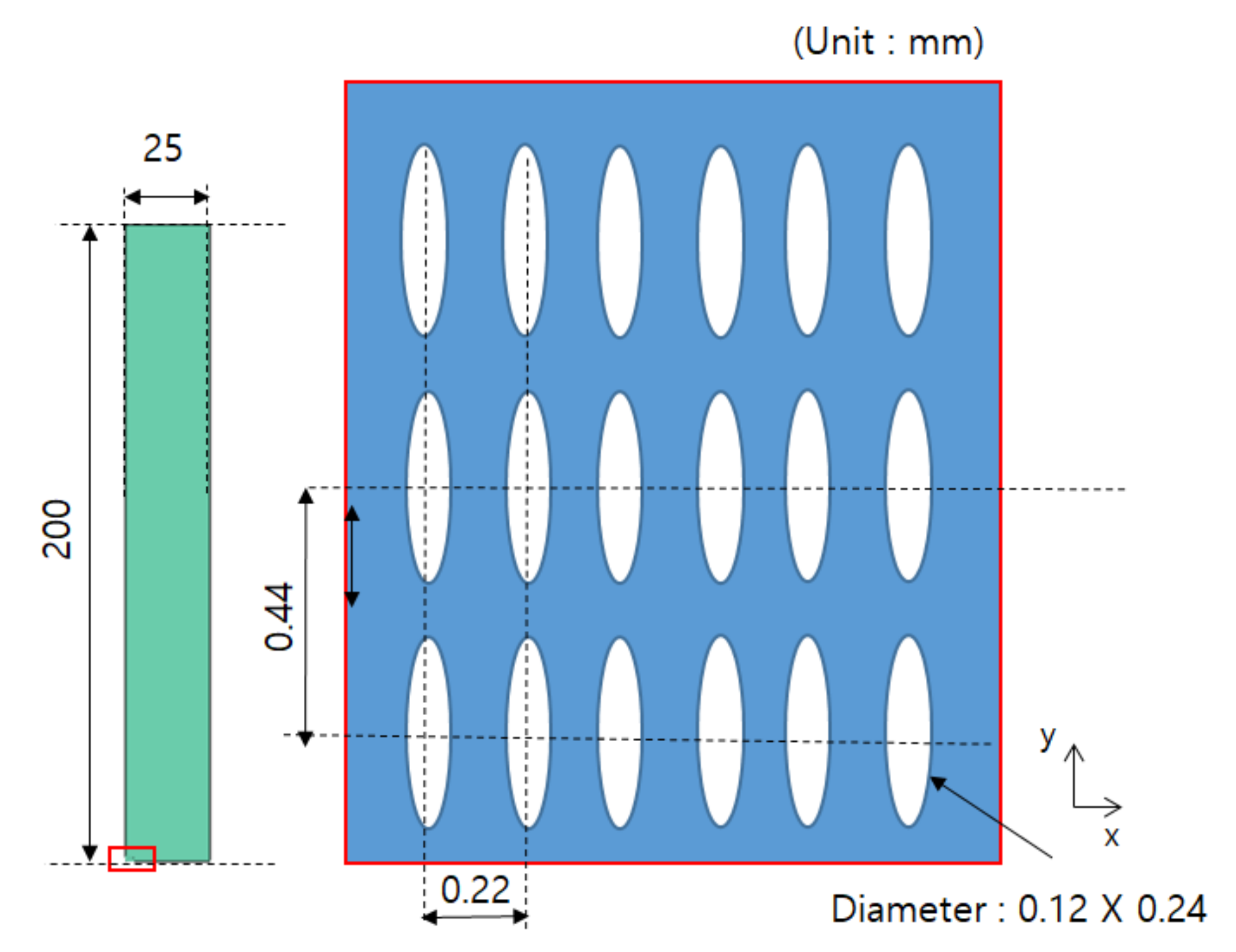



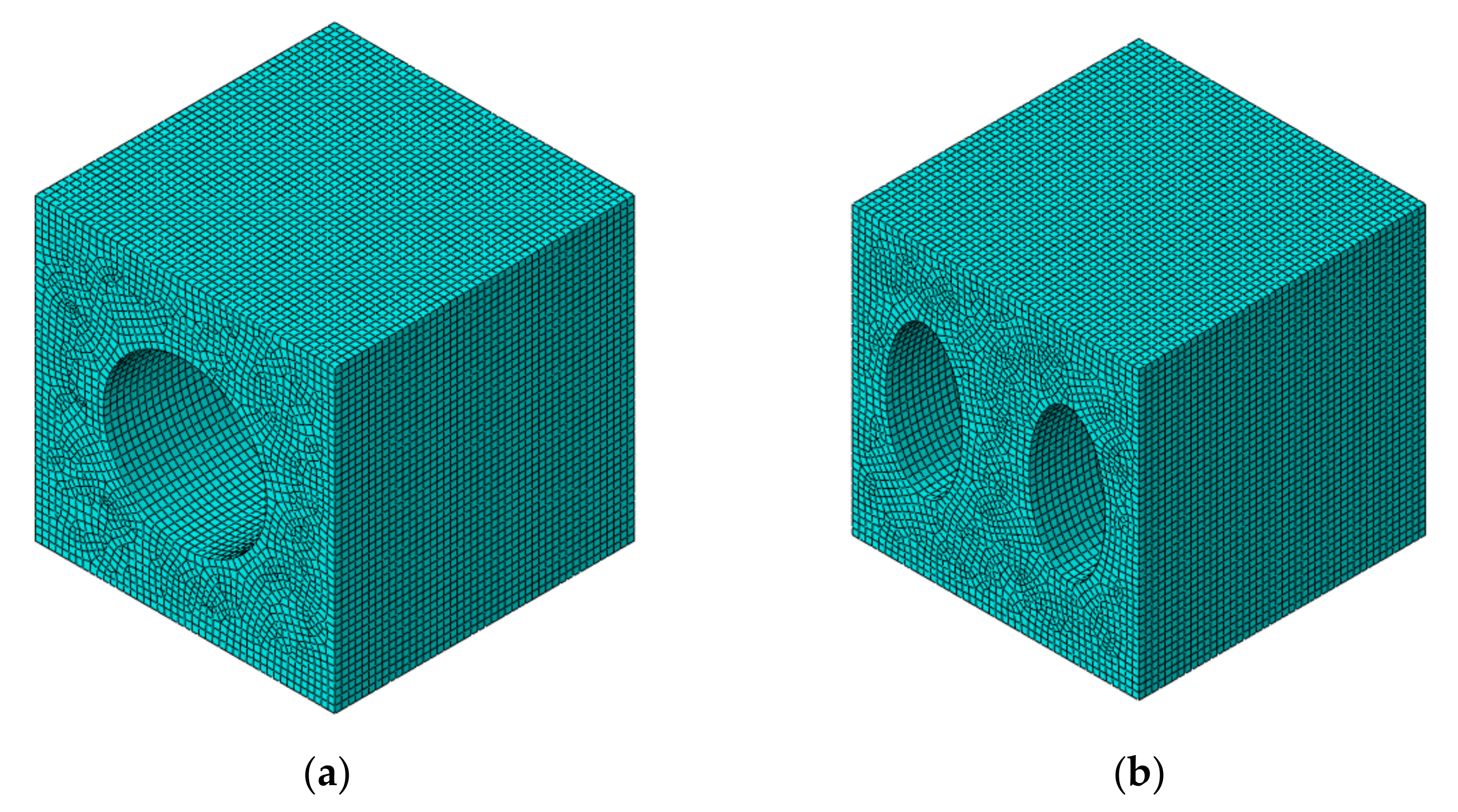
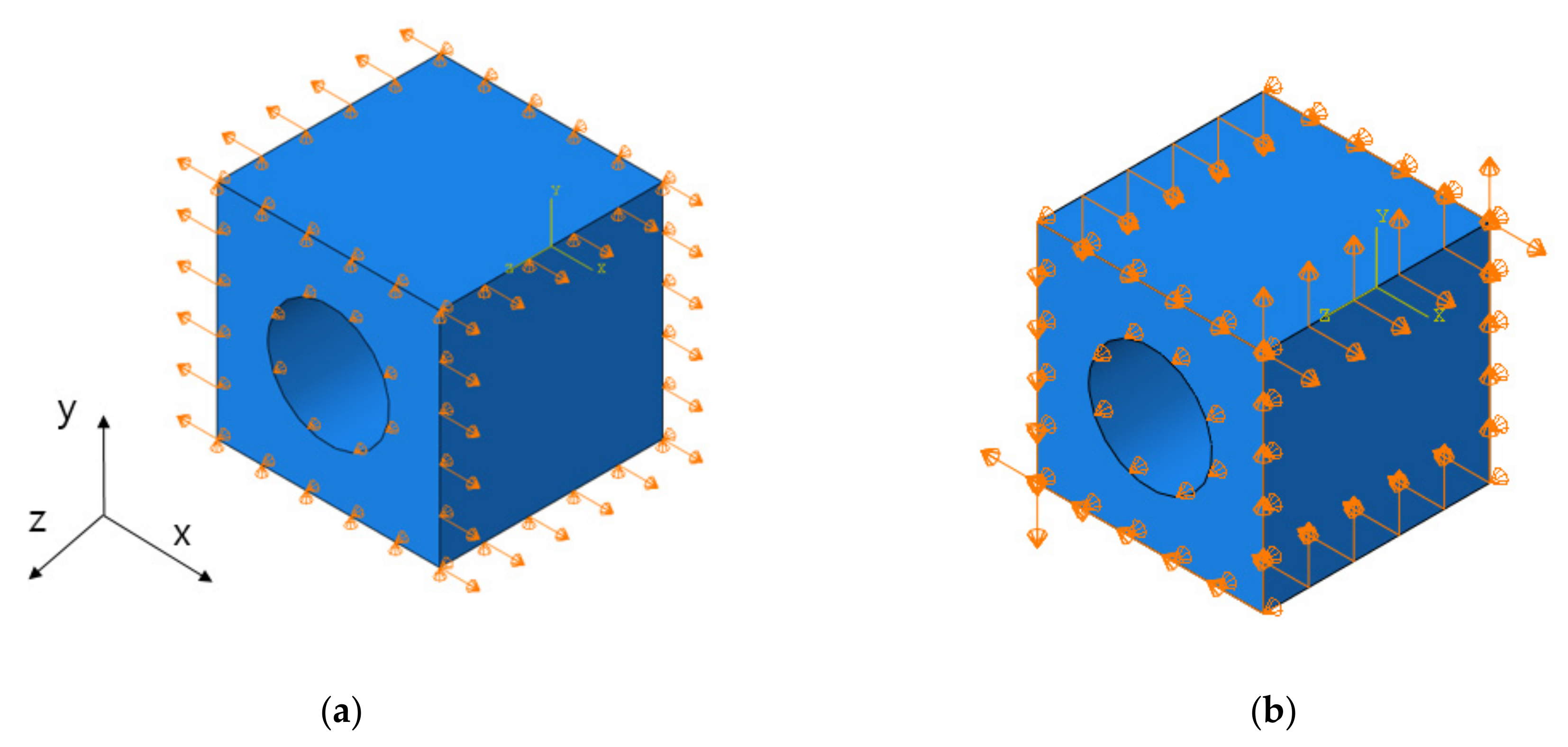
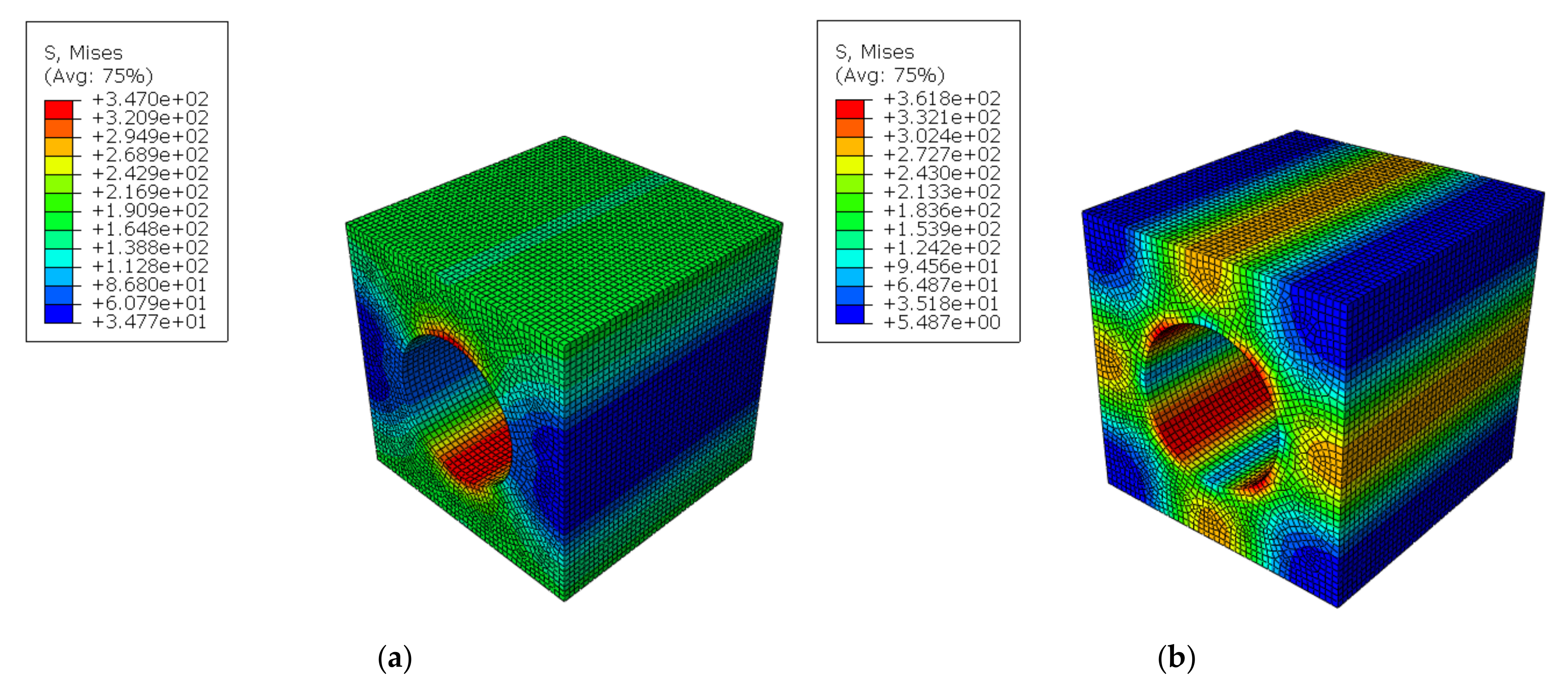

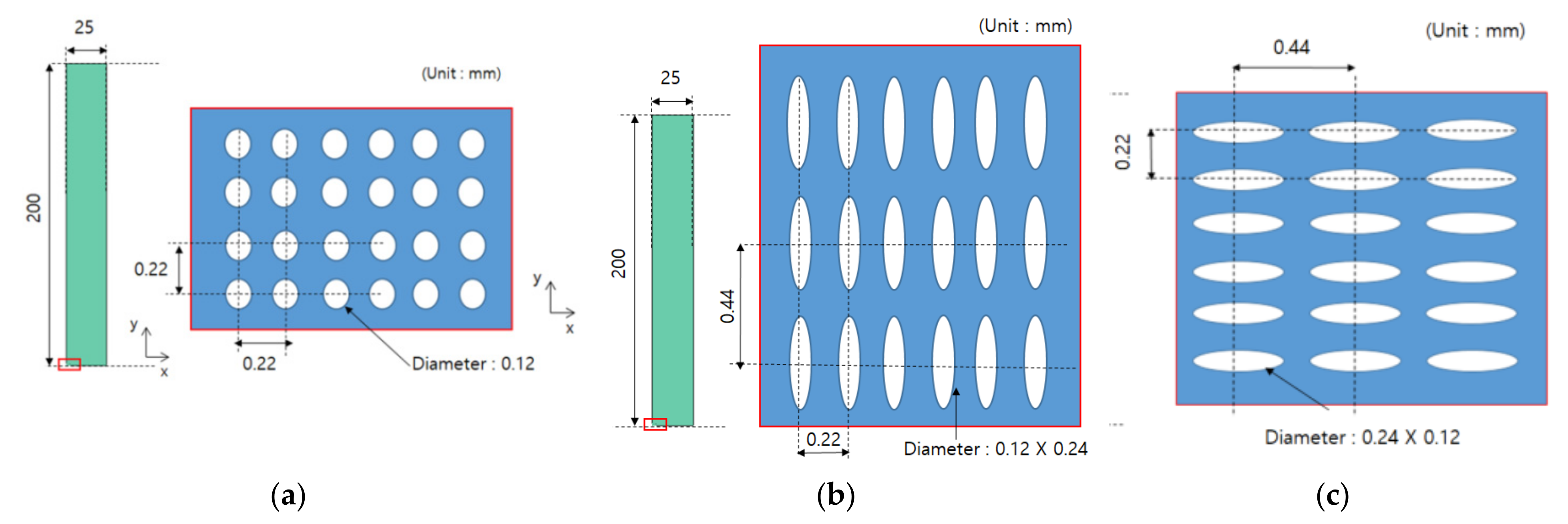

| Design | Real | |||
|---|---|---|---|---|
| Circular pore | Length of unit cell | 220.0 | 221.25 | |
| Hole diameter | 120.0 | 116.25 | ||
| Elliptical pore | Length of unit cell | 440.0 | 433.13 | |
| Hole diameter | Short | 120.0 | 120.00 | |
| Long | 240.0 | 233.13 | ||
| Contents | Value | Unit |
|---|---|---|
| Density | 8000 | kg/m3 |
| Modulus of elasticity | 193.0 | GPa |
| Poisson’s ratio | 0.29 | - |
| Contents | Value | Unit |
|---|---|---|
| Elastic modulus (Ex) | 112.3 | GPa |
| Elastic modulus (Ey) | 112.3 | GPa |
| Elastic modulus (Ez) | 147.9 | GPa |
| Poisson’s ratio (νyx) | 0.230 | m/m |
| Poisson’s ratio (νxy) | 0.230 | m/m |
| Poisson’s ratio (νzx) | 0.290 | m/m |
| Poisson’s ratio (νzy) | 0.290 | m/m |
| Contents | Value | Unit |
|---|---|---|
| Elastic modulus (Ex) | 106.2 | GPa |
| Elastic modulus (Ey) | 127.6 | GPa |
| Elastic modulus (Ez) | 150.5 | GPa |
| Poisson’s ratio (νyx) | 0.235 | m/m |
| Poisson’s ratio (νxy) | 0.196 | m/m |
| Poisson’s ratio (νzx) | 0.290 | m/m |
| Poisson’s ratio (νzy) | 0.290 | m/m |
| Test No. | Modulus of Elasticity (GPa) | Poisson’s Ratio (mm/mm) |
|---|---|---|
| 1 | 116.0 | 0.226 |
| 2 | 117.0 | 0.228 |
| 3 | 117.0 | 0.243 |
| 4 | 118.0 | 0.248 |
| 5 | 118.0 | 0.242 |
| 6 | 117.0 | 0.231 |
| Average | 117.17 | 0.2363 |
| Standard Deviation | 0.687 | 0.0083 |
| Test No. | Modulus of Elasticity (GPa) | Poisson’s Ratio (mm/mm) |
|---|---|---|
| 1 | 124.0 | 0.211 |
| 2 | 124.0 | 0.233 |
| 3 | 124.0 | 0.212 |
| 4 | 127.0 | 0.223 |
| 5 | 123.0 | 0.219 |
| 6 | 122.0 | 0.226 |
| Average | 124.0 | 0.221 |
| Standard Deviation | 1.53 | 0.0077 |
| Test No. | Modulus of Elasticity (GPa) | Poisson’s Ratio (mm/mm) |
|---|---|---|
| 1 | 110.0 | 0.196 |
| 2 | 109.0 | 0.196 |
| 3 | 111.0 | 0.188 |
| 4 | 110.0 | 0.206 |
| 5 | 109.0 | 0.194 |
| 6 | 109.0 | 0.199 |
| Average | 109.7 | 0.197 |
| Standard Deviation | 0.75 | 0.0054 |
| Modulus of Elasticity (GPa) | Poisson’s Ratio (mm/mm) | |
|---|---|---|
| Simulation | 112.3 | 0.232 |
| Measurement | 117.2 | 0.236 |
| Difference (%) | 4.18 (%) | 1.69 (%) |
| Modulus of Elasticity (Ey, GPa) | Poisson’s Ratio (νyx, m/m) | |
|---|---|---|
| Simulation | 127.6 | 0.236 |
| Measurement | 124.0 | 0.221 |
| Difference (%) | 2.82 (%) | 6.36 (%) |
| Modulus of Elasticity (Ex, GPa) | Poisson’s Ratio (νxy, m/m) | |
|---|---|---|
| Simulation | 106.2 | 0.196 |
| Measurement | 109.7 | 0.197 |
| Difference (%) | 3.19 (%) | 0.51 (%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pyo, C.; Kim, Y.; Kim, J.; Kang, S. A Study to Derive Equivalent Mechanical Properties of Porous Materials with Orthotropic Elasticity. Materials 2021, 14, 5132. https://doi.org/10.3390/ma14185132
Pyo C, Kim Y, Kim J, Kang S. A Study to Derive Equivalent Mechanical Properties of Porous Materials with Orthotropic Elasticity. Materials. 2021; 14(18):5132. https://doi.org/10.3390/ma14185132
Chicago/Turabian StylePyo, Changmin, Younghyun Kim, Jaewoong Kim, and Sungwook Kang. 2021. "A Study to Derive Equivalent Mechanical Properties of Porous Materials with Orthotropic Elasticity" Materials 14, no. 18: 5132. https://doi.org/10.3390/ma14185132
APA StylePyo, C., Kim, Y., Kim, J., & Kang, S. (2021). A Study to Derive Equivalent Mechanical Properties of Porous Materials with Orthotropic Elasticity. Materials, 14(18), 5132. https://doi.org/10.3390/ma14185132







