Pseudogap Isotope Effect as a Probe of Bipolaron Mechanism in High Temperature Superconductors
Abstract
1. Introduction
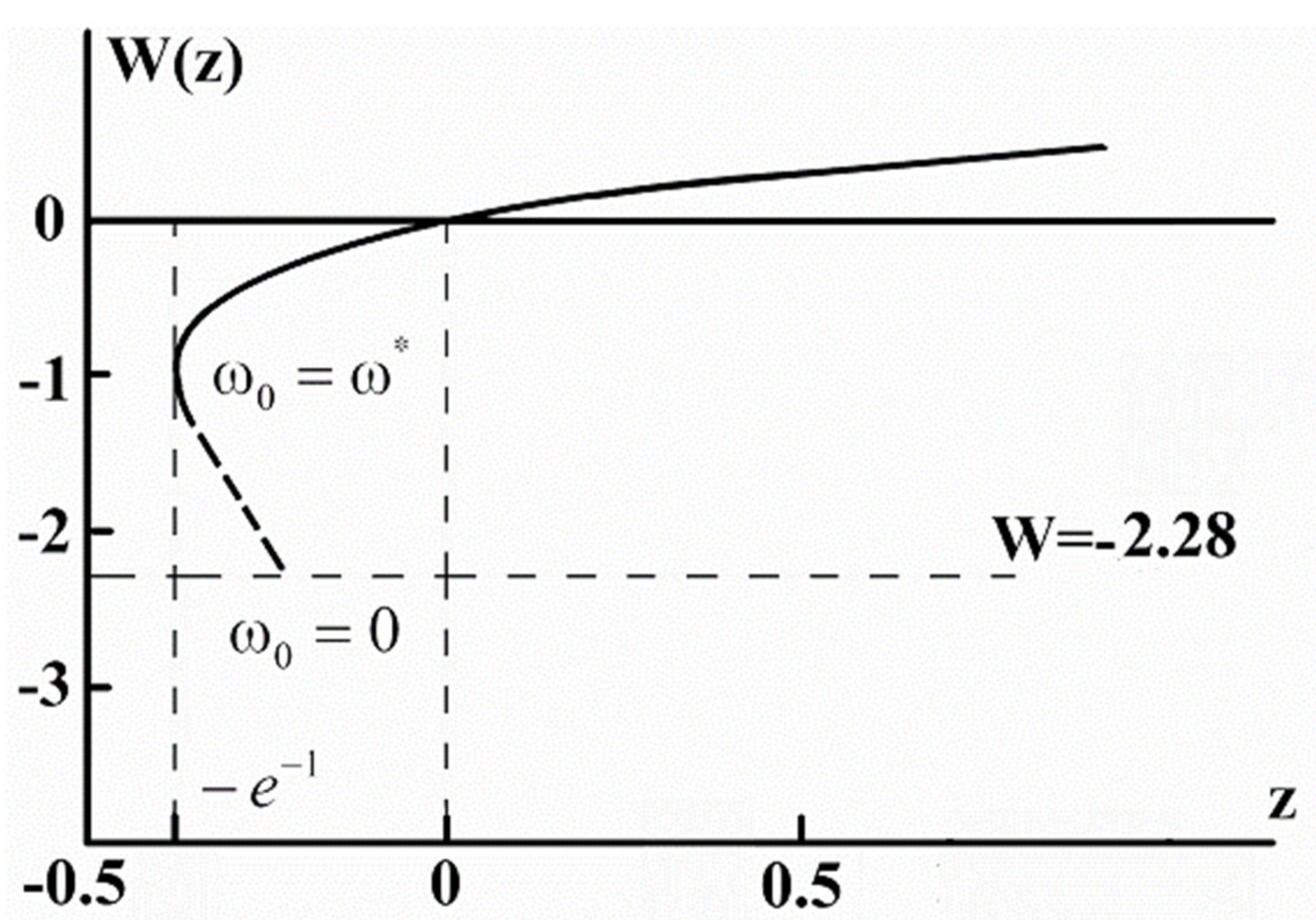
2. The Critical Temperature of a Pseudogap Phase
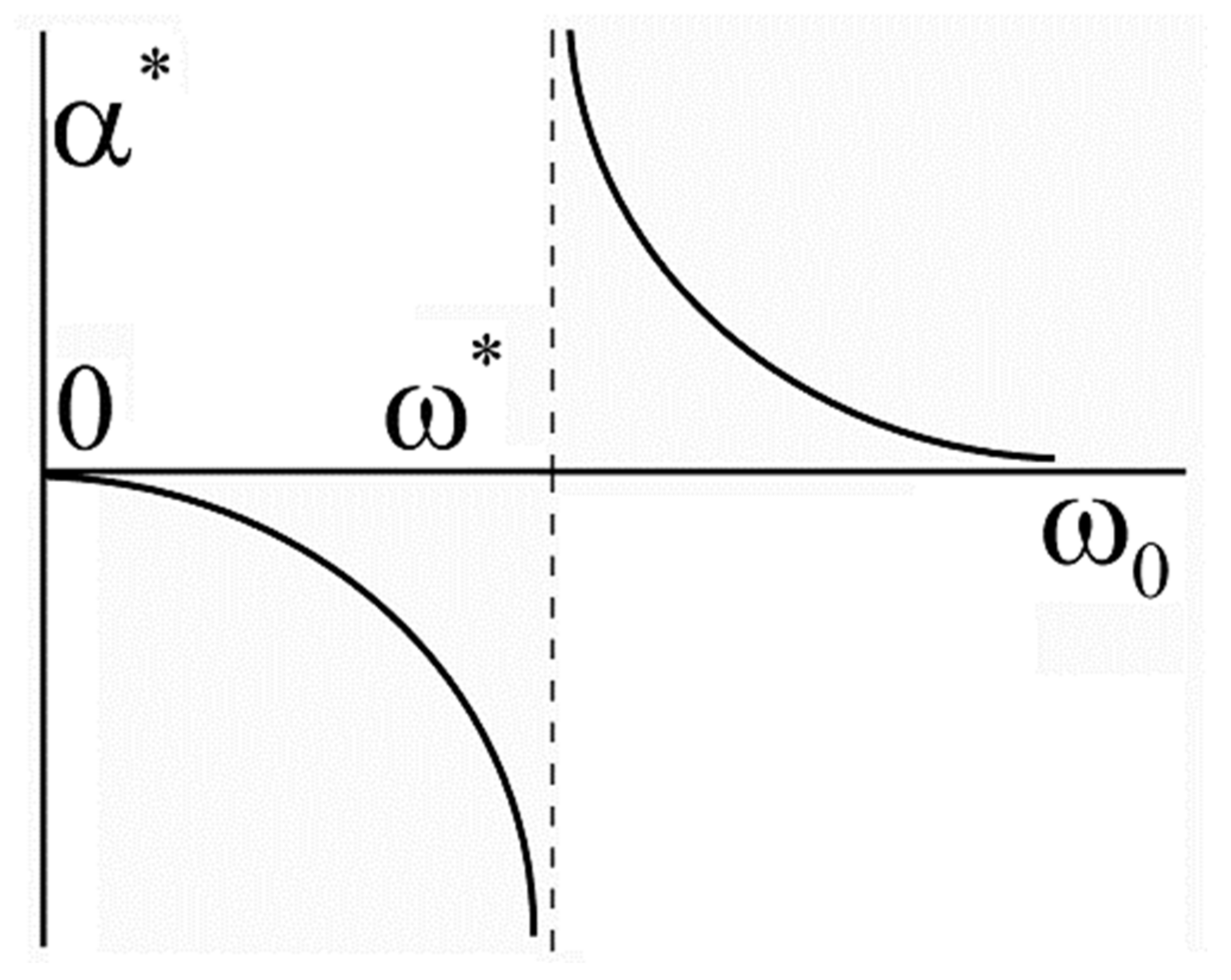
3. Isotope Coefficient for the Pseudogap Phase
4. Isotope Coefficient for Pseudogap Phase in Magnetic Field
5. Discussion
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of Formula (13)
References
- Norman, M.R.; Pines, D.; Kallin, C. The pseudogap: Friend or foe of highTc? Adv. Phys. 2005, 54, 715–733. [Google Scholar] [CrossRef]
- Vishik, I.M.; Lee, W.S.; He, R.-H.; Hashimoto, M.; Hussain, Z.; Devereaux, T.P.; Shen, Z.-X. ARPES studies of cuprate Fermiology: Superconductivity, pseudogap and quasiparticle dynamics. New J. Phys. 2010, 12, 105008. [Google Scholar] [CrossRef]
- Timusk, T.; Statt, B. The pseudogap in high-temperature superconductors: An experimental survey. Rep. Prog. Phys. 1999, 62, 61–122. [Google Scholar] [CrossRef]
- Hüfner, S.; Hossain, M.A.; Damascelli, A.; A Sawatzky, G. Two gaps make a high-temperature superconductor? Rep. Prog. Phys. 2008, 71, 062501. [Google Scholar] [CrossRef]
- Lee, P.A.; Nagaosa, N.; Wen, X.-G. Doping a Mott insulator: Physics of high-temperature superconductivity. Rev. Mod. Phys. 2006, 78, 17–85. [Google Scholar] [CrossRef]
- Randeria, M.; Trivedi, N. Pairing correlations above Tc and pseudogaps in underdoped cuprates. J. Phys. Chem. Solids 1998, 59, 1754–1758. [Google Scholar] [CrossRef]
- Franz, M. Importance of fluctuations. Nat. Phys. 2007, 3, 686–687. [Google Scholar] [CrossRef]
- Emery, V.J.; A Kivelson, S. Importance of phase fluctuations in superconductors with small superfluid density. Nature 1995, 374, 434–437. [Google Scholar] [CrossRef]
- Curty, P.; Beck, H. Thermodynamics and Phase Diagram of High Temperature Superconductors. Phys. Rev. Lett. 2003, 91, 257002. [Google Scholar] [CrossRef] [PubMed]
- Moon, E.G.; Sachdev, S. Competition between spin density wave order and superconductivity in the underdoped cuprates. Phys. Rev. B 2009, 80, 035117. [Google Scholar] [CrossRef]
- Sadovskii, M.V. Pseudogap in high-temperature superconductors. Physics-Uspekhi 2001, 44, 515–539. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef]
- Lakhno, V.D. Superconducting Properties of 3D Low-Density Translation-Invariant Bipolaron Gas. Adv. Condens. Matter Phys. 2018, 2018, 1–12. [Google Scholar] [CrossRef]
- Lakhno, V. Superconducting properties of a nonideal bipolaron gas. Phys. C Supercond. 2019, 561, 1–8. [Google Scholar] [CrossRef]
- Lakhno, V.D. Superconducting Properties of 3D Low-Density TI-Bipolaron Gas in Magnetic Field. Condens. Matter 2019, 4, 43. [Google Scholar] [CrossRef]
- Lakhno, V.D. Translational-Invariant Bipolarons and Superconductivity. Condens. Matter 2020, 5, 30. [Google Scholar] [CrossRef]
- Kagan, M.Y. Modern Trends in Superconductivity and Superfluidity; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Temprano, D.R.; Mesot, J.; Janssen, S.; Conder, K.; Furrer, A.; Mutka, H.; Müller, K.A. Large Isotope Effect on the Pseudogap in the High-Temperature SuperconductorHoBa2Cu4O8. Phys. Rev. Lett. 2000, 84, 1990–1993. [Google Scholar] [CrossRef] [PubMed]
- Bendele, M.; Von Rohr, F.; Guguchia, Z.; Pomjakushina, E.; Conder, K.; Bianconi, A.; Simon, A.; Bussmann-Holder, A.; Keller, H. Evidence for strong lattice effects as revealed from huge unconventional oxygen isotope effects on the pseudogap temperature in La2−xSrxCuO4. Phys. Rev. B 2017, 95, 014514. [Google Scholar] [CrossRef]
- Furrer, A. Neutron Scattering Investigations of Charge Inhomogeneities and the Pseudogap State in High-Temperature Superconductors. In Superconductivity in Complex Systems; Structure and Bonding book series (STRUCTURE, v. 114); Müller, A., Bussmann-Holder, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar] [CrossRef]
- Bill, A.; Kresin, V.Z.; Wolf, S.A. The isotope Effect in Superconductors. In Pair Correlations in Many-Fermion Systems; Plenum Press: New York, NY, USA, 1998; pp. 25–56. [Google Scholar] [CrossRef]
- Solov’Ev, A.L.; Dmitriev, V.M. Fluctuation conductivity and pseudogap in YBCO high-temperature superconductors (Review). Low Temp. Phys. 2009, 35, 169–197. [Google Scholar] [CrossRef]
- Madan, I.; Kurosawa, T.; Toda, Y.; Oda, M.; Mertelj, T.; Mihailović, D. Evidence for carrier localization in the pseudogap state of cuprate superconductors from coherent quench experiments. Nat. Commun. 2015, 6, 6958. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kordyuk, A. Pseudogap from ARPES experiment: Three gaps in cuprates and topological superconductivity (Review Article). Low Temp. Phys. 2015, 41, 319–341. [Google Scholar] [CrossRef]
- Labbé, J.; Bok, J. Superconductivity in Alcaline-Earth-Substituted La2CuO4: A Theoretical Model. EPL Europhys. Lett. 1987, 3, 1225–1230. [Google Scholar] [CrossRef]
- Radtke, R.J.; Norman, M.R. Relation of extended Van Hove singularities to high-temperature superconductivity within strong-coupling theory. Phys. Rev. B 1994, 50, 9554–9560. [Google Scholar] [CrossRef] [PubMed]
- Schüttler, H.-B.; Pao, C.-H. Isotope Effect ind-Wave Superconductors. Phys. Rev. Lett. 1995, 75, 4504–4507. [Google Scholar] [CrossRef] [PubMed]
- Nazarenko, A.; Dagotto, E. Possible phononic mechanism for dx2−y2 superconductivity in the presence of short-range antiferromagnetic correlations. Phys. Rev. B 1996, 53, R2987–R2990. [Google Scholar] [CrossRef] [PubMed]
- Greco, A.; Zeyher, R. Electronic correlations, electron-phonon interaction, and isotope effect in high-Tccuprates. Phys. Rev. B 1999, 60, 1296–1302. [Google Scholar] [CrossRef]
- Perali, A.; Innocenti, D.; Valletta, A.; Bianconi, A. Anomalous isotope effect near a 2.5 Lifshitz transition in a multi-band multi-condensate superconductor made of a superlattice of stripes. Supercond. Sci. Technol. 2012, 25. [Google Scholar] [CrossRef]
- Valletta, A.; Bianconi, A.; Perali, A.; Saini, N. Electronic and superconducting properties of a superlattice of quantum stripes at the atomic limit. Eur. Phys. J. B 1997, 104, 707–713. [Google Scholar] [CrossRef]
- Medicherla, V.R.R.; Patil, S.; Singh, R.S.; Maiti, K. Origin of ground state anomaly in LaB6 at low temperatures. Appl. Phys. Lett. 2007, 90, 62507. [Google Scholar] [CrossRef]
- Chainani, A.; Yokoya, T.; Kiss, T.; Shin, S.; Nishio, T.; Uwe, H. Electron-phonon coupling induced pseudogap and the superconducting transition in Ba0.67K0.33BiO3. Phys. Rev. B 2001, 64, 180509. [Google Scholar] [CrossRef]
- Yokoya, T.; Chainani, A.; Kiss, T.; Shin, S.; Hirata, K.; Kameda, N.; Tamegai, T.; Nishio, T.; Uwe, H. High-resolution photoemission study of low-Tc superconductors: Phonon-induced electronic structures in low-Tc superconductors and comparison with the results of high-Tc cuprates. Phys. C: Supercond. 2002, 378-381, 97–101. [Google Scholar] [CrossRef]
- Sacépé, B.; Chapelier, C.; Baturina, T.I.; Vinokur, V.M.; Baklanov, M.R.; Sanquer, M. Pseudogap in a thin film of a conventional superconductor. Nat. Commun. 2010, 1, 140. [Google Scholar] [CrossRef]
- Mondal, M.; Kamlapure, A.; Chand, M.; Saraswat, G.; Kumar, S.; Jesudasan, J.; Benfatto, L.; Tripathi, V.; Raychaudhuri, P. Phase Fluctuations in a Strongly Disordereds-Wave NbN Superconductor Close to the Metal-Insulator Transition. Phys. Rev. Lett. 2011, 106, 047001. [Google Scholar] [CrossRef]
- Thakur, S.; Biswas, D.; Sahadev, N.; Biswas, P.K.; Balakrishnan, G.; Maiti, K. Complex spectral evolution in a BCS superconductor, ZrB12. Sci. Rep. 2013, 3, 3342. [Google Scholar] [CrossRef] [PubMed]
- Patil, S.; Medicherla, V.R.R.; Ali, K.; Singh, R.S.; Manfrinetti, P.; Wrubl, F.; Dhar, S.K.; Maiti, K. Observation of pseudogap in MgB2. J. Phys. Condens. Matter 2017, 29, 465504. [Google Scholar] [CrossRef]
- Lanzara, A.; Zhao, G.-M.; Saini, N.L.; Bianconi, A.; Conder, K.; Keller, H.; A Müller, K. Oxygen-isotope shift of the charge-stripe ordering temperature in La2−xSrxCuO4 from x-ray absorption spectroscopy. J. Phys. Condens. Matter 1999, 11, L541–L546. [Google Scholar] [CrossRef]
- Lakhno, V.D. Translation invariant theory of polaron (bipolaron) and the problem of quantizing near the classical solution. J. Exp. Theor. Phys. 2013, 116, 892–896. [Google Scholar] [CrossRef][Green Version]
- Lakhno, V.D. Isotope Effect in the Translation-Invariant Bipolaron Theory of High-Temperature Superconductivity. Condens. Matter 2020, 5, 80. [Google Scholar] [CrossRef]
- Alexandrov, A.S. Superconducting Polarons and Bipolarons. In Polarons in Advanced Materials; Alexandrov, A.S., Ed.; v.103; Springer: Berlin/Heidelberg, Germany, 2007; pp. 257–310. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lakhno, V.D. Pseudogap Isotope Effect as a Probe of Bipolaron Mechanism in High Temperature Superconductors. Materials 2021, 14, 4973. https://doi.org/10.3390/ma14174973
Lakhno VD. Pseudogap Isotope Effect as a Probe of Bipolaron Mechanism in High Temperature Superconductors. Materials. 2021; 14(17):4973. https://doi.org/10.3390/ma14174973
Chicago/Turabian StyleLakhno, Victor D. 2021. "Pseudogap Isotope Effect as a Probe of Bipolaron Mechanism in High Temperature Superconductors" Materials 14, no. 17: 4973. https://doi.org/10.3390/ma14174973
APA StyleLakhno, V. D. (2021). Pseudogap Isotope Effect as a Probe of Bipolaron Mechanism in High Temperature Superconductors. Materials, 14(17), 4973. https://doi.org/10.3390/ma14174973





