A Theoretical Model for Debonding Prediction in the RC Beams Externally Strengthened with Steel Strip and Inorganic Matrix
Abstract
:1. Introduction
2. Theoretical Modelling
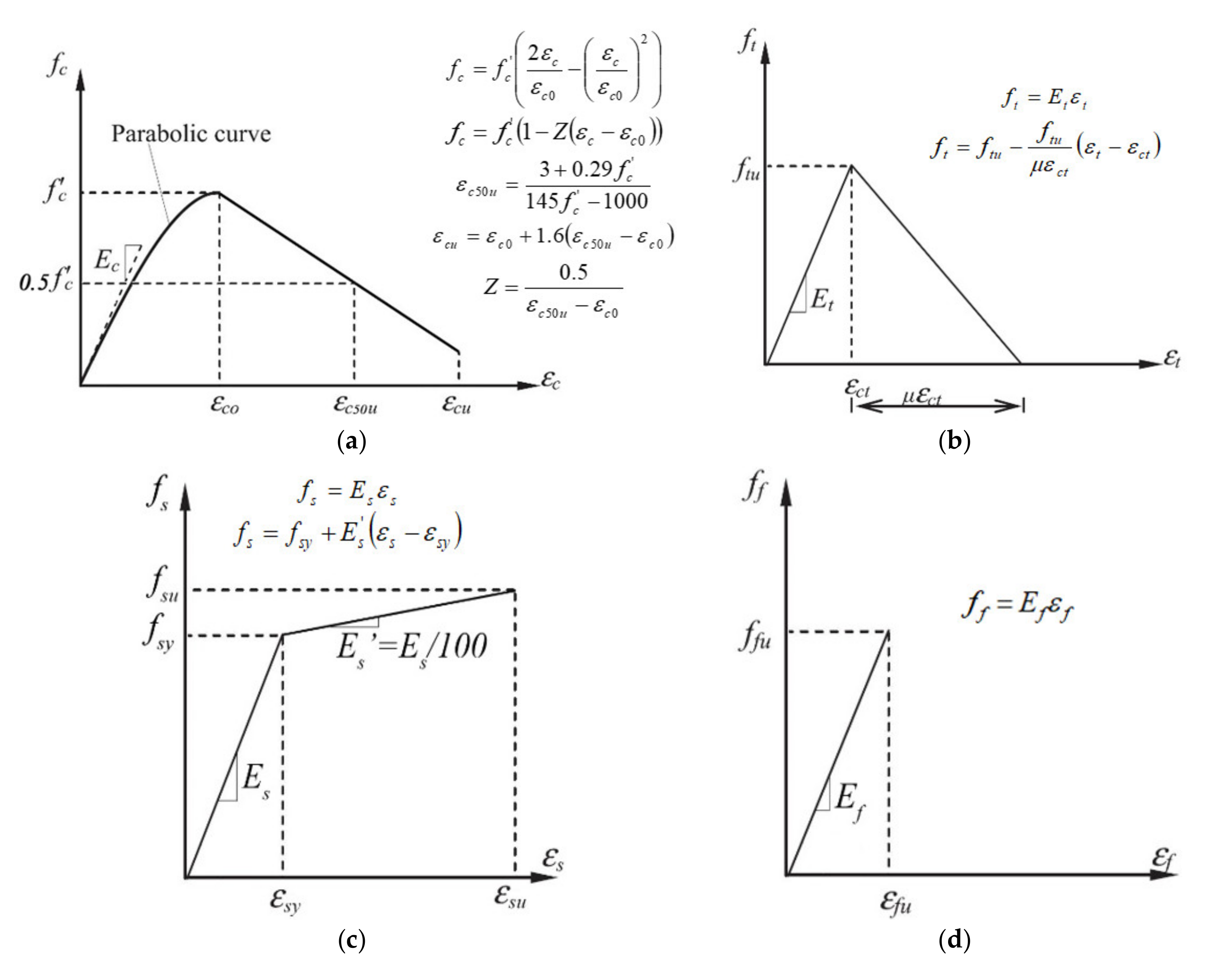
2.1. Stress–Strain Material Models
2.2. Moment–Curvature/Load–Deflection Relationships
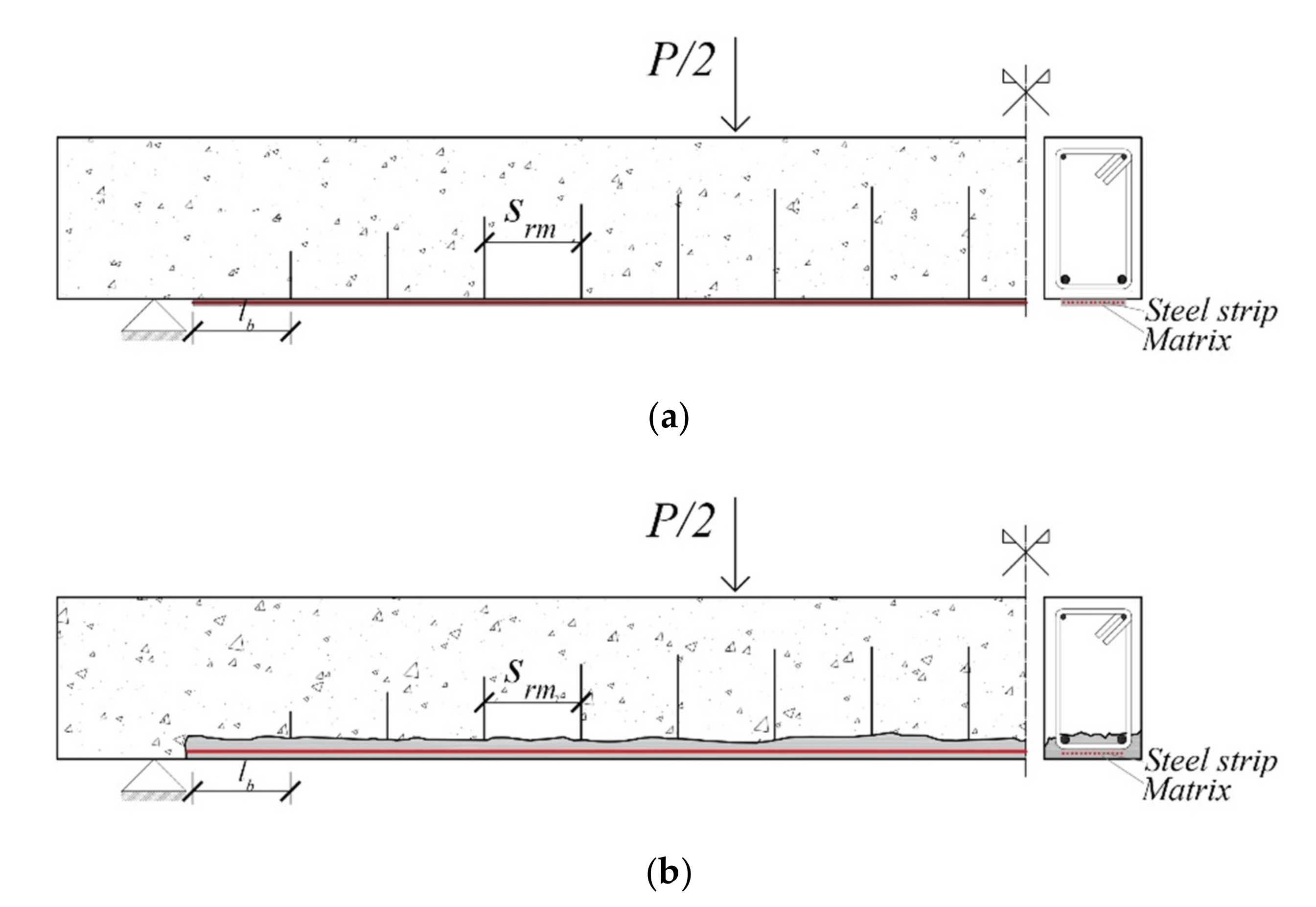
2.3. Debonding Predictions
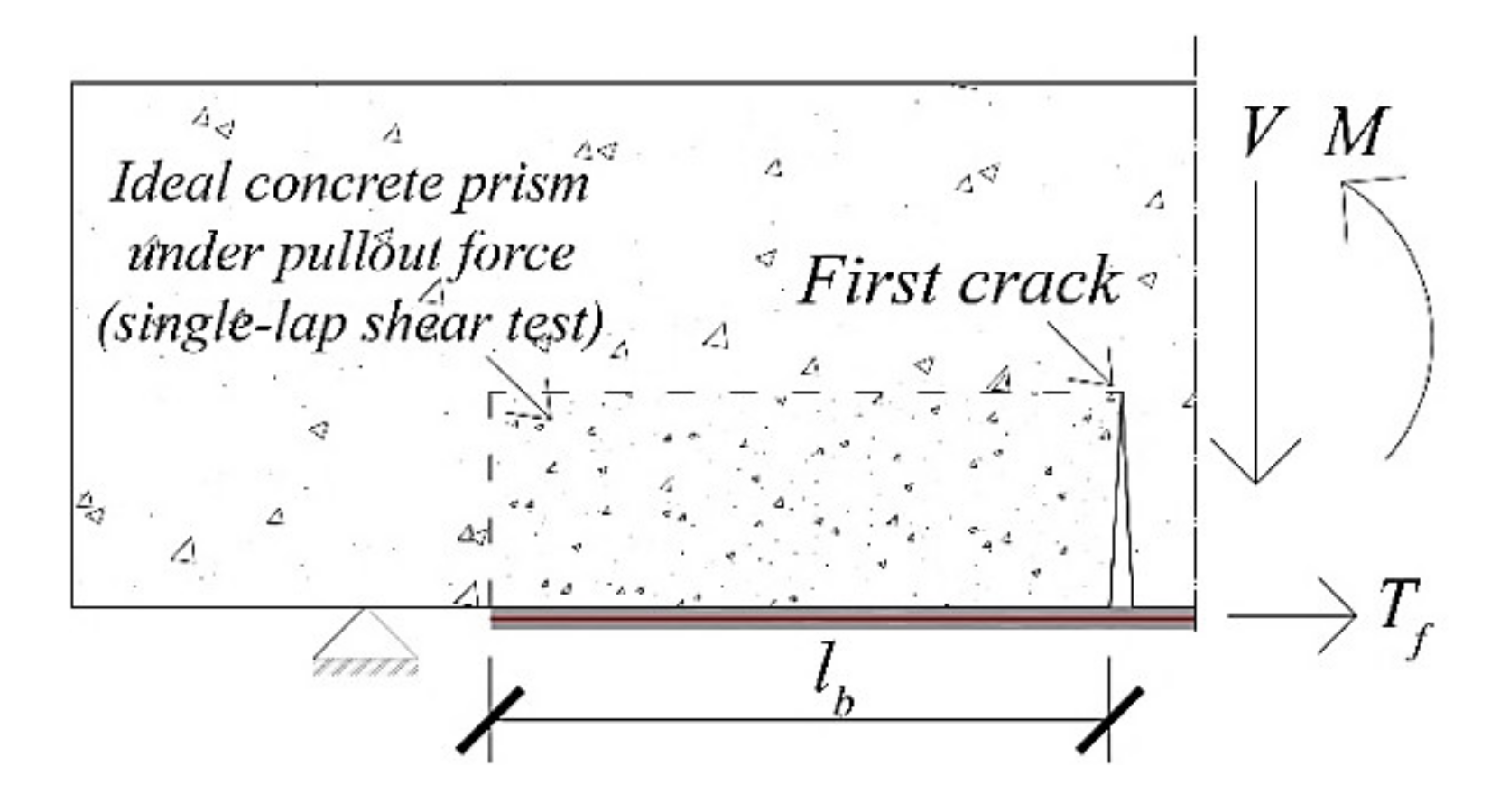
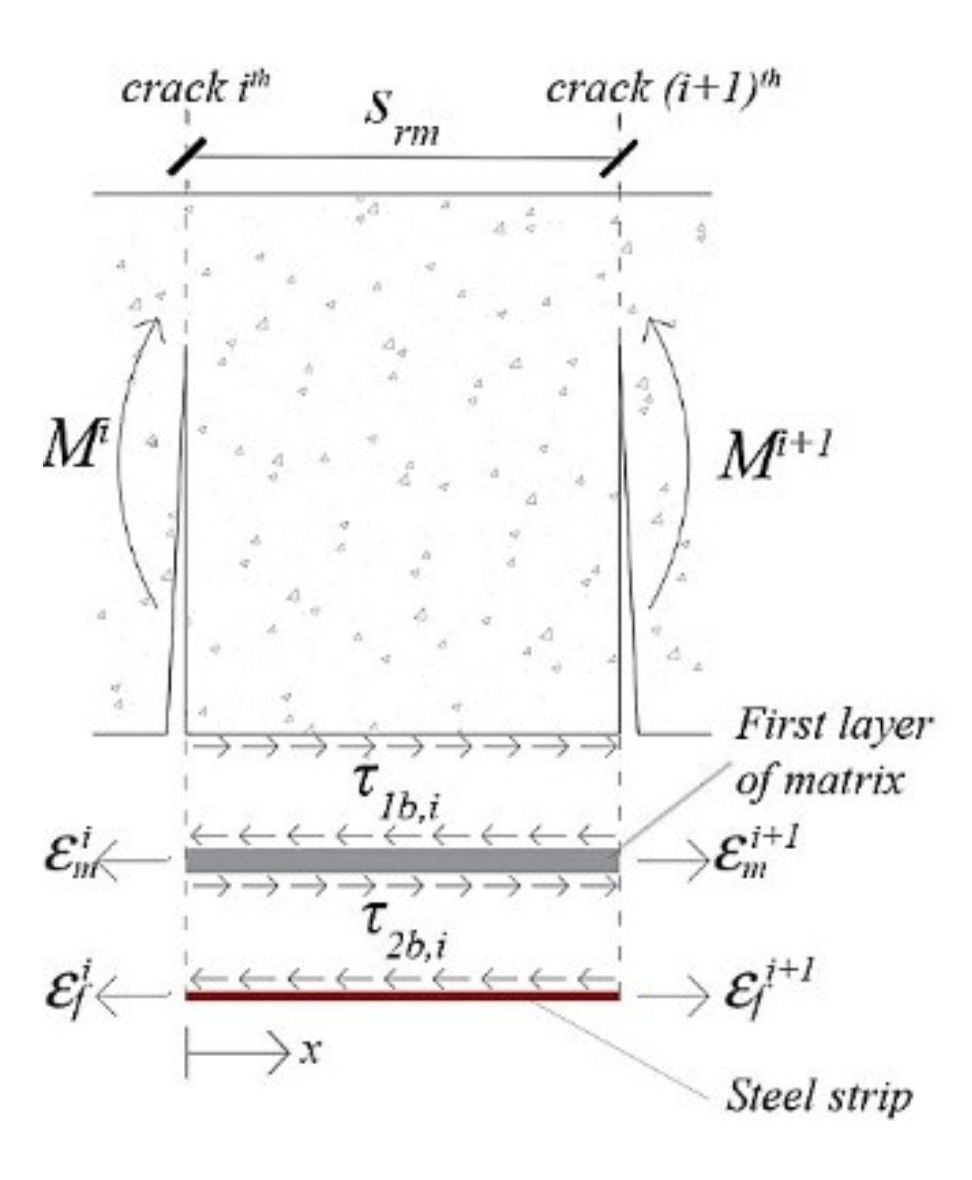
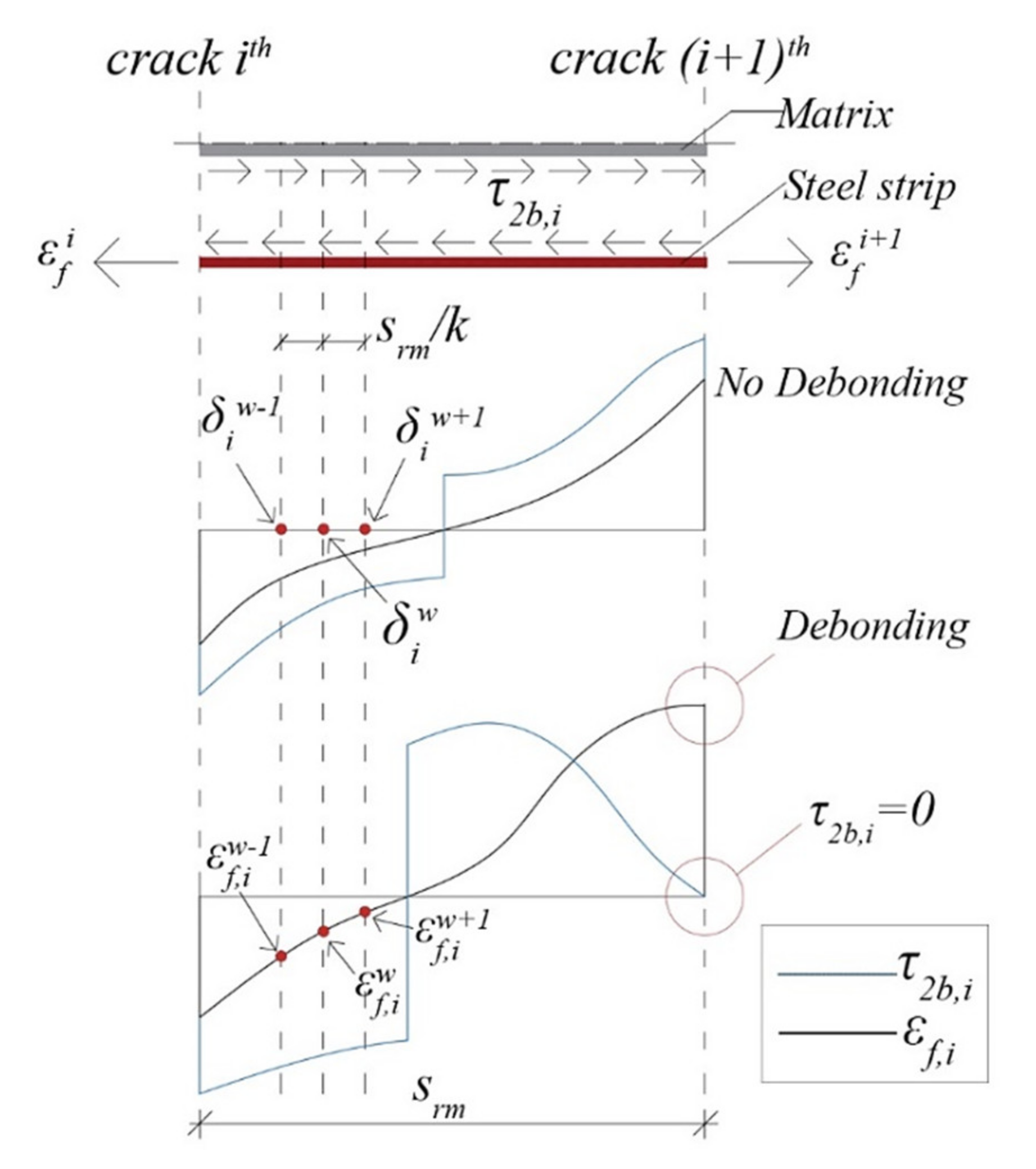
2.3.1. Interfacial Behaviour of SRGM System Bonded to Concrete
2.3.2. End Debonding
2.3.3. Intermediate Debonding
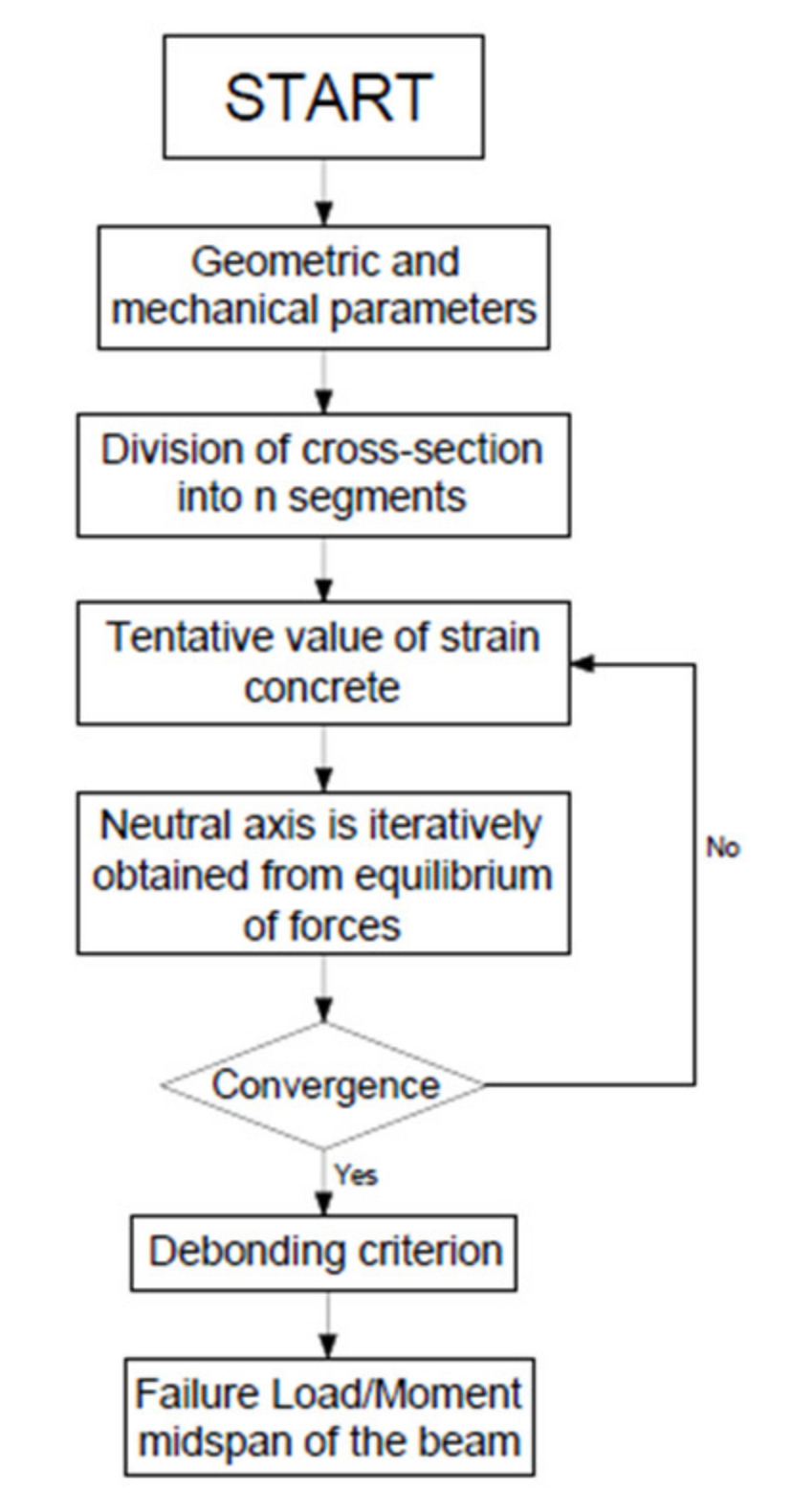
2.3.4. Flowchart of the Standard Procedure
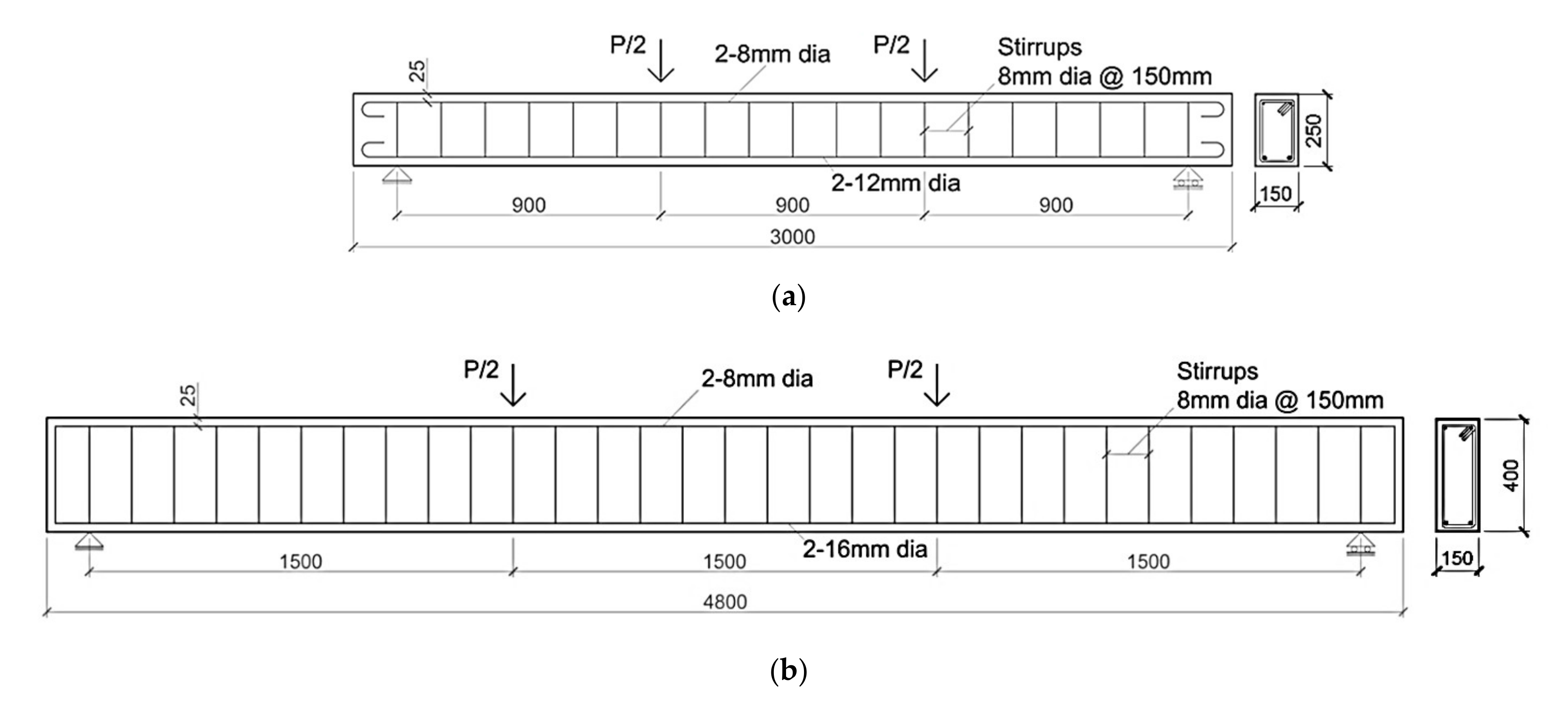
3. RC Beams Strengthened with EB/IRS-SRGM
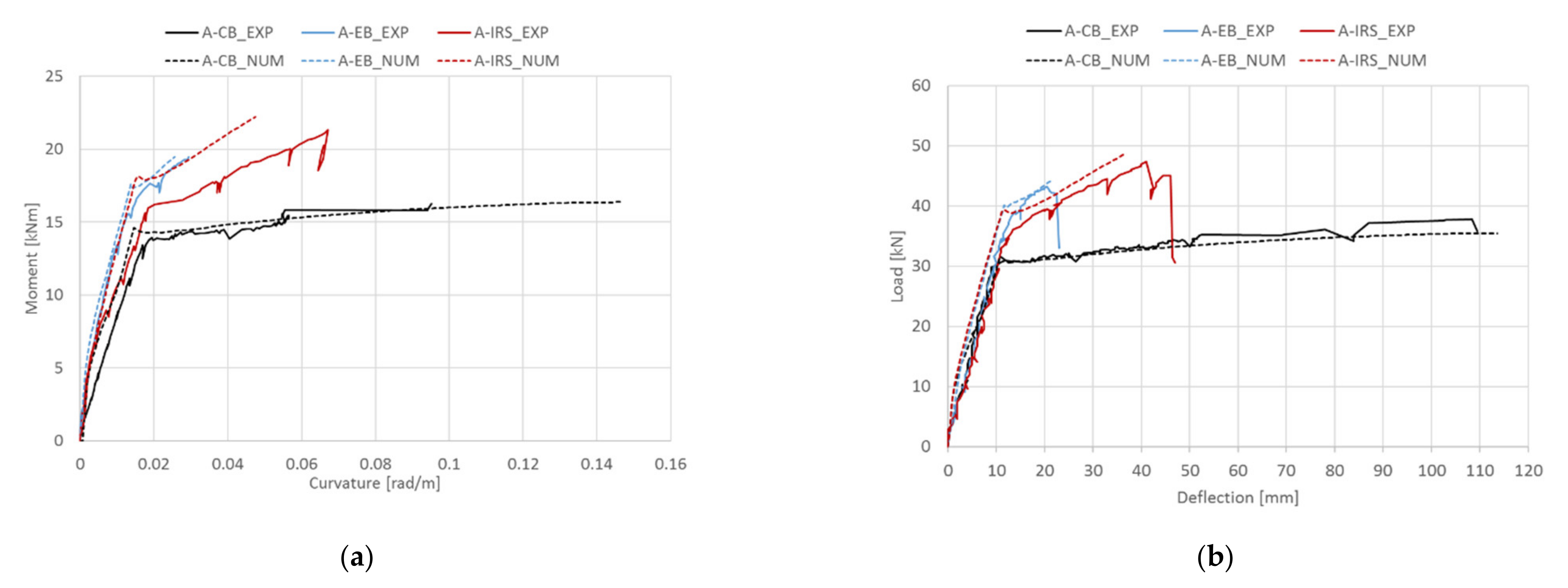
4. Validation of the Theoretical Procedure
5. Theoretical Results and Comparisons
6. Conclusions
- The end debonding failure, for bonded lengths equal to or greater than effective bonded length, can be predicted by limiting the strain in the external strengthening strip, at first flexural crack, to the maximum analytical strain calibrated on single-lap shear bond tests. For bonded lengths lower than the effective bonded length a parabolic relationship can be used for reducing the maximum strain.
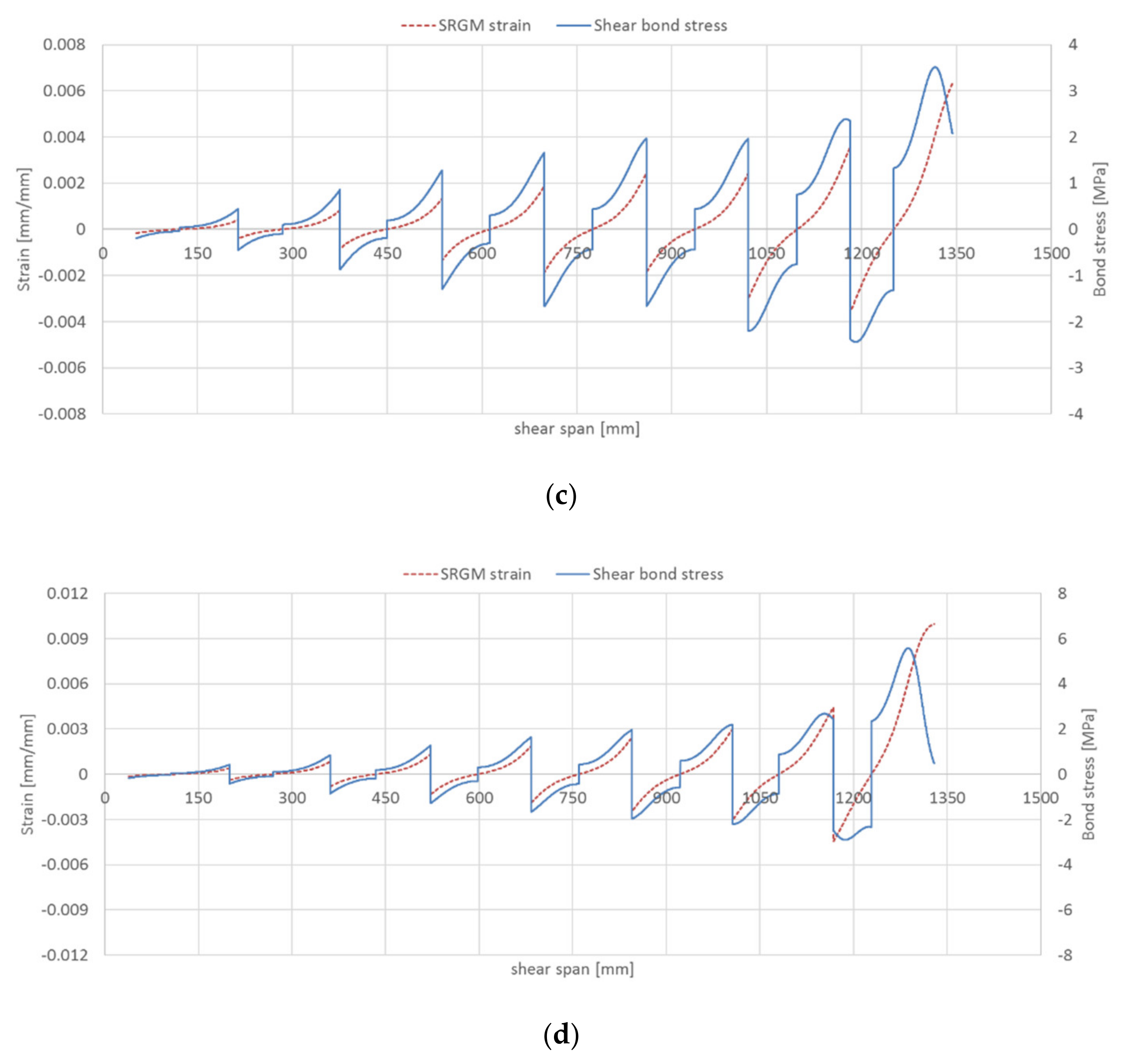
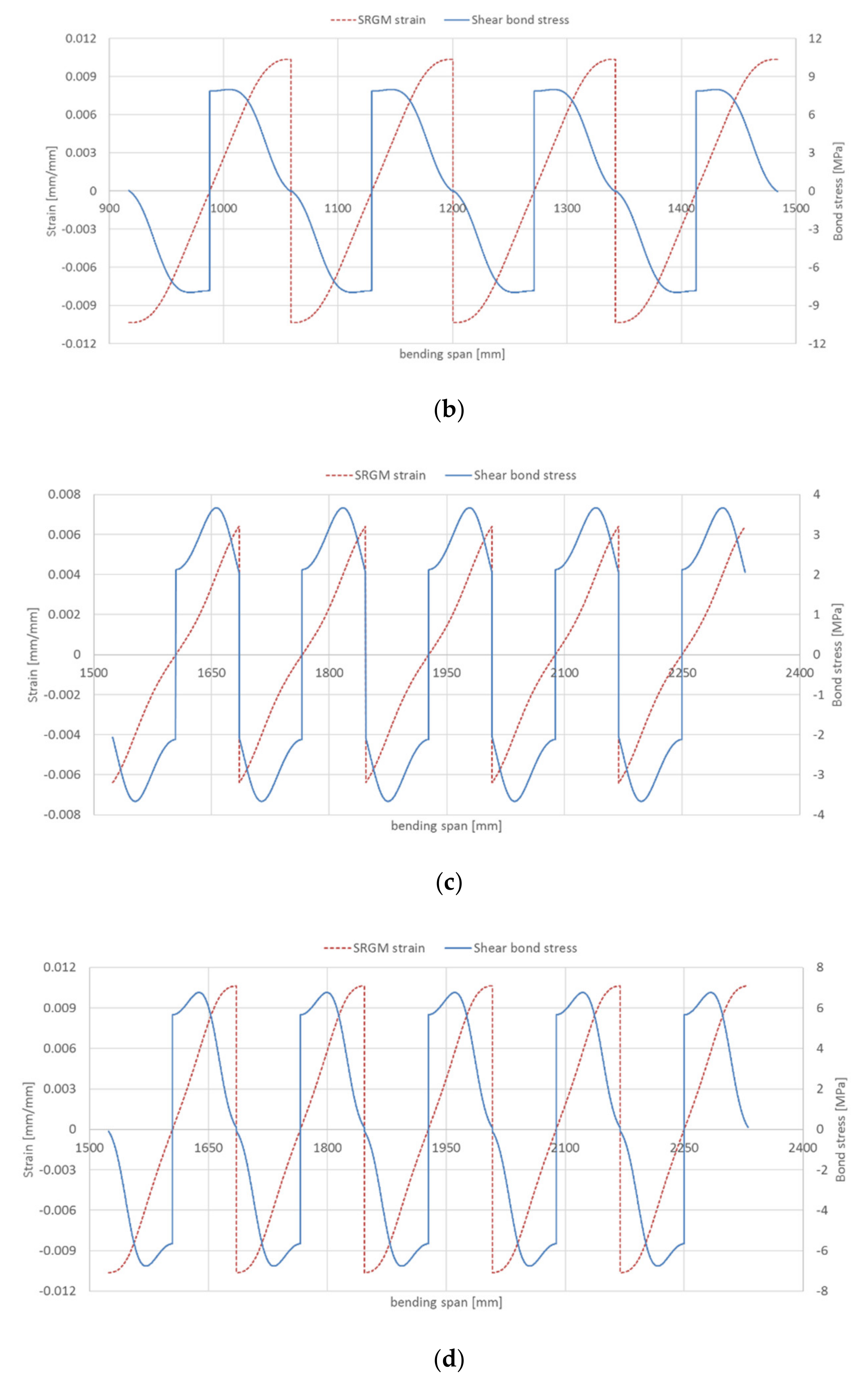
- The maximum strain value in the strengthening system for intermediate debonding at steel strip–matrix interface is about 1.30–1.40 times the end debonding strain (7.82‰). As a result, the load carrying capacity of strengthened RC beams for debonding failure at fibre–matrix interface can be predicted by limiting the average axial strain in the strengthening strip to 10–11‰.
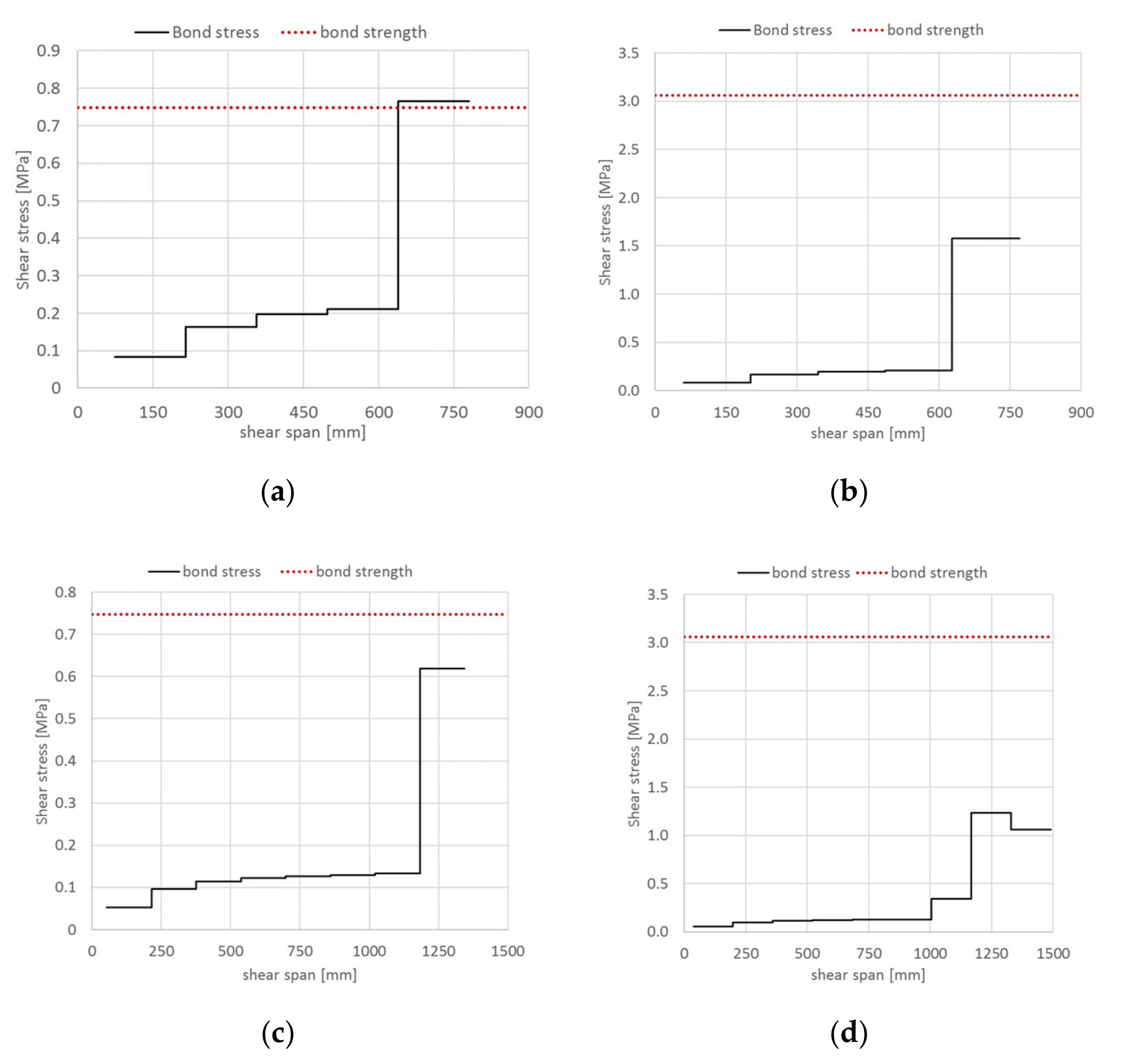
- The brittle intermediate debonding at concrete–matrix interface can be predicted by limiting the maximum shear bond stress to the interface shear strength.
- Approach 2 proposed by Fib 14 for FRP systems provides conservative values of failure load compared with the values calculated according to the proposed model.
- The assumption of a perfect bond between materials leads to slightly stiffer behaviour of the numerical curves in the first stage (until the yielding of the internal tensile reinforcements). In any case, the yielding and failure loads are accurately predicted by the calculation procedure. Further development of the code could take into account a suitable bond–slip law between reinforcing steel bars/concrete and external composite material/concrete.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- ACI 440. 2R-08 Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures; American Concrete Institute: Farmington Hills, MI, USA, 2008. [Google Scholar]
- CNR-DT 200 R1/2013 Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Existing Structures–Materials, RC and PC Structures, Masonry Structures; Italian National Research Council: Rome, Italy, 2013.
- Fib 14. Externally Bonded FRP Reinforcement for RC Structures; Technical Report; Fib CEB-FI: Lausanne, Switzerland, 2001. [Google Scholar]
- Wang, X.; Zhou, C.; Ai, J.; Petrů, M.; Liu, Y. Numerical investigation for the fatigue performance of reinforced concrete beams strengthened with external prestressed HFRP sheet. Constr. Build. Mater. 2020, 237, 117601. [Google Scholar] [CrossRef]
- Wang, X.; Petrů, M. Experimental study on fracture properties of CFRP-to-concrete interfacesubject to salt water. Compos. Struct. 2021, 258, 113179. [Google Scholar] [CrossRef]
- Ashour, A.F.; El-Refaie, S.A.; Garrity, S.W. Flexural strengthening of RC continuous beams using CFRP laminates. Cem. Concr. Compos. 2004, 26, 765–775. [Google Scholar] [CrossRef]
- Bakis, C.E.; Bank, L.C.; Brown, V.L.; Cosenza, E.; Davalos, J.F.; Lesko, J.J.; Machida, A.; Rizkalla, S.H.; Triantafillou, T.C. Fiber reinforced polymer composites for construction—state-of-the-art review. J. Compos. Constr. 2002, 6, 73–87. [Google Scholar] [CrossRef] [Green Version]
- Sebastian, W.M. Significance of midspan debonding failure in FRP-plated concrete beams. J. Struct. Eng. 2001, 127, 792–798. [Google Scholar] [CrossRef]
- Spadea, G.; Bencardino, F.; Sorrenti, F.; Swamy, R.N. Structural effectiveness of FRP materials in strengthening RC beams. Eng. Struct. 2015, 99, 631–641. [Google Scholar] [CrossRef]
- Bruckner, A.; Ortlepp, R.; Curbach, M. Textile reinforced concrete for strengthening in bending and shear. Mater. Struct. 2006, 39, 741–748. [Google Scholar] [CrossRef]
- Larbi, A.S.; Agbossou, A.; Hamelin, P. Experimental and numerical investigations about textile-reinforced concrete and hybrid solutions for repairing and/or strengthening reinforced concrete beams. Compos. Struct. 2013, 99, 152–162. [Google Scholar] [CrossRef]
- Triantafillou, T.C. Recent developments in strengthening of concrete structures with advanced composites textile-reinforced mortar (TRM) jacketing. In Proceedings of the International Conference on Structural Composites for Infrastructure Applications, Alexandria, Egypt, 17–20 December 2004. [Google Scholar]
- Triantafillou, T.C.; Papanicolau, C.G. Shear strengthening of reinforced concrete members with textile reinforced mortar (TRM) jackets. Mater. Struct. 2006, 39, 85–93. [Google Scholar]
- D’Ambrisi, A.; Focacci, F. Flexural Strengthening of RC beams with cement-based composites. J. Compos. Constr. 2011, 15, 707–720. [Google Scholar] [CrossRef]
- Loreto, G.; Leardini, L.; Arboleda, D.; Nanni, A. Performance of RC slab-type elements strengthened with fabric-reinforced-cementitious-matrix (FRCM) composites. J. Compos. Constr. 2013, 18, A4013003. [Google Scholar]
- Bencardino, F.; Condello, A. Innovative solution to retrofit RC members: Inhibiting-Repairing-Strengthening (IRS). Constr. Build. Mater. 2016, 117, 171–181. [Google Scholar] [CrossRef]
- Bencardino, F.; Condello, A. Eco-friendly external strengthening system for existing reinforced concrete beams. Compos. Part B Eng. 2016, 93, 163–173. [Google Scholar] [CrossRef]
- Katakalos, K.; Papakonstantinou, C.G. Fatigue of Reinforced Concrete Beams Strengthened with Steel-Reinforced Inorganic Polymers. J. Compos. Constr. 2009, 13, 103–112. [Google Scholar] [CrossRef]
- Menna, C.; Asprone, D.; Ferone, C.; Colangelo, C.; Balsamo, A.; Prota, A.; Cioffi, R.; Manfredi, G. Use of geopolymers for composite external reinforcement of RC members. Compos. Part B Eng. 2013, 45, 1667–1676. [Google Scholar] [CrossRef]
- Balsamo, A.; Nardone, F.; Iovinella, I.; Ceroni, F.; Pecce, M. Flexural strengthening of concrete beams with EB-FRP, SRP and SRCM: Experimental investigation. Compos. Part B Eng. 2013, 46, 91–101. [Google Scholar] [CrossRef]
- Barton, B.; Wobbe, E.; Dharani, L.R.; Silva, P.; Birman, V.; Nanni, A.; Alkhrdaji, T.; Thomas, J.; Tunis, G. Characterization of reinforced concrete beams strengthened by steel reinforced polymer and grout (SRP and SRG) composites. Mater. Sci. Eng. 2005, 412, 129–136. [Google Scholar] [CrossRef]
- Bencardino, F.; Condello, A. Structural behaviour of RC beams externally strengthened in flexure with SRG and SRP systems. Int. J. Struct. Eng. 2014, 5, 346–368. [Google Scholar] [CrossRef]
- Napoli, A.; Realfonzo, R. Reinforced concrete beams strengthened with SRP/SRG systems: Experimental investigation. Constr. Build. Mater. 2015, 93, 654–677. [Google Scholar] [CrossRef]
- Pecce, M.; Ceroni, F.; Prota, A.; Manfredi, G. Response prediction of RC beams externally bonded with steel-reinforced polymers. J. Compos. Constr. 2006, 10, 195–203. [Google Scholar] [CrossRef]
- Vasconcelos, E.; Fernandes, S.; Barroso de Aguiar, J.L.; Pacheco-Torgal, S. Concrete retrofitting using metakaolin geopolymer mortars and CFRP. Constr. Build. Mater. 2011, 25, 3213–3221. [Google Scholar] [CrossRef] [Green Version]
- ACI 549. 4R-20 Guide to Design and Construction of Externally Bonded Fabric-Reinforced Cementitious Matrix and Steel-Reinforced Grout Systems for Repair and Strengthening of Concrete Structures; American Concrete Institute: Farmington Hills, MI, USA, 2020. [Google Scholar]
- Carloni, C.; D’Antino, T.; Sneed, L.; Pellegrino, C. Role of the Matrix Layers in the Stress-Transfer Mechanism of FRCM Composites Bonded to a Concrete Substrate. J. Eng. Mech. 2015, 141, 04014165. [Google Scholar] [CrossRef]
- Bencardino, F.; Condello, A. Reliability and adaptability of the analytical models proposed for the FRP systems to the Steel Reinforced Polymer and Steel Reinforced Grout strengthening systems. Compos. Part B Eng. 2015, 76, 249–259. [Google Scholar] [CrossRef]
- Bencardino, F.; Condello, A. SRG/SRP-concrete bond-slip laws for externally strengthened RC beams. Compos. Struct. 2015, 132, 804–815. [Google Scholar] [CrossRef]
- MATLAB R2020a; The MathWorks Inc.: Natick, MA, USA, 2020.
- Kara, I.F.; Ashour, A.F.; Köroğlu, M.A. Flexural performance of reinforced concrete beams strengthened with prestressed near-surface-mounted FRP reinforcements. Compos. Part B Eng. 2016, 91, 371–383. [Google Scholar] [CrossRef] [Green Version]
- Kara, I.F.; Ashour, A.F.; Köroğlu, M.A. Flexural behavior of hybrid FRP/steel reinforced concrete beams. Compos. Struct. 2015, 129, 111–121. [Google Scholar] [CrossRef]
- Kara, I.F.; Ashour, A.F. Flexural performance of FRP reinforced concrete beams. Compos. Struct. 2012, 94, 1616–1625. [Google Scholar] [CrossRef] [Green Version]
- Kent, D.C.; Park, R. Flexural Members with Confined Concrete. J. Struct. Div. 1971, 97, 1969–1990. [Google Scholar] [CrossRef]
- Aram, M.R.; Czaderski, C.; Motavalli, M. Debonding failure modes of flexural FRP-strengthened RC beams. Compos. Part B Eng. 2008, 39, 826–841. [Google Scholar] [CrossRef]
- Pham, H.; Al-Mahaidi, R. Assessment of available prediction models for the strength of FRP retrofitted RC beams. Compos. Struct. 2004, 66, 601–610. [Google Scholar] [CrossRef]
- Gunes, O.; Buyukozturk, O.; Karaca, E. A fracture-based model for FRP debonding in strengthened beams. Eng. Fract. Mech. 2009, 76, 1897–1909. [Google Scholar] [CrossRef]
- Eurocode 2: Design of Concrete Structures–Part 1–1: General Rules and Rules for Buildings; EN 1992–1–1; European Committee for Standardization: Brussels, Belgium, 2005.
- Bencardino, F.; Condello, A.; Ashour, A.F. Single-lap shear bond tests on Steel Reinforced Geopolymeric Matrix-concrete joints. Compos. Part B Eng. 2017, 110, 62–71. [Google Scholar] [CrossRef] [Green Version]
- Dai, J.; Ueda, T.; Sato, Y. Development of the nonlinear bond stress-slip model of fiber reinforced plastics sheet-concrete interfaces with a simple method. J. Compos. Constr. 2005, 9, 52–62. [Google Scholar] [CrossRef] [Green Version]
- Oehlers, D.J. Reinforced concrete beams with plates glued to their soffits. J. Struct. Eng. 1992, 118, 2023–2038. [Google Scholar] [CrossRef]
- Zhang, S.; Raoof, M.; Wood, L.A. Prediction of peeling failure of reinforced concrete beams with externally bonded steel plates. Proc. Inst. Civ. Eng. Struct. Build. 1995, 110, 257–268. [Google Scholar] [CrossRef]
- Ziraba, Y.N.; Baluch, M.H.; Basunbul, I.A.; Sharif, A.M.; Azad, A.K.; Al-Sulaimani, G.J. Guidelines towards the design of reinforced concrete beams with external plates. ACI Struct. J. 1994, 91, 639–646. [Google Scholar]
- ACI 318-19 Building Code Requirements for Structural Concrete and Commentary; American Concrete Institute: Farmington Hills, MI, USA, 2019.




| Experimental Work | Specimen | Dimensions (b × h × l) | fc’ (MPa) | ftu (MPa) | fsy (MPa) | As (mm2) | Af (mm2) | Ef (MPa) | εfu | bf/bc | N. Plies | Anchorage System |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bencardino and Condello [16,17] | A-EB | 150 × 250 × 3000 | 16.80 | 1.70 | 367.10 | 226.08 | 24.00 | 188,360 | 0.02 | 0.67 | 1 | - |
| A-IRS | ||||||||||||
| B-EB | 150 × 400 × 4500 | 492.00 | 401.92 | 36.00 | 1.00 | |||||||
| B-IRS | ||||||||||||
| Barton et al. [21] | SRG-1 | 203 × 305 × 2438 | 36.50 | 3.36 | 436.00 | 401.92 | 57.76 | 206,000 | 0.02 | 0.75 | 1 | - |
| SRG-2 | 115.52 | 2 | ||||||||||
| Pecce et al. [24] | B-2 | 400 × 200 × 3700 | 33.30 | 3.10 | 500.00 | 392.50 | 54.00 | 184,000 | 0.02 | 0.50 | 1 | - |
| B-3 | 0.50 | 1 | Nails | |||||||||
| B-4 | 108.00 | 0.50 | 2 | Nails | ||||||||
| Menna et al. [19] | S(1) | 400 × 200 × 3800 | 25.00 | 2.38 | 450.00 | 392.50 | 72.00 | 210,000 | 0.01 | 0.50 | 1 | - |
| S(2) | - | |||||||||||
| Bencardino and Condello [22] | G1 | 150 × 250 × 3000 | 34.00 | 3.50 | 604.20 | 157.00 | 28.50 | 206,000 | 0.02 | 1.00 | 1 | - |
| G1-U | U-wrap | |||||||||||
| Napoli and Realfonzo [23] | SRG-1LD | 400 × 200 × 3700 | 15.14 | 2.60 | 460.00 | 392.50 | 16.80 | 206,000 | 0.02 | 0.50 | 1 | - |
| SRG-2LD | 33.60 | 2 | - | |||||||||
| SRG-1MD | 50.80 | 1 | - | |||||||||
| SRG-1MD-A | 1 | - | ||||||||||
| SRG-1MD-B | 1 | - | ||||||||||
| SRG-2MD | 101.60 | 2 | - |
| Specimen | Failure Mode | Ultimate Load (kN) | Fnum./Fexp. | ||
|---|---|---|---|---|---|
| Experimental | Theoretical | Experimental (Fexp.) | Theoretical (Fnum.) | ||
| A-EB | End debonding | Int. debonding | 43.22 | 44.29 | 1.02 |
| A-IRS | Int. debonding | Int. debonding | 47.39 | 48.53 | 1.02 |
| B-EB | End debonding | End debonding | 89.52 | 94.26 | 1.05 |
| B-IRS | Concrete crushing | Concrete crushing | 98.96 | 102.33 | 1.03 |
| SRG-1 | Int. debonding | Int. debonding | 81.80 | 87.17 | 1.07 |
| SRG-2 | Int. debonding | Int. debonding | 92.40 | 93.17 | 1.01 |
| B-2 | Int. debonding | Int. debonding | 72.70 | 74.50 | 1.02 |
| B-3 | Int. debonding | Int. debonding | 71.50 | 74.50 | 1.04 |
| B-4 | Int. debonding | Int. debonding | 86.70 | 88.47 | 1.02 |
| S(1) | Steel cord failure | Int. debonding | 85.70 | 76.58 | 0.89 |
| S(2) | Steel cord failure | Int. debonding | 86.30 | 76.58 | 0.89 |
| G1 | Int. debonding | Int. debonding | 54.93 | 62.44 | 1.14 |
| G1-U | End-anch. deb/slip | Int. debonding | 54.93 | 62.44 | 1.14 |
| SRG-1LD | Rupture SRG | End debonding | 61.85 | 66.45 | 1.07 |
| SRG-2LD | Delam. SRG system | End debonding | 68.70 | 67.70 | 0.99 |
| SRG-1MD | Delam. SRG system | End debonding | 69.55 | 69.12 | 0.99 |
| SRG-1MD-A | Delam. SRG system | End debonding | 70.25 | 69.12 | 0.98 |
| SRG-1MD-B | Delam. SRG system | End debonding | 64.28 | 69.12 | 1.08 |
| SRG-2MD | Delam. SRG system | End debonding | 87.58 | 77.03 | 0.88 |
| Average | 1.02 | ||||
| Standard deviation | 0.07 | ||||
| Beam | Experimental (Fexp.) | Theoretical | ||||
|---|---|---|---|---|---|---|
| End Deb. | Int. Deb. Concrete–Matrix | Int. deb. Fibre–Matrix | Approach 2 Fib 14 | Failure (Fnum.) | ||
| A-CB | 37.22 | - | - | - | - | 35.46 |
| A-EB | 43.22 | 51.54 | 44.29 | 50.54 | 47.54 | 44.29 |
| A-IRS | 47.39 | 54.31 | 61.02 | 48.53 | 45.27 | 48.53 |
| B-CB | 76.33 | - | - | - | - | 81.62 |
| B-EB | 89.52 | 94.26 | 96.29 | 104.26 | 94.38 | 94.26 |
| B-IRS | 98.96 | 103.67 | 106.96 | 102.33 | 92.01 | 102.33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bencardino, F.; Nisticò, M. A Theoretical Model for Debonding Prediction in the RC Beams Externally Strengthened with Steel Strip and Inorganic Matrix. Materials 2021, 14, 4961. https://doi.org/10.3390/ma14174961
Bencardino F, Nisticò M. A Theoretical Model for Debonding Prediction in the RC Beams Externally Strengthened with Steel Strip and Inorganic Matrix. Materials. 2021; 14(17):4961. https://doi.org/10.3390/ma14174961
Chicago/Turabian StyleBencardino, Francesco, and Mattia Nisticò. 2021. "A Theoretical Model for Debonding Prediction in the RC Beams Externally Strengthened with Steel Strip and Inorganic Matrix" Materials 14, no. 17: 4961. https://doi.org/10.3390/ma14174961
APA StyleBencardino, F., & Nisticò, M. (2021). A Theoretical Model for Debonding Prediction in the RC Beams Externally Strengthened with Steel Strip and Inorganic Matrix. Materials, 14(17), 4961. https://doi.org/10.3390/ma14174961







