Characterization of Monte Carlo Dynamic/Kinetic Properties of Local Structure in Bond Fluctuation Model of Polymer System
Abstract
1. Introduction
1.1. Bond Fluctuation Model and Simulations of Physical Phenomena in Polymer Systems
1.2. Local Free Volume—Static Characterization of Mosaic-Like States
1.3. Heterogeneous Dynamics and Complexity
1.4. Objective
2. Materials and Methods
2.1. Monte Carlo Bond Fluctuation Model
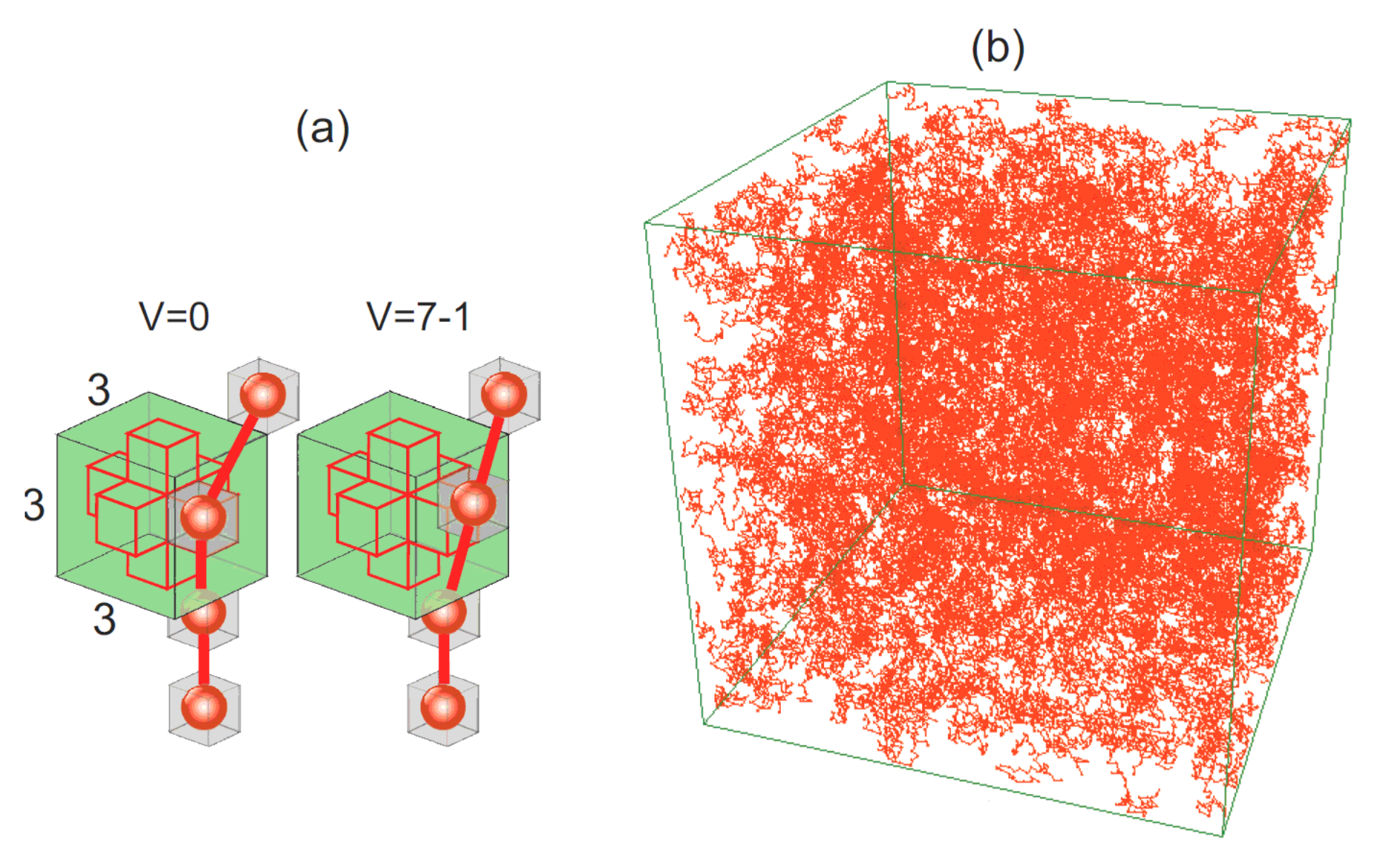
2.2. Local Void Parameter
2.3. Local Mobility Parameter
2.4. Parameter
3. Results
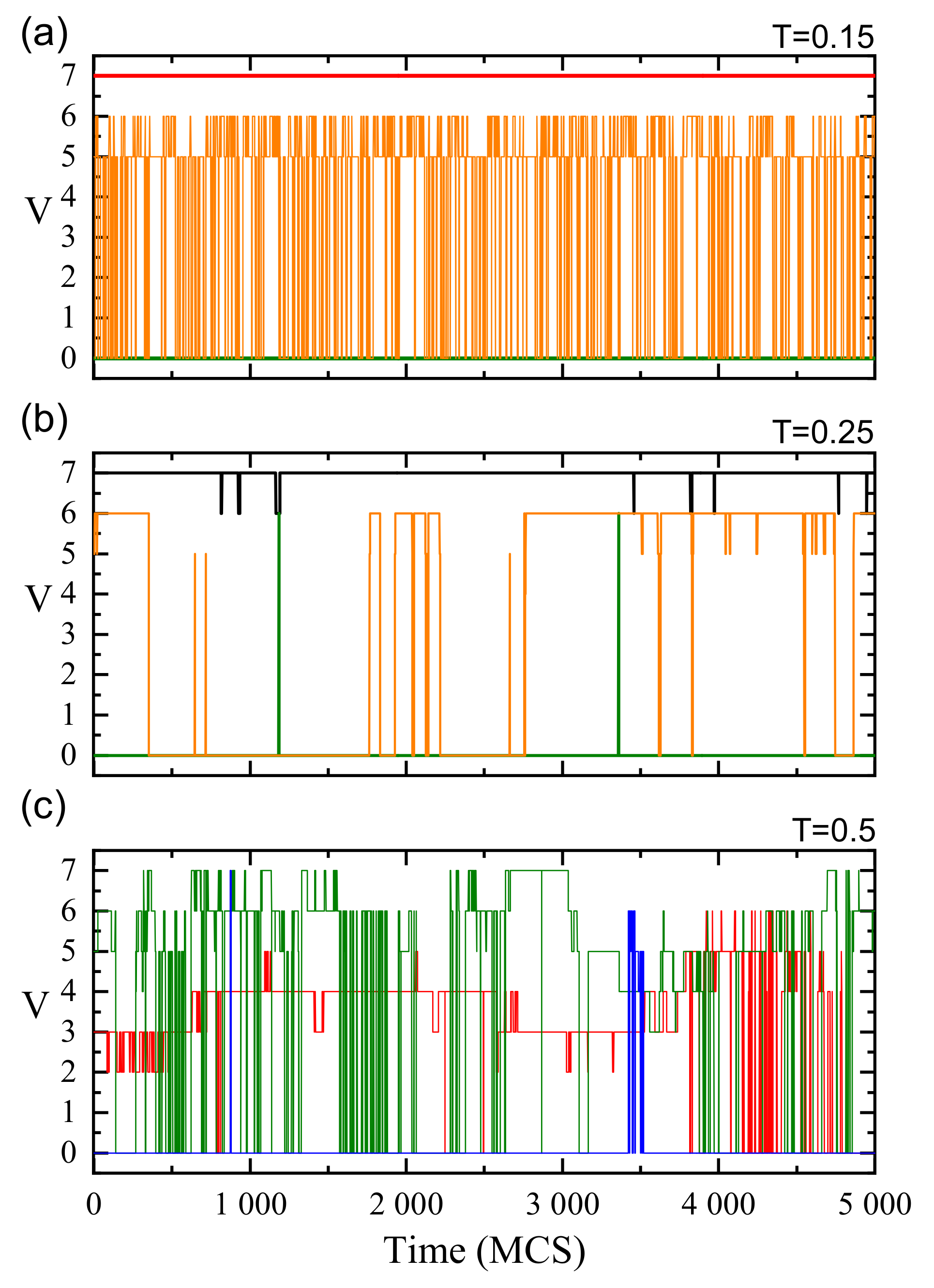
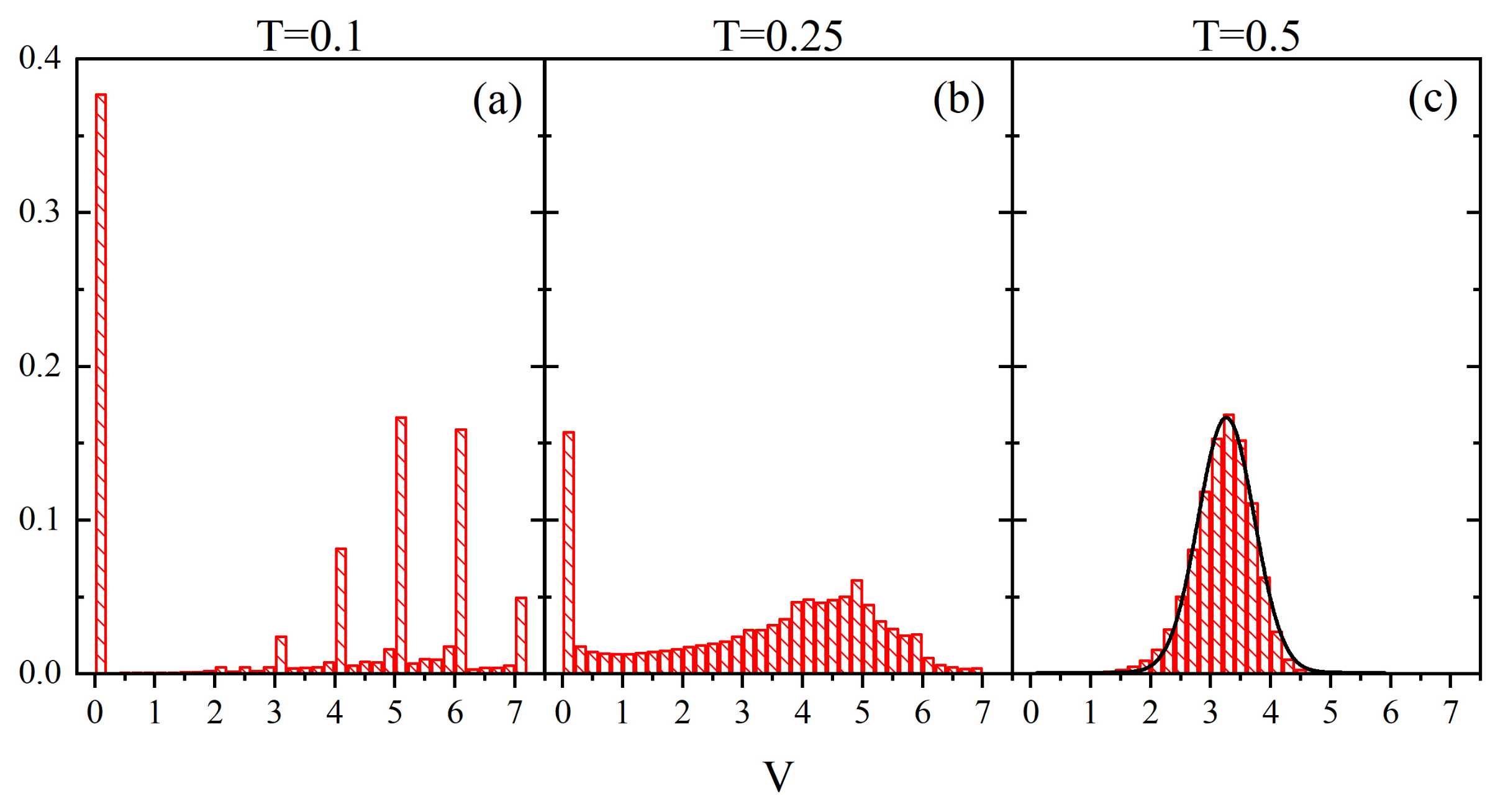
3.1. Evolution in Time of Local Free Volume: Parameter
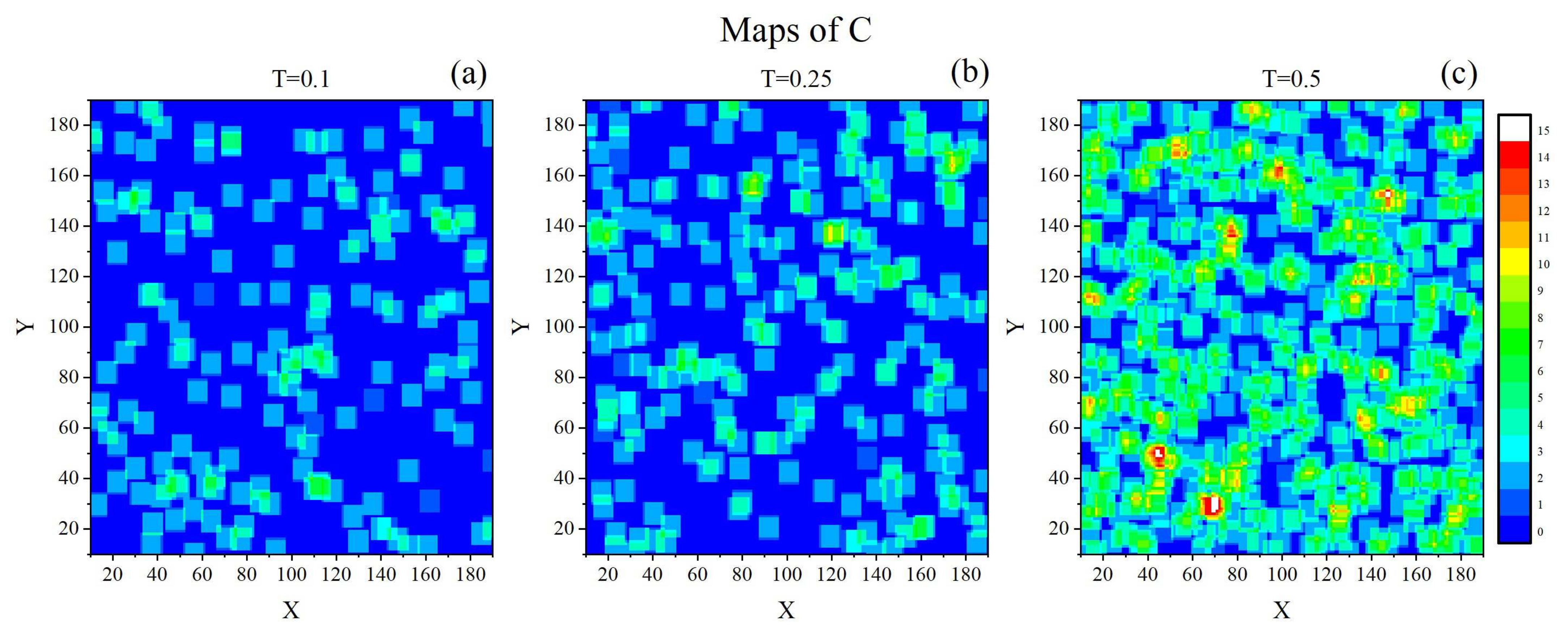
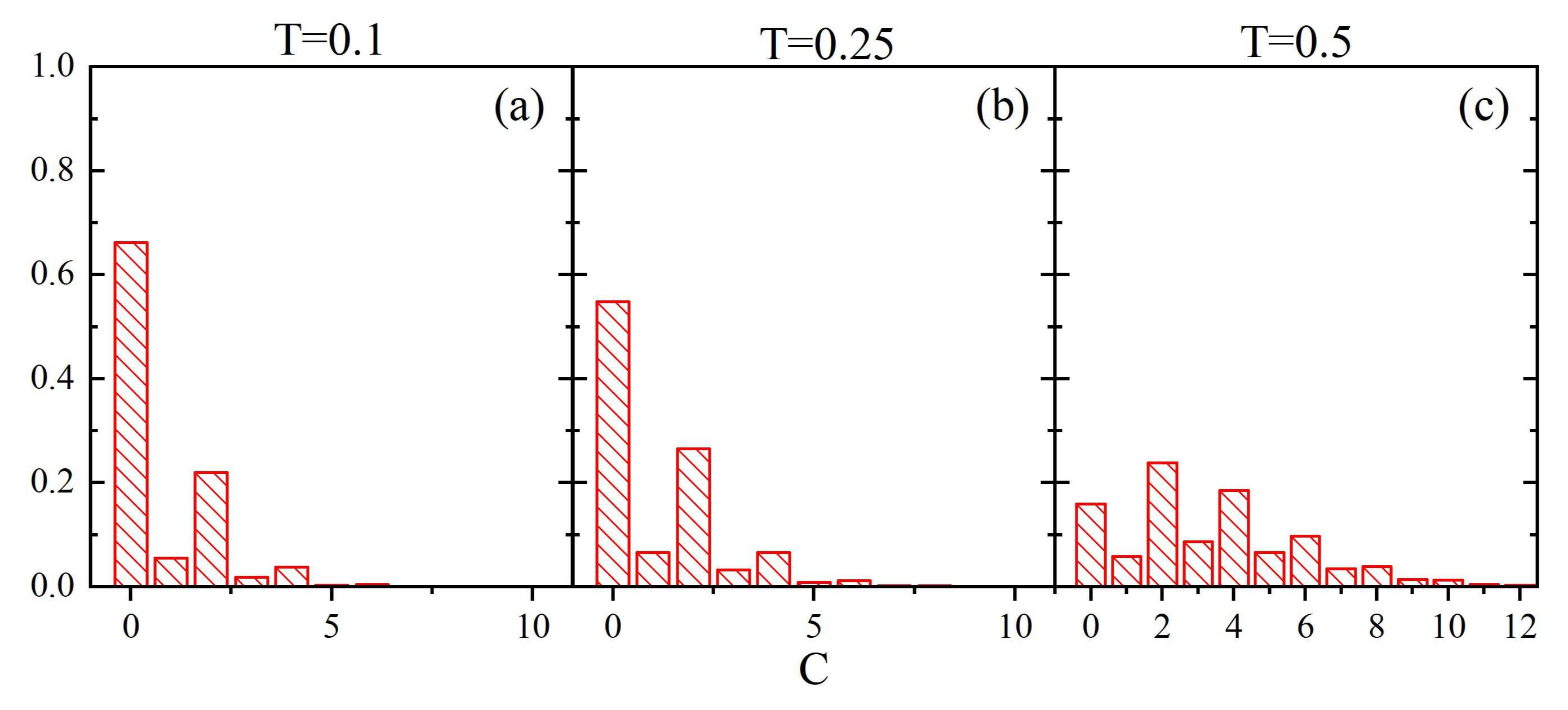
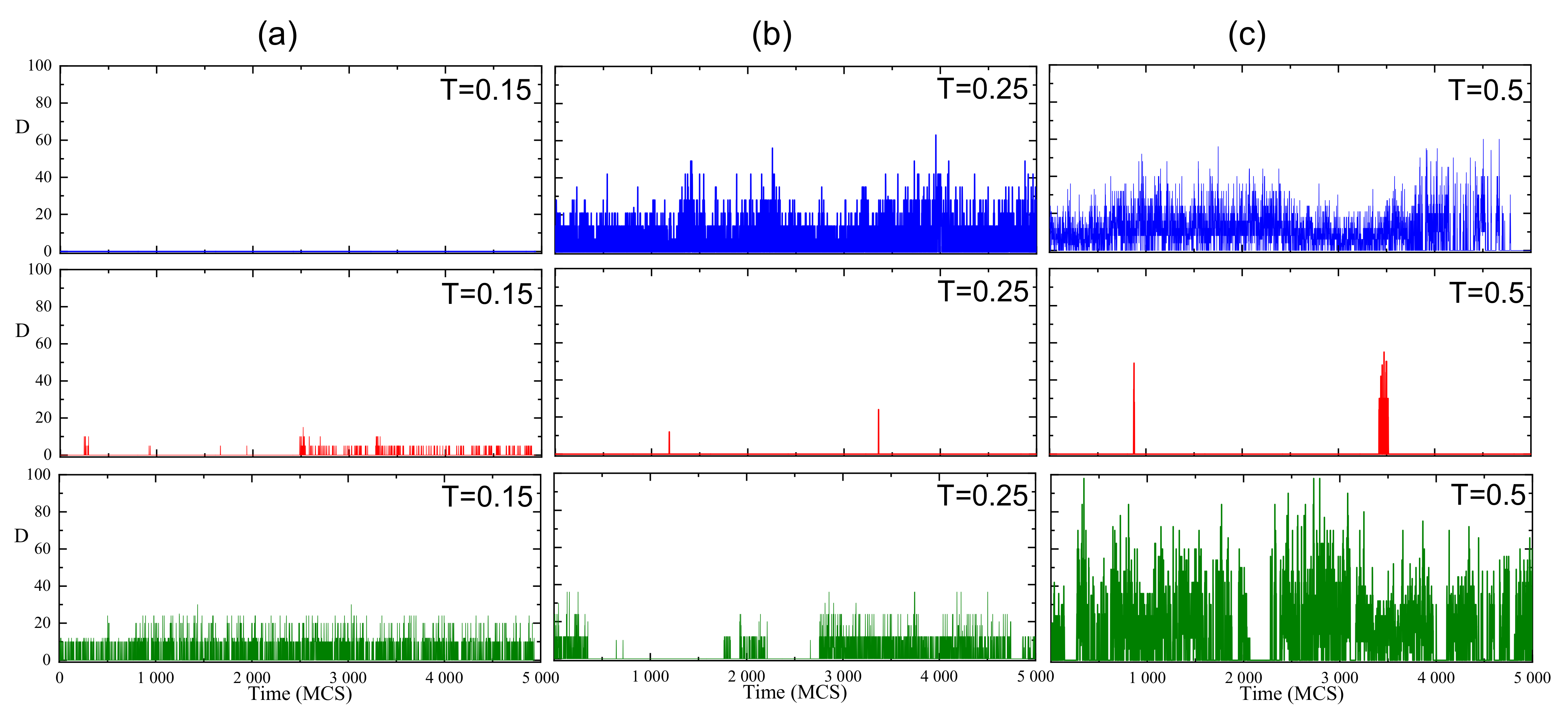
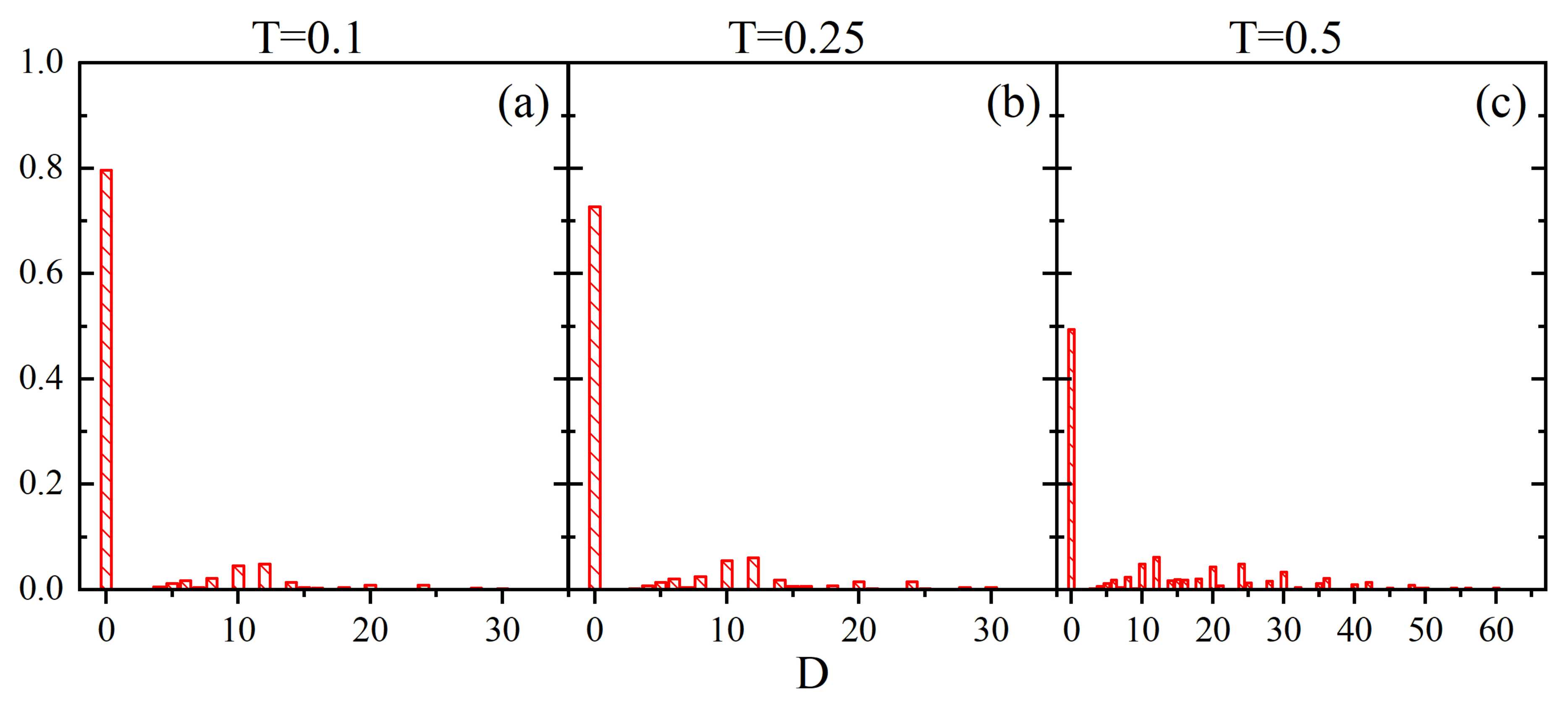
3.2. Evolution in Time of Local Mobility Parameter
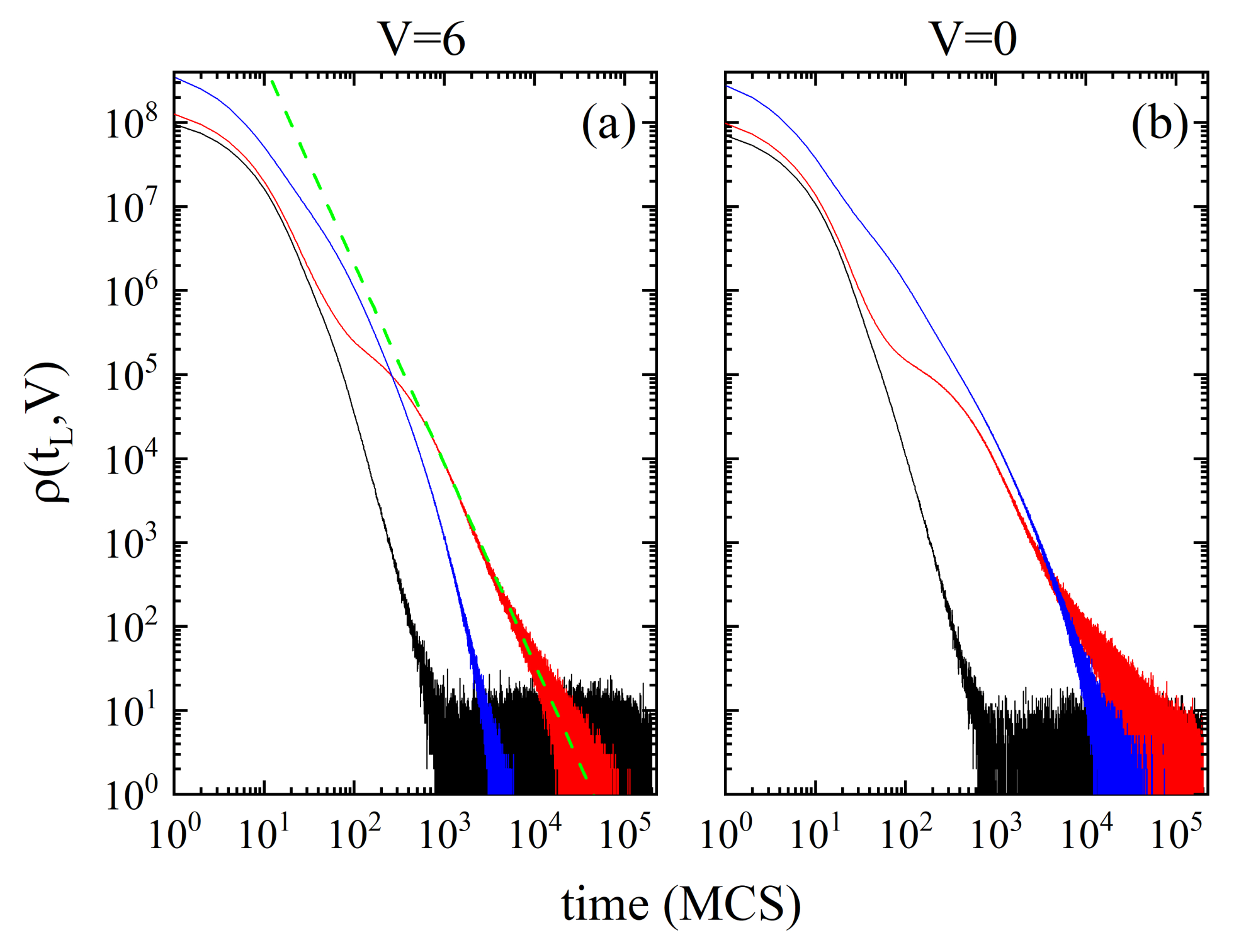
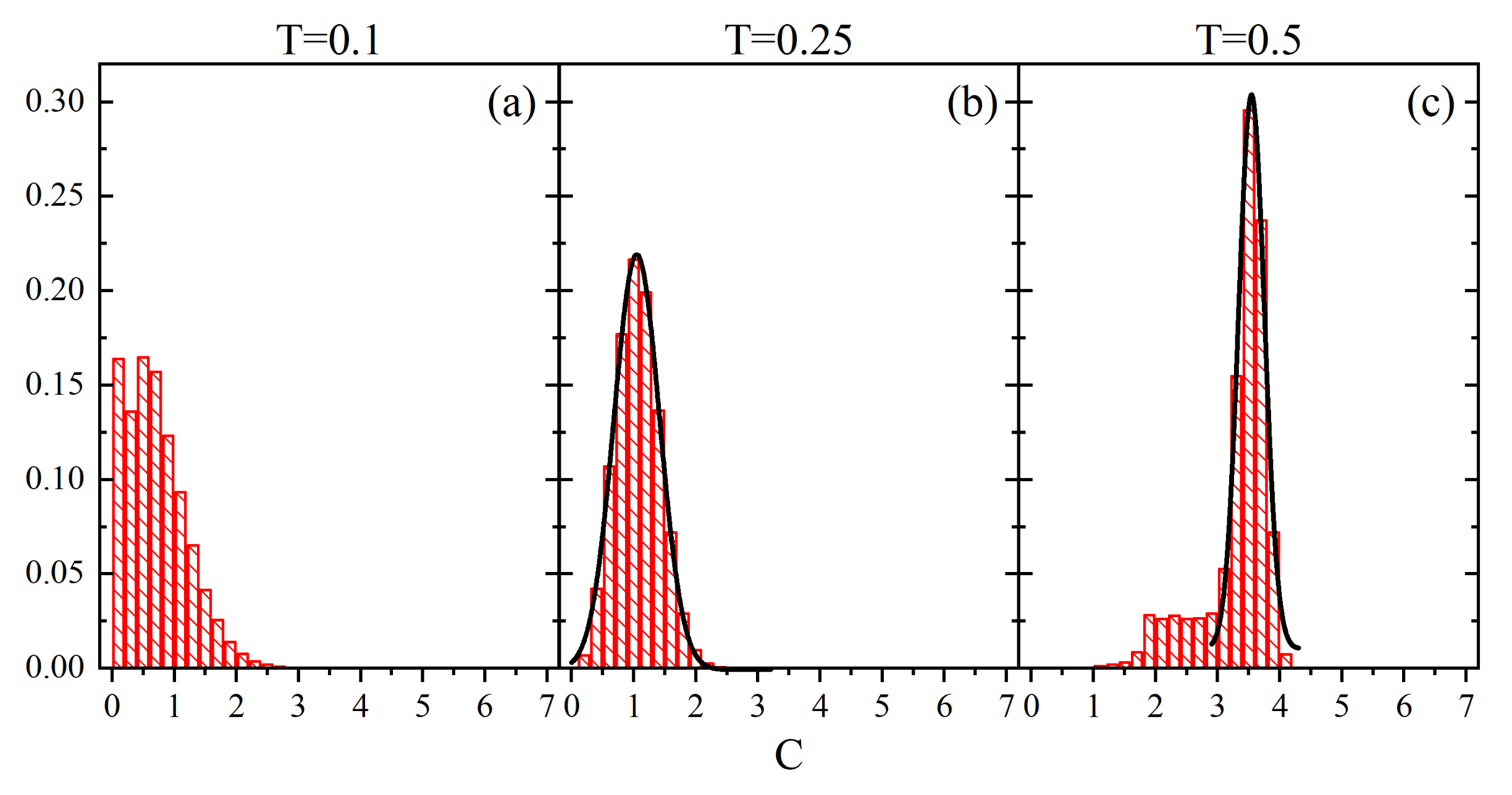
3.3. Parameter
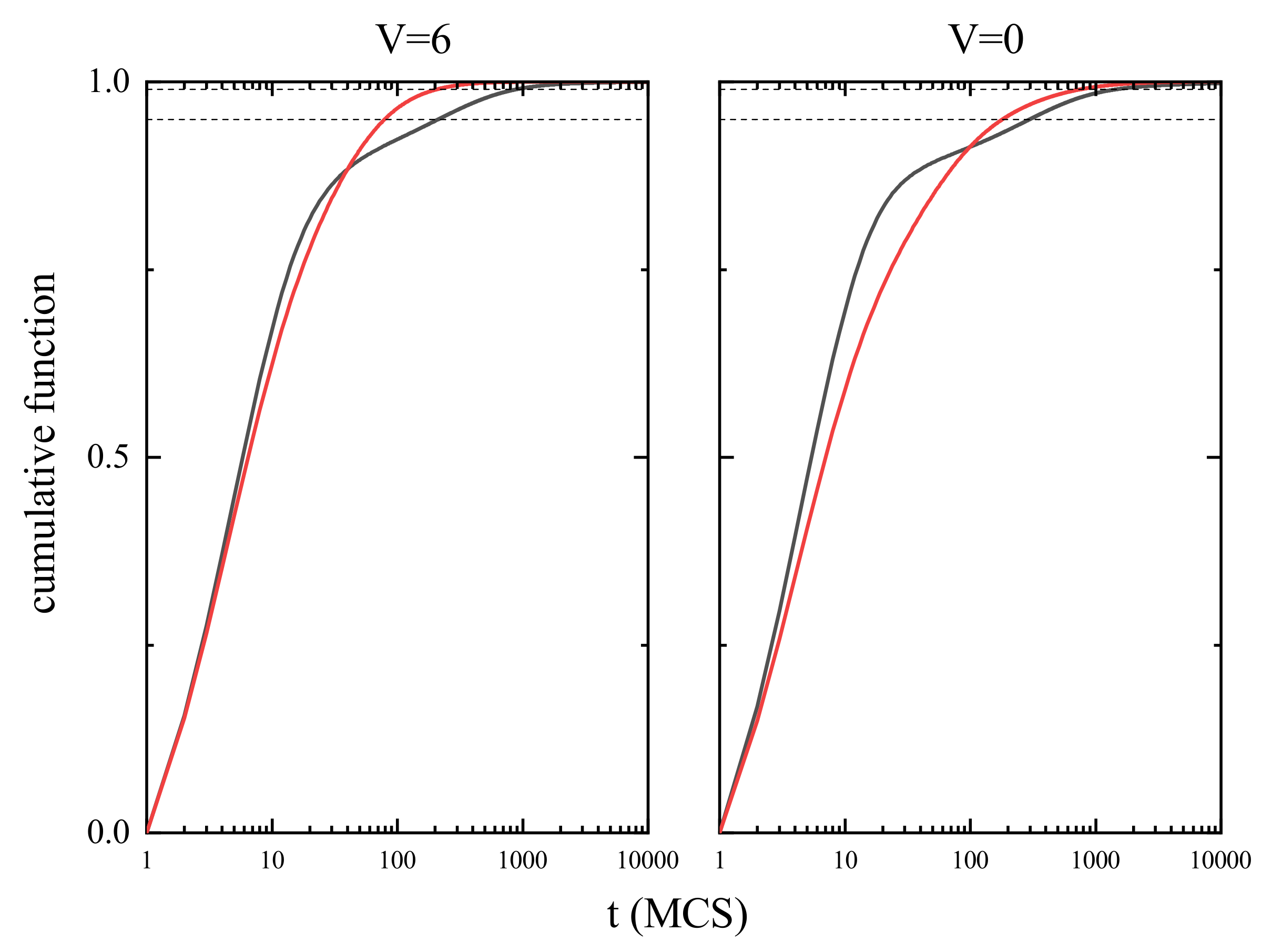
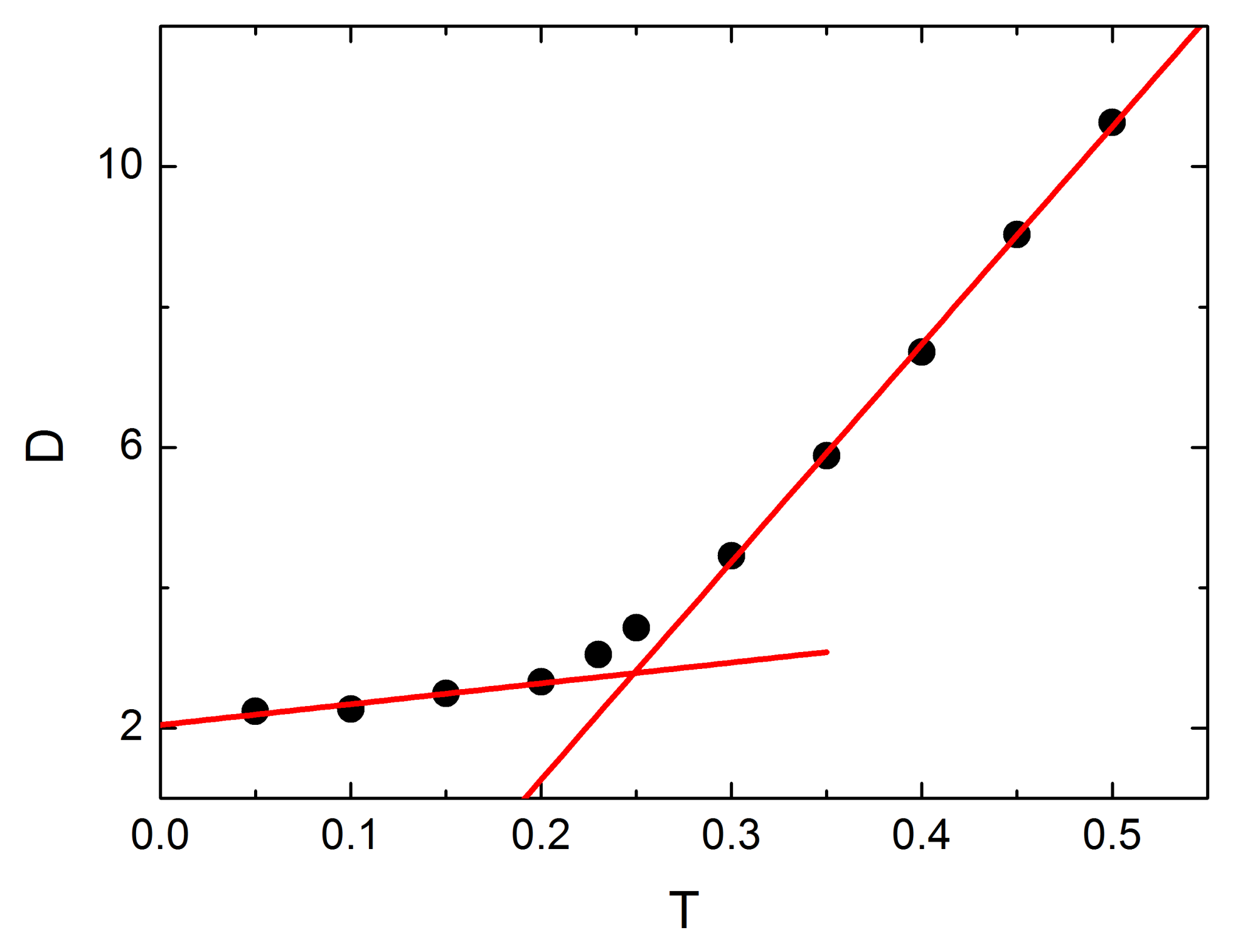
3.4. Localization of Glass Transition
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynaics; Oxford Univesity Press: New York, NY, USA, 1986. [Google Scholar]
- Binder, K. Monte Carlo and Molecular Dynamics Simulations in Polymer Science; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Kremer, K. Computer Simulations for Macromolecular Science. Macromol. Chem. Phys. 2003, 204, 257–264. [Google Scholar] [CrossRef]
- Binder, K.; Ciccotti, G. Monte Carlo and Molecular Dynamics of Condensed Matter Systems; Italian Physical Society: Bologna, Italy, 1996. [Google Scholar]
- Carmesin, I.; Kremer, K. The Bond Fluctuation Method: A New Effective Algorithm for the Dynamics of Polymers in All Spatial Dimensions. Macromolecules 1988, 21, 2819–2823. [Google Scholar] [CrossRef]
- Wittmann, H.-P.; Kremer, K. Vectorized version of the bond fluctuation method for lattice polymers. Comp. Phys. Commun. 1990, 61, 309–330. [Google Scholar] [CrossRef]
- Paul, W.; Binder, K.; Heermann, D.; Kremer, K. Dynamics of polymer solutions and melts. Reptation predictions and scaling of relaxation Times. J. Chem. Phys. 1991, 95, 7726. [Google Scholar] [CrossRef]
- Deutsch, H.; Dickman, R. Equation of state for athermal lattice chains in a 3d fluctuating bond model. J. Chem. Phys. 1990, 93, 8983. [Google Scholar] [CrossRef]
- Deutsch, H.-P.; Binder, K. Interdiffusion and self-diffusion in polymer mixtures: A Monte Carlo study. J. Chem. Phys. 1991, 94, 2294–2304. [Google Scholar] [CrossRef]
- Paul, W.; Binder, K.; Heermann, D.; Kremer, K. Crossover scaling in semidilute polymer solutions: A Monte Carlo test. J. Phys. II 1991, 1, 37. [Google Scholar] [CrossRef]
- Muller, M.; Paul, W. Measuring the chemical potential of polymer solutions and melts in computer simulations. J. Chem. Phys. 1994, 100, 719. [Google Scholar] [CrossRef]
- Wilding, N.; Muller, M. Accurate measurements of the chemical potential of polymeric systems by Monte Carlo simulation. J. Chem. Phys. 1994, 101, 4324. [Google Scholar] [CrossRef]
- Muller, M.; Binder, K.; Schafer, L. Intra- and Interchain Correlations in Semidilute Polymer Solutions: Monte Carlo Simulations and Renormalization Group Results. Macromolecules 2000, 33, 4568. [Google Scholar] [CrossRef]
- Stukan, M.; Ivanov, V.; Muller, M.; Paul, W.; Binder, K. Finite size effects in pressure measurements for Monte Carlo simulations of lattice polymer models. J. Chem. Phys. 2002, 117, 9934. [Google Scholar] [CrossRef]
- Wittmer, J.P.; Meyer, H.; Baschnagel, J.; Johner, A.; Obukhov, S.P.; Mattioni, L.; Muller, M.; Semenov, A.N. Long Range Bond-Bond Correlations in Dense Polymer Solutions. Phys. Rev. Lett. 2004, 93, 147801. [Google Scholar] [CrossRef] [PubMed]
- Wittmer, J.P.; Beckrich, P.; Johner, A.; Semenov, A.N.; Obukhov, S.P.; Meyer, H.; Baschnagel, J. Why polymer chains in a melt are not random walks. Europhys. Lett. 2007, 77, 56003. [Google Scholar] [CrossRef]
- Beckrich, P.; Johner, A.; Semenov, A.N.; Obukhov, S.P.; Benoit, H.; Wittmer, J.P. Intramolecular Form Factor in Dense Polymer Systems: Systematic Deviations from the Debye Formula. Macromolecules 2007, 40, 3805. [Google Scholar] [CrossRef]
- Wittmer, J.P.; Beckrich, P.; Meyer, H.; Cavallo, A.; Johner, A.; Baschnagel, J.; Johner, A.; Semenov, A.N.; Obukhov, S.P.; Benoit, H. Intramolecular long-range correlations in polymer melts: The segmental size distribution and its moments. Phys. Rev. E 2007, 76, 011803. [Google Scholar] [CrossRef]
- Meyer, H.; Wittmer, J.P.; Kreer, T.; Beckrich, P.; Johner, A.; Farago, J.; Baschnagel, J. Static Rouse modes and related quantities: Corrections to chain ideality in polymer melts. Eur. Phys. J. E 2008, 26, 25. [Google Scholar] [CrossRef] [PubMed]
- Muller, M.; Wittmer, J.P.; Cates, M.E. Topological effects in ring polymers: A computer simulation study. Phys. Rev. E 1996, 53, 5063. [Google Scholar] [CrossRef]
- Muller, M.; Wittmer, J.P.; Barrat, J.-L. On two intrinsic length scales in polymer physics: Topological constraints vs. entanglement length. Europhys. Lett. 2000, 52, 406. [Google Scholar] [CrossRef]
- Muller, M. Miscibility behavior and single chain properties in polymer blends: A bond fluctuation model study. Macromol. Theory Simul. 1999, 8, 343. [Google Scholar] [CrossRef]
- Cavallo, A.; Muller, M.; Binder, K. Anomalous scaling of the critical temperature of unmixing with chain length for two-dimensional polymer blends. Europhys. Lett. 2003, 61, 214. [Google Scholar] [CrossRef]
- Sommer, J.-U.; Saalwachter, K. Segmental order in end-linked polymer networks: A Monte Carlo study. Eur. Phys. J. E 2005, 18, 167. [Google Scholar] [CrossRef]
- Binder, K.; Baschnagel, J.; Paul, W. Glass transition of polymer melts: Test of theoretical concepts by computer simulation. Prog. Polym. Sci. 2003, 28, 115. [Google Scholar] [CrossRef]
- Baschnagel, J.; Binder, K.; Wittmann, H.-P. The influence of the cooling rate on the glass transition and the glassy state in three-dimensional dense polymer melts: A Monte Carlo study. J. Phys. Condens. Matter 1993, 5, 1597. [Google Scholar] [CrossRef]
- Wittmann, H.-P.; Kremer, K.; Binder, K. Glass transition of polymer melts: A two-dimensional Monte Carlo study in the framework of the bond fluctuation method. J. Chem. Phys. 1996, 96, 6291. [Google Scholar] [CrossRef]
- Deutsch, H.-P.; Binder, K. Critical Behavior and Crossover Scaling in Symmetric Polyme Mixtures: A Monte Carlo Investigation. Macromolecules 1992, 25, 6214–6230. [Google Scholar] [CrossRef]
- Werner, A.; Schmid, F.; Muller, M. Monte Carlo simulations of copolymers at homopolymer interfaces: Interfacial structure as a function of the copolymer density. J. Chem. Phys. 1999, 110, 5370. [Google Scholar] [CrossRef]
- Wittmer, J.; Johner, A.; Joanny, J.F.; Binder, K. Chain desorption from a semidilute polymer brush: A Monte Carlo simulation. J. Chem. Phys. 1994, 101, 4379. [Google Scholar] [CrossRef]
- Kopf, A.; Baschnagel, J.; Wittmer, J.; Binder, K. On the Adsorption Process in Polymer Brushes: A Monte Carlo Study. Macromolecules 1996, 29, 1433. [Google Scholar] [CrossRef]
- Wittmer, J.P.; Cates, M.E.; Johner, A.; Turner, M.S. Diffusive growth of a polymer layer by in situ polymerization. Europhys. Lett. 1996, 33, 397. [Google Scholar] [CrossRef][Green Version]
- Lang, M.; Werner, M.; Dockhorn, R.; Kreer, T. Arm Retraction Dynamics in Dense Polymer Brushes. Macromolecules 2016, 49, 5190–5201. [Google Scholar] [CrossRef]
- Lang, M.; Hoffmann, M.; Dockhorn, R.; Werner, M.; Sommer, J.-U. Fluctuation driven height reduction of crosslinked polymer brushes: A Monte Carlo study. J. Chem. Phys. 2013, 139, 164903. [Google Scholar] [CrossRef] [PubMed]
- Lai, P.-Y.; Binder, K. Structure and dynamics of grafted polymer layers: A Monte Carlo simulation. J. Chem. Phys. 1991, 95, 9288. [Google Scholar] [CrossRef]
- Lai, P.-Y. Grafted polymer layers with chain exchange: A Monte Carlo simulation. J. Chem. Phys. 1993, 98, 669. [Google Scholar] [CrossRef]
- Khalatur, P.; Khokhlov, A.; Prokhorova, S.; Sheiko, S.; Moller, M.; Reineker, P.; Shirvanyanz, D. Unusual conformation of molecular cylindrical brushes strongly adsorbed on a flat solid Surface. Eur. Phys. J. E 2000, 1, 99. [Google Scholar] [CrossRef]
- Mischler, C.; Baschnagel, J.; Binder, K. Polymer films in the normal-liquid and supercooled state: A review of recent Monte Carlo simulation results. Adv. Colloid Interface Sci. 2001, 94, 197. [Google Scholar] [CrossRef]
- Cavallo, A.; Müller, M.; Wittmer, J.P.; Johner, A. Single chain structure in thin polymer films: Corrections to Flory’s and Silberberg’s hypotheses. J. Phys. Condens. Matter. 2005, 17, S1697. [Google Scholar] [CrossRef]
- Wittmer, J.P.; Milchev, A.; Cates, M.E. Dynamical Monte Carlo study of equilibrium polymers: Static properties. J. Chem. Phys. 1998, 109, 834. [Google Scholar] [CrossRef]
- Wittmer, J.P.; Beckrich, P.; Crevel, F.; Huang, C.C.; Cavallo, A.; Kreer, T.; Meyer, H. Are polymer melts “ideal”? Comput. Phys. Commun. 2007, 177, 146. [Google Scholar] [CrossRef][Green Version]
- Cavallo, A.; Muller, M.; Binder, K. Formation of Micelles in Homopolymer-Copolymer Mixtures: Quantitative Comparison between Simulations of Long Chains and Self- Consistent Field Calculations. Macromolecules 2006, 39, 9539. [Google Scholar] [CrossRef]
- Cavallo, A.; Muller, M.; Binder, K. Monte Carlo Simulation of a Homopolymer-Copolymer Mixture Interacting with a Surface: Bulk versus Surface Micelles and Brush Formation. Macromolecules 2008, 41, 4937. [Google Scholar] [CrossRef]
- Wengenmayr, M.; Dockhorn, R.; Sommer, J.-U. Multicore Unimolecular Structure Formation in Single Dendritic-Linear Copolymers under Selective Solvent Conditions. Macromolecules 2016, 49, 9215–9227. [Google Scholar] [CrossRef]
- Lang, M.; Müller, T. Analysis of the Gel Point of Polymer Model Networks by Computer Simulations. Macromolecules 2020, 53, 498–512. [Google Scholar] [CrossRef]
- Muller, T.; Sommer, J.-U.; Lang, M. Tendomers—Force sensitive bis-rotaxanes with jump-like deformation behavior. Soft Matter 2019, 15, 3671–3679. [Google Scholar] [CrossRef] [PubMed]
- Rabbel, H.; Breier, P.; Sommer, J.-U. Swelling Behavior of Single-Chain Polymer Nanoparticles: Theory and Simulation. Macromolecules 2017, 50, 7410–7418. [Google Scholar] [CrossRef]
- Lang, M.; Schwenke, K.; Sommer, J.-U. Short Cyclic Structures in Polymer Model Networks: A Test of Mean Field Approximation by Monte Carlo Simulations. Macromolecules 2012, 45, 4886–4895. [Google Scholar] [CrossRef]
- Lang, M.; Fischer, J.; Werner, M.; Sommer, J.-U. Olympic Gels: Concatenation and Swelling. Macromol. Symp. 2015, 358, 140–147. [Google Scholar] [CrossRef]
- Fischer, J.; Lang, M.; Sommer, J.-U. The formation and structure of Olympic gels. J. Chem. Phys. 2015, 143, 243114. [Google Scholar] [CrossRef]
- Lang, M.; Fischer, J.; Werner, M.; Sommer, J.-U. Swelling of Olympic Gels. PRL 2014, 112, 238001. [Google Scholar] [CrossRef]
- Dockhorn, R.; Pluuschke, L.; Geisler, M.; Zessin, J.; Lindner, P.; Mundil, R.; Merna, J.; Sommer, J.-U.; Lederer, A. Polyolefins Formed by Chain Walking Catalysis—A Matter of Branching Density Only? J. Am. Chem. Soc. 2019, 141, 15586–15596. [Google Scholar] [CrossRef]
- Jurjiu, A.; Dockhorn, R.; Mironova, O.; Sommer, J.-U. Two universality classes for random hyperbranched polymers. Soft Matter 2014, 10, 4935–4946. [Google Scholar] [CrossRef]
- Wengenmayr, M.; Dockhorn, R.; Sommer, J.-U. Dendrimers in Solution of Linear Polymers: Crowding Effects. Macromolecules 2019, 52, 2616–2626. [Google Scholar] [CrossRef]
- Klos, J.S.; Sommer, J.-U. Dendrimer solutions: A Monte Carlo study. Soft Matter 2016, 12, 9007–9013. [Google Scholar] [CrossRef]
- Sommer, J.-U.; Klos, J.S.; Mironova, O. Adsorption of branched and dendritic polymers onto flat surfaces: A Monte Carlo study. J. Chem. Phys. 2013, 139, 244903. [Google Scholar] [CrossRef]
- Klos, J.S.; Sommer, J.-U. Simulations of Terminally Charged Dendrimers with Flexible Spacer Chains and Explicit Counterions. Macromolecules 2010, 43, 4418–4427. [Google Scholar] [CrossRef]
- Checkervarty, A.; Werner, M.; Sommer, J.-U. Formation and stabilization of pores in bilayermembranes by peptide-like amphiphilic polymers. Soft Matter 2018, 14, 2526–2534. [Google Scholar] [CrossRef] [PubMed]
- Rabbel, H.; Werner, M.; Sommer, J.-U. Interactions of Amphiphilic Triblock Copolymers with Lipid Membranes: Modes of Interaction and Effect on Permeability Examined by Generic Monte Carlo Simulations. Macromolecules 2015, 48, 4724–4732. [Google Scholar] [CrossRef]
- Werner, M.; Sommer, J.-U. Translocation and Induced Permeability of Random AmphiphilicCopolymers Interacting with Lipid Bilayer Membranes. Biomacromolecules 2015, 16, 125–135. [Google Scholar] [CrossRef] [PubMed]
- Sommer, J.-U.; Werner, M.; Baulin, V.A. Critical adsorption controls translocation of polymer chains through lipid bilayers and permeation of solvent. EPL 2012, 98, 18003. [Google Scholar] [CrossRef][Green Version]
- Baschnagel, J.; Wittmer, J.P.; Meyer, H. From Synthetic Polymers to Proteins. Comput. Soft Matter 2004, 23, 83. [Google Scholar]
- Muller, M. Handbook of Materials Modeling; Springer: New Yorkg, NY, USA, 2005. [Google Scholar]
- Wittmer, J.P.; Cavallo, A.; Kreer, T.; Baschnagel, J.; Johner, A. A finite excluded volume bond-fluctuation model: Static properties of dense polimer melts revisited. J. Chem. Phys. 2009, 131, 064901. [Google Scholar] [CrossRef]
- Wittmer, J.P.; Paul, W.; Binder, K. Rouse and reptation dynamics at finite temperatures: A Monte Carlo simulation. Macromolecules 1992, 25, 7211. [Google Scholar] [CrossRef]
- Kreer, T.; Baschnagel, J.; Muller, M.; Binder, K. Monte Carlo Simulation of Long Chain Polymer Melts: Crossover from Rouse to Reptation Dynamics. Macromolecules 2001, 34, 1105. [Google Scholar] [CrossRef]
- Mattioni, L.; Wittmer, J.P.; Baschnagel, J.; Barrat, J.-L.; Luijten, E. Dynamical properties of the slithering-snake algorithm: A numerical test of the activated-reptation hypothesis. Eur. Phys. J. E 2003, 10, 369. [Google Scholar] [CrossRef]
- Azuma, R.; Takayama, H. Diffusion of single long polymers in fixed and low density matrix of obstacles confined to two dimensions. J. Chem. Phys. 1999, 111, 8666. [Google Scholar] [CrossRef][Green Version]
- Mitus, A.C.; Saphiannikova, M.; Radosz, W.; Toshchevikov, V.; Pawlik, G. Modeling of Nonlinear Optical Phenomena in Host-Guest Systems Using Bond Fluctuation Monte Carlo Model: A Review. Materials 2021, 14, 1454. [Google Scholar] [CrossRef]
- Adam, G.; Gibbs, J.H. On the temperature dependence of cooperative relaxation properties in glass-forming liquids. J. Chem. Phys. 1965, 43, 139–146. [Google Scholar] [CrossRef]
- Radosz, W.; Orlik, R.; Pawlik, G.; Mitus, A.C. On complex structure of local free volume in bond fluctuation model of polymer matrix. Polymer 2019, 177, 1–9. [Google Scholar] [CrossRef]
- Patashinski, A.Z.; Ratner, M.A.; Grzybowski, B.A.; Orlik, R.; Mitus, A.C. Heterogeneous structure, heterogeneous dynamics, and complex behavior in two-dimensional liquids. J. Phys. Chem. Lett. 2012, 3, 2431–2435. [Google Scholar] [CrossRef] [PubMed]
- Patashinski, A.Z.; Ratner, M.A.; Orlik, R.; Mitus, A.C. Nanofluidic Manifestations of Structure in Liquids: A Toy Model. J. Phys. Chem. C 2019, 123, 16787–16795. [Google Scholar] [CrossRef]
- Stanislavsky, A.; Weron, K. Stochastic tools hidden behind the empirical dielectric relaxation laws. Rep. Prog. Phys. 2017, 80, 036001. [Google Scholar] [CrossRef][Green Version]
- Metzler, R.; Klafter, J. From stretched exponential to inverse power-law: Franctional dynamics, Cole-Cole relaxation processes, and beyond. J. Non-Cryst. Solids 2002, 305, 81–87. [Google Scholar] [CrossRef]
- Vainstein, M.H.; Costa, I.V.; Morgado, R.; Oliveira, F.A. Non-exponential relaxation for anomalous diffusion. EPL 2006, 73, 726–732. [Google Scholar] [CrossRef][Green Version]
- Bohmer, R.; Ngai, K.; Angell, C.; Plazek, D. Nonexponential relaxations in strong and fragile glass formers. J. Chem. Phys. 1993, 99, 4201–4209. [Google Scholar] [CrossRef]
- Shlesinger, M.F. Fractal time in condensed matter. Annu. Rev. Phys. Chem. 1988, 39, 269–290. [Google Scholar] [CrossRef]
- Radosz, W.; Pawlik, G.; Mitus, A.C. Complex Dynamics of Photo-Switchable Guest Molecules in All-Optical Poling Close to the Glass Transition: Kinetic Monte Carlo Modeling. J. Phys. Chem. B 2018, 122, 1756–1765. [Google Scholar] [CrossRef] [PubMed]
- Pawlik, G.; Wysoczanski, T.; Mitus, A.C. Complex Dynamics of Photoinduced Mass Transport and Surface Relief Gratings Formation. Nanomaterials 2019, 9, 352. [Google Scholar] [CrossRef] [PubMed]
- Pawlik, G.; Sobolewska, A.; Miniewicz, A.; Mitus, A.C. Generic stochastic Monte Carlo model of the photoinduced mass transport in azo-polymers and fine structure of surface relief gratings. Europhys. Lett. 2014, 105, 26002. [Google Scholar] [CrossRef]
- Pawlik, G.; Mitus, A.C. Photoinduced Mass Transport in Azo-Polymers in 2D: Monte Carlo Study of Polarization Effects. Materials 2020, 13, 4724. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.N.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Pawlik, G.; Orlik, R.; Radosz, W.; Mitus, A.C.; Kuzyk, M.G. Towards understanding the photomechanical effect in polymeric fibers: Analysis of free volume in a model polymeric matrix. Proc. SPIE 2008, 2012, 84740A1. [Google Scholar]
- Pawlik, G.; Mitus, A.C.; Miniewicz, A.; Sobolewska, A.; Kajzar, F. Temperature dependence of the kinetics of diffraction gratings formation in a polymer matrix containing azobenzene chromophores: Monte Carlo simulations and experiment. Mol. Cryst. Liq. Cryst. 2005, 426, 243–252. [Google Scholar] [CrossRef]
- Pawlik, G.; Rau, I.; Kajzar, F.; Mitus, A.C. Second-harmonic generation in poled polymers: Pre-poling history paradigm. Opt. Express 2010, 18, 18793–18804. [Google Scholar] [CrossRef]
- Pawlik, G.; Mitus, A.C.; Mysliwiec, J.; Miniewicz, A.; Grote, J.G. Photochromic dye semi-intercalation into DNA-based polymeric matrix: Computer modeling and experiment. Chem. Phys. Lett. 2010, 484, 321–323. [Google Scholar] [CrossRef]
- Pawlik, G.; Radosz, W.; Mitus, A.C.; Mysliwiec, J.; Miniewicz, A.; Kajzar, F.; Rau, I. Holographic grating inscription in DR1: DNA-CTMA thin films: The puzzle of time scales. Cent. Eur. J. Chem. 2014, 12, 886–892. [Google Scholar] [CrossRef]
- Kawakatsu, K. Statistical Physics of Polymers; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Pawlik, G.; Mitus, A.C.; Miniewicz, A.; Kajzar, F. Monte Carlo simulations of temperature dependence of the kinetics of diffraction gratings formation in a polymer matrix containing azobenzene chromophores. J. Non. Opt. Phys. Mat. 2004, 13, 481–489. [Google Scholar] [CrossRef]
- Pawlik, G.; Mitus, A.C.; Rau, I.; Kajzar, F. Monte Carlo modelling of chosen non-linear optical effects for systems of guest molecules in polymeric and liquid-crystal matrices. J. Nonlinear Opt. Quantum Opt. 2009, 38, 227–244. [Google Scholar]
- Feller, W. An Introduction to Probability Theory and Its Applications; John Wiley and Sons: Hoboken, NJ, USA, 1968. [Google Scholar]
- Krauklis, A.E.; Akulichev, A.G.; Gagani, A.I.; Echtermeyer, A.T. Time–Temperature–Plasticization Superposition Principle: Predicting Creep of a Plasticized Epoxy. Polymers 2019, 11, 1848. [Google Scholar] [CrossRef]
- Lalwani, S.M.; Eneh, C.I.; Lutkenhaus, J.L. Emerging trends in the dynamics of polyelectrolyte complexes. Phys. Chem. Chem. Phys. 2020, 22, 24157. [Google Scholar] [CrossRef] [PubMed]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radosz, W.; Pawlik, G.; Mituś, A.C. Characterization of Monte Carlo Dynamic/Kinetic Properties of Local Structure in Bond Fluctuation Model of Polymer System. Materials 2021, 14, 4962. https://doi.org/10.3390/ma14174962
Radosz W, Pawlik G, Mituś AC. Characterization of Monte Carlo Dynamic/Kinetic Properties of Local Structure in Bond Fluctuation Model of Polymer System. Materials. 2021; 14(17):4962. https://doi.org/10.3390/ma14174962
Chicago/Turabian StyleRadosz, Wojciech, Grzegorz Pawlik, and Antoni C. Mituś. 2021. "Characterization of Monte Carlo Dynamic/Kinetic Properties of Local Structure in Bond Fluctuation Model of Polymer System" Materials 14, no. 17: 4962. https://doi.org/10.3390/ma14174962
APA StyleRadosz, W., Pawlik, G., & Mituś, A. C. (2021). Characterization of Monte Carlo Dynamic/Kinetic Properties of Local Structure in Bond Fluctuation Model of Polymer System. Materials, 14(17), 4962. https://doi.org/10.3390/ma14174962






