A 2D Front-Tracking Lagrangian Model for the Modeling of Anisotropic Grain Growth
Abstract
:1. Introduction
2. Numerical Method
2.1. Grain Boundary Motion by Capillarity: Anisotropic Context for the TRM Model
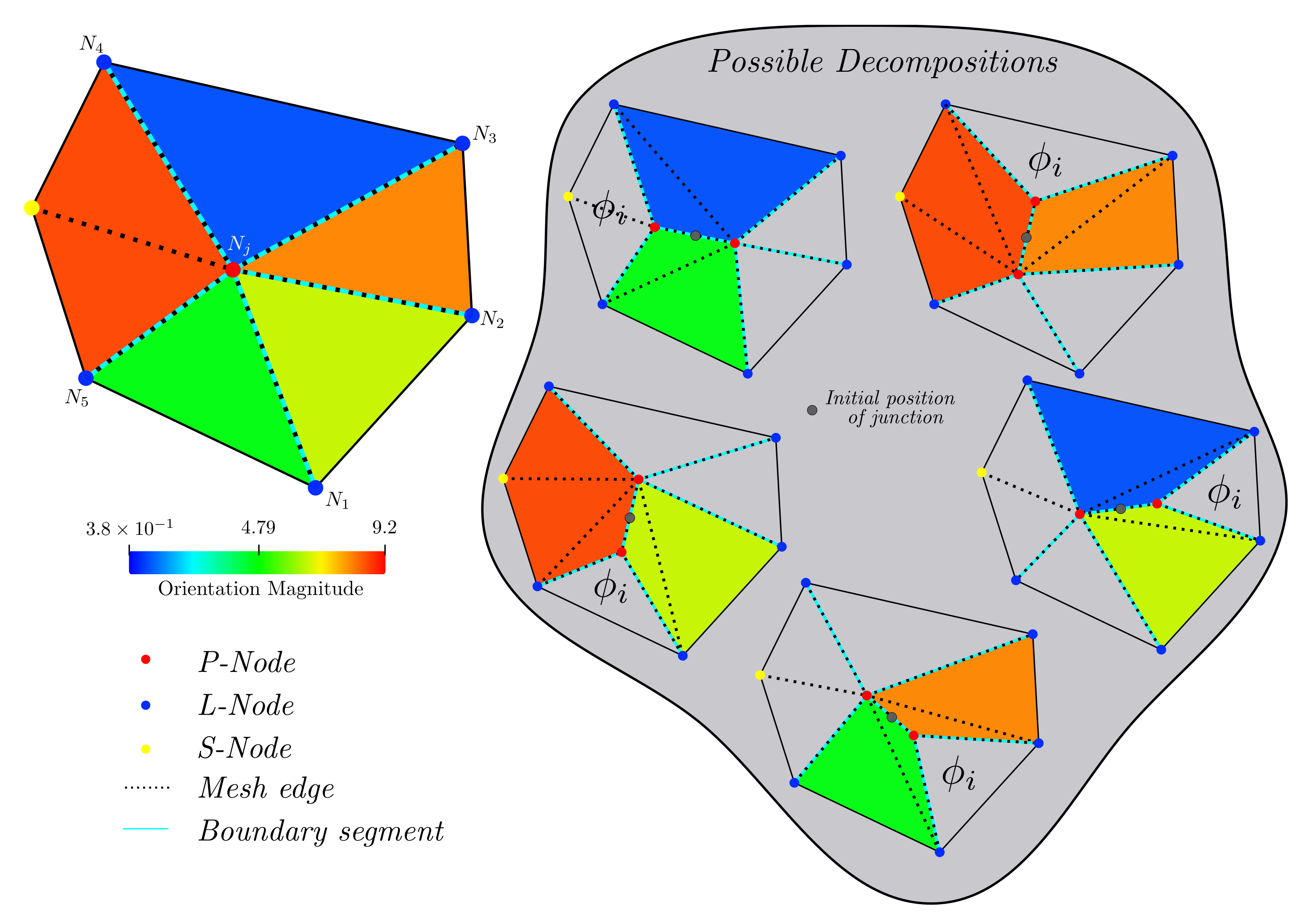
2.2. Minimal-State Energy of High-Order MJs
2.3. Algorithm for the Decomposition of High-Order Multiple Junctions
| Algorithm 1 MJ decomposition algorithm for the TRM model |
| 1: for all Points do |
| 2: if then |
| 3: ← Node representing |
| 4: ← Elements() |
| 5: ← |
| 6: ← |
| 7: ←∞ |
| 8: ← tuple |
| 9: i← 2 |
| 10: for all number of connections of : j do |
| 11: ← |
| 12: Separate from by adding a new Node |
| 13: Create new boundary (PP-Connection) |
| 14: ←∪ |
| 15: if then |
| 16: ← |
| 17: ← Elements() ∪ |
| 18: ← tuple |
| 19: if then |
| 20: Replace by |
| 21: else if then |
| 22: i← |
| 23: goto 10: |
3. Numerical Results
3.1. Triple Junction Test Case
3.2. 2D GG with Heterogeneous GB Properties
4. Discussion, Conclusions and Perspectives
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DOF | Degrees of freedom |
| DOAJ | Directory of open access journals |
| GB | Grain boundary |
| GBM | Grain boundary motion |
| GG | Grain growth |
| FE | Finite elements |
| MDPI | Multidisciplinary Digital Publishing Institute |
| MJ | Multiple junction |
| LS | Level-set |
| TRM | ToRealMotion |
| RS | Read–Shockley |
Appendix A. Computation of the Disorientation Angle
Appendix B. Sensitivity Analysis on GG Simulations: Mesh Size and Time Step



References
- Humphreys, J.; Rohrer, G.S.; Rollett, A. Recrystallization and Related Annealing Phenomena, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar] [CrossRef]
- Watanabe, T. Grain boundary engineering: Historical perspective and future prospects. J. Mater. Sci. 2011, 46, 4095–4115. [Google Scholar] [CrossRef]
- Fausty, J. Towards the Full Field Modeling and Simulation of Annealing Twins Using a Finite Element Level Set Method. Ph.D. Thesis, PSL, Mines-ParisTech, Paris, France, 2020. [Google Scholar]
- Fausty, J.; Murgas, B.; Florez, S.; Bozzolo, N.; Bernacki, M. A new level set-finite element formulation for anisotropic grain boundary migration. arXiv 2020, arXiv:2006.15531. [Google Scholar]
- Murgas, B.; Florez, S.; Bozzolo, N.; Fausty, J.; Bernacki, M. Comparative study and limits of different level-set formulations for the modeling of anisotropic grain growth. arXiv 2021, arXiv:2106.03565. [Google Scholar]
- DeWit, G.; Koehler, J.S. Interaction of Dislocations with an Applied Stress in Anisotropic Crystals. Phys. Rev. 1959, 116, 1113–1120. [Google Scholar] [CrossRef]
- Grest, G.S.; Srolovitz, D.J.; Anderson, M.P. Computer simulation of grain growth-IV. Anisotropic grain boundary energies. Acta Metall. 1985, 33, 509–520. [Google Scholar] [CrossRef]
- Fausty, J.; Bozzolo, N.; Pino Muñoz, D.; Bernacki, M. A novel Level-Set Finite Element formulation for grain growth with heterogeneous grain boundary energies. Mater. Des. 2018, 160, 578–590. [Google Scholar] [CrossRef]
- Fausty, J.; Bozzolo, N.; Bernacki, M. A 2D level set finite element grain coarsening study with heterogeneous grain boundary energies. Appl. Math. Model. 2020, 78, 505–518. [Google Scholar] [CrossRef]
- Miyoshi, E.; Takaki, T. Multi-phase-field study of the effects of anisotropic grain-boundary properties on polycrystalline grain growth. J. Cryst. Growth 2017, 474, 160–165. [Google Scholar] [CrossRef]
- Hallberg, H.; Bulatov, V.V. Modeling of grain growth under fully anisotropic grain boundary energy Modeling of grain growth under fully anisotropic grain boundary energy. Model. Simul. Mater. Sci. Eng. 2019, 27, 045002. [Google Scholar] [CrossRef]
- Barrales Mora, L.A. 2D vertex modeling for the simulation of grain growth and related phenomena. Math. Comput. Simul. 2010, 80, 1411–1427. [Google Scholar] [CrossRef]
- Elsey, M.; Esedoglu, S.; Smereka, P. Simulations of anisotropic grain growth: Efficient algorithms and misorientation distributions. Acta Mater. 2013, 61, 2033–2043. [Google Scholar] [CrossRef] [Green Version]
- Mießen, C.; Velinov, N.; Gottstein, G.; Barrales-Mora, L.A. A highly efficient 3D level-set grain growth algorithm tailored for ccNUMA architecture. Model. Simul. Mater. Sci. Eng. 2017, 25. [Google Scholar] [CrossRef] [Green Version]
- Kawasaki, K.; Nagai, T.; Nakashima, K. Vertex models for two-dimensional grain growth. Philos. Mag. B 1989, 60, 399–421. [Google Scholar] [CrossRef]
- Chang, K.; Chen, L.Q.; Krill, C.E.; Moelans, N. Effect of strong nonuniformity in grain boundary energy on 3-D grain growth behavior: A phase-field simulation study. Comput. Mater. Sci. 2017, 127, 67–77. [Google Scholar] [CrossRef] [Green Version]
- Florez, S.; Alvarado, K.; Muñoz, D.P.; Bernacki, M. A novel highly efficient Lagrangian model for massively multidomain simulation applied to microstructural evolutions. Comput. Methods Appl. Mech. Eng. 2020, 367, 113107. [Google Scholar] [CrossRef]
- Florez, S.; Fausty, J.; Alvarado, K.; Murgas, B.; Bernacki, M. Parallelization of an efficient 2D-Lagrangian model for massive multi-domain simulations. Model. Simul. Mater. Sci. Eng. 2020, 29, 065005. [Google Scholar] [CrossRef]
- Florez, S.; Alvarado, K.; Bernacki, M. A new front-tracking Lagrangian model for the modeling of dynamic and post-dynamic recrystallization. Model. Simul. Mater. Sci. Eng. 2021, 29, 035004. [Google Scholar] [CrossRef]
- Florez, S.; Alvarado, K.; Bernacki, M. Statistical behaviour of interfaces subjected to curvature flow and torque effects applied to microstructural evolutions. arXiv 2021, arXiv:2106.05605. [Google Scholar]
- Mackenzie, J.K. Second paper on statistics associated with the random disorientation of cubes. Biometrika 1958, 45, 229–240. [Google Scholar] [CrossRef]
- Herring, C. Surface tension as a motivation for sintering. In Fundamental Contributions to the Continuum Theory of Evolving Phase Interfaces in Solids; Springer: Berlin/Heidelberg, Germany, 1999; pp. 33–69. [Google Scholar]
- Stanley, R. Enumerative Combinatorics; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Merriman, B.; Bence, J.K.; Osher, S.J. Motion of Multiple Junctions: A Level Set Approach. J. Comput. Phys. 1994, 112, 334–363. [Google Scholar] [CrossRef]
- Bernacki, M.; Chastel, Y.; Coupez, T.; Logé, R.E. Level set framework for the numerical modelling of primary recrystallization in polycrystalline materials. Scr. Mater. 2008, 58, 1129–1132. [Google Scholar] [CrossRef]
- Scholtes, B.; Shakoor, M.; Settefrati, A.; Bouchard, P.O.; Bozzolo, N.; Bernacki, M. New finite element developments for the full field modeling of microstructural evolutions using the level-set method. Comput. Mater. Sci. 2015, 109, 388–398. [Google Scholar] [CrossRef]
- Read, W.T.; Shockley, W. Dislocation Models of Crystal Grain Boundaries. Phys. Rev. 1950, 78, 275–289. [Google Scholar] [CrossRef]
- Hitti, K.; Laure, P.; Coupez, T.; Silva, L.; Bernacki, M. Precise generation of complex statistical Representative Volume Elements (RVEs) in a finite element context. Comput. Mater. Sci. 2012, 61, 224–238. [Google Scholar] [CrossRef]
- Hitti, K.; Bernacki, M. Optimized Dropping and Rolling (ODR) method for packing of poly-disperse spheres. Appl. Math. Model. 2013, 37, 5715–5722. [Google Scholar] [CrossRef]
- Florez, S. Towards Highly Efficient Massive-Multidomain Simulations in the Context of Microstructural Evolutions. Ph.D. Thesis, PSL, Mines-ParisTech, Paris, France, 2020. [Google Scholar]
- Maire, L. Full Field and Mean Field Modeling of Dynamic and Post-Dynamic Recrystallization in 3D—Application to 304L Steel. Ph.D. Thesis, PSL, Mines-ParisTech, Paris, France, 2019. [Google Scholar]
- Beladi, H.; Rohrer, G.S. The relative grain boundary area and energy distributions in a ferritic steel determined from three-dimensional electron backscatter diffraction maps. Acta Mater. 2013, 61, 1404–1412. [Google Scholar] [CrossRef]
- Dapogny, C.; Dobrzynski, C.; Frey, P. Three-dimensional adaptive domain remeshing, implicit domain meshing, and applications to free and moving boundary problems. J. Comput. Phys. 2014, 262, 358–378. [Google Scholar] [CrossRef] [Green Version]
- Barrales Mora, L.; Gottstein, G.; Shvindlerman, L. Three-dimensional grain growth: Analytical approaches and computer simulations. Acta Mater. 2008, 56, 5915–5926. [Google Scholar] [CrossRef]













| Function | IS 1 | IS 2 | IS 3 | IS 4 | Mean |
|---|---|---|---|---|---|
| Homogeneous | 0 h 56 min 16 s | 0 h 55 min 16 s | 0 h 57 min 53 s | 0 h 58 min 11 s | 0 h 56 min 54 s |
| RS | 7 h 5 min 48 s | 6 h 58 min 36 s | 7 h 5 min 15 s | 7 h 0 min 17 s | 7 h 2 min 29 s |
| RS+ | 7 h 30 min 8 s | 7 h 19 min 21 s | 7 h 25 min 35 s | 7 h 21 min 25 s | 7 h 24 min 7 s |
| Gaussian | 7 h 49 min 6 s | 7 h 48 min 22 s | 7 h 50 min 28 s | 7 h 51 min 30 s | 7 h 49 min 51 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Florez, S.; Fausty, J.; Alvarado, K.; Murgas, B.; Bernacki, M. A 2D Front-Tracking Lagrangian Model for the Modeling of Anisotropic Grain Growth. Materials 2021, 14, 4219. https://doi.org/10.3390/ma14154219
Florez S, Fausty J, Alvarado K, Murgas B, Bernacki M. A 2D Front-Tracking Lagrangian Model for the Modeling of Anisotropic Grain Growth. Materials. 2021; 14(15):4219. https://doi.org/10.3390/ma14154219
Chicago/Turabian StyleFlorez, Sebastian, Julien Fausty, Karen Alvarado, Brayan Murgas, and Marc Bernacki. 2021. "A 2D Front-Tracking Lagrangian Model for the Modeling of Anisotropic Grain Growth" Materials 14, no. 15: 4219. https://doi.org/10.3390/ma14154219
APA StyleFlorez, S., Fausty, J., Alvarado, K., Murgas, B., & Bernacki, M. (2021). A 2D Front-Tracking Lagrangian Model for the Modeling of Anisotropic Grain Growth. Materials, 14(15), 4219. https://doi.org/10.3390/ma14154219






