Tetragonal–Cubic Phase Transition and Low-Field Dielectric Properties of CH3NH3PbI3 Crystals
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
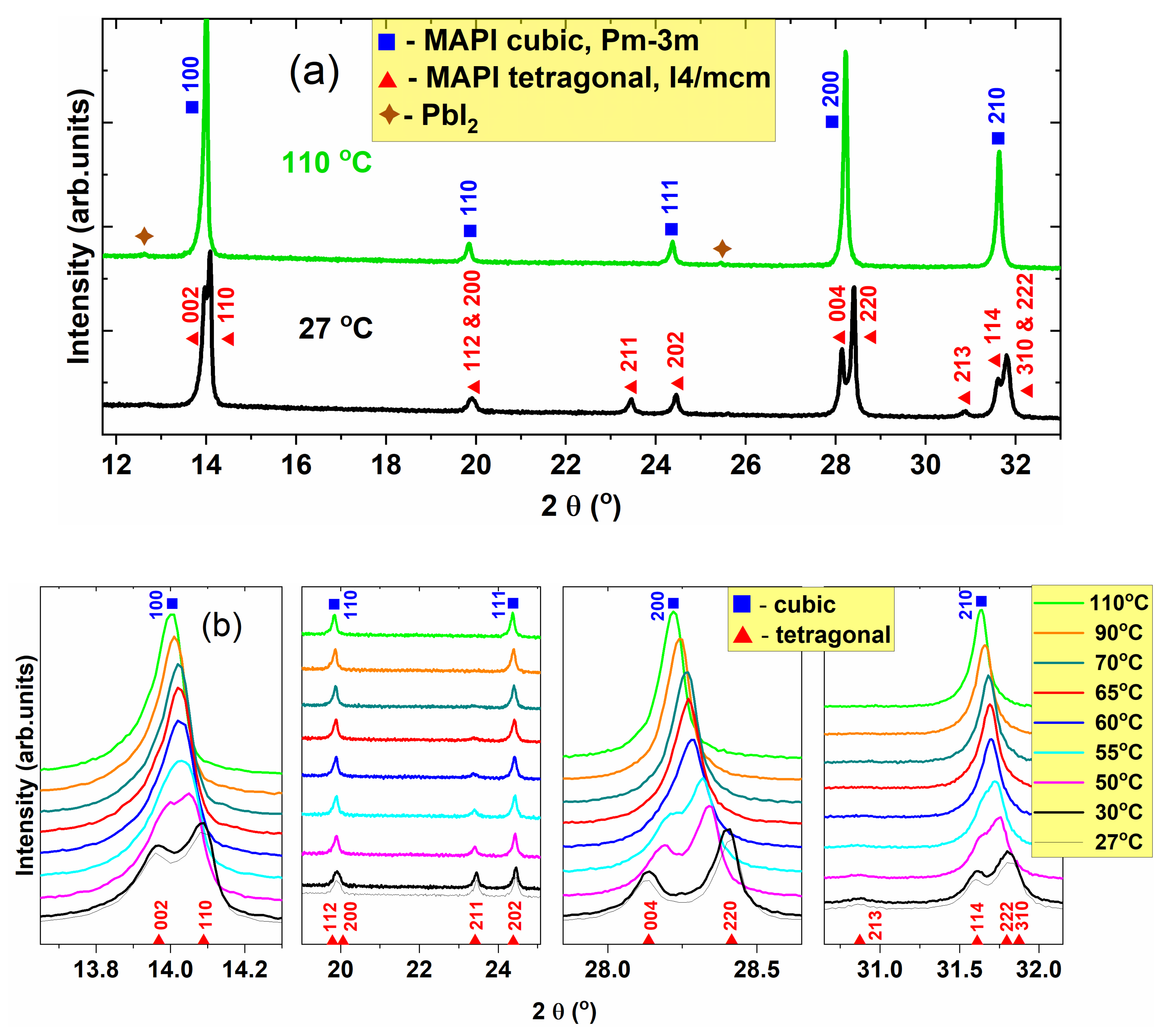
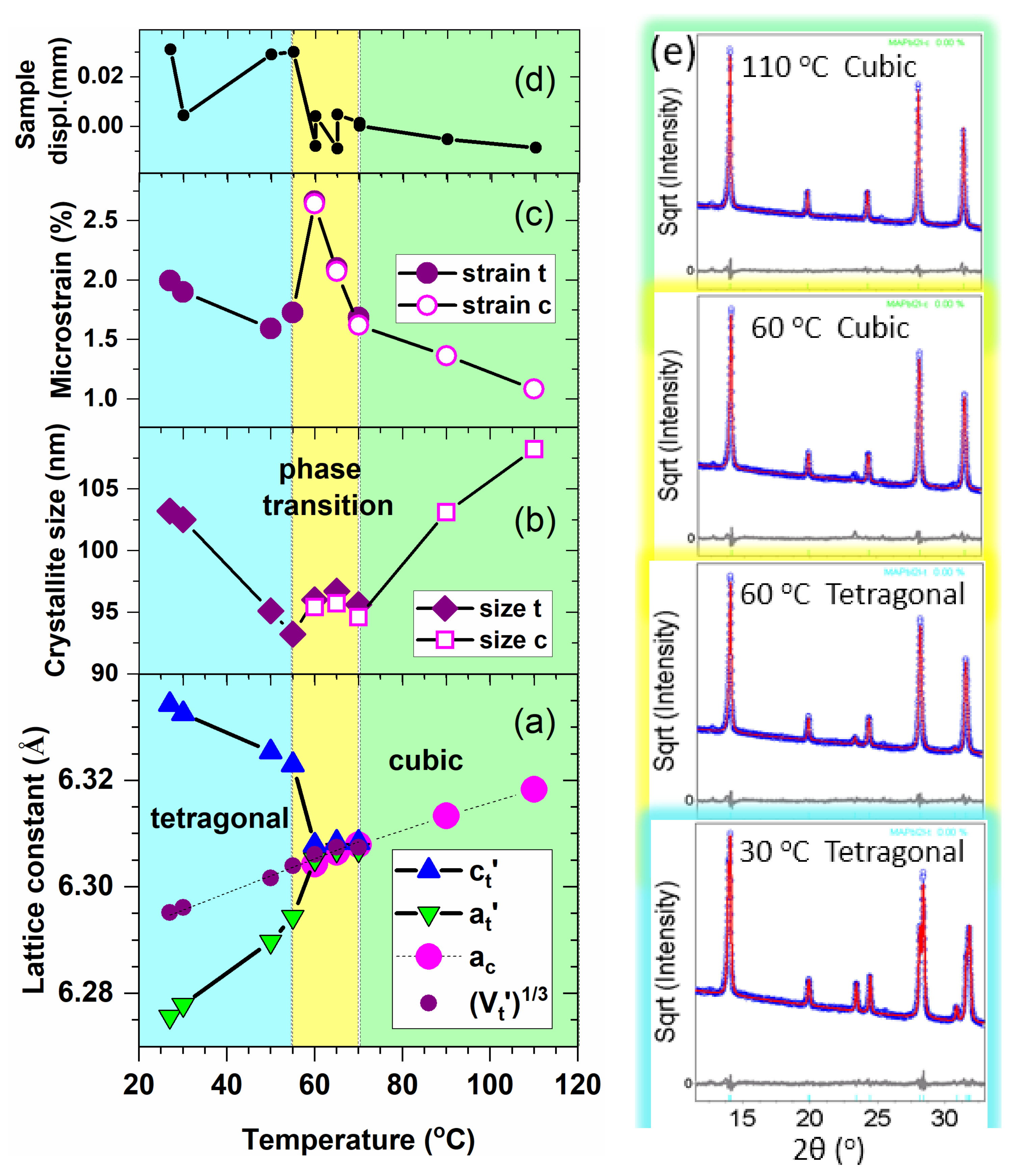
3.1. Structural and Microstructural Investigation
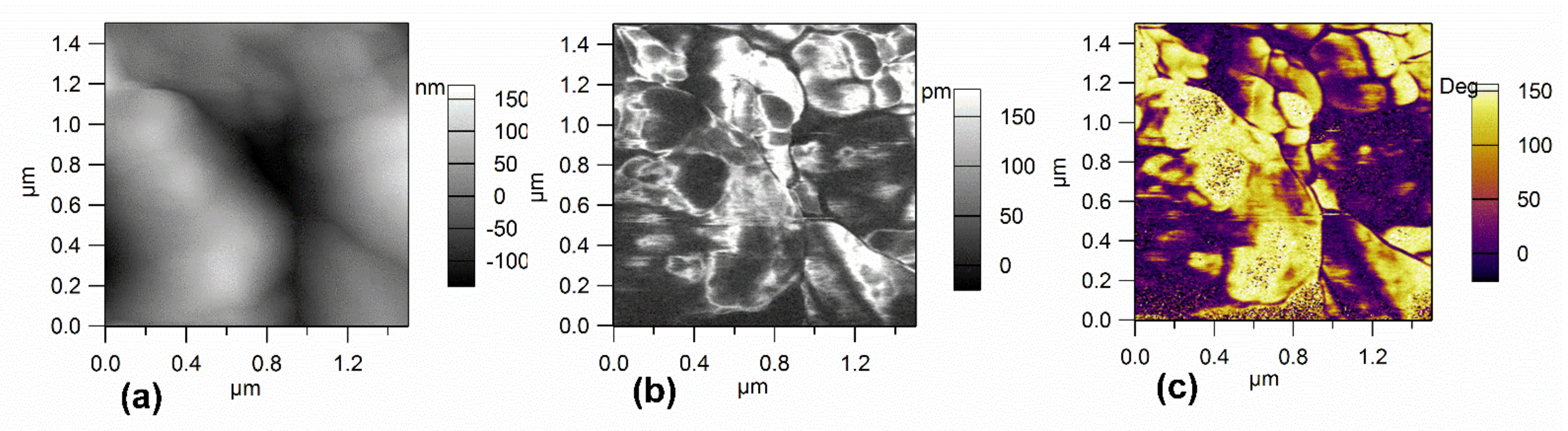
3.2. Surface Morphology
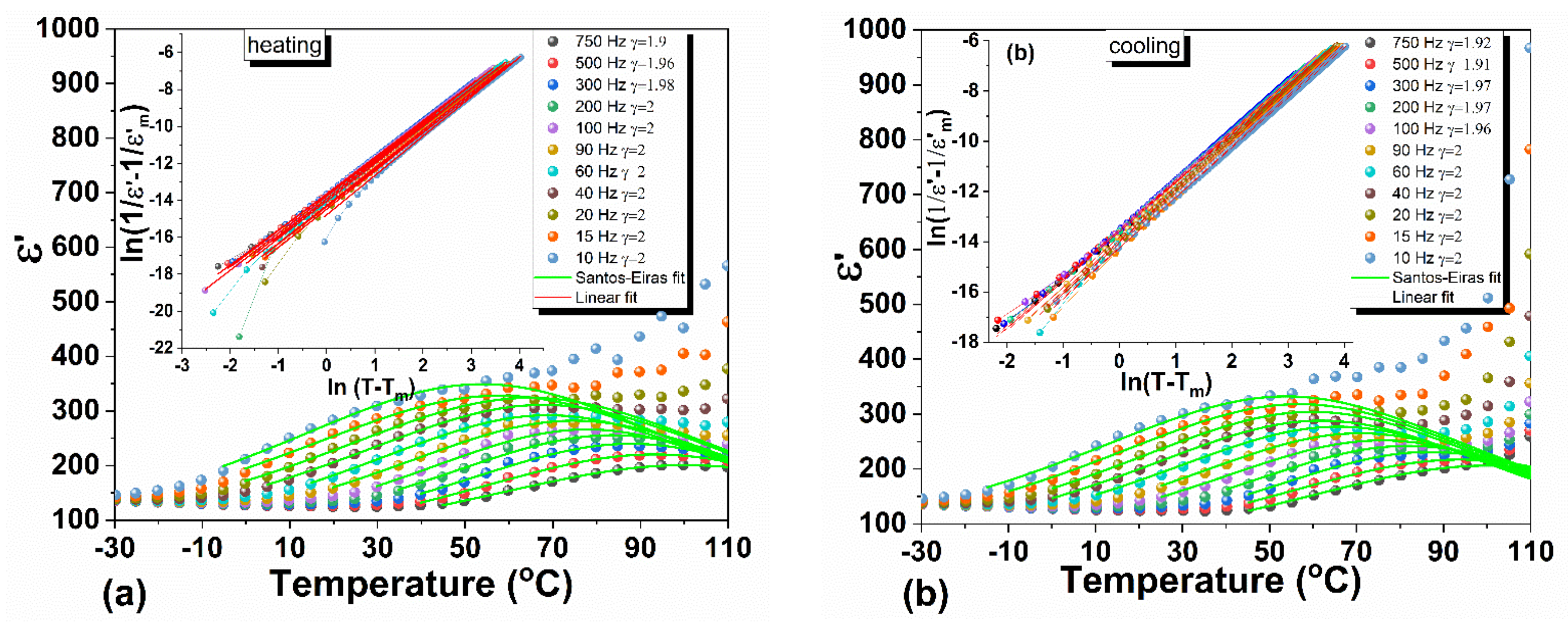
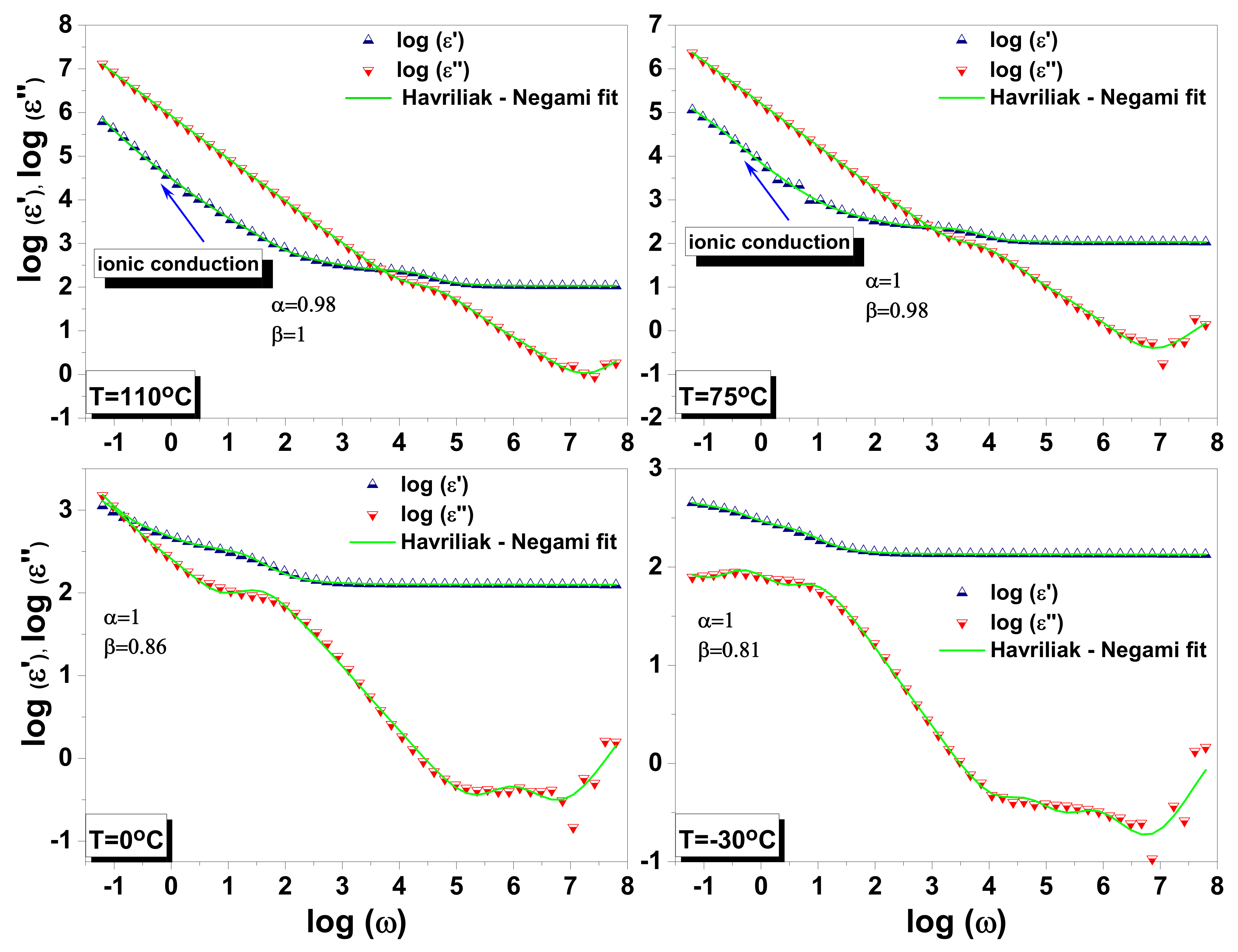
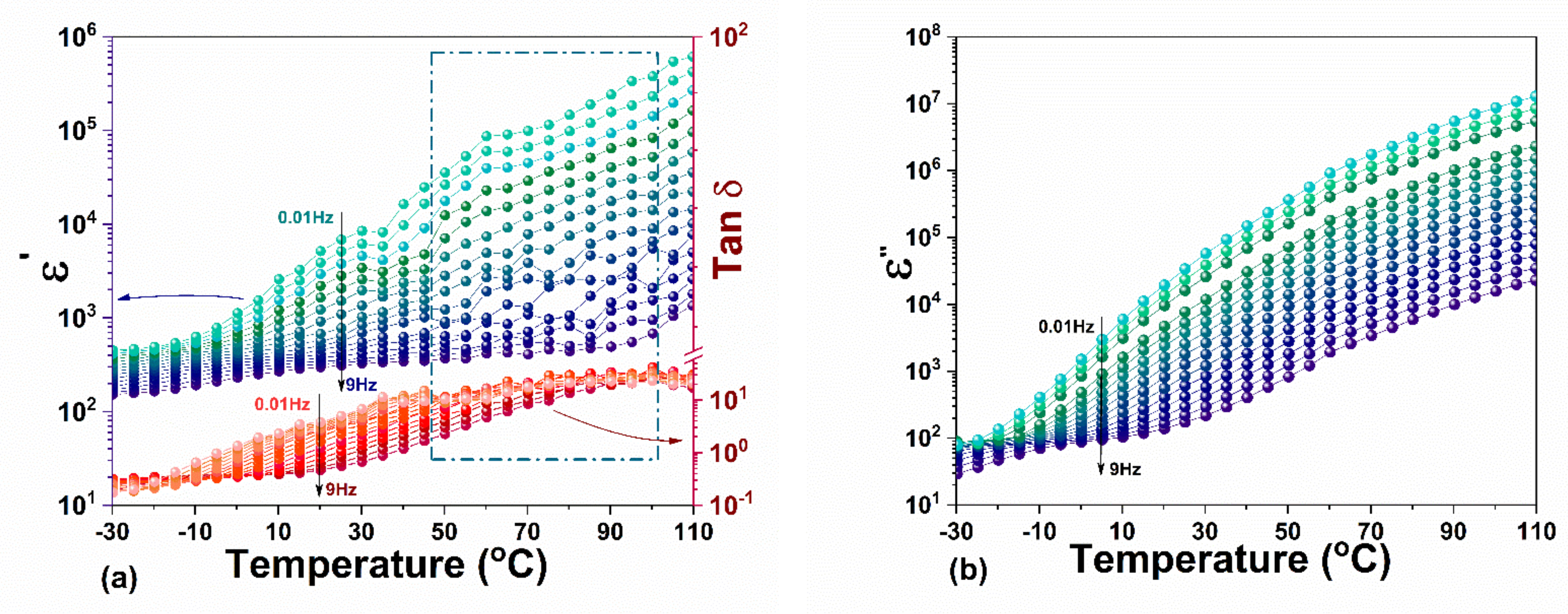
3.3. Dielectric Spectroscopy
3.3.1. Dielectric Function and Curie Weiss Analyses
3.3.2. Dielectric Relaxations
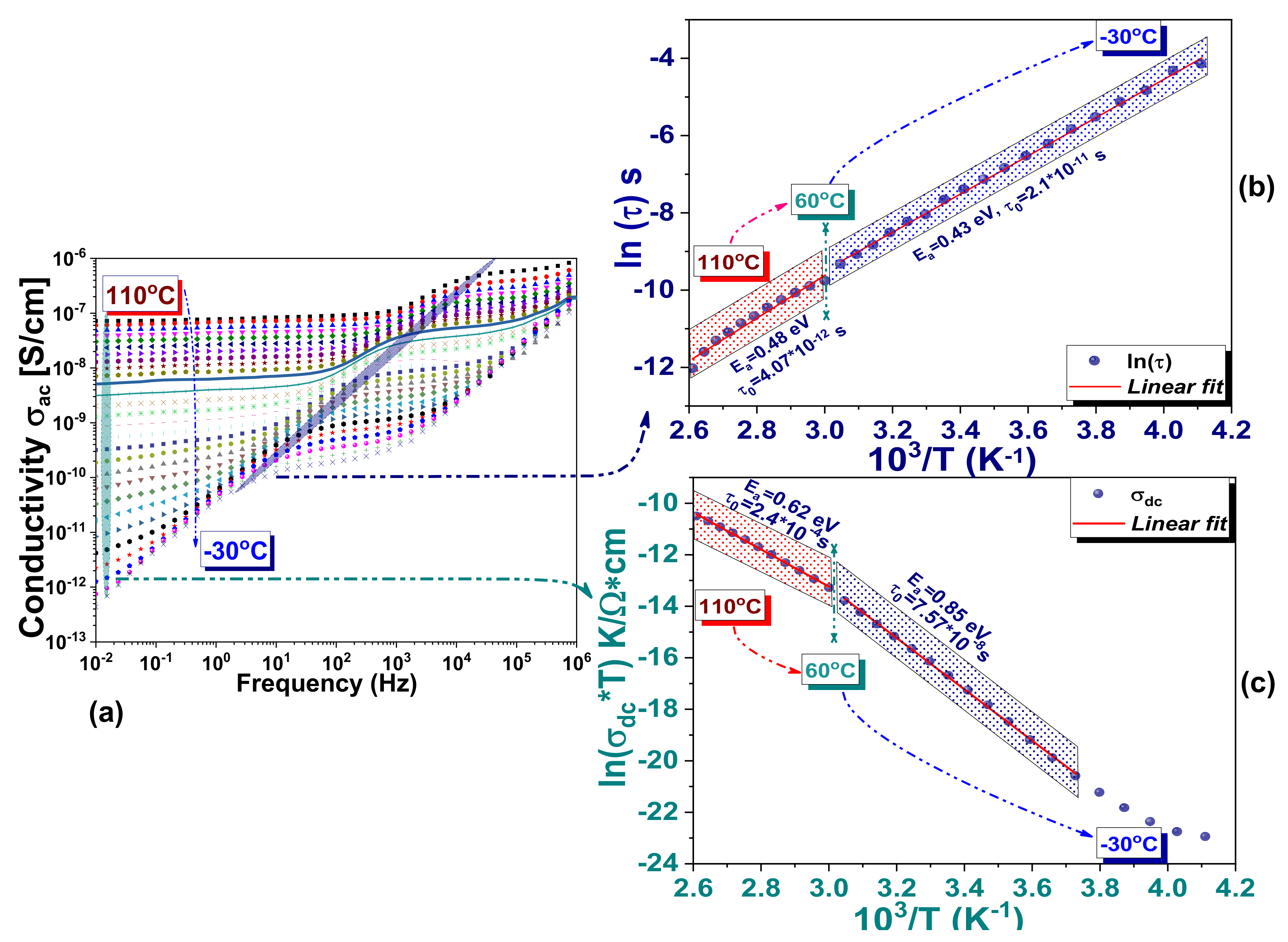
3.3.3. Electrical Conductivity Properties
3.3.4. Impedance Analysis
- (i)
- The geometrical resistance/capacitance of the bulk perovskite grains (Rg/Cg) in the high-frequency range, with the corresponding τgrains time constant;
- (ii)
- The grain boundaries resistance/capacitance (Rgb/Cgb elements corrected by CPE) [82] in the mid-frequency range with the corresponding τbounderies time constant;
- (iii)
- The accumulation/diffusion of charges at low-frequency by considering the Rct − ZW/Cdl group with the corresponding τinterfaces time constant. Rct accounts for the resistance of coupled electron/ion transport, Cdl is the capacitance associated with the charges accumulated or adsorbed at the dielectric–electrode interfaces of the opposing polarity. and the Warburg ZW complex impedance accounts for the diffusion of the electroactive species [89]. We define three-time constants for each of the RC branches in the equivalent circuit in Figure 13d, τgrains, τboundaries, and τinterfaces.
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Jiang, Q.; Zhao, Y.; Zhang, X.; Yang, X.; Chen, Y.; Chu, Z.; Ye, Q.; Li, X.; Yin, Z.; You, J. Surface Passivation of Perovskite Film for Efficient Solar Cells. Nat. Photonics 2019, 13, 460–466. [Google Scholar] [CrossRef]
- Jeong, J.; Kim, M.; Seo, J.; Lu, H.Z.; Ahlawat, P.; Mishra, A.; Yang, Y.G.; Hope, M.A.; Eickemeyer, F.T.; Kim, M.; et al. Pseudo-halide anion engineering for alpha-FAPbI(3) perovskite solar cells. Nature 2021, 592, 381–385. [Google Scholar] [CrossRef]
- Gao, X.-X.; Xue, D.-J.; Gao, D.; Han, Q.; Ge, Q.-Q.; Ma, J.-Y.; Ding, J.; Zhang, W.; Zhang, B.; Feng, Y.; et al. High-Mobility Hydrophobic Conjugated Polymer as Effective Interlayer for Air-Stable Efficient Perovskite Solar Cells. Sol. RRL 2019, 3, 1800232. [Google Scholar] [CrossRef] [Green Version]
- Wang, P.; Li, R.; Chen, B.; Hou, F.; Zhang, J.; Zhao, Y.; Zhang, X. Gradient Energy Alignment Engineering for Planar Perovskite Solar Cells with Efficiency Over 23%. Adv. Mater. 2020, 32, 1905766. [Google Scholar] [CrossRef] [PubMed]
- Ansari, F.; Shirzadi, E.; Salavati-Niasari, M.; LaGrange, T.; Nonomura, K.; Yum, J.-H.; Sivula, K.; Zakeeruddin, S.M.; Nazeeruddin, M.K.; Grätzel, M.; et al. Passivation Mechanism Exploiting Surface Dipoles Affords High-Performance Perovskite Solar Cells. J. Am. Chem. Soc. 2020, 142, 11428–11433. [Google Scholar] [CrossRef] [PubMed]
- Yang, W.S.; Park, B.W.; Jung, E.H.; Jeon, N.J.; Kim, Y.C.; Lee, D.U.; Shin, S.S. Iodide Management in Formamidinium-Lead-Halide–Based Perovskite Layers for Efficient Solar Cells. Science 2017, 356, 1376–1379. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Li, T.; Dong, Q.; Mosconi, E.; Song, J.; Chen, Z.; Deng, Y.; Liu, Y.; Ducharme, S.; Gruverman, A.; et al. Large Electrostrictive Response in Lead Halide Perovskites. Nat. Mater. 2018, 17, 1020–1026. [Google Scholar] [CrossRef]
- Frost, J.M.; Butler, K.T.; Brivio, F.; Hendon, C.H.; van Schilfgaarde, M.; Walsh, A. Atomistic Origins of High-Performance in Hybrid Halide Perovskite Solar Cells. Nano Lett. 2014, 14, 2584–2590. [Google Scholar] [CrossRef] [Green Version]
- Li, W.; Wang, Z.; Deschler, F.; Gao, S.; Friend, R.H.; Cheetham, A.K. Chemically Diverse and Multifunctional Hybrid Organic–Inorganic Perovskites. Nat. Rev. Mater. 2017, 2, 16099. [Google Scholar] [CrossRef]
- Frost, J.M.; Butler, K.T.; Walsh, A. Molecular Ferroelectric Contributions to Anomalous Hysteresis in Hybrid Perovskite Solar Cells. APL Mater. 2014, 2, 081506. [Google Scholar] [CrossRef] [Green Version]
- Glazer, A.M. The Classification of Tilted Octahedra in Perovskites. Acta Crystallogr. 1972, 28, 3384–3392. [Google Scholar] [CrossRef]
- Stroppa, A.; Quarti, C.; De Angelis, F.; Picozzi, S. Ferroelectric Polarization of CH3NH3PbI3: A Detailed Study Based on Density Functional Theory and Symmetry Mode Analysis. J. Phys. Chem. Lett. 2015, 6, 2223–2231. [Google Scholar] [CrossRef] [PubMed]
- Weller, M.T.; Weber, O.J.; Henry, P.F.; Di Pumpo, A.M.; Hansen, T.C. Complete Structure and Cation Orientation in the Perovskite Photovoltaic Methylammonium Lead Iodide between 100 and 352 K. Chem. Commun. 2015, 51, 4180–4183. [Google Scholar] [CrossRef] [Green Version]
- Quarti, C.; Mosconi, E.; De Angelis, F. Interplay of Orientational Order and Electronic Structure in Methylammonium Lead Iodide: Implications for Solar Cells Operation. Chem. Mater. 2014, 26, 6557–6569. [Google Scholar] [CrossRef]
- Zheng, F.; Takenaka, H.; Wang, F.; Koocher, N.Z.; Rappe, A.M. First-Principles Calculation of the Bulk Photovoltaic Effect in CH3NH3PbI3 and CH3NH3PbI3-xClx. J. Phys. Chem. Lett. 2015, 6, 31–37. [Google Scholar] [CrossRef] [Green Version]
- Stroppa, A.; Di Sante, D.; Barone, P.; Bokdam, M.; Kresse, G.; Franchini, C.; Whangbo, M.-H.; Picozzi, S. Tunable Ferroelectric Polarization and Its Interplay with Spin-Orbit Coupling in Tin Iodide Perovskites. Nat. Commun. 2014, 5, 3335–3339. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Shi, J.; Zheng, X.; Zhou, Y.; Zhu, K.; Priya, S. Ferroelectric Solar Cells Based on Inorganic–Organic Hybrid Perovskites. J. Mater. Chem. A 2015, 3, 7699–7705. [Google Scholar] [CrossRef]
- Kutes, Y.; Ye, L.; Zhou, Y.; Pang, S.; Huey, B.D.; Padture, N.P. Direct Observation of Ferroelectric Domains in Solution-Processed CH3NH3PbI3 Perovskite Thin Films. J. Phys. Chem. Lett. 2014, 5, 3335–3339. [Google Scholar] [CrossRef]
- Coll, M.; Gomez, A.; Mas Marzá, E.; Almora, O.; Garcia-Belmonte, G.; Campoy-Quiles, M.; Bisquert, J. Polarization Switching and Light-Enhanced Piezoelectricity in Lead Halide Perovskites. J. Phys. Chem. Lett. 2015, 6, 1408–1413. [Google Scholar] [CrossRef] [PubMed]
- Fan, Z.; Xiao, J.; Sun, K.; Chen, L.; Hu, Y.; Ouyang, J.; Ong, K.P.; Zeng, K.; Wang, J. Ferroelectricity of CH3NH3PbI3 Perovskite. J. Phys. Chem. Lett. 2015, 6, 1155–1161. [Google Scholar] [CrossRef] [PubMed]
- Cordero, F.; Craciun, F.; Trequattrini, F.; Imperatori, P.; Paoletti, A.M.; Pennesi, G. Competition Between Polar and Antiferrodistortive Modes and Correlated Dynamics of the Methylammonium Molecules in MAPbI3 from Anelastic and Dielectric Measurements. J. Phys. Chem. Lett. 2018, 9, 4401–4406. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stoumpos, C.C.; Malliakas, C.D.; Kanatzidis, M.G. Semiconducting Tin and Lead Iodide Perovskites with Organic Cations: Phase Transitions, High Mobilities, and Near-Infrared Photoluminescent Properties. Inorg. Chem. 2013, 52, 9019–9038. [Google Scholar] [CrossRef]
- Baikie, T.; Fang, Y.; Kadro, J.M.; Schreyer, M.; Wei, F.; Mhaisalkar, S.G.; Graetzeld, M.; White, T.J. Synthesis and Crystal Chemistry of the Hybrid Perovskite (CH3NH3)PbI3 for Solid-State Sensitised Solar Cell Applications. J. Mater. Chem. A 2013, 1, 5628–5641. [Google Scholar] [CrossRef]
- Khassaf, H.; Yadavalli, S.K.; Zhou, Y.; Padture, N.P.; Kingon, A.I. Effect of Grain Boundaries on Charge Transport in Methylammonium Lead Iodide Perovskite Thin Films. J. Phys. Chem. C 2019, 123, 5321–5325. [Google Scholar] [CrossRef]
- Khassaf, H.; Yadavalli, S.K.; Game, O.S.; Zhou, Y.; Padture, N.P.; Kingon, A.I. Comprehensive Elucidation of Ion Transport and Its Relation to Hysteresis in Methylammonium Lead Iodide Perovskite Thin Films. J. Phys. Chem. C 2019, 123, 4029–4034. [Google Scholar] [CrossRef]
- Nemnes, G.A.; Besleaga, C.; Tomulescu, A.G.; Palici, A.; Pintilie, L.; Manolescu, A.; Pintilie, I. How Measurement Protocols Influence the Dynamic J-V Characteristics of Perovskite Solar Cells: Theory and Experiment. Sol. Energy 2018, 173, 976–983. [Google Scholar] [CrossRef] [Green Version]
- Saidaminov, M.I.; Abdelhady, A.L.; Murali, B.; Alarousu, E.; Burlakov, V.M.; Peng, W.; Dursun, I.; Wang, L.; He, Y.; Maculan, G.; et al. High-Quality Bulk Hybrid Perovskite Single Crystals within Minutes by Inverse Temperature Crystallization. Nat. Commun. 2015, 6, 7586. [Google Scholar] [CrossRef] [Green Version]
- Ming, W.; Yang, D.; Li, T.; Zhang, L.; Du, M.-H. Formation and Diffusion of Metal Impurities in Perovskite Solar Cell Material CH3NH3PbI3: Implications on Solar Cell Degradation and Choice of Electrode. Adv. Sci. 2018, 5, 1700662. [Google Scholar] [CrossRef] [Green Version]
- Shi, T.; Chen, J.; Zheng, J.; Li, X.; Zhou, B.; Cao, H.; Wang, Y. Ti/Au Cathode for Electronic Transport Material-Free Organic Inorganic Hybrid Perovskite Solar Cells. Sci. Rep. 2016, 6, 39132. [Google Scholar] [CrossRef] [Green Version]
- Whitfield, P.S.; Herron, N.; Guise, W.E.; Page, K.; Cheng, Y.Q.; Milas, I.; Crawford, M.K. Structures, Phase Transitions and Tricritical Behavior of the Hybrid Perovskite Methyl Ammonium Lead Iodide. Sci. Rep. 2016, 6, 35685. [Google Scholar] [CrossRef] [Green Version]
- Kawamura, Y.; Mashiyama, H.; Hasebe, K. Structural Study on Cubic-Tetragonal Transition of CH3NH3PbI3. J. Phys. Soc. Jpn. 2002, 71, 1694–1697. [Google Scholar] [CrossRef] [Green Version]
- Dinnebier, R.E.; Billinge, S.J.L. Powder Diffraction. Theory and Practice; The Royal Society of Chemistry: Cambridge, UK, 2008; pp. 381–384. [Google Scholar]
- Kremer, F.; Schonhals, A. Broadband Dielectric Spectroscopy; Springer: Berlin/Heidelberg, Germany, 2003; pp. 58–98. [Google Scholar]
- Ciomaga, C.E.; Guzu, A.; Airimioaei, M.; Curecheriu, L.P.; Lukacs, V.A.; Avadanei, O.G.; Stoian, G.; Grigoras, M.; Lupu, N.; Asandulesa, M.; et al. Comparative Study of Magnetoelectric BaTiO3–Co0.8Zn0.2Fe2O4 Bi-Tunable Ceramics Sintered by Spark Plasma Sintering and Classical Method. Ceram. Int. 2019, 45, 24168–24175. [Google Scholar] [CrossRef]
- Ciomaga, C.E.; Neagu, A.M.; Pop, M.V.; Airimioaei, M.; Tascu, S.; Schileo, G.; Galassi, C.; Mitoseriu, L. Ferroelectric and Dielectric Properties of Ferrite-Ferroelectric Ceramic Composites. J. Appl. Phys. 2013, 113, 074103. [Google Scholar] [CrossRef]
- You, Y.-M.; Liao, W.-Q.; Zhao, D.; Ye, H.-Y.; Zhang, Y.; Zhou, Q.; Niu, X.; Wang, J.; Li, P.-F.; Fu, D.-W.; et al. An Organic-Inorganic Perovskite Ferroelectric with Large Piezoelectric Response. Science 2017, 357, 306–309. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Egger, D.A.; Rappe, A.M.; Kronik, L. Hybrid Organic-Inorganic Perovskites on the Move. Acc. Chem. Res. 2016, 49, 573–581. [Google Scholar] [CrossRef]
- Mashiyama, H.; Kawamura, Y.; Magome, E.; Kubota, Y. Displacive Character of the Cubic-Tetragonal Transition in CH3NH3PbIX3. J. Korean Phys. Soc. 2003, 42, 1026–1029. [Google Scholar]
- Swainson, I.P.; Stock, C.; Parker, S.F.; Van Eijck, L.; Russina, M.; Taylor, J.W. From Soft Harmonic Phonons to Fast Relaxational Dynamics in CH3NH3PbBr3. Phys. Rev. B Condens. Matter Mater. Phys. 2015, 92, 100303. [Google Scholar] [CrossRef] [Green Version]
- Brivio, F.; Frost, J.M.; Skelton, J.M.; Jackson, A.J.; Weber, O.J.; Weller, M.T.; Goñi, A.R.; Leguy, A.M.A.; Barnes, P.R.F.; Walsh, A. Lattice Dynamics and Vibrational Spectra of the Orthorhombic, Tetragonal, and Cubic Phases of Methylammonium Lead Iodide. Phys. Rev. B Condens. Matter Mater. Phys. 2015, 92, 144308. [Google Scholar] [CrossRef] [Green Version]
- Knop, O.; Wasylishen, R.E.; White, M.A.; Cameron, T.S.; Van Voort, M.J.M. Alkylammonium Lead Halides. Part 2. CH3NH3PbX3 (X = C1, Br, I) Perovskites: Cuboctahedral Halide Cages with Isotropic Cation Reorientation. Can. J. Chem. 1990, 68, 412–422. [Google Scholar] [CrossRef] [Green Version]
- Onoda-Yamamuro, N.; Matsuo, T.; Suga, H. Calorimetric and IR Spectroscopic Studies of Phase Transitions in Methylammonium Trihalogenplumbates (II). J. Phys. Chem. Solids 1990, 51, 1383–1395. [Google Scholar] [CrossRef]
- Grigoriadis, C.; Duran, H.; Steinhart, M.; Kappl, M.; Butt, H.-J.; Floudas, G. Suppression of Phase Transitions in a Confined Rodlike Liquid Crystal. ACS Nano 2011, 5, 9208. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, P.; Wu, H.; Ren, W.; Ye, Z.-G. Synthesis, Structure, and Properties of the PbZrO3-PbTiO3-Bi(Zn2/3Nb1/3)O3 Ternary Solid Solution System Around the Morphotropic Phase Boundary. Phys. Status Solidi A 2018, 215, 1701007. [Google Scholar] [CrossRef]
- Chen, S.-C.; Wu, P.-C.; Lee, W. Dielectric and Phase Behaviors of Blue-Phase Liquid Crystals. Opt. Mater. Express 2014, 4, 2392. [Google Scholar] [CrossRef]
- Santos, I.A.; Garcia, D.; Eiras, J.A.; Arantes, V.L. Features of Diffuse Phase Transition in Lead Barium Niobate Ferroelectric Ceramics. J. Appl. Phys. 2003, 93, 1701. [Google Scholar] [CrossRef]
- Uchino, K.; Nomura, S. Critical Exponents of the Dielectric Constants in Diffused-Phase-Transition Crystals. Ferroelectr. Lett. 1982, 44, 55–61. [Google Scholar] [CrossRef]
- Debye, P.J.W. Polar Molecules; Dover Publ. Inc.: New York, NY, USA, 1945. [Google Scholar]
- Debye, P.J.W. Dielectric Constant. Energy Absorption in Dielectrics with Polar Molecules. Trans. Faraday Soc. 1934, 30, 679–683. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and Absorption in Dielectrics I. Alternating Current Characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar] [CrossRef] [Green Version]
- Devidson, D.W.; Cole, R.H. Dielectric Relaxation in Glycerol, Propylene Glycol, and nPropanol. J. Chem. Phys. 1951, 19, 1484. [Google Scholar] [CrossRef]
- Jonscher, A.K. Review. A New Understanding of the Dielectric Relaxation of Solids. J. Mater. Sci. 1981, 16, 2037–2060. [Google Scholar] [CrossRef]
- Kohlrausch, R. Theorie des Elektrischen Ruckstandes in Leidener Flasche. Ann. Phys. 1854, 167, 179–214. [Google Scholar] [CrossRef] [Green Version]
- Williams, G.; Watts, D.C. Non-Symmetrical Dielectric Relaxation Behaviour Arising from a Simple Empirical Decay Function. Trans. Faraday Soc. 1970, 66, 80–85. [Google Scholar] [CrossRef]
- Havriliak, S.; Negami, S. A Complex Plane Representation of Dielectric and Mechanical Relaxation Processes in Some Polymers. Polymer 1967, 8, 161–210. [Google Scholar] [CrossRef]
- Zorn, R. Applicability of Distribution Functions for the Havriliak–Negami Spectral Function. J. Polym. Sci. B. Polym. Phys. 1999, 37, 1043–1044. [Google Scholar] [CrossRef]
- Volkov, A.S.; Koposov, G.D.; Perfiliev, R.O. On the Physical Meaning of Disperse Parameters of Frequency Dependence of Dielectric Permittivity in the Havriliak–Negami Model. Opt. Spectrosc. 2018, 125, 379–382. [Google Scholar] [CrossRef]
- Lvovich, V.F. Impedance Spectroscopy, Applications to Electrochemical and Dielectric Phenomena; Chapter 1; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; p. 10. [Google Scholar]
- Almora, O.; Zarazua, I.; Mas-Marza, E.; Mora-Sero, I.; Bisquert, J.; Garcia-Belmonte, G. Capacitive Dark Currents, Hysteresis, and Electrode Polarization in Lead Halide Perovskite Solar Cells. J. Phys. Chem. Lett. 2015, 6, 1645–1652. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Man, Z.-Y.; Zeng, J.; Zheng, L.; Li, G.; Kassiba, A. Relationship of Giant Dielectric Constant and Ion Migration in CH3NH3PbI3 Single Crystal Using Dielectric Spectroscopy. J. Phys. Chem. C 2020, 124, 13348–13355. [Google Scholar] [CrossRef]
- Minussi, F.B.; Reis, S.P.; Araújo, E.B. An Unusual Frequency Dispersion of the Dielectric Permittivity Maxima at Temperatures Around the Tetragonal–Cubic Phase Transition of Methylammonium Lead Iodide. J. Appl. Phys. 2020, 127, 244103. [Google Scholar] [CrossRef]
- Labram, J.G.; Fabini, D.H.; Perry, E.E.; Lehner, A.J.; Wang, H.; Glaudell, A.M.; Wu, G.; Evans, H.; Buck, D.; Cotta, R.; et al. Temperature-Dependent Polarization in Field-Effect Transport and Photovoltaic Measurements of Methylammonium Lead Iodide. J. Phys. Chem. Lett. 2015, 6, 3565–3571. [Google Scholar] [CrossRef] [Green Version]
- Juarez-Perez, E.J.; Sanchez, R.S.; Badia, L.; Garcia-Belmonte, G.; Kang, Y.S.; Mora-Sero, I.; Bisquert, J. Photoinduced Giant Dielectric Constant in Lead Halide Perovskite Solar Cells. J. Phys. Chem. Lett. 2014, 5, 2390–2394. [Google Scholar] [CrossRef]
- Govinda, S.; Kore, B.P.; Bokdam, M.; Mahale, P.; Kumar, A.; Pal, S.; Bhattacharyya, B.; Lahnsteiner, J.; Kresse, G.; Franchini, C.; et al. Behavior of Methylammonium Dipoles in MAPbX3 (X=Br and I). J. Phys. Chem. Lett. 2017, 8, 4113–4121. [Google Scholar] [CrossRef] [Green Version]
- Bakulin, A.A.; Selig, O.; Bakker, H.J.; Rezus, Y.L.A.; Müller, C.; Glaser, T.; Lovrincic, R.; Sunm, Z.; Chen, Z.; Walsh, A.; et al. Real-Time Observation of Organic Cation Reorientation in Methylammonium Lead Iodide Perovskites. J. Phys. Chem. Lett. 2015, 6, 3663–3669. [Google Scholar] [CrossRef] [Green Version]
- Hoque, M.N.F.; Islam, N.; Li, Z.; Ren, G.; Zhu, K.; Fan, Z. Ionic and Optical Properties of Methylammonium Lead Iodide Perovskite across the Tetragonal–Cubic Structural Phase Transition. Spec. Issue Stab. Perovskite Sol. Cells Devices 2016, 9, 2692–2968. [Google Scholar] [CrossRef] [Green Version]
- Eames, C.; Frost, J.M.; Barnes, P.R.F.; O’Regan, B.C.; Walsh, A.; Islam, M.S. Ionic Transport in Hybrid Lead Iodide Perovskite Solar Cells. Nat. Commun. 2015, 6, 7497. [Google Scholar] [CrossRef] [Green Version]
- Yang, D.; Ming, W.; Shi, H.; Zhang, L.; Du, M.-H. Fast Diffusion of Native Defects and Impurities in Perovskite Solar Cell Material CH3NH3PbI3. Chem. Mater. 2016, 28, 4349–4357. [Google Scholar] [CrossRef]
- Almora, O.; González-Lezcano, A.; Guerrero, A.; Brabec, C.J.; Garcia-Belmonte, G. Ion-Mediated Hopping Electrode Polarization Model for Impedance Spectra of CH3NH3PbI3. J. Appl. Phys. 2020, 128, 075104. [Google Scholar] [CrossRef]
- Game, O.S.; Buchsbaum, G.J.; Zhou, Y.; Padture, N.P.; Kingon, A.I. Ions Matter: Description of the Anomalous Electronic Behavior in Methylammonium Lead Halide Perovskite Devices. Adv. Funct. Mater. 2017, 27, 1606584. [Google Scholar] [CrossRef]
- Azpiroz, J.M.; Mosconi, E.; Bisquert, J.; De Angelis, F. Defects Migration in Methylammonium Lead Iodide and their Role in Perovskite Solar Cells Operation. Energy Environ. Sci. 2015, 8, 2118–2127. [Google Scholar] [CrossRef]
- Yuan, Y.B.; Huang, J.S. Ion Migration in Organometal Trihalide Perovskite and Its Impact on Photovoltaic Efficiency and Stability. Acc. Chem. Res. 2016, 49, 286–293. [Google Scholar] [CrossRef] [Green Version]
- Delugas, P.; Caddeo, C.; Filippetti, A.; Mattoni, A. Thermally Activated Point Defect Diffusion in Methylammonium Lead Trihalide: Anisotropic and Ultrahigh Mobility of Iodine. J. Phys. Chem. Lett. 2016, 7, 2356–2361. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Tscheuschner, S.; Paulus, F.; Hopkinson, P.E.; Kießling, J.; Köhler, A.; Vaynzof, Y.; Huettner, S. Iodine Migration and its Effect on Hysteresis in Perovskite Solar Cells. Adv. Mater. 2016, 28, 2446–2454. [Google Scholar] [CrossRef] [PubMed]
- Meloni, S.; Moehl, T.; Tress, W.; Franckevičius, M.; Saliba, M.; Lee, Y.H.; Gao, P.; Nazeeruddin, M.K.; Zakeeruddin, S.M.; Rothlisberger, U.; et al. Ionic Polarization Induced Current-Voltage Hysteresis in CH3NH3PbX3 Perovskite Solar Cells. Nat. Commun. 2016, 7, 10334. [Google Scholar] [CrossRef] [PubMed]
- Haruyama, J.; Sodeyama, K.; Han, L.Y.; Tateyama, Y. First-Principles Study of Ion Diffusion in Perovskite Solar Cell Sensitizers. J. Am. Chem. Soc. 2015, 137, 10048–10051. [Google Scholar] [CrossRef]
- Futscher, M.H.; Lee, J.M.; McGovern, L.; Muscarella, L.A.; Wang, T.; Haider, M.I.; Fakharuddin, A.; Schmidt-Mende, L.; Ehrler, B. Quantification of Ion Migration in CH3NH3PbI3 Perovskite Solar Cells by Transient Capacitance Measurements. Mater. Horiz. 2019, 6, 1497–1503. [Google Scholar] [CrossRef] [Green Version]
- Yang, T.-Y.; Gregori, G.; Pellet, N.; Gratzel, M.; Maier, J. The Significance of Ion Conduction in a Hybrid Organic-Inorganic Lead Iodide-Based Perovskite Photosensitizer. Angew. Chem. Int. Ed. 2015, 54, 7905–7910. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Chae, J.; Shao, Y.; Wang, Q.; Xiao, Z.; Centrone, A.; Huang, J. Photovoltaic Switching Mechanism in Lateral Structure, Hybrid Perovskite Solar Cells. Adv. Energy Mater. 2015, 5, 1500615. [Google Scholar] [CrossRef]
- Moure, C.; Peña, O. Recent advances in perovskites: Processing and properties. Progress Solid State Chem. 2015, 43, 123–148. [Google Scholar] [CrossRef]
- Huang, V.M.-W.; Vivier, V.; Orazem, M.E.; Pébère, N.; Tribollet, B. The Apparent Constant-Phase-Element Behavior of an Ideally Polarized Blocking Electrode. J. Electrochem. Soc. 2007, 154, C81–C88. [Google Scholar] [CrossRef]
- Macdonald, J.R. Impedance Spectroscopy: Emphasizing Solid Materials and Systems; John Wiley & Sons: New York, NY, USA, 1987. [Google Scholar]
- Bisquert, J. Theory of the Impedance of Electron Diffusion and Recombination in a Thin Layer. J. Phys. Chem. B 2002, 106, 325–333. [Google Scholar] [CrossRef]
- Oldenburger, M.; Bedürftig, B.; Gruhle, A.; Grimsmann, F.; Richter, E.; Findeisen, R.; Hintennach, A. Investigation of the Low Frequency Warburg Impedance of Li-Ion Cells by Frequency Domain Measurements. J. Energy Storage 2019, 21, 272–280. [Google Scholar] [CrossRef]
- Jorcin, J.B.; Orazem, M.E.; Pebere, N.; Tribollet, B. CPE analysis by local electrochemical impedance spectroscopy. Electrochim. Acta 2006, 51, 1473–1479. [Google Scholar] [CrossRef]
- Córdoba-Torres, P.; Mesquita, T.J.; Devos, O.; Tribollet, B.; Roche, V.; Nogueira, R.P. On the Intrinsic Coupling between Constant-Phase Element Parameters A and Q in Electrochemical Impedance Spectroscopy. Electrochim. Acta 2012, 72, 172–178. [Google Scholar] [CrossRef]
- Ahmad, Z.; Shikoh, A.S.; Paek, S.; Nazeeruddin, M.K.; Al-Muhtaseb, S.A.; Touati, F.; Bhadra, J.; Al-Thani, N.J. Degradation Analysis in Mixed (MAPbI3 and MAPbBr3) Perovskite Solar Cells under Thermal Stress. J. Mater. Sci. Mater. Electron. 2019, 30, 1354–1359. [Google Scholar] [CrossRef]
- Bag, M.; Renna, L.A.; Adhikari, R.Y.; Karak, S.; Liu, F.; Lahti, P.M.; Russe, T.P.; Tuominen, M.T.; Venkataraman, D. Kinetics of Ion Transport in Perovskite Active Layers and Its Implications for Active Layer Stability. J. Am. Chem. Soc. 2015, 137, 13130–13137. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Wang, Q.; Huang, J. Ion Migration in Hybrid Perovskite Solar Cells. In Organic-Inorganic Halide Perovskite Photovoltaics: From Fundamentals to Device Architectures; Park, N.G., Grätzel, M., Miyasaka, T., Miyasaka, T., Eds.; Springer: Cham, Switzerland, 2016; p. 137. [Google Scholar] [CrossRef]
- Almeida, P.M.V.; Gozzo, C.B.; Thaines, E.H.N.S.; Sales, A.J.M.; Freitas, R.G.; Terezo, A.J.; Sombra, A.S.B.; Costa, M.M. Dielectric Relaxation Study of the Ceramic Matrix BaBi4Ti4O15:Bi2O3. Mater. Chem. Phys. 2018, 205, 72–83. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patru, R.E.; Khassaf, H.; Pasuk, I.; Botea, M.; Trupina, L.; Ganea, C.-P.; Pintilie, L.; Pintilie, I. Tetragonal–Cubic Phase Transition and Low-Field Dielectric Properties of CH3NH3PbI3 Crystals. Materials 2021, 14, 4215. https://doi.org/10.3390/ma14154215
Patru RE, Khassaf H, Pasuk I, Botea M, Trupina L, Ganea C-P, Pintilie L, Pintilie I. Tetragonal–Cubic Phase Transition and Low-Field Dielectric Properties of CH3NH3PbI3 Crystals. Materials. 2021; 14(15):4215. https://doi.org/10.3390/ma14154215
Chicago/Turabian StylePatru, Roxana E., Hamidreza Khassaf, Iuliana Pasuk, Mihaela Botea, Lucian Trupina, Constantin-Paul Ganea, Lucian Pintilie, and Ioana Pintilie. 2021. "Tetragonal–Cubic Phase Transition and Low-Field Dielectric Properties of CH3NH3PbI3 Crystals" Materials 14, no. 15: 4215. https://doi.org/10.3390/ma14154215
APA StylePatru, R. E., Khassaf, H., Pasuk, I., Botea, M., Trupina, L., Ganea, C.-P., Pintilie, L., & Pintilie, I. (2021). Tetragonal–Cubic Phase Transition and Low-Field Dielectric Properties of CH3NH3PbI3 Crystals. Materials, 14(15), 4215. https://doi.org/10.3390/ma14154215







