Computer Simulation of Hydrodynamic and Thermal Processes in DLD Technology
Abstract
:1. Introduction
2. Materials and Methods
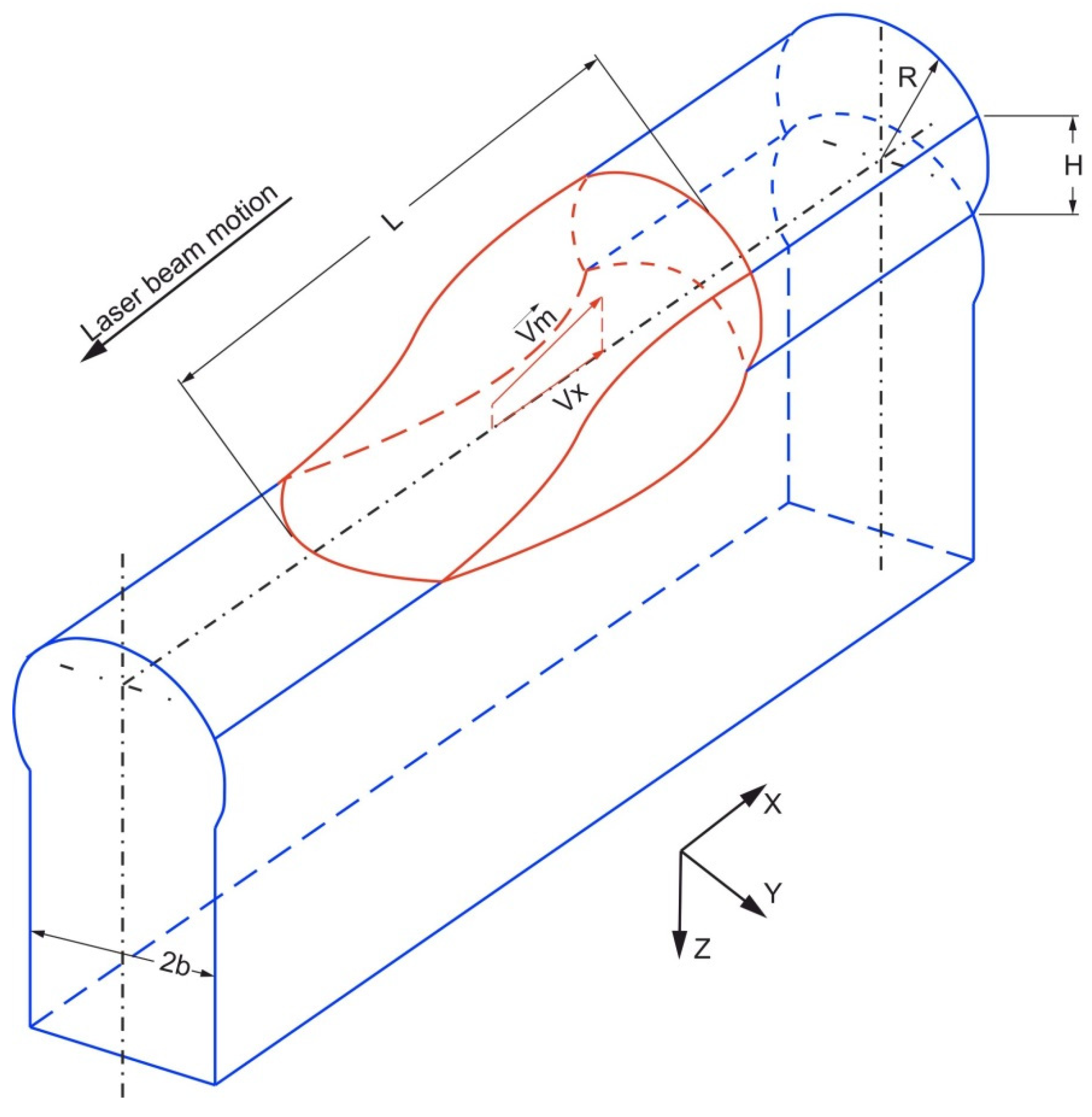
2.1. Melt Flow Description
2.2. Influence of the Powder Jet on the Heat Transfer in the Deposited Wall
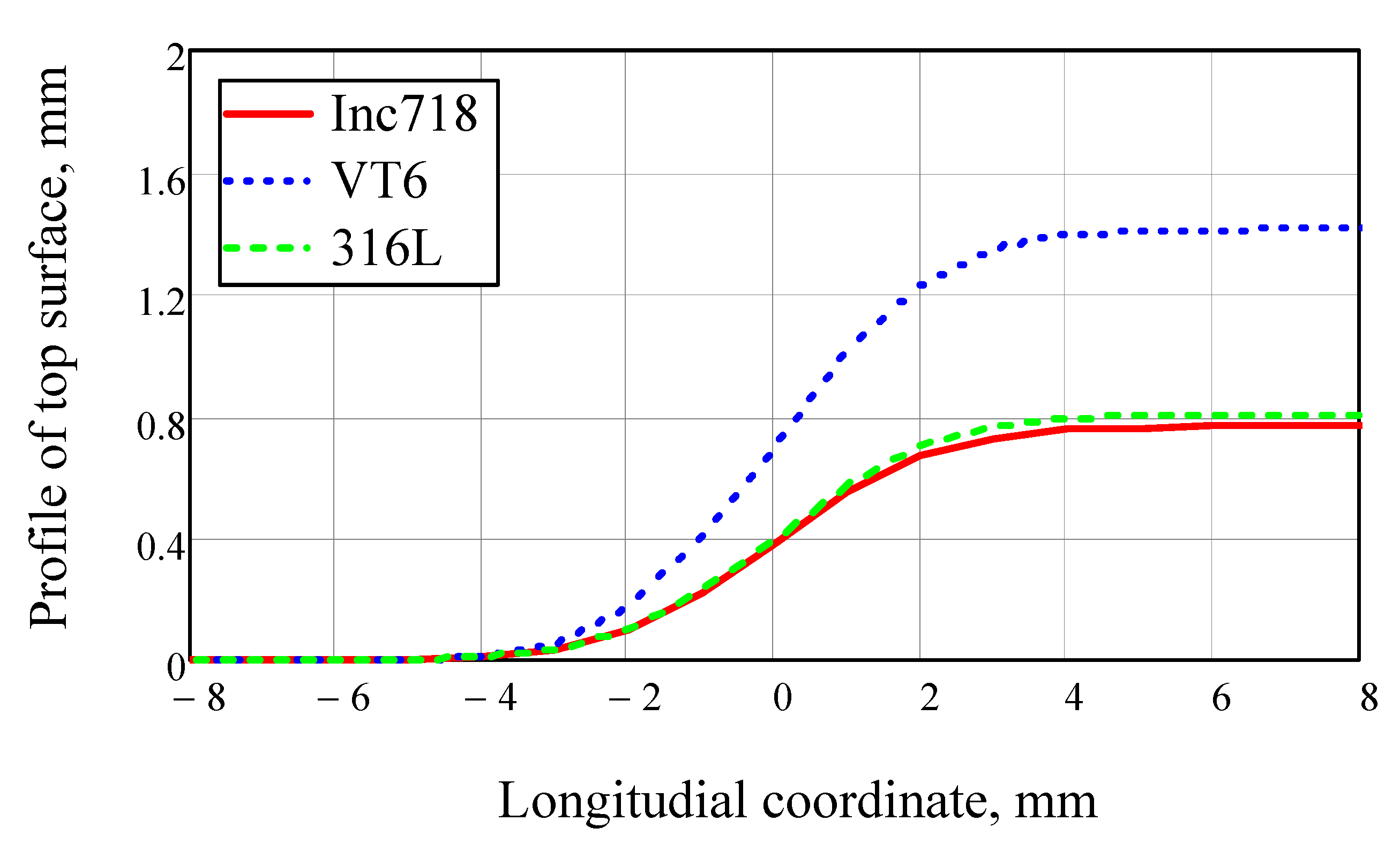
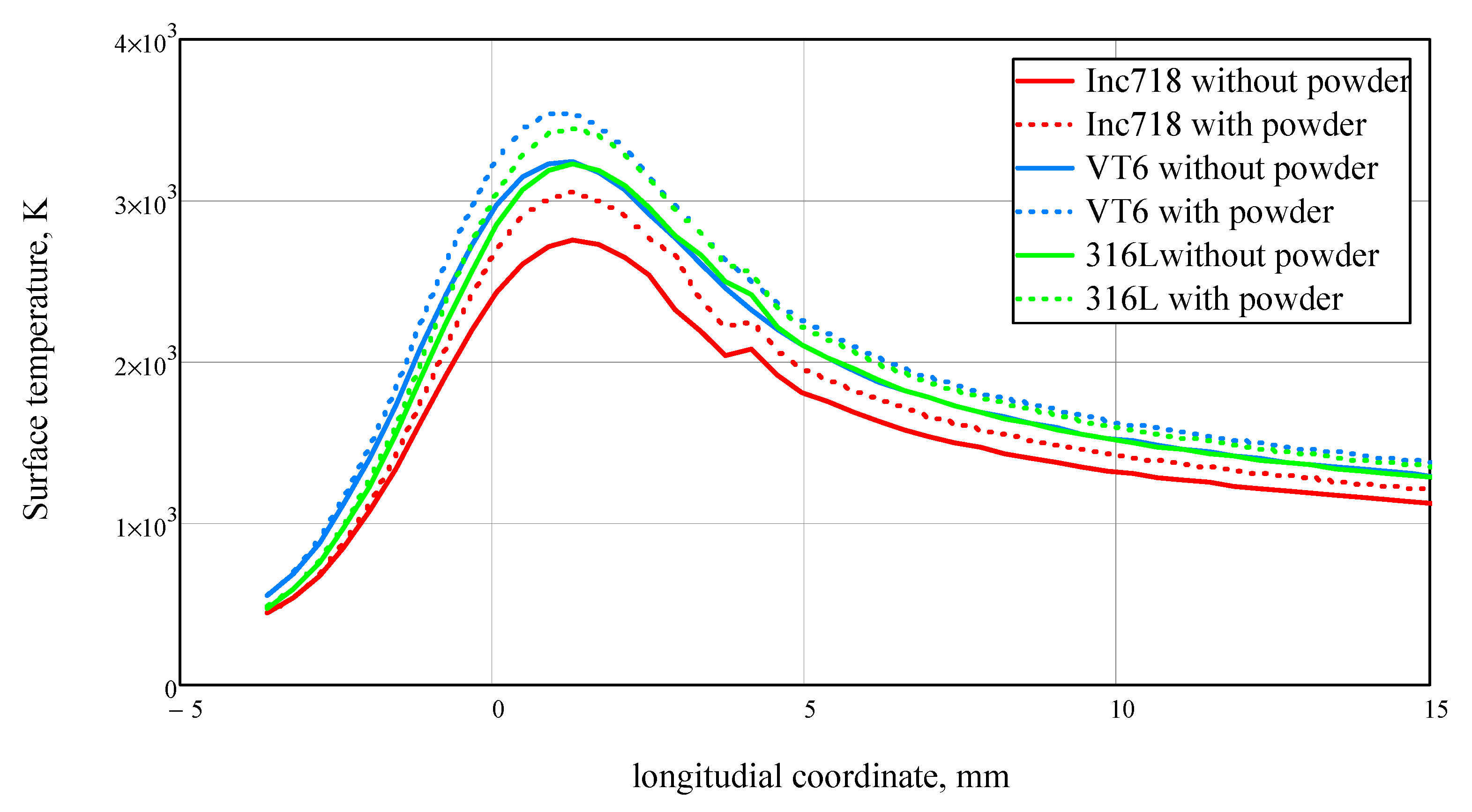
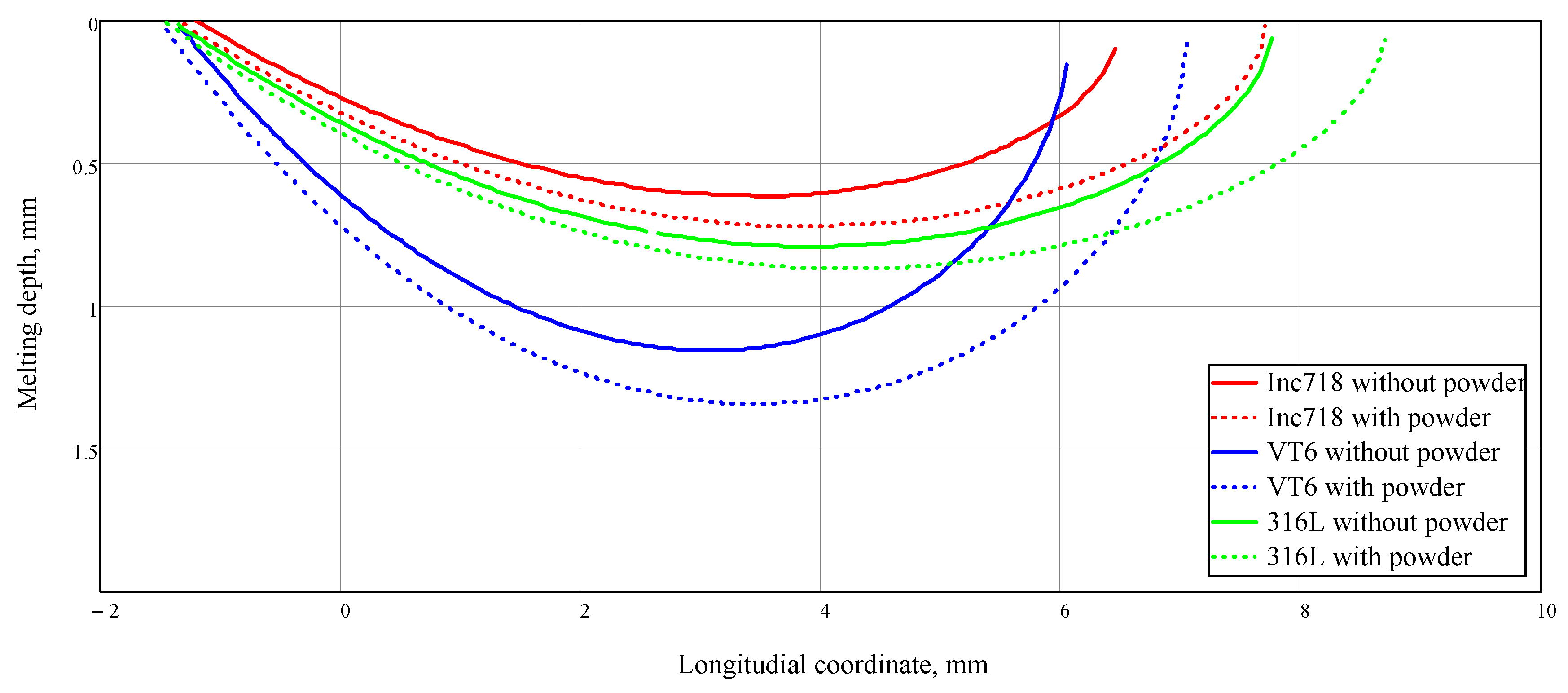
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| L | Melt pool length, mm |
| H | Melt pool depth, mm |
| b | Melt pool half-width, mm |
| R | Curvature radius of a bead profile |
| V | Laser beam motion speed, mm/s |
| Vm(x,y,z) | Liquid metal flow velocity, mm/s |
| Vx, Vy, Vz | X, Y, and Z components of the liquid metal flow velocity, mm/s |
| c | Heat capacity, J/(kg·K) |
| λ | Heat conductivity, W/(m·K) |
| χ | Thermal diffusivity, m2/s |
| ρ | Density, kg/m3 |
| ν | Kinematic viscosity of the liquid melt, m2/s |
| η | Dynamic viscosity of the liquid melt, Pa·s |
| α, β, γ | Coefficients of the parabolic equation of the melt velocity X component |
| σ, σ* | Surface tension, N/m |
| T0 | Initial temperature, environment temperature, K |
| Tm | Melting point, K |
| Tb | Boiling point, K |
| Ts | Maximum surface temperature, K |
| Tw | Residual temperature of the previous deposited bead, K |
| p | Pressure, Pa |
| padd | Additional pressure over change of the longitudinal curvature radius, Pa |
| j(x) | Powder mass flow density, kg/(s·m2) |
| q(x) | Distribution of the total energy flux on the melt pool surface, W/m |
| I(x) | Intensity of the laser beam radiation, W/m |
| A | Light energy absorption coefficient |
| Ti(r,t) | Temperature of a particle at co-ordinate r and heating time t, K |
| Tp(x) | Temperature distribution in the powder jet along the X axis, K |
References
- Thompson, S.M.; Bian, L.; Shamsaei, N.; Yadollahi, A. An overview of Direct Laser Deposition for additive manufacturing; Part I: Transport phenomena, modeling and diagnostics. Addit. Manuf. 2015, 8, 36–62. [Google Scholar] [CrossRef]
- Staiano, G.; Gloria, A.; Ausanio, G.; Lanzotti, A.; Pensa, C.; Martorelli, M. Experimental study on hydrodynamic performances of naval propellers to adopt new additive manufacturing processes. Int. J. Interact. Des. Manuf. (IJIDeM) 2016, 12, 1–14. [Google Scholar] [CrossRef]
- Ding, Y.; Dwivedi, R.; Kovacevic, R. Process planning for 8-axis robotized laser-based direct metal deposition system: A case on building revolved part. Robot. Comput. Manuf. 2017, 44, 67–76. [Google Scholar] [CrossRef]
- Korsmik, R.; Tsybulskiy, I.; Rodionov, A.; Klimova-Korsmik, O.; Gogolukhina, M.; Ivanov, S.; Zadykyan, G.; Mendagaliev, R. The approaches to design and manufacturing of large-sized marine machinery parts by direct laser deposition. Procedia CIRP 2020, 94, 298–303. [Google Scholar] [CrossRef]
- Mendagaliev, R.; Klimova-Korsmik, O.; Promakhov, V.; Schulz, N.; Zhukov, A.; Klimenko, V.; Olisov, A. Heat Treatment of Corrosion Resistant Steel for Water Propellers Fabricated by Direct Laser Deposition. Materials 2020, 13, 2738. [Google Scholar] [CrossRef] [PubMed]
- Turichin, G.; Klimova-Korsmik, O.; Babkin, K.; Ivanov, S.Y. Additive manufacturing of large parts. Addit. Manuf. 2021, 531–568. [Google Scholar] [CrossRef]
- Turichin, G.; Zemlyakov, E.; Klimova, O.; Babkin, K. Hydrodynamic Instability in High-speed Direct Laser Deposition for Additive Manufacturing. Phys. Procedia 2016, 83, 674–683. [Google Scholar] [CrossRef] [Green Version]
- Turichin, G.; Zemlyakov, E.; Babkin, K.; Ivanov, S.; Vildanov, A. Analysis of distortion during laser metal deposition of large parts. Procedia CIRP 2018, 74, 154–157. [Google Scholar] [CrossRef]
- Fu, G.; Zhang, D.Z.; He, A.N.; Mao, Z.; Zhang, K. Finite Element Analysis of Interaction of Laser Beam with Material in Laser Metal Powder Bed Fusion Process. Materials 2018, 11, 765. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Razavykia, A.; Brusa, E.; Delprete, C.; Yavari, R. An Overview of Additive Manufacturing Technologies—A Review to Technical Synthesis in Numerical Study of Selective Laser Melting. Materials 2020, 13, 3895. [Google Scholar] [CrossRef]
- Guo, Z.; Wang, L.; Wang, C.; Ding, X.; Liu, J. Heat Transfer, Molten Pool Flow Micro-Simulation, and Experimental Research on Molybdenum Alloys Fabricated via Selective Laser Melting. Materials 2020, 14, 75. [Google Scholar] [CrossRef] [PubMed]
- Ning, J.; Sievers, D.E.; Garmestani, H.; Liang, S.Y. Analytical Thermal Modeling of Metal Additive Manufacturing by Heat Sink Solution. Materials 2019, 12, 2568. [Google Scholar] [CrossRef] [Green Version]
- Caiazzo, F.; Alfieri, V. Simulation of Laser-assisted Directed Energy Deposition of Aluminum Powder: Prediction of Geometry and Temperature Evolution. Materials 2019, 12, 2100. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Turichin, G.; Valdaytseva, E.; Pozdeeva, E.; Zemlykov, E. Influence of aerodynamic force on powder transfer to flat substrate in laser cladding, BTLA. In Proceedings of the Six International Scientific and Technical Conference, Saint Petersburg, Russia, 2–6 September 2009; pp. 42–47. [Google Scholar]
- Turichin, G.A.; Somonov, V.V.; Klimova, O.G. Investigation and Modeling of the Process of Formation of the Pad Weld and its Microstructure during Laser Cladding by Radiation of High Power Fiber Laser. Appl. Mech. Mater. 2014, 682, 160–165. [Google Scholar] [CrossRef]
- Bitzadze, A.V.; Kalinichenko, D.F. Collection of Problems on Equations of Mathematical Physics; Nauka: Moscow, Russia, 1986; p. 224. [Google Scholar]
- Stankevich, S.L.; Korsmik, R.S.; Valdaytseva, E.A. Modeling of bead formation process during laser cladding. J. Phys. Conf. Ser. 2017, 857, 12045. [Google Scholar] [CrossRef] [Green Version]
- Stankevich, S.L.; Topalov, I.K.; Golovin, P.A.; Valdaytseva, E.A. Study of metallic powder flow in discrete coaxial nozzles. J. Phys. Conf. Ser. 2018, 1109, 012008. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical constants of transition metals: Ti, V, Cr, Mn, Fe, Co, Ni, and Pd. Phys. Rev. B 1974, 9, 5056–5070. [Google Scholar] [CrossRef]
- Werner, W.S.M.; Glantschnig, K.; Draxl, C. Optical Constants and Inelastic Electron-Scattering Data for 17 Elemental Metals. J. Phys. Chem. Ref. Data 2009, 38, 1013–1092. [Google Scholar] [CrossRef]
- Ordal, M.A.; Bell, R.J.; Alexander, R.W.; Long, L.L.; Querry, M.R. Optical properties of Au, Ni, and Pb at submillimeter wavelengths. Appl. Opt. 1987, 26, 744–752. [Google Scholar] [CrossRef]
- Rakić, A.D.; Djurišić, A.B.; Elazar, J.M.; Majewski, M.L. Optical properties of metallic films for vertical-cavity optoelectronic devices. Appl. Opt. 1998, 37, 5271–5283. [Google Scholar] [CrossRef] [PubMed]
- Querry, M.R. Optical Constants; Contra University of Missouri-Kansas City: Kansas City, MO, USA, 1985. [Google Scholar]
- Palm, K.; Murray, J.; Narayan, T.C.; Munday, J.N. Dynamic Optical Properties of Metal Hydrides. Acs Photonics 2018, 5, 4677–4686. [Google Scholar] [CrossRef] [Green Version]
- Xie, J.; Kar, A. Laser welding of thin sheet steel with surface oxidation. Weld. J. 1999, 78, 343-s. [Google Scholar]
- Juan, J.; Peter, N. Thermophysical Properties. ASM Handb. 2008, 15, 468–481. [Google Scholar]

| Properties | Inconel 718 | VT6 | 316 L |
|---|---|---|---|
| Heat capacity, J/(G·K) | 0.435 | 0.546 | 0.45 |
| Heat conductivity W/(m·K) | 8.9 | 26 | 30 |
| Density, kg/m3 | 8190 | 4430 | 7800 |
| Melting point, K | 1600 | 1920 | 1710 |
| Reflectivity for 1.06 μm, % | 77 | 61 | 68 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turichin, G.A.; Valdaytseva, E.A.; Stankevich, S.L.; Udin, I.N. Computer Simulation of Hydrodynamic and Thermal Processes in DLD Technology. Materials 2021, 14, 4141. https://doi.org/10.3390/ma14154141
Turichin GA, Valdaytseva EA, Stankevich SL, Udin IN. Computer Simulation of Hydrodynamic and Thermal Processes in DLD Technology. Materials. 2021; 14(15):4141. https://doi.org/10.3390/ma14154141
Chicago/Turabian StyleTurichin, Gleb A., Ekaterina A. Valdaytseva, Stanislav L. Stankevich, and Ilya N. Udin. 2021. "Computer Simulation of Hydrodynamic and Thermal Processes in DLD Technology" Materials 14, no. 15: 4141. https://doi.org/10.3390/ma14154141
APA StyleTurichin, G. A., Valdaytseva, E. A., Stankevich, S. L., & Udin, I. N. (2021). Computer Simulation of Hydrodynamic and Thermal Processes in DLD Technology. Materials, 14(15), 4141. https://doi.org/10.3390/ma14154141






