Eurocode Shear Design of Coarse Recycled Aggregate Concrete: Reliability Analysis and Partial Factor Calibration
Abstract
:1. Introduction
1.1. Shear Resistance of Recycled Aggregate Concrete Elements
- At the same time, the mechanical and durability properties of concrete are detrimentally affected by the incorporation of RAs: for the same compressive strength, RAC is typically found to have a smaller Young’s modulus, larger creep and shrinkage and worse durability properties [9,10,11]. Fracture energy and tensile strength are also detrimentally affected, especially when the strength class of concrete is larger [12,13];
- The influence of the incorporation ratio of RAs on shear resistance [21];
- The shear resistance of prestressed RAC beams [22];
- The shear resistance of RAC elements made with RAs that are treated with beneficiation methods [23];
- Meta-analyses that compare the shear resistance of NAC and RAC based on several investigations [24];
- The previous finding is validated by a meta-analysis [24] that compares the model uncertainties () [30] of Eurocode shear resistance models for NAC and RAC design. These show that the resistance models of EN1992 [31] and prEN1992 [32] for elements without shear reinforcement overestimate the resistance of RAC in comparison to NAC elements;
- Aggregate interlock is a preponderant mechanism in shear strength mobilisation [39];
1.2. Codified Shear Design of Recycled Aggregate Concrete
- Partial factors = 1.35 and increase actions. Permanent loads are multiplied by and variable loads are multiplied by ;
- Partial factors = 1.15 and decrease material properties or resistance (depending on the resistance model). In most cases, the characteristic yield stress of the reinforcement is divided by , while the compressive strength of concrete is divided by ;
- may be modelled as , where is a partial factor for material variability and is a partial factor that accounts for the uncertainty in geometry and in resistance modelling.
- The behaviour of RAC may be more variable than that of NAC;
- The resistance models used for NAC may not be as representative for RAC.
1.3. Objectives
- Proposal of a resistance format with a specific partial factor for RAC design;
- Reliability analyses for representative cases of design using the stochastic models for proposed in [24];
- Calibration of to be used in the resistance format proposed;
- Sensitivity analyses to understand the robustness of the calibrated for the shear design of elements with shear reinforcement.
2. Design Equations of the Eurocode Format
2.1. Design of Members without Shear Reinforcement
- is the partial factor for concrete;
- is the width of the web of the beam;
- is the effective depth of the beam;
- accounts for size effects. In this equation, is in mm;
- is the geometric ratio of the longitudinal tensile reinforcement. In this equation, ;
- is the characteristic compressive strength of concrete and is in MPa;
- is the minimum shear stress. This condition is always complied with in this paper and is not mentioned from here on.
- In the case of NAC, is replaced with ;
- In the case of RAC, is replaced with .
- if
- if ;
- , where ;
- if ;
- ;
- is the characteristic yielding stress of the longitudinal reinforcement;
- is the partial factor of steel reinforcement;
- and are the bending moment and shear stress at the control section;
- In this code, no limit on the of EC2 (2004) is imposed.
2.2. Design of Members with Shear Reinforcement
- is the shear reinforcement area;
- is the distance between shear reinforcement;
- is the characteristic yield stress of the shear reinforcement;
- is the partial factor for reinforcement strength, including geometric and modelling uncertainty;
- is the angle of the strut with the longitudinal axis of the element. This angle may be assumed as any value in the region of 21.8 to 45°.
3. Reliability Analysis for Partial Factor Calibration
3.1. Calibration Procedure and Reliability Method
- Cases of design are defined;
- The load combination presented in Equation (10) is used to determine ;
- An iterative process takes place, beginning with the preliminary proposal of the authors [24] for and . For a given , the equation for the design value of resistance is used to design the structural element;
- A reliability analysis takes place, in which a limit state function of the type is used to determine . is the random outcome of resistance and is the random outcome of load-effects. The limit state functions used are presented in Section 3.2 and Section 3.3;
- When is below expectations, a new partial factor is checked and a new iteration (starting at step 3 of this bullet list) takes place;
- The calibration criteria for shear design of elements without shear reinforcement are that:
- In the case of NAC, ensures that the target reliability index ( = 3.8, since reliability class 2 and a 50-year reference period are considered [44]) is complied with in the majority of cases of design. Moreover, the value should be similar to those obtained in seminal reliability assessments of the Eurocodes [55,56];
- In the case of RAC, the criterion is that results in a similar β value to that obtained when is used for NAC design;
- In the case of the shear design of elements with shear reinforcement, no partial factor for NAC is used and the criterion is that the calibrated leads to a similar value to that when NAC elements are designed.
- The partial factors for shear resistance of elements without shear reinforcement are calibrated for the shear design of slabs;
- The partial factor for shear resistance of elements with shear reinforcement is calibrated for the shear design of beams.
3.2. Limit State Function for Slabs without Shear Reinforcement
3.3. Limit State Function for Beams with Shear Reinforcement
4. Cases of Design and Modelling
4.1. Cases of Design
- The uncertainty in the outcome of resistance of this type of design is virtually lognormally distributed and reliability is predominantly dependent on the moments of and , which do not depend on the case of design. This occurs because Equation (13) has a multiplicative nature, is mainly composed of lognormal distributions, and depends mostly on and ;
- The uncertainty in the outcome of load-effects depends on , , and only. Since the statistics of are fixed for all cases of design, loads are given by + and the variability of and are defined in terms of their coefficient of variation (CoV), different cases of design lead to similar uncertainty in the outcome of load-effects.
4.2. Deterministic and Stochastic Modelling
- Assumption 1, in which the statistics of NAC are those presented in fib Bulletin 80 [79] for ∙ between 1 and 2 MPa. Concerning RAC, this case assumes that the mean value of is unaffected by the incorporation of RAs, but the standard deviation increases as the RA incorporation ratio increases;
- Assumption 2, in which the statistics of NAC are those presented in fib Bulletin 80 [79] for ∙ between 1 and 2 MPa and pessimistic expectations for the influence of RAs on the mean value and standard deviation of are assumed.
5. Results
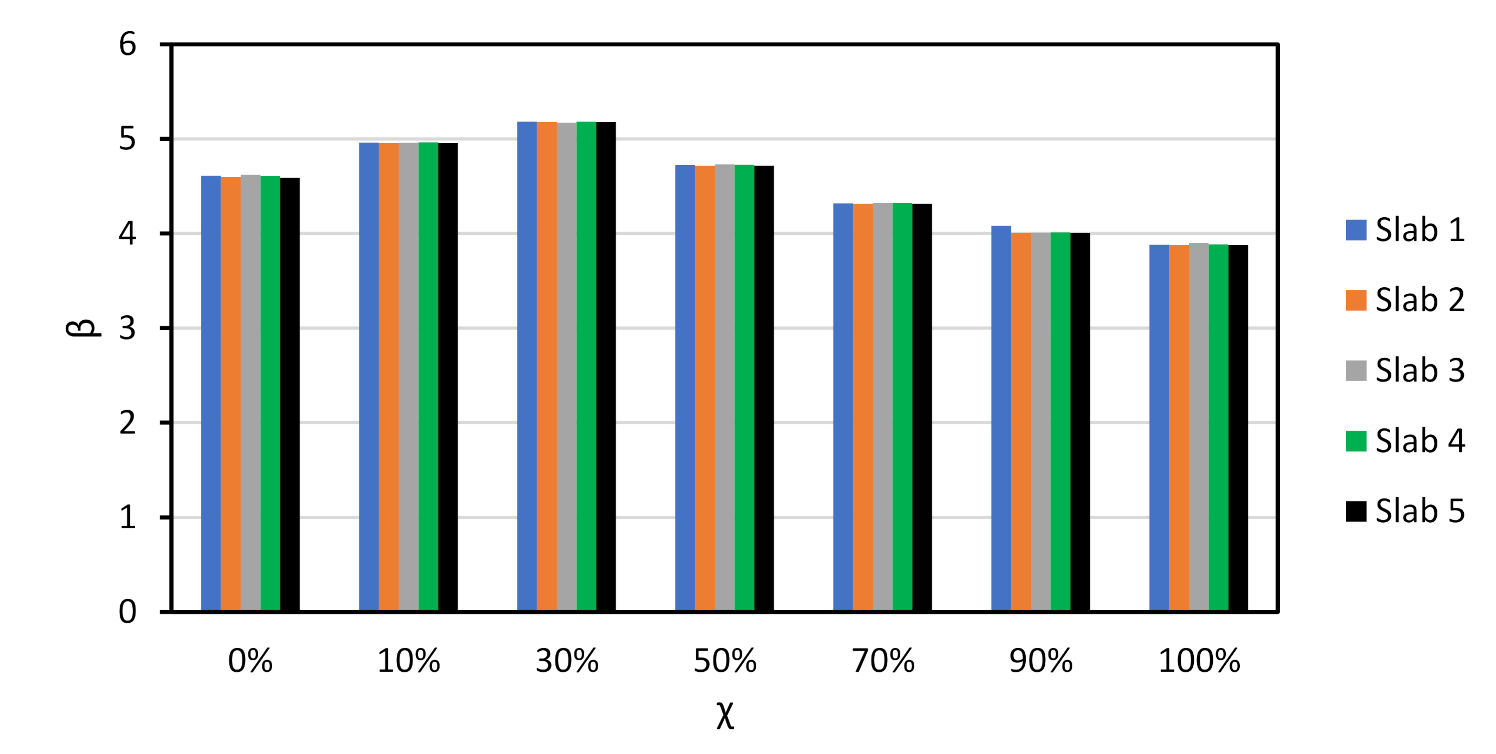
5.1. Slabs without Shear Reinforcement
5.1.1. Design with prEN1992
5.1.2. Design with EN1992
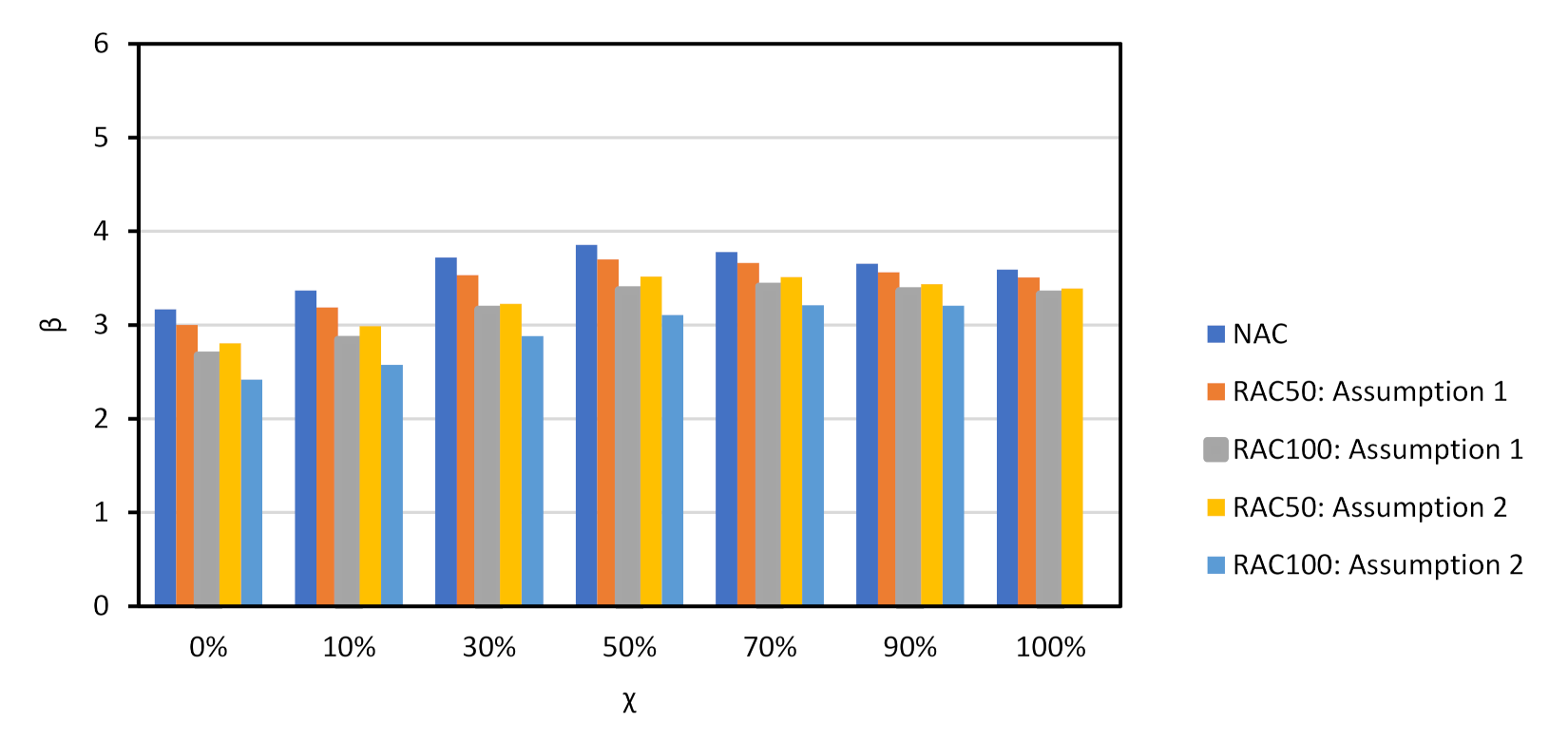
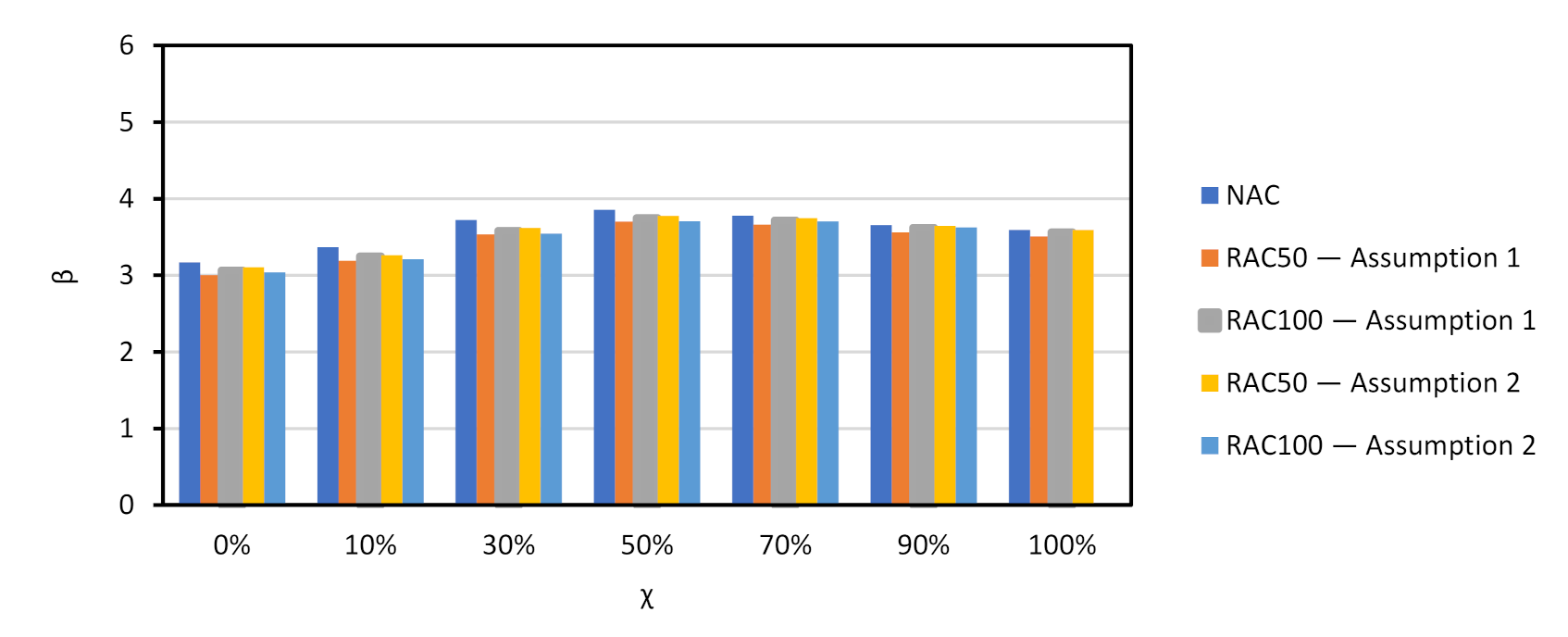
5.2. Beams with Shear Reinforcement
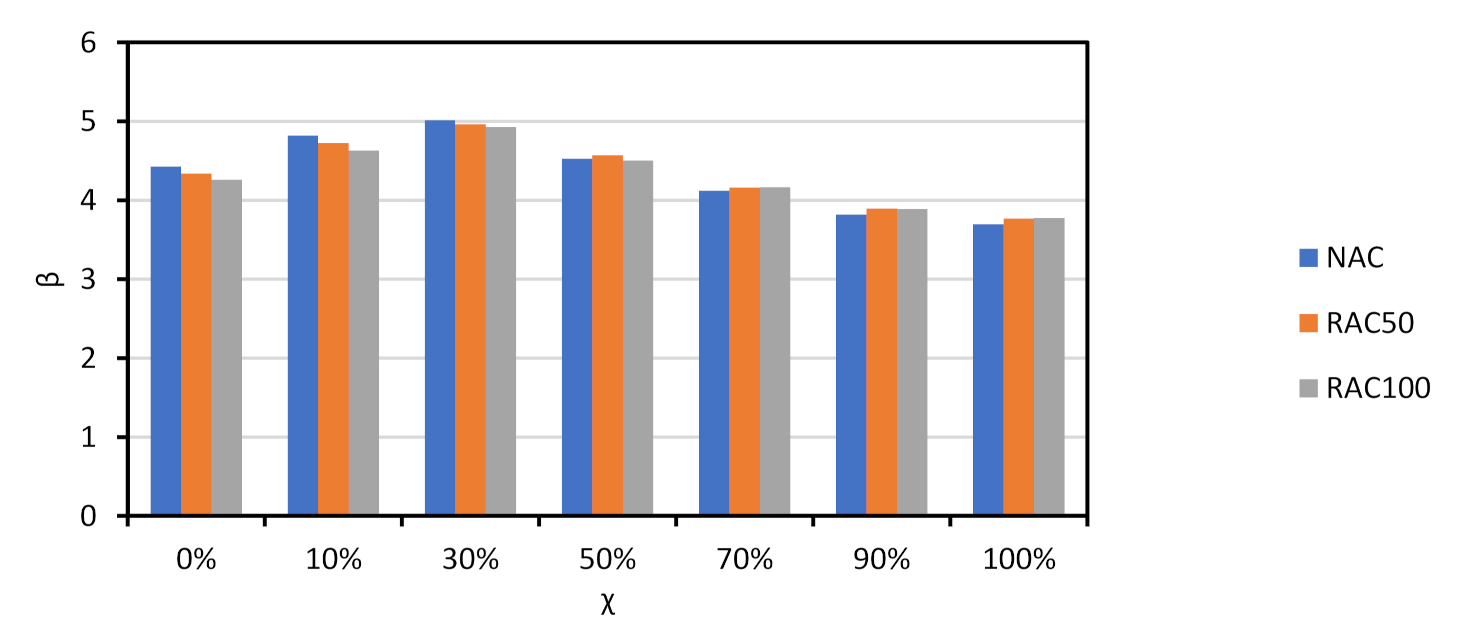
- For Assumption 1 and χ = 50%, the beam made with RAC100 has a 50-year of 3.75. Assumption 1 models with a mean of 1.25;
- If the mean of is 1.20 instead of 1.25, the actual 50-year would correspond to roughly:
5.3. Recommendations for Design
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
List of Acronyms and Symbols
| CDW | construction and demolition waste |
| CoV | coefficient of variation |
| NA | coarse natural aggregate |
| RA | coarse recycled aggregate |
| RAC | concrete with partial or total incorporation of coarse recycled aggregate concrete |
| RAC50 | recycled aggregate concrete elements with 50% incorporation of coarse recycled aggregates |
| RAC100 | recycled aggregate concrete elements with full incorporation of coarse recycled aggregates |
| cross-sectional area of the reinforcement | |
| area of shear reinforcement | |
| random outcome of load-effects | |
| design value of load-effects | |
| Young’s modulus of reinforcement | |
| conversion of delivered strength measured on standard specimens to the strength within structural elements | |
| height of the beam | |
| bending moment at the control section | |
| random outcome of permanent loading | |
| characteristic value of permanent loading | |
| random outcome of variable loading | |
| characteristic value of variable loading | |
| random outcome of resistance | |
| shear stress at the control section | |
| design value of shear resistance | |
| design value of the minimum shear resistance of elements without shear reinforcement | |
| design value of the shear resistance of the compression struts of the resistance model of beams with shear reinforcement | |
| design value of the shear resistance of the ties of the resistance model of beams with shear reinforcement | |
| width of the web of the beam | |
| concrete cover | |
| effective depth of the beam | |
| maximum aggregate diameter | |
| random outcome of the compressive strength of concrete | |
| characteristic value of the compressive strength of concrete | |
| random outcome of the yield stress of the reinforcement | |
| design value of the yield stress of the reinforcement | |
| characteristic yield stress of the reinforcement | |
| limit state function | |
| distance between reinforcement | |
| uncertainty in the width of the beam | |
| diameter of longitudinal reinforcement | |
| angle of the compression strut with the longitudinal axis used in the resistance model of elements with shear reinforcement | |
| α | direction cosine of a stochastic variable |
| β | reliability index |
| target reliability index | |
| partial factor for the strength of concrete | |
| partial factor for the variability of the strength of concrete | |
| partial factor for permanent loads | |
| partial factor for variable loads | |
| partial factor for shear design of natural aggregate concrete elements without shear reinforcement | |
| partial factor for shear design of recycled aggregate concrete elements | |
| partial factor for shear design of recycled aggregate concrete elements with 50% incorporation of coarse recycled aggregates | |
| partial factor for shear design of recycled aggregate concrete elements with full incorporation of coarse recycled aggregates | |
| partial factor for the uncertainty in geometry and in resistance modelling | |
| partial factor for the yield stress of the reinforcement | |
| model uncertainty of load-effect modelling | |
| model uncertainty of the resistance model | |
| stochastic model for the conversion of specified to delivered strength | |
| geometric ratio of longitudinal tensile reinforcement | |
| geometric ratio of shear reinforcement | |
| minimum shear stress of the resistance model of elements without shear reinforcement | |
| ratio of the design value of the variable loading to the total design value of loading |
References
- Pacheco, J.; De Brito, J.; Ferreira, J.; Soares, D. Destructive horizontal load tests of full-scale recycled aggregate concrete structures. Aci Struct. J. 2015, 112, 815–826. [Google Scholar] [CrossRef] [Green Version]
- Rangel, C.S.; Amario, M.; Pepe, M.; Yao, Y.; Mobasher, B.; Filho, R.T. Tension stiffening approach for interface characterization in recycled aggregate concrete. Cem. Concr. Compos. 2017, 82, 176–189. [Google Scholar] [CrossRef]
- European Environment Agency. Construction and Demolition Waste: Challenges and Opportunities in a Circular Economy; Briefing no. 14/2019; European Environment Agency: Copenhagen, Denmark, 2020. [Google Scholar]
- Pacheco, J.; De Brito, J.; Chastre, C.; Evangelista, L. Uncertainty models of reinforced concrete beams in bending: Code comparison and recycled aggregate incorporation. J. Struct. Eng. 2019, 145, 04019013. [Google Scholar] [CrossRef]
- Silva, R.; De Brito, J. Reinforced recycled aggregate concrete slabs: Structural design based on Eurocode 2. Eng. Struct. 2020, 204, 110047. [Google Scholar] [CrossRef]
- Pacheco, J.; De Brito, J. Recycled aggregate concrete: Properties and behaviour, applications and production challenges. In Proceedings of the fib Symposium 2021: Concrete structures: New Trends for Eco-Efficiency and Performance, Lisbon, Portugal, 13–16 June 2021. [Google Scholar]
- Del Bosque, I.S.; Zhu, W.; Howind, T.; Matías, A.; de Rojas, M.S.; Medina, C. Properties of interfacial transition zones (ITZs) in concrete containing recycled mixed aggregate. Cem. Concr. Compos. 2017, 81, 25–34. [Google Scholar] [CrossRef] [Green Version]
- Pepe, M.; Grabois, T.M.; Silva, M.A.; Tavares, L.M.; Filho, R.D.T. Mechanical behaviour of coarse lightweight, recycled and natural aggregates for concrete. Proc. Inst. Civ. Eng. Constr. Mater. 2018, 173, 1–9. [Google Scholar] [CrossRef]
- Bravo, M.; de Brito, J.; Pontes, J.; Evangelista, L. Mechanical performance of concrete made with aggregates from construction and demolition waste recycling plants. J. Clean. Prod. 2015, 99, 59–74. [Google Scholar] [CrossRef]
- Xiao, J.; Li, W.; Fan, Y.; Huang, X. An overview of study on recycled aggregate concrete in China (1996–2011). Constr. Build. Mater. 2012, 31, 364–383. [Google Scholar] [CrossRef]
- Tošić, N.; Torrenti, J.M.; Sedran, T.; Ignjatović, I. Toward a codified design of recycled aggregate concrete structures: Background for the new fib Model Code 2020 and Eurocode 2. Struct. Concr. 2021. [Google Scholar] [CrossRef]
- Pacheco, J.; de Brito, J.; Chastre, C.; Evangelista, L. Scatter of constitutive models of the mechanical properties of concrete: Comparison of major international codes. J. Adv. Concr. Technol. 2019, 17, 102–125. [Google Scholar] [CrossRef] [Green Version]
- Pacheco, J. Reliability Analysis of Eco-Concrete. Ph.D. Thesis, Civil Engineering, Department of Civil Engineering, Architecture and Gerorresources, Instituto Superior Técnico, University of Lisbon, Lisbon, Portugal, 2020. [Google Scholar]
- Pacheco, J.; de Brito, J.; Ferreira, J.G.; Soares, D. Flexural load tests of full-scale recycled aggregates concrete structures. Constr. Build. Mater. 2015, 101, 65–71. [Google Scholar] [CrossRef]
- Tošić, N.; Marinković, S.; De Brito, J. Deflection control for reinforced recycled aggregate concrete beams: Experimental database and extension of the fib Model Code 2010 model. Struct. Concr. 2019, 20, 2015–2029. [Google Scholar] [CrossRef]
- Silva, R.; de Brito, J.; Dhir, R. Properties and composition of recycled aggregates from construction and demolition waste suitable for concrete production. Constr. Build. Mater. 2014, 65, 201–217. [Google Scholar] [CrossRef]
- Choi, H.; Yi, C.; Cho, H.; Kang, K.; Choi, H.; Yi, C.; Cho, H.; Kang, K. Experimental study on the shear strength of recycled aggregate concrete beams. Mag. Concr. Res. 2010, 62, 103–114. [Google Scholar] [CrossRef]
- Yun, H.-D.; Choi, W.-C. Shear Strength of Reinforced Recycled Aggregate Concrete Beams Without Shear Reinforcements. J. Civ. Eng. Manag. 2016, 23, 76–84. [Google Scholar] [CrossRef]
- Schubert, S.; Hoffmann, C.; Leemann, A.; Moser, K.; Motavalli, M. Recycled aggregate concrete: Experimental shear resistance of slabs without shear reinforcement. Eng. Struct. 2012, 41, 490–497. [Google Scholar] [CrossRef]
- Ignjatović, I.S.; Marinković, S.B.; Tošić, N. Shear behaviour of recycled aggregate concrete beams with and without shear reinforcement. Eng. Struct. 2017, 141, 386–401. [Google Scholar] [CrossRef]
- Arezoumandi, M.; Drury, J.; Volz, J.S.; Khayat, K. Effect of Recycled Concrete Aggregate Replacement Level on Shear Strength of Reinforced Concrete Beams. ACI Mater. J. 2015, 112, 559–568. [Google Scholar] [CrossRef]
- Brandes, M.R.; Kurama, Y.C. Behavior of shear-critical prestressed concrete beams with recycled concrete aggregates under ultimate loads. Eng. Struct. 2018, 165, 237–246. [Google Scholar] [CrossRef]
- Katkhuda, H.; Shatarat, N. Shear behavior of reinforced concrete beams using treated recycled concrete aggregate. Constr. Build. Mater. 2016, 125, 63–71. [Google Scholar] [CrossRef]
- Pacheco, J.; de Brito, J.; Chastre, C.; Evangelista, L. Uncertainty of shear resistance models: Influence of recycled concrete aggregate on beams with and without shear reinforcement. Eng. Struct. 2020, 204, 109905. [Google Scholar] [CrossRef]
- Francesconi, L.; Pani, L.; Stochino, F. Punching shear strength of reinforced recycled concrete slabs. Constr. Build. Mater. 2016, 127, 248–263. [Google Scholar] [CrossRef]
- Reis, N.; de Brito, J.; Correia, J.R.; Arruda, M.R.T. Punching behaviour of concrete slabs incorporating coarse recycled concrete aggregates. Eng. Struct. 2015, 100, 238–248. [Google Scholar] [CrossRef]
- Sahoo, S.; Singh, B. Punching shear capacity of recycled-aggregate concrete slab-column connections. J. Build. Eng. 2021, 41, 102430. [Google Scholar] [CrossRef]
- Etxeberria, M.; Mari, A.; Vázquez, E. Recycled aggregate concrete as structural material. Mater. Struct. 2006, 40, 529–541. [Google Scholar] [CrossRef]
- Han, B.C.; Yun, H.D.; Chung, S.Y. Shear capacity of reinforced concrete beams made with recycled-aggregate. ACI Spec. Publ. 2001, 200, 503–516. [Google Scholar]
- Sýkora, M.; Holicky, M. Assessment of Uncertainties in Mechanical Models. Appl. Mech. Mater. 2013, 378, 13–18. [Google Scholar] [CrossRef]
- EN1992-1-1. Eurocode 2-Design of Concrete Structures: Part 1-1: General Rules and Rules for Buildings; Comité Européen de Normalisation (CEN): Brussels, Belgium, 2008. [Google Scholar]
- CEN/TC-250/SC-2. prEN 1992-1-1 D6 Working File (2020-10-05 Rev. 7); CEN: Brussels, Belgium, 2020. [Google Scholar]
- Waseem, S.; Singh, B. An experimental study on shear capacity of interfaces in recycled aggregate concrete. Struct. Concr. 2018, 19, 230–245. [Google Scholar] [CrossRef] [Green Version]
- Khaldoun, N.R.; Abdul-Lateef, A.-K. Shear-friction behavior of recycled and natural aggregate concrete—an experimental investigation. ACI Struct. J. 2015, 112, 725–734. [Google Scholar]
- Fakitsas, C.G.; Papakonstantinou, P.E.A.; Kiousis, P.D.; Savva, A. Effects of recycled concrete agregates on the compressive and shear strength of high-strength self-consolidating concrete. J. Mater. Civ. Eng. 2012, 24, 356–361. [Google Scholar] [CrossRef]
- Xiao, J.; Sun, C.; Lange, D.A. Effect of joint interface conditions on shear transfer behavior of recycled aggregate concrete. Constr. Build. Mater. 2016, 105, 343–355. [Google Scholar] [CrossRef]
- Waseem, S.A.; Singh, B. Shear transfer strength of normal and high-strength recycled aggregate concrete—An experimental investigation. Constr. Build. Mater. 2016, 125, 29–40. [Google Scholar] [CrossRef]
- Xiao, J.; Xie, H.; Yang, Z. Shear transfer across a crack in recycled aggregate concrete. Cem. Concr. Res. 2012, 42, 700–709. [Google Scholar] [CrossRef]
- Walraven, J. Aggregate Interlock: A Theoretical and Experimental Analysis. Ph.D. Thesis, TU Delft, Delft, The Netherlands, 1980. [Google Scholar]
- Pacheco, J.; de Brito, J.; Chastre, C.; Evangelista, L. Bond of recycled coarse aggregate concrete: Model uncertainty and reliability-based calibration of design equations. Eng. Struct. 2021, 239, 112290. [Google Scholar] [CrossRef]
- Khoury, E.; Ambrós, W.; Cazacliu, B.; Sampaio, C.H.; Remond, S. Heterogeneity of recycled concrete aggregates, an intrinsic variability. Constr. Build. Mater. 2018, 175, 705–713. [Google Scholar] [CrossRef]
- Xiao, J.; Li, W.; Sun, Z.; Shah, P.S. Crack propagation in recycled aggregate concrete under uniaxial compressive loading. Mater. J. 2012, 109, 451–461. [Google Scholar]
- Guo, M.; Alam, S.Y.; Bendimerad, A.Z.; Grondin, F.; Rozière, E.; Loukili, A. Fracture process zone characteristics and identification of the micro-fracture phases in recycled concrete. Eng. Fract. Mech. 2017, 181, 101–115. [Google Scholar] [CrossRef]
- EN1990. Eurocode: Basis of Structural Design; Comité Européen de Normalisation (CEN): Brussels, Belgium, 2002. [Google Scholar]
- ISO2394. General Principles on Reliability for Structures; ISO: Geneve, Switzerland, 2014. [Google Scholar]
- Yousefpour, H.; Bayrak, O. Shear design of beams without stirrups: Survey of participants in the fib workshop on beam shear. Fib Bulletin 85: Towards a Rational Understanding of Shear in Beams and Slabs; Fib: Zurich, Switzerland, 2016. [Google Scholar]
- PT-SC2-T1. D3BG-Background Documents to the Final PT1 Draft prEN 1992-1-1:2018; CEN: Brussels, Belgium, 2018. [Google Scholar]
- Pacheco, J.; de Brito, J.; Chastre, C.; Evangelista, L. Experimental investigation on the variability of the main mechanical properties of recycled aggregate concrete. Constr. Build. Mater. 2019, 201, 110–120. [Google Scholar] [CrossRef]
- Pacheco, J.N.; De Brito, J.; Chastre, C.; Evangelista, L. Probabilistic Conversion of the Compressive Strength of Cubes to Cylinders of Natural and Recycled Aggregate Concrete Specimens. Materials 2019, 12, 280. [Google Scholar] [CrossRef] [Green Version]
- Fib. Bulletin 65. Model Code 2010 Final Draft; Fib: Lausanne, Switzerland, 2010; Volume 1. [Google Scholar]
- CEN/TC-250/SC-2. Updated Draft by SC2/WG1/CDG prEN 1992-1-1-D5 Working File (Rev. 11) 2020-05-2; CEN: Brussels, Belgium, 2020. [Google Scholar]
- ACI318-14. Building Code Requirements for Structural Concrete (ACI 318-14) and Commentary; The American Concrete Institute: Farmington Hills, MI, USA, 2014. [Google Scholar]
- Fib. Bulletin 66. Model Code 2010 Final Draft; Fib: Lausanne, Switzerland, 2010; Volume 2. [Google Scholar]
- Albuquerque, A.; Pacheco, J.; Brito, J. Eurocode Design of Recycled Aggregate Concrete for Chloride Environments: Stochastic Modeling of Chloride Migration and Reliability-Based Calibration of Cover. Crystals 2021, 11, 284. [Google Scholar] [CrossRef]
- BRE. Client Report 210297. An Independent Technical Expert Review of the SAKO Report; Gulvanessian, H., Calgaro, J.A., Spehl, P., Jensen, B., Eds.; BRE: Watford, UK, 2003. [Google Scholar]
- NKB/SAKO. NKB1999:01E Basis of design of structures. In Proposals for Modification of Partial Safety Factors in Eurocodes, I.-B.; Nordic Committee on Building Regulations (NBK): Oslo, Norway, 1999. [Google Scholar]
- Rackwitz, R.; Fiessler, B. Structural reliability under combined random load sequences. Comput. Struct. 1978, 9, 489–494. [Google Scholar] [CrossRef]
- Lemaire, M. Structural Reliability; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Ditlevsen, O.; Madsen, H.O. Structural Reliability Methods; Department of Mechanical Engineering, Technical University of Denmark: Lyngby, Denmark, 2005. [Google Scholar]
- EN206. Concrete: Specification, Performance, Production and Conformity. In Incorporating Corrigendum May 2014; CEN: Brussels, Belgium, 2013. [Google Scholar]
- LNEC E471. Guide for the Use of Coarse Recycled Aggregates in Concret-Guia Para a Utilização de Agregados Reciclados Grossos em Betões de Ligantes Hidráulicos; LNEC: Portugal, Spain, 2009. [Google Scholar]
- JCSS. Probabilistic Model Code. In Part 3: Material Properties; Danish Technical University: Lyngby, Denmark, 2001. [Google Scholar]
- Bartlett, F.M.; MacGregor, J.G. Statistical analysis of the compressive strength of concrete in structures. Mater. J. 1996, 93, 158–168. [Google Scholar]
- Pacheco, J.; de Brito, J.; Chastre, C.; Evangelista, L. Statistical analysis of Portuguese ready-mixed concrete production. Constr. Build. Mater. 2019, 209, 283–294. [Google Scholar] [CrossRef]
- Gulvanessian, H.; Holicky, M. Eurocodes: Using reliability analysis to combine action effects. Proc. Inst. Civ. Eng. Struct. Build. 2005, 158, 243–252. [Google Scholar] [CrossRef] [Green Version]
- Holicky, M. Reliability-based analysis of codified design allowing for production quality. In Proceedings of the 4th International ASRANet Colloquium, Athens, Greece, 25–27 June 2008. [Google Scholar]
- Gulvanessian, H.; Holický, M. Reliability based calibration of Eurocodes considering a steel member. In Proceedings of the JCSS Workshop on Reliability Based Code Calibration, Zurich, Switzerland, 21–22 March 2002. [Google Scholar]
- Holicky, M.; Markova, J. Calibration of reliability elements for a column. In Proceedings of the JCSS Workshop on Reliability Based Code Calibration, Joint Committee for Structural Safety, Zurich, Switzerland, 21–22 March 2002. [Google Scholar]
- Caspeele, R.S.; Miroslav, S.; Taerwe, L. Influence of quality control of concrete on structural reliability: Assessment using a Bayesian approach. Mater. Struct. 2014, 47, 105–116. [Google Scholar] [CrossRef]
- Caspeele, R.; Taerwe, L. Influence of concrete strength estimation on the structural safety assessment of existing structures. Constr. Build. Mater. 2014, 62, 77–84. [Google Scholar] [CrossRef]
- Gulvanessian, H.; Holický, M. Annex C-Calibration procedure. In Implementation of Eurocodes: Development of Skills Facilitating Implementation of Eurocodes. Handbook 2: Reliability Backgrounds; Leonardo da Vinci Pilot Project CZ/02/B/F/PP-134007; Prague, Czech Republic, 2005. [Google Scholar]
- Holický, M.; Retief, J.; Wium, J. Partial factors for selected reinforced concrete members: Background to a revision of SANS 10100-1. J. S. Afr. Inst. Civ. Eng. 2010, 52, 36–44. [Google Scholar]
- Gulvanessian, H.; Calgaro, J.A.; Holicky, M. Designers’ Guide to EN1990 Eurocode: Basis of Structural Design. In Designers’ Guide to the Eurocodes; Gulvanessian, H., Ed.; Thomas Telford: London, UK, 2002. [Google Scholar]
- EN1991-1. Eurocode 1: Actions on Structures-Part 1-1: General actions-Densities, Self-Weight, Imposed Loads for Buildings; CEN: Brussels, Belgium, 2002. [Google Scholar]
- Gulvanessian, H.; Formichi, P.; Calgaro, J.A. Designers’ guide to Eurocode 1: Actions on buildings. In Designers’ Guide to the Eurocodes; Harding, G., Ed.; Thomas Telford: London, UK, 2009; Volume 266. [Google Scholar]
- Sedlacek, G.; Gulvanessian, H. Eurocode 1: Basis of Design and Actions on Structures: Part 2.1: Densities, Self Weight, Imposed Loads; IABSE Rep; IABSE: Zurich, Switzerland, 1996; Volume 74. [Google Scholar]
- Holický, M.A. Chapter 1-Self-weight and imposed loads on buildings. In Implementation of Eurocodes: Development of Skills Facilitating Implementation of Eurocodes. Handbook 3: Action Effects for Buildings; Leonardo da Vinci Pilot Project CZ/02/B/F/PP-134007; Aachen, Germany, 2005. [Google Scholar]
- Holický, M.; Retief, J.V.; Sýkora, M. Assessment of model uncertainties for structural resistance. Probabilistic Eng. Mech. 2016, 45, 188–197. [Google Scholar] [CrossRef]
- Fib. Bulletin 80: Partial Factor Methods for Existing Concrete Structures; Fib: Lausanne, Switzerland, 2016. [Google Scholar]
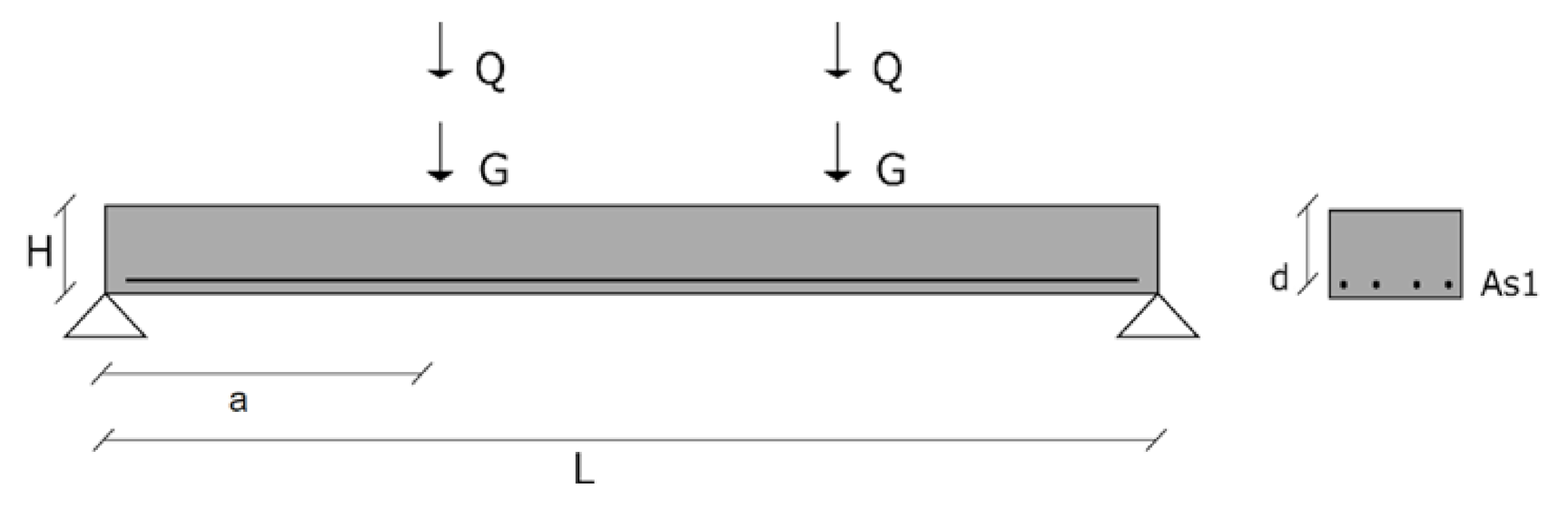

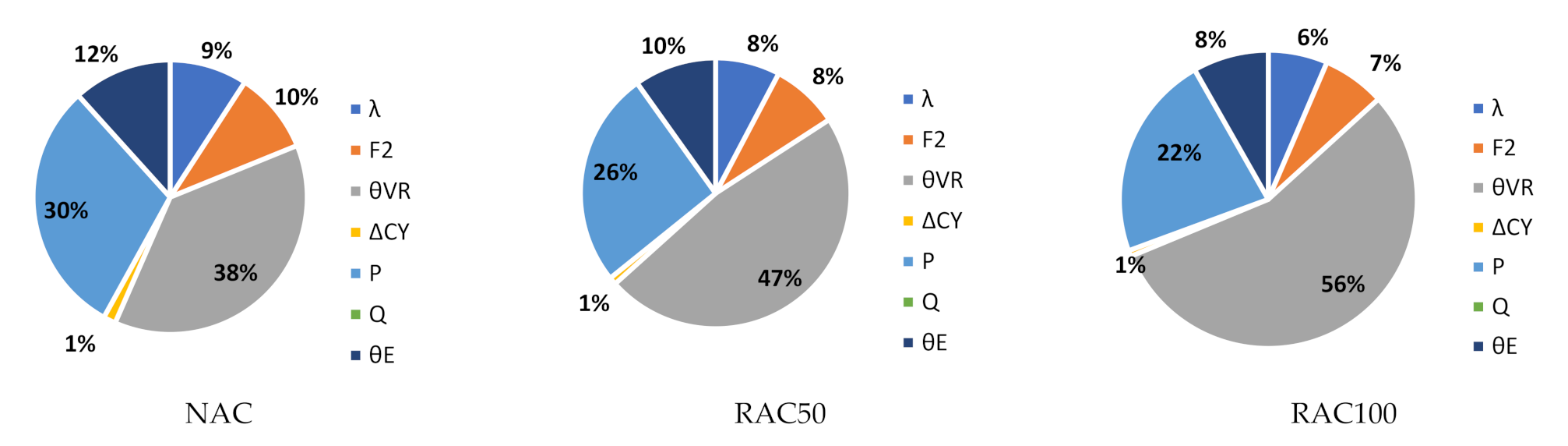

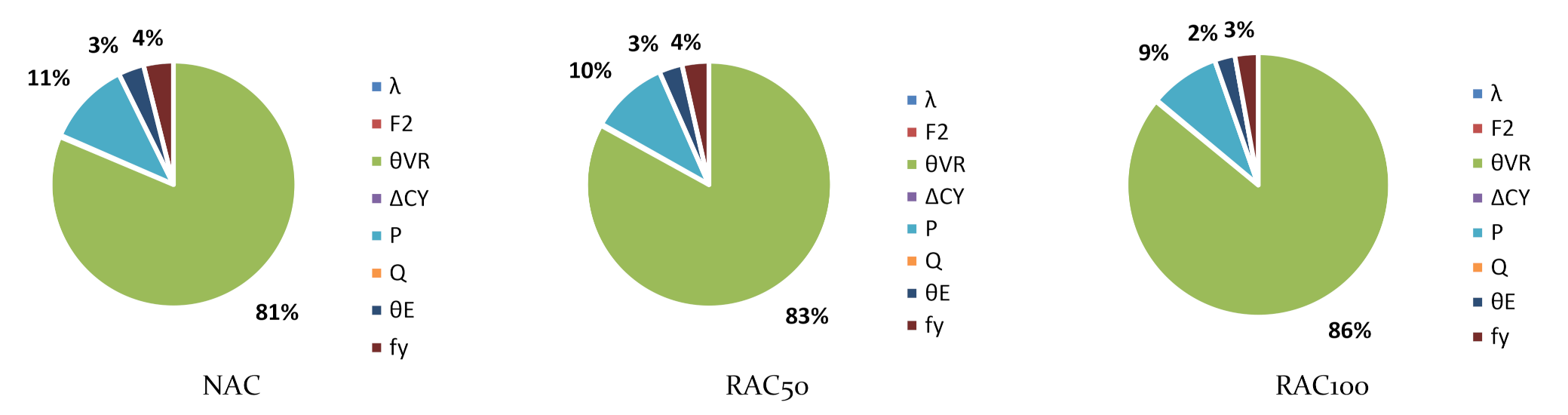
| Slab | (MPa) | (mm) | (mm) | (mm) | (m) | (mm) | (mm) | (kN) | ||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 25 | 20 | 170 | 25 | 5.0 | 2.5 | 12 | 100 | 0.81% | 122.1 |
| 2 | 25 | 20 | 140 | 25 | 5.0 | 2.5 | 16 | 100 | 1.88% | 135.5 |
| 3 | 25 | 20 | 210 | 25 | 5.0 | 2.5 | 16 | 150 | 0.76% | 140.0 |
| 4 | 40 | 20 | 170 | 25 | 6.5 | 2.5 | 16 | 150 | 0.97% | 150.4 |
| 5 | 40 | 20 | 145 | 25 | 6.5 | 2.5 | 16 | 75 | 2.39% | 177.1 |
| Code | |||
|---|---|---|---|
| EN1992 [32] | 1.45 | 1.55 | 1.60 |
| prEN1992 [31] | 1.40 | 1.60 | 1.70 |
| Slab | (MPa) | (mm) | (mm) | (m) | (mm) | (mm) | (kN) | ||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 25 | 190 | 25 | 5.0 | 2.5 | 16 | 104.1 | 1.23% | 122.1 |
| 2 | 25 | 190 | 25 | 5.0 | 2.5 | 16 | 86.2 | 1.49% | 135.5 |
| 3 | 25 | 215 | 25 | 5.0 | 2.5 | 16 | 100 | 1.10% | 140.0 |
| 4 | 40 | 175 | 25 | 6.5 | 2.5 | 16 | 73 | 1.94% | 150.4 |
| 5 | 40 | 200 | 25 | 6.5 | 2.5 | 20 | 94.2 | 2.02% | 177.1 |
(MPa) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (mm) | (cm2/mm) | (MPa) | Ω | (kN) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 25 | 250 | 450 | 25 | 407 | 16 | 8 | 150 | 6.7 | 0.27% | 1.17 | 30° | 185.9 |
| Parameter | Deterministic Model | Stochastic Model | Reference | ||||
|---|---|---|---|---|---|---|---|
| Symbol | Fractile | Symbol | Mean | Standard Deviation (σ) | Probability Distribution | ||
| Permanent load | 50 % | 0.10 × | Normal | [44] | |||
| Maximum variable load (50 years) | * | 0.60 | 0.35 | Gumbel | [65,66,67,68,69,70] | ||
| Model uncertainty of load-effects | Absent from deterministic modelling | 1.00 | 0.05 | Lognormal | [55,71] | ||
| Compressive strength | 5% fractile | , with assumed deterministic | [63,64] | ||||
| Specified to delivered strength | Absent from deterministic modelling | 1.20 | 0.17 | Lognormal | |||
| Standard to strength-in-structures | Absent from deterministic modelling | 0.95 | 0.13 | Lognormal | |||
| Yield stress of the reinforcement | 5% fractile | 30 MPa | Lognormal | [55,56,62,72]; | |||
| Young’s modulus of the reinforcement | = 200 GPa assumed as deterministic | ||||||
| Cross-sectional area of the reinforcement | assumed as deterministic | ||||||
| Height of the cross-section | H assumed as deterministic | ||||||
| Concrete cover (vertical) | Nominal value | : 5 mm (slabs) : −5 mm (beams) | : 5 mm (slabs) : −5 mm (beams) | : Normal is deterministic | [13,62] | ||
| Incorporation Ratio of RAs | Mean Value | Standard Deviation (σ) | Probability Distribution | |
|---|---|---|---|---|
| EN 1992 [31] | NAC | 1.03 | 0.113 | Lognormal |
| RAC50 | 1.00 | 0.120 | Lognormal | |
| RAC100 | 0.95 | 0.114 | Lognormal | |
| prEN 1992 [32] | NAC | 0.98 | 0.088 | Lognormal |
| RAC50 | 0.93 | 0.102 | Lognormal | |
| RAC100 | 0.93 | 0.121 | Lognormal |
| Incorporation Ratio of RA | Mean | Standard Deviation (σ) | Probability Distribution | Source | |
|---|---|---|---|---|---|
| Assumption 1 | NAC | 1.25 | 0.312 (CoV = 25.0%) | Lognormal | NAC: fib Bulletin 80 [79] RAC: Same mean value as NAC; pessimistic expectation of the CoV |
| RAC50 | 1.25 | 0.343 (CoV = 27.5%) | Lognormal | ||
| RAC100 | 1.25 | 0.375 (CoV = 30.0%) | Lognormal | ||
| Assumption 2 | NAC | 1.25 | 0.312 (CoV = 25.0%) | Lognormal | NAC: fib Bulletin 80 [79] RAC: Pessimistic expectation of the mean value and CoV |
| RAC50 | 1.21 | 0.333 (CoV = 27.5%) | Lognormal | ||
| RAC100 | 1.17 | 0.351 (CoV = 30.0%) | Lognormal |
| RA | Slab | χ | ||||||
|---|---|---|---|---|---|---|---|---|
| 0% | 10% | 30% | 50% | 70% | 90% | 100% | ||
| RAC50 | Slab 1 | 98% | 98% | 99% | 101% | 101% | 102% | 102% |
| Slab 2 | 98% | 98% | 99% | 101% | 101% | 102% | 102% | |
| Slab 3 | 98% | 98% | 100% | 101% | 102% | 102% | 102% | |
| Slab 4 | 98% | 98% | 99% | 101% | 103% | 103% | 102% | |
| Slab 5 | 100% | 102% | 103% | 104% | 104% | 104% | 104% | |
| RAC100 | Slab 1 | 96% | 96% | 98% | 100% | 101% | 102% | 102% |
| Slab 2 | 93% | 92% | 96% | 99% | 101% | 102% | 102% | |
| Slab 3 | 94% | 93% | 100% | 97% | 102% | 102% | 103% | |
| Slab 4 | 94% | 93% | 96% | 100% | 101% | 102% | 102% | |
| Slab 5 | 94% | 93% | 96% | 99% | 101% | 102% | 102% | |
| RA | Slab | χ | ||||||
|---|---|---|---|---|---|---|---|---|
| 0% | 10% | 30% | 50% | 70% | 90% | 100% | ||
| RAC50 | Slab 1 | 100% | 100% | 100% | 101% | 101% | 100% | 102% |
| Slab 2 | 100% | 100% | 100% | 101% | 101% | 102% | 102% | |
| Slab 3 | 102% | 100% | 101% | 101% | 101% | 101% | 102% | |
| Slab 4 | 100% | 101% | 100% | 101% | 101% | 102% | 102% | |
| Slab 5 | 101% | 100% | 100% | 101% | 101% | 102% | 102% | |
| RAC100 | Slab 1 | 98% | 98% | 99% | 100% | 100% | 98% | 100% |
| Slab 2 | 98% | 97% | 98% | 99% | 100% | 100% | 100% | |
| Slab 3 | 101% | 101% | 98% | 97% | 101% | 100% | 99% | |
| Slab 4 | 98% | 98% | 99% | 99% | 100% | 100% | 100% | |
| Slab 5 | 98% | 97% | 98% | 99% | 100% | 100% | 100% | |
| Elasticity (%) | NAC | RAC50 Assumption 1 | RAC100 Assumption 1 | RAC50 Assumption 2 | RAC100 Assumption 2 |
|---|---|---|---|---|---|
| Mean | 2.01 | 2.04 | 1.99 | 1.97 | 1.94 |
| Standard deviation | −0.86 | −0.88 | −0.89 | −0.89 | −0.91 |
| Design | ||||
|---|---|---|---|---|
| Type of Concrete | Shear without Shear Reinforcement | Shear with Shear Reinforcement—EN1992 [31] and prEN1992 [32] | ||
| EN1992 [31] | prEN1992 [32] | Assumption 1 (Moderate) | Assumption 2 (Pessimistic) | |
| NAC | 1.45 | 1.40 | 1.00 | 1.00 |
| RAC50 | 1.55 | 1.50 | 1.00 | 1.10 |
| RAC100 | 1.60 | 1.60 | 1.05 | 1.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pacheco, J.; de Brito, J.; Chastre, C.; Evangelista, L. Eurocode Shear Design of Coarse Recycled Aggregate Concrete: Reliability Analysis and Partial Factor Calibration. Materials 2021, 14, 4081. https://doi.org/10.3390/ma14154081
Pacheco J, de Brito J, Chastre C, Evangelista L. Eurocode Shear Design of Coarse Recycled Aggregate Concrete: Reliability Analysis and Partial Factor Calibration. Materials. 2021; 14(15):4081. https://doi.org/10.3390/ma14154081
Chicago/Turabian StylePacheco, João, Jorge de Brito, Carlos Chastre, and Luís Evangelista. 2021. "Eurocode Shear Design of Coarse Recycled Aggregate Concrete: Reliability Analysis and Partial Factor Calibration" Materials 14, no. 15: 4081. https://doi.org/10.3390/ma14154081
APA StylePacheco, J., de Brito, J., Chastre, C., & Evangelista, L. (2021). Eurocode Shear Design of Coarse Recycled Aggregate Concrete: Reliability Analysis and Partial Factor Calibration. Materials, 14(15), 4081. https://doi.org/10.3390/ma14154081