Analysis of Flexural Vibrations of a Piezoelectric Semiconductor Nanoplate Driven by a Time-Harmonic Force
Abstract
:1. Introduction
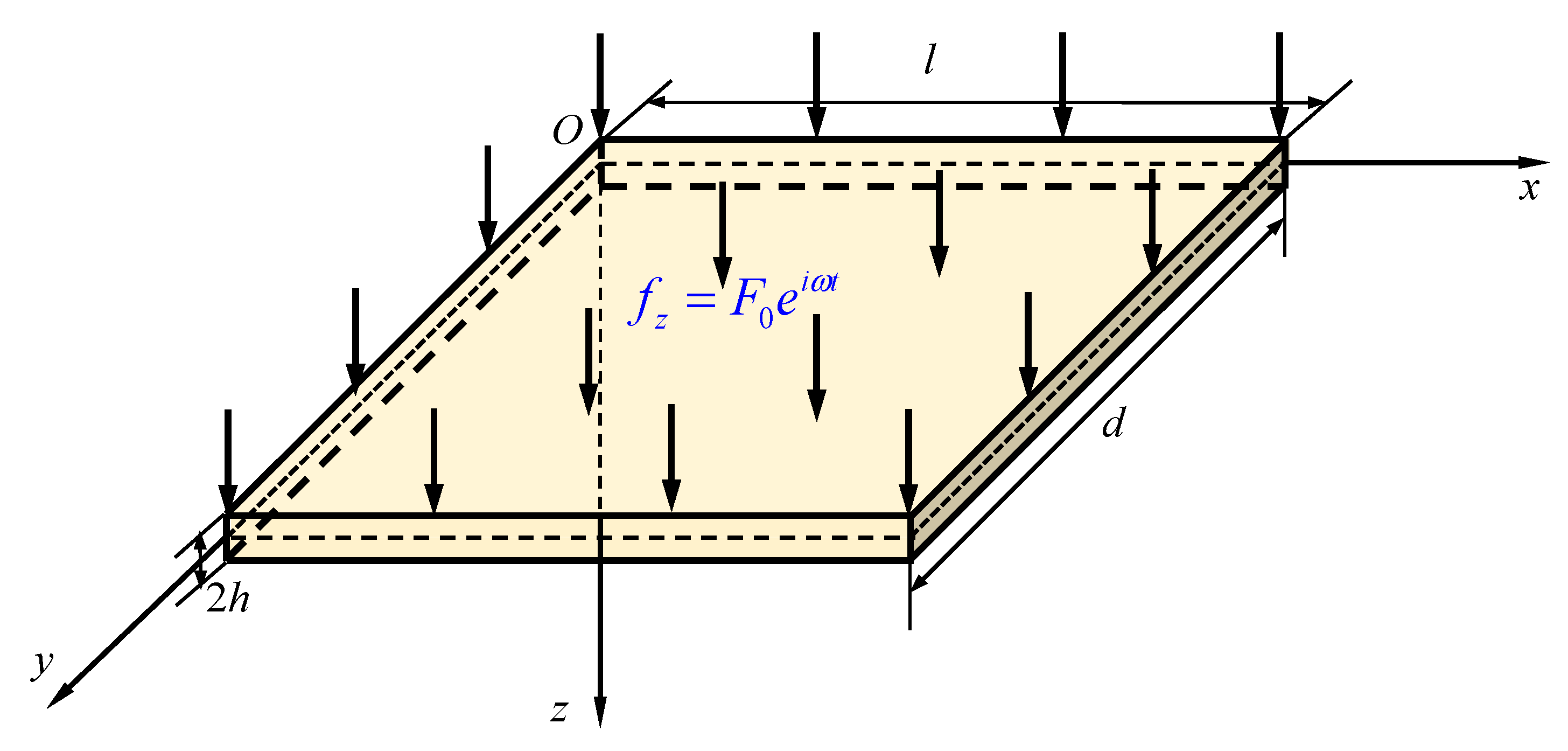
2. Piezoelectric Semiconductor Plate Model
3. Modal Analysis
4. Numerical Examples
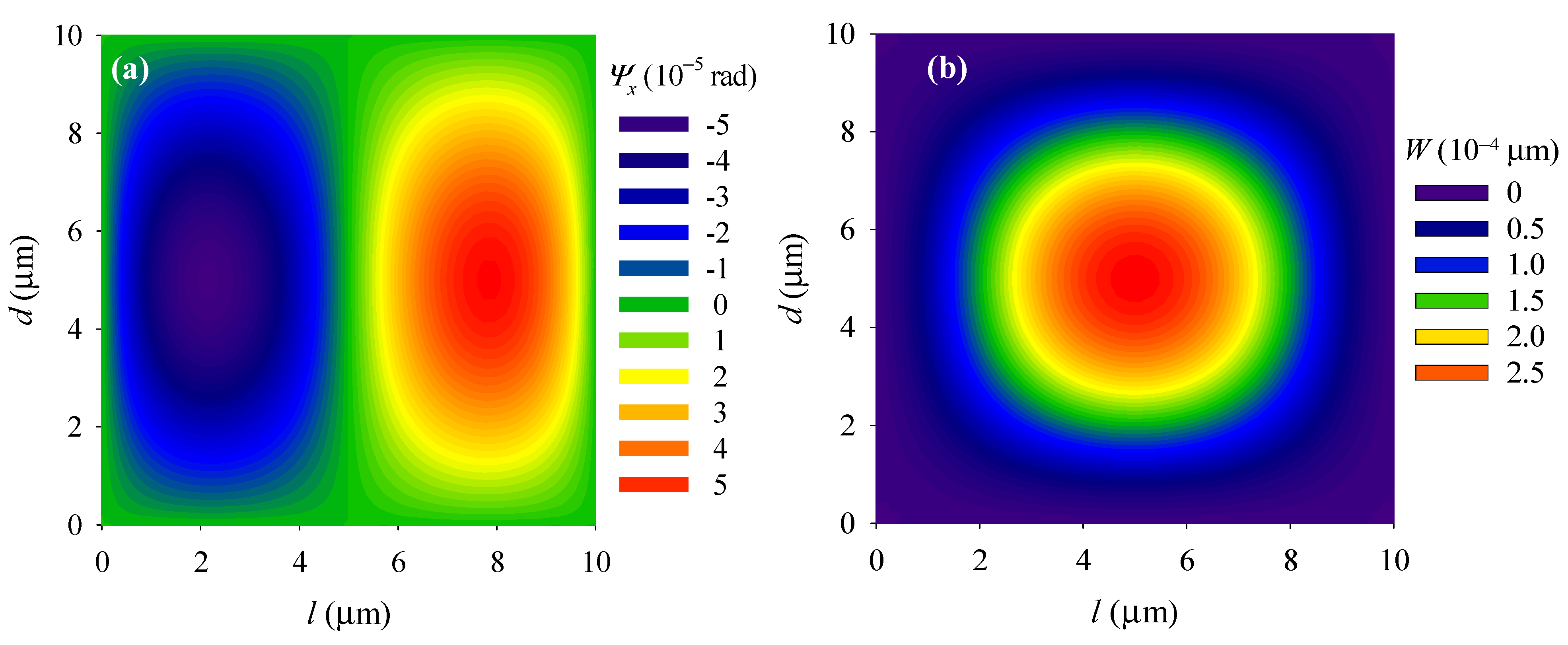
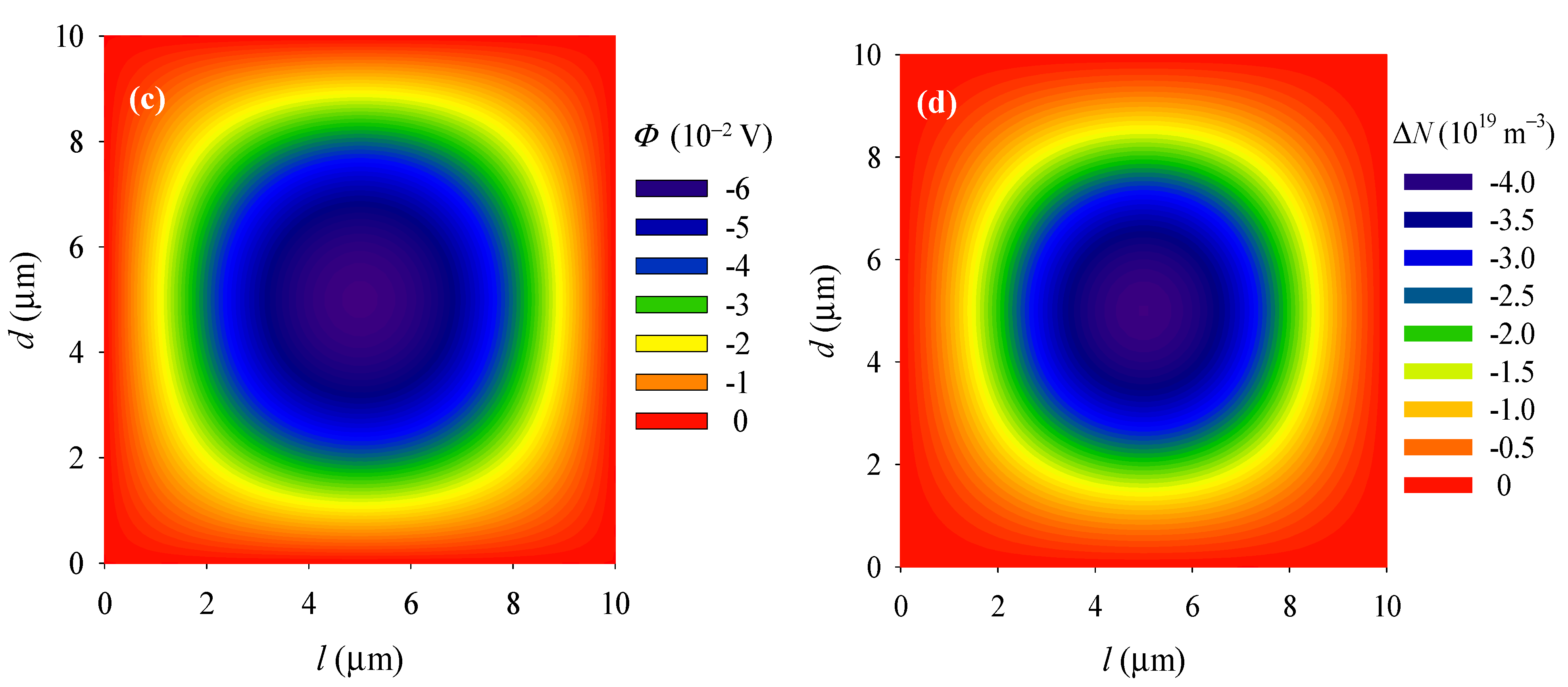
4.1. Vibration Behaviors
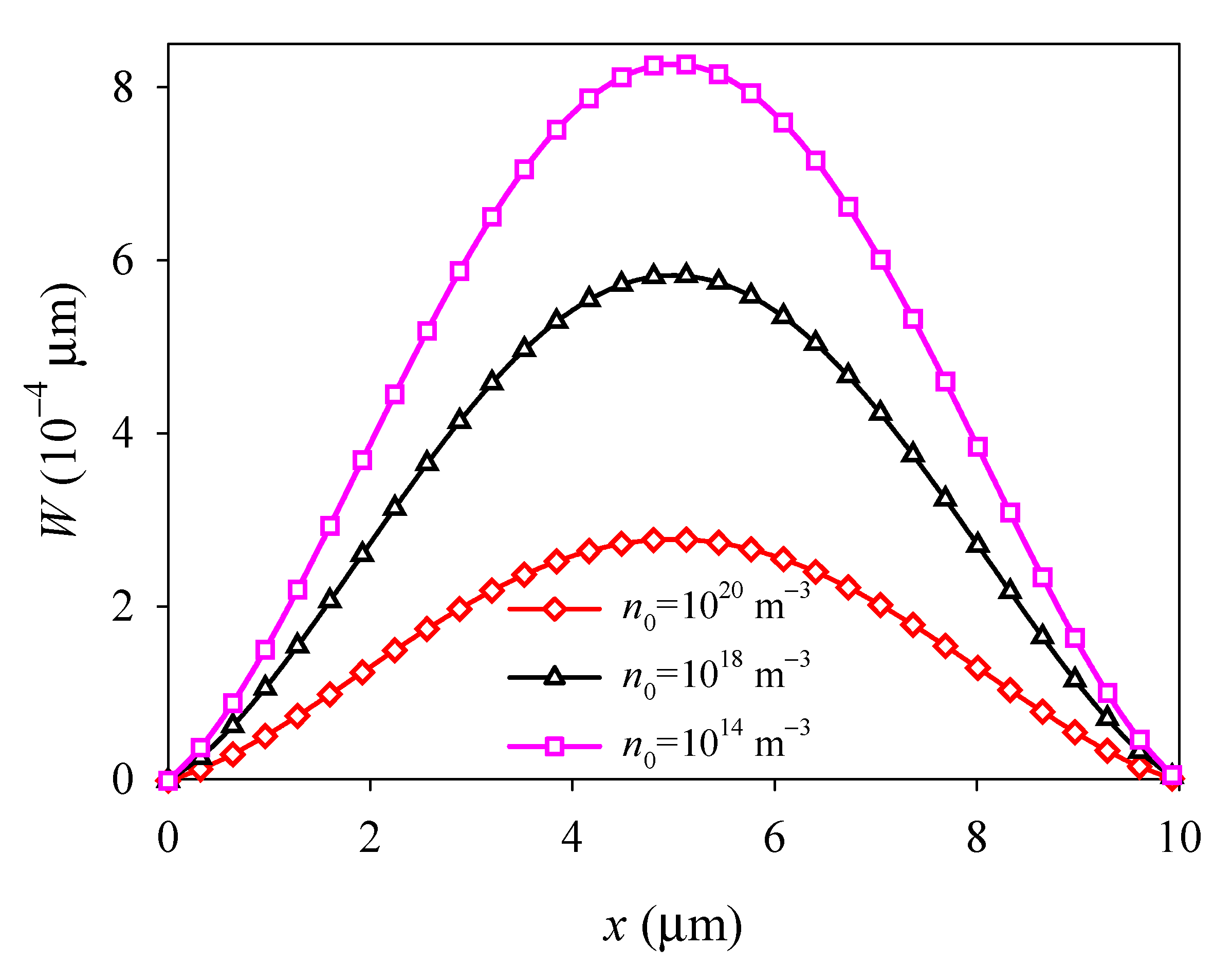
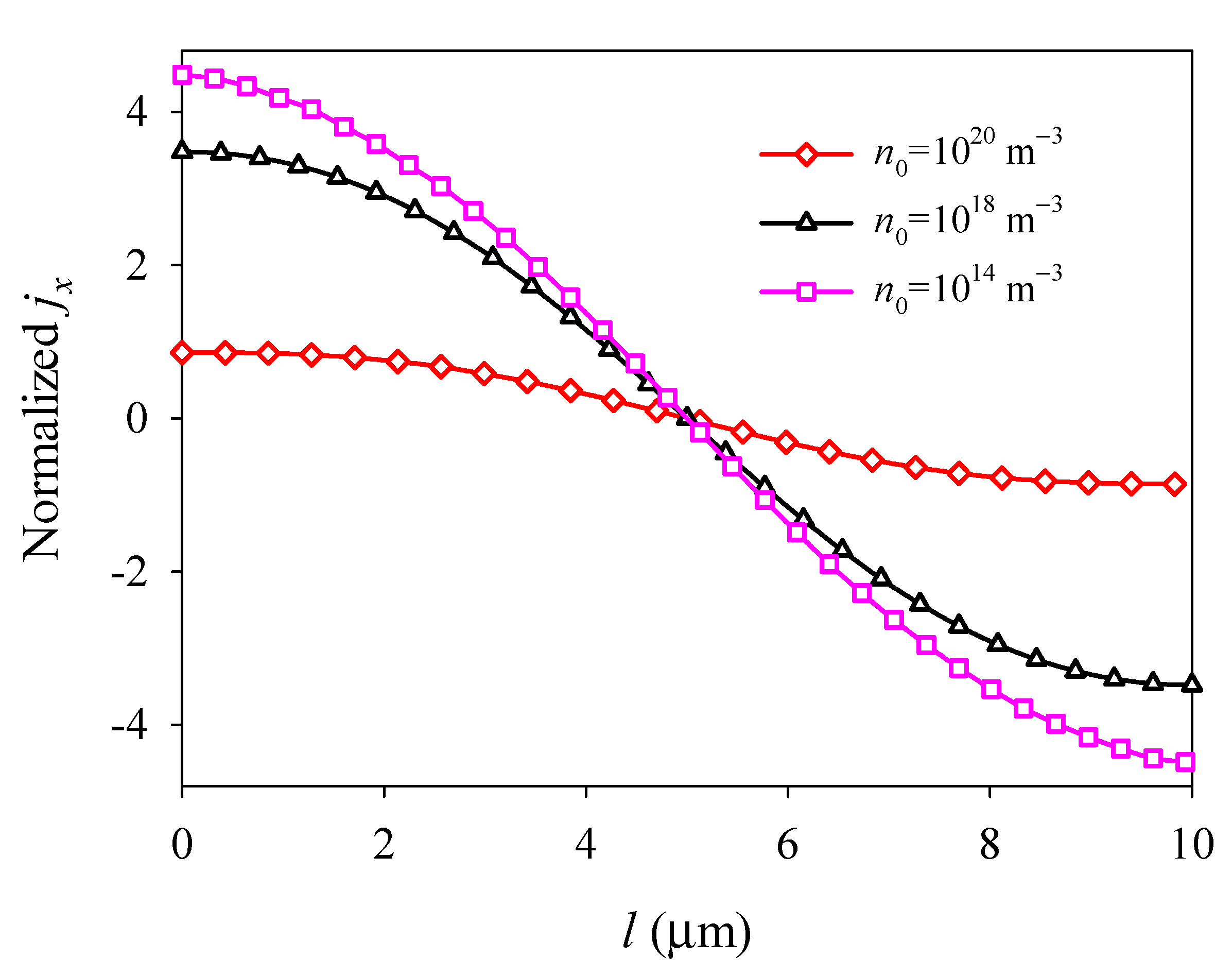
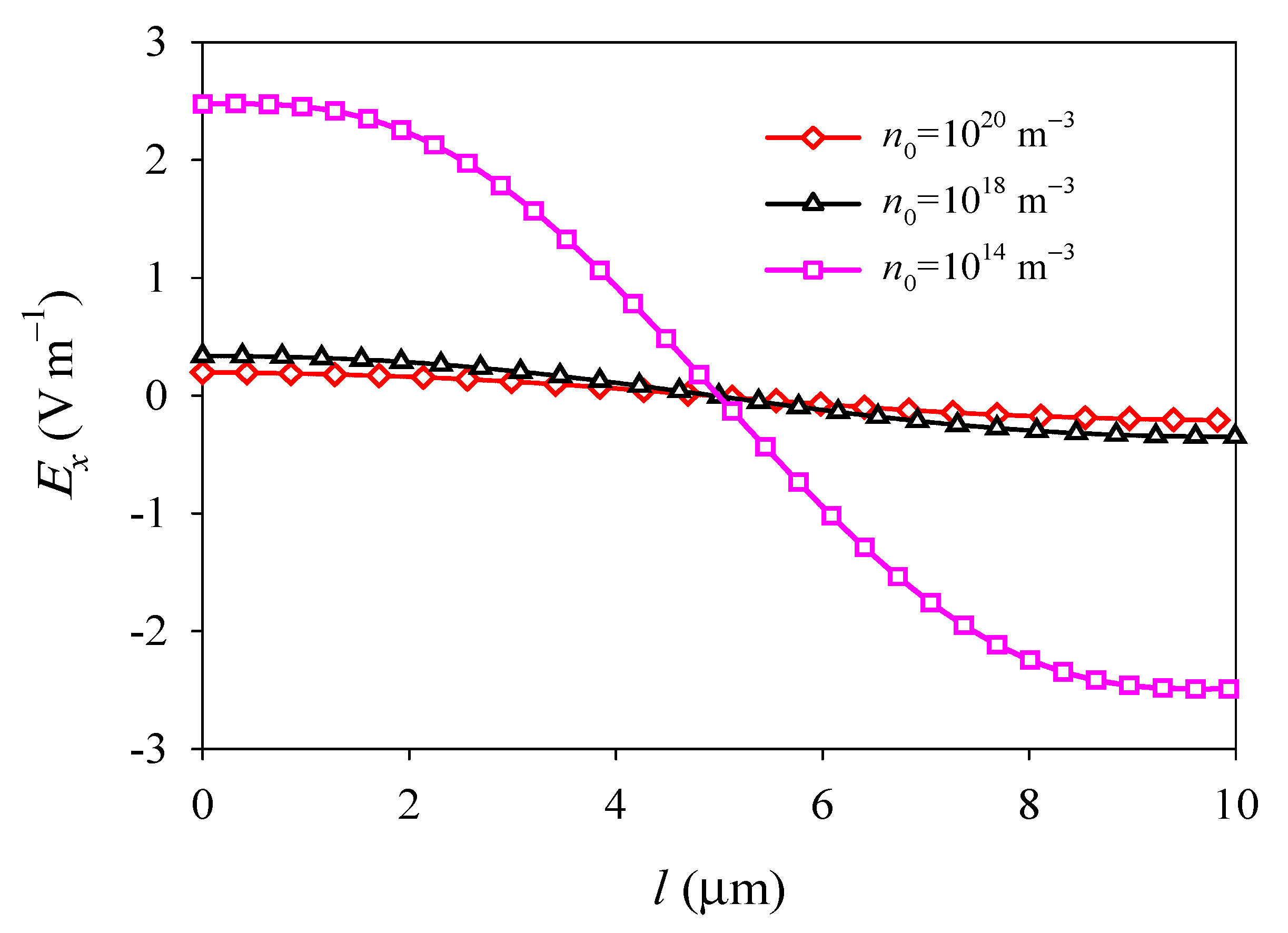
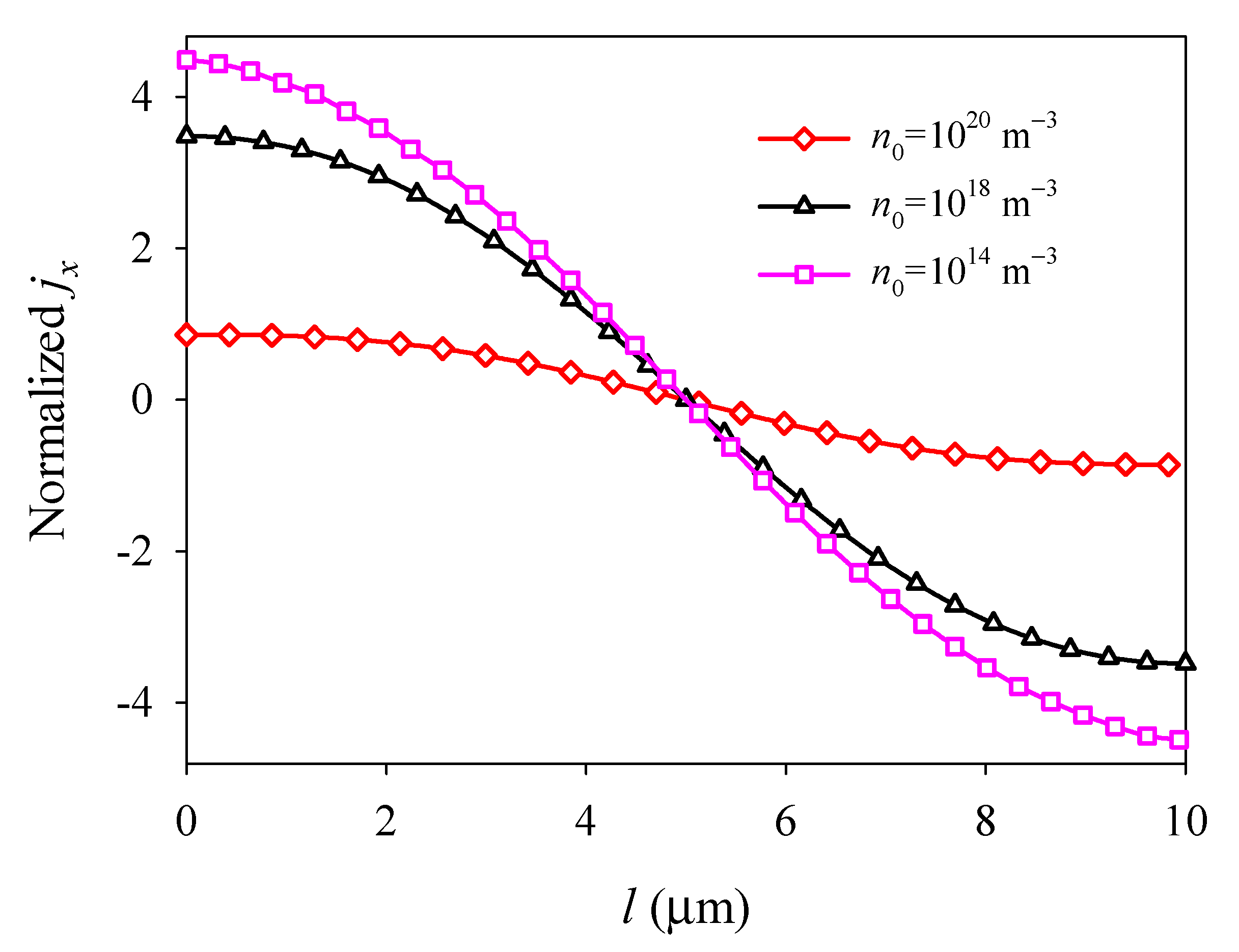
4.2. Effects of Initial Electron Concentration
5. Conclusions
- The amplitude of the deflection corresponding to the first resonant frequency is much larger than those at higher resonant frequencies, and a high energy conversion efficiency for conversing mechanical energy into electrical energy can be realized in a resonance state;
- With the increase in the initial electron concentration, the first-order nature frequency decreases until it reaches a constant value. This phenomenon indicates that initial electron concentration plays a role in the stiffness reduction;
- Due to the electron screen effect, the deflection, electric field, and electric current density in the PSC plate all decrease with the increase in the initial electron concentration.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Hutson, A.R. Piezoelectricity and Conductivity in ZnO and CdS. Phys. Rev. Lett. 1960, 4, 505–507. [Google Scholar] [CrossRef]
- Zhang, X.B.; Taliercio, T.; Kolliakos, S.; Lefebvre, P. Influence of electron-phonon interaction on the optical properties of III nitride semiconductors. J. Phys.-Condens. Matter. 2001, 13, 7053–7074. [Google Scholar] [CrossRef]
- He, J.H.; Hsin, C.L.; Liu, J.; Chen, L.J.; Wang, Z.L. Piezoelectric gated diode of a single ZnO nanowire. Adv. Mater. 2009, 19, 781–784. [Google Scholar] [CrossRef]
- Wang, Z.L. Piezopotential gated nanowire devices: Piezotronics and piezo-phototronics. Nano Today 2010, 5, 540–552. [Google Scholar] [CrossRef]
- Wang, Z.L. The new field of nanopiezotronics. Mater. Today 2007, 10, 20–28. [Google Scholar] [CrossRef]
- Yang, Q.; Guo, X.; Wang, W.H.; Zhang, Y.; Xu, S.; Lien, D.H.; Wang, Z.L. Enhancing Sensitivity of a Single ZnO Micro-/Nanowire Photo detector by Piezo-Phototronic Effect. ACS Nano 2010, 4, 6285–6291. [Google Scholar] [CrossRef]
- Zhu, G.; Yang, R.S.; Wang, S.H.; Wang, Z.L. Flexible high-output nanogenerator based on lateral ZnO nanowire array. Nano Lett. 2010, 10, 3151–3155. [Google Scholar] [CrossRef] [Green Version]
- Torrisi, G.; Crupi, I.; Mirabella, S.; Terrasi, A. Robustness and electrical reliability of AZO/Ag/AZO thin film after bending stress. Sol. Energy. Mater. Sol. Cell 2017, 165, 88–93. [Google Scholar] [CrossRef]
- Zhang, C.L.; Wang, X.Y.; Chen, W.Q.; Yang, J.S. An analysis of the extension of a ZnO piezoelectric semiconductor nanofiber under an axial force. Smart Mater. Struct. 2017, 26, 025030. [Google Scholar] [CrossRef]
- Yang, W.L.; Hu, Y.T.; Yang, J.S. Transient extensional vibration in a ZnO piezoelectric semiconductor nanofiber under a suddenly applied end force. Mater. Res. Express 2019, 6, 025902. [Google Scholar] [CrossRef]
- Zhang, Q.Y.; Fan, C.Y.; Xu, G.T.; Zhao, M.H. Iterative boundary element method for crack analysis of two-dimensional piezoelectric semiconductor. Eng. Anal. Bound. Elem. 2017, 83, 87–95. [Google Scholar] [CrossRef]
- Zhao, M.H.; Yang, C.H.; Fan, C.Y.; Xu, G.T. Extended displacement discontinuity method for analysis of penny-shaped cracks in three-dimensional thermal piezoelectric semiconductors. Eur. J. Mech. A-Solids. 2018, 70, 23–36. [Google Scholar] [CrossRef]
- Luo, Y.X.; Zhang, C.L.; Chen, W.Q.; Yang, J.S. An analysis of PN junctions in piezoelectric semiconductors. J. Appl. Phys. 2017, 122, 204502. [Google Scholar] [CrossRef]
- Yang, W.L.; Liu, J.X.; Hu, Y.T. Mechanical tuning methodology on the barrier configuration near a piezoelectric PN interface and the regulation mechanism on I-V characteristics of the junction. Nano Energy 2021, 81, 105581. [Google Scholar] [CrossRef]
- Dai, X.Y.; Zhu, F.; Qian, Z.H.; Yang, J.S. Electric potential and carrier distribution in a piezoelectric semiconductor nanowire in time-harmonic bending vibration. Nano Energy 2018, 43, 22–28. [Google Scholar] [CrossRef]
- Cheng, R.R.; Zhang, C.L.; Chen, W.Q.; Yang, J.S. Electrical behaviors of a piezoelectric semiconductor fiber under a local temperature change. Nano Energy 2019, 66, 104081. [Google Scholar] [CrossRef]
- Jin, Z.H.; Yang, J.S. Analysis of a sandwiched piezoelectric semiconducting thermoelectric structure. Mech. Res. Commun. 2019, 98, 31–36. [Google Scholar] [CrossRef]
- Jiao, F.H.; Wei, J.P.; Zhou, Y.H.; Zhou, X.L. Wave propagation through a piezoelectric semiconductor slab sandwiched by two piezoelectric half-spaces. Eur. J. Mech. A-Solids 2019, 75, 70–81. [Google Scholar] [CrossRef]
- Liang, Y.X.; Hu, Y.T. Effect of interaction among the three time scales on the propagation characteristics of coupled waves in a piezoelectric semiconductor rod. Nano Energy 2020, 68, 104345. [Google Scholar] [CrossRef]
- Yang, J.S.; Zhou, H.G. Amplification of acoustic waves in piezoelectric semiconductor plates. Int. J. Solids Struct. 2005, 42, 3171–3183. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.S.; Yang, X.M.; Turner, J.A. Amplification of acoustic waves in laminated piezoelectric semiconductor plates. Arch. Appl. Mech. 2004, 3, 288–298. [Google Scholar] [CrossRef]
- Li, P.; Jin, F.; Yang, J.S. Effects of semiconduction on electromechanical energy conversion in piezoelectrics. Smart Mater. Struct. 2015, 24, 025021. [Google Scholar] [CrossRef]
- Tian, R.; Liu, J.X.; Pan, E.; Wang, Y.S.; Soh, A.K. Some characteristics of elastic waves in a piezoelectric semiconductor plate. J. Appl. Phys. 2019, 126, 125701. [Google Scholar] [CrossRef]
- Tian, R.; Liu, J.X.; Pan, E.; Wang, Y.S. SH waves in multilayered piezoelectric semiconductor plates with imperfect interfaces. Eur. J. Mech. A-Solid. 2020, 81, 103961. [Google Scholar] [CrossRef]
- Luo, Y.X.; Zhang, C.L.; Chen, W.Q.; Yang, J.S. Piezotronic effect of a thin film with elastic and piezoelectric semiconductor layers under a static flexural loading. J. Appl. Mech-Trans. ASME 2019, 86, 051003. [Google Scholar] [CrossRef]
- Luo, Y.X.; Cheng, R.R.; Zhang, C.L. Analysis of Flexural Vibrations of Laminated Piezoelectric Semiconductor Plates. CJSM 2020, 41, 15–29. [Google Scholar]
- Zhao, M.H.; Yang, C.H.; Fan, C.Y.; Zhang, Q.Y. A shooting method for nonlinear boundary value problems in a thermal piezoelectric semiconductor plate. ZAMM-Z. Angew. Math. Mech. 2020, 100, e201900302. [Google Scholar] [CrossRef]
- Zhao, M.H.; Zhang, Q.Y.; Fan, C.Y. An efficient iteration approach for nonlinear boundary value problems in 2D piezoelectric semiconductors. Appl. Math. Model. 2019, 74, 170–183. [Google Scholar] [CrossRef]




| Property | Parameter | Value | Unit |
|---|---|---|---|
| Elastic constant | c11 | 293.7 | GPa |
| c12 | 124.1 | GPa | |
| c13 | 158.5 | GPa | |
| c33 | 282.0 | GPa | |
| c44 | 22.3 | GPa | |
| Piezoelectric constant | e13 | −0.52 | C m−2 |
| Dielectric constant | ε33 | 9.385 × 10−11 | C V−1 m−1 |
| Electron mobility | μ11 | 9.62 × 10−2 | m2 V−1 s−1 |
| Diffusion constant | d11 | 2.49 × 10−3 | m2 s−1 |
| NE | n0 = 1020 (m−3) | n0 = 1014 (m−3) | ||||
|---|---|---|---|---|---|---|
| W (10−4 m) | Φ (10−2 V) | ΔN (1018 m−3) | W (10−4 m) | Φ (10−1 V) | ΔN (1014 m−3) | |
| 36 × 36 | 2.549 | 6.643 | 4.020 | 8.252 | 8.632 | 1.796 |
| 78 × 78 | 2.784 | 6.555 | 4.307 | 8.273 | 8.653 | 1.802 |
| 100 × 100 | 2.791 | 6.552 | 4.316 | 8.273 | 8.654 | 1.802 |
| 150 × 150 | 2.795 | 6.550 | 4.321 | 8.274 | 8.654 | 1.802 |
| 200 × 200 | 2.796 | 6.551 | 4.321 | 8.274 | 8.654 | 1.802 |
| 300 × 300 | 2.795 | 6.550 | 4.321 | 8.274 | 8.654 | 1.802 |
| 400 × 400 | 2.795 | 6.550 | 4.321 | 8.274 | 8.654 | 1.802 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, M.; Zhang, Q.; Wang, B.; Zhao, M. Analysis of Flexural Vibrations of a Piezoelectric Semiconductor Nanoplate Driven by a Time-Harmonic Force. Materials 2021, 14, 3926. https://doi.org/10.3390/ma14143926
Li M, Zhang Q, Wang B, Zhao M. Analysis of Flexural Vibrations of a Piezoelectric Semiconductor Nanoplate Driven by a Time-Harmonic Force. Materials. 2021; 14(14):3926. https://doi.org/10.3390/ma14143926
Chicago/Turabian StyleLi, Mengen, Qiaoyun Zhang, Bingbing Wang, and Minghao Zhao. 2021. "Analysis of Flexural Vibrations of a Piezoelectric Semiconductor Nanoplate Driven by a Time-Harmonic Force" Materials 14, no. 14: 3926. https://doi.org/10.3390/ma14143926
APA StyleLi, M., Zhang, Q., Wang, B., & Zhao, M. (2021). Analysis of Flexural Vibrations of a Piezoelectric Semiconductor Nanoplate Driven by a Time-Harmonic Force. Materials, 14(14), 3926. https://doi.org/10.3390/ma14143926





