Higher Order Multiscale Finite Element Method for Heat Transfer Modeling
Abstract
:1. Introduction
- The specific properties, shapes [11] and weight/volume ratios of the constituents;
- The particle-based mesoscopic modeling based on a coarse-grained analysis, e.g., Monte Carlo method, lattice Boltzmann method [30];
1.1. Microscale Modeling
1.2. Mesoscale (Particle-Based) Modeling
1.3. Macroscale Modeling
2. Problem Formulation
- Dirichlet boundary conditions: on ;
- Neumann boundary conditions: on ( is the unit outward normal vector, denotes the heat flux across ).
3. Upscaling
3.1. Idea
| Algorithm 1 Solve a heat transfer problem within a heterogeneous domain. |
| Require: define the problem (heterogeneous domain and boundary conditions) Ensure: a coarse mesh and an appropriate refinement of each coarse element for n=1 to do {loop over coarse mesh elements} for m=1 to M do {loop over n-th element shape functions} solve local problem (5) in the n-th element for the m-th shape function end for compute and for the n-th element end for solve the coarse mesh problem using the effective matrices and vectors |
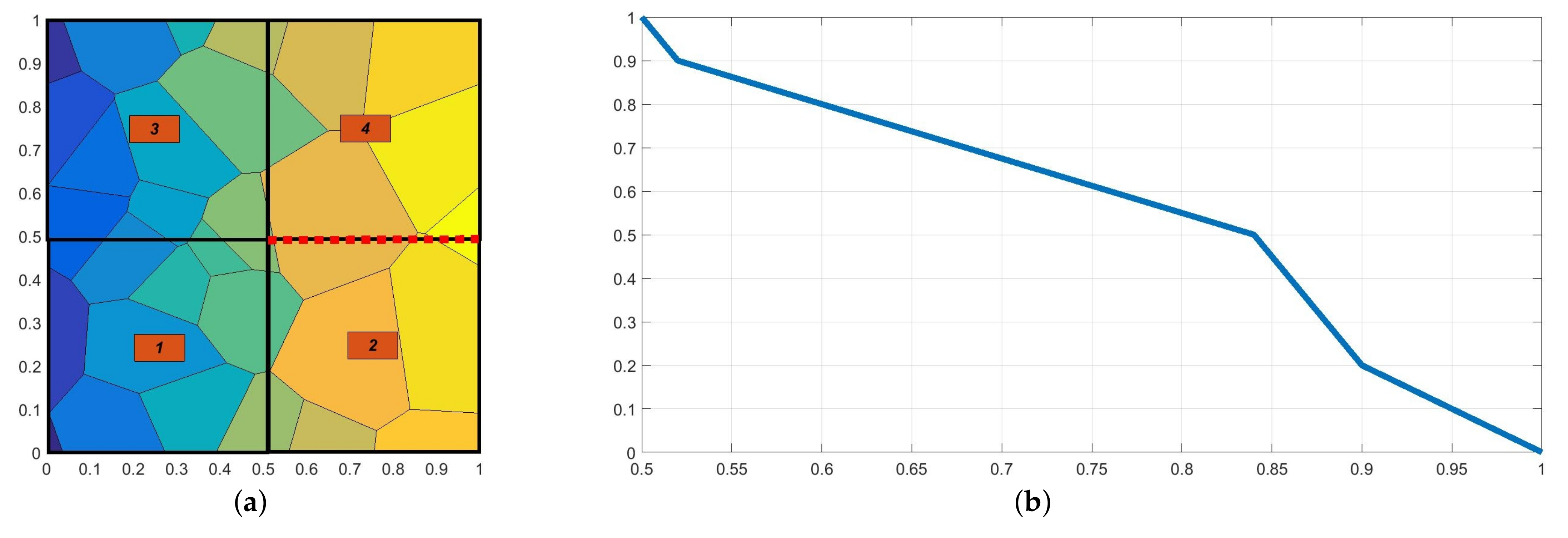
3.2. Formulation
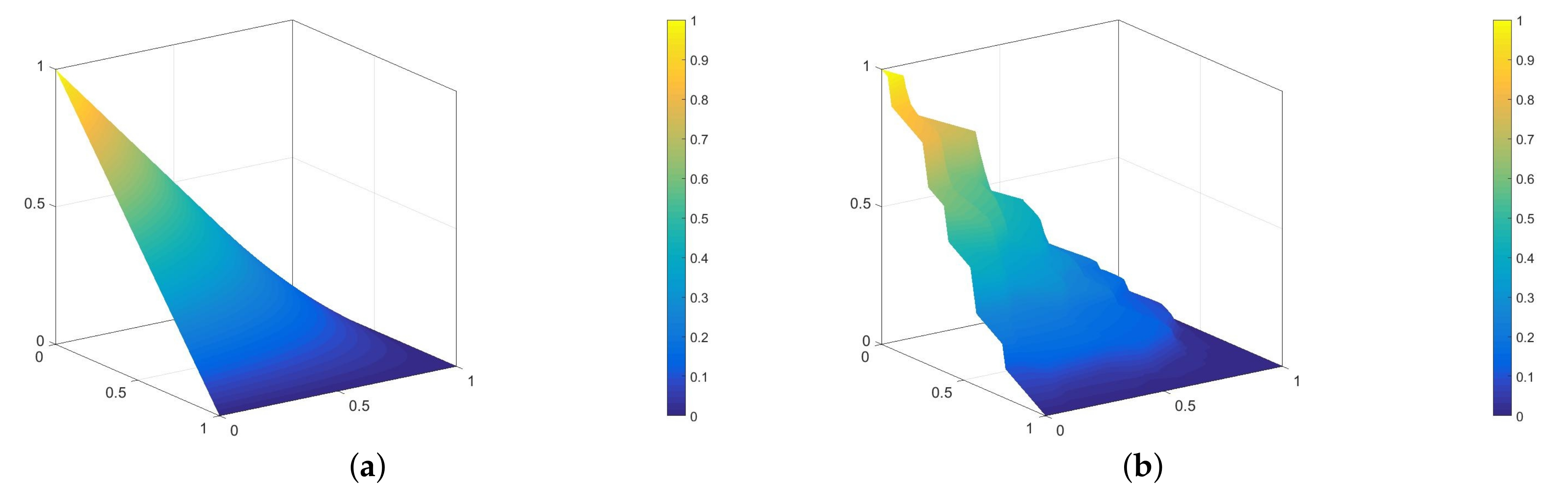
- In 1D, we only solve the reduced Equation (5) (), obtaining the modified shape function. For the linear shape functions, we use 0 and 1 as the boundary conditions. For the “bubble” ones, is equal to zero. Exemplary standard and modified “bubble” shape functions for this case are shown in Figure 2. The horizontal thick lines represent the material distribution; thus, the standard shape function (Figure 2a) is the solution of problem (5) for the material with constant thermal conductivity in . The solution presented in Figure 2b was obtained using 50 finite elements, which comply with the microstructure schematically marked with the horizontal line. The green material is characterized by a thermal conductivity 10 times larger than the other one;
- In 3D, we need to solve reduced problems (5) along the edges and, subsequently, within the faces of the domain. Finally, Equation (5) is solved with the Dirichlet boundary conditions resulting from the lower scales auxiliary computations. A number of 3D-modified shape function examples for the linear elasticity problem can be found in [14,18].
3.3. Implementation
- For the periodic heterogeneous domains, we compute the effective stiffness matrix once, and use it for every coarse mesh element—the effective load vectors are different in most cases;
- For non-periodic heterogeneous domains, we can parallelize the computations of the coarse-mesh-element matrices and vectors and .
4. Numerical Results
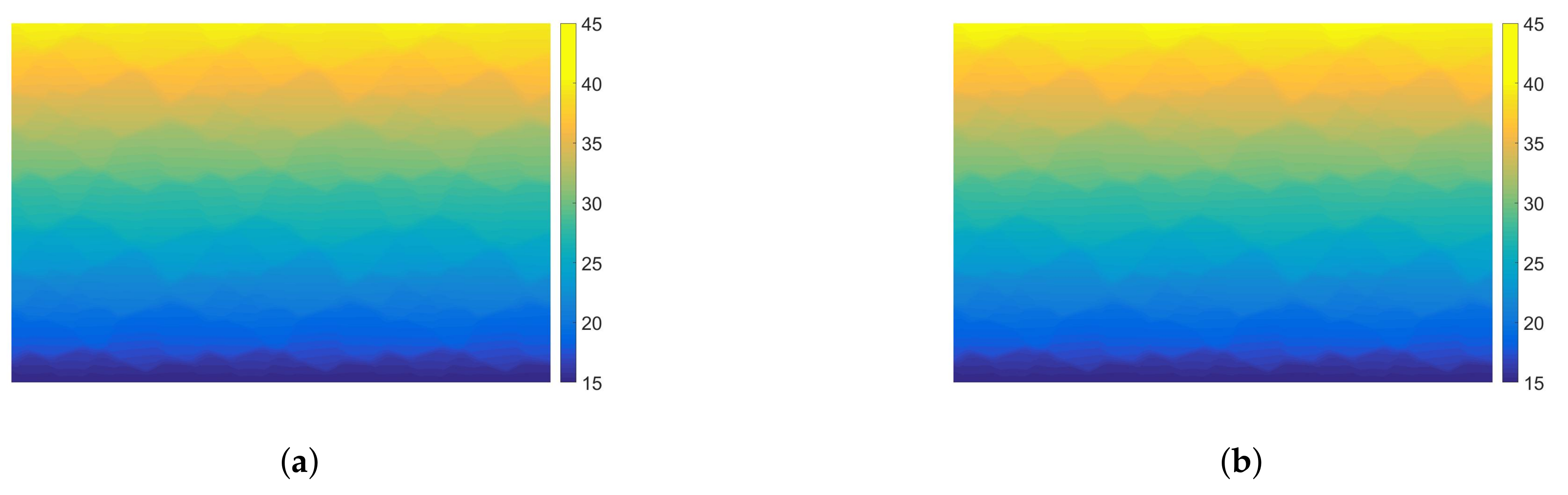
4.1. Asphalt Concrete
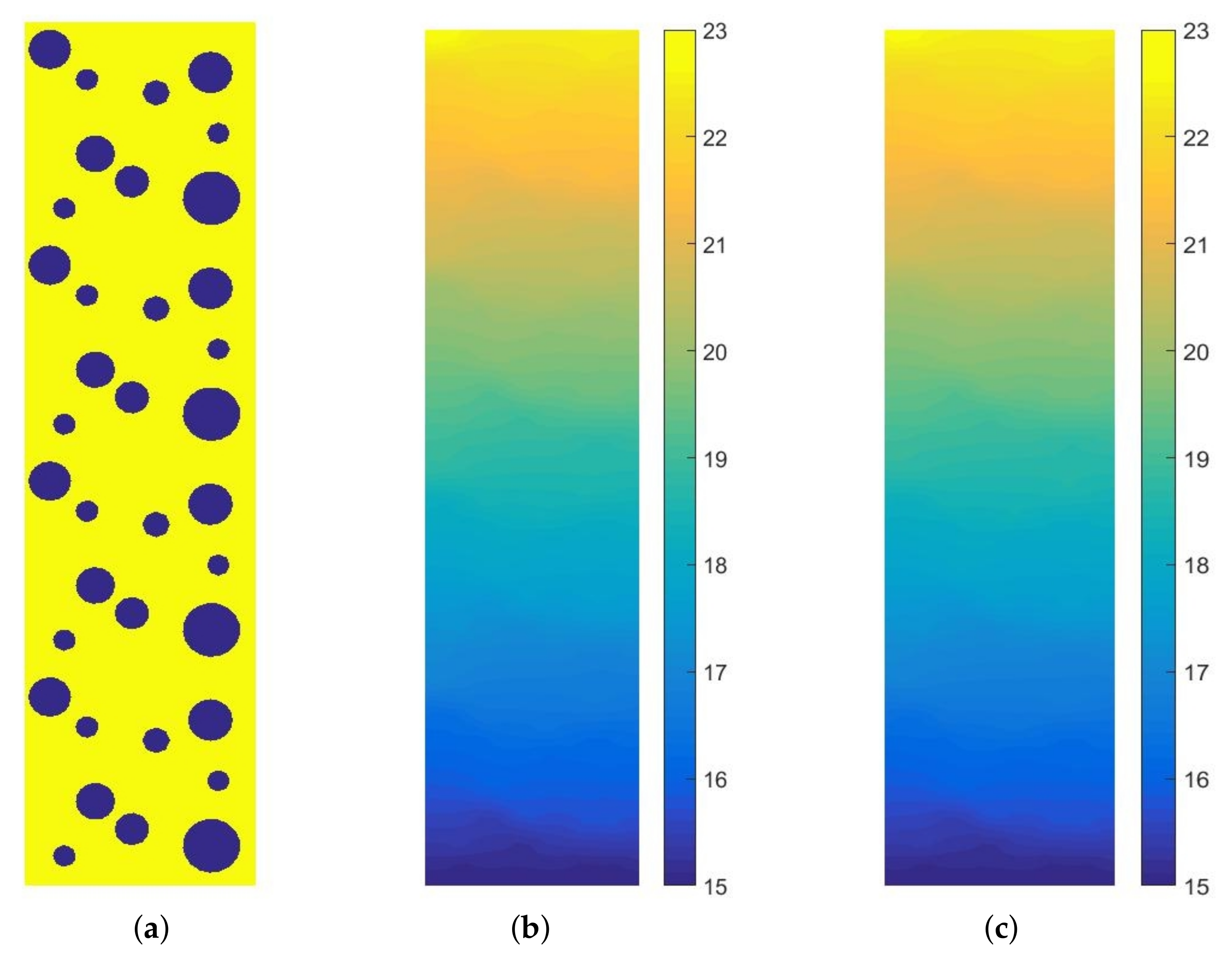
4.2. Metal Foam
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- You, T.; Al-Rub, R.; Darabi, M.; Masad, E.; Little, D. Three-dimensional microstructural modeling of asphalt concrete using a unified viscoelastic-viscoplastic-viscodamage model. Constr. Build. Mater. 2012, 28, 531–548. [Google Scholar] [CrossRef]
- Jia, L.; Sun, L.; Huang, L.; Qin, J. Numerical temperature prediction model for asphalt concrete pavement. J. Tongji Univ. 2007, 35, 1039–1043. [Google Scholar]
- Israr, H.; King, W.; Rivallant, S. Numerical Modelling Strategies for Composite Structures crashworthiness: A Review. J. Adv. Res. Mater. Sci. 2018, 42, 8–23. [Google Scholar]
- Pinho, S.; Camanho, P.; Moura, M.D. Numerical simulation of the crushing process of composite materials. Int. J. Crashworthiness 2004, 9, 263–276. [Google Scholar] [CrossRef]
- Jaworska, I. Higher order multipoint Meshless Finite Difference Method for two-scale analysis of heterogeneous materials. Int. J. Multiscale Comput. Eng. 2019, 17, 239–260. [Google Scholar] [CrossRef]
- Wang, Y.H.; Nie, J.G.; Cai, C. Numerical modeling on concrete structures and steel-concrete composite frame structures. Compos. Part Eng. 2013, 51, 58–67. [Google Scholar] [CrossRef]
- Ožbolt, J.; Balabanić, G.; Kušter, M. 3D Numerical modelling of steel corrosion in concrete structures. Corros. Sci. 2011, 53, 4166–4177. [Google Scholar] [CrossRef]
- Guinard, S.; Bouclier, R.; Toniolli, M.; Passieux, J.C. Multiscale analysis of complex aeronautical structures using robust non-intrusive coupling. Adv. Model. Simul. Eng. Sci. 2018, 5, 1–27. [Google Scholar] [CrossRef] [Green Version]
- Guan, Z.; Cantwell, W.; Abdullah, M. Numerical Modeling of the Impact Response of Fiber-Metal Laminates. Polym. Compos. 2009, 30, 603–611. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, X.T.; He, N.B.; Jia, G.H. Numerical Material Model for Composite Laminates in High-Velocity Impact Simulation. Lat. Am. J. Solids Struct. 2017, 14, 1912–1931. [Google Scholar] [CrossRef] [Green Version]
- Liu, P.; Hu, J.; Wang, D.; Oeser, M.; Alber, S.; Ressel, W.; Fala, G. Modelling and evaluation of aggregate morphology on asphalt compression behavior. Constr. Build. Mater. 2017, 133, 196–208. [Google Scholar] [CrossRef]
- Liu, Y.; Dai, Q.; You, Z. Viscoelastic Model for Discrete Element Simulation of Asphalt Mixtures. J. Eng. Mech. 2009, 135, 324–333. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, Y. A domain decomposition technique based on the multiscale seamless-domain method. Mech. Eng. J. 2017, 4, 17–00145. [Google Scholar] [CrossRef] [Green Version]
- Klimczak, M.; Cecot, W. An adaptive MsFEM for non periodic viscoelastic composites. Int. J. Numer. Methods Eng. 2018, 114, 861–881. [Google Scholar] [CrossRef]
- Demkowicz, L.; Rachowicz, W.; Devloo, P. A Fully Automatic hp-Adaptivity. J. Sci. Comput. 2002, 17, 117–142. [Google Scholar] [CrossRef]
- Demkowicz, L.; Kurtz, J.; Pardo, D.; Paszynski, M.; Rachowicz, W.; Zdunek, A. Computing with hp-Adaptive Finite Elements. Vol 2. Frontiers: Three-Dimensional Elliptic and Maxwell Problems with Applications; Chapman & Hall/CRC: New York, NY, USA, 2008. [Google Scholar]
- Schüller, T.; Jänicke, R.; Steeb, H. Nonlinear modeling and computational homogenization of asphalt concrete on the basis of XRCT scans. Constr. Build. Mater. 2016, 109, 96–108. [Google Scholar] [CrossRef]
- Klimczak, M.; Cecot, W. Towards asphalt concrete modeling by the multiscale finite element method. Finite Elem. Anal. Des. 2020, 171, 103367. [Google Scholar] [CrossRef]
- Efendiev, Y.; Hou, T. Multiscale Finite Element Methods; Springer: New York, NY, USA, 2009. [Google Scholar]
- Fish, J. (Ed.) Multiscale Methods. Bridging the Scales in Science and Engineering; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Fish, J. Practical Multiscaling; Wiley: Chichester, UK, 2014. [Google Scholar]
- Geers, M.; Kouznetsova, V.; Brekelmans, W. Multi-scale computational homogenization: Trends and challenges. J. Comput. Appl. Math. 2010, 234, 2175–2182. [Google Scholar] [CrossRef]
- Cecot, W.; Oleksy, M. High order FEM for multigrid homogenization. Comput. Math. Appl. 2015, 70, 1391–1400. [Google Scholar] [CrossRef]
- Klimczak, M.; Cecot, W. Synthetic Microstructure Generation and Multiscale Analysis of Asphalt Concrete. Appl. Sci. 2020, 10, 765. [Google Scholar] [CrossRef] [Green Version]
- Murthy, J.; Mathur, S. Computational Heat Transfer in Complex Systems: A Review of Needs and Opportunities. J. Heat Transf. 2012, 134, 031016. [Google Scholar] [CrossRef]
- He, Y.L.; Tao, W.Q. Numerical Solutions of Nano/Microphenomena Coupled With Macroscopic Process of Heat Transfer and Fluid Flow: A Brief Review. J. Heat Transf. 2015, 137, 090801. [Google Scholar] [CrossRef]
- Tong, Z.X.; He, Y.L.; Tao, W.Q. A review of current progress in multiscale simulations for fluid flow and heat transfer problems: The frameworks, coupling techniques and future perspectives. Int. J. Heat Mass Transf. 2019, 137, 1263–1289. [Google Scholar] [CrossRef]
- Chantrenne, P. Multiscale simulations: Application to the heat transfer simulation of sliding solids. Int. J. Mater. Form. 2008, 1, 31–37. [Google Scholar] [CrossRef]
- Sun, H.; Li, F.; Wang, M.; Xin, G.; Wang, X. Molecular dynamics study of convective heat transfer mechanism in a nano heat exchanger. RSC Adv. 2020, 10, 23097–23107. [Google Scholar] [CrossRef]
- Teschner, T.; Könözsy, L.; Jenkins, K. Progress in particle-based multiscale and hybrid methods for flow applications. Microfluid. Nanofluid. 2016, 20, 68. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, Y. Multiscale Seamless-Domain Method for Nonperiodic Fields: Nonlinear Heat Conduction Analysis. Int. J. Multiscale Comput. Eng. 2019, 17, 1–28. [Google Scholar] [CrossRef]
- Khan, A.A.; Bukhari, S.R.; Marin, M.; Ellahi, R. Effects of Chemical Reaction on Third-Grade MHD Fluid Flow Under the Influence of Heat and Mass Transfer With Variable Reactive Index. Heat Transf. Res. 2019, 50, 1061–1080. [Google Scholar] [CrossRef]
- Murashima, T.; Urata, S.; Li, S. Coupling finite element method with large scale atomic/molecular massively parallel simulator (LAMMPS) for hierarchical multiscale simulations. Eur. Phys. J. 2019, 92. [Google Scholar] [CrossRef] [Green Version]
- O’Connell, S.; Thompson, P. Molecular dynamics-continuum hybrid computations: A tool for studying complex fluid flows. Phys. Rev. E 1995, 52, 5792–5795. [Google Scholar] [CrossRef] [PubMed]
- Hadjiconstantinou, N.; Patera, A. Heterogeneous Atomistic-Continuum Representations for Dense Fluid Systems. Int. J. Mod. Phys. C 1997, 8, 967–976. [Google Scholar] [CrossRef]
- Wang, Y.C.; He, G.W. A dynamic coupling model for hybrid atomistic–continuum computations. Chem. Eng. Sci. 2007, 62, 3574–3579. [Google Scholar] [CrossRef] [Green Version]
- Kamali, R.; Kharazmi, A. Investigation of multiscale fluid flow characteristics based on a hybrid atomistic–continuum method. Comput. Phys. Commun. 2013, 184, 2316–2320. [Google Scholar] [CrossRef]
- Flekkøy, E.; Wagner, G.; Feder, J. Hybrid model for combined particle and continuum dynamics. Europhys. Lett. 2000, 52, 271–276. [Google Scholar] [CrossRef]
- Delgado-Buscalioni, R.; Coveney, P. USHER: An algorithm for particle insertion in dense fluids. J. Chem. Phys. 2003, 119, 978–987. [Google Scholar] [CrossRef] [Green Version]
- E, W.; Engquist, B.; Huang, Z. Heterogeneous multiscale method: A general methodology for multiscale modeling. Phys. Rev. B 2003, 67, 092101. [Google Scholar] [CrossRef] [Green Version]
- Fedosov, D.; Karniadakis, G. Triple-decker: Interfacing atomistic-mesoscopic-continuum flow regimes. J. Comput. Phys. 2009, 228, 1157–1171. [Google Scholar] [CrossRef]
- Liang, T.; Ye, W. An Efficient Hybrid DSMC/MD Algorithm for Accurate Modeling of Micro Gas Flows. Commun. Comput. Phys. 2014, 15, 246–264. [Google Scholar] [CrossRef]
- Bensoussan, A.; Lions, J.L.; Papanicolaou, G. Asymptotic Analysis for Periodic Structures; North Holland: Amsterdam, The Netherlands, 1978. [Google Scholar]
- Sanchez-Palencia, E. Non-homogeneous media and vibration theory. In Lecture Notes in Physics 127; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Donato, P.; Paulin, J.S.J. Homogenization of the Poisson equation in a porous medium with double periodicity. Jpn. J. Ind. Appl. Math. 1993, 10, 333–349. [Google Scholar] [CrossRef]
- Melnyk, T. Homogenization of the Poisson Equation in a Thick Periodic Junction. J. Anal. Its Appl. 1999, 18, 953–975. [Google Scholar] [CrossRef]
- Feyel, F.; Chaboche, L. FE2 multiscale approach for modelling the elasto-visco-plastic behaviour of long fibre SiC/Ti composite materials. Comput. Methods Appl. Mech. Eng. 2000, 183, 309–330. [Google Scholar] [CrossRef]
- Feyel, F. A multilevel finite element method (FE2) to describe the response of highly non-linear structures using generalized continua. Comput. Methods Appl. Mech. Eng. 2003, 192, 3233–3244. [Google Scholar] [CrossRef]
- Özdemir, I.; Brekelmans, W.; Geers, M. Computational homogenization for heat conduction in heterogeneous solids. Int. J. Numer. Methods Eng. 2008, 73, 185–204. [Google Scholar] [CrossRef] [Green Version]
- Radermacher, A.; Bednarcyk, B.; Stier, B.; Simon, J.; Zhou, L.; Reese, S. Displacement-based multiscale modeling of fiber-reinforced composites by means of proper orthogonal decomposition. Adv. Model. Simul. Eng. Sci. 2016, 3, 1–23. [Google Scholar] [CrossRef] [Green Version]
- Cook, R.D.; Malkus, D.S.; Plesha, M.E.; Witt, R.J. Concepts and Applications of Finite Element Analysis; Wiley: Chichester, UK, 2002. [Google Scholar]
- Liu, X.Q. Multiscale Finite Element Methods for Heat Equation in Three Dimension Honeycomb Structure. In Proceedings of the Third International Conference on Artificial Intelligence and Computational Intelligence, AICI’11, Taiyuan, China, 24–25 September 2011; Volume 3, pp. 186–194. [Google Scholar]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klimczak, M.; Cecot, W. Higher Order Multiscale Finite Element Method for Heat Transfer Modeling. Materials 2021, 14, 3827. https://doi.org/10.3390/ma14143827
Klimczak M, Cecot W. Higher Order Multiscale Finite Element Method for Heat Transfer Modeling. Materials. 2021; 14(14):3827. https://doi.org/10.3390/ma14143827
Chicago/Turabian StyleKlimczak, Marek, and Witold Cecot. 2021. "Higher Order Multiscale Finite Element Method for Heat Transfer Modeling" Materials 14, no. 14: 3827. https://doi.org/10.3390/ma14143827
APA StyleKlimczak, M., & Cecot, W. (2021). Higher Order Multiscale Finite Element Method for Heat Transfer Modeling. Materials, 14(14), 3827. https://doi.org/10.3390/ma14143827





