Mechanical Properties of a Chiral Cellular Structure with Semicircular Beams
Abstract
1. Introduction
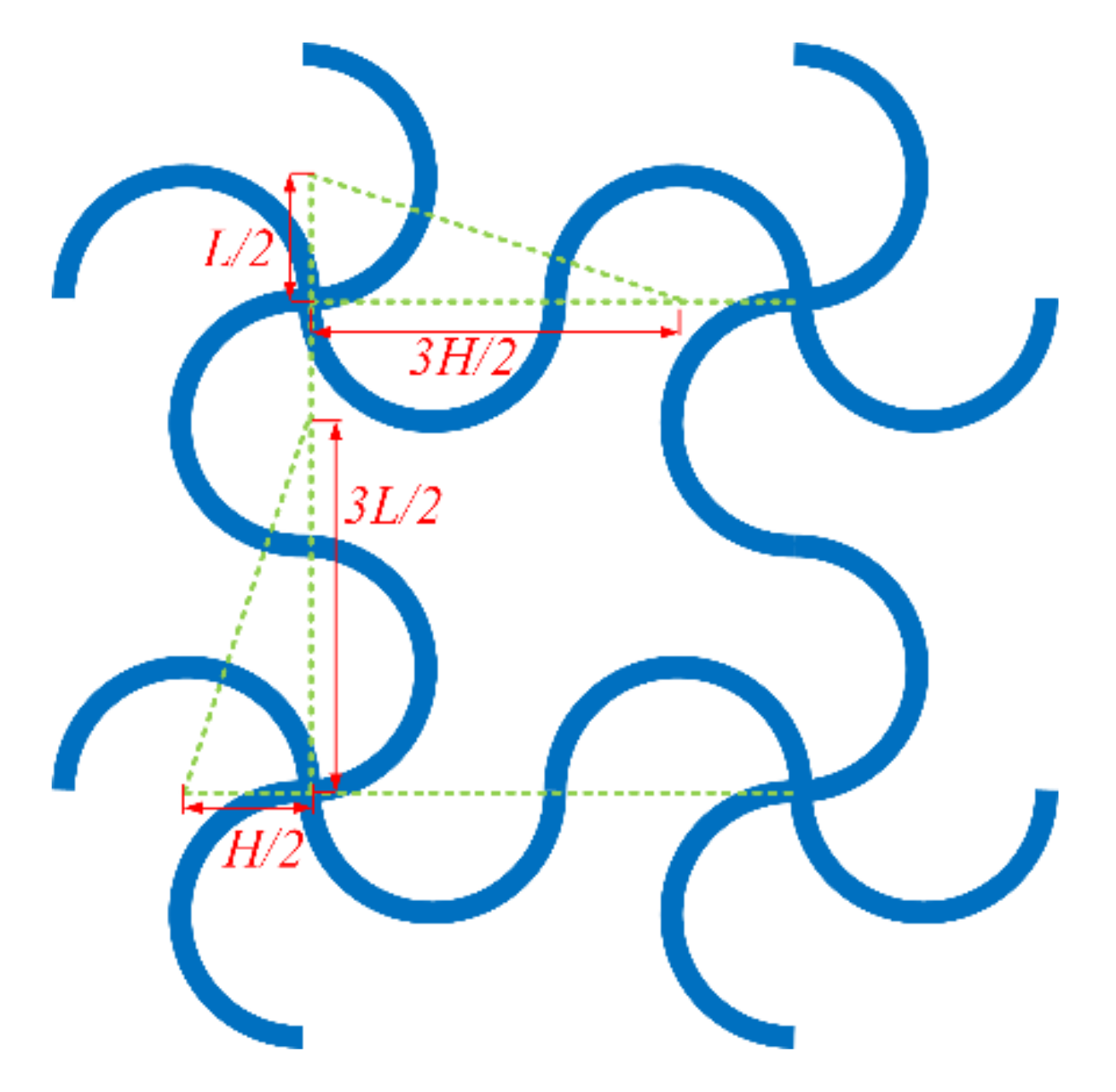
2. Geometry of the Structure
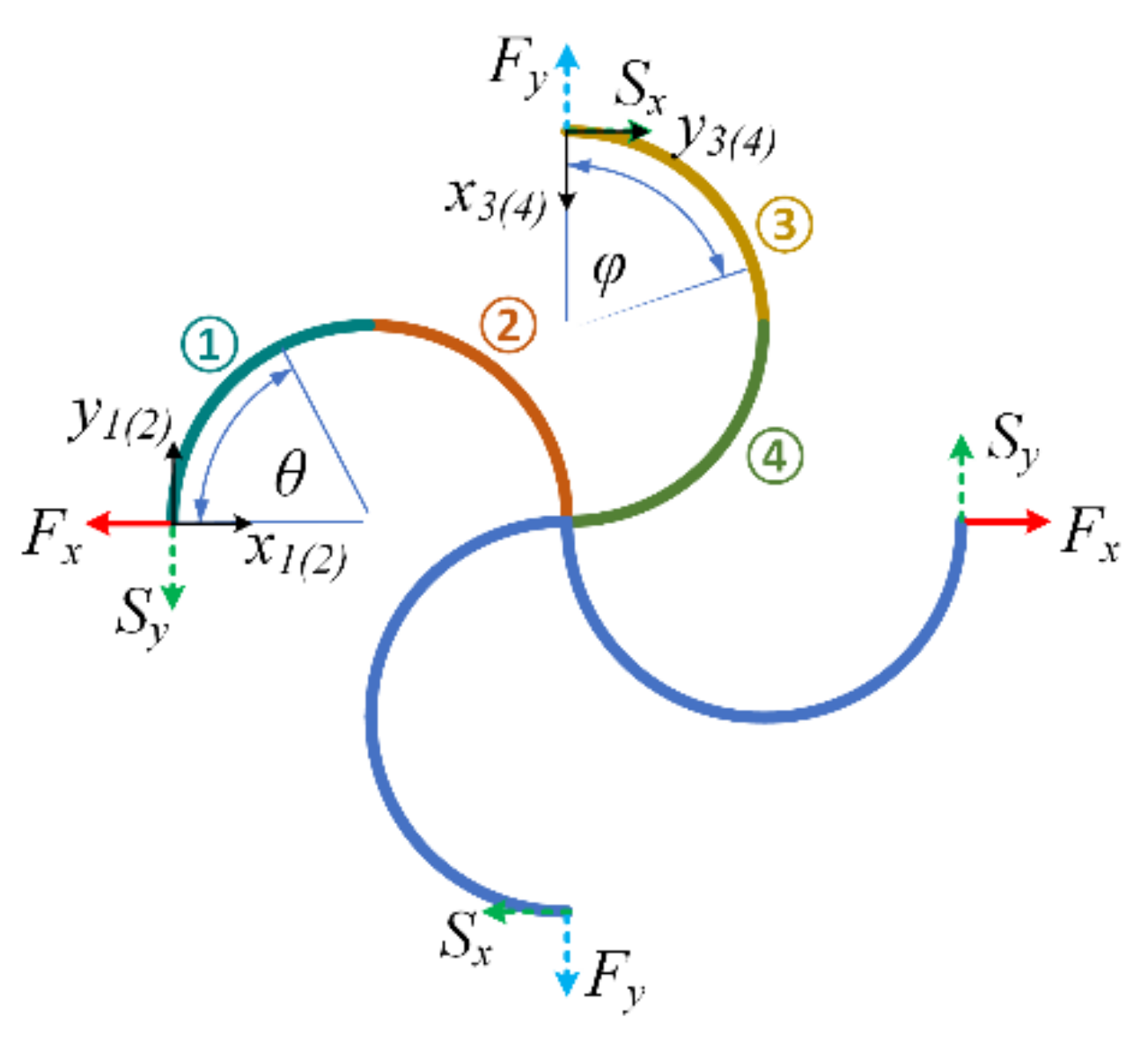
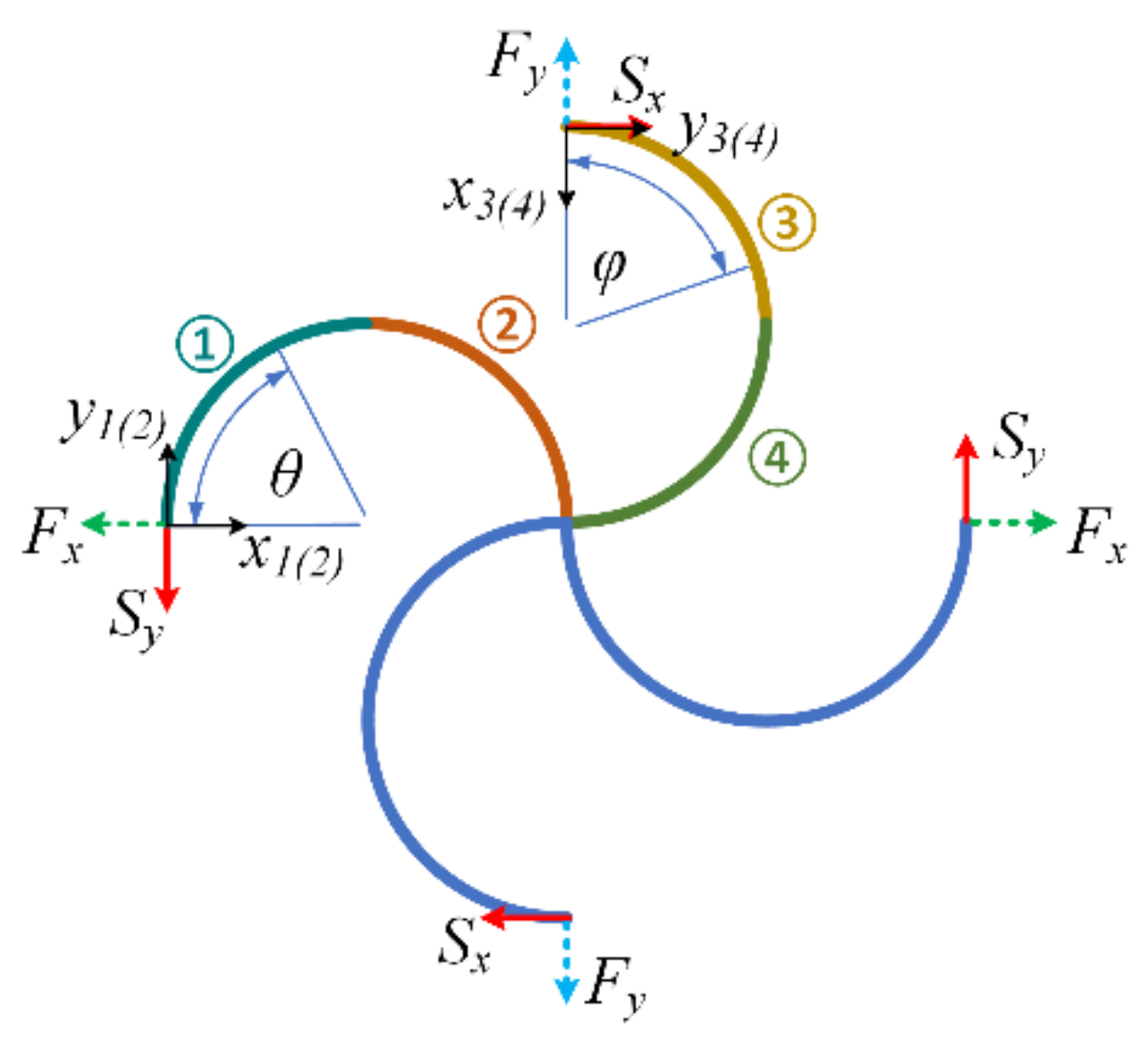
3. Modeling of the Elastic Properties
3.1. Tensile Properties in the X-Direction
3.2. Shear Properties in the X–Y Plane
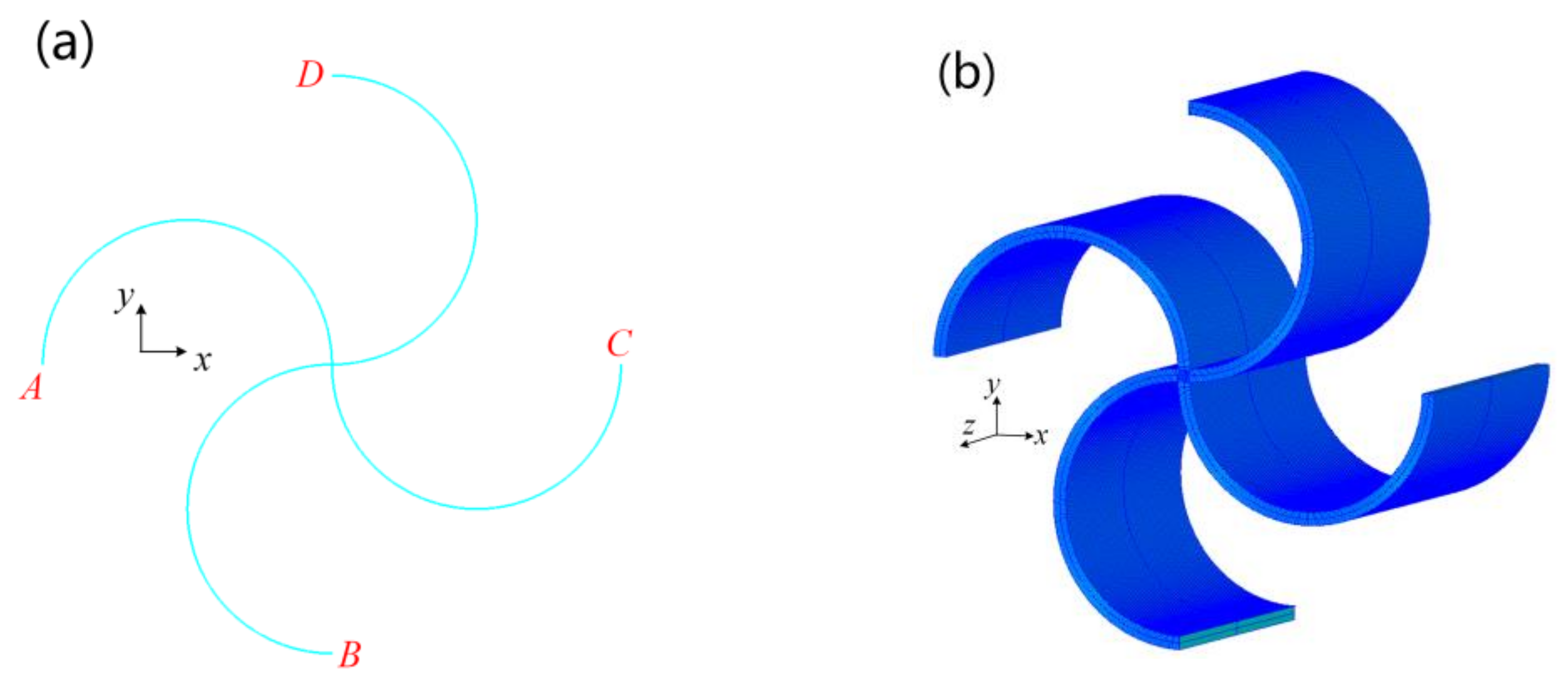
4. Finite Element Analyses
5. Results and Discussion
5.1. Elastic Modulus in the X-Direction
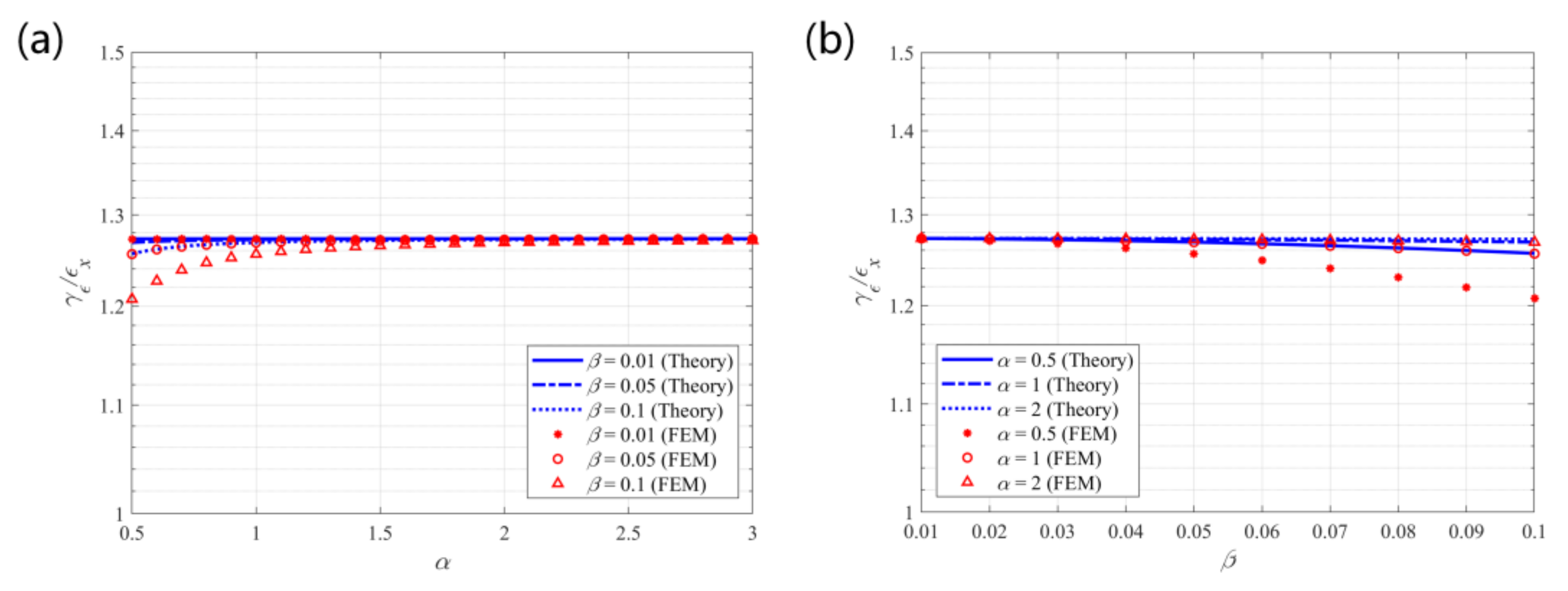
5.2. Tensile–Shear Coupling Effect
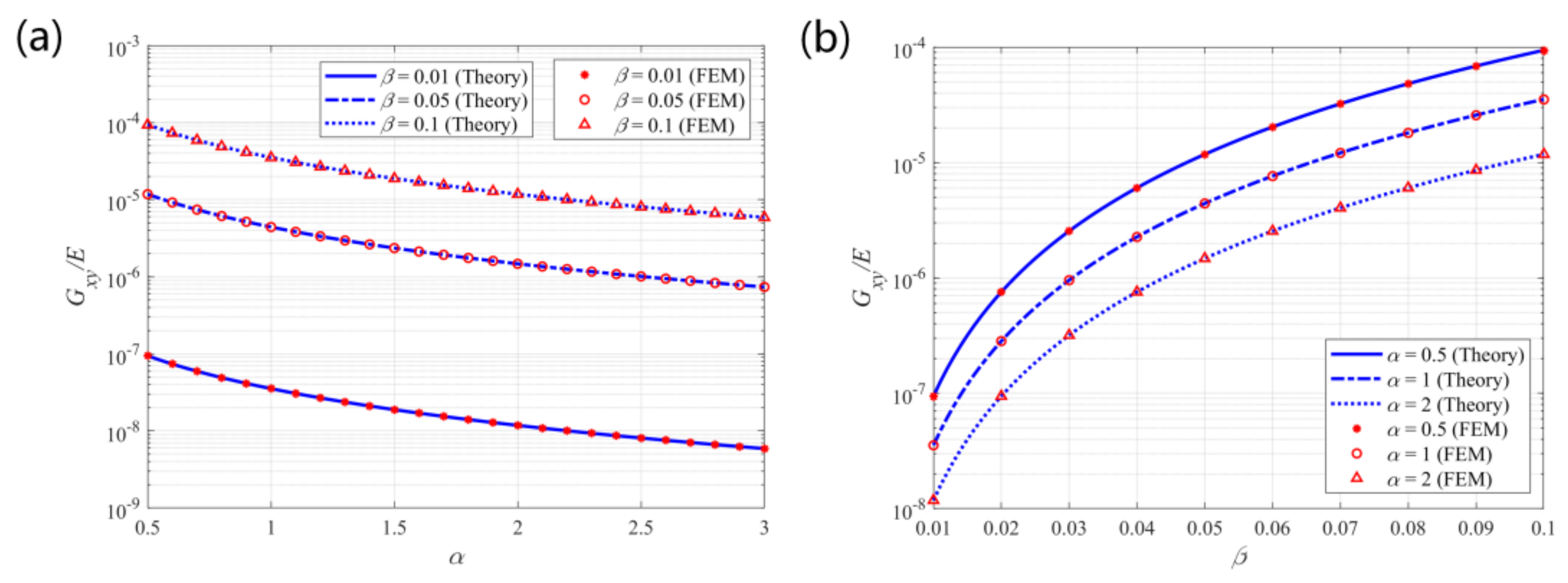
5.3. Shear Modulus in the X–Y Plane
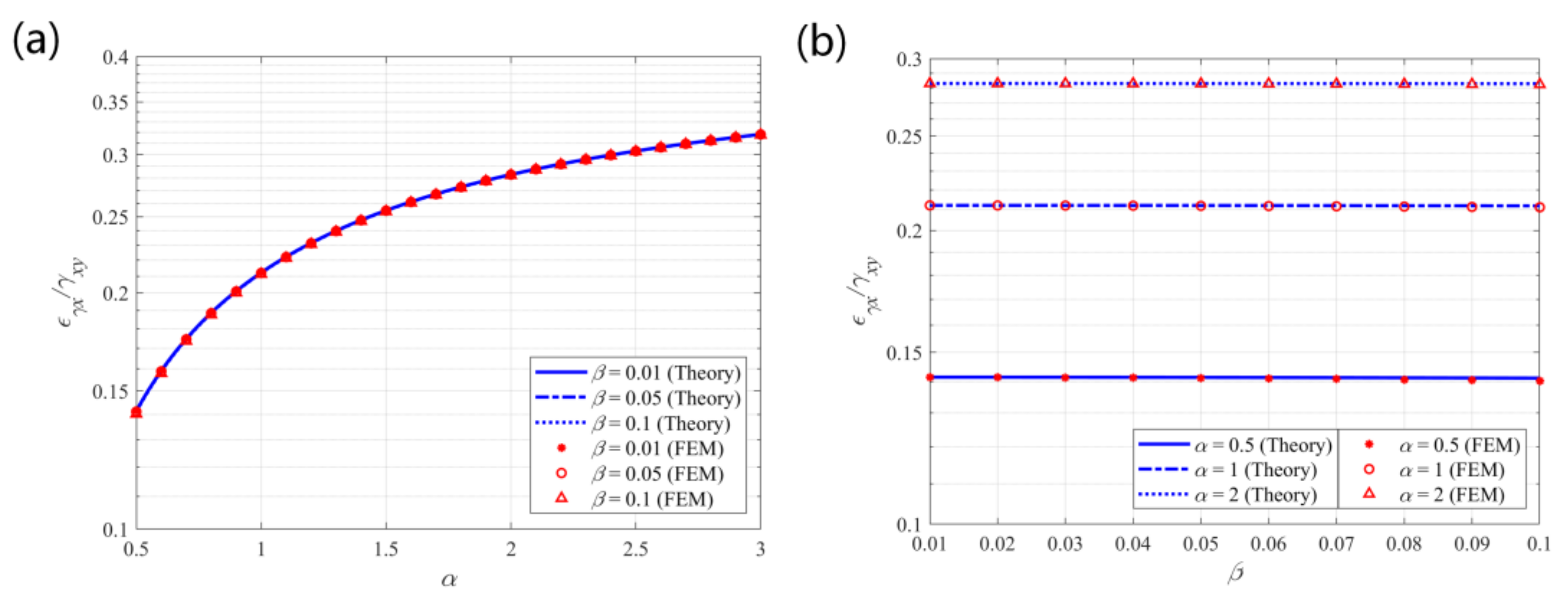
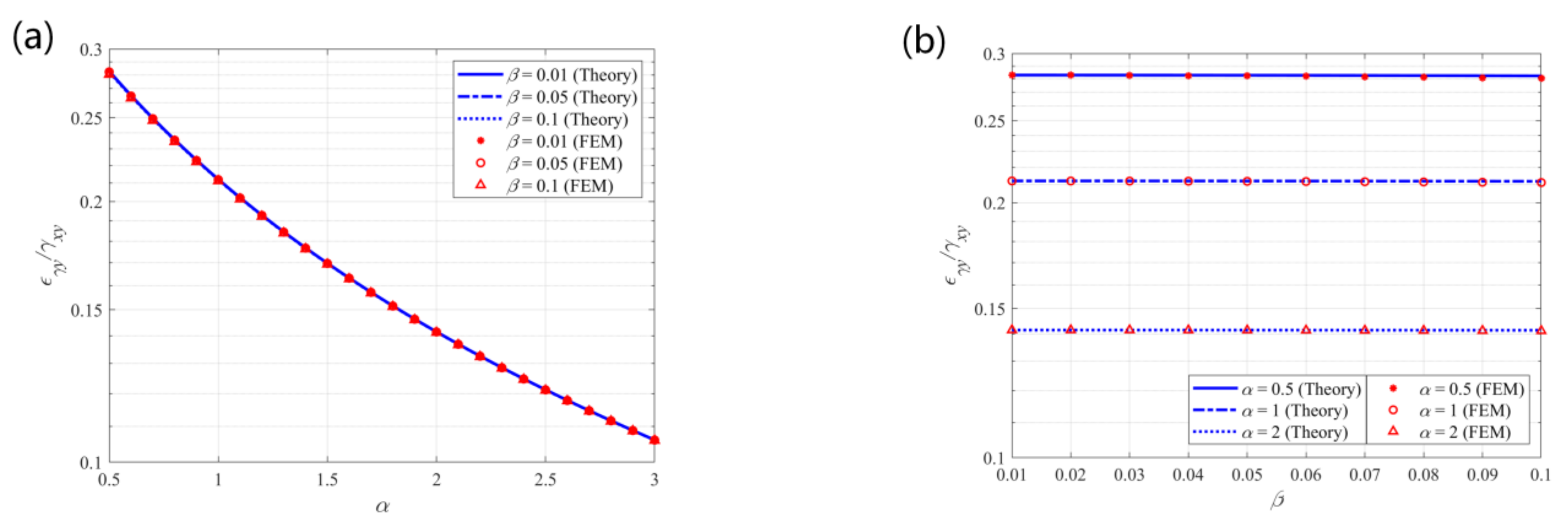
5.4. Shear–Tensile Coupling Effects
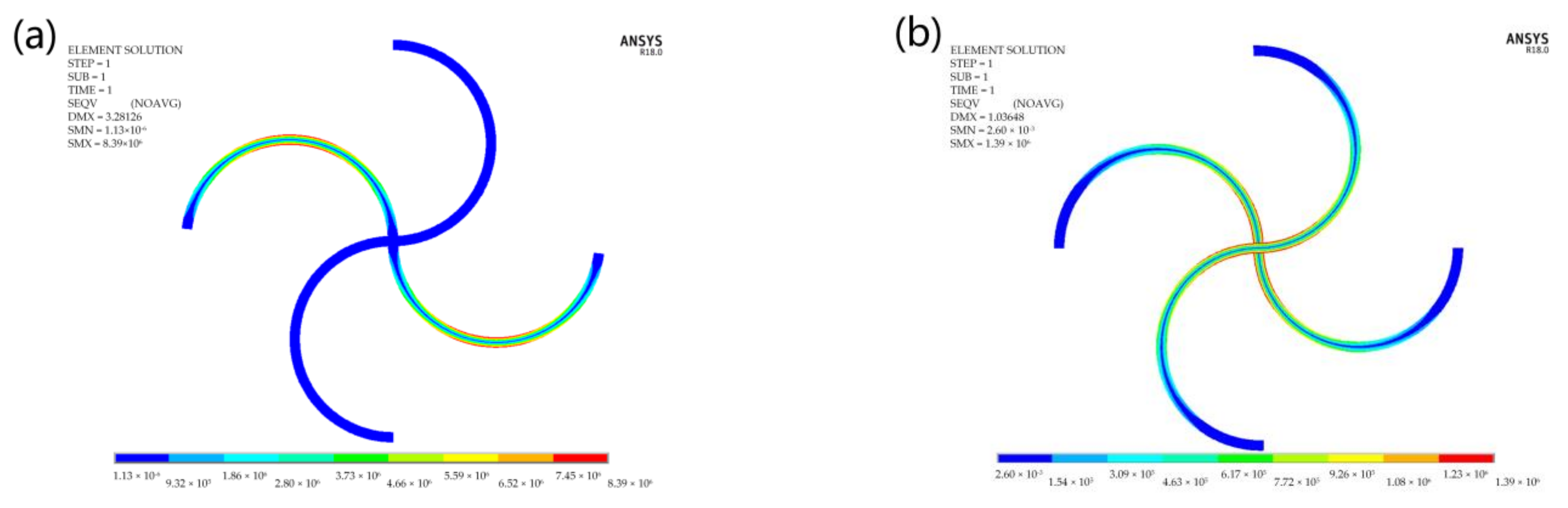
5.5. Failure Mechanism of the Structure
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, L.-M.; Chen, M.-J.; Pei, Y.-M.; Zhang, Y.-H.; Fang, D.-N. Optimal design of sandwich beams with lightweight cores in three-point bending. Int. J. Appl. Mech. 2012, 4. [Google Scholar] [CrossRef]
- Parsons, E.M. Lightweight Cellular Metal Composites with Zero and Tunable Thermal Expansion Enabled by Ultrasonic Ad-ditive Manufacturing: Modeling, Manufacturing, and Testing. Compos. Struct. 2019, 223, 110656. [Google Scholar] [CrossRef]
- Tabatabaei, M.; Atluri, S.N. Ultralight cellular composite materials with architected geometrical structure. Compos. Struct. 2018, 196, 181–198. [Google Scholar] [CrossRef]
- Calladine, C.R. Buckminster Fuller’s “Tensegrity” Structures and Clerk Maxwell’s Rules for the Construction of Stiff Frames. Int. J. Solids Struct. 1978, 14, 161–172. [Google Scholar] [CrossRef]
- Chen, M.; Zhu, X.; Lei, H.; Chen, H.; Fang, D. Effect of Defect on the Compressive Response of Sandwich Structures with Carbon Fiber Pyramidal Truss Cores. Int. J. Appl. Mech. 2015, 7, 1550004. [Google Scholar] [CrossRef]
- Fowler, P.W.; Guest, S.D. A Symmetry Extension of Maxwell’s Rule for Rigidity of Frames. Int. J. Solids Struct. 2000, 37, 1793–1804. [Google Scholar] [CrossRef]
- Hu, Z.; Thiyagarajan, K.; Bhusal, A.; Letcher, T.; Fan, Q.H.; Liu, Q.; Salem, D. Design of ultra-lightweight and high-strength cellular structural composites inspired by biomimetics. Compos. Part B Eng. 2017, 121, 108–121. [Google Scholar] [CrossRef]
- Palucka, T. Mechanical metamaterials produce ultralight, ultrastiff lattices. MRS Bull. 2014, 39, 759–760. [Google Scholar] [CrossRef][Green Version]
- Sun, F.; Zheng, Q.; Fan, H.; Fang, D. The Mechanical Properties of Hierarchical Truss-Walled Lattice Materials. Int. J. Appl. Mech. 2017, 9, 1750027. [Google Scholar] [CrossRef]
- Zheng, X.; Lee, H.; Weisgraber, T.H.; Shusteff, M.; DeOtte, J.; Duoss, E.B.; Kuntz, J.D.; Biener, M.M.; Ge, Q.; Jackson, J.A.; et al. Ultralight, ultrastiff mechanical metamaterials. Science 2014, 344, 1373–1377. [Google Scholar] [CrossRef]
- Barbarino, S.; Bilgen, O.; Ajaj, R.M.; Friswell, M.I.; Inman, D.J. A Review of Morphing Aircraft. J. Intell. Mater. Syst. Struct. 2011, 22, 823–877. [Google Scholar] [CrossRef]
- Thill, C.; Etches, J.; Bond, I.; Potter, K.; Weaver, P. Morphing skins. Aeronaut. J. 2008, 112, 117–139. [Google Scholar] [CrossRef]
- Lachenal, X.; Daynes, S.; Weaver, P.M. Review of morphing concepts and materials for wind turbine blade applications. Wind. Energy 2012, 16, 283–307. [Google Scholar] [CrossRef]
- Loth, E.; Selig, M.; Moriarty, P. Morphing segmented wind turbine concept. In Proceedings of the 28th AIAA Applied Aerodynamics Conference, Chicago, IL, USA, 28 June–1 July 2010; p. 4400. [Google Scholar] [CrossRef]
- Thomsen, O.T. Sandwich Materials for Wind Turbine Blades—Present and Future. J. Sandw. Struct. Mater. 2009, 11, 7–26. [Google Scholar] [CrossRef]
- Daynes, S.; Weaver, P.M. Review of shape-morphing automobile structures: Concepts and outlook. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2013, 227, 1603–1622. [Google Scholar] [CrossRef]
- Hao, X.P.; Xu, Z.; Li, C.Y.; Hong, W.; Zheng, Q.; Wu, Z.L. Kirigami-Design-Enabled Hydrogel Multimorphs with Application as a Multistate Switch. Adv. Mater. 2020, 32, e2000781. [Google Scholar] [CrossRef] [PubMed]
- Mark, A.G.; Palagi, S.; Qiu, T.; Fischer, P. Auxetic metamaterial simplifies soft robot design. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 4951–4956. [Google Scholar]
- Yu, X.; Zhou, J.; Liang, H.; Jiang, Z.; Wu, L. Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review. Prog. Mater. Sci. 2018, 94, 114–173. [Google Scholar] [CrossRef]
- Gibson, L.J.; Ashby, M.F. Cellular Solids: Structure and Properties; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Masters, I.; Evans, K. Models for the elastic deformation of honeycombs. Compos. Struct. 1996, 35, 403–422. [Google Scholar] [CrossRef]
- Olympio, K.R.; Gandhi, F. Zero Poisson’s Ratio Cellular Honeycombs for Flex Skins Undergoing One-Dimensional Morphing. J. Intell. Mater. Syst. Struct. 2010, 21, 1737–1753. [Google Scholar] [CrossRef]
- Gong, X.; Huang, J.; Scarpa, F.; Liu, Y.; Leng, J. Zero Poisson’s Ratio Cellular Structure for Two-Dimensional Morphing Ap-plications. Compos. Struct. 2015, 134, 384–392. [Google Scholar] [CrossRef]
- Grima, J.N.; Gatt, R.; Farrugia, P.-S. On the properties of auxetic meta-tetrachiral structures. Phys. Status Solidi 2008, 245, 511–520. [Google Scholar] [CrossRef]
- Grima, J.N.; Oliveri, L.; Attard, D.; Ellul, B.; Gatt, R.; Cicala, G.; Recca, G. Hexagonal Honeycombs with Zero Poisson’s Ratios and Enhanced Stiffness. Adv. Eng. Mater. 2010, 12, 855–862. [Google Scholar] [CrossRef]
- Huang, J.; Gong, X.; Zhang, Q.; Scarpa, F.; Liu, Y.; Leng, J. In-Plane Mechanics of a Novel Zero Poisson’s Ratio Honeycomb Core. Compos. Part B Eng. 2016, 89, 67–76. [Google Scholar] [CrossRef]
- Karakoç, A.; Freund, J. A direct simulation method for the effective in-plane stiffness of cellular materials. Int. J. Appl. Mech. 2013, 5, 1350034. [Google Scholar] [CrossRef]
- Li, X.; Yang, Z.; Lu, Z. Design 3D metamaterials with compression-induced-twisting characteristics using shear–compression coupling effects. Extreme Mech. Lett. 2019, 29, 100471. [Google Scholar] [CrossRef]
- Liu, W.; Li, H.; Zhang, J.; Bai, Y. In-plane mechanics of a novel cellular structure for multiple morphing applications. Compos. Struct. 2019, 207, 598–611. [Google Scholar] [CrossRef]
- Liu, W.; Li, H.; Zhang, J.; Li, H. Elastic Properties of a Novel Cellular Structure with Trapezoidal Beams. Aerosp. Sci. Technol. 2018, 75, 315–328. [Google Scholar] [CrossRef]
- Zhong, R.; Fu, M.; Chen, X.; Zheng, B.; Hu, L. A novel three-dimensional mechanical metamaterial with compression-torsion properties. Compos. Struct. 2019, 226, 111232. [Google Scholar] [CrossRef]
- Lakes, R. Deformation Mechanisms in Negative Poisson’s Ratio Materials: Structural Aspects. J. Mater. Sci. 1991, 26, 2287–2292. [Google Scholar] [CrossRef]
- Prall, D.; Lakes, R.S. Properties of a Chiral Honeycomb with a Poisson’s Ratio of—1. Int. J. Mech. Sci. 1997, 39, 305–314. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L.; Attard, D.; Evans, K.E.; Gatt, R.; Grima, J.N.; Miller, W.; Ravirala, N.; Smith, C.W.; Zied, K. Elastic constants of 3-, 4- and 6-connected chiral and anti-chiral honeycombs subject to uniaxial in-plane loading. Compos. Sci. Technol. 2010, 70, 1042–1048. [Google Scholar] [CrossRef]
- Alderson, A.; Alderson, K.L.; Chirima, G.T.; Ravirala, N.; Zied, K. The in-plane linear elastic constants and out-of-plane bending of 3-coordinated ligament and cylinder-ligament honeycombs. Compos. Sci. Technol. 2010, 70, 1034–1041. [Google Scholar] [CrossRef]
- Lorato, A.; Innocenti, P.; Scarpa, F.; Alderson, A.; Alderson, K.L.; Zied, K.; Ravirala, N.; Miller, W.; Smith, C.W.; Evans, K.E. The transverse elastic properties of chiral honeycombs. Compos. Sci. Technol. 2010, 70, 1057–1063. [Google Scholar] [CrossRef]
- Qi, D.; Yu, H.; Hu, W.; He, C.; Wu, W.; Ma, Y. Bandgap and wave attenuation mechanisms of innovative reentrant and anti-chiral hybrid auxetic metastructure. Extrem. Mech. Lett. 2019, 28, 58–68. [Google Scholar] [CrossRef]
- Ruan, X.L.; Li, J.J.; Song, X.K.; Zhou, H.J.; Yuan, W.X.; Wu, W.W.; Xia, R. Mechanical Design of Antichiral-Reentrant Hybrid Intravascular Stent. Int. J. Appl. Mech. 2018, 10. [Google Scholar] [CrossRef]
- Wu, W.; Geng, L.; Niu, Y.; Qi, D.; Cui, X.; Fang, D. Compression Twist Deformation of Novel Tetrachiral Architected Cylin-drical Tube Inspired by Towel Gourd Tendrils. Extrem. Mech. Lett. 2018, 20, 104–111. [Google Scholar] [CrossRef]
- Wu, W.; Hu, W.; Qian, G.; Liao, H.; Xu, X.; Berto, F. Mechanical design and multifunctional applications of chiral mechanical metamaterials: A review. Mater. Des. 2019, 180, 107950. [Google Scholar] [CrossRef]
- Wu, W.; Tao, Y.; Xia, Y.; Chen, J.; Lei, H.; Sun, L.; Fang, D. Mechanical Properties of Hierarchical Anti-Tetrachiral Meta-structures. Extrem. Mech. Lett. 2017, 16, 18–32. [Google Scholar] [CrossRef]
- Sha, Z.; She, C.; Xu, G.; Pei, Q.; Liu, Z.; Wang, T.; Gao, H. Metallic glass-based chiral nanolattice: Light weight, auxeticity, and superior mechanical properties. Mater. Today 2017, 20, 569–576. [Google Scholar] [CrossRef]
- Ma, C.; Lei, H.; Hua, J.; Bai, Y.; Liang, J.; Fang, D. Experimental and simulation investigation of the reversible bi-directional twisting response of tetra-chiral cylindrical shells. Compos. Struct. 2018, 203, 142–152. [Google Scholar] [CrossRef]
- Ma, C.; Lei, H.; Liang, J.; Wu, W.; Wang, T.; Fang, D. Macroscopic Mechanical Response of Chiral-Type Cylindrical Meta-structures Under Axial Compression Loading. Mater. Des. 2018, 158, 198–212. [Google Scholar] [CrossRef]
- Bettini, P.; Airoldi, A.; Sala, G.; Di Landro, L.; Ruzzene, M.; Spadoni, A. Composite chiral structures for morphing airfoils: Numerical analyses and development of a manufacturing process. Compos. Part B Eng. 2010, 41, 133–147. [Google Scholar] [CrossRef]
- Heo, H.; Ju, J.; Kim, D.-M. Compliant cellular structures: Application to a passive morphing airfoil. Compos. Struct. 2013, 106, 560–569. [Google Scholar] [CrossRef]
- Smith, C.; Grima, J.; Evans, K. A novel mechanism for generating auxetic behaviour in reticulated foams: Missing rib foam model. Acta Mater. 2000, 48, 4349–4356. [Google Scholar] [CrossRef]
- Bahaloo, H.; Li, Y. Micropolar Modeling of Auxetic Chiral Lattices with Tunable Internal Rotation. J. Appl. Mech. 2019, 86, 0410024. [Google Scholar] [CrossRef]
- Liu, W.; Li, H.; Yang, Z.; Zhang, J.; Ge, X. In-plane elastic properties of a 2D chiral cellular structure with V-shaped wings. Eng. Struct. 2020, 210, 110384. [Google Scholar] [CrossRef]
- Cristescu, N.D.; Craciun, E.-M.; Soós, E. Mechanics of Elastic Composites. Mech. Elastic Compos. 2003, 1. [Google Scholar] [CrossRef]
- Groza, G.; Mitu, A.-M.; Pop, N.; Sireteanu, T. Transverse vibrations analysis of a beam with degrading hysteretic behavior by using Euler-Bernoulli beam model. Analele Univ. Ovidius Constanta Ser. Mat. 2018, 26, 125–139. [Google Scholar] [CrossRef]
- Asad, J.; Florea, O. Numerical aspects of two coupled harmonic oscillators. Analele Univ. Ovidius Constanta Ser. Mat. 2020, 28, 5–15. [Google Scholar] [CrossRef]
- Khodadadian, A.; Noii, N.; Parvizi, M.; Abbaszadeh, M.; Wick, T.; Heitzinger, C. A Bayesian estimation method for variational phase-field fracture problems. Comput. Mech. 2020, 66, 827–849. [Google Scholar] [CrossRef]
- Khodadadian, A.; Parvizi, M.; Abbaszadeh, M.; Dehghan, M.; Heitzinger, C. A multilevel Monte Carlo finite element method for the stochastic Cahn–Hilliard–Cook equation. Comput. Mech. 2019, 64, 937–949. [Google Scholar] [CrossRef] [PubMed]
- Ferdous, W.; Manalo, A.; Peauril, J.; Salih, C.; Reddy, K.R.; Yu, P.; Schubel, P.; Heyer, T. Testing and modelling the fatigue behaviour of GFRP composites—Effect of stress level, stress concentration and frequency. Eng. Sci. Technol. Int. J. 2020, 23, 1223–1232. [Google Scholar] [CrossRef]
- Ferdous, W.; Manalo, A.; AlAjarmeh, O.; Mohammed, A.A.; Salih, C.; Yu, P.; Khotbehsara, M.M.; Schubel, P. Static behaviour of glass fibre reinforced novel composite sleepers for mainline railway track. Eng. Struct. 2021, 229, 111627. [Google Scholar] [CrossRef]



| Conditions | Tensile Loading in the x-Direction | Shear Loading in the x–y Plane |
|---|---|---|
| Periodic conditions | ||
| Boundary conditions | ||
| z-direction~SYMM for all nodes | ||
| Parameters | β = 0.01 | |||||
|---|---|---|---|---|---|---|
| α = 0.5 | α = 0.6 | α = 0.7 | α = 0.8 | α = 0.9 | α = 1 | |
| Theoretical result | 1.2731 | 1.2731 | 1.2732 | 1.2732 | 1.2732 | 1.2732 |
| FE result | 1.2725 | 1.2728 | 1.2729 | 1.2730 | 1.2730 | 1.2731 |
| Error | 4.12 × 10−4 | 2.86 × 10−4 | 2.10 × 10−4 | 1.61 × 10−4 | 1.27 × 10−4 | 1.03 × 10−4 |
| Parameters | β = 0.05 | |||||
| α = 0.5 | α = 0.6 | α = 0.7 | α = 0.8 | α = 0.9 | α = 1 | |
| Theoretical result | 1.2690 | 1.2703 | 1.2711 | 1.2716 | 1.2719 | 1.2722 |
| FE result | 1.2561 | 1.2613 | 1.2644 | 1.2665 | 1.2679 | 1.2689 |
| Error | 1.03 × 10−2 | 0.71 × 10−2 | 0.52 × 10−2 | 0.40 × 10−2 | 0.32 × 10−2 | 0.26 × 10−2 |
| Parameters | β = 0.1 | |||||
| α = 0.5 | α = 0.6 | α = 0.7 | α = 0.8 | α = 0.9 | α = 1 | |
| Theoretical result | 1.2565 | 1.2616 | 1.2646 | 1.2666 | 1.2680 | 1.2690 |
| FE result | 1.2074 | 1.2268 | 1.2388 | 1.2467 | 1.2522 | 1.2561 |
| Error | 4.06 × 10−2 | 2.83 × 10−2 | 2.09 × 10−2 | 1.60 × 10−2 | 1.27 × 10−2 | 1.03 × 10−2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bai, Y.; Zhao, T.; Yuan, C.; Liu, W.; Zhang, H.; Yang, L.; She, C. Mechanical Properties of a Chiral Cellular Structure with Semicircular Beams. Materials 2021, 14, 2887. https://doi.org/10.3390/ma14112887
Bai Y, Zhao T, Yuan C, Liu W, Zhang H, Yang L, She C. Mechanical Properties of a Chiral Cellular Structure with Semicircular Beams. Materials. 2021; 14(11):2887. https://doi.org/10.3390/ma14112887
Chicago/Turabian StyleBai, Yalei, Tong Zhao, Chengxu Yuan, Weidong Liu, Haichao Zhang, Lei Yang, and Chongmin She. 2021. "Mechanical Properties of a Chiral Cellular Structure with Semicircular Beams" Materials 14, no. 11: 2887. https://doi.org/10.3390/ma14112887
APA StyleBai, Y., Zhao, T., Yuan, C., Liu, W., Zhang, H., Yang, L., & She, C. (2021). Mechanical Properties of a Chiral Cellular Structure with Semicircular Beams. Materials, 14(11), 2887. https://doi.org/10.3390/ma14112887







