Electron-Phonon Coupling Parameter of Ferromagnetic Metal Fe and Co
Abstract
1. Introduction
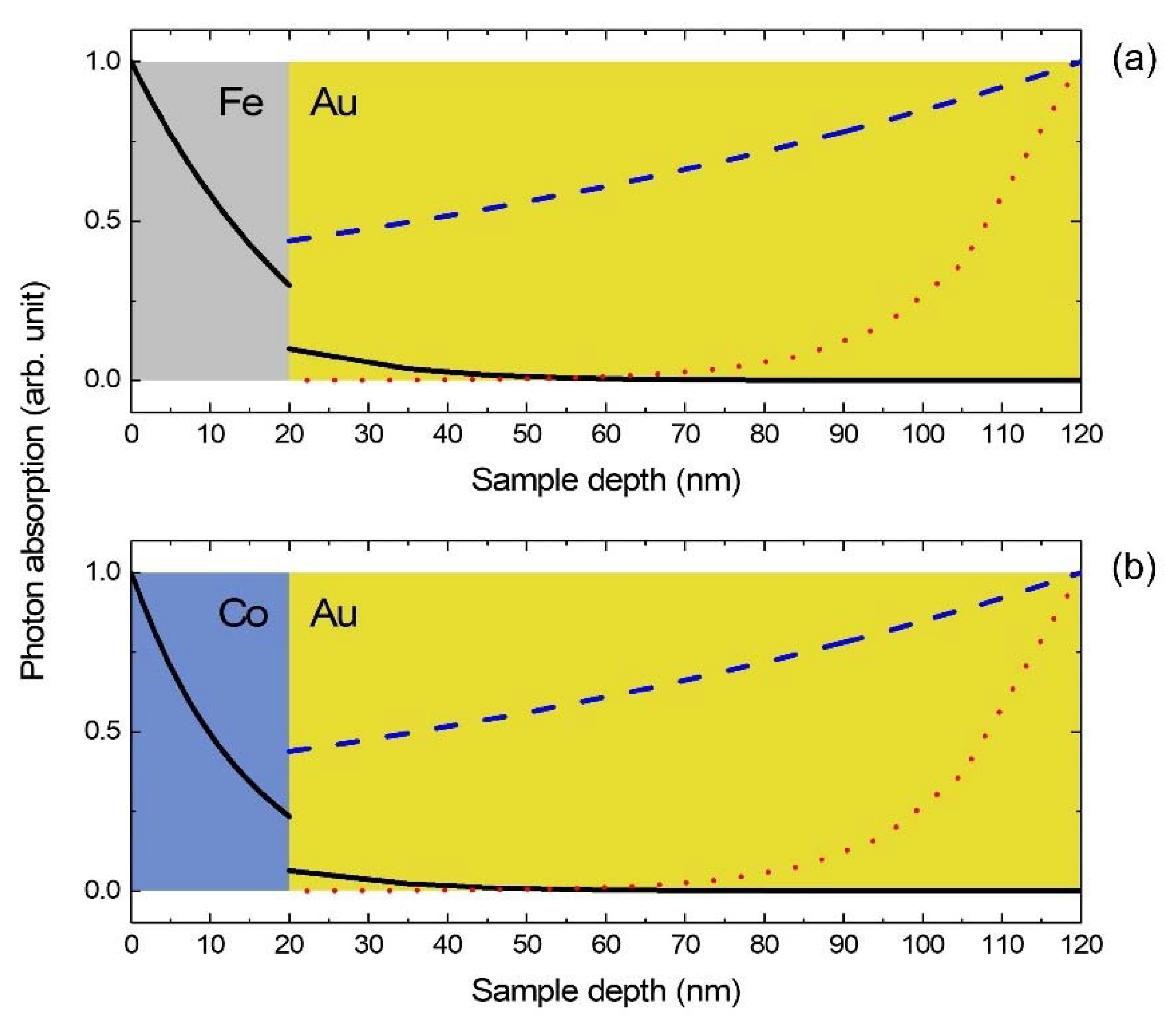
2. Materials and Methods
3. Results
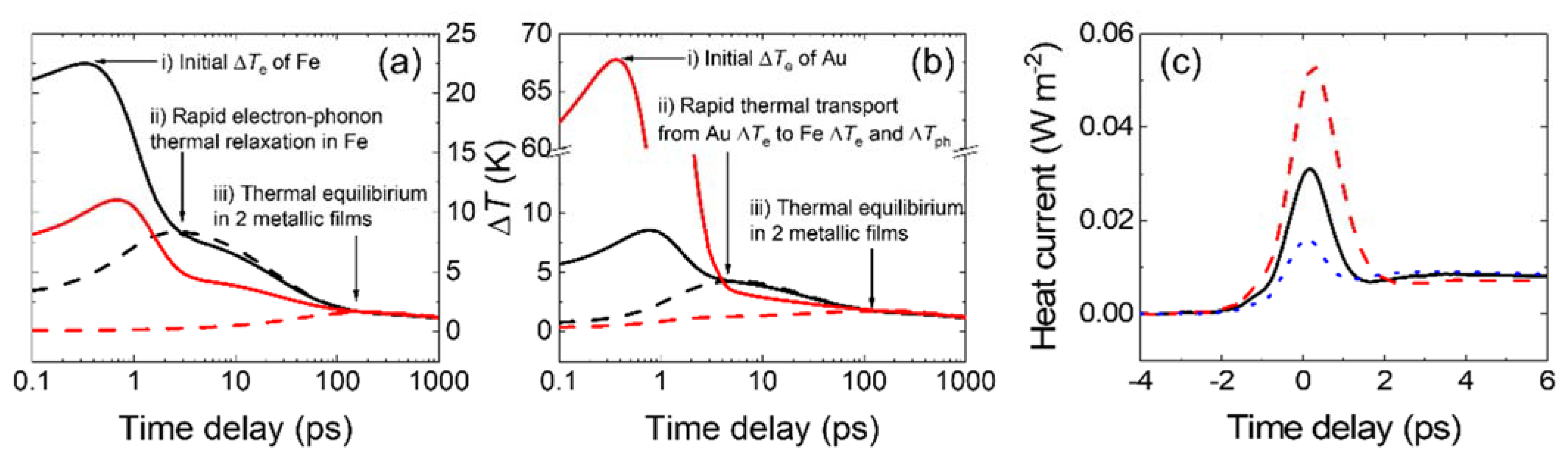
3.1. Overview
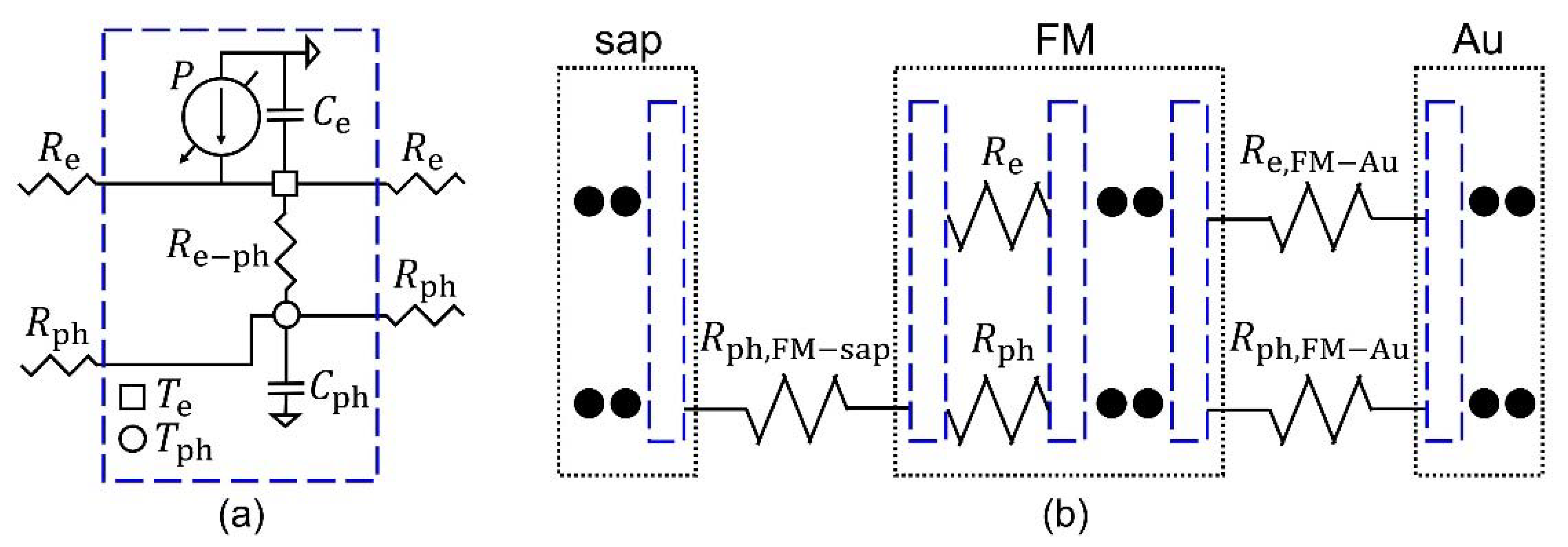
3.2. Thermal Circuit Model
3.3. Fitting Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Anisimov, S.; Kapeliovich, B.; Perel’Man, T. Electron emission from metal surfaces exposed to ultrashort laser pulses. Sov. J. Exp. Theor. Phys. 1974, 39, 776–781. [Google Scholar]
- Fujimoto, J.G.; Liu, J.M.; Ippen, E.P.; Bloembergen, N. Femtosecond Laser Interaction with Metallic Tungsten and Nonequilibrium Electron and Lattice Temperatures. Phys. Rev. Lett. 1984, 53, 1837–1840. [Google Scholar] [CrossRef]
- Philip, B. Allen Theory of Thermal Relaxation of Electrons in Metals. Phys. Rev. Lett. 1987, 59, 1460. [Google Scholar]
- Brorson, S.D.; Kazeroonian, A.; Moodera, J.S.; Face, D.W.; Cheng, T.K.; Ippen, E.P.; Dresselhaus, M.S.; Dresselhaus, G. Femtosecond room-temperature measurement of the electron-phonon coupling constant γ in metallic superconductors. Phys. Rev. Lett. 1990, 64, 2172–2175. [Google Scholar] [CrossRef]
- Elsayed-Ali, H.E.; Juhasz, T.; Smith, G.O.; Bron, W.E. Femtosecond thermoreflectivity and thermotransmissivity of polycrystalline and single-crystalline gold films. Phys. Rev. B 1991, 43, 4488–4491. [Google Scholar] [CrossRef] [PubMed]
- Groeneveld, R.H.M.; Sprik, R.; Lagendijk, A. Femtosecond spectroscopy of electron-electron and electron-phonon energy relaxation in Ag and Au. Phys. Rev. B 1995, 51, 11433–11445. [Google Scholar] [CrossRef] [PubMed]
- Hostetler, J.L.; Smith, A.N.; Czajkowsky, D.M.; Norris, P.M. Measurement of the electron-phonon coupling factor dependence on film thickness and grain size in Au, Cr, and Al. Appl. Opt. 1999, 38, 3614–3620. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.; Zhigilei, L.; Celli, V. Electron-phonon coupling and electron heat capacity of metals under conditions of strong electron-phonon nonequilibrium. Phys. Rev. B 2008, 77, 1–17. [Google Scholar] [CrossRef]
- Caffrey, A.P.; Hopkins, P.E.; Klopf, J.M.; Norris, P.M. Thin Film Non-Noble Transition Metal Thermophysical Properties. Microscale Thermophys. Eng. 2005, 9, 365–377. [Google Scholar] [CrossRef]
- Beaurepaire, E.; Merle, J.-C.; Daunois, A.; Bigot, J.-Y. Ultrafast Spin Dynamics in Ferromagnetic Nickel. Phys. Rev. Lett. 1996, 76, 4250–4253. [Google Scholar] [CrossRef]
- Kang, K.; Choi, G.-M. Thermal coupling parameters between electron, phonon, and magnon of Nickel. J. Magn. Magn. Mater. 2020, 514, 167156. [Google Scholar] [CrossRef]
- Petrov, Y.V.; Inogamov, N.A.; Migdal, K.P. Thermal conductivity and the electron-ion heat transfer coefficient in condensed media with a strongly excited electron subsystem. JETP Lett. 2013, 97, 20–27. [Google Scholar] [CrossRef]
- Ritzmann, U.; Oppeneer, P.M.; Maldonado, P. Theory of out-of-equilibrium electron and phonon dynamics in metals after femtosecond laser excitation. Phys. Rev. B 2020, 102, 214305. [Google Scholar] [CrossRef]
- Medvedev, N.; Milov, I. Electron-phonon coupling in metals at high electronic temperatures. Phys. Rev. B 2020, 102, 064302. [Google Scholar] [CrossRef]
- Jang, H.; Marnitz, L.; Huebner, T.; Kimling, J.; Kuschel, T.; Cahill, D.G. Thermal Conductivity of Oxide Tunnel Barriers in Magnetic Tunnel Junctions Measured by Ultrafast Thermoreflectance and Magneto-Optic Kerr Effect Thermometry. Phys. Rev. Appl. 2020, 13, 1. [Google Scholar] [CrossRef]
- Wang, W.; Cahill, D.G. Limits to Thermal Transport in Nanoscale Metal Bilayers due to Weak Electron-Phonon Coupling in Au and Cu. Phys. Rev. Lett. 2012, 109, 175503. [Google Scholar] [CrossRef]
- Choi, G.-M.; Wilson, R.B.; Cahill, D.G. Indirect heating of Pt by short-pulse laser irradiation of Au in a nanoscale Pt/Au bilayer. Phys. Rev. B 2014, 89, 064307. [Google Scholar] [CrossRef]
- Schoenlein, R.W.; Lin, W.Z.; Fujimoto, J.G.; Eesley, G.L. Femtosecond studies of nonequilibrium electronic processes in metals. Phys. Rev. Lett. 1987, 58, 1680–1683. [Google Scholar] [CrossRef]
- Groeneveld, R.H.M.; Sprik, R.; Lagendijk, A. Effect of a nonthermal electron distribution on the electron-phonon energy relaxation process in noble metals. Phys. Rev. B 1992, 45, 5079–5082. [Google Scholar] [CrossRef] [PubMed]
- Giri, A.; Gaskins, J.T.; Foley, B.M.; Cheaito, R.; Hopkins, P.E. Experimental evidence of excited electron number density and temperature effects on electron-phonon coupling in gold films. J. Appl. Phys. 2015, 117, 044305. [Google Scholar] [CrossRef]
- Cahill, D.G. Analysis of heat flow in layered structures for time-domain thermoreflectance. Rev. Sci. Instrum. 2004, 75, 5119–5122. [Google Scholar] [CrossRef]
- Huxtable, S.; Cahill, D.G.; Fauconnier, V.; White, J.O.; Zhao, J.-C. Thermal conductivity imaging at micrometre-scale resolution for combinatorial studies of materials. Nat. Mater. 2004, 3, 298–301. [Google Scholar] [CrossRef]
- Costescu, R.M.; Wall, M.A.; Cahill, D.G. Thermal conductance of epitaxial interfaces. Phys. Rev. B 2003, 67, 054302. [Google Scholar] [CrossRef]
- Pratt, W.; Bass, J. Perpendicular-current studies of electron transport across metal/metal interfaces. Appl. Surf. Sci. 2009, 256, 399–403. [Google Scholar] [CrossRef][Green Version]
- Wang, H.; Xu, Y.; Shimono, M.; Tanaka, Y.; Yamazaki, M. Computation of Interfacial Thermal Resistance by Phonon Diffuse Mismatch Model. Mater. Trans. 2007, 48, 2349–2352. [Google Scholar] [CrossRef]
- Van Kampen, M.; Kohlhepp, J.T.; De Jonge, W.J.M.; Koopmans, B.; Coehoorn, R. Sub-picosecond electron and phonon dynamics in nickel. J. Physics: Condens. Matter 2005, 17, 6823–6834. [Google Scholar] [CrossRef]
- Hohlfeld, J.; Wellershoff, S.-S.; Güdde, J.; Conrad, U.; Jähnke, V.; Matthias, E. Electron and lattice dynamics following optical excitation of metals. Chem. Phys. 2000, 251, 237–258. [Google Scholar] [CrossRef]
- Brorson, S.D.; Fujimoto, J.G.; Ippen, E.P. Femtosecond electronic heat-transport dynamics in thin gold films. Phys. Rev. Lett. 1987, 59, 1962–1965. [Google Scholar] [CrossRef]
- Wilson, R.B.; Apgar, B.A.; Martin, L.W.; Cahill, D.G. Thermoreflectance of metal transducers for optical pump-probe studies of thermal properties. Opt. Express 2012, 20, 28829–28838. [Google Scholar] [CrossRef] [PubMed]
- Purdue University, Thermophysical Properties Research Center. Thermophysical Properties of High Temperature Solid Materials; Touloukian, Y.S., Ed.; Macmillan: New York, NY, USA, 1967. [Google Scholar]
- Bruce, H.B.; Dwight, E. American Institute of Physics Handbook, 3rd ed.; McGraw-Hill: New York, NY, USA, 1972. [Google Scholar]
- Klemens, P.G.; Williams, R.K. Thermal conductivity of metals and alloys. Int. Met. Rev. 1986, 31, 197. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, Z.; Ruan, X. First principles calculation of lattice thermal conductivity of metals considering phonon-phonon and phonon-electron scattering. J. Appl. Phys. 2016, 119, 225109. [Google Scholar] [CrossRef]
- Parchovianský, M.; Galusek, D.; Švančárek, P.; Sedláček, J.; Šajgalík, P. Thermal behavior, electrical conductivity and microstructure of hot pressed Al2O3/SiC nanocomposites. Ceram. Int. 2014, 40, 14421–14429. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical Constant of the Nobel Metals. Phys. Rev. B 1972, 6, 4370–4379. [Google Scholar] [CrossRef]
- Johnson, P.; Christy, R. Optical constants of transition metals: Ti, V, Cr, Mn, Fe, Co, Ni, and Pd. Phys. Rev. B 1974, 9, 5056–5070. [Google Scholar] [CrossRef]
- Malitson, I.H. and M.J. Dodge. Refractive-index and birefringence of synthetic sapphire. J. Opt. Soc. Am. 1972, 62, 1405. [Google Scholar]

| Au | Fe | Co | Sapphire | |
|---|---|---|---|---|
| () | 2.5 1 | 3.5 1 | 3.76 1 | 3.08 1 |
| () | 67.6 2 | 705 2 | 710 2 | |
| () | 2.47 3 | 3.32 3 | 3.55 3 | 3.08 3 |
| () | 0.7 4 | 0.17 5 | 0.18 5 | |
| () | 2.5 6 | 9 5 | 5 5 | 30 7 |
| () | 0.22 8 | 8.8–9.4 9 | 9.6–12.2 9 | |
| () | 20 10 | 14 10 | ||
| () | 1 11 | 1 11 | ||
| () | 0.35 9 | 0.6 9 | ||
| 0.15 + 4.8j 12 | 2.9 + 3.33j 13 | 2.46 + 4.75j 13 | 1.76 14 | |
| () | 2 15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, K.; Choi, G.-M. Electron-Phonon Coupling Parameter of Ferromagnetic Metal Fe and Co. Materials 2021, 14, 2755. https://doi.org/10.3390/ma14112755
Kang K, Choi G-M. Electron-Phonon Coupling Parameter of Ferromagnetic Metal Fe and Co. Materials. 2021; 14(11):2755. https://doi.org/10.3390/ma14112755
Chicago/Turabian StyleKang, Kyuhwe, and Gyung-Min Choi. 2021. "Electron-Phonon Coupling Parameter of Ferromagnetic Metal Fe and Co" Materials 14, no. 11: 2755. https://doi.org/10.3390/ma14112755
APA StyleKang, K., & Choi, G.-M. (2021). Electron-Phonon Coupling Parameter of Ferromagnetic Metal Fe and Co. Materials, 14(11), 2755. https://doi.org/10.3390/ma14112755






