Magnetic Anisotropy and Damping Constant of Ferrimagnetic GdCo Alloy near Compensation Point
Abstract
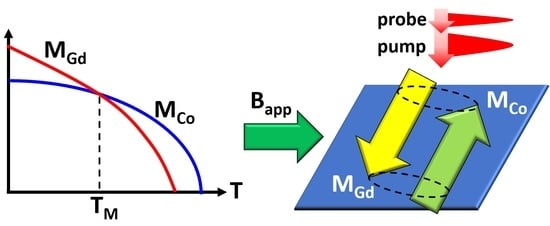
1. Introduction
2. Materials and Methods
3. Results
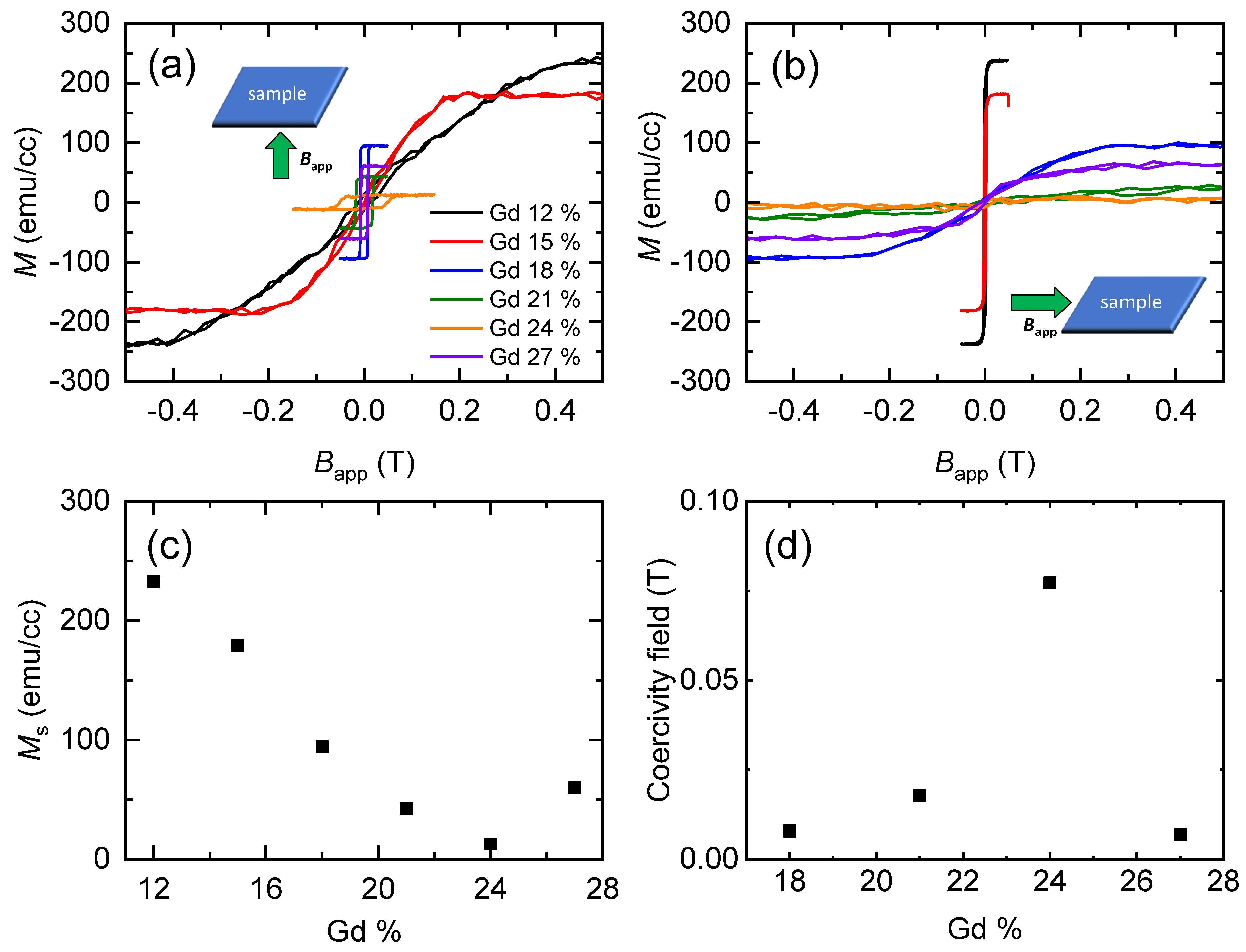
3.1. Basic Magnetic Properties
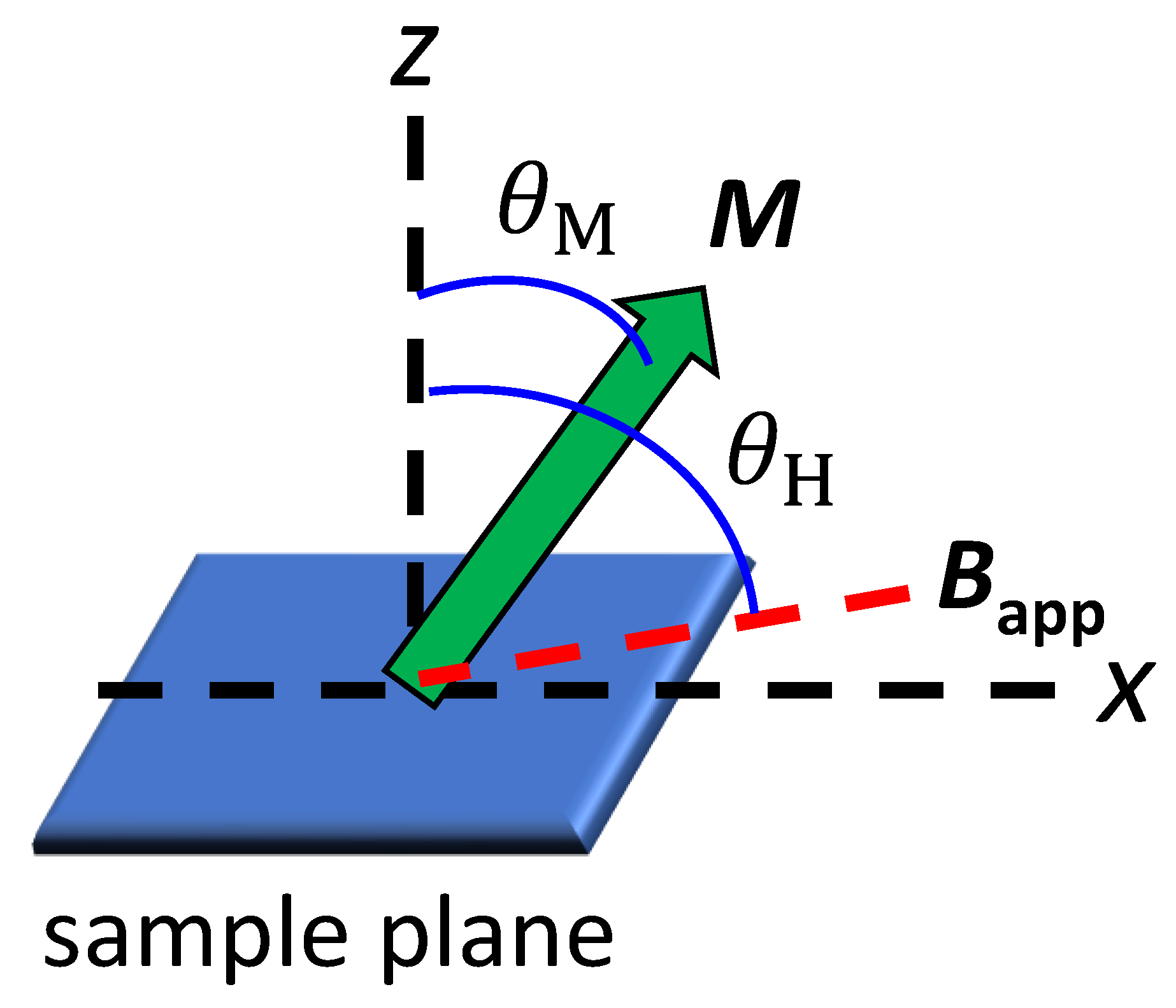
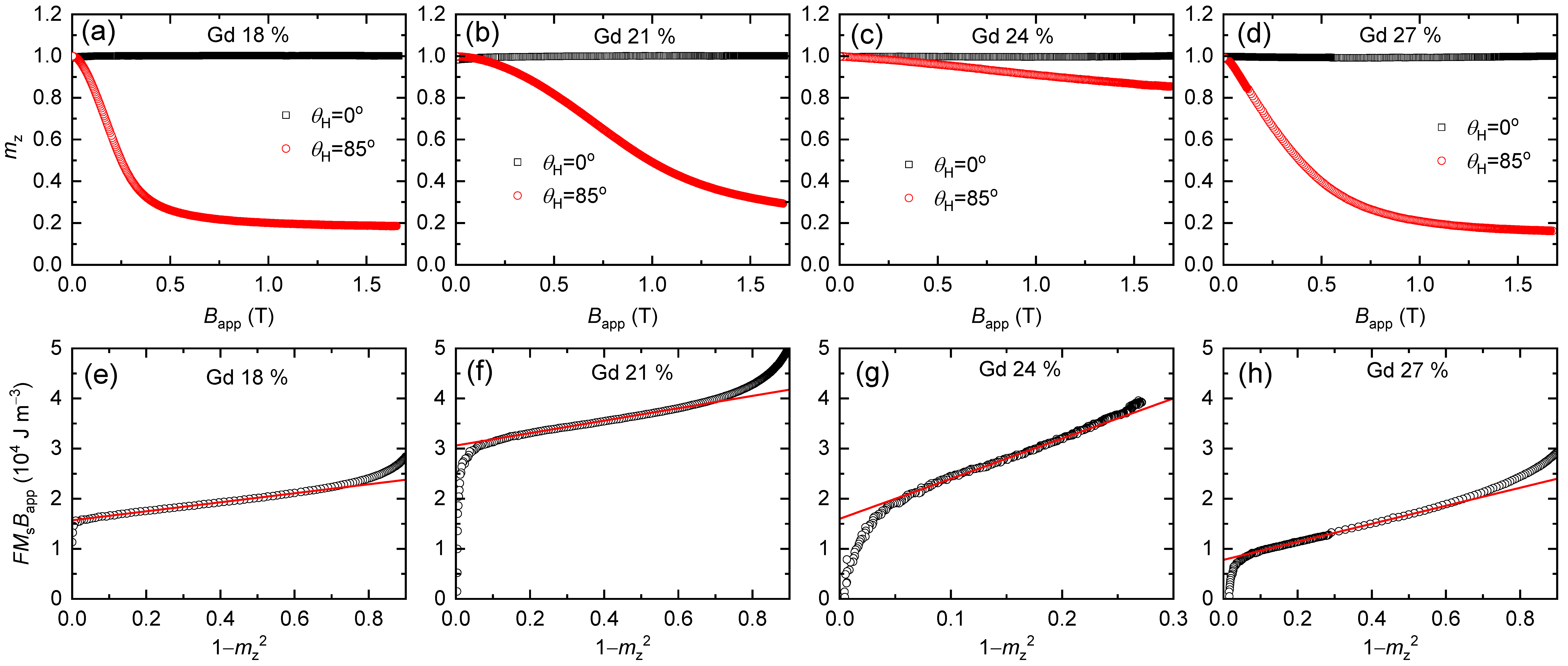
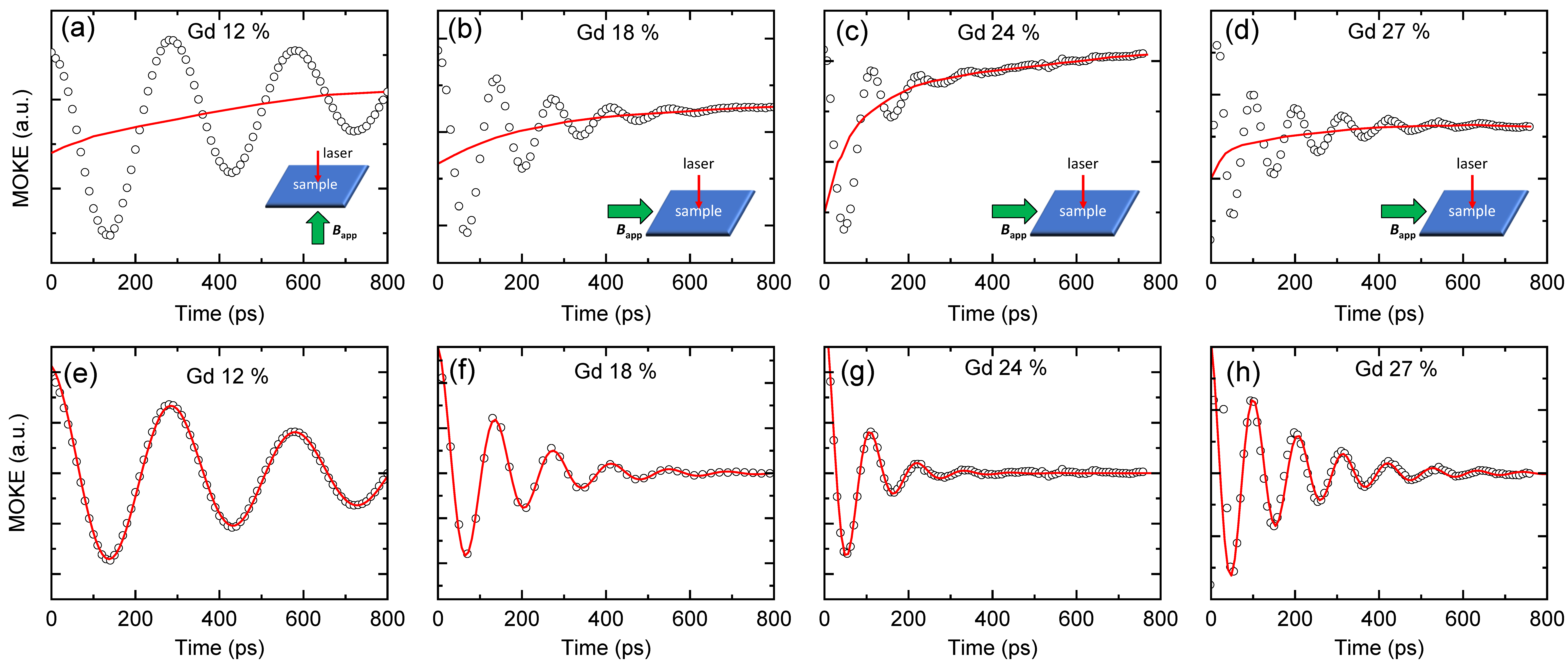
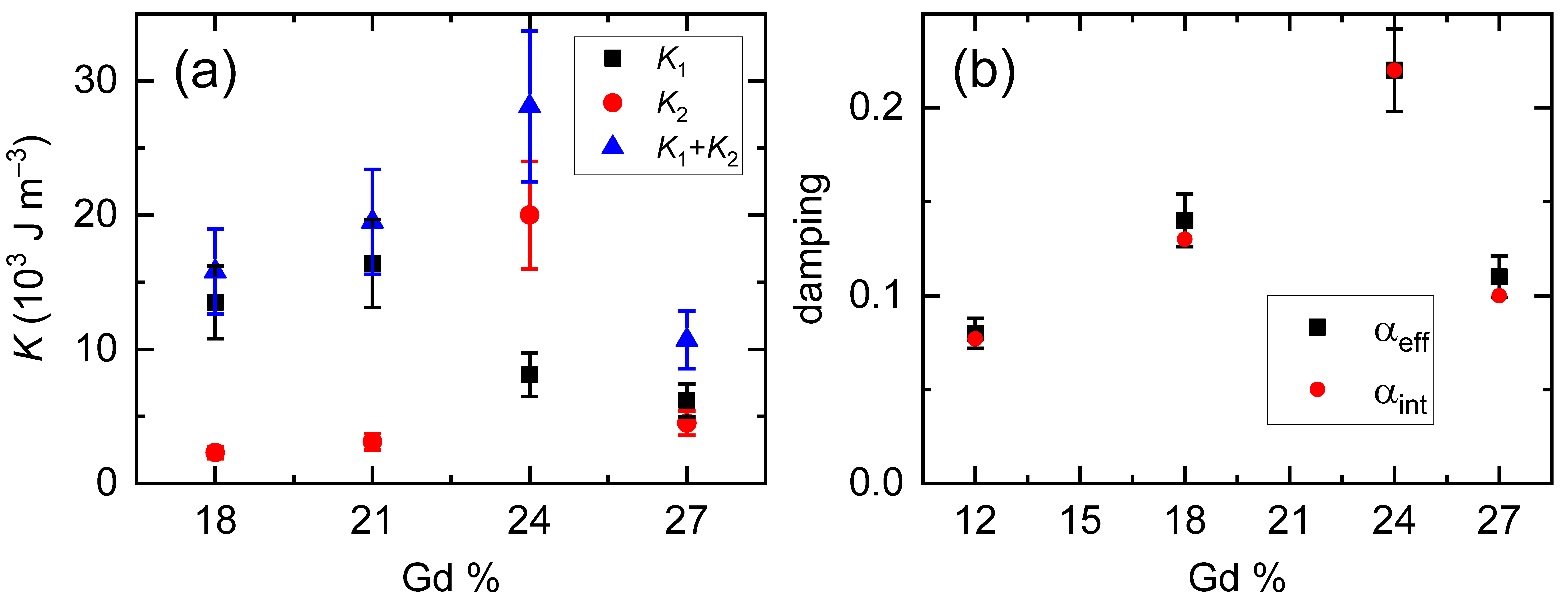
3.2. Determination of Magnetic Anisotropy
3.3. Determination of Damping Constant
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Esho, S.; Fujiwara, S. Growth Induced Anisotropy in Sputtered GdCo Films. In Magnetism and Magnetic Materials, Proceedings of the First Joint MMM-Intermag Conference, Pittsburgh, PA, USA, 15–18 June 1976; AIP Publishing: College Park, MD, USA, 1976; Volume 34, pp. 331–333. [Google Scholar]
- Taylor, R.; Gangulee, A. Magnetization and magnetic anisotropy in evaporated GdCo amorphous films. J. Appl. Phys. 1976, 47, 4666–4668. [Google Scholar] [CrossRef]
- Mizoguchi, T.; Cargill, G., III. Magnetic anisotropy from dipolar interactions in amorphous ferrimagnetic alloys. J. Appl. Phys. 1979, 50, 3570–3582. [Google Scholar] [CrossRef]
- Ostler, T.A.; Evans, R.F.L.; Chantrell, R.W.; Atxitia, U.; Chubykalo-Fesenko, O.; Radu, I.; Abrudan, R.; Radu, F.; Tsukamoto, A.; Itoh, A.; et al. Crystallographically amorphous ferrimagnetic alloys: Comparing a localized atomistic spin model with experiments. Phys. Rev. B 2011, 84, 024407. [Google Scholar] [CrossRef]
- Stanciu, C.D.; Hansteen, F.; Kimel, A.V.; Kirilyuk, A.; Tsukamoto, A.; Itoh, A.; Rasing, T. All-optical magnetic recording with circularly polarized light. Phys. Rev. Lett. 2007, 99, 047601. [Google Scholar] [CrossRef]
- Kirilyuk, A.; Kimel, A.V.; Rasing, T. Laser-induced magnetization dynamics and reversal in ferrimagnetic alloys. Rep. Prog. Phys. 2013, 76, 026501. [Google Scholar] [CrossRef] [PubMed]
- Hansen, P.; Clausen, C.; Much, G.; Rosenkranz, M.; Witter, K. Magnetic and magneto-optical properties of rare-earth transition-metal alloys containing Gd, Tb, Fe, Co. J. Appl. Phys. 1989, 66, 756–767. [Google Scholar] [CrossRef]
- Jiang, X.; Gao, L.; Sun, J.Z.; Parkin, S.S.P. Temperature dependence of current-induced magnetization switching in spin valves with a ferrimagnetic CoGd free layer. Phys. Rev. Lett. 2006, 97, 217202. [Google Scholar] [CrossRef]
- Yang, Y.; Wilson, R.B.; Gorchon, J.; Lambert, C.-H.; Salahuddin, S.; Bokor, J. Ultrafast magnetization reversal by picosecond electrical pulses. Sci. Adv. 2017, 3, e1603117. [Google Scholar] [CrossRef]
- Mishra, R.; Yu, J.; Qiu, X.; Motapothula, M.; Venkatesan, T.; Yang, H. Anomalous current-induced spin torques in ferrimagnets near compensation. Phys. Rev. Lett. 2017, 118, 167201. [Google Scholar] [CrossRef]
- Cai, K.; Zhu, Z.; Lee, J.M.; Mishra, R.; Ren, L.; Pollard, S.D.; He, P.; Liang, G.; Teo, K.L.; Yang, H. Ultrafast and energy-efficient spin–orbit torque switching in compensated ferrimagnets. Nat. Electron. 2020, 3, 37–42. [Google Scholar] [CrossRef]
- Sala, G.; Krizakova, V.; Grimaldi, E.; Lambert, C.-H.; Devolder, T.; Gambardella, P. Real-time Hall-effect detection of current-induced magnetization dynamics in ferrimagnets. Nat. Commun. 2021, 12, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.-J.; Kim, S.K.; Hirata, Y.; Oh, S.-H.; Tono, T.; Kim, D.-H.; Okuno, T.; Ham, W.S.; Kim, S.; Go, G.; et al. Fast domain wall motion in the vicinity of the angular momentum compensation temperature of ferrimagnets. Nat. Mater. 2017, 16, 1187–1192. [Google Scholar] [CrossRef] [PubMed]
- Siddiqui, S.A.; Han, J.; Finley, J.T.; Ross, C.A.; Liu, L. Current-induced domain wall motion in a compensated ferrimagnet. Phys. Rev. Lett. 2018, 121, 057701. [Google Scholar] [CrossRef] [PubMed]
- Caretta, L.; Mann, M.; Büttner, F.; Ueda, K.; Pfau, B.; Günther, C.M.; Hessing, P.; Churikova, A.; Klose, C.; Schneider, M.; et al. Fast current-driven domain walls and small skyrmions in a compensated ferrimagnet. Nat. Nanotechnol. 2018, 13, 1154–1160. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, S.; Miura, K.T.; Yamamoto, H.; Mizunuma, K.; Gan, H.D.; Endo, M.; Kanai, S.; Hayakawa, J.; Matsukura, F.; Ohno, H. A perpendicular-anisotropy CoFeB–MgO magnetic tunnel junction. Nat. Mater. 2010, 9, 721–724. [Google Scholar] [CrossRef]
- Ohmori, H.; Hatori, T.; Nakagawa, S. Perpendicular magnetic tunnel junction with tunneling magnetoresistance ratio of 64% using MgO (100) barrier layer prepared at room temperature. J. Appl. Phys. 2008, 103, 07A911. [Google Scholar] [CrossRef]
- Yoshikawa, M. Tunnel magnetoresistance over 100% in MgO-based magnetic tunnel junction films with perpendicular magnetic L10-FePt electrodes. IEEE Trans. Magn. 2008, 44, 2573–2576. [Google Scholar] [CrossRef]
- Rahman, M.T.; Liu, X.; Morisako, A. TiN underlayer and overlayer for TbFeCo perpendicular magnetic recording media. J. Magn. Magn. Mater. 2006, 303, e133–e136. [Google Scholar] [CrossRef]
- Ceballos, A.; Pattabi, A.; El-Ghazaly, A.; Ruta, S.; Simon, C.P.; Evans, R.F.L.; Ostler, T.; Chantrell, R.W.; Kennedy, E.; Scott, M.; et al. Role of element-specific damping in ultrafast, helicity-independent, all-optical switching dynamics in amorphous (Gd,Tb)Co thin films. Phys. Rev. B 2021, 103, 024438. [Google Scholar] [CrossRef]
- Sucksmith, W.; Thompson, J.E. The magnetic anisotropy of cobalt. R. Soc. Lond. Ser. A Math. Phys. Sci. 1954, 225, 362–375. [Google Scholar]
- Okamoto, S.; Kikuchi, N.; Kitakami, O.; Miyazaki, T.; Shimada, Y.; Fukamichi, K. Chemical-order-dependent magnetic anisotropy and exchange stiffness constant of FePt (001) epitaxial films. Phys. Rev. B 2002, 66, 024413. [Google Scholar] [CrossRef]
- Choi, G.-M.; Min, B.-C.; Shin, K.-H. L10 Ordering of FePtB Films on a Thin MgO Layer. Appl. Phys. Express 2011, 4, 023001. [Google Scholar] [CrossRef]
- Nagaosa, N.; Sinova, J.; Onoda, S.; Macdonald, A.H.; Ong, N.P. Anomalous hall effect. Rev. Mod. Phys. 2010, 82, 1539–1592. [Google Scholar] [CrossRef]
- Van Kampen, M.M.; Jozsa, C.C.; Kohlhepp, J.J.; LeClair, P.P.; Lagae, L.L.; De Jonge, W.J.M.; Koopmans, B.B. All-optical probe of coherent spin waves. Phys. Rev. Lett. 2002, 88, 227201. [Google Scholar] [CrossRef] [PubMed]
- Binder, M.; Weber, A.; Mosendz, O.; Woltersdorf, G.; Izquierdo, M.; Neudecker, I.; Dahn, J.R.; Hatchard, T.D.; Thiele, J.-U.; Back, C.H.; et al. Magnetization dynamics of the ferrimagnet CoGd near the compensation of magnetization and angular momentum. Phys. Rev. B 2006, 74, 134404. [Google Scholar] [CrossRef]
- Stanciu, C.D.; Kimel, A.V.; Hansteen, F.; Tsukamoto, A.; Itoh, A.; Kirilyuk, A.; Rasing, T. Ultrafast spin dynamics across compensation points in ferrimagnetic GdFeCo: The role of angular momentum compensation. Phys. Rev. B. 2006, 73, 220402. [Google Scholar] [CrossRef]
- Kato, T.; Nakazawa, K.; Komiya, R.; Nishizawa, N.; Tsunashima, S.; Iwata, S. Compositional dependence of g-factor and damping constant of GdFeCo amorphous alloy films. IEEE Trans. Magn. 2008, 44, 3380–3383. [Google Scholar] [CrossRef]
- Wangsness, R.K. Sublattice effects in magnetic resonance. Phys. Rev. 1953, 91, 1085–1091. [Google Scholar] [CrossRef]
- Mizukami, S. Fast magnetization precession obsereved in L10-FePt epitaxial thin film. Appl. Phys. Lett. 2011, 98, 052501. [Google Scholar] [CrossRef]
- Kim, D.-H.; Okuno, T.; Kim, S.K.; Oh, S.-H.; Nishimura, T.; Hirata, Y.; Futakawa, Y.; Yoshikawa, H.; Tsukamoto, A.; Tserkovnyak, Y.; et al. Low magnetic damping of ferrimagnetic GdFeCo alloys. Phys. Rev. Lett. 2019, 122, 127203. [Google Scholar] [CrossRef]
| Colume Heading | Gd18Co82 | Gd21Co79 | Gd24Co76 | Gd27Co73 |
|---|---|---|---|---|
| K1eff (J m−3) | 7.9 × 103 | 15.3 × 103 | 8 × 103 | 3.9 × 103 |
| μ0M2/2 (J m−3) | 5.6 × 103 | 1.1 × 103 | 0.1 × 103 | 2.3 × 103 |
| K1 (J m−3) | 13.5 × 103 | 16.4 × 103 | 8.1 × 103 | 6.2 × 103 |
| K2 (J m−3) | 2.3 × 103 | 3.1 × 103 | 20 × 103 | 4.5 × 103 |
| K1 + K2 (J m−3) | 15.8 × 103 | 19.5 × 103 | 28.1 × 103 | 10.7 × 103 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joo, S.; Alemayehu, R.S.; Choi, J.-G.; Park, B.-G.; Choi, G.-M. Magnetic Anisotropy and Damping Constant of Ferrimagnetic GdCo Alloy near Compensation Point. Materials 2021, 14, 2604. https://doi.org/10.3390/ma14102604
Joo S, Alemayehu RS, Choi J-G, Park B-G, Choi G-M. Magnetic Anisotropy and Damping Constant of Ferrimagnetic GdCo Alloy near Compensation Point. Materials. 2021; 14(10):2604. https://doi.org/10.3390/ma14102604
Chicago/Turabian StyleJoo, Sungjung, Rekikua Sahilu Alemayehu, Jong-Guk Choi, Byong-Guk Park, and Gyung-Min Choi. 2021. "Magnetic Anisotropy and Damping Constant of Ferrimagnetic GdCo Alloy near Compensation Point" Materials 14, no. 10: 2604. https://doi.org/10.3390/ma14102604
APA StyleJoo, S., Alemayehu, R. S., Choi, J.-G., Park, B.-G., & Choi, G.-M. (2021). Magnetic Anisotropy and Damping Constant of Ferrimagnetic GdCo Alloy near Compensation Point. Materials, 14(10), 2604. https://doi.org/10.3390/ma14102604