A Parallel Coupled Lattice Boltzmann-Volume of Fluid Framework for Modeling Porous Media Evolution
Abstract
1. Introduction
2. The Description of the Physicochemical Model
2.1. The Governing Equations
| Dirichlet: | , | , | |
| Neumann: | , | , | |
| Robin: | , | , |
2.2. Factorized Central-Moment Lattice Boltzmann Method for Modeling Mass Transport
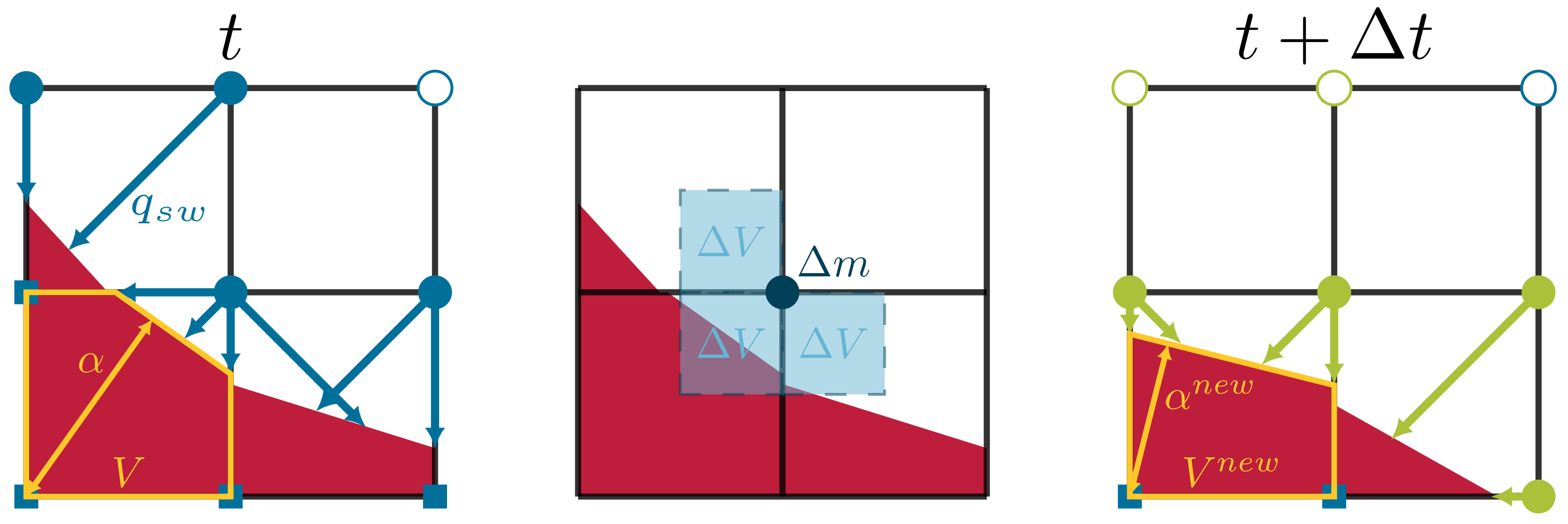
2.3. Volume of Fluid with Piecewise Linear Interface Construction
3. Implementation Details
4. Results and Discussion
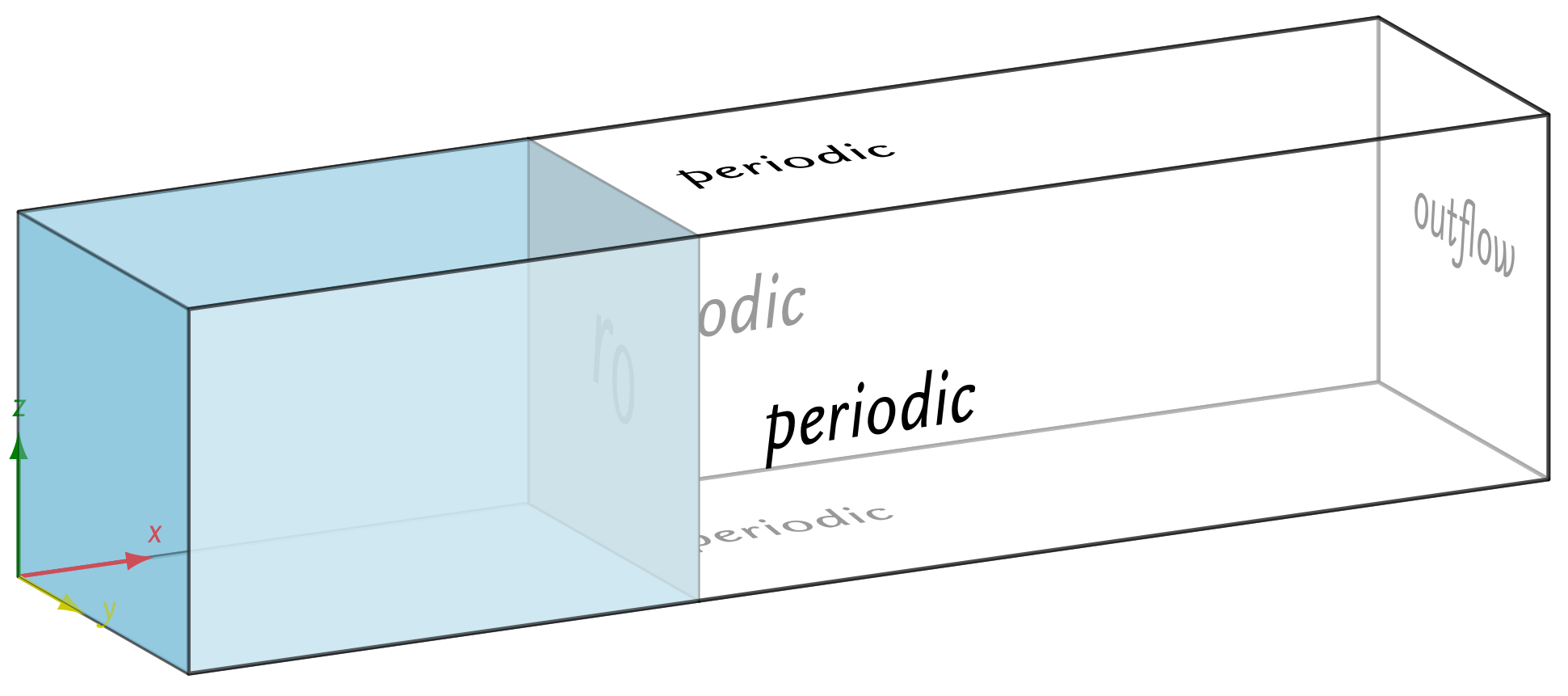
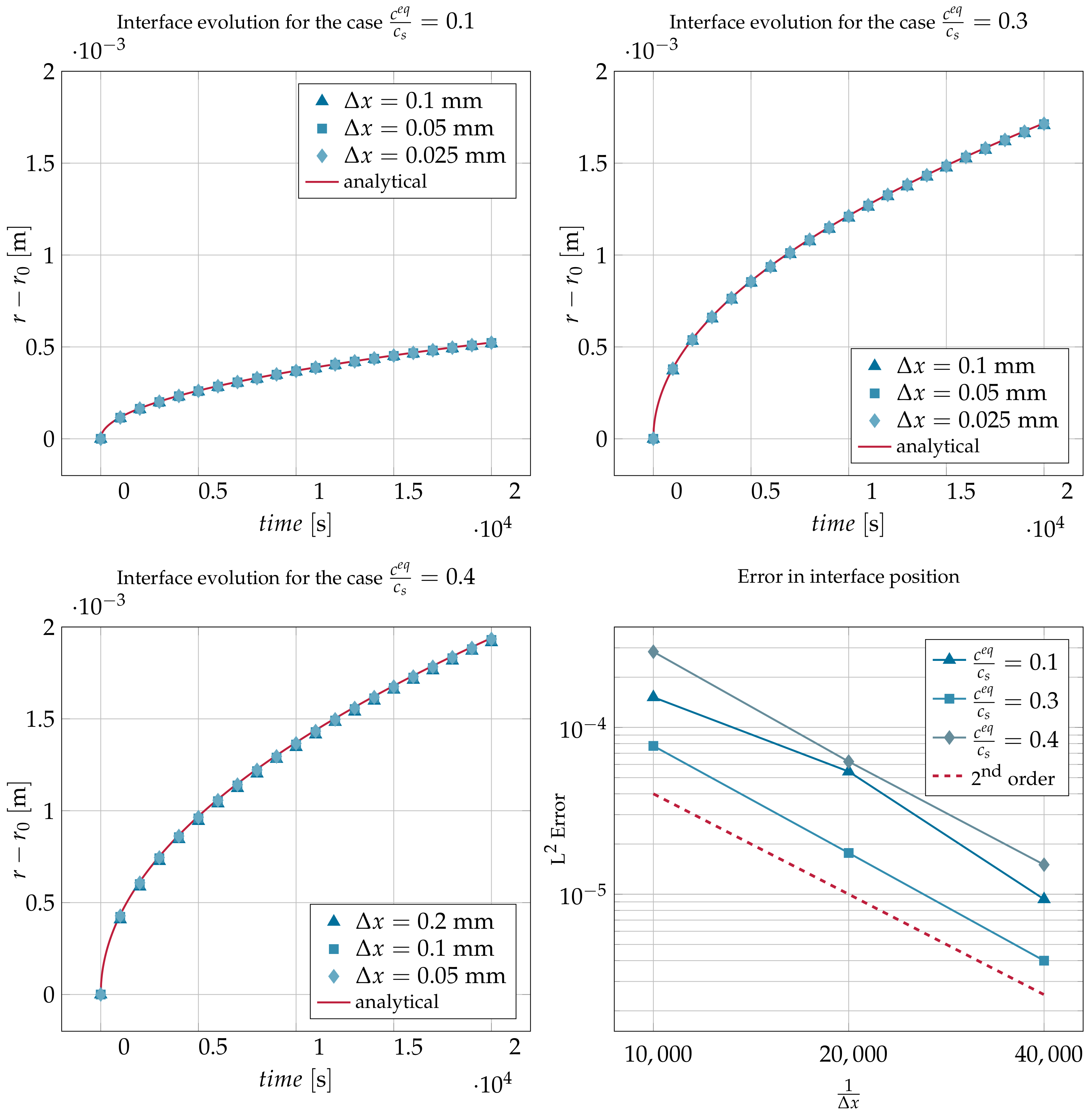
4.1. Channel with Moving Interface: Diffusion Controlled
4.2. Transport and Morphology Change of Tomographic Images of Cement-Based Materials
4.2.1. Preprocessing of the CT Scans
4.2.2. Diffusion through Capillary Pores in HCP Microstructures
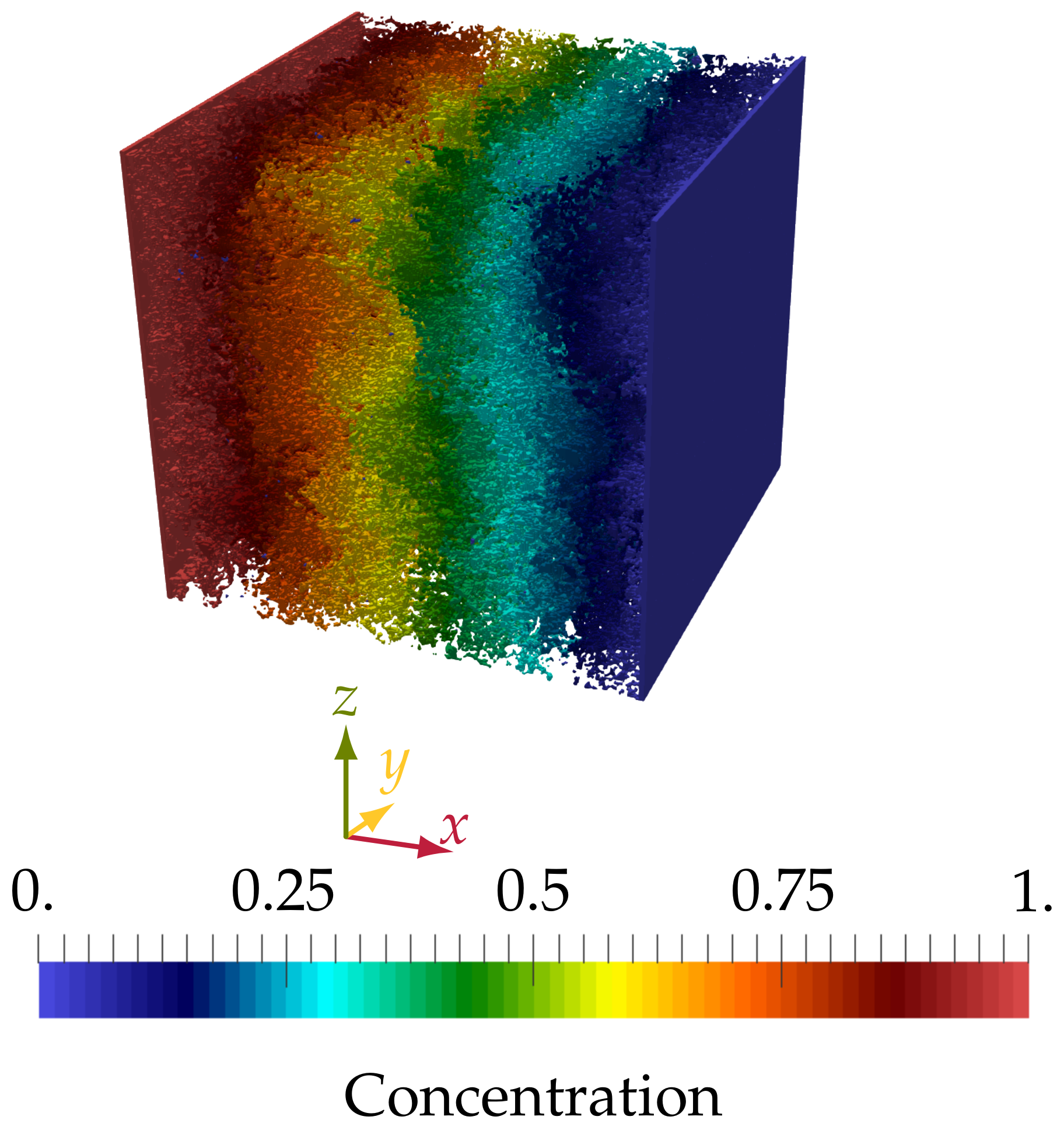
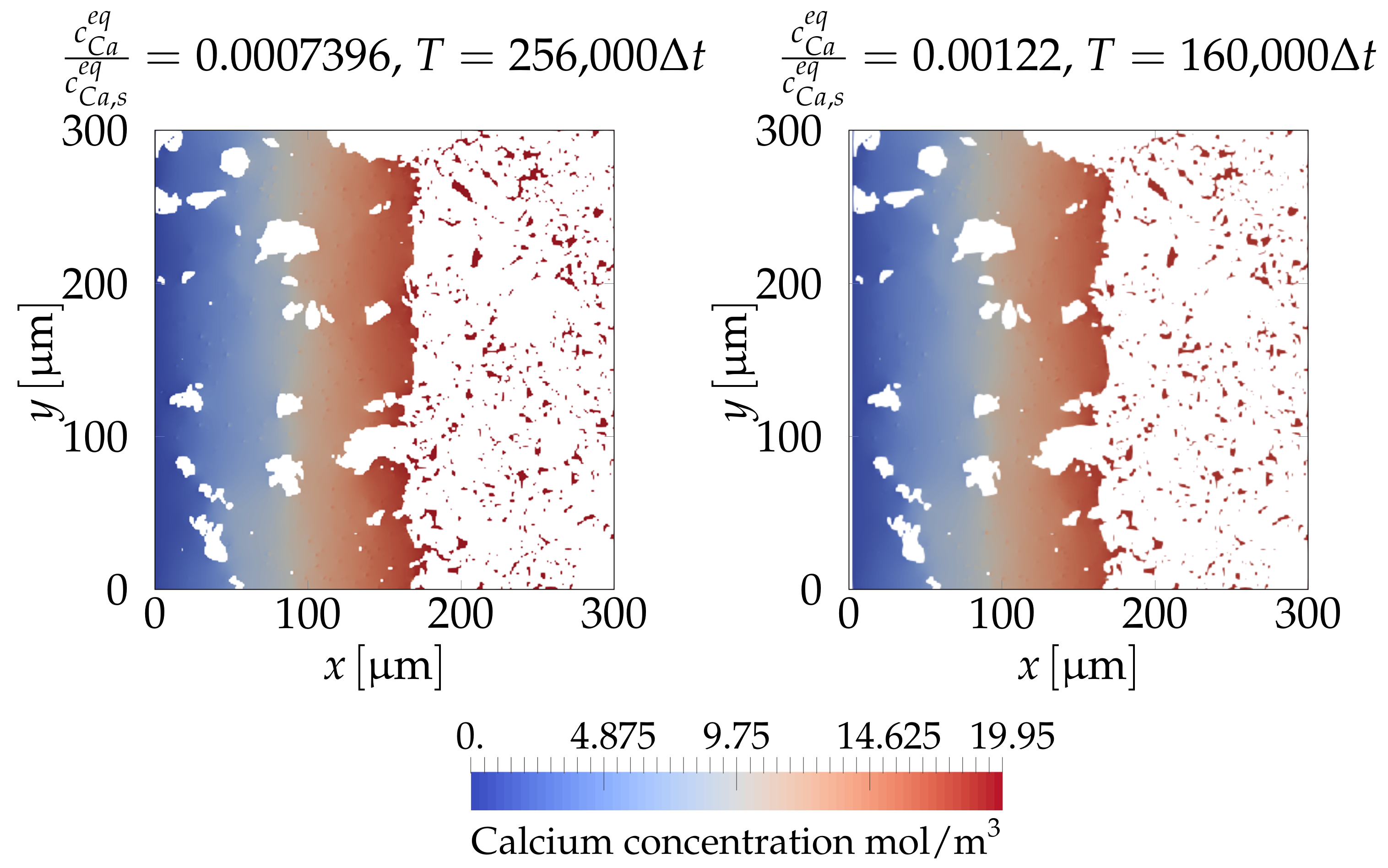
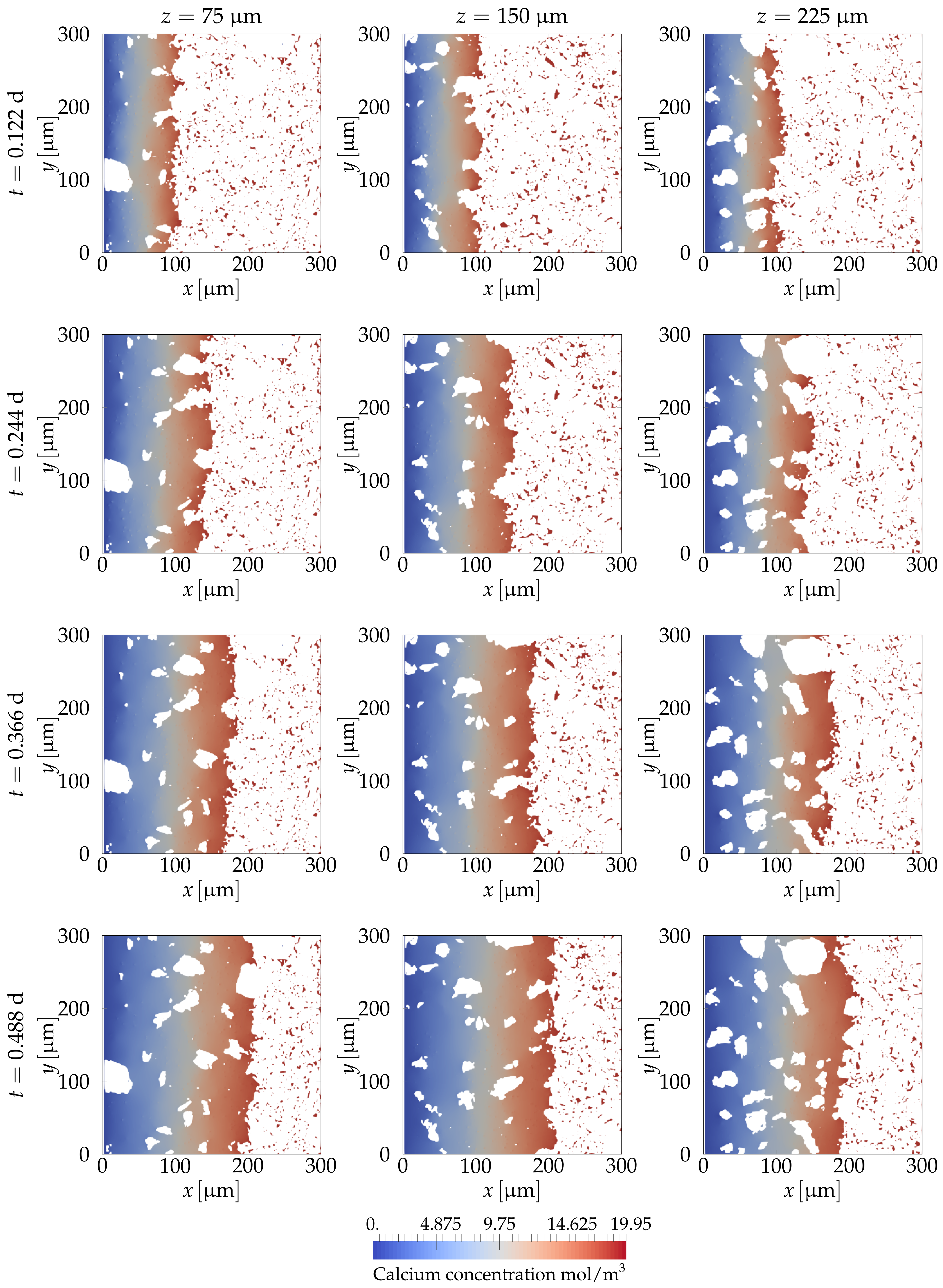
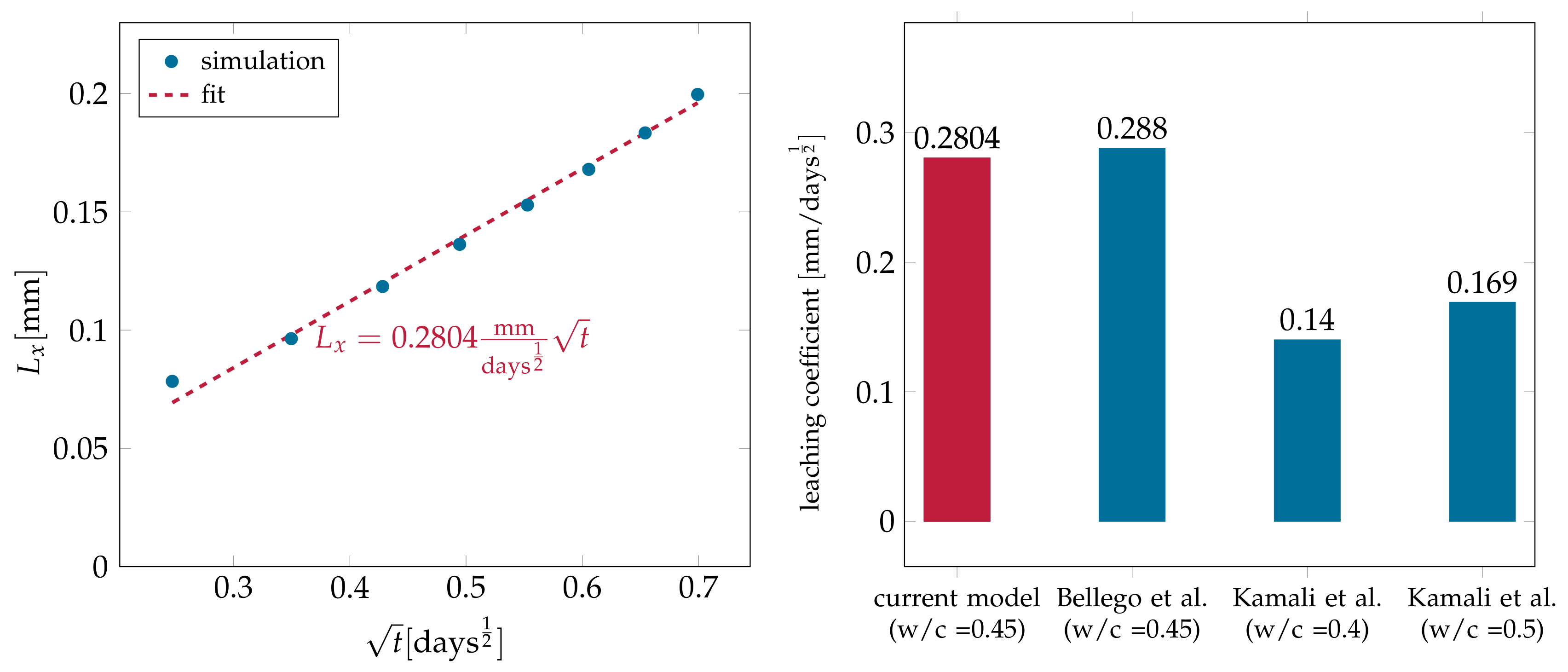
4.2.3. Simulating Calcium Leaching in HCP Microstructures
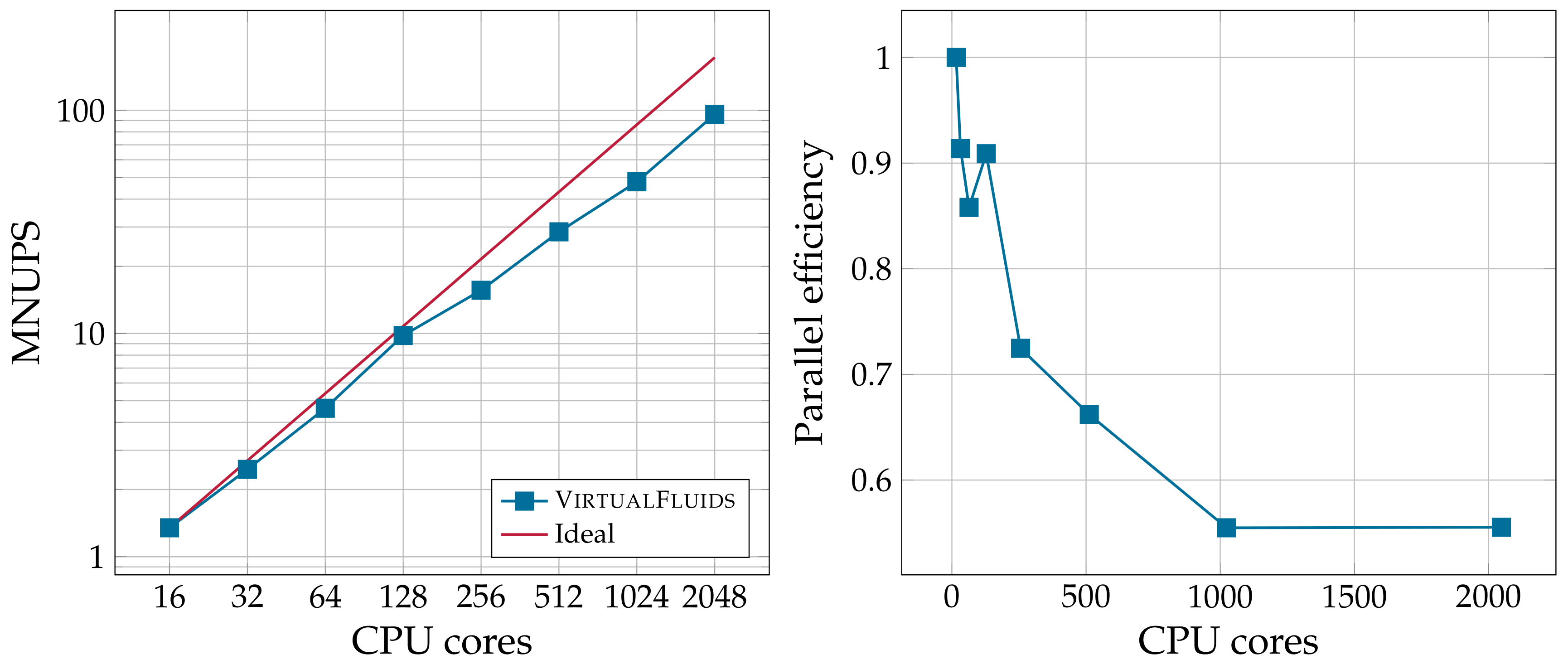
4.3. Parallel Performance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BGK | Bhatnagar, Gross, and Krook |
| CCRL | Cement and Concrete Reference Laboratory |
| CH | Calcium hydroxide |
| CSH | Calcium silicate hydrate |
| CT | Computer tomography |
| ESRF | European Synchrotron Radiation Facility |
| FCM | Factorized central moment |
| HCP | Hydrated cement paste |
| LBM | Lattice Boltzmann method |
| MNUPS | Million nodal updates per second |
| MPI | Message passing interface |
| MRT | Multiple relaxation time |
| NIST | National institure of standards and technology |
| PLIC | Piecewise linear interface construction |
| REV | Rrepresentative elementary volume |
| SLIC | Simple line interfac calculation |
| VOF | Volume of fluid |
Appendix A. From Moments to Distributions and Vice Versa
Appendix B. Expanding and Inverse Calculation of Equation (18)
Appendix C. Analysis of Finite Differences for Interface Normal
Appendix D. Homogenization Procedure of the Hydrated Phases
References
- Steefel, C.I.; DePaolo, D.J.; Lichtner, P.C. Reactive transport modeling: An essential tool and a new research approach for the Earth sciences. Earth Planet. Sci. Lett. 2005, 240, 539–558. [Google Scholar] [CrossRef]
- Yabusaki, S.B.; Steefel, C.I.; Wood, B. Multidimensional, multicomponent, subsurface reactive transport in nonuniform velocity fields: Code verification using an advective reactive streamtube approach. J. Contam. Hydrol. 1998, 30, 299–331. [Google Scholar] [CrossRef]
- Mostaghimi, P.; Liu, M.; Arns, C.H. Numerical simulation of reactive transport on micro-CT images. Math. Geosci. 2016, 48, 963–983. [Google Scholar] [CrossRef]
- Kang, Q.; Lichtner, P.C.; Viswanathan, H.S.; Abdel-Fattah, A.I. Pore scale modeling of reactive transport involved in geologic CO 2 sequestration. Transp. Porous Media 2010, 82, 197–213. [Google Scholar] [CrossRef]
- Singh, R.; Chakma, S.; Birke, V. Numerical modelling and performance evaluation of multi-permeable reactive barrier system for aquifer remediation susceptible to chloride contamination. Groundw. Sustain. Dev. 2020, 10, 100317. [Google Scholar] [CrossRef]
- De Windt, L.; Spycher, N. Reactive Transport Modeling: A Key Performance Assessment Tool for the Geologic Disposal of Nuclear Waste. Elements 2019, 15, 99–102. [Google Scholar] [CrossRef]
- Hajirezaie, S.; Wu, X.; Soltanian, M.R.; Sakha, S. Numerical simulation of mineral precipitation in hydrocarbon reservoirs and wellbores. Fuel 2019, 238, 462–472. [Google Scholar] [CrossRef]
- Chen, L.; Kang, Q.; Tao, W. Pore-Scale Study of Reactive Transport Processes in Catalyst Layer Agglomerates of Proton Exchange Membrane Fuel Cells. Electrochim. Acta 2019, 306, 454–465. [Google Scholar] [CrossRef]
- Patel, R.A. Lattice Boltzmann Method Based Framework for Simulating Physico-Chemical Processes in Heterogeneous Porous Media and Its Application to Cement Paste. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2016. [Google Scholar]
- Mcdonald, M.Z.P. Lattice Boltzmann simulations of the permeability and capillary adsorption of cement model microstructures. Cem. Concr. Res. 2012, 1601–1610. [Google Scholar] [CrossRef]
- Patel, R.A.; Perko, J.; Jacques, D.; De Schutter, G.; Van Breugel, K.; Ye, G. A versatile pore-scale multicomponent reactive transport approach based on lattice Boltzmann method: Application to portlandite dissolution. Phys. Chem. Earth Parts A/B/C 2014, 127–137. [Google Scholar] [CrossRef]
- Carrara, P.; De Lorenzis, L.; Bentz, D.P. Chloride diffusivity in hardened cement paste from microscale analyses and accounting for binding effects. Model. Simul. Mater. Sci. Eng. 2016, 24, 065009. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M. Multiscale Lattice Boltzmann-Finite Element Modeling of Transport Properties in Cement-Based Materials. Ph.D. Thesis, Technische Universiteit Delft, Delft, The Netherlands, 2013. [Google Scholar]
- Van Breugel, K. Simulation of Hydration and Formation of Structure in Hardening Cement-Based Materials. Ph.D. Thesis, TU Delft, Delft, The Netherlands, 1993. [Google Scholar]
- Bentz, D.P.; Coveney, P.V.; Garboczi, E.J.; Kleyn, M.F.; Stutzman, P.E. Cellular automaton simulations of cement hydration and microstructure development. Model. Simul. Mater. Sci. Eng. 1994, 2, 783. [Google Scholar] [CrossRef]
- Van Breugel, K. Numerical simulation of hydration and microstructural development in hardening cement-based materials (I) theory. Cem. Concr. Res. 1995, 25, 319–331. [Google Scholar] [CrossRef]
- Patel, R.A.; Perko, J.; Jacques, D.; De Schutter, G.; Ye, G.; Van Breugel, K. Can a reliable prediction of cement paste transport properties be made using microstructure models? In Proceedings of the International RILEM Conference on Materials, Systems and Structures in Civil Engineering Conference Segment on Service Life of Cement-Based Materials and Structures, Lyngby, Denmark, 15–29 August 2016; Volume 109, pp. 203–210. [Google Scholar]
- Mainguy, M.; Coussy, O. Propagation fronts during calcium leaching and chloride penetration. J. Eng. Mech. 2000, 126, 250–257. [Google Scholar] [CrossRef]
- Scardovelli, R.; Zaleski, S. Analytical relations connecting linear interfaces and volume fractions in rectangular grids. J. Comput. Phys. 2000, 164, 228–237. [Google Scholar] [CrossRef]
- Guimaraes, L.d.N.; Gens, A.; Olivella, S. Coupled Analysis of Damage Formation Around Wellbores; Elsevier Geo-Engineering Book Series; Elsevier: Amsterdam, The Netherlands, 2004; Volume 2, pp. 599–604. [Google Scholar]
- Chen, L.; Kang, Q.; Tang, Q.; Robinson, B.A.; He, Y.L.; Tao, W.Q. Pore-scale simulation of multicomponent multiphase reactive transport with dissolution and precipitation. Int. J. Heat Mass Transf. 2015, 85, 935–949. [Google Scholar] [CrossRef]
- Schweizer, B.; Bodea, S.; Surulescu, C.; Surovtsova, I. Fluid Flows and Free Boundaries. In Reactive Flows, Diffusion and Transport; Springer: Berlin, Germany, 2007; pp. 5–24. [Google Scholar]
- Geier, M.; Greiner, A.; Korvink, J.G. A factorized central moment lattice Boltzmann method. Eur. Phys. J. Spec. Top. 2009, 171, 55–61. [Google Scholar] [CrossRef]
- Yang, X.; Mehmani, Y.; Perkins, W.A.; Pasquali, A.; Schönherr, M.; Kim, K.; Perego, M.; Parks, M.L.; Trask, N.; Balhoff, M.T.; et al. Intercomparison of 3D pore-scale flow and solute transport simulation methods. Adv. Water Resour. 2016, 95, 176–189. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Geier, M.; Schönherr, M.; Pasquali, A.; Krafczyk, M. The cumulant lattice Boltzmann equation in three dimensions: Theory and validation. Comput. Math. Appl. 2015, 70, 507–547. [Google Scholar] [CrossRef]
- Verhaeghe, F.; Arnout, S.; Blanpain, B.; Wollants, P. Lattice-Boltzmann modeling of dissolution phenomena. Phys. Rev. E 2006, 73, 036316. [Google Scholar] [CrossRef] [PubMed]
- Nichols, B.; Hirt, C. Methods for calculating multidimensional, transient free surface flows past bodies. In Proceedings of the First International Conference on Numerical Ship Hydrodynamics, Gaithersburg, MD, USA, 20 October 1975; Naval Ship Research and Development Center: Bethesda, MD, USA, 1975; pp. 253–277. [Google Scholar]
- Noh, W.F.; Woodward, P. SLIC (simple line interface calculation). In Proceedings of the Fifth International Conference on Numerical Methods in Fluid Dynamics, June 28 July 2, 1976 Twente University, Enschede; Springer: Cham, Switzerland, 1976; pp. 330–340. [Google Scholar]
- Youngs, D.L. Time-dependent multi-material flow with large fluid distortion. In Numerical Methods for Fluid Dynamics; Academic Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Puckett, E.G. A volume-of-fluid interface tracking algorithm with applications to computing shock wave refraction. In Proceedings of the Fourth International Symposium on Computational Fluid Dynamics, Davis, CA, USA, 9–12 September 1991; pp. 933–938. [Google Scholar]
- Pilliod, J.E. An Analysis of Piecewise Linear Interface Reconstruction Algorithms for Volume-of-Fluid Methods; University of California: Davis, CA, USA, 1992. [Google Scholar]
- Ginzburg, I.; Wittum, G. Two-phase flows on interface refined grids modeled with VOF, staggered finite volumes, and spline interpolants. J. Comput. Phys. 2001, 166, 302–335. [Google Scholar] [CrossRef]
- Puckett, E.; Saltzman, J. A 3D adaptive mesh refinement algorithm for multimaterial gas dynamics. Phys. D Nonlinear Phenom. 1992, 60, 84–93. [Google Scholar] [CrossRef]
- Janssen, C.; Krafczyk, M. A lattice Boltzmann approach for free-surface-flow simulations on non-uniform block-structured grids. Comput. Math. Appl. 2010, 59, 2215–2235. [Google Scholar] [CrossRef]
- Parker, B.; Youngs, D. Two and three dimensional Eulerian simulation of fluid flow with material interfaces, Atomic Weapons Establishment (AWE). Preprint 1992, 1, 92. [Google Scholar]
- Pilliod, J.E., Jr.; Puckett, E.G. Second-order accurate volume-of-fluid algorithms for tracking material interfaces. J. Comput. Phys. 2004, 199, 465–502. [Google Scholar] [CrossRef]
- IRMB Research Code VirtualFluids. Available online: https://www.tu-braunschweig.de/irmb/forschung/virtualfluids (accessed on 11 November 2020).
- Aaron, H.B.; Fainstein, D.; Kotler, G.R. Diffusion Limited Phase Transformations: A Comparison and Critical Evaluation of the Mathematical Approximations. J. Appl. Phys. 1970, 41, 4404–4410. [Google Scholar] [CrossRef]
- Smolarkiewicz, P.K. A simple positive definite advection scheme with small implicit diffusion. Mon. Weather Rev. 1983, 111, 479–486. [Google Scholar] [CrossRef]
- Perko, J.; Patel, R.A. Single-relaxation-time lattice Boltzmann scheme for advection-diffusion problems with large diffusion-coefficient heterogeneities and high-advection transport. Phys. Rev. E 2014, 89, 053309. [Google Scholar] [CrossRef]
- Bossa, N.; Chaurand, P.; Vicente, J.; Borschneck, D.; Levard, C.; Aguerre-Chariol, O.; Rose, J. Micro-and nano-X-ray computed-tomography: A step forward in the characterization of the pore network of a leached cement paste. Cem. Concr. Res. 2015, 67, 138–147. [Google Scholar] [CrossRef]
- Bentz, D.P.; Mizell, S.; Satterfield, S.; Devaney, J.; George, W.; Ketcham, P.; Graham, J.; Porterfield, J.; Quenard, D.; Vallee, F.; et al. The Visible Cement Data Set. J. Res. Natl. Inst. Stand. Technol. 2002, 107, 137–148. [Google Scholar] [CrossRef]
- The Visible Cement Data Set. Available online: https://visiblecement.nist.gov/ (accessed on 11 November 2020).
- Powers, T. Physical properties of cement paste. In Proceedings of the 4th International Symposium on the Chemistry of Cement, Washington DC, USA, 2–7 October 1960; Volume 2, pp. 577–613. [Google Scholar]
- Karim, M.; Krabbenhoft, K. Extraction of effective cement paste diffusivities from X-ray microtomography scans. Transp. Porous Media 2010, 84, 371–388. [Google Scholar] [CrossRef]
- Van der Wegen, G.; Polder, R.B.; van Breugel, K. Guideline for service life design of structural concrete–a performance based approach with regard to chloride induced corrosion. Heron 2012, 57, 153–168. [Google Scholar]
- Ichikawa, Y.; Kawamura, K.; Fujii, N.; Nattavut, T. Molecular dynamics and multiscale homogenization analysis of seepage/diffusion problem in bentonite clay. Int. J. Numer. Methods Eng. 2002, 54, 1717–1749. [Google Scholar] [CrossRef]
- Patel, R.A.; Perko, J.; Jacques, D.; De Schutter, G.; Ye, G.; Van Bruegel, K. Effective diffusivity of cement pastes from virtual microstructures: Role of gel porosity and capillary pore percolation. Constr. Build. Mater. 2018, 165, 833–845. [Google Scholar] [CrossRef]
- Zhang, M.; Ye, G.; Van Breugel, K. Microstructure-based modeling of water diffusivity in cement paste. Constr. Build. Mater. 2011, 25, 2046–2052. [Google Scholar] [CrossRef]
- Garboczi, E.; Bentz, D. Computer simulation of the diffusivity of cement-based materials. J. Mater. Sci. 1992, 27, 2083–2092. [Google Scholar] [CrossRef]
- Nakarai, K.; Ishida, T.; Maekawa, K. Modeling of calcium leaching from cement hydrates coupled with micro-pore formation. J. Adv. Concr. Technol. 2006, 4, 395–407. [Google Scholar] [CrossRef]
- Gérard, B.; Le Bellego, C.; Bernard, O. Simplified modelling of calcium leaching of concrete in various environments. Mater. Struct. 2002, 35, 632–640. [Google Scholar] [CrossRef]
- Delagrave, A.; Gérard, B.; Marchand, J. Modeling the calcium leaching mechanisms in hydrated cement pastes. In Mechanisms of Chemical Degradation of Cement-Based Systems; CRC Press: Boca Raton, FL, USA, 1997; pp. 38–49. [Google Scholar]
- Haga, K.; Sutou, S.; Hironaga, M.; Tanaka, S.; Nagasaki, S. Effects of porosity on leaching of Ca from hardened ordinary Portland cement paste. Cem. Concr. Res. 2005, 35, 1764–1775. [Google Scholar] [CrossRef]
- Buil, M.; Revertegat, E.; Oliver, J. A model of the attack of pure water or undersaturated lime solutions on cement. In Stabilization and Solidification of Hazardous, Radioactive, and Mixed Wastes; ASTM International: West Conshohocken, PA, USA, 1992; Volume 2. [Google Scholar]
- Adenot, F.; Buil, M. Modeling of the corrosion of the cement paste by deionized water. Cem. Concr. Res. 1992, 22, 489–496. [Google Scholar] [CrossRef]
- Carde, C.; Francois, R.; Torrenti, J.M. Leaching of both calcium hydroxide and CSH from cement paste: Modeling the mechanical behavior. Cem. Concr. Res. 1996, 26, 1257–1268. [Google Scholar] [CrossRef]
- Jennings, H.M.; Tennis, P.D. Model for the developing microstructure in Portland cement pastes. J. Am. Ceram. Soc. 1994, 77, 3161–3172. [Google Scholar] [CrossRef]
- Taylor, H.; Barret, P.; Brown, P.; Double, D.; Frohnsdorff, G.; Johansen, V.; Ménétrier-Sorrentino, D.; Odler, I.; Parrott, L.; Pommersheim, J.; et al. The hydration of tricalcium silicate. Mater. Struct. 1984, 17, 457–468. [Google Scholar] [CrossRef]
- Tennis, P.D.; Jennings, H.M. A model for two types of calcium silicate hydrate in the microstructure of Portland cement pastes. Cem. Concr. Res. 2000, 30, 855–863. [Google Scholar] [CrossRef]
- Huang, J.; Krabbenhoft, K.; Lyamin, A. Statistical homogenization of elastic properties of cement paste based on X-ray microtomography images. Int. J. Solids Struct. 2013, 50, 699–709. [Google Scholar] [CrossRef]
- Perko, J.; Jacques, D. Numerically accelerated pore-scale equilibrium dissolution. J. Contam. Hydrol. 2019, 220, 119–127. [Google Scholar] [CrossRef]
- Bellego, C.L.; Gérard, B.; Pijaudier-Cabot, G. Chemo-mechanical effects in mortar beams subjected to water hydrolysis. J. Eng. Mech. 2000, 126, 266–272. [Google Scholar] [CrossRef]
- Kamali, S.; Moranville, M.; Leclercq, S. Material and environmental parameter effects on the leaching of cement pastes: Experiments and modelling. Cem. Concr. Res. 2008, 38, 575–585. [Google Scholar] [CrossRef]
- Berner, U. Modeling the incongruent dissolution of hydrated cement minerals. Radiochim. Acta 1988, 44, 387–394. [Google Scholar]
- Wan, K.; Li, L.; Sun, W. Solid–liquid equilibrium curve of calcium in 6 mol/L ammonium nitrate solution. Cem. Concr. Res. 2013, 53, 44–50. [Google Scholar] [CrossRef]
- Varzina, A.; Cizer, Ö.; Yu, L.; Liu, S.; Jacques, D.; Perko, J. A new concept for pore-scale precipitation-dissolution modelling in a lattice Boltzmann framework—Application to portlandite carbonation. Appl. Geochem. 2020, 123, 104786. [Google Scholar] [CrossRef]
- Kang, Q.; Lichtner, P.C.; Zhang, D. Lattice Boltzmann pore-scale model for multicomponent reactive transport in porous media. J. Geophys. Res. Solid Earth 2006, 111. [Google Scholar] [CrossRef]
- Luo, H.; Quintard, M.; Debenest, G.; Laouafa, F. Properties of a diffuse interface model based on a porous medium theory for solid–liquid dissolution problems. Comput. Geosci. 2012, 16, 913–932. [Google Scholar] [CrossRef]
- Promentilla, M.A.B.; Sugiyama, T.; Hitomi, T.; Takeda, N. Characterizing the 3D pore structure of hardened cement paste with synchrotron microtomography. J. Adv. Concr. Technol. 2008, 6, 273–286. [Google Scholar] [CrossRef]
- Marone, F.; Schlepütz, C.M.; Marti, S.; Fusseis, F.; Velásquez-Parra, A.; Griffa, M.; Jiménez-Martínez, J.; Dobson, K.J.; Stampanoni, M. Time Resolved in situ X-Ray Tomographic Microscopy Unraveling Dynamic Processes in Geologic Systems. Front. Earth Sci. 2020, 7, 346. [Google Scholar] [CrossRef]
- Taylor, H.F. Cement Chemistry; Thomas Telford London: London, UK, 1997; Volume 2. [Google Scholar]
- Bernard, O.; Ulm, F.J.; Lemarchand, E. A multiscale micromechanics-hydration model for the early-age elastic properties of cement-based materials. Cem. Concr. Res. 2003, 33, 1293–1309. [Google Scholar] [CrossRef]

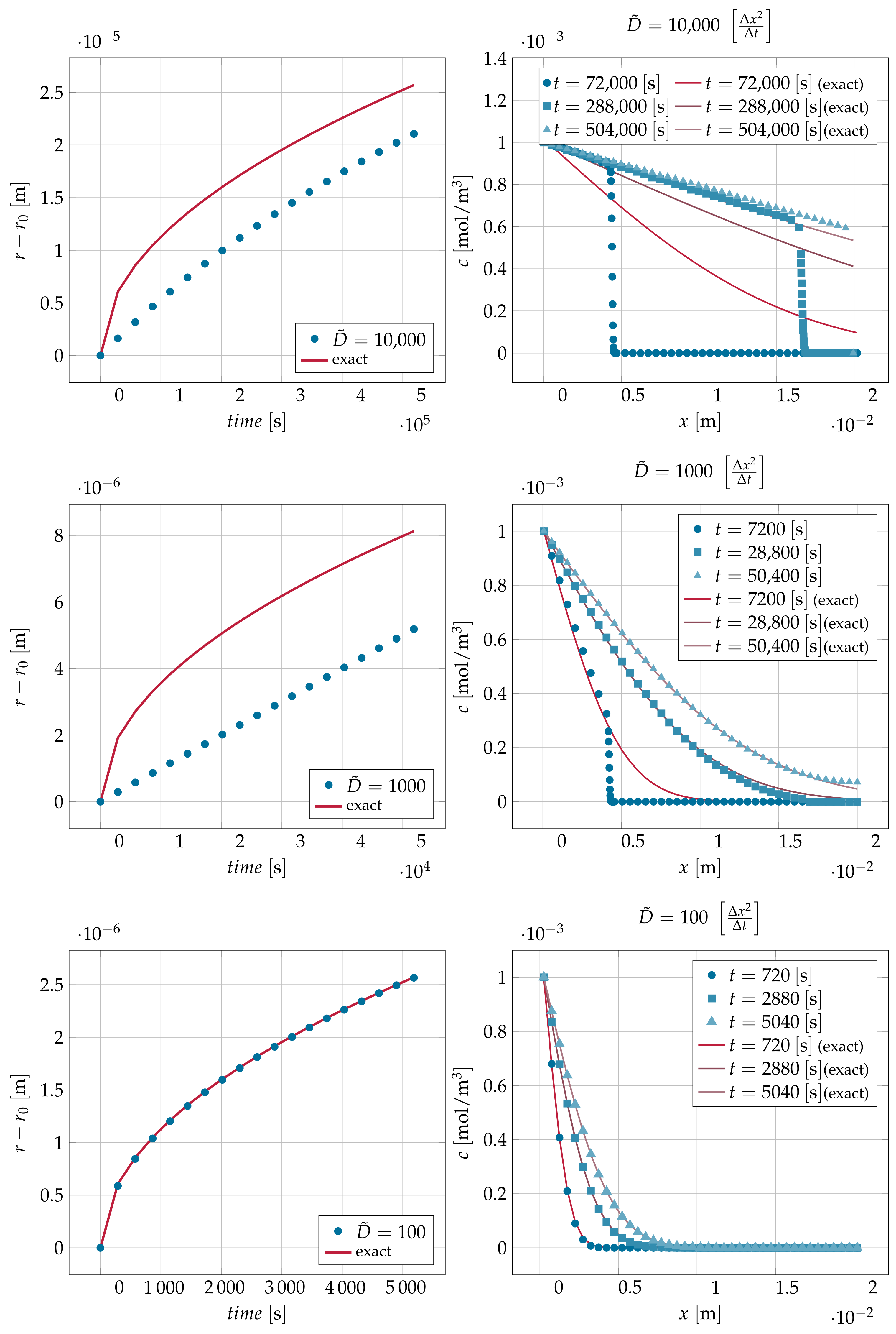


| 10,000 | 72,000 | 0.4128 |
| 10,000 | 288,000 | 1.6643 |
| 1000 | 7200 | 0.4028 |
| 1000 | 28,800 | 1.6719 |
| Along x Direction | Along y Direction | Along z Direction | |
|---|---|---|---|
| (Equation (33)) | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alihussein, H.; Geier, M.; Krafczyk, M. A Parallel Coupled Lattice Boltzmann-Volume of Fluid Framework for Modeling Porous Media Evolution. Materials 2021, 14, 2510. https://doi.org/10.3390/ma14102510
Alihussein H, Geier M, Krafczyk M. A Parallel Coupled Lattice Boltzmann-Volume of Fluid Framework for Modeling Porous Media Evolution. Materials. 2021; 14(10):2510. https://doi.org/10.3390/ma14102510
Chicago/Turabian StyleAlihussein, Hussein, Martin Geier, and Manfred Krafczyk. 2021. "A Parallel Coupled Lattice Boltzmann-Volume of Fluid Framework for Modeling Porous Media Evolution" Materials 14, no. 10: 2510. https://doi.org/10.3390/ma14102510
APA StyleAlihussein, H., Geier, M., & Krafczyk, M. (2021). A Parallel Coupled Lattice Boltzmann-Volume of Fluid Framework for Modeling Porous Media Evolution. Materials, 14(10), 2510. https://doi.org/10.3390/ma14102510






