Strain Hardening in an AZ31 Alloy Submitted to Rotary Swaging
Abstract
1. Introduction
2. Materials and Methods
3. Results
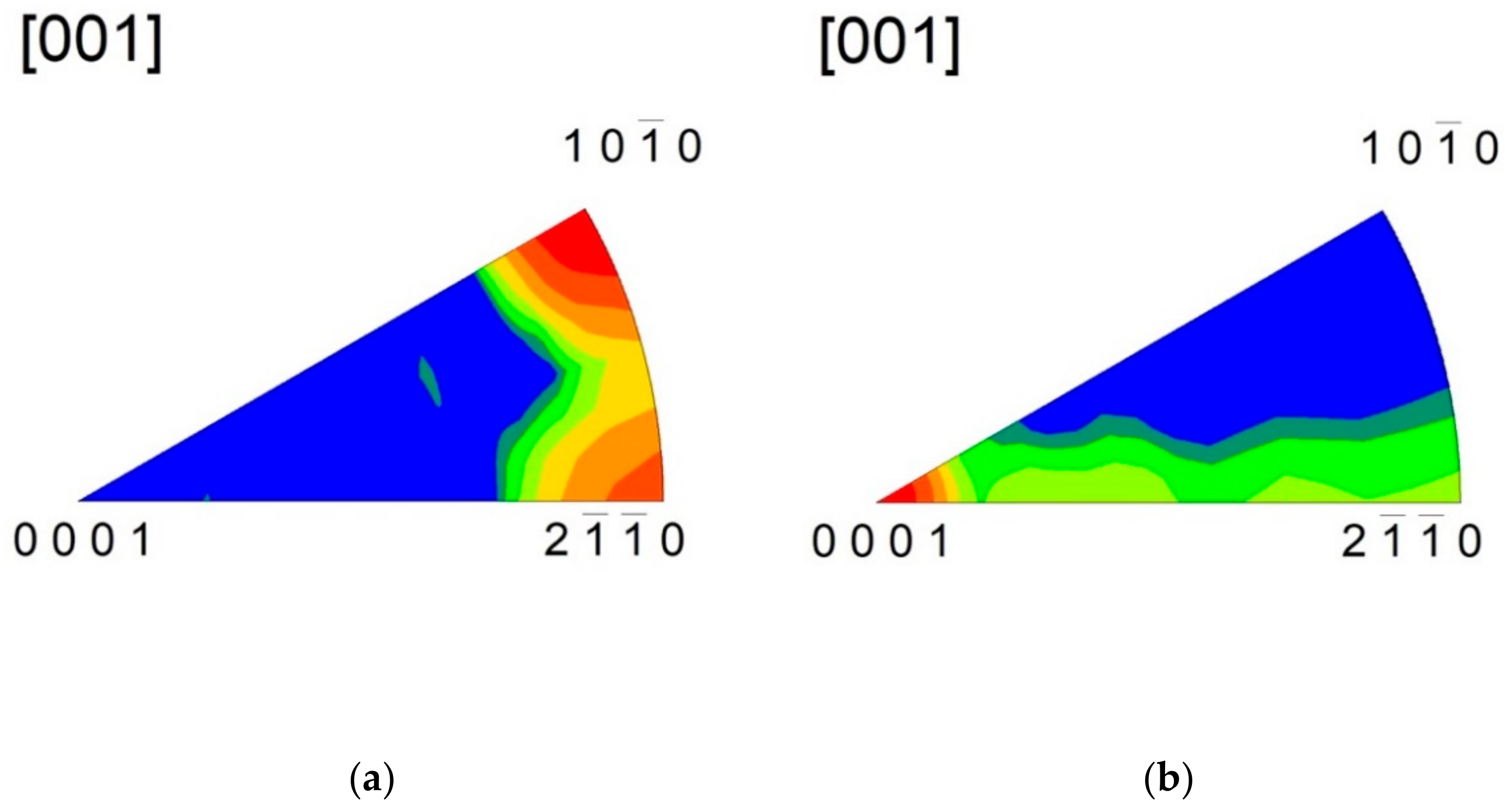
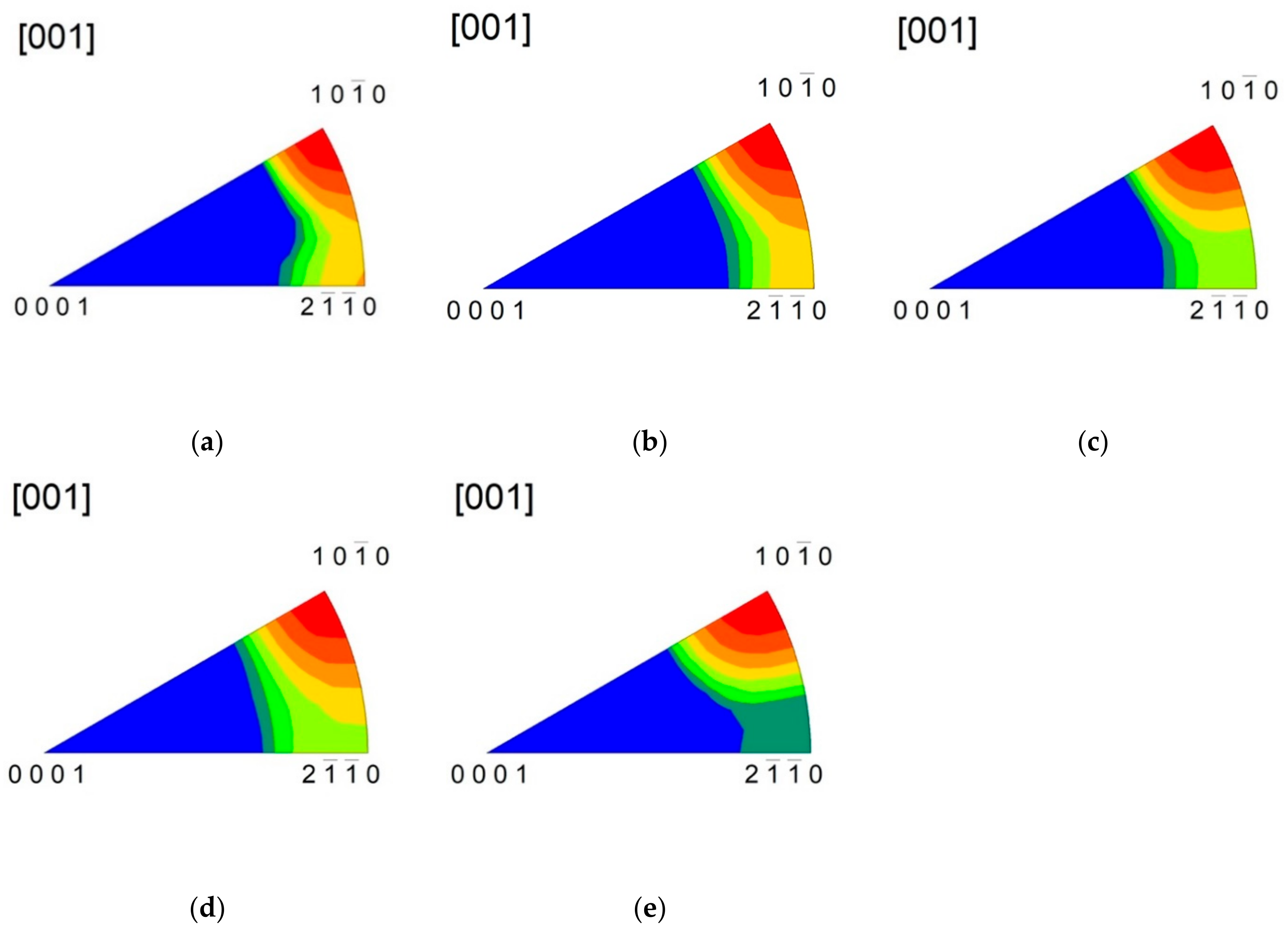
3.1. Microstructure and Texture
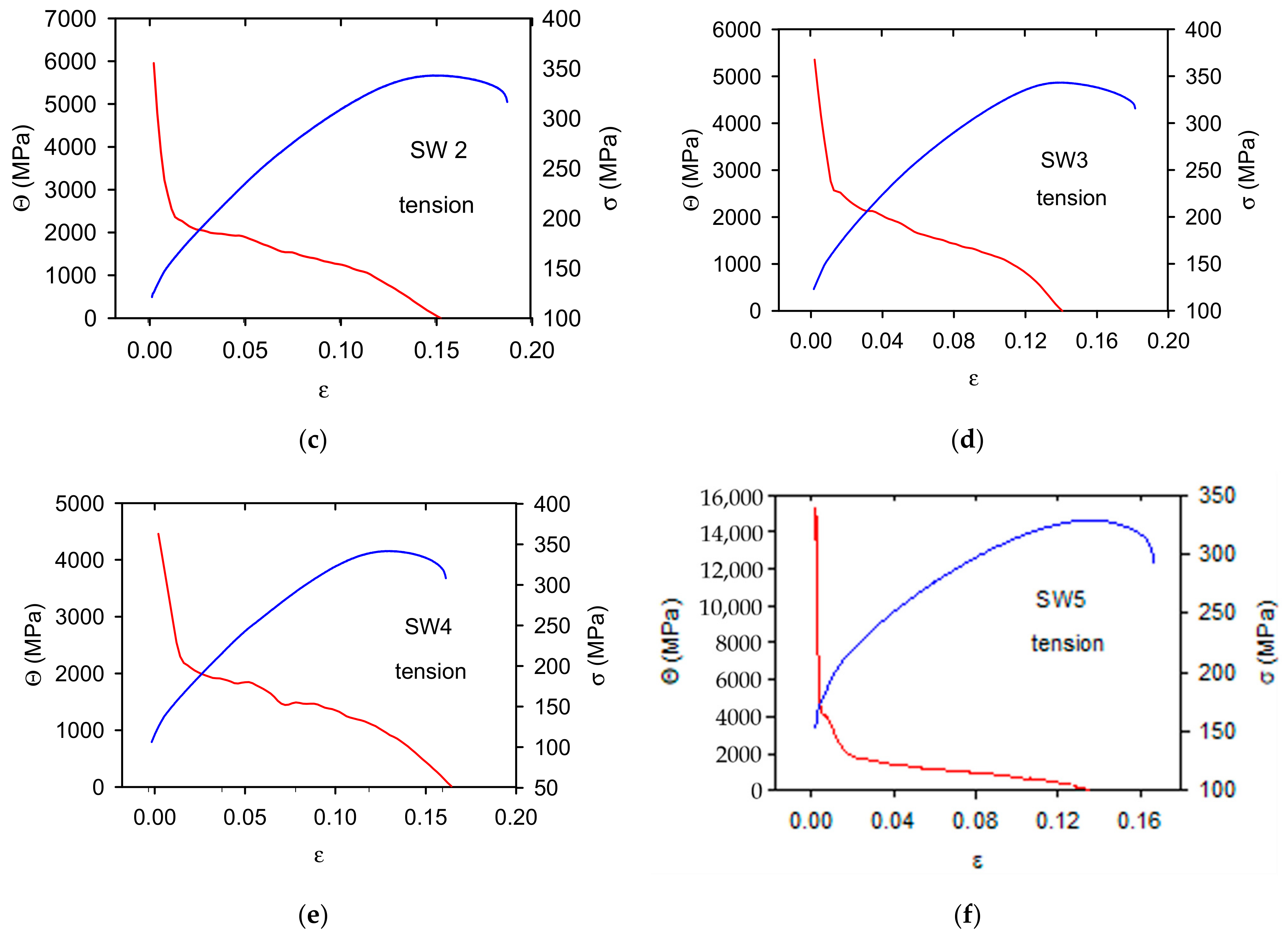
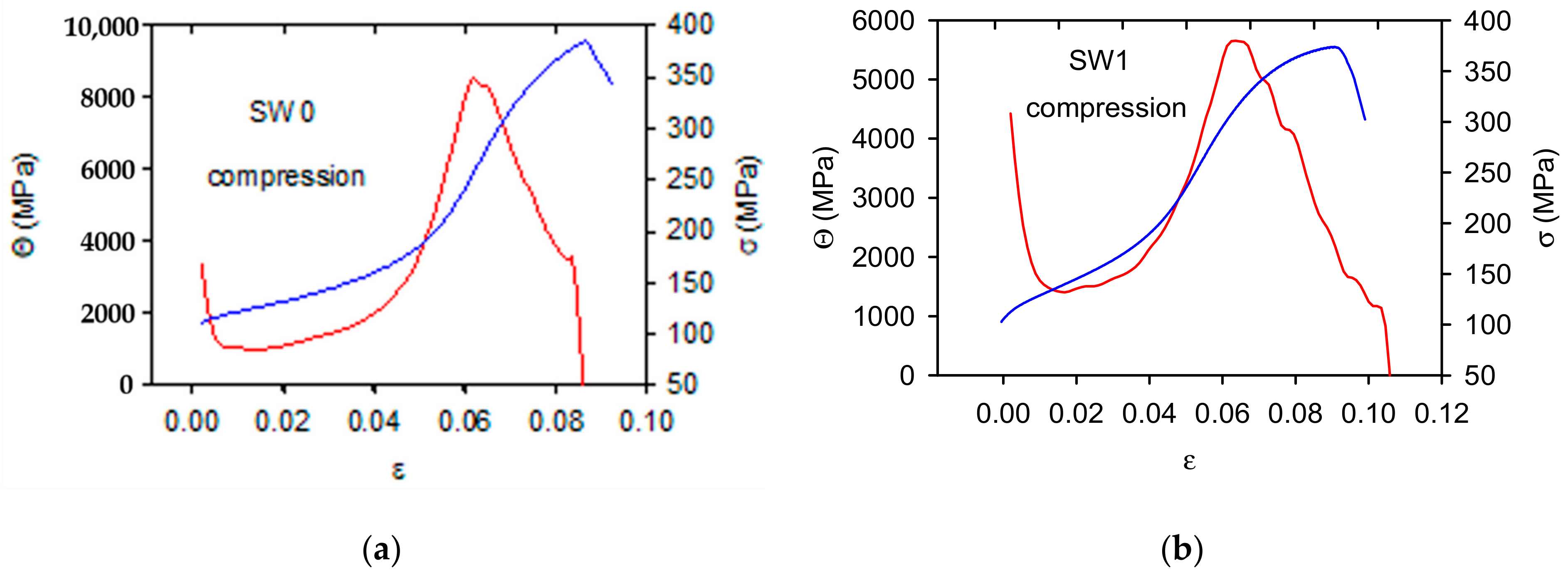
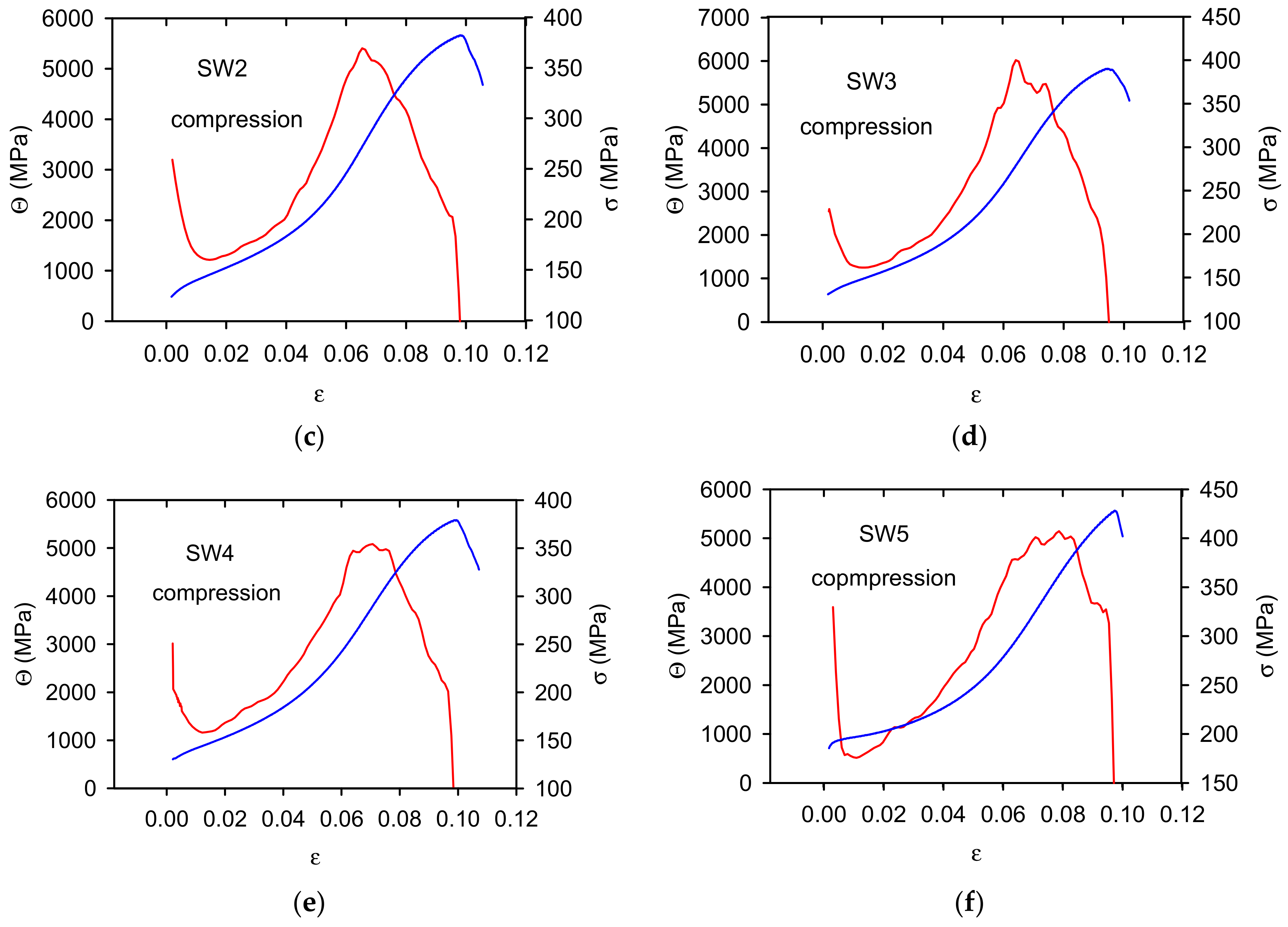
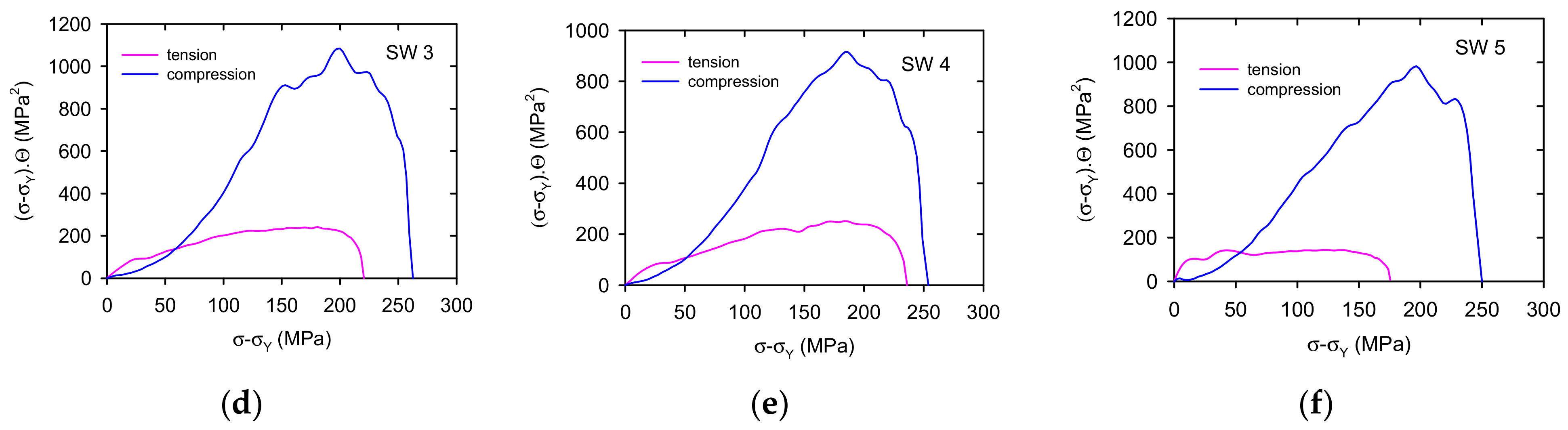
3.2. Work Hardening Coefficient
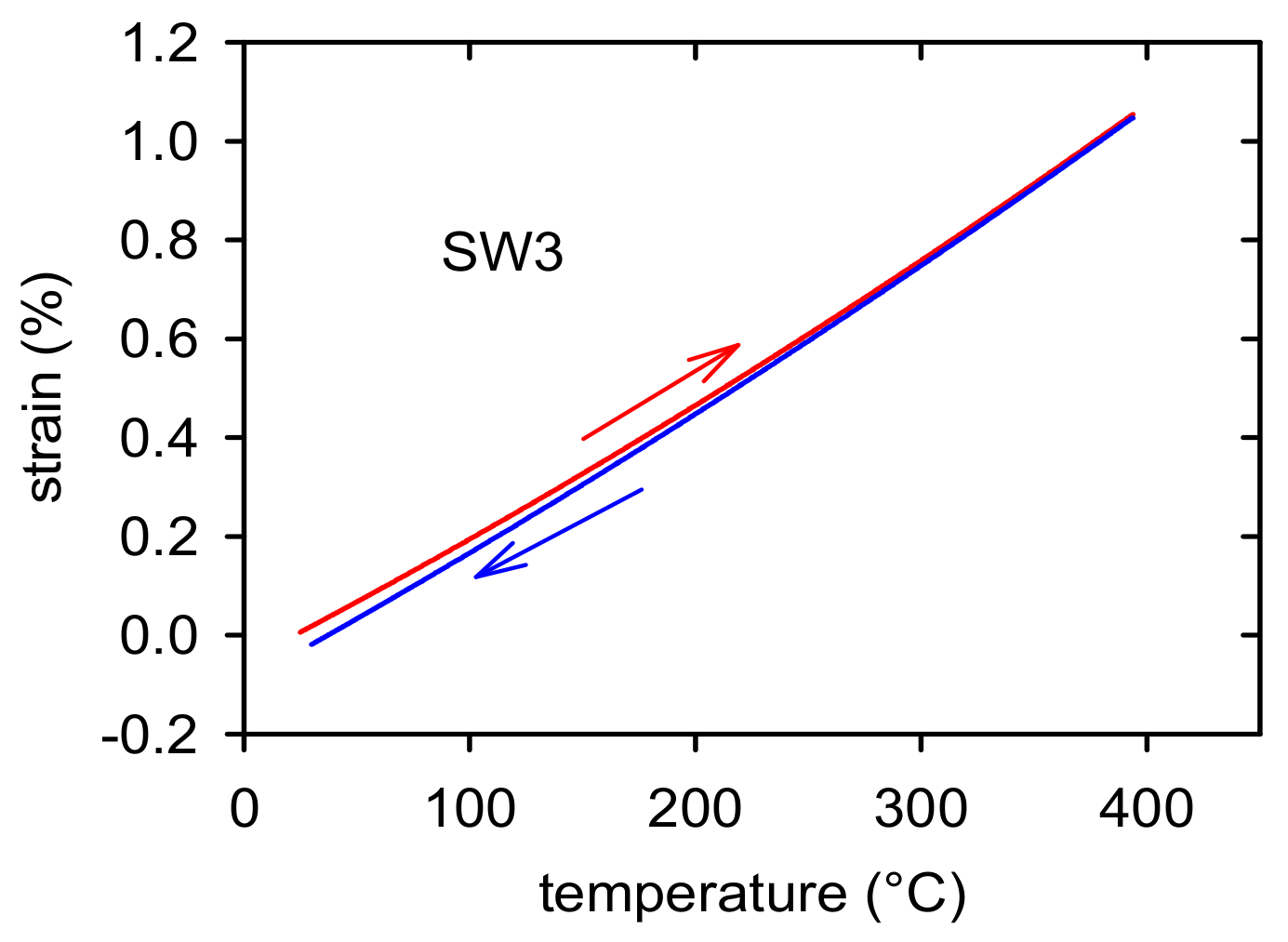
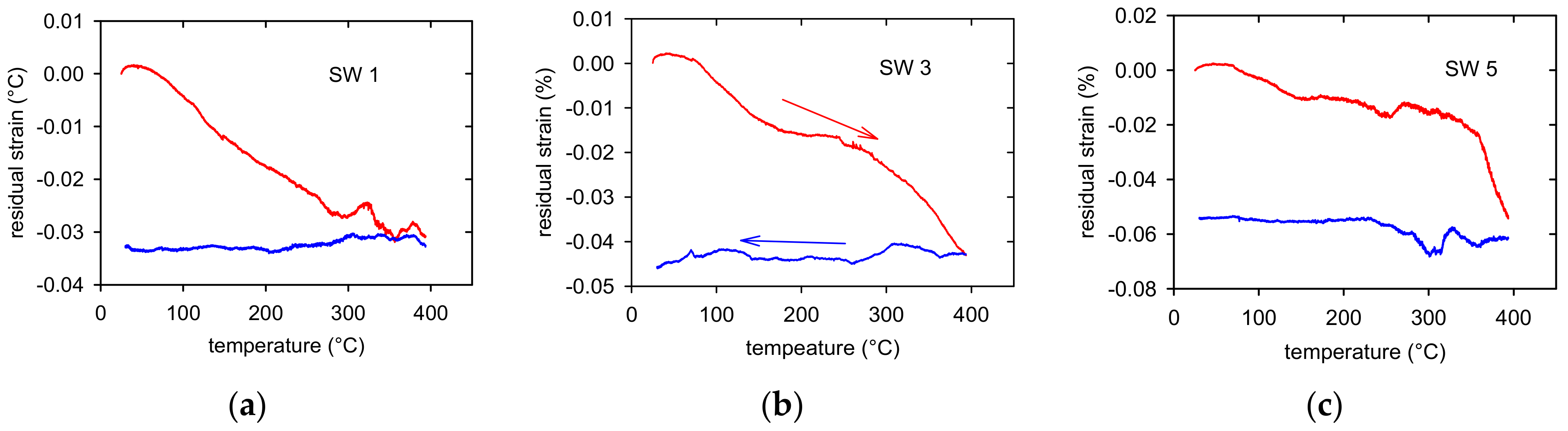
3.3. Thermal Expansion
4. Discussion
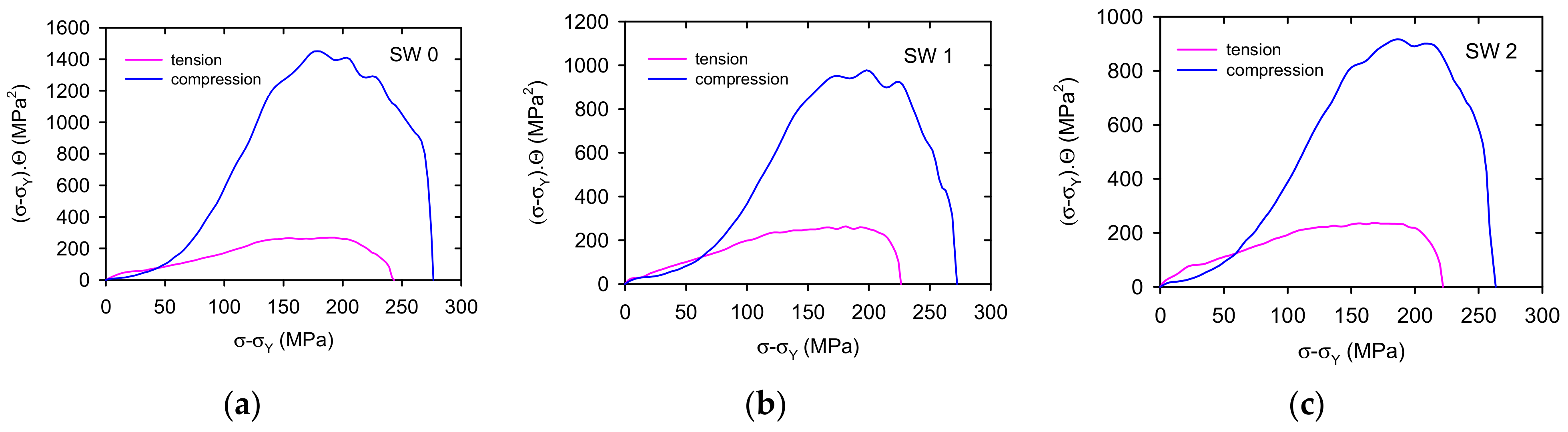
4.1. Strain Hardening
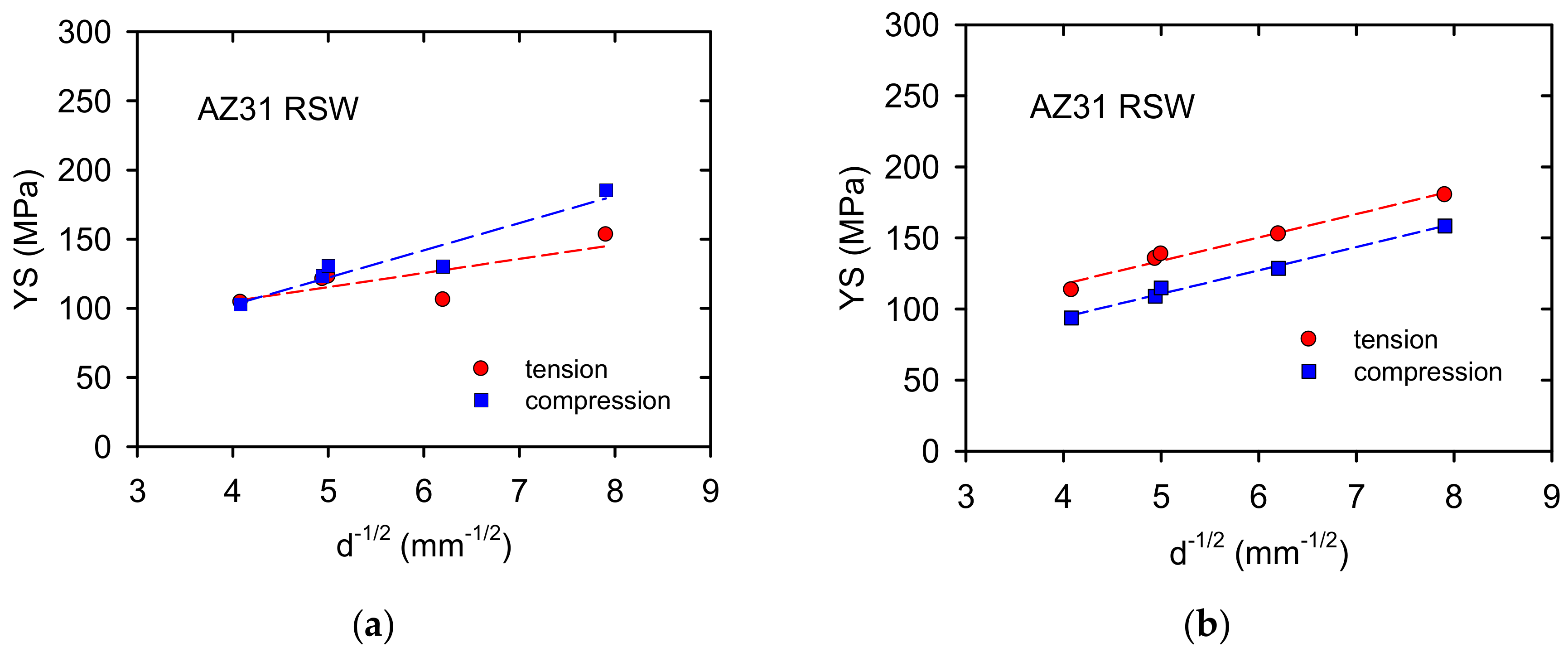
4.2. Hall-Petch Strengthening
5. Conclusions
- (1)
- Rotary swaging developed a pronounced fibre texture.
- (2)
- The grain size decreased with stepwise swaging.
- (3)
- The strain hardening behaviour of samples is influenced by the deformation mode and texture.
- (4)
- Massive formation of twins and their interaction with dislocations caused high strain hardening in the compression tests.
- (5)
- The main softening mechanism is very probably cross-slip of <c + a> dislocations between pyramidal planes of the second and first order.
- (6)
- The yield stresses measured in compression are higher compared to the yield stress found in tension. Internal stresses originated during swaging are the reason for this behaviour.
- (7)
- Mechanical twinning increased the grain size sensitivity of the yield stress.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kocks, U.F.; Mecking, H. Dislocation Modelling of Physical Systems; Ashby, M.F., Hartley, C.S., Bullough, R., Hirth, J.P., Eds.; Pergamon Press: Oxford, UK, 1981; pp. 197–211. ISBN 978-0-08-026724-1. [Google Scholar] [CrossRef]
- Lukáč, P.; Balík, J. Kinetics of Plastic Deformation. Key Eng. Mater. 1994, 97–98, 307–322. [Google Scholar] [CrossRef]
- Král, R.; Lukáč, P. Mechanisms of plastic deformation in Al-Mg and Al-Zn-Mg alloys. Acta Univ. Carol. Math. Phys. 1998, 39, 49–90. [Google Scholar]
- Máthis, K.; Trojanová, Z.; Lukáč, P. Hardening and softening in deformed magnesium alloys. Mater. Sci. Eng. A 2002, 324, 141–144. [Google Scholar] [CrossRef]
- Balik, J.; Dobroň, P.; Chmelík, F.; Kužel, R.; Dozdenko, D.; Bohlen, J.; Letzig, D.; Lukáč, P. Modelling of work hardening in magnesium alloy sheets. Int. J. Plast. 2016, 76, 166–185. [Google Scholar] [CrossRef]
- Trojanová, Z.; Lukáč, P. Physical aspects of plastic deformation in Mg–Al alloys with Sr and Ca. Inter. J. Mater. Res. 2009, 100, 270–276. [Google Scholar] [CrossRef]
- Trojanová, Z.; Lukáč, P.; Dlouhý, A. Hardening and softening in Zr-Sn polycrystals. Mater. Sci. Eng. A 1993, 164, 246–251. [Google Scholar] [CrossRef]
- Máthis, K.; Trojanová, Z.; Lukáč, P.; Cáceres, C.H.; Ledvai, J. Modeling of hardening and softening processes in Mg alloys. J. Alloys Compd. 2004, 378, 176–179. [Google Scholar] [CrossRef]
- Cáceres, C.H.; Lukáč, P.; Blake, A. Strain hardening due to {10 12} twinning in pure magnesium. Phil. Mag. 2008, 88, 991–1003. [Google Scholar] [CrossRef]
- Oppendal, A.L.; El Kadiri, H.; Tomé, C.N.; Kaschner, G.C.; Vogel, S.C.; Baird, J.C.; Horstenmeyer, M.F. Effect of dislocation transmutation on modeling hardening mechanisms by twinning in magnesium. Inter. J. Plasticity 2012, 30–31, 41–61. [Google Scholar] [CrossRef]
- Cáceres, C.H.; Blake, A.H. On the strain hardening behaviour of magnesium at room temperature. Mater. Sci. Eng. A 2007, 462, 193–196. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, D.; Bu, F.; Li, X.; Li, B.; Yan, T.; Guan, K.; Yang, Q.; Liu, X.; Meng, J. Excellent ductility and strong work hardening effect of as cast Mg-Zn-Zr-Yb alloy at room temperature. J. Alloys Compd. 2017, 728, 404–412. [Google Scholar] [CrossRef]
- Guo, L.; Chen, Z.; Gao, L. Effect of grain size, texture and twinning on mechanical properties and work hardening behavior of AZ31magnesium alloy. Mater. Sci. Eng. A 2011, 528, 8537–8545. [Google Scholar] [CrossRef]
- Del Valle, J.A.; Carreño, F.; Ruano, O.A. Influence of texture and grain size on work hardening and ductility in magnesium -based alloys processed by ECAP and rolling. Acta Mater. 2006, 54, 4247–4259. [Google Scholar] [CrossRef]
- Koike, J.; Kobayashi, T.; Mukai, T.; Watanabe, H.; Suzuki, M.; Maruyama, K.; Hogashi, K. The activity of non-basal slip systems and dynamic recovery at room temperature in fine grained AZ31 B magnesium alloys. Acta Mater. 2003, 51, 2055–2065. [Google Scholar] [CrossRef]
- Liao, H.; Kim, J.; Liu, T.; Tang, A.; She, J.; Peng, P.; Pan, F. Effect of Mn addition on the microstructure, mechanical properties and work-hardening of Mg-1Mn alloy. Mater. Sci. Eng. A. 2019, 754, 778–785. [Google Scholar] [CrossRef]
- Knezevic, M.; Levinson, A.; Harris, R.; Mishra, R.K.; Doherty, R.D.; Kalidindi, S. Deformation twinning in AZ31: Influence on strain hardening and texture evolution. Acta Mater. 2010, 58, 6230–6242. [Google Scholar] [CrossRef]
- Kula, A.; Lia, X.; Mishra, R.K.; Niewczas, M. Flow stress and work hardening of Mg-Y alloys. Int. J. Plasticity 2017, 92, 96–121. [Google Scholar] [CrossRef]
- Shou, H.; Zheng, J.; Zhang, Y.; Long, D.; Rao, J.; Liu, Q. Quasi-in-situ analysis of dependency of deformation mechanism and work-hardening behavior on texture in Mg-2Zn-0.1Ca alloy. J. Alloy. Compd. 2019, 784, 1187–1197. [Google Scholar] [CrossRef]
- Zhao, J.; Jiang, B.; Yuan, Y.; Tang, A.; Sheng, H.; Yang, T.; Huang, G.; Zhang, D.; Pan, F. Influence of Zn addition on the microstructure, tensile properties and work-hardening behavior of Mg-1Gd alloy. Mater. Sci. Eng. A 2020, 772, 138779. [Google Scholar] [CrossRef]
- Figueiredo, R.B.; Száraz, Z.; Trojanová, Z.; Lukáč, P.; Langdon, T.G. Significance of twinning in the anisotropic behavior of a magnesium alloy processed by equal-channel angular pressing. Scripta Mater. 2010, 63, 504–507. [Google Scholar] [CrossRef]
- Trojanová, Z.; Máthis, K.; Lukáč, P.; Janeček, M.; Farkas, G. Plastic Properties of a Mg-Al-Ca Alloy Reinforced with Short Saffil Fibers. Metall. Mater. Trans. A 2014, 45A, 29–35. [Google Scholar] [CrossRef]
- Vinogradov, A.; Agletdinov, E.; Yasnikov, I.S.; Máthis, K.; Estrin, Y. A phenomenological model of twinning-mediated strain hardening. Mater. Sci. Eng. 2020, A780, 139194. [Google Scholar] [CrossRef]
- Trojanová, Z.; Drozd, Z.; Škraban, T.; Minárik, P.; Džugan, J.; Halmešová, K.; Németh, G.; Lukáč, P.; Chmelík, F. Effect of Rotary Swaging on Microstructure and Mechanical Properties of an AZ31 Magnesium Alloy. Adv. Eng. Mater. 2020, 1900596. [Google Scholar] [CrossRef]
- Heiple, C.R.; Carpenter, S.H. Acoustic Emission; Matthews, J.R., Ed.; Gordon and Breach Science Publishers: New York, NY, USA, 1983; ISBN 0-677-16490-4. [Google Scholar] [CrossRef]
- Chmelík, F.; Trojanová, Z.; Převorovský, Z.; Lukáč, P. The Portevin-Le Chatelier effect in Al-2.92%Mg-0.38%Mn and linear location of acoustic emission. Mater. Sci. Eng. A 1993, 164, 260–265. [Google Scholar] [CrossRef]
- Boiko, V.S.; Garber, H.I.; Krivenko, L.F. Acoustic emission during annihilation of dislocation pile ups. Fizika Tverd. Tela. 1974, 16, 1233–1235. (In Russian) [Google Scholar]
- Trojanová, Z.; Száraz, Z.; Chmelík, F.; Lukáč, P. Acoustic emission from deformed magnesium alloy-based composites. Mater. Sci. Eng. A 2011, 528, 2479–2483. [Google Scholar] [CrossRef]
- Máthis, K.; Čapek, J.; Zdražilová, Z.; Trojanová, Z. Investigation of tension-compression asymmetry of magnesium by use of the acoustic emission technique. Mater. Sci. Eng. A 2011, 528, 5904–5907. [Google Scholar] [CrossRef]
- Kocks, U.F.; Mecking, H. Physics and phenomenology of strain hardening: The FCC case. Progr. Mater. Sci. 2003, 48, 171–273. [Google Scholar] [CrossRef]
- Máthis, K.; Csiszar, G.; Čapek, J.; Gubicza, J.; Clausen, B.; Lukáš, P.; Vinogradov, A.; Agnew, S.R. Effect of the loading mode on the evolution of the deformation mechanisms in randomly textured magnesium polycrystals—Comparison of experimental and modeling results. Inter. J. Plast. 2015, 72, 127–150. [Google Scholar] [CrossRef]
- Barnett, M.R. Twinning and the ductility of magnesium alloys part I: Tension twins. Mater. Sci. Eng. A 2007, 464, 1–7. [Google Scholar] [CrossRef]
- Barnett, M.R. Twinning and the ductility of magnesium alloys part II. “contraction” twins. Mater. Sci. Eng. A 2007, 464, 8–16. [Google Scholar] [CrossRef]
- Koike, J. Enhanced deformation mechanisms by anisotropic plasticity in polycrystalline Mg alloys. Metall. Mater. Trans. A 2007, 36, 1689–1696. [Google Scholar] [CrossRef]
- Lou, X.Y.; Li, M.; Boger, R.K.; Agnew, S.R.; Wagoner, R.H. Hardening evolution of AZ31 B Mg sheet. Int. J. Plasticity 2007, 23, 44–86. [Google Scholar] [CrossRef]
- Lavrentev, F.F. The type of dislocation interaction as the factor determining work hardening. Mater. Sci. Eng. 1980, 46, 191–208. [Google Scholar] [CrossRef]
- Molodov, K.D.; Al-Samman, T.; Molodov, D.A. Profuse slip transmission across twin boundaries in magnesium. Acta Mater. 2017, 124, 397–409. [Google Scholar] [CrossRef]
- Molodov, K.D.; Al-Samman, T.; Molodov, T.D.; Korte-Kerz, S. On the twinning shear of twins in magnesium: Experimental determination and formal description. Acta Mater. 2017, 134, 267–273. [Google Scholar] [CrossRef]
- Yang, H.; Jiang, B.; He, J.; Jiang, Z.; Yang, H.; Jiang, B.; He, J.; Zhang, Z.; Pang, F. twinning behavior in magnesium bicrystal. J. Alloys Compd. 2017, 725, 1282–1287. [Google Scholar] [CrossRef]
- Buey, D.; Ghazisaeidi, M. Atomistic simulation of <c + a> screw dislocation cross slip in Mg. Scripta Mater. 2016, 117, 51–54. [Google Scholar] [CrossRef]
- Ando, S.; Tonda, H. Non-Basal Slip in Magnesium-Lithium Alloy Single Crystals. Mater. Trans. JIM 2000, 41, 1188–1191. [Google Scholar] [CrossRef]
- Tonda, H.; Ando, S. Effect of temperature and shear direction on yield stress by slip in HCP metals slip in HCP metals. Metall. Mater. Trans. A 2002, 33, 831–836. [Google Scholar] [CrossRef]
- Ahmad, R.; Wu, Z.; Curtin, W.A. Analysis of double cross slip of pyramidalI <c + a> dislocations and implications for ductility in Mg alloys. Acta Mater. 2020, 183, 228–241. [Google Scholar] [CrossRef]
- Armstrong, R.W.; Balasubramanian, N. Unified Hall-Petch description of nano-grain nickel hardness, flow stress and strain rate sensitivity measurements. AIP Adv. 2017, 7. [Google Scholar] [CrossRef]
- Mann, G.; Griffith, J.R.; Cácers, C.H. Hall-Petch parameters in tension and compression in cast Mg-2Zn alloys. J. Alloys Compd. 2004, 178, 188–191. [Google Scholar] [CrossRef]
- Yu, H.; Xin, Y.; Wang, M.; Liu, Q. Hall-Petch relationship in Mg alloys: A review. J. Mater. Sci. Technol. 2018, 34, 248–256. [Google Scholar] [CrossRef]
- Cáceres, C.H.; Lukáč, P. Strain hardening behaviour and the Taylor factor of pure magnesium. Phil. Mag. 2008, 88, 977–989. [Google Scholar] [CrossRef]
- Somekawa, H.; Mukai, T. Hall-Petch relation for deformation twinning in solid solution magnesium alloys. Mater. Sci. Eng. A 2013, 561, 378–385. [Google Scholar] [CrossRef]
- Meyers, M.A.; Vohringer, O.; Lubarda, V.A. The onset of twinning in metals: A constitutive description. Acta Mater. 2001, 49, 4025–4039. [Google Scholar] [CrossRef]




| Sample | SW1 | SW2 | SW3 | SW4 | SW5 |
|---|---|---|---|---|---|
| Grain size (μm) | 60.5 ± 55.2 | 41.5 ± 28.6 | 40.3 ± 26.8 | 26.3 ± 13.9 | 16.2 ± 12.6 |
| Swaging Counts | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| Permanent strain % | 0.02 | 0.030 | 0.035 | 0.045 | 0.05 | 0.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Trojanová, Z.; Drozd, Z.; Halmešová, K.; Džugan, J.; Škraban, T.; Minárik, P.; Németh, G.; Lukáč, P. Strain Hardening in an AZ31 Alloy Submitted to Rotary Swaging. Materials 2021, 14, 157. https://doi.org/10.3390/ma14010157
Trojanová Z, Drozd Z, Halmešová K, Džugan J, Škraban T, Minárik P, Németh G, Lukáč P. Strain Hardening in an AZ31 Alloy Submitted to Rotary Swaging. Materials. 2021; 14(1):157. https://doi.org/10.3390/ma14010157
Chicago/Turabian StyleTrojanová, Zuzanka, Zdeněk Drozd, Kristýna Halmešová, Ján Džugan, Tomáš Škraban, Peter Minárik, Gergely Németh, and Pavel Lukáč. 2021. "Strain Hardening in an AZ31 Alloy Submitted to Rotary Swaging" Materials 14, no. 1: 157. https://doi.org/10.3390/ma14010157
APA StyleTrojanová, Z., Drozd, Z., Halmešová, K., Džugan, J., Škraban, T., Minárik, P., Németh, G., & Lukáč, P. (2021). Strain Hardening in an AZ31 Alloy Submitted to Rotary Swaging. Materials, 14(1), 157. https://doi.org/10.3390/ma14010157







