Mercury Removal from Aqueous Solution Using ETS-4 in the Presence of Cations of Distinct Sizes
Abstract
1. Introduction
2. Materials and Methods
2.1. Chemicals
2.2. Engelhard Titanium Silicate No. 4 (ETS-4)
2.3. Ion Exchange Studies and Analytical Procedures
2.3.1. Ion Exchange of TPA+ Solution (without Hg2+) Using Na-ETS-4
2.3.2. Ion Exchange of Hg2+ Solution Using Na-ETS-4
3. Modelling
4. Results and Discussion
4.1. Check that Tetrapropylammonium Cation (TPA+) Cannot Penetrate ETS-4 Pores
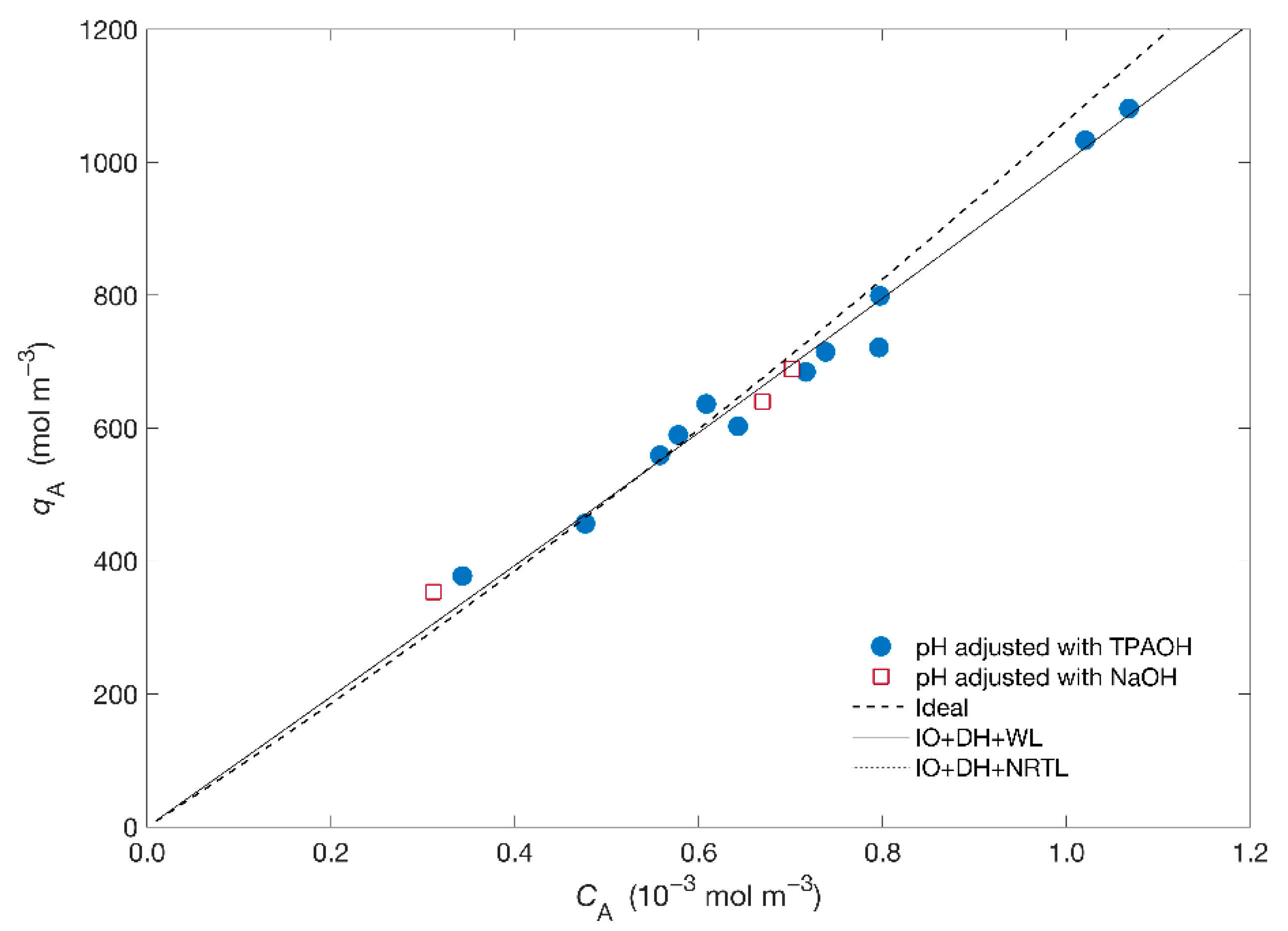
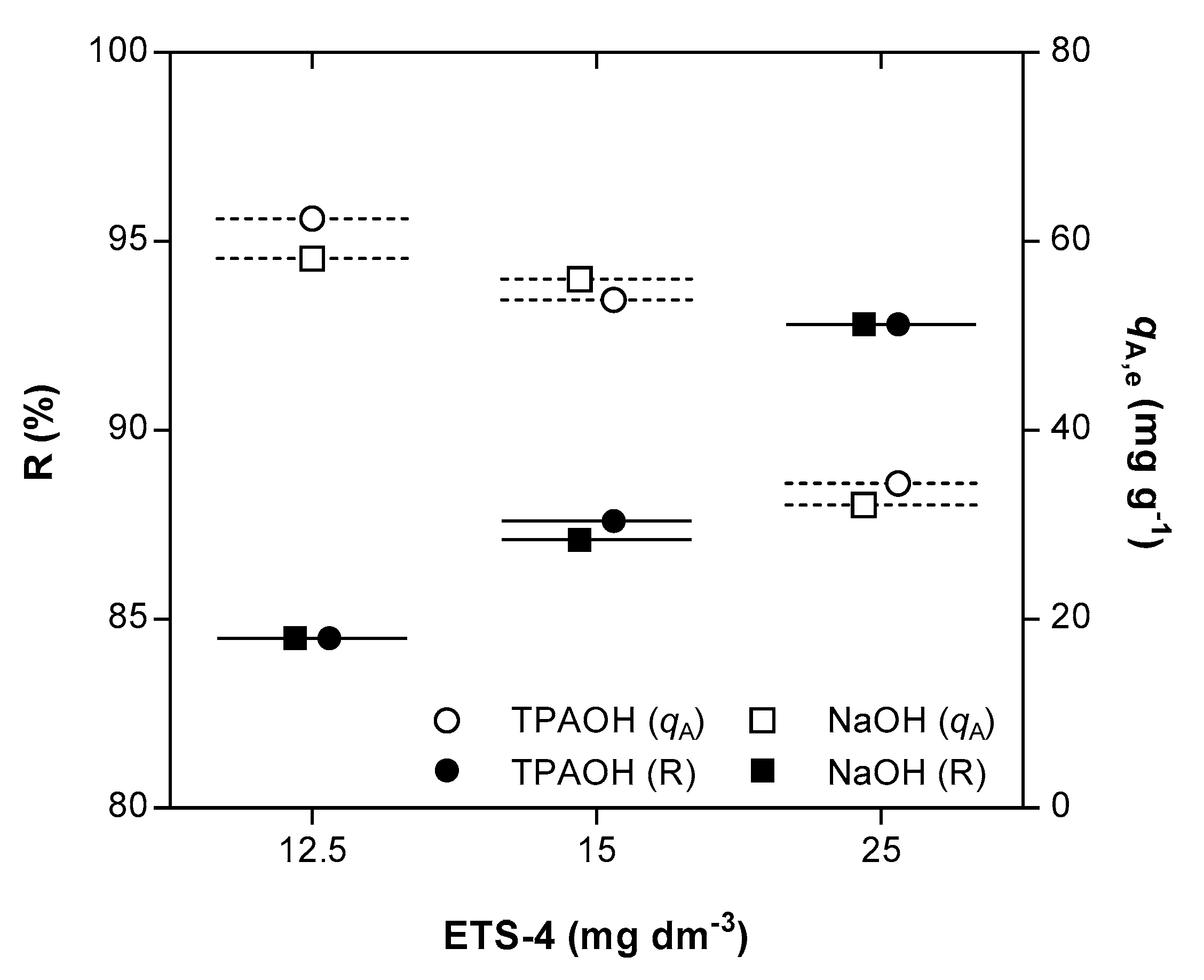
4.2. Isotherm of the Hg2+/Na+/ETS-4 System
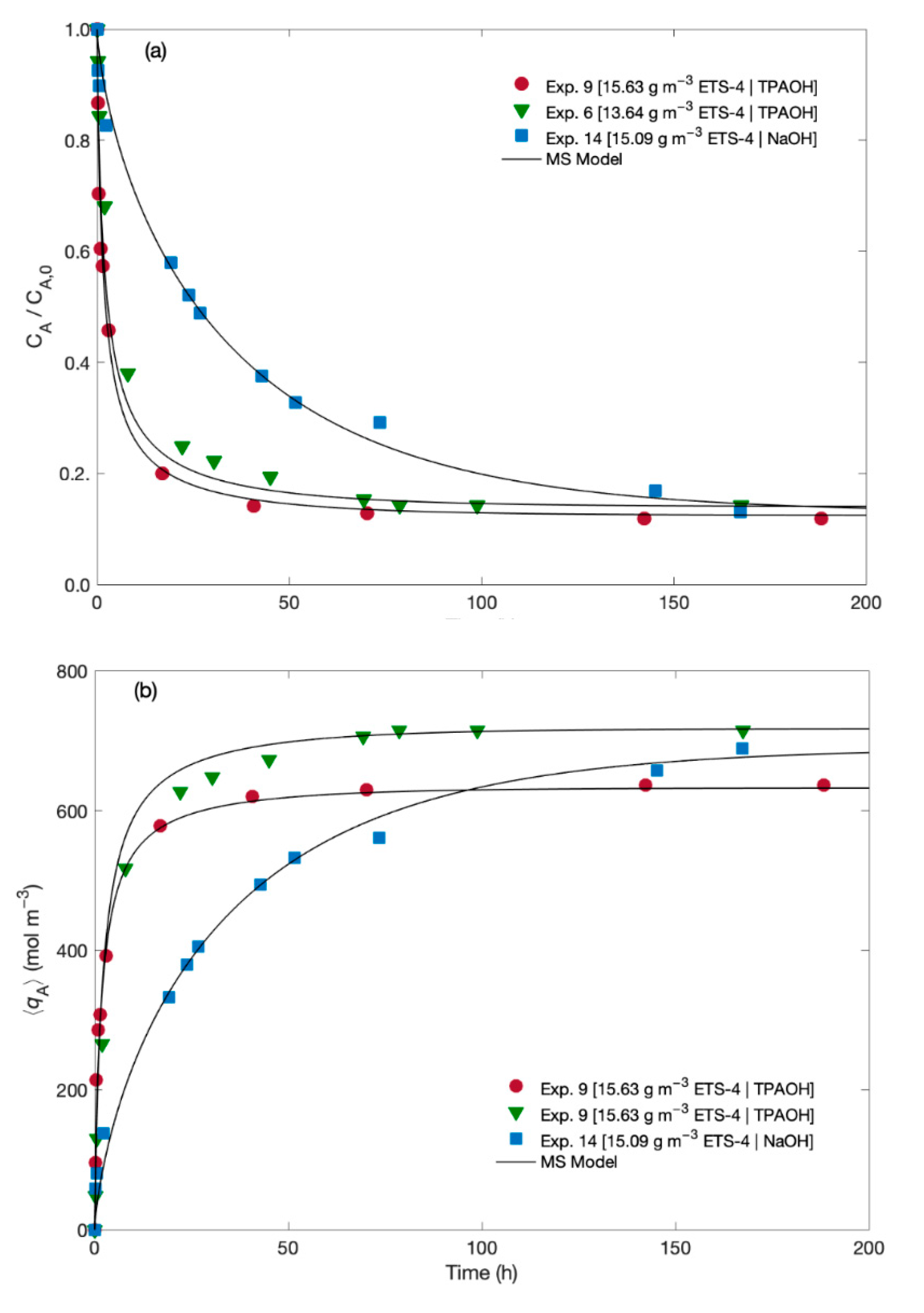
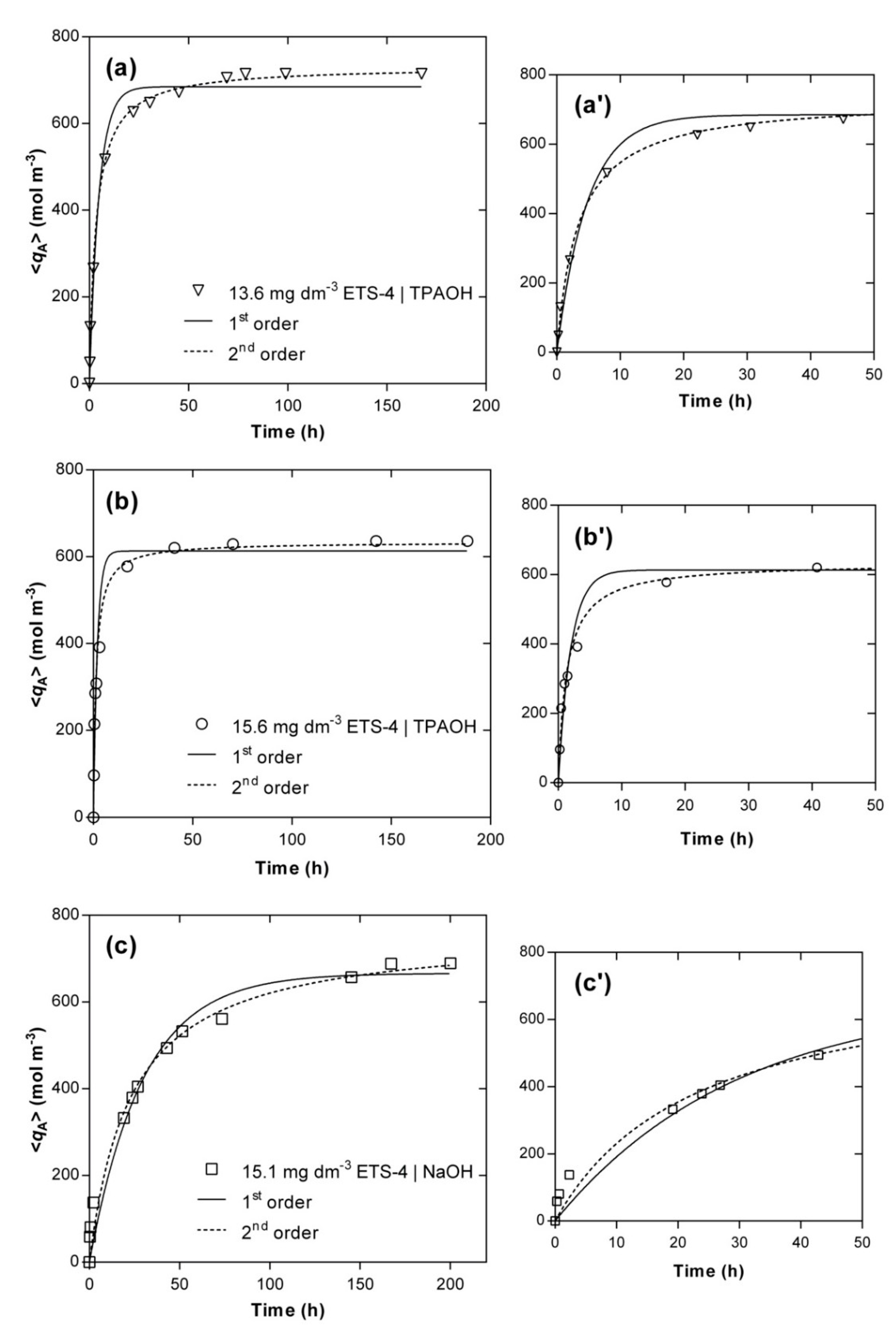
4.3. Kinetics Modelling of the Hg2+/Na+/ETS-4 System
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lopes, C.B.; Lito, P.F.; Cardoso, S.P.; Pereira, E.; Duarte, A.C.; Silva, C.M. Metal Recovery, Separation and/or Pre-concentration. In Ion Exchange Technology II—Applications; Inamuddin, D., Luqman, M., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 237–322. [Google Scholar]
- Coelho, J.P.; Santos, H.; Reis, A.T.; Falcão, J.; Rodrigues, E.T.; Pereira, M.E.; Duarte, A.C.; Pardal, M.A. Mercury bioaccumulation in the spotted dogfish (Scyliorhinus canicula) from the Atlantic Ocean. Mar. Pollut. Bull. 2010, 60, 1372–1375. [Google Scholar] [CrossRef] [PubMed]
- European Union. Directive 2013/39/EU of the European Parliament and of the Council of 12 August 2013 amending Directives 2000/60/EC and 2008/105/EC as regards priority substances in the field of water policy. Off. J. Eur. Union. 2013, 226, 1–17. [Google Scholar]
- ATSDR. ATSDR 2015 Subst. Prior. List. (n.d.). Available online: http://www.atsdr.cdc.gov/spl/index.html (accessed on 20 January 2019).
- Krabbenhoft, D.P.; Rickert, D.A. Mercury Contamination of Aquatic Ecosystems. Available online: http://pubs.usgs.gov/fs/1995/fs216-95/ (accessed on 1 April 2020).
- Sylvester, P.; Behrens, E.A.; Graziano, G.M.; Clearfield, A. An Assessment of Inorganic Ion-Exchange Materials for the Removal of Strontium from Simulated Hanford Tank Wastes. Sep. Sci. Technol. 1999, 34, 1981–1992. [Google Scholar] [CrossRef]
- Zhao, G.X.S.; Lee, J.L.; Chia, P.A. Unusual Adsorption Properties of Microporous Titanosilicate ETS-10 toward Heavy Metal Lead. Langmuir 2003, 19, 1977–1979. [Google Scholar] [CrossRef]
- Lopes, C.B.; Coimbra, J.; Otero, M.; Pereira, E.; Duarte, A.C.; Lin, Z.; Rocha, J. Uptake of Hg2+ from aqueous solutions by microporous titano- and zircono-silicates. Quim. Nova 2008, 31, 321–325. [Google Scholar] [CrossRef]
- Camarinha, E.D.; Lito, P.F.; Antunes, B.M.; Otero, M.; Lin, Z.; Rocha, J.; Pereira, E.; Duarte, A.C.; Silva, C.M. Cadmium(II) removal from aqueous solution using microporous titanosilicate ETS-10. Chem. Eng. J. 2009, 155, 108–114. [Google Scholar] [CrossRef]
- Barreira, L.D.; Lito, P.F.; Antunes, B.M.; Otero, M.; Lin, Z.; Rocha, J.; Pereira, E.; Duarte, A.C.; Silva, C.M. Effect of pH on cadmium (II) removal from aqueous solution using titanosilicate ETS-4. Chem. Eng. J. 2009, 155, 728–735. [Google Scholar] [CrossRef]
- Ferreira, T.R.; Lopes, C.B.; Lito, P.F.; Otero, M.; Lin, Z.; Rocha, J.; Pereira, E.; Duarte, A.C.; Silva, C.M. Cadmium(II) removal from aqueous solution using microporous titanosilicate ETS-4. Chem. Eng. J. 2009, 147, 173–179. [Google Scholar] [CrossRef]
- Cardoso, S.P.; Lopes, C.B.; Pereira, E.; Duarte, A.C.; Silva, C.M. Competitive removal of Cd2+ and Hg2+ ions from water using titanosilicate ETS-4: Kinetic behaviour and selectivity. Water. Air. Soil Pollut. 2013, 224, 1535. [Google Scholar] [CrossRef]
- Cardoso, S.P.; Azenha, I.S.; Lin, Z.; Portugal, I.; Rodrigues, A.E.; Silva, C.M. Experimental measurement and modeling of ion exchange equilibrium and kinetics of cadmium(II) solutions over microporous stannosilicate AV-6. Chem. Eng. J. 2016, 295, 139–151. [Google Scholar] [CrossRef]
- Figueiredo, B.R.; Ananias, D.; Portugal, I.; Rocha, J.; Silva, C.M. Tb/Eu-AV-9: A lanthanide silicate for the sensing and removal of cesium ions from aqueous solutions. Chem. Eng. J. 2016, 286, 679–688. [Google Scholar] [CrossRef]
- Figueiredo, B.R.; Portugal, I.; Rocha, J.; Silva, C.M. Fixed-bed removal of Cs+ from aqueous solutions by microporous silicate ETS-4: Measurement and modeling of loading-regeneration cycles. Chem. Eng. J. 2016, 301, 276–284. [Google Scholar] [CrossRef]
- Figueiredo, B.R.; Ananias, D.; Rocha, J.; Silva, C.M. Cs+ ion exchange over lanthanide silicate Eu-AV-20: Experimental measurement and modelling. Chem. Eng. J. 2015, 268, 208–218. [Google Scholar] [CrossRef]
- Duan, C.; Ma, T.; Wang, J.; Zhou, Y. Removaal of heavy metals from aqueous solution using carbon-based adsorbents: A review. J. Water Process. Eng. 2020, 37, 101339. [Google Scholar] [CrossRef]
- Filice, S.; Mazurkiewicz-Pawlicka, M.; Malolepszy, A.; Stobinski, L.; Kwiatkowski, R.; Boczkowska, A.; Gradon, L.; Scalese, S. Sulfonated Pentablock Copolymer Membranes and Graphene Oxide Addition for Efficient Removal of Metal Ions from Water. Nanomaterials 2020, 10, 1157. [Google Scholar] [CrossRef]
- Wadhawan, S.; Jain, A.; Nayyar, J.; Mehta, S.K. Role of nanomaterials as adsorbents in heavy metal ion removal from waste water: A review. J. Water. Process Eng. 2020, 33, 101038. [Google Scholar] [CrossRef]
- Upadhyay, U.; Sreedhar, I.; Singh, S.A.; Patel, C.M.; Anitha, K.L. Recent advances in heavy metal removal by chitosan based adsorbents. Carbohydr. Polym. 2021, 251, 117000. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, W.; Zhao, Y.; Bai, H.; Wen, T.; Kang, S.; Song, G.; Song, S.; Komarneni, S. Removal of heavy metals and dyes by clay-based adsorbents: From natural clays to 1D and 2D nano-composites. Chem. Eng. J. 2021, in press. [Google Scholar] [CrossRef]
- Fabre, E.; Dias, M.; Costa, M.; Henriques, B.; Vale, C.; Lopes, C.B.; Pinheiro-Torres, J.; Silva, C.M.; Pereira, E. Negligible effect of potentially toxic elements and rare earth elements on mercury removal from contaminated waters by green, brown and red living marine macroalgae. Sci. Total Environ. 2020, 724, 138133. [Google Scholar] [CrossRef]
- Fabre, E.; Rocha, A.; Cardoso, S.P.; Brandão, P.; Vale, C.; Lopes, C.B.; Pereira, E.; Silva, C.M. Purification of mercury-contaminated water using new AM-11 and AM-14 microporous silicates. Sep. Purif. Technol. 2020, 239, 116438. [Google Scholar] [CrossRef]
- Fabre, E.; Lopes, C.B.; Vale, C.; Pereira, E.; Silva, C.M. Valuation of banana peels as an effective biosorbent for mercury removal under low environmental concentrations. Sci. Total Environ 2020, 709, 135883. [Google Scholar] [CrossRef]
- Clearfield, A.; Poojary, D.M.; Behrens, E.A.; Cahill, R.A.; Bortun, A.I.; Bortun, L.N. Structural Basis of Selectivity in Tunnel Type Inorganic Ion Exchangers. In Metal-Ion Separation and Preconcentration; Bond, A.H., Dietz, M.L., Rogers, R.D., Eds.; American Chemical Society: Washington, DC, USA, 1999; pp. 168–182. [Google Scholar]
- Helfferich, F.G. Ion Exchange; Dover Publications: New York, NY, USA, 1962. [Google Scholar]
- Nair, S.; Jeong, H.-K.; Chandrasekaran, A.; Braunbarth, C.M.; Tsapatsis, M.; Kuznicki, S.M. Synthesis and Structure Determination of ETS-4 Single Crystals. Chem. Mater. 2001, 13, 4247–4254. [Google Scholar] [CrossRef]
- Oleksiienko, O.; Wolkersdorfer, C.; Sillanpää, M. Titanosilicates in cation adsorption and cation exchange—A review. Chem. Eng. J. 2017, 317, 570–585. [Google Scholar] [CrossRef]
- Al Attar, L.; Dyer, A. Sorption of uranium onto titanosilicate materials. J. Radioanal. Nucl. Chem. 2001, 247, 121–128. [Google Scholar]
- Popa, K.; Pavel, C.C.; Bilba, N.; Cecal, A. Purification of waste waters containing 60Co2+, 115mCd2+ and 203Hg2+ radioactive ions by ETS-4 titanosilicate. J. Radioanal. Nucl. Chem. 2006, 269, 155–160. [Google Scholar] [CrossRef]
- Popa, K.; Pavel, C.C.; Bilba, N.; Cecal, A. Radioactive wastewaters purification using titanosilicates materials: State of the art and perspectives. Desalination 2012, 293, 78–86. [Google Scholar] [CrossRef]
- Lopes, C.B.; Otero, M.; Lin, Z.; Pereira, E.; Silva, C.M.; Rocha, J.; Duarte, A.C. Removal of Mercury From Aqueous Solutions by ETS-4 Microporous Titanosilicate: Effect of Contact Time, Titanosilicate Mass and Initial Metal Concentration. In Proceedings of the 11th International Conference on Environmental Remediation and Radioactive Waste Management (ICEM2007), Bruges, Belgium, 2–6 September 2007. [Google Scholar]
- Lopes, C.B.; Otero, M.; Lin, Z.; Silva, C.M.; Rocha, J.; Pereira, E.; Duarte, A.C. Removal of Hg2+ ions from aqueous solution by ETS-4 microporous titanosilicate—Kinetic and equilibrium studies. Chem. Eng. J. 2009, 151, 247–254. [Google Scholar] [CrossRef]
- Lopes, C.B.; Otero, M.; Lin, Z.; Silva, C.M.; Pereira, E.; Rocha, J.; Duarte, A.C. Effect of pH and temperature on Hg2+ water decontamination using ETS-4 titanosilicate. J. Hazard. Mater. 2010, 175, 439–444. [Google Scholar] [CrossRef]
- Tolosana, S.; Ehrlich, R. Composition of liquid effluent discharged by medical institutions in Cape Town. S. Afr. J. Sci. 2000, 96, 417–420. [Google Scholar]
- Chojnacki, A.; Chojnacka, K.; Hoffmann, J.; Górecki, H. The application of natural zeolites for mercury removal: From laboratory tests to industrial scale. Miner. Eng. 2004, 17, 933–937. [Google Scholar] [CrossRef]
- Álvarez-Ayuso, E.; García-Sánchez, A.; Querol, X. Purification of metal electroplating waste waters using zeolites. Water Res. 2003, 37, 4855–4862. [Google Scholar] [CrossRef] [PubMed]
- Philippou, A.; Anderson, M.W. Structural investigation of ETS-4. Zeolites 1996, 16, 98–107. [Google Scholar] [CrossRef]
- Lito, P.F.; Cardoso, S.P.; Loureiro, J.M.; Silva, C.M. Ion Exchange Equilibria and Kinetics. In Ion Exchange Technology I—Theory and Materials; Inamuddin, D., Luqman, M., Eds.; Springer: Dordrecht, The Netherlands, 2012; pp. 51–120. [Google Scholar]
- Zemaitis, J.F.; Clark, D.M.; Rafal, M.; Scricvner, N.C. Handbook of Aqueous Electrolyte Thermodynamics: Theory & Application; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Lito, P.F.; Aniceto, J.P.S.; Silva, C.M. Maxwell–Stefan based modelling of ion exchange systems containing common species (Cd2+, Na+) and distinct sorbents (ETS-4, ETS-10). Int. J. Environ. Sci. Technol. 2013, 12, 183–192. [Google Scholar] [CrossRef][Green Version]
- Lito, P.F.; Aniceto, J.P.S.; Silva, C.M. Modelling ion exchange kinetics in zeolyte-type materials using Maxwell–Stefan approach. Desalin. Water Treat. 2013, 52, 5333–5342. [Google Scholar] [CrossRef]
- Ioannidis, S.; Anderko, A.; Sanders, S.J. Internally consistent representation of binary ion exchange equilibria. Chem. Eng. Sci. 2000, 55, 2687–2698. [Google Scholar] [CrossRef]
- Kuznicki, S.M.; Bell, V.A.; Nair, S.; Hillhouse, H.W.; Jacubinas, R.M.; Braunbarth, C.M.; Toby, B.H.; Tsapatsis, M. A titanosilicate molecular sieve with adjustable pores for size-selective adsorption of molecules. Nature 2001, 412, 720–724. [Google Scholar] [CrossRef]
- Barrer, R.M.; Rees, L.V.C. Energies of Activation for Self-diffusion of Alkali Metal Ions in Analcite. Nature 1960, 187, 768–769. [Google Scholar] [CrossRef]
- Coker, E.N.; Rees, L.V.C. Kinetics of ion exchange in quasi-crystalline aluminosilicate zeolite precursors. Microporous Mesoporous Mater. 2005, 84, 171–178. [Google Scholar] [CrossRef]
- Lopes, C.B.; Lito, P.F.; Otero, M.; Lin, Z.; Rocha, J.; Silva, C.M.; Pereira, E.; Duarte, A.C. Mercury removal with titanosilicate ETS-4: Batch experiments and modelling. Microporous Mesoporous Mater. 2008, 115, 98–105. [Google Scholar] [CrossRef]
- Armenante, P.M.; Kirwan, D.J. Mass transfer to microparticles in agitated systems. Chem. Eng. Sci. 1989, 44, 2781–2796. [Google Scholar] [CrossRef]
- Silva, C.M.; Lito, P.F. Application of the Maxwell–Stefan approach to ion exchange in microporous materials. Batch process modelling. Chem. Eng. Sci. 2007, 62, 6939–6946. [Google Scholar] [CrossRef]
- Lopes, C.B.; Oliveira, J.R.; Rocha, L.S.; Tavares, D.S.; Silva, C.M.; Silva, S.P.; Hartog, N.; Duarte, A.C.; Pereira, E. Cork stoppers as an effective sorbent for water treatment: The removal of mercury at environmentally relevant concentrations and conditions. Environ. Sci. Pollut. Res. 2014, 21, 2108–2121. [Google Scholar] [CrossRef] [PubMed]
- Tavares, D.S.; Lopes, C.B.; Daniel-da-Silva, A.L.; Duarte, A.C.; Trindade, T.; Pereira, E. The role of operational parameters on the uptake of mercury by dithiocarbamate functionalized particles. Chem. Eng. J. 2014, 254, 559–570. [Google Scholar] [CrossRef]
- Rocha, L.S.; Almeida, Â.; Nunes, C.; Henriques, B.; Coimbra, M.A.; Lopes, C.B.; Silva, C.M.; Duarte, A.C.; Pereira, E. Simple and effective chitosan based films for the removal of Hg from waters: Equilibrium, kinetic and ionic competition. Chem. Eng. J. 2016, 300, 217–229. [Google Scholar] [CrossRef]
- Rocha, L.S.; Lopes, C.B.; Borges, J.A.; Duarte, A.C.; Pereira, E. Valuation of Unmodified Rice Husk Waste as an Eco-Friendly Sorbent to Remove Mercury: A Study Using Environmental Realistic Concentrations. Water, Air, Soil Pollut. 2013, 224, 1599. [Google Scholar] [CrossRef]
- Henriques, B.; Rocha, L.S.; Lopes, C.B.; Figueira, P.; Monteiro, R.J.R.; Duarte, A.C.; Pardal, M.A.; Pereira, E. Study on bioaccumulation and biosorption of mercury by living marine macroalgae: Prospecting for a new remediation biotechnology applied to saline waters. Chem. Eng. J. 2015, 281, 759–770. [Google Scholar] [CrossRef]
| Experiment No. | Experiment Type | Dose of ETS-4 (g m−3) | (10−3 mol m−3) | pH Adjust Solution |
|---|---|---|---|---|
| 1 | Equilibrium | 7.15 | 4.58 | TPAOH |
| 2 | Equilibrium | 8.33 | 4.93 | TPAOH |
| 3 | Equilibrium | 11.10 | 4.83 | TPAOH |
| 4 | Equilibrium | 12.56 | 4.62 | TPAOH |
| 5 | Equilibrium | 12.62 | 4.93 | TPAOH |
| 6 | Equilibrium & Kinetic | 13.64 | 5.17 | TPAOH |
| 7 | Equilibrium | 14.52 | 4.62 | TPAOH |
| 8 | Equilibrium | 15.28 | 4.67 | TPAOH |
| 9 | Equilibrium & Kinetic | 15.63 | 5.13 | TPAOH |
| 10 | Equilibrium | 17.63 | 5.04 | TPAOH |
| 11 | Equilibrium | 20.23 | 4.67 | TPAOH |
| 12 | Equilibrium | 25.85 | 4.87 | TPAOH |
| 13 | Equilibrium | 12.55 | 4.31 | NaOH |
| 14 | Equilibrium & Kinetic | 15.09 | 5.43 | NaOH |
| 15 | Equilibrium | 25.19 | 4.34 | NaOH |
| Model | Parameter 1 of | Parameter 2 of | AARD (%) | |
|---|---|---|---|---|
| Ideal | - | - | 0.93 | |
| Debye–Hückel + Wilson | 0.4132 | 2.4199 | 0.89 | |
| Debye–Hückel + NRTL | −2934 | 2667.1 | 0.89 |
| Model | Maxwell–Stefan | Pseudo-first Order | Pseudo-Second Order |
|---|---|---|---|
| Parameters | Ðij (m2 s−1); kf (m s−1) | k1 (10−1 h−1) | k2 (10−4 m3 mol−1 h−1) |
| 5.09 × 10−4 | - | - | |
| TPAOH (Exp. 6 and Exp. 9) | ÐAB = 4.33 × 10−18 | k1(Exp. 9) = 5.04 ± 0.72 | k2(Exp. 9) =11.70 ± 1.30 |
| ÐAS = 4.25 × 10−20 | k1(Exp. 6) = 2.07 ± 0.26 | k2(Exp. 6) = 4.03 ± 0.04 | |
| ÐBS = 1.04 × 10−20 | |||
| NaOH (Exp. 14) | ÐAB = 2.36 × 10−16 | k1(Exp. 14) = 0.34 ± 0.04 | k2(Exp. 14) = 0.56 ± 0.10 |
| ÐAS = 3.09 × 10−19 | |||
| ÐBS = 5.03 × 10−21 | |||
| Global AARD (%) | 5.81 | 14.50 | 8.30 |
| System | Pore Diameter (Å) | (m2s−1) | (m2s−1) | (m2s−1) | (m s−1) | Ref. |
|---|---|---|---|---|---|---|
| Hg2+/Na+/ETS-4 (*) | 3–4 | [49] | ||||
| Cd2+/Na+/AV-6 (*) | [13] | |||||
| Cd2+/Na+/ETS-4 (*) | 3–4 | [41] | ||||
| Cd2+/Na+/ETS-10 (*) | [41] | |||||
| Hg2+/Na+/ETS-4 (*) | 3–4 | This work | ||||
| Hg2+/Na+/ETS-4 (**) | 3–4 | This work |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cardoso, S.P.; Faria, T.L.; Pereira, E.; Portugal, I.; Lopes, C.B.; Silva, C.M. Mercury Removal from Aqueous Solution Using ETS-4 in the Presence of Cations of Distinct Sizes. Materials 2021, 14, 11. https://doi.org/10.3390/ma14010011
Cardoso SP, Faria TL, Pereira E, Portugal I, Lopes CB, Silva CM. Mercury Removal from Aqueous Solution Using ETS-4 in the Presence of Cations of Distinct Sizes. Materials. 2021; 14(1):11. https://doi.org/10.3390/ma14010011
Chicago/Turabian StyleCardoso, Simão P., Tiago L. Faria, Eduarda Pereira, Inês Portugal, Cláudia B. Lopes, and Carlos M. Silva. 2021. "Mercury Removal from Aqueous Solution Using ETS-4 in the Presence of Cations of Distinct Sizes" Materials 14, no. 1: 11. https://doi.org/10.3390/ma14010011
APA StyleCardoso, S. P., Faria, T. L., Pereira, E., Portugal, I., Lopes, C. B., & Silva, C. M. (2021). Mercury Removal from Aqueous Solution Using ETS-4 in the Presence of Cations of Distinct Sizes. Materials, 14(1), 11. https://doi.org/10.3390/ma14010011











