FEM-Based Wave Propagation Modelling for SHM: Certain Numerical Issues in 1D Structures
Abstract
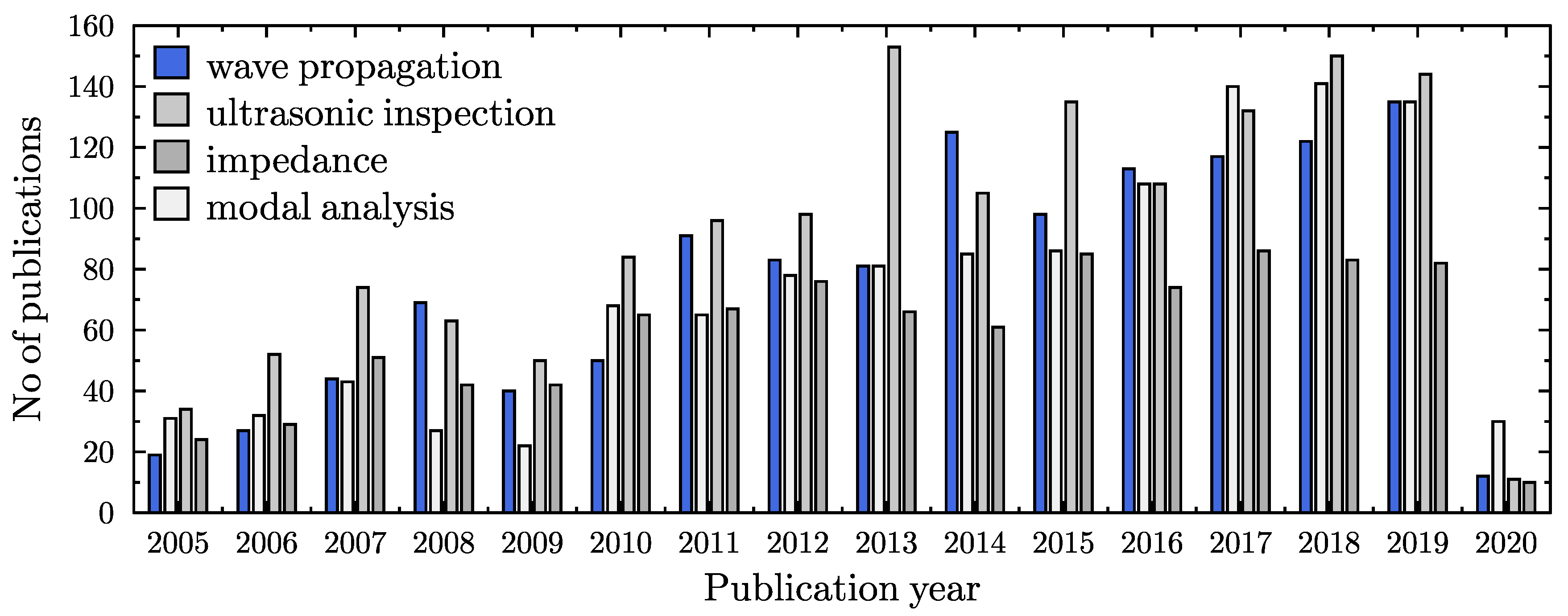
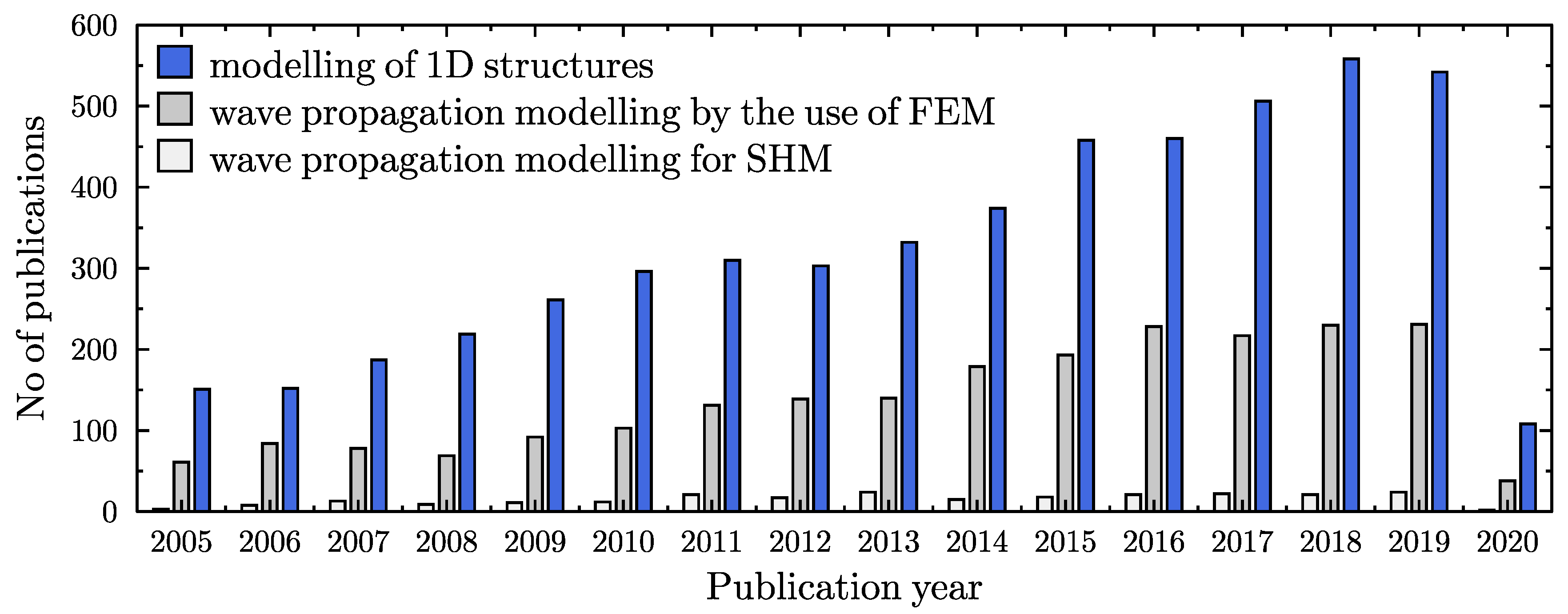
1. Introduction
2. Technical Background
- Division of the analysed structure into a finite number of geometrically simple elements, called spectral finite elements with a certain number of characteristic points called nodes. The spectral finite elements are connected together in a finite number of nodes located at their edges. The number of nodes in the element indicates a selection of the function used for description of the distribution of the physical quantities within the spectral finite elements, depending on their node values. These functions are called node functions or shape functions—Lobatto, Chebyshew, or Laguerre polynomials.
- Transformation of the ordinary or differential equations describing the analysed physical phenomenon to equations of the spectral finite element method. This transformation may be a weak formulation of the method, where there is a weighted residual method applied or a strong formulation, where there the method of minimising the variation functional of the phenomenon is applied. The aforementioned equations, being the problem description, are composed at the level of individual elements and are called local equations, whereas the transformations mentioned correspond to the characteristic matrices of the elements, which are derived. At this step the element matrices are aggregated to form the global characteristic matrices.
- Implementation of boundary conditions.
- Starting the solution process with the appropriate numerical method, leading to obtaining values of sought physical quantities in nodes of individual elements.
3. Numerical Considerations
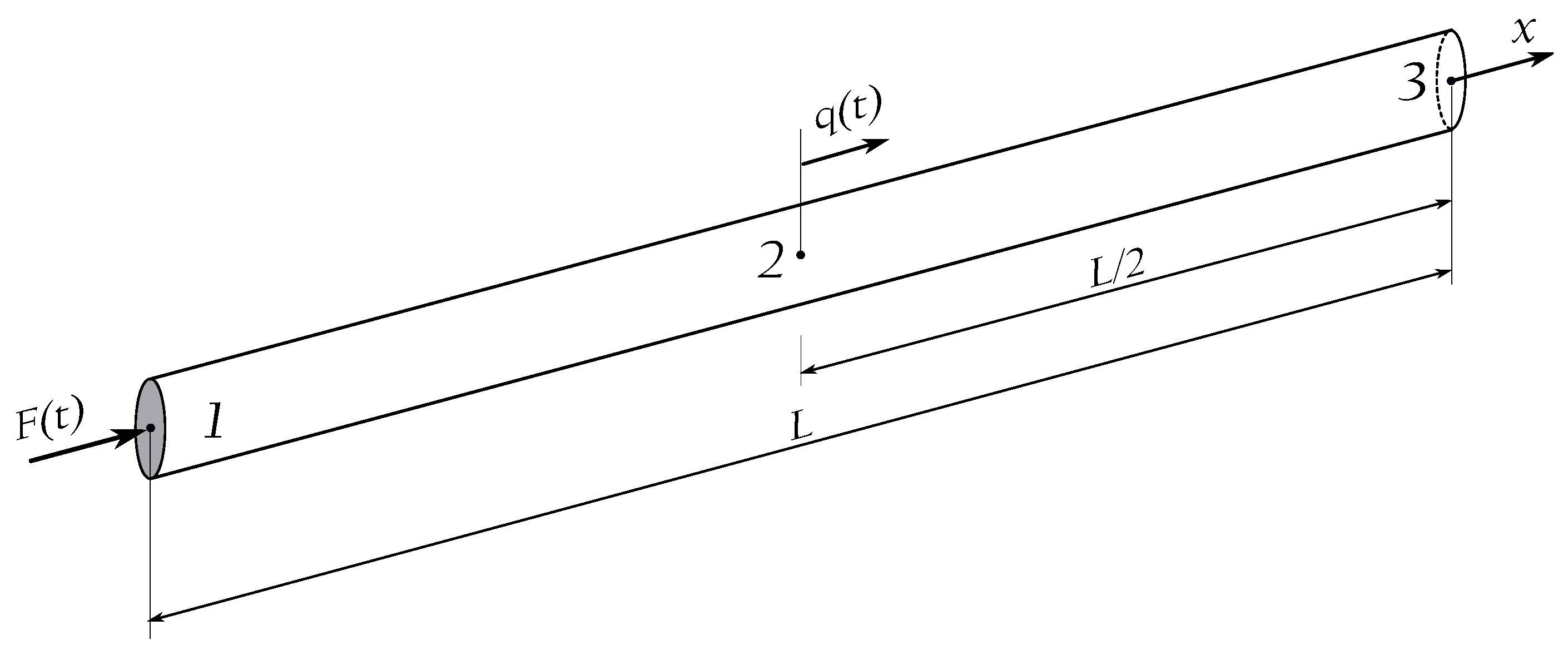
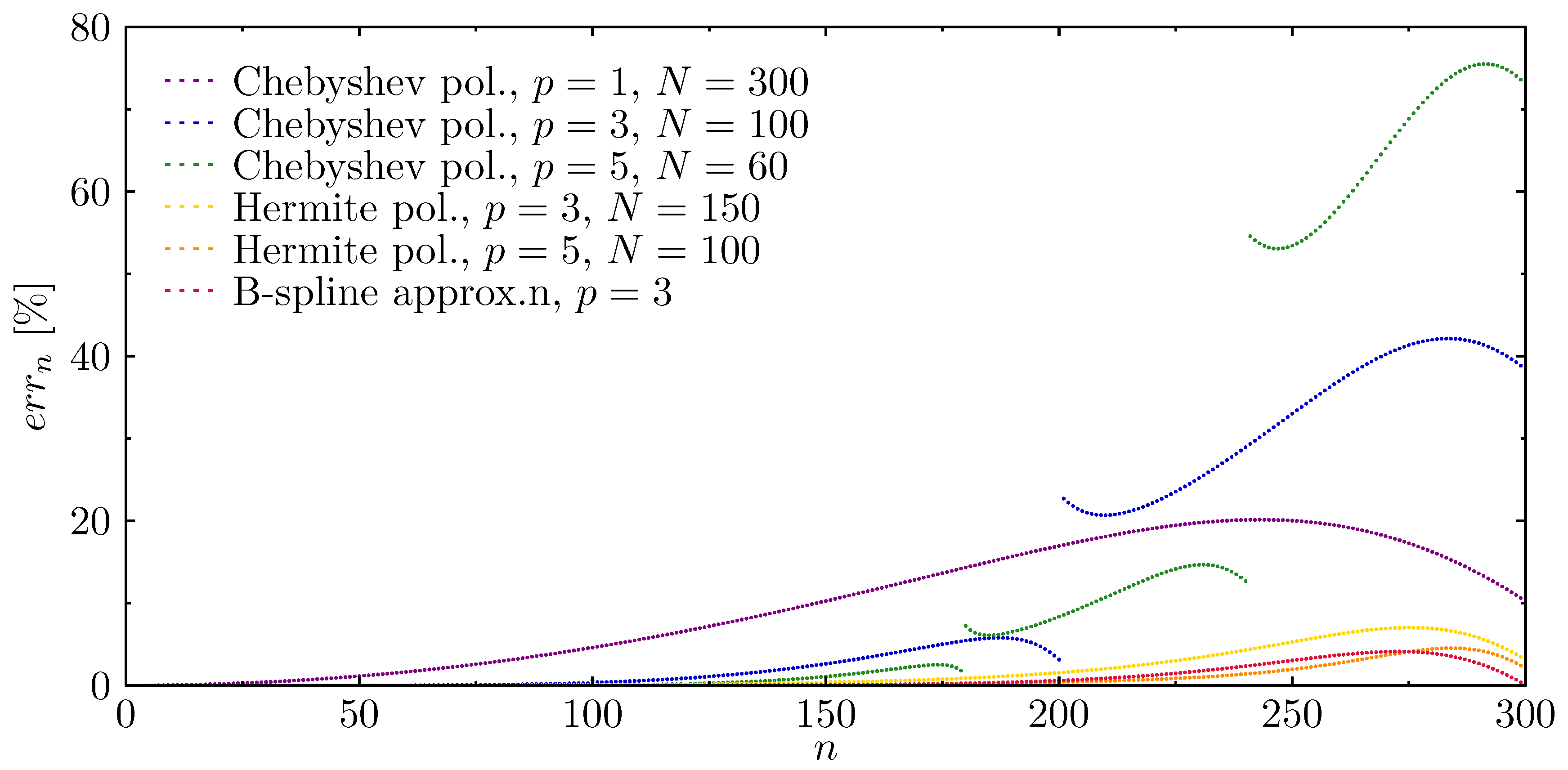
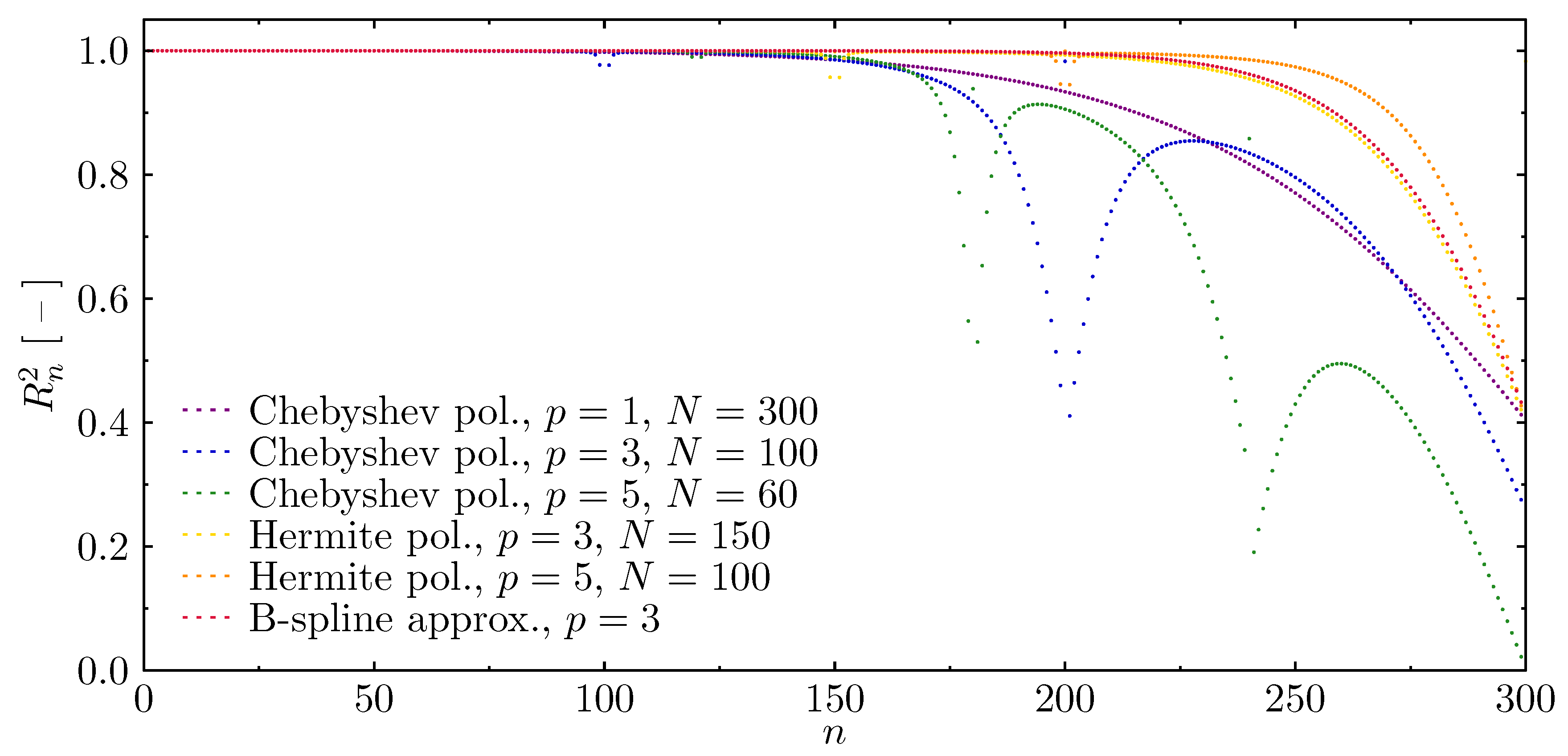
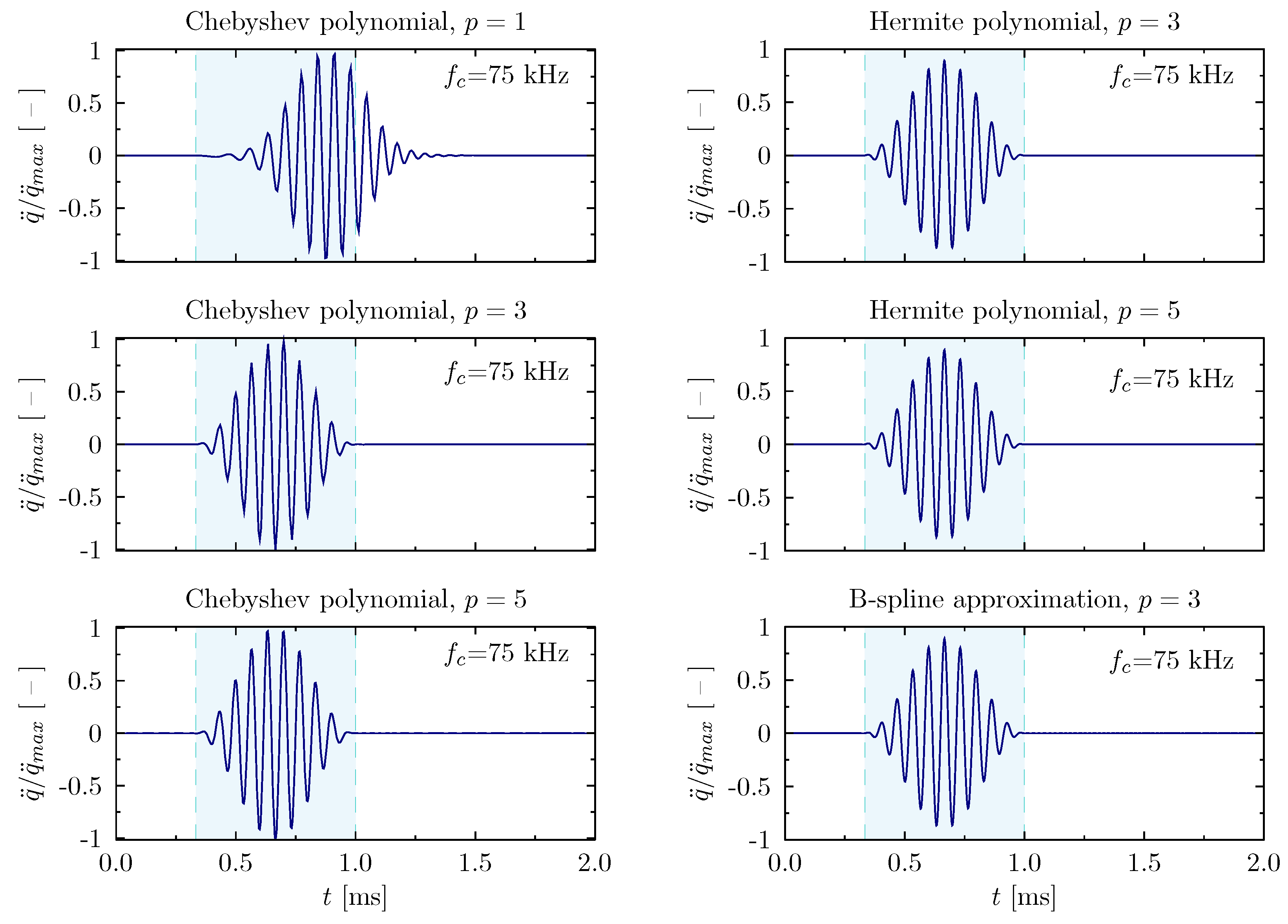
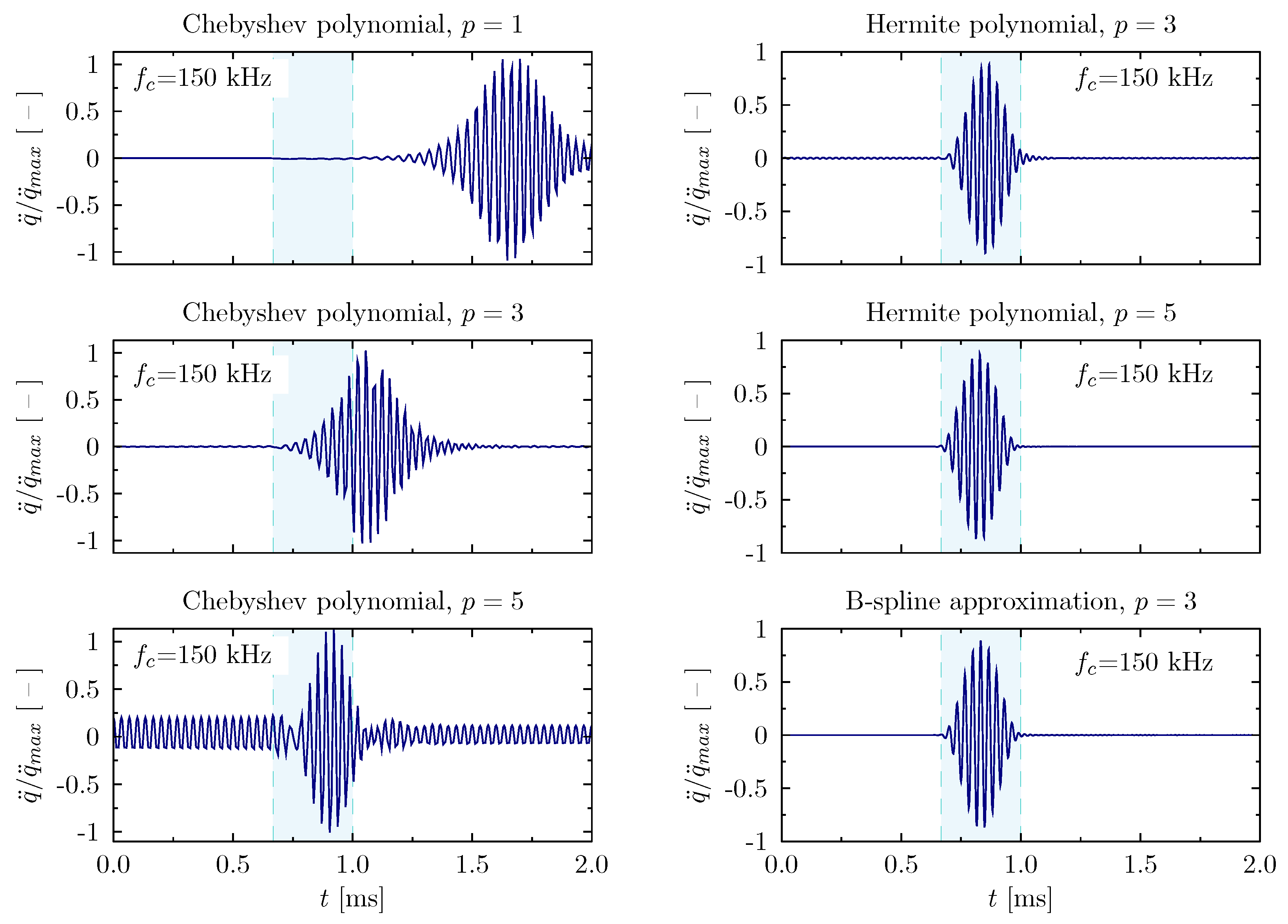
3.1. Rod Structure
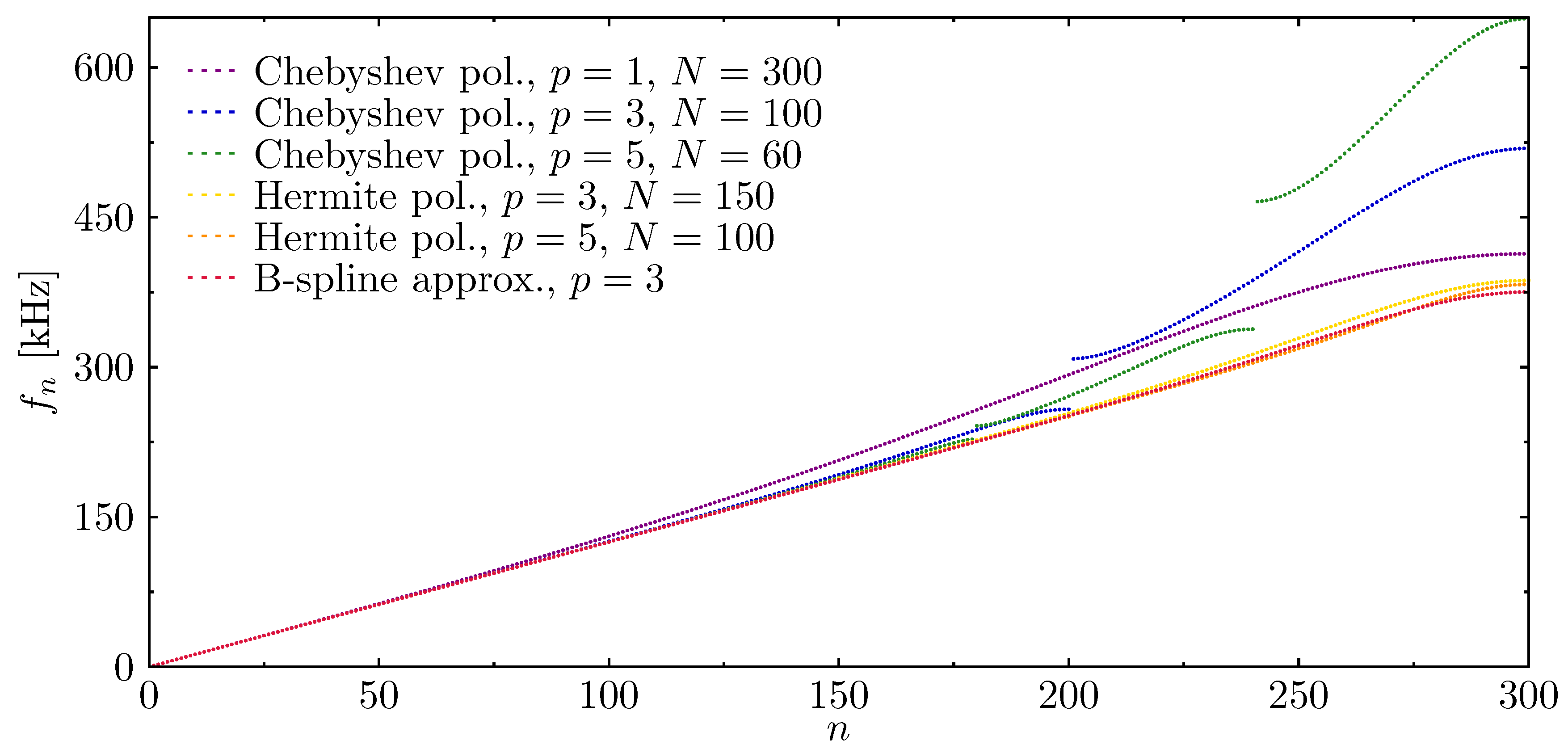
- Two-node element, Chebyshev polynomial, , 300 finite elements, 301 DOFs;
- Four-node element, Chebyshev polynomial, , 100 finite elements, 301 DOFs;
- Six-node element, Chebyshev polynomial, , 60 finite elements, 301 DOFs;
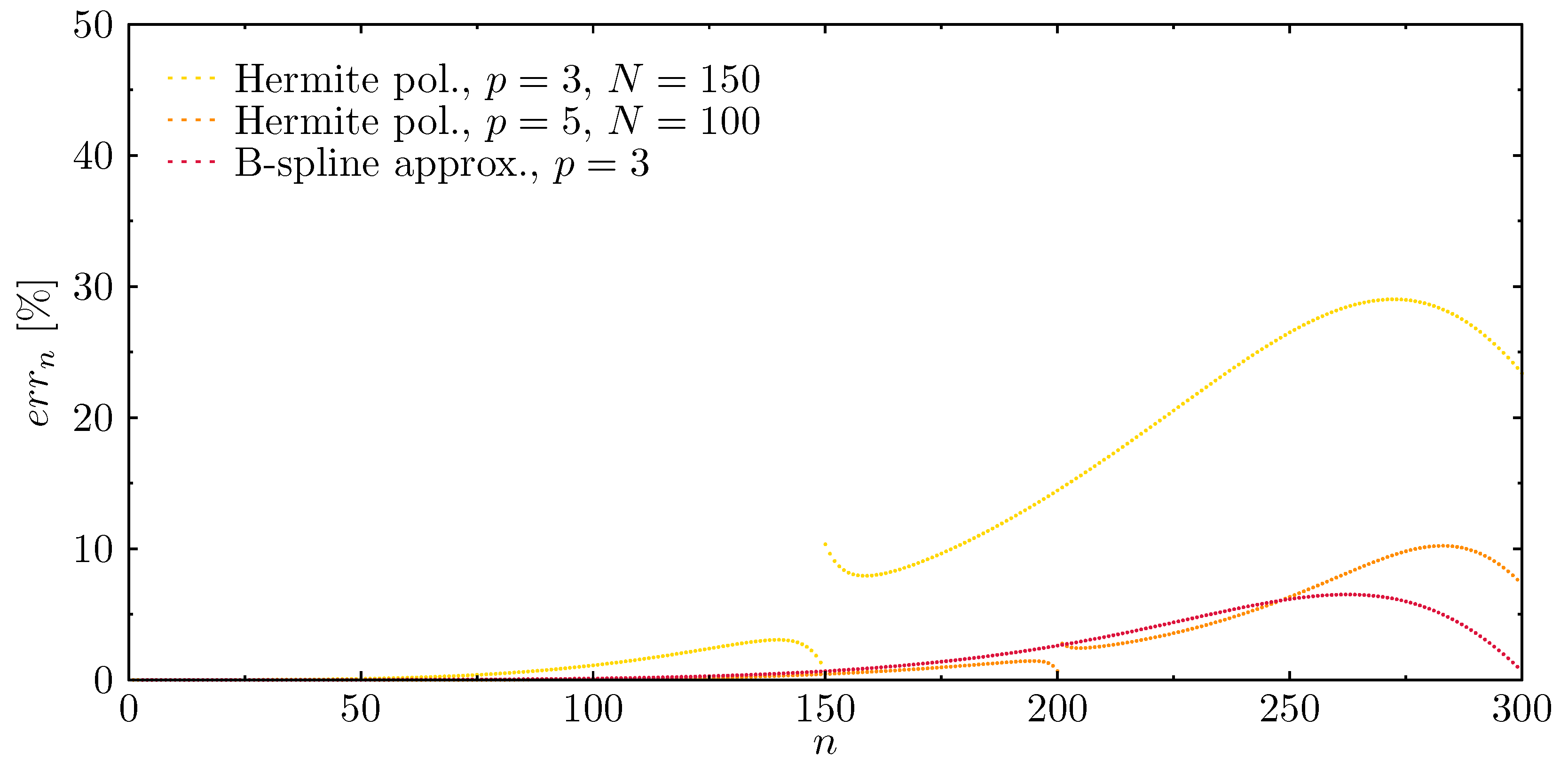
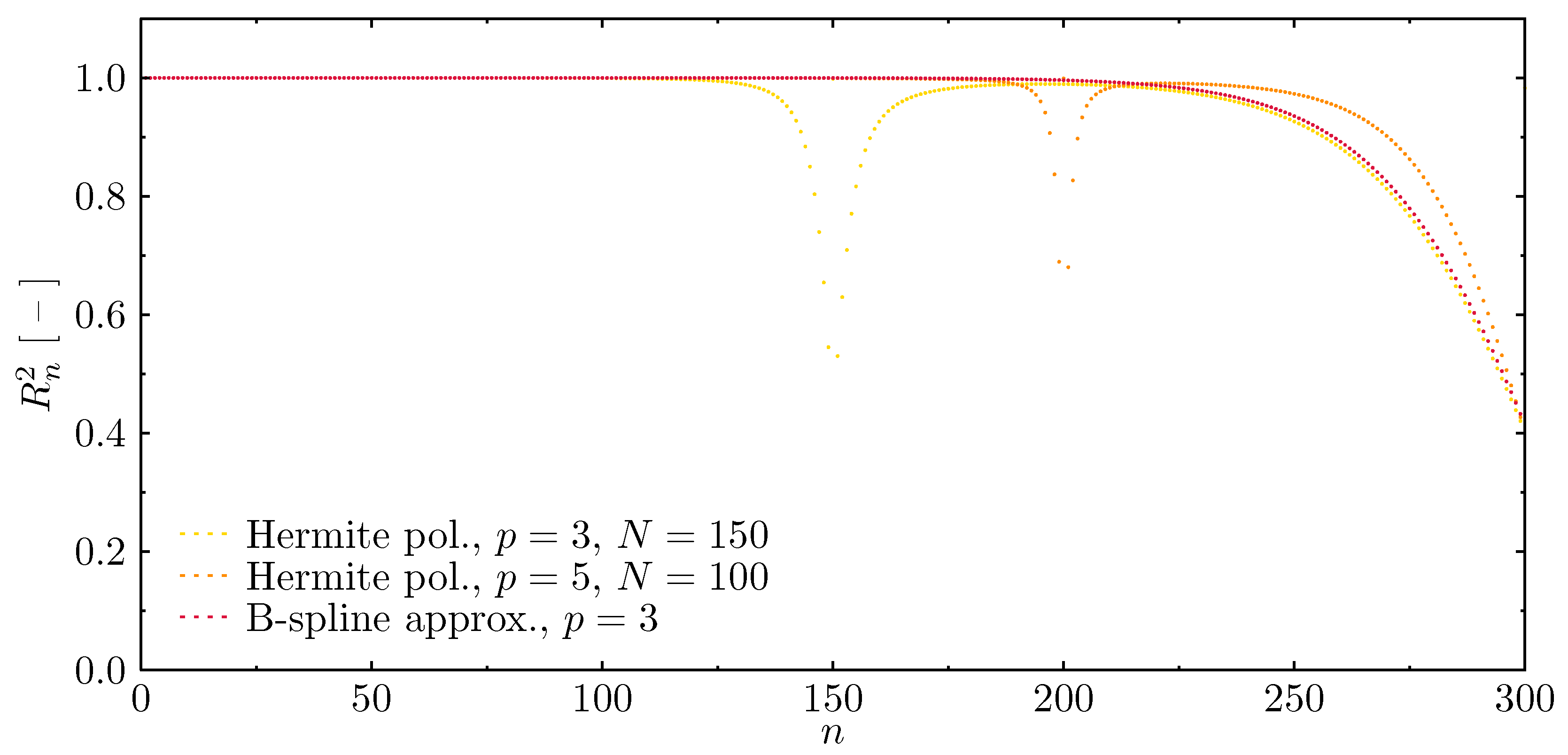
- Two-node element, Hermite polynomial, , 150 finite elements, 302 DOFs;
- Two-node element, Hermite polynomial, , 100 finite elements, 303 DOFs;
- B-spline polynomial, , 300 nodes, 302 DOFs.
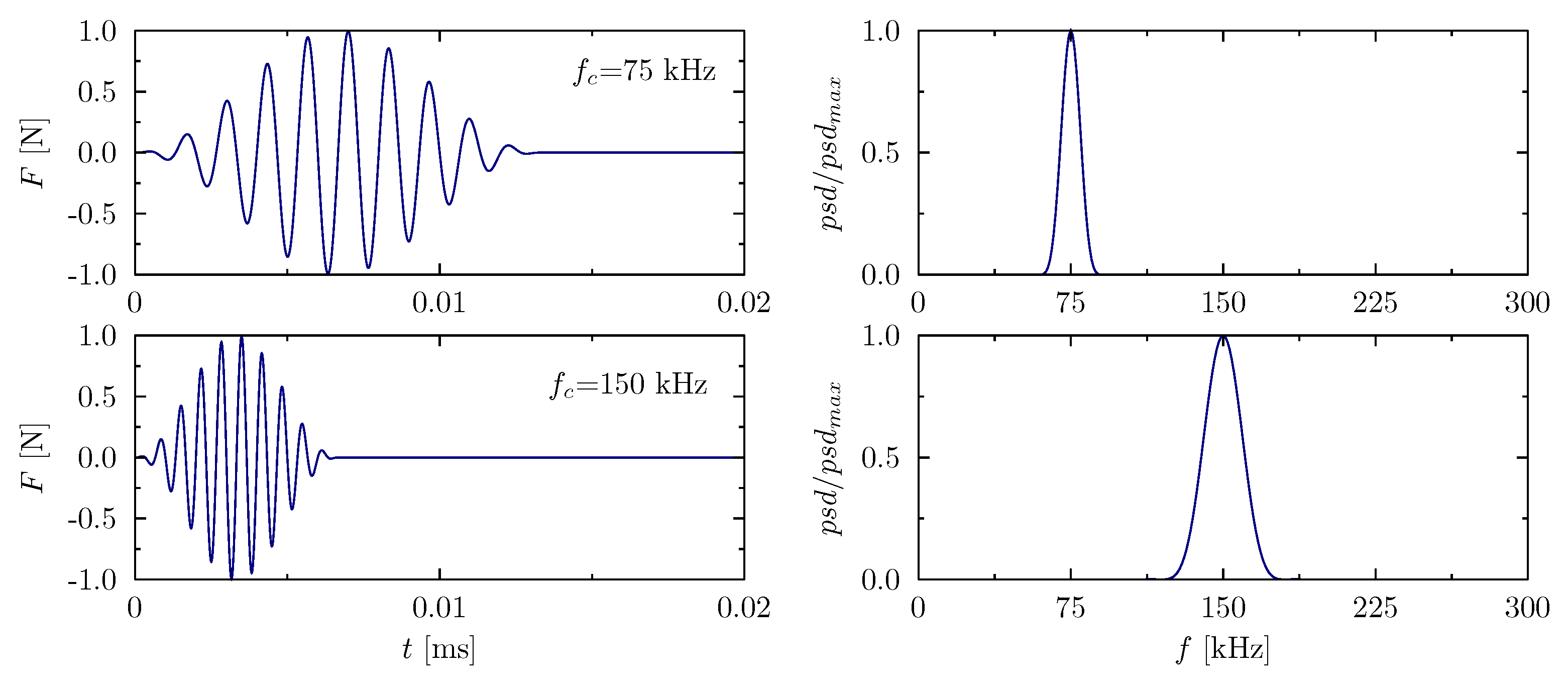
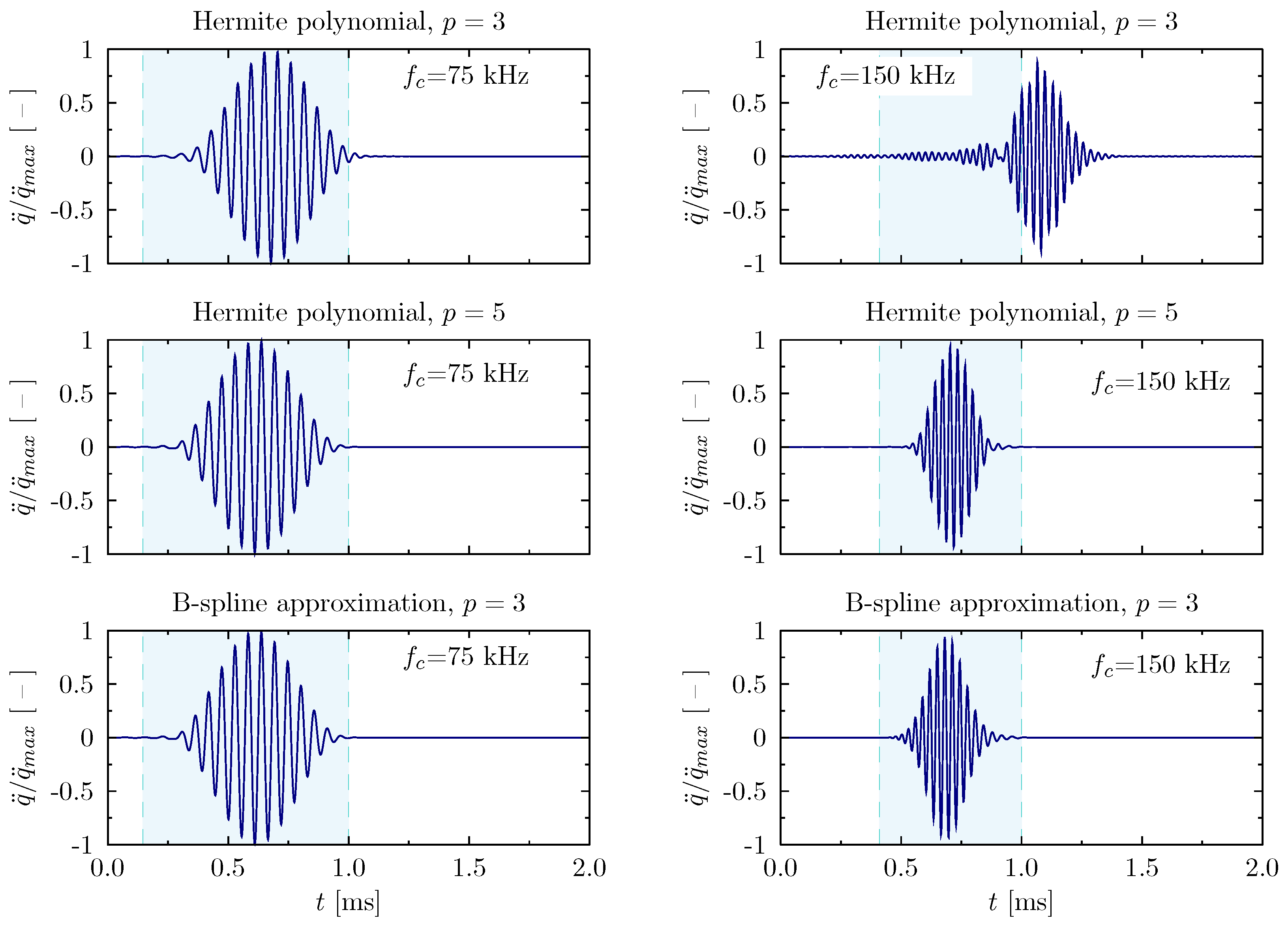
Wave Propagation Analysis
3.2. Beam Structure
Wave Propagation Analysis
4. Discussion and Conclusions
- Numerical models based on the use of finite elements may be thought of as representing periodic structures of certain properties as long as the they include a large number of finite elements of the same or similar size.
- The periodic nature of these models results from the level of the discontinuity of the displacement fields and the order of approximation polynomials employed to build appropriate finite elements, and manifests by the presence of so-called frequency band gaps in calculated frequency spectra.
- As a result of that, the frequency spectra are divided into a number of regions separated by these frequency band gaps, which effectively limits the usable parts of available frequency spectra, based on which the calculated dynamics responses remain unaffected by the periodic nature of discrete numerical models used.
- The number of regions is correlated with the order of approximation polynomials and the level of continuity of the displacement field (1 corresponds to the continuity of the displacement field, 2 to the continuity of the strain and stress fields, and 3 to the continuity of their derivatives).
- The biggest number of such regions was observed in the case of Chebyshev approximation polynomials and the continuity of the displacement field only, which is typical for classical FEM and TDSFEM. The only exceptions are the approximation polynomials of the first degree , where there are no visible frequency band gaps in the calculated spectrum and where the order of approximation polynomials is the same as the level of the continuity of the displacement field. However, the application of such approximation polynomials is characterised by the greatest average errors.
- Application of other types of approximation polynomials, such as Hermite polynomials, leads to smooth frequency spectra only in the case of rods. For calculated beam elements, the use of Hermite approximation polynomials does not improve the situation. In their cases, the orders of approximation polynomials and are greater than the level of the continuity of the displacement fields, which are equal to 2 and 3, respectively.
- Only in the case of B-spline approximation polynomials of the third degree is the observed behaviour different, and the calculated characteristics remain smooth. In this case the order of approximation polynomials is equal to the level of the continuity of the displacement field. As a result the entire spectrum is free of frequency band gaps.
- The influence of frequency band gaps is typically associated to the upper part of the calculated frequency spectra; however, it may significantly influence the representation of modal responses in much lower parts of these spectra.
- This influence may lead to significant numerical errors, as a result of which calculated wave propagation responses may be misrepresented and possess artificial features; for example, they may suggest the presence of strong damping or dispersion.
- As a consequence it is strongly recommended by the authors, prior any wave propagation analysis, that one performs a thorough analysis of natural frequencies and modes of natural vibrations in order to recognise the regions affected by the periodicity of numerical models employed.
- The features discussed in this paper may even more profoundly influence dynamic responses of two-dimensional and three-dimensional structures. This is the subject of the authors’ future research.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SHM | Structural health monitoring |
| FEM | Finite element method |
| TDSFEM | Time domain spectral finite element method |
References
- Boller, C.; Chang, F.; Fujino, Y. (Eds.) Encyclopedia of Structural Health Monitoring; John Wiley and Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Kessler, S.; Spearing, S.; Soutis, C. Damage detection in composite materials using Lamb wave methods. Smart Mater. Struct. Struct. 2002, 11, 269–278. [Google Scholar] [CrossRef]
- Inman, D.; Farrar, C.; Lopes, V., Jr.; Steffen, V., Jr. (Eds.) Damage Prognosis for Aerospace, Civil and Mechanical Systems; John Wiley and Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Farrar, C.; Doebling, S. An Overview of Modal-Based Damage Identification Methods; Technical Report; Los Alamos National Laboratory: Los Alamos, NM, USA, 1997.
- Doebling, S.; Farrar, C.; Prime, M. A Summary Review of Vibration-based Damage Identification Methods. Shock Vib. Digest 1998, 30, 91–105. [Google Scholar] [CrossRef]
- Israr, A.; Cartmell, M.; Krawczuk, M.; Ostachowicz, W.; Manoach, E.; Trendafilova, I.; Shishkina, E.; Palacz, M. On approximate anatytical solutions for vibrations in cracked plates. Appl. Mech. Mater. 2006, 5–6, 315–322. [Google Scholar] [CrossRef]
- Raja, S.; Prathima Adya, H.; Viswanath, S. Analysis of Piezoelectric Composite Beam and Plate with Multiple Delaminations. Struct. Health Monit. 2006, 5, 255–266. [Google Scholar] [CrossRef]
- Wang, J.; Qiao, P. Improved Damage Detection for Beam-type Structures using a Unigorm Load Surface. Struct. Health Monit. 2007, 6, 99–110. [Google Scholar] [CrossRef]
- Sinou, J. chapter A Review of Damage Detection and Health Monitoring of Mechanical Systems from Changes in the Measurement of Linear and Non-linear Vibrations. In Mechanical Vibrations: Measurement, Effects and Control; Nova Science Publishers: Hauppauge, NY, USA, 2009; pp. 643–702. [Google Scholar]
- Giurgiutiu, V.; Zagrai, A. Damage Detection in Thin Plates and Aerospace Structures with the Electro-Mechanical Impedance Method. Struct. Health Monit. 2005, 4, 99–118. [Google Scholar] [CrossRef]
- Dhakal, D.; Neupane, K.; Thapa, C.H.; Ramanjaneyulu, G. Different techniques of structural health monitoring. Int. J. Civ. Struct. Infrastruct. Eng. Res. Dev. 2013, 3, 55–66. [Google Scholar]
- Ludwig, R.; Lord, W. Afbeams-element formulation for the study of ultrasonic NDT systems. IEEE Trans. Ultrason. Ferroelectr. Frequency Control 1988, 35, 809–820. [Google Scholar] [CrossRef]
- Kishore, N.; Sridhar, I.; Iyengar, N. Finite element modelling of the scattering of ultrasonic waves by isolated flaws. NDT E Int. 2000, 33, 297–305. [Google Scholar] [CrossRef]
- Rizzo, P.; Lanza di Scalea, F. Feature Extraction for Defect Detection in Strands by Guided Ultrasonic Waves. Struct. Health Monit. 2006, 5, 297–308. [Google Scholar] [CrossRef]
- Broda, D.; Staszewski, W.; Martowicz, A.; Uhl, T.; Silberschmidt, V. Modelling of non-linear crack-wave interactions for damage detection based on ultrasound—A review. J. Sound Vib. 2014, 333, 1097–1118. [Google Scholar] [CrossRef]
- Su, Z.; Ye, L. Fundamental Lamb Mode-based Delamination Detection for CF/EP Composite Laminates Using Distributed Piezoelectrics. Struct. Health Monit. 2004, 3, 43–68. [Google Scholar] [CrossRef]
- Mal, A.; Ricci, F.; Banerjee, S.; Shih, F. A Conceptual Structural Health Monitoring System based on Vibration and Wave Propagation. Struct. Health Monit. 2005, 4, 283–293. [Google Scholar] [CrossRef]
- Monnier, T. Lamb Waves-based Impact Damage Monitoring of a Stiffened Aircraft Panel using Piezoelectric Transducers. J. Intell. Mater. Syst. Struct. 2006, 17, 411–421. [Google Scholar] [CrossRef]
- Lestari, W.; Qiao, P. Application of Wave Propagation Analysis for Damage Identification in Composite Laminated Beams. Compos. Mater. 2005, 39, 1967–1984. [Google Scholar] [CrossRef]
- Su, Z.; Ye, L.; Lu, Y. Guided Lamb waves for identification of damage in composite structures: A review. J. Sound Vib. 2006, 295, 753–780. [Google Scholar] [CrossRef]
- Raghavan, A.; Cesnik, C. Review of Guided-wave Structural Health Monitoring. Shock Vib. Digest 2007, 39, 91–114. [Google Scholar] [CrossRef]
- Grabowska, J.; Palacz, M.; Krawczuk, M.; Ostachowicz, W.; Trendafilova, I.; Manoach, E.; Cartmell, M. Wavelet analysis for damage identification in composite structures. Key Eng. Mater. 2007, 347, 253–258. [Google Scholar] [CrossRef]
- Grabowska, J.; Palacz, M.; Krawczuk, M. Damage identification by wavelet analysis. Mech. Syst. Signal Process. 2008, 22, 1623–1635. [Google Scholar] [CrossRef]
- Ng, C.; Veidt, M.; Lam, H. Guided wave damage characterisation in beams utilising probabilistic optimisation. Eng. Struct. 2009, 31, 2842–2850. [Google Scholar] [CrossRef]
- Joglekar, D.M.; Mitra, M. Nonlinear analysis of flexural wave propagation through 1D waveguides with a breathing crack. J. Sound Vib. 2015, 344, 242–257. [Google Scholar] [CrossRef]
- Mitra, M.; Gopalakrishnan, S. Guided wave based structural health monitoring: A review. Smart Mater. Struct. 2016, 25, 1–28. [Google Scholar] [CrossRef]
- Nazeer, N.; Ratassepp, M.; Fan, Z. Damage detection in bent plates using shear horizontal guided waves. Ultrasonics 2017, 75, 155–163. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Yan, N. Numerical Study on Guided Wave Propagation in Wood Utility Poles: Finite Element Modelling and Parametric Sensitivity Analysis. Appl. Sci. 2017, 7, 1063. [Google Scholar]
- Martinez, M.; Pant, S.; Yanishevsky, M.; Backman, D. Residual stress effects of a fatigue crack on guided Lamb waves. Smart Mater. Struct. 2017, 26, 1–16. [Google Scholar] [CrossRef]
- Kudela, P.; Radzieński, M.; Ostachovicz, W.; Yang, Z. Structural Health Monitoring system based on a concept of Lamb wave focusing by the piezoelectric array. Mech. Syst. Signal Process. 2018, 108, 21–23. [Google Scholar] [CrossRef]
- Murayama, H.; Kageyama, K.; Naruse, H.; Shimada, A.; Uzawa, K. Application of Fiber-Optic Distributed Sensors to Health Monitoring for Full-Scale Composite Structures. J. Intell. Mater. Syst. Struct. 2003, 14, 3–13. [Google Scholar] [CrossRef]
- Giurgiutiu, V.; Cuc, C. Embedded Non-destructive Evaluation for Structural Health Monitoring, Damage Detection, and Failure Prevention. Shock Vib. Digest 2005, 37, 83–105. [Google Scholar] [CrossRef]
- Montalvao, D.; Maia, N.; Ribeiro, A. A Review of Vibration-based Structural Health Monitoring with Special Emphasis on Composite Materials. Shock Vib. Digest 2006, 38(4), 295–324. [Google Scholar] [CrossRef]
- Reda Taha, M.; Noureldin, A.; Lucero, J.; Baca, T. Wavelet Transform for Structural Health Monitoring: A Compendium of Uses and Features. Struct. Health Monit. 2006, 5, 267–295. [Google Scholar] [CrossRef]
- Nichols, J.; Trickey, S.; Seaver, M.; Moniz, L. Use of Fiber-optic Strain Sensors and Holder Exponents for Detecting and Localizing Damage in an Experimental Plate Structure. J. Intell. Mater. Syst. Struct. 2007, 18, 51–67. [Google Scholar] [CrossRef]
- Ostachowicz, W.; Kudela, P.; Krawczuk, M.; Żak, A. Guided Waves in Structures for SHM: The Time-Domain Spectral Element Method; Wiley & Sons: West Sussex, UK, 2012. [Google Scholar]
- Hall, S. The effective management and use of structural health data. In Proceedings of the 2nd International Workshop on Structural Health Monitoring, Stanford, CA, USA, 8–10 September 1999; pp. 265–275. [Google Scholar]
- de Basabe, J.; Sen, M. A comparison of finite-difference and spectral-element methods for elastic wave propagation in media with a fluid-solid interface. Geophys. J. Int. 2015, 200, 278–298. [Google Scholar] [CrossRef]
- Chakraborty, A.; Gopalakrishnan, S. A spectrally formulated finite element for wave propagation analysis in functionally graded beams. Int. J. Solids Struct. 2003, 40, 2421–2448. [Google Scholar] [CrossRef]
- Chakraborty, A.; Gopalakrishnan, S. A spectral finite element model for wave propagation analysis in laminated composite plate. J. Vib. Acoust. 2006, 128, 477–488. [Google Scholar] [CrossRef]
- Palacz, M.; Krawczuk, M. Analysis of longitudinal wave propagation in a cracked rod by the spectral element method. Comput. Struct. 2002, 80, 1809–1816. [Google Scholar] [CrossRef]
- Rucka, M. Guided Wave Propagation in Structures. Modelling, Experimental Studies adn Application to Damage Detection; Politechnika Gdańska: Gdańsk, Poland, 2011. [Google Scholar]
- Żak, A.; Krawczuk, M. Certain numerical issues of wave propagation modelling in rods by the Spectral Finite Element Method. Finite Elements Anal. Des. 2011, 47, 1036–1046. [Google Scholar] [CrossRef]
- Żak, A.; Krawczuk, M. Assessment of flexural beam behaviour theories used for dynamics and wave propagation problems. J. Sound Vib. 2012, 331, 5715–5731. [Google Scholar] [CrossRef]
- Faccioli, E.; Maggio, F.; Paolucci, R.; Quarteroni, A. 2D and 3D elastic wave propagation by a pseudo-spectral domain decomposition method. J. Seismol. 1997, 1, 237–251. [Google Scholar] [CrossRef]
- Ham, S.; Bathe, K. A finite element method enriched for wave propagation problems. Comput. Struct. 2012, 94–95, 1–12. [Google Scholar] [CrossRef]
- Chakraborty, A.; Gopalakrishnan, S. A higher-order spectral element for wave propagation analysis in functionally graded materials. Acta Mech. 2004, 172, 17–43. [Google Scholar] [CrossRef]
- Joglekar, D.M.; Mitra, M. Analysis of flexural wave propagation through beams with a breathing crack using wavelet spectral finite element method. Mech Syst. Signal Process. 2016, 76–77, 576–591. [Google Scholar] [CrossRef]
- Komijani, M.; Gracie, R. An enriched finite element model for wave propagation in fractured media. Finite Elements Anal. Des. 2017, 125, 14–23. [Google Scholar] [CrossRef]
- Wang, Y.; Hao, H.; Zhu, X.; Ou, J. Spectral Element Modelling of Wave Propagation with Boundary and Structural Discontinuity Reflections. Adv. Struct. Eng. 2012, 15, 855–870. [Google Scholar] [CrossRef]
- Simonetti, F.; Cawley, P. On the nature of shear horizontal wave propagation in elastic plates coated with viscoelastic materials. Proc. R. Soc. A 2004, 204, 2197–2221. [Google Scholar] [CrossRef]
- Ajith, V.; Gopalakrishnan, S. Wave propagation in a porous composite beam: Porosity determination, location and quantification. Int. J. Solids Struct. 2013, 50, 556–569. [Google Scholar] [CrossRef]
- Ahmida, K.; Arruda, J. On the relation between complex modes and wave propagation phenomena. J. Sound Vib. 2002, 255, 663–684. [Google Scholar] [CrossRef]
- Patera, A. A Spectral Element Method for Fluid Dynamics: Laminar Flow in a Channel Expansion. J. Comput. Phys. 1984, 54, 468–488. [Google Scholar] [CrossRef]
- Bottero, A.; Cristini, P.; Komatitsch, D. An axisymmetric time-domain spectral-element method for full-wave simulations: Application to ocean acoustics. J. Acoust. Soc. Am. 2016, 140, 3520–3530. [Google Scholar] [CrossRef]
- Doliński, L.; Krawczuk, M.; Palacz, M.; Żak, A. Spectral finite element method in condition monitoring and damage detection. In Proceedings of the 8th European Workshop on Structural Health Monitoring, EWSHM 2016, Bilbao, Spain, 5–8 July 2016; Volume 2, pp. 1172–1181. [Google Scholar]
- Komatitsch, D.; Vilotte, J.; Vai, R.; Castillo-Covarrubias, J.; Sanchez-Sesma, F. The spectral element method for elastic wave equations-application to 2-D and 3-D seismic problems. Int. J. Numer. Methods Eng. 1999, 45, 1139–1164. [Google Scholar] [CrossRef]
- Ha, S.; Chang, F.K. Optimizing a spectral element for modeling PZT-induced Lamb wave propagation in thin plates. Smart Mater. Struct. 2010, 19, 015015. [Google Scholar] [CrossRef]
- Rucka, M. Modelling of in-plane wave propagation in a plate using spectral element method and Kane-Mindlin theory with application to damage detection. Arch. Appl. Mech. 2011, 81, 1877–1888. [Google Scholar] [CrossRef]
- Żak, A.; Krawczuk, M. A higher order transversely deformable shell-type spectral finite element for dynamic analysis of isotropic structures. Finite Elements Anal. Des. 2018, 142, 17–29. [Google Scholar] [CrossRef]
- Palacz, M. Spectral Methods for Modelling of Wave Propagation in Structures in Terms of Damage Detection—A Review. Appl. Sci. 2018, 8, 1124. [Google Scholar] [CrossRef]
- Boyd, J. Chebyshew and Fourier Spectral Methods; Dover Publications, Inc.: Miniola, NY, USA, 2000. [Google Scholar]
- Żak, A.; Krawczuk, M.; Palacz, M. Periodic Properties of 1D FE Discrete Models in High Frequency Dynamics. Math. Probl. Eng. 2016, 2016, 1–15. [Google Scholar] [CrossRef][Green Version]
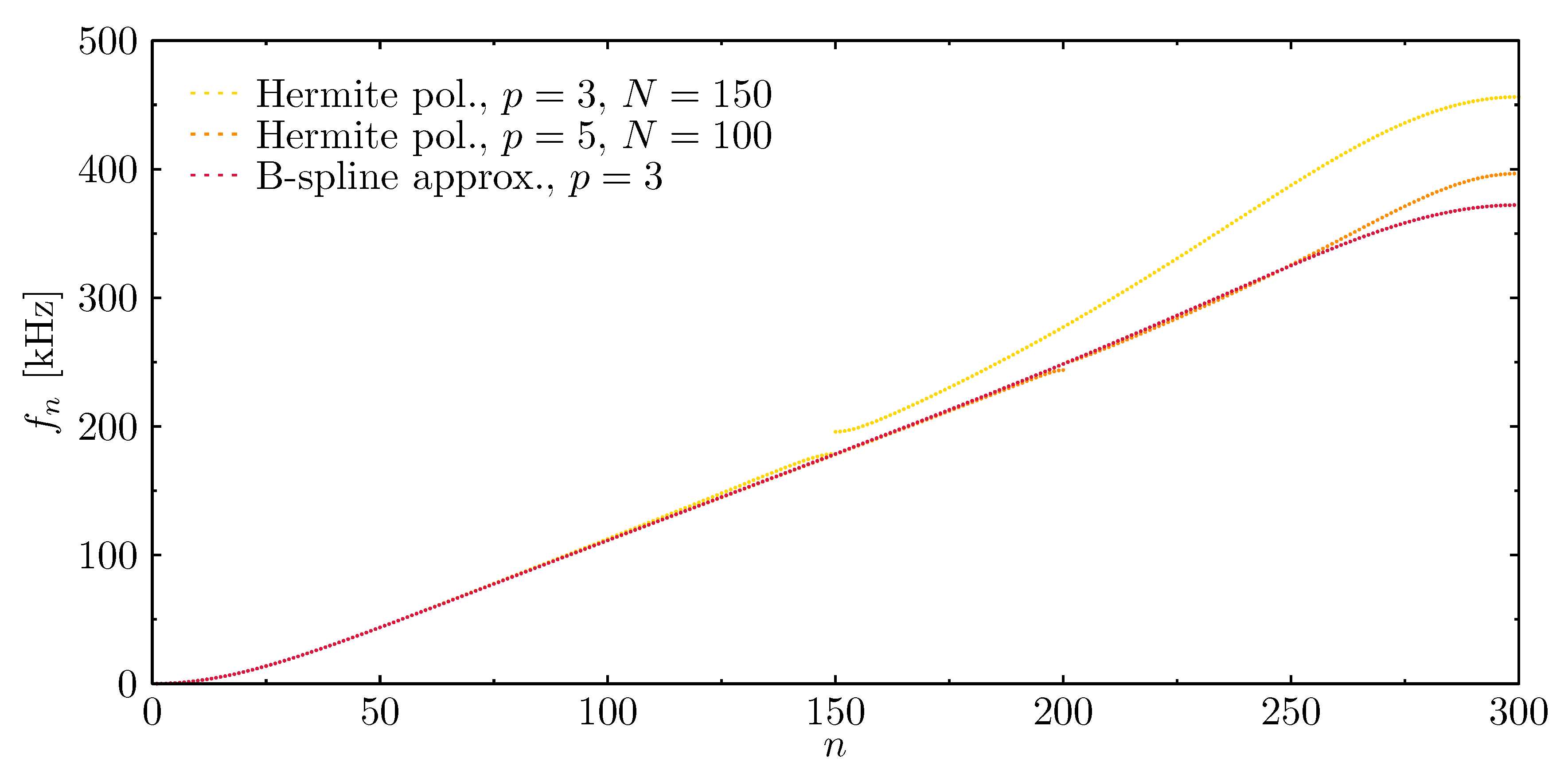
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palacz, M.; Żak, A.; Krawczuk, M. FEM-Based Wave Propagation Modelling for SHM: Certain Numerical Issues in 1D Structures. Materials 2020, 13, 2051. https://doi.org/10.3390/ma13092051
Palacz M, Żak A, Krawczuk M. FEM-Based Wave Propagation Modelling for SHM: Certain Numerical Issues in 1D Structures. Materials. 2020; 13(9):2051. https://doi.org/10.3390/ma13092051
Chicago/Turabian StylePalacz, Magdalena, Arkadiusz Żak, and Marek Krawczuk. 2020. "FEM-Based Wave Propagation Modelling for SHM: Certain Numerical Issues in 1D Structures" Materials 13, no. 9: 2051. https://doi.org/10.3390/ma13092051
APA StylePalacz, M., Żak, A., & Krawczuk, M. (2020). FEM-Based Wave Propagation Modelling for SHM: Certain Numerical Issues in 1D Structures. Materials, 13(9), 2051. https://doi.org/10.3390/ma13092051






