Numerical Validation of a Population Balance Model Describing Cement Paste Rheology
Abstract
1. Introduction
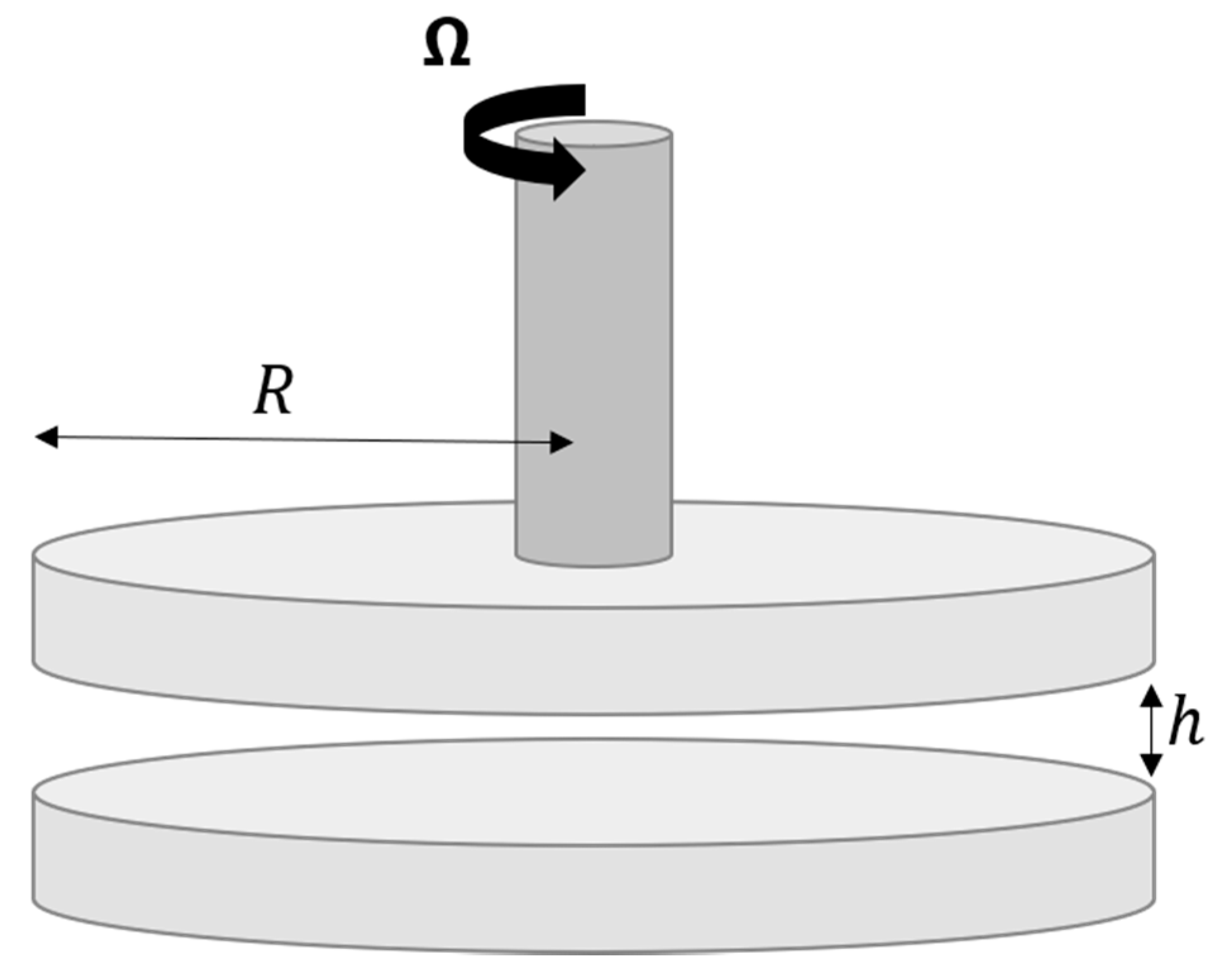
2. Model
3. Results and Discussion
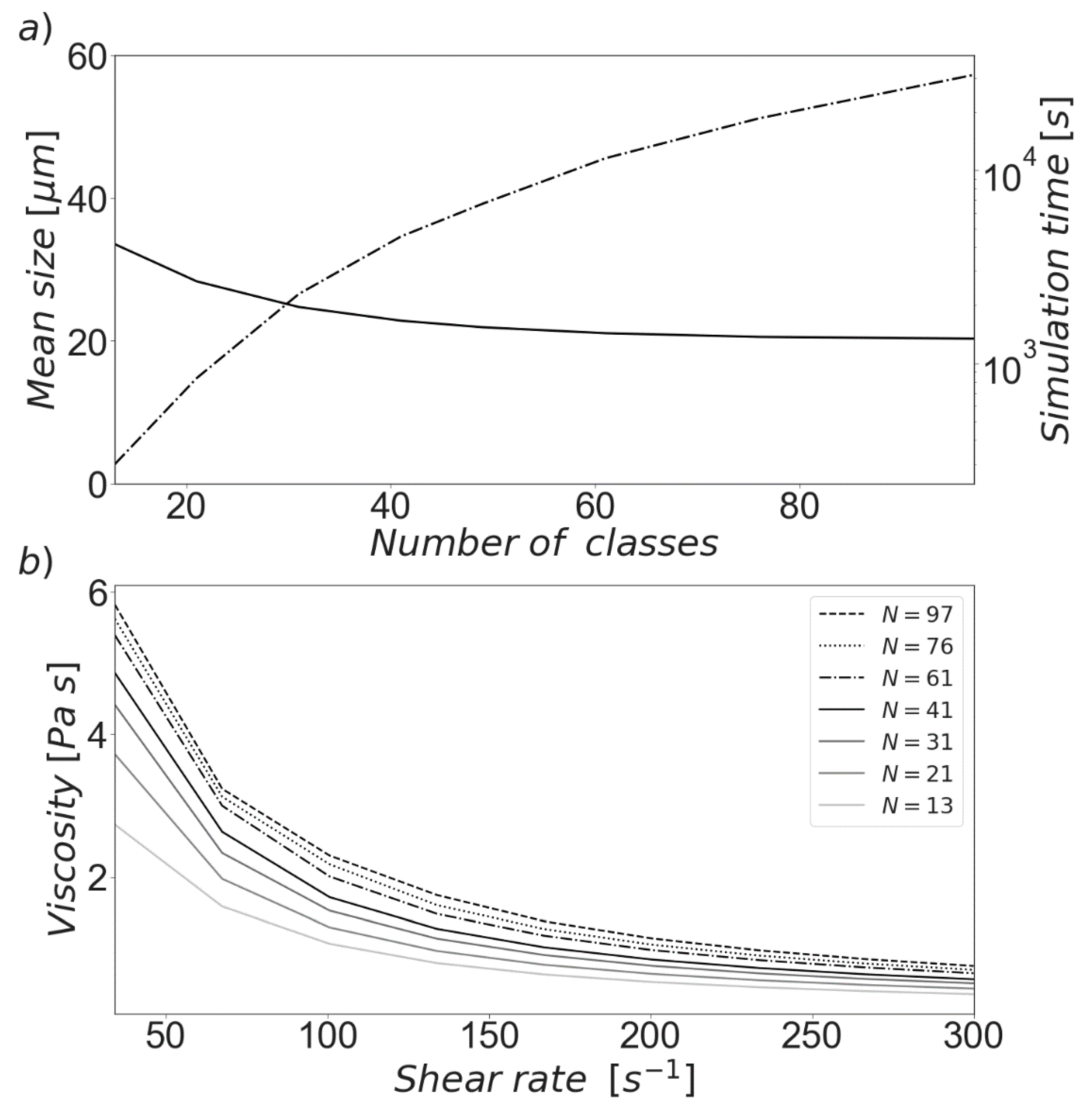
3.1. Grid Independence
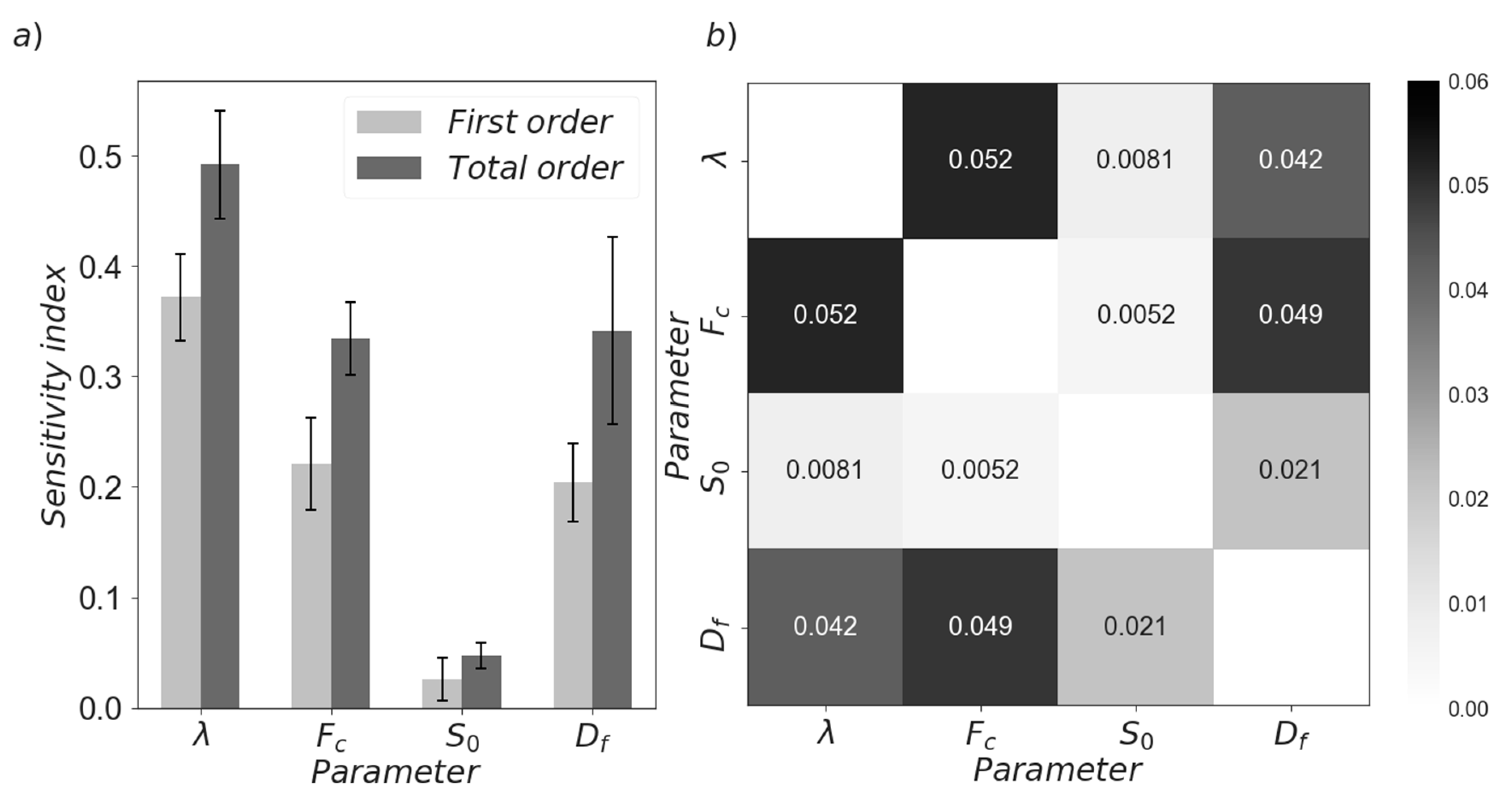
3.2. Sensitivity Analysis
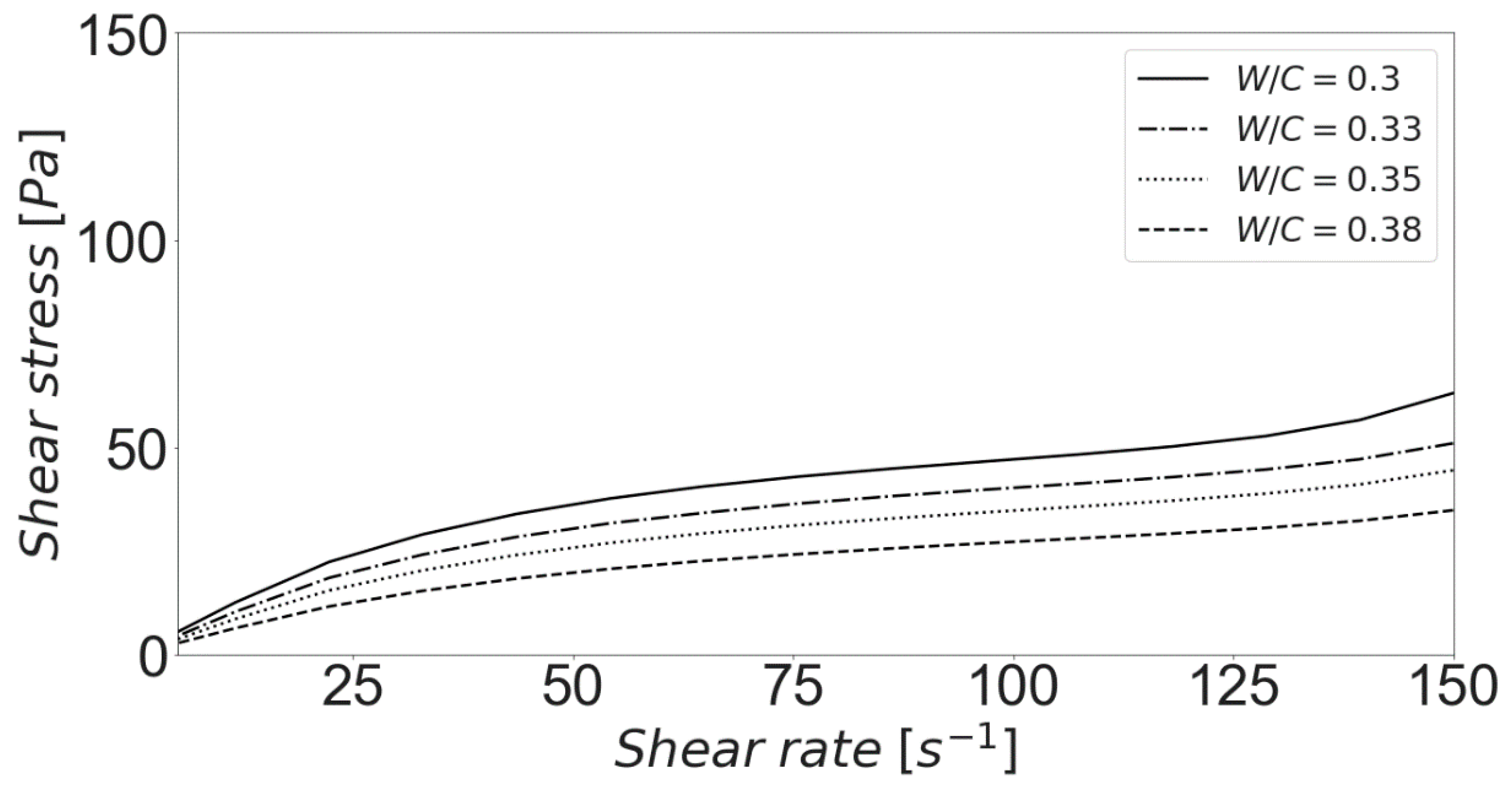
3.3. Predicted Rheological Responses
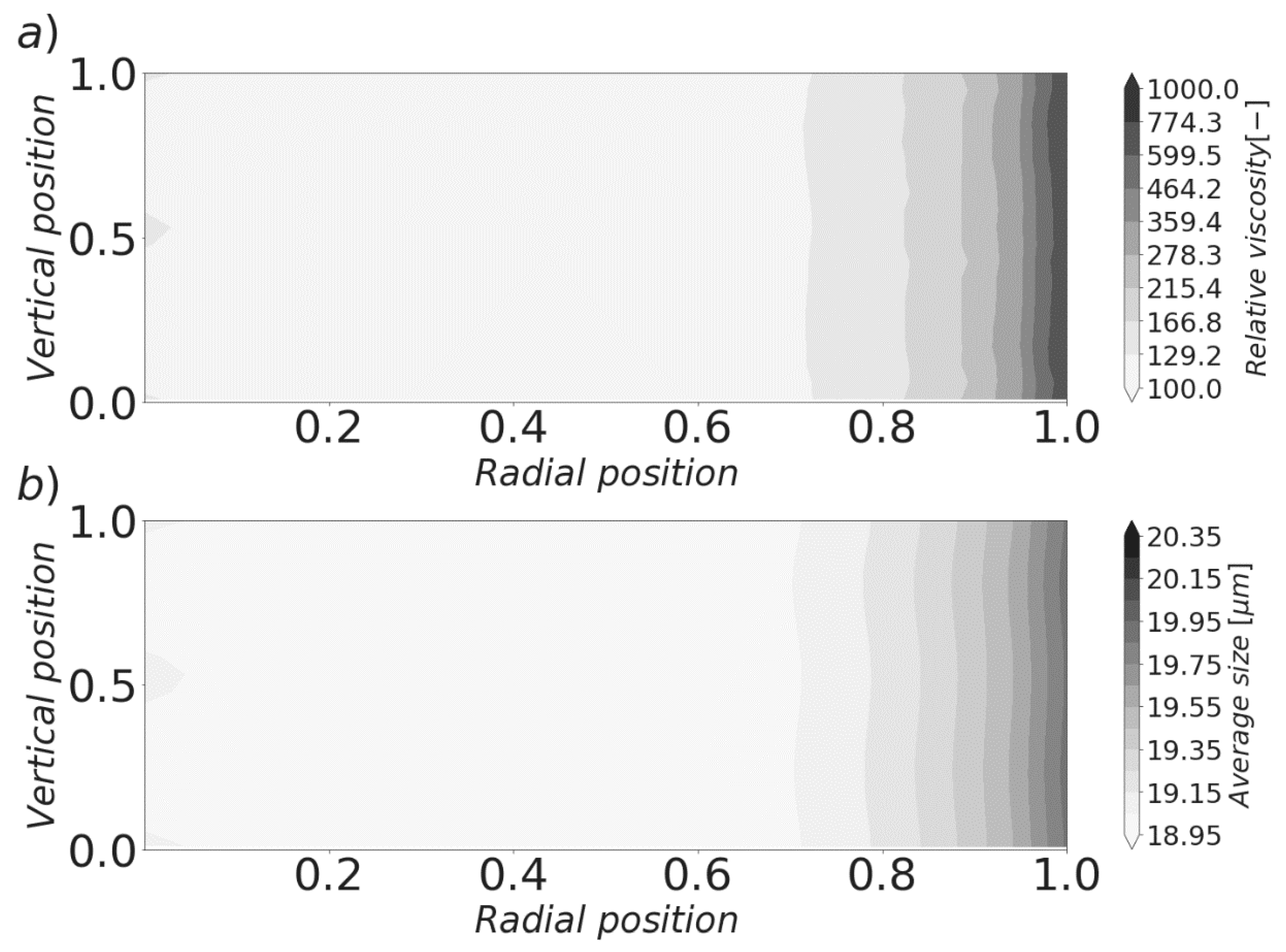
3.4. Spatially Resolved Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Flatt, R.J.; Roussel, N.; Cheeseman, C.R. Concrete: An eco material that needs to be improved. J. Eur. Ceram. Soc. 2012, 32, 2787–2798. [Google Scholar] [CrossRef]
- Roussel, N.; Lemaître, A.; Flatt, R.J.; Coussot, P. Steady state flow of cement suspensions: A micromechanical state of the art. Cem. Concr. Res. 2010, 40, 77–84. [Google Scholar] [CrossRef]
- Chidiac, S.E.; Mahmoodzadeh, F. Plastic viscosity of fresh concrete—A critical review of predictions methods. Cem. Concr. Compos. 2009, 31, 535–544. [Google Scholar] [CrossRef]
- Flatt, R.J.; Bowen, P. Electrostatic repulsion between particles in cement suspensions: Domain of validity of linearized Poisson-Boltzmann equation for nonideal electrolytes. Cem. Concr. Res. 2003, 33, 781–791. [Google Scholar] [CrossRef]
- Toutpu, Z.; Roussel, N. Multi Scale Experimental Study of Concrete Rheology: From Water Scale to Gravel Scale. Mater. Struct. Constr. 2006, 39, 189–199. [Google Scholar] [CrossRef]
- Ferraris, C.F.; de Larrard, F. Testing and Modelling of Fresh Concrete Rheology; Technical Report No. 6094; National Institute of Standards and Technology (NIST): Gaithersburg, MD, USA, 1998; p. 61.
- Flatt, R.J.; Martys, N.; Bergström, L. The rheology of cementitious materials. MRS Bull. 2004, 29, 314–318. [Google Scholar] [CrossRef]
- Flatt, R.J. Towards a prediction of superplasticized concrete rheology. Mater. Struct. Constr. 2004, 37, 289–300. [Google Scholar] [CrossRef]
- Farizhandi, A.A.K.; Zhao, H.; Lau, R. Modeling the change in particle size distribution in a gas-solid fluidized bed due to particle attrition using a hybrid artificial neural network-genetic algorithm approach. Chem. Eng. Sci. 2016, 155, 210–220. [Google Scholar] [CrossRef]
- Jiao, D.; Shi, C.; Yuan, Q.; An, X.; Liu, Y.; Li, H. Effect of constituents on rheological properties of fresh concrete-A review. Cem. Concr. Compos. 2017, 83, 146–159. [Google Scholar] [CrossRef]
- Krieger, I.; Dougherty, T. A Mechanism for Non-Newtonian Flow in Suspensions of Rigid Spheres. Trans. Soc. Rheol. 1937, 3, 137–152. [Google Scholar] [CrossRef]
- Vikan, H.; Justnes, H.; Winnefeld, F.; Figi, R. Correlating cement characteristics with rheology of paste. Cem. Concr. Res. 2007, 37, 1502–1511. [Google Scholar] [CrossRef]
- Zhou, Z.; Solomon, M.J.; Scales, P.J.; Boger, D.V. The yield stress of concentrated flocculated suspensions of size distributed particles. J. Rheol. 2002, 43, 651–671. [Google Scholar] [CrossRef]
- Mwasame, P.M.; Wagner, N.J.; Beris, A.N. Modeling the effects of polydispersity on the viscosity of noncolloidal hard sphere suspensions. J. Rheol. 2016, 60, 225–240. [Google Scholar] [CrossRef]
- Pednekar, S.; Chun, J.; Morris, J. Bidisperse and polydisperse suspension rheology at large solid fraction. J. Rheol. 2018, 62, 513–526. [Google Scholar] [CrossRef]
- Bentz, D.P.; Ferraris, C.F.; Galler, M.A.; Hansen, A.S.; Guynn, J.M. Influence of particle size distributions on yield stress and viscosity of cement-fly ash pastes. Cem. Concr. Res. 2012, 42, 404–409. [Google Scholar] [CrossRef]
- Barthelmes, G.; Pratsinis, S.E.; Buggisch, H. Particle size distributions and viscosity of suspensions undergoing shear-induced coagulation and fragmentation. Chem. Eng. Sci. 2003, 58, 2893–2902. [Google Scholar] [CrossRef]
- Mohtaschemi, M.; Puisto, A.; Illa, X.; Alava, M.J. Rheology dynamics of aggregating colloidal suspensions. Soft Matter 2014, 10, 2971. [Google Scholar] [CrossRef]
- Farr, R.S. Simple heuristic for the viscosity of polydisperse hard spheres. J. Chem. Phys. 2014, 141, 1–9. [Google Scholar] [CrossRef]
- Mendoza, C.I. A simple semiempirical model for the effective viscosity of multicomponent suspensions. Rheol. Acta 2017, 56, 487–499. [Google Scholar] [CrossRef]
- Desmond, K.W.; Weeks, E.R. Influence of Particle Size Distribution on Random Close Packing of Spheres. Phys. Rev. E 2014, 90, 022204. [Google Scholar] [CrossRef]
- Quemada, D. Rheological modelling of complex fluids. I. The concept of effective volume fraction revisited. Eur. Phys. J. Appl. Phys. 1998, 1, 119–127. [Google Scholar] [CrossRef]
- Chougnet, A.; Audibert, A.; Moan, M. Linear and non-linear rheological behaviour of cement and silica suspensions. Effect of polymer addition. Rheol. Acta 2007, 46, 793–802. [Google Scholar] [CrossRef]
- Chougnet, A.; Palermo, T.; Audibert, A.; Moan, M. Rheological behaviour of cement and silica suspensions: Particle aggregation modelling. Cem. Concr. Res. 2008, 38, 1297–1301. [Google Scholar] [CrossRef]
- Ramkrishna, D.; Singh, M.R. Population Balance Modeling: Current Status and Future Prospects. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 123–146. [Google Scholar] [CrossRef]
- Puisto, A.; Illa, X.; Mohtaschemi, M.; Alava, M.J. Modeling the viscosity and aggregation of suspensions of highly anisotropic nanoparticles. Eur. Phys. J. E 2012, 35, 1–7. [Google Scholar] [CrossRef]
- Farris, R.J. Prediction of the Viscosity of Multimodal Suspensions from Unimodal Viscosity Data. Trans. Soc. Rheol. 1968, 12, 281–301. [Google Scholar] [CrossRef]
- Ramkrishna, D. Population Balances: Theory and Applications to Particulate Systems in Engineering; Academic Press: Cambridge, MA, USA, 2000; ISBN 0125769709. [Google Scholar]
- Yeoh, G.H.; Cheung, C.; Tu, J. Multiphase Flow Analysis Using Population Balance Modeling; Elsevier: Amsterdam, The Netherlands, 2014; ISBN 9780080982298. [Google Scholar]
- Kumar, J.; Peglow, M.; Warnecke, G.; Heinrich, S. An efficient numerical technique for solving population balance equation involving aggregation, breakage, growth and nucleation. Powder Technol. 2008, 182, 81–104. [Google Scholar] [CrossRef]
- Giri, A.K.; Hausenblas, E. Convergence analysis of sectional methods for solving aggregation population balance equations: The fixed pivot technique. Nonlinear Anal. Real World Appl. 2013, 14, 2068–2090. [Google Scholar] [CrossRef]
- Kumar, J.; Peglow, M.; Warnecke, G.; Heinrich, S.; Mörl, L. Improved accuracy and convergence of discretized population balance for aggregation: The cell average technique. Chem. Eng. Sci. 2006, 61, 3327–3342. [Google Scholar] [CrossRef]
- Somasundaran, P.; Runkana, V. Modeling flocculation of colloidal mineral suspensions using population balances. Int. J. Miner. Process. 2003, 72, 33–55. [Google Scholar] [CrossRef]
- Jeldres, R.I.; Concha, F.; Toledo, P.G. Population balance modelling of particle flocculation with attention to aggregate restructuring and permeability. Adv. Colloid Interface Sci. 2015, 224, 62–71. [Google Scholar] [CrossRef] [PubMed]
- Jeldres, R.; Fawell, O.; Florio, B. Population balance modelling to describe the particle aggregation process: A review. Powder Technol. 2018, 326, 190–207. [Google Scholar] [CrossRef]
- Meyer, C.J.; Deglon, D.A. Particle collision modeling—A review. Miner. Eng. 2011, 24, 719–730. [Google Scholar] [CrossRef]
- Roussel, N.; Ovarlez, G.; Garrault, S.; Brumaud, C. The origins of thixotropy of fresh cement pastes. Cem. Concr. Res. 2012, 42, 148–157. [Google Scholar] [CrossRef]
- Wheeler, J.; Chatterji, S. Settling of Particles in Fresh Cement Pastes. J. Am. Ceram. Soc. 1972, 55, 461–464. [Google Scholar] [CrossRef]
- Chatterji, S. On the properties of freshly made Portland cement paste. Part 2. sedimentation and strength of flocculation. Cem. Concr. Res. 1988, 18, 615–620. [Google Scholar] [CrossRef]
- Smoluchowski, M.V. Versuch einer mathematischen Theorie der Koagulationskinetik kolloider Lösungen. Zeitschrift Phys. Chem. 1917, 92, 129–168. [Google Scholar] [CrossRef]
- Feys, D.; Cepuritis, R.; Jacobsen, S.; Lesage, K.; Secrieru, E.; Yahia, A. Measuring Rheological Properties of Cement Pastes: Most common Techniques, Procedures and Challenges. RILEM Tech. Lett. 2017, 2, 129–135. [Google Scholar] [CrossRef]
- Ferron, R.D.; Shah, S.; Fuente, E.; Negro, C. Aggregation and breakage kinetics of fresh cement paste. Cem. Concr. Res. 2013, 50, 1–10. [Google Scholar] [CrossRef]
- Yeung, A.K.C.; Pelton, R. Micromechanics: A New Approach to Studying the Strength and Breakup of Flocs. J. Colloid Interface Sci. 1996, 184, 579–585. [Google Scholar] [CrossRef]
- Heath, A.; Bahri, P.; Fawell, P.; Farrow, J. Polymer Flocculation of Calcite: Population Balance Model. AIChE J. 2006, 52, 1641–1653. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Fractal Geometry of Nature; W. H. Freeman and Company: New York, NY, USA, 1982. [Google Scholar]
- Flesch, J.C.; Spicer, P.T.; Pratsinis, S.E. Laminar and Turbulent Shear-Induced Flocculation of Fractal Aggregates. AiChE J. 1999, 45, 1114–1123. [Google Scholar] [CrossRef]
- Yang, X.; Wang, F.; Yang, X.; Zhou, Q. Fractal dimension in concrete and implementation for meso-simulation. Constr. Build. Mater. 2017, 143, 464–472. [Google Scholar] [CrossRef]
- Quemada, D. Rheology of concentrated disperse systems and minimum energy dissipation principle. Rheol. Acta 1977, 16, 82–94. [Google Scholar] [CrossRef]
- Brown, P.N.; Byrne, G.D.; Hindmarsh, A.C. VODE: A Variable-Coefficient ODE Solver. SIAM J. Sci. Stat. Comput. 1989, 10, 1038–1051. [Google Scholar] [CrossRef]
- Macosko, C. Rheology: Principles, Measurements and Applications; Wiley: New York, NY, USA, 1994; ISBN 1560815795. [Google Scholar]
- Homma, T.; Saltelli, A. Importance measures in global sensitivity analysis of nonlinear models. Reliab. Eng. Syst. Saf. 1996, 52, 1–17. [Google Scholar] [CrossRef]
- Zhang, X.; Trame, M.N.; Lesko, L.J.; Schmidt, S. Sobol Sensitivity Analysis: A Tool to Guide the Development and Evaluation of Systems Pharmacology Models. CPT Pharmacomet. Syst. Pharmacol. 2015, 4, 69–79. [Google Scholar] [CrossRef]
- Flatt, R.J. Dispersion forces in cement suspensions. Cem. Concr. Res. 2004, 34, 399–408. [Google Scholar] [CrossRef]
- Derjaguin, B.; Landau, L. Theory of the stability of strongly charged lyophobic soils and of the adhesion of strongly charged particles in solutions of electrolytes. Prog. Surf. Sci. 1993, 43, 30–59. [Google Scholar] [CrossRef]
- Selomulya, C.; Bushell, G.; Amal, R.; Waite, T.D. Understanding the role of restructuring in flocculation: The application of a population balance model. Chem. Eng. Sci. 2003, 58, 327–338. [Google Scholar] [CrossRef]
- De Gennes, P.G. Polymers at an interface; a simplified view. Adv. Colloid Interface Sci. 1987, 27, 189–209. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S. Numerical Optimization; Springer Series in Operations Research and Financial Engineering; Springer: New York, NY, USA, 2006; ISBN 978-0-387-30303-1. [Google Scholar]
- Jiang, Q.; Logan, B.E. Fractal Dimensions of Aggregates Determined from Steady-State Size Distributions. Environ. Sci. Technol. 1991, 25, 2031–2038. [Google Scholar] [CrossRef]
- Kaleta, A.; Grzeszczyk, S. The Influence of Chosen Factors on the Rheological Properties of Cement Paste. Procedia Eng. 2015, 108, 568–574. [Google Scholar] [CrossRef][Green Version]
- Jones, T.E.R.; Taylor, S.; Tattersall, G.H. A mathematical model relating the flow curve of a cement paste to its water/cement ratio. Mag. Concr. Res. 1978, 30, 229–230. [Google Scholar] [CrossRef]
- De Larrard, F.; Ferraris, C.F.; Sedran, T. Fresh concrete: A Herschel-Bulkley material. Mater. Struct. 1998, 31, 494–498. [Google Scholar] [CrossRef]
- Yahia, A. Shear-thickening behavior of high-performance cement grouts—Influencing mix-design parameters. Cem. Concr. Res. 2011, 41, 230–235. [Google Scholar] [CrossRef]
- Savins, J.G.; Metzner, A.B. Radial (secondary) flows in rheogoniometric devices. Rheol. Acta 1970, 9, 365–373. [Google Scholar] [CrossRef]
- McCoy, D.H.; Denn, M.M. Secondary flow in a parallel-disk viscometer. Rheol. Acta 1971, 10, 408–411. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Initial condition | Uniform polydispersion |
| Size range [µm] | 1–100 |
| Total volume [m3] | 1 × 10−5 |
| Type of grid | Uniform |
| Number of size classes | 13–97 |
| Simulation type | Shear rate sweep (30–300 s−1) |
| Simulation hardware | Intel i7 6700k 4.0 GHz, 16GB RAM |
| Parameter | Value |
|---|---|
| Initial condition | Experimental [42] |
| Size range [µm] | 1–100 |
| Total volume [m3] | 1 × 10−5 |
| Type of grid | Non-uniform |
| Studied parameters | Aggregation efficiency (λ), effective bound force (Fc), breakage efficiency (S0), fractal dimension (Df) |
| Studied output | Viscosity (η) |
| Simulation type | Constant shear rate (100 s−1) |
| Number of samples | 20000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gallo-Molina, J.P.; Lesage, K.; Nopens, I. Numerical Validation of a Population Balance Model Describing Cement Paste Rheology. Materials 2020, 13, 1249. https://doi.org/10.3390/ma13051249
Gallo-Molina JP, Lesage K, Nopens I. Numerical Validation of a Population Balance Model Describing Cement Paste Rheology. Materials. 2020; 13(5):1249. https://doi.org/10.3390/ma13051249
Chicago/Turabian StyleGallo-Molina, Juan Pablo, Karel Lesage, and Ingmar Nopens. 2020. "Numerical Validation of a Population Balance Model Describing Cement Paste Rheology" Materials 13, no. 5: 1249. https://doi.org/10.3390/ma13051249
APA StyleGallo-Molina, J. P., Lesage, K., & Nopens, I. (2020). Numerical Validation of a Population Balance Model Describing Cement Paste Rheology. Materials, 13(5), 1249. https://doi.org/10.3390/ma13051249







