Experimental Study on Shear Capacity of High Strength Reinforcement Concrete Deep Beams with Small Shear Span–Depth Ratio
Abstract
1. Introduction
2. Test Overview
2.1. Experiment Material
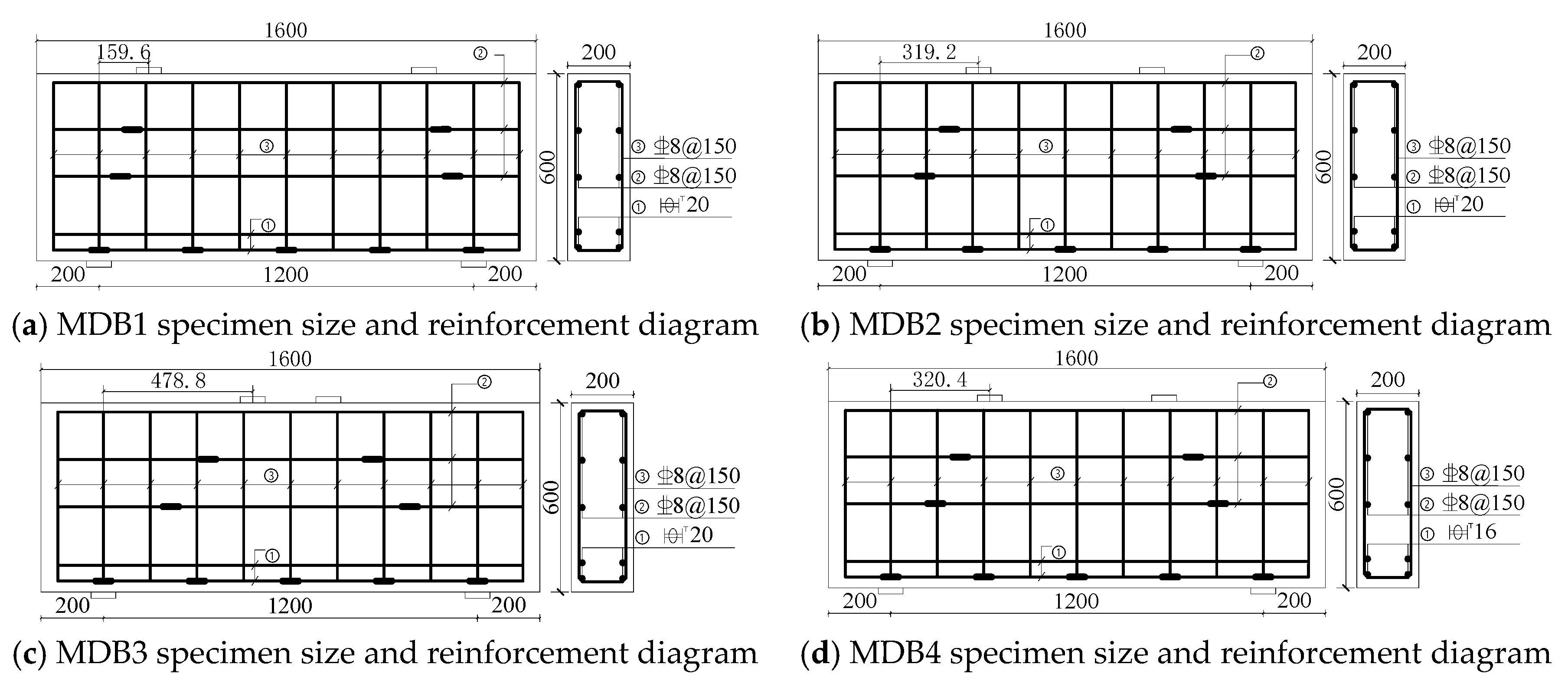
2.2. Specimen Design
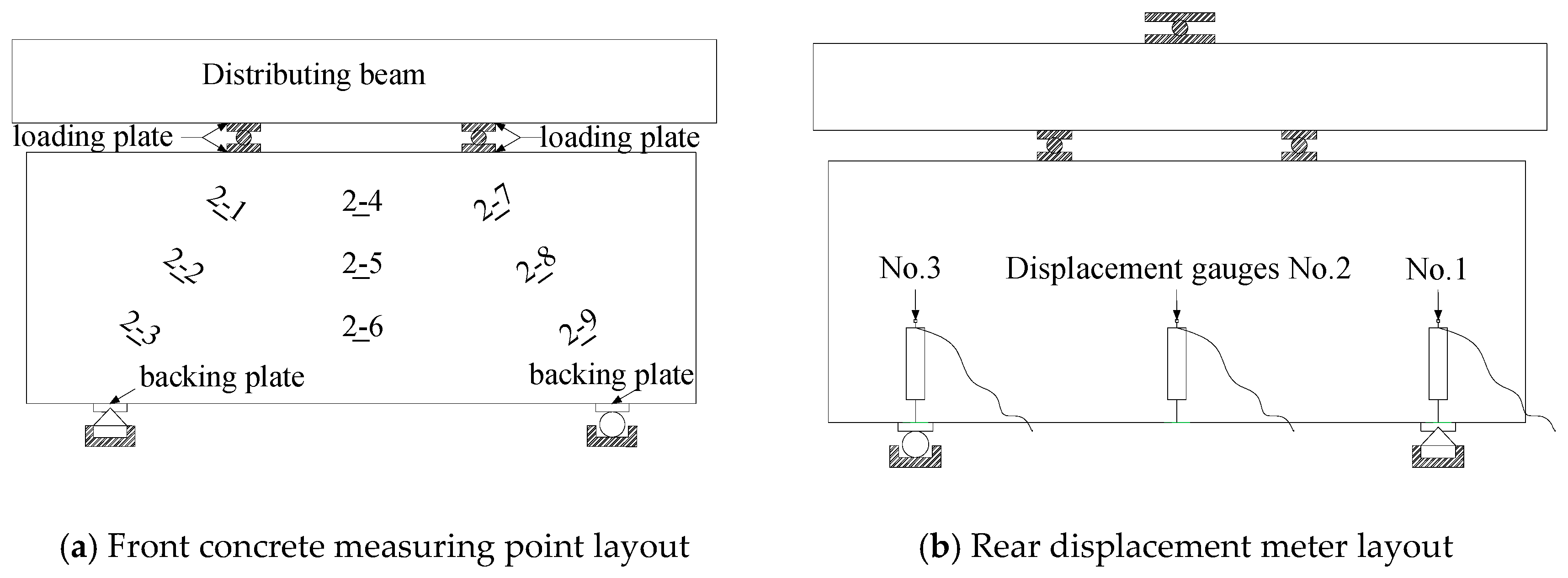
2.3. Test Setup and Instrumentation
3. Behavior of Test Specimens and Failure Modes
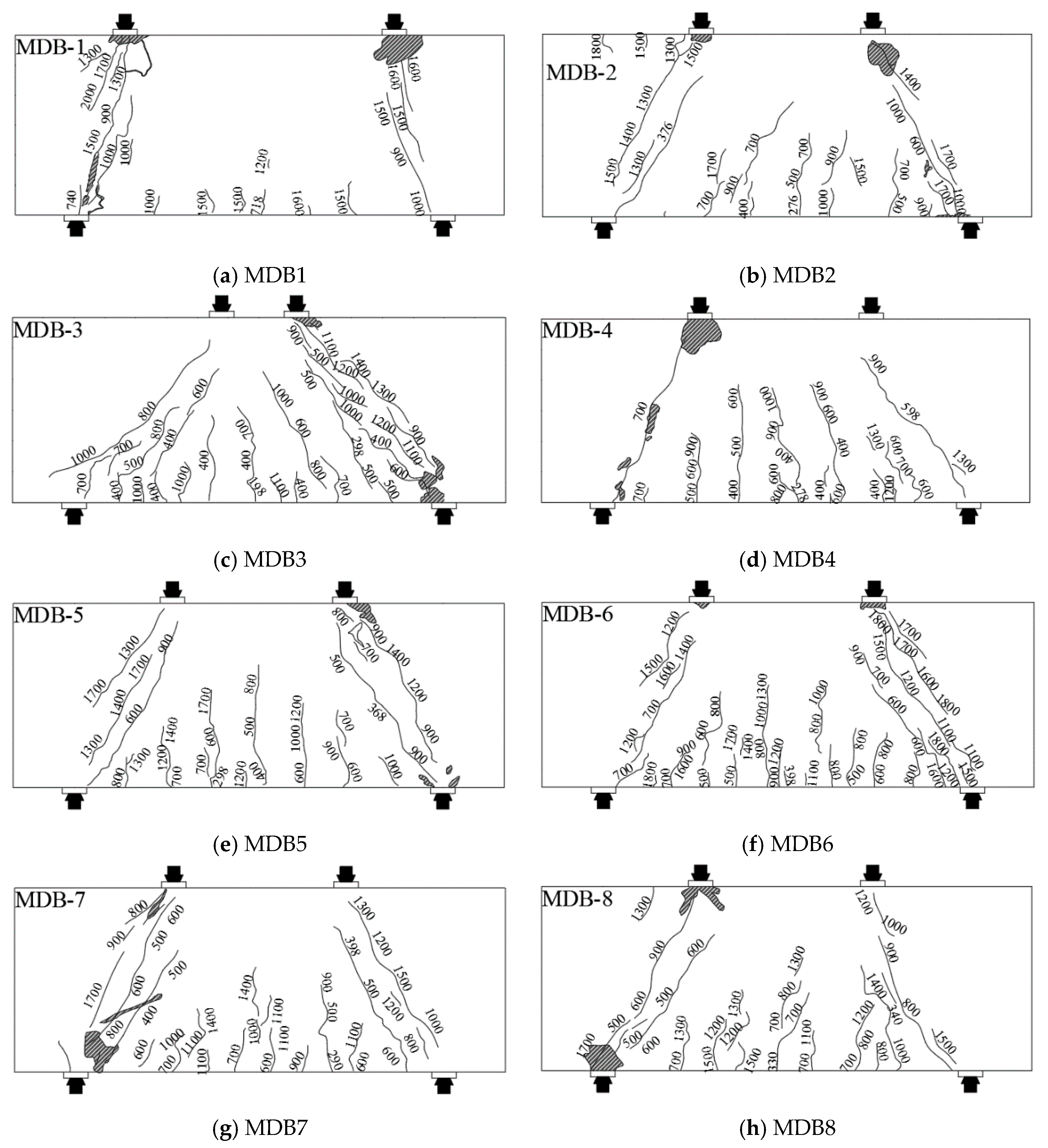
3.1. Failure Modes
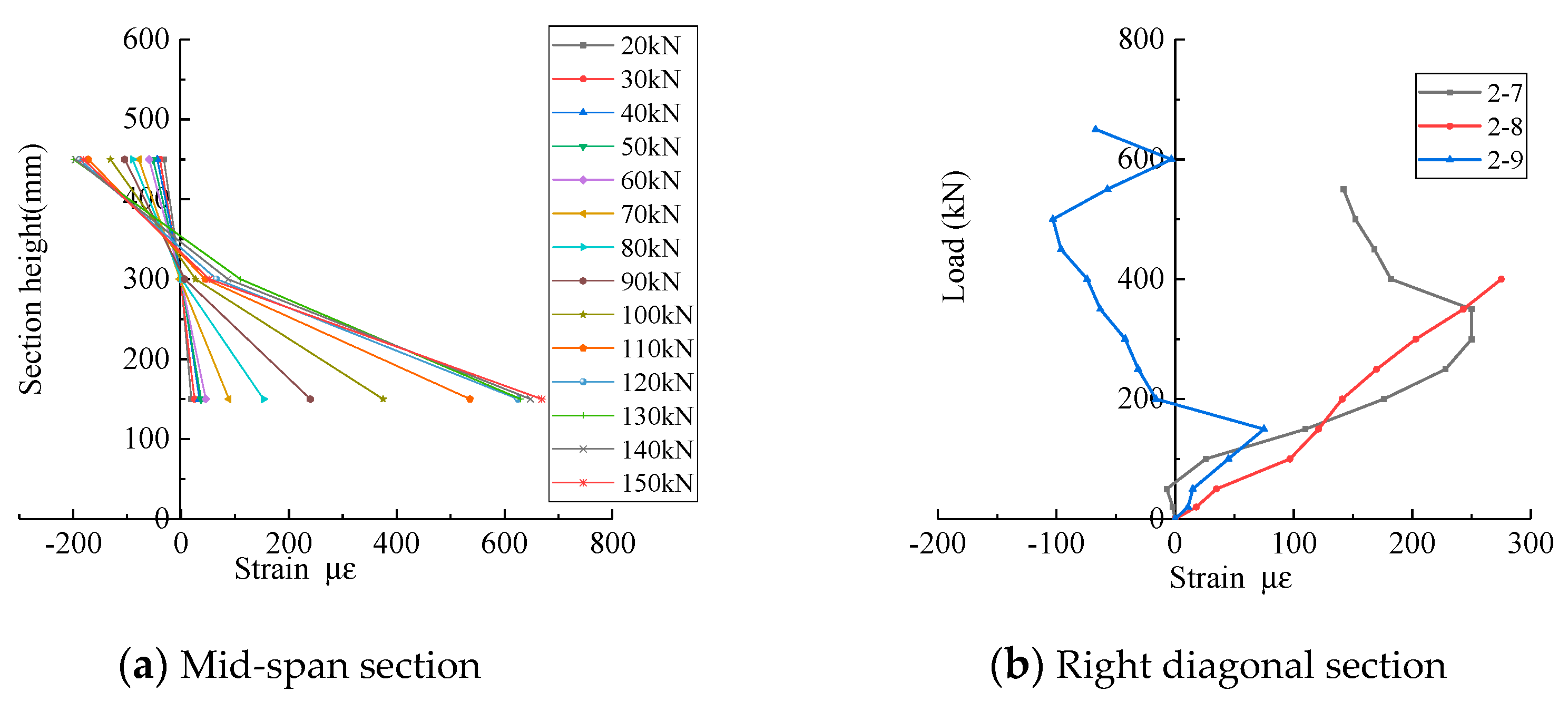
3.2. Failure Process of Test Specimens
3.3. Influencing Factor Analysis
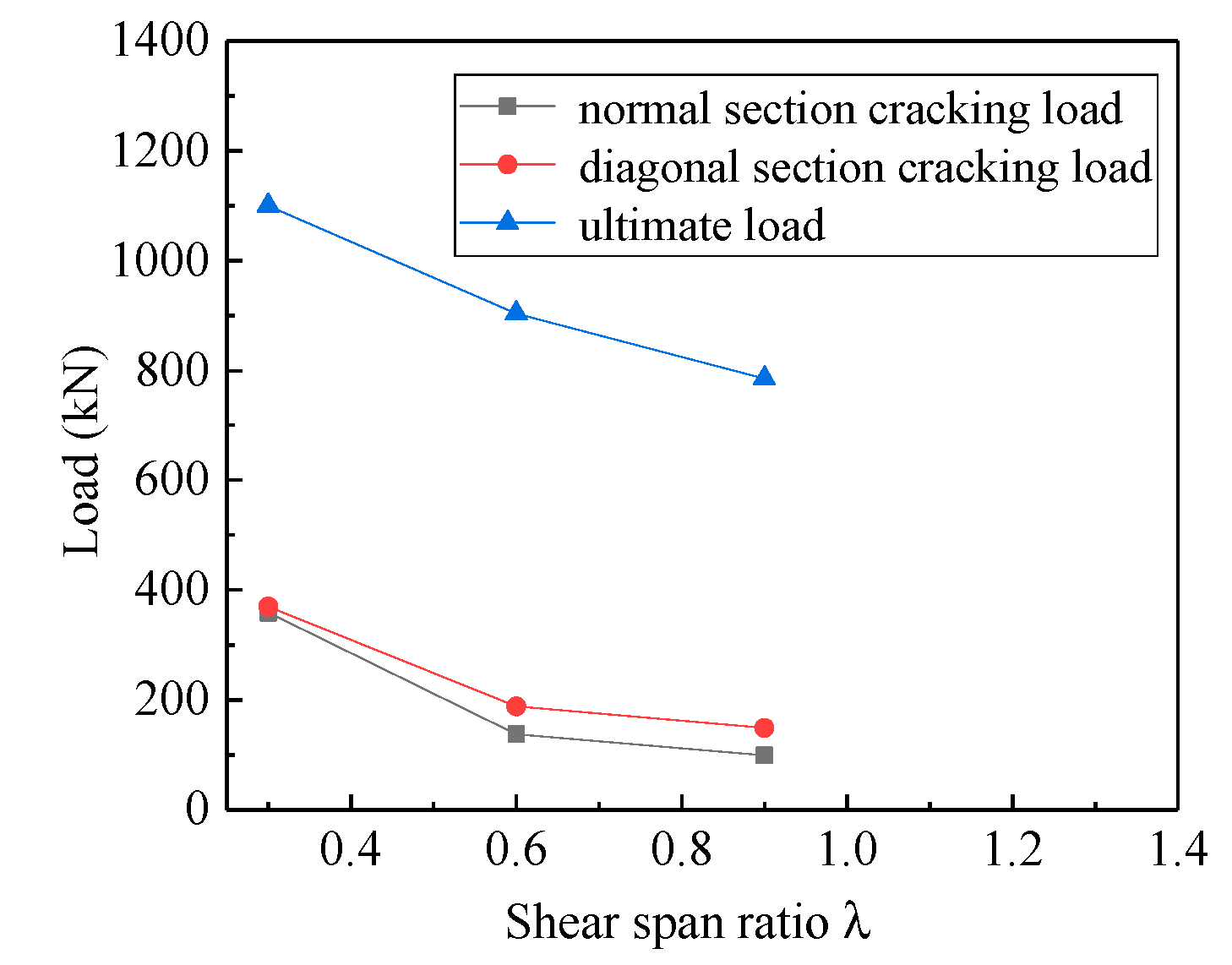
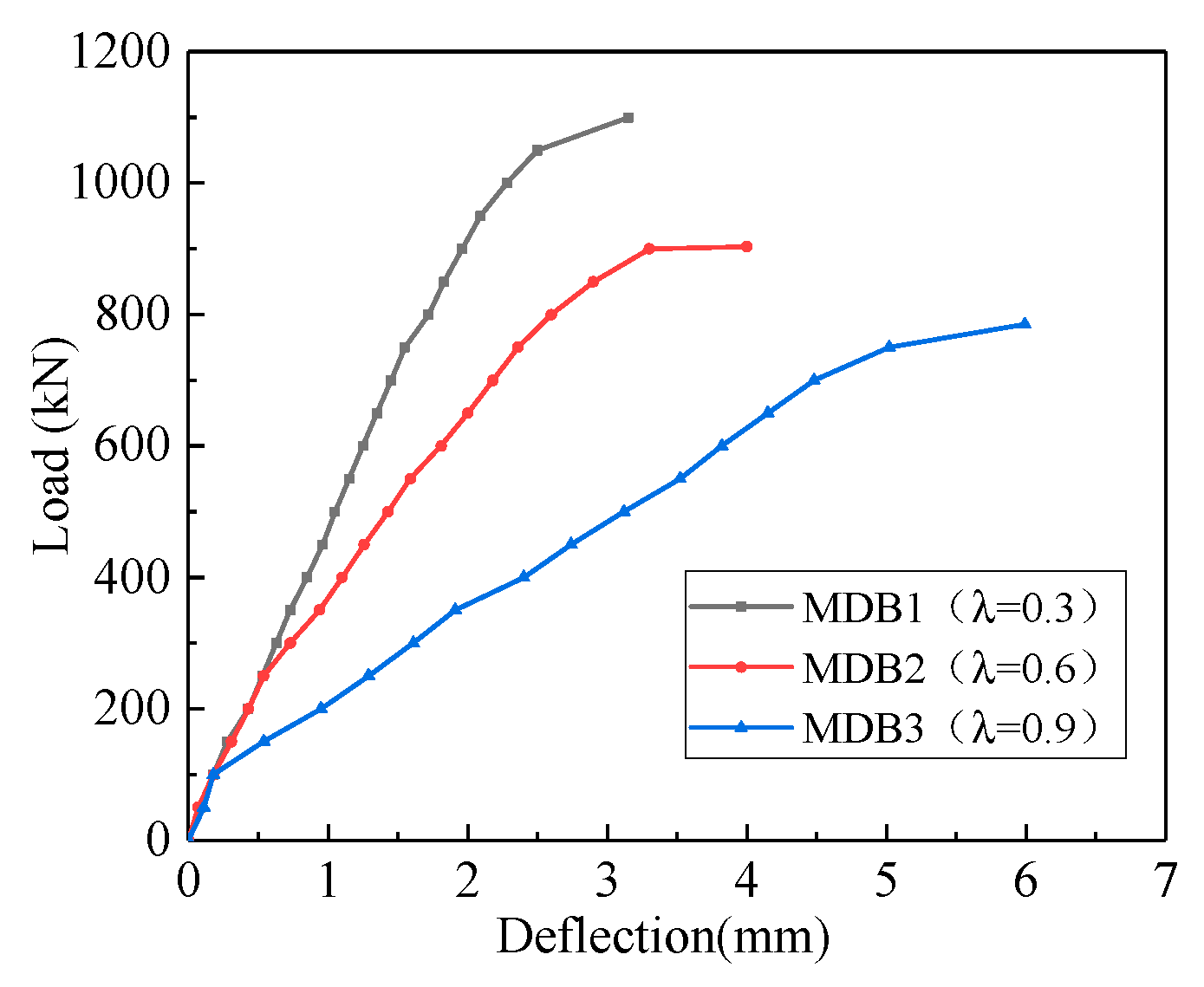
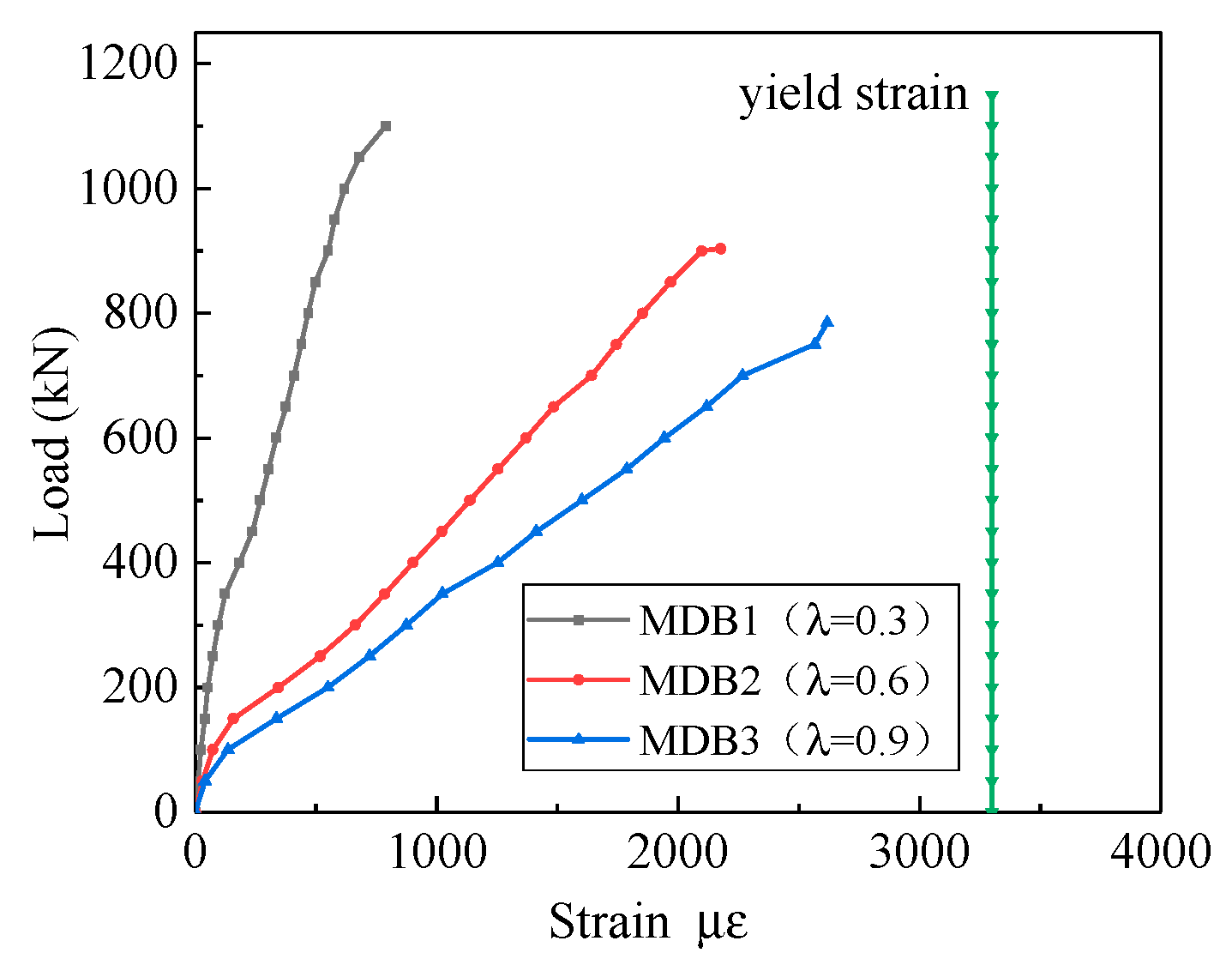
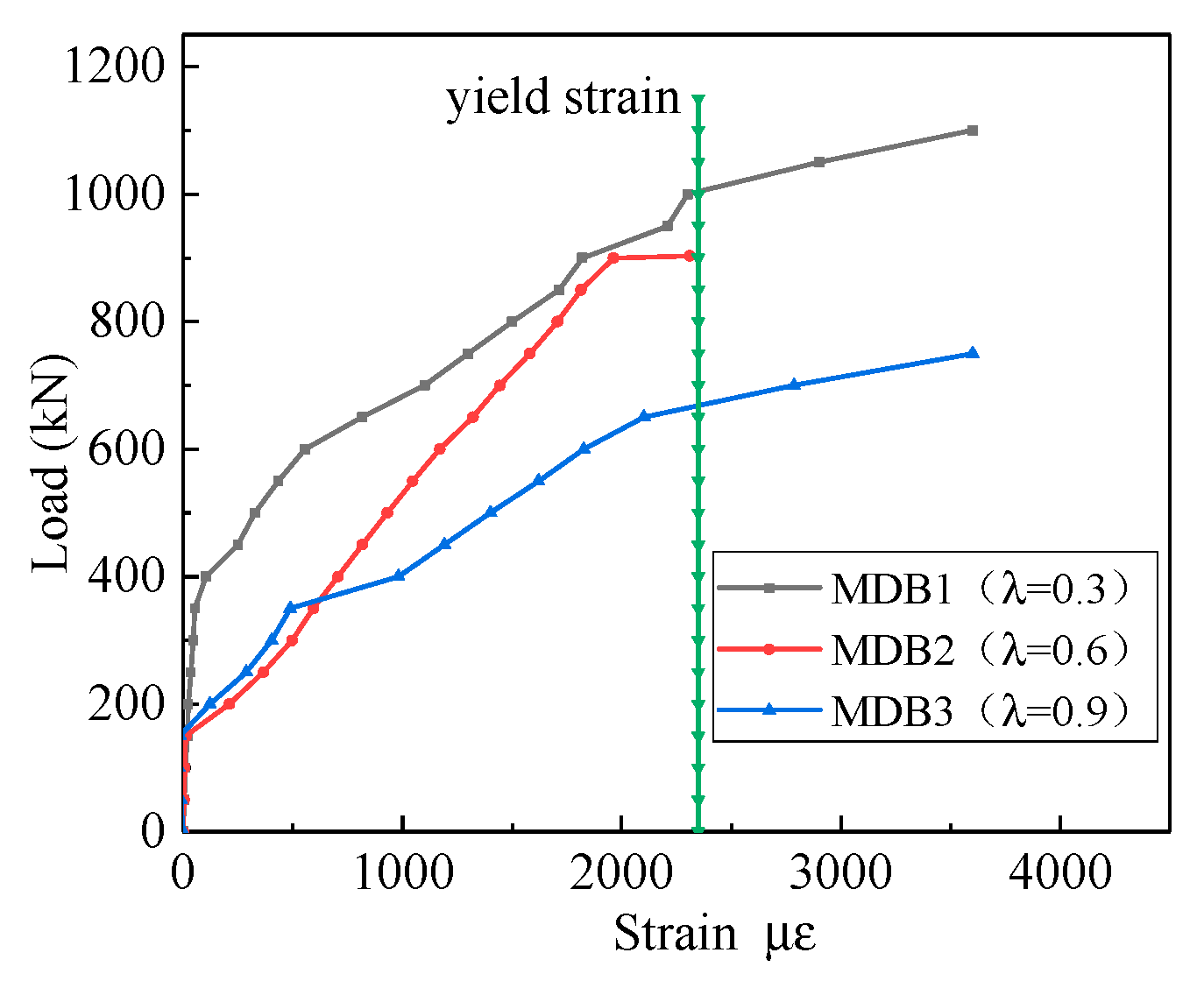
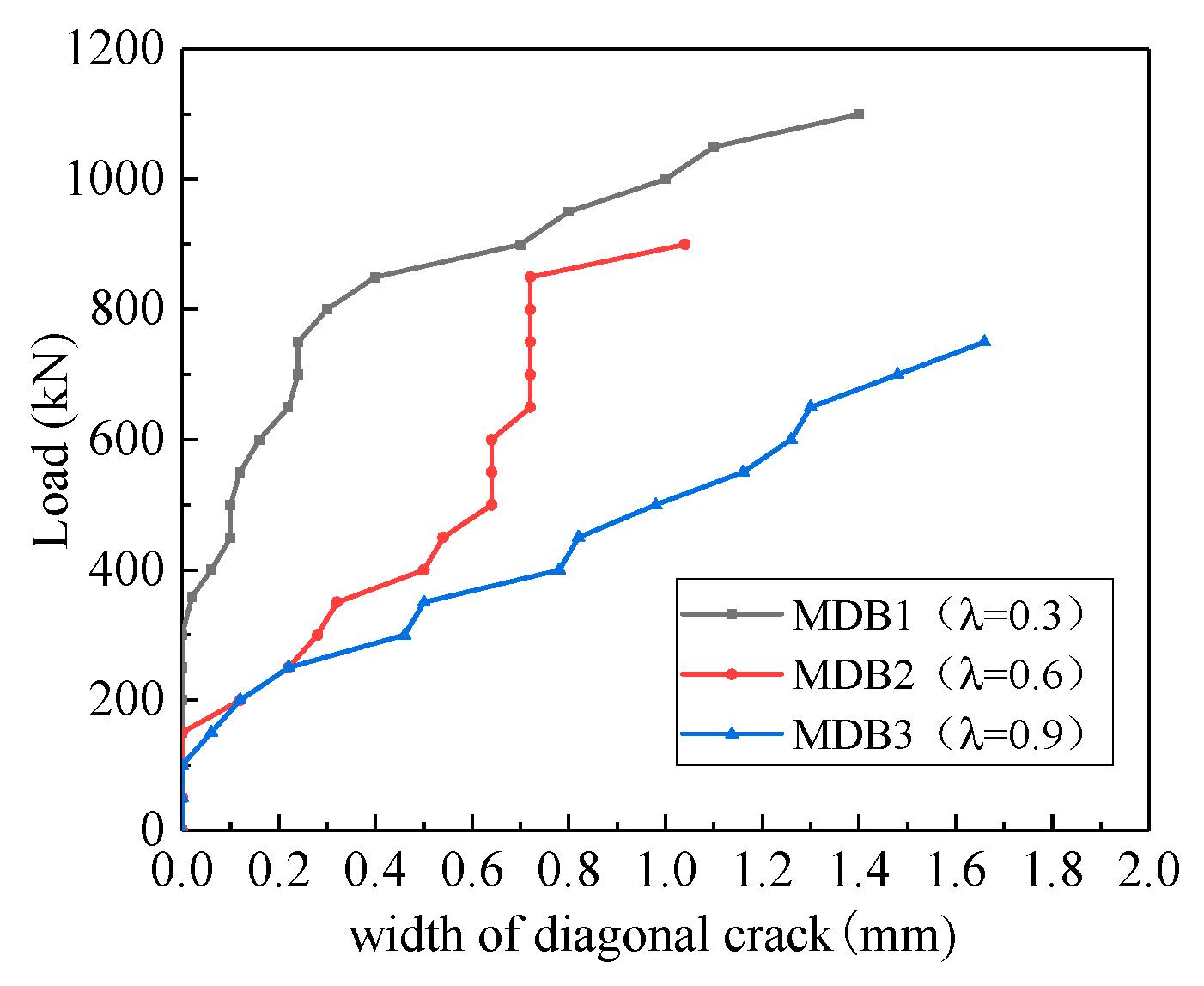
3.3.1. Shear Span–Depth Ratio
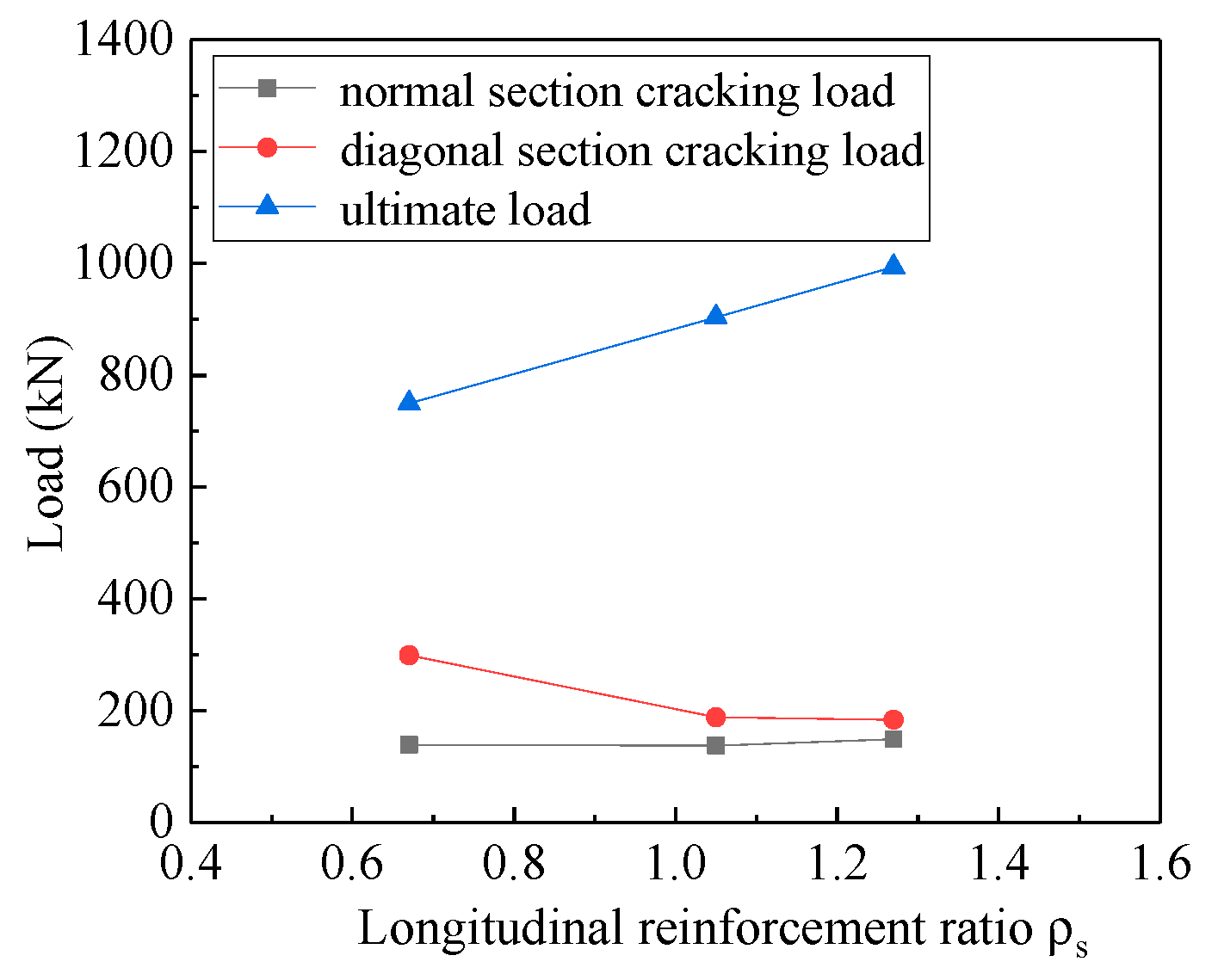
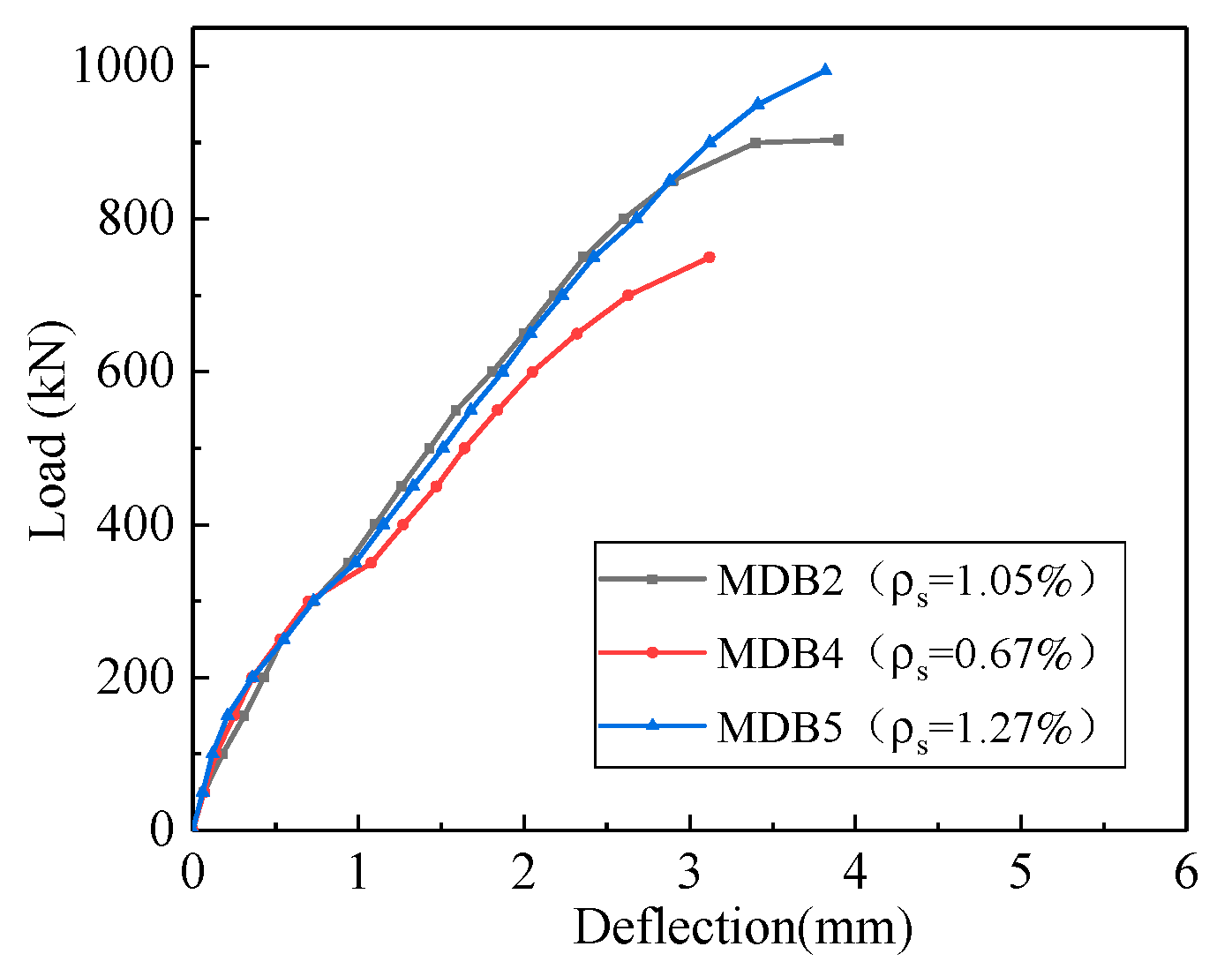
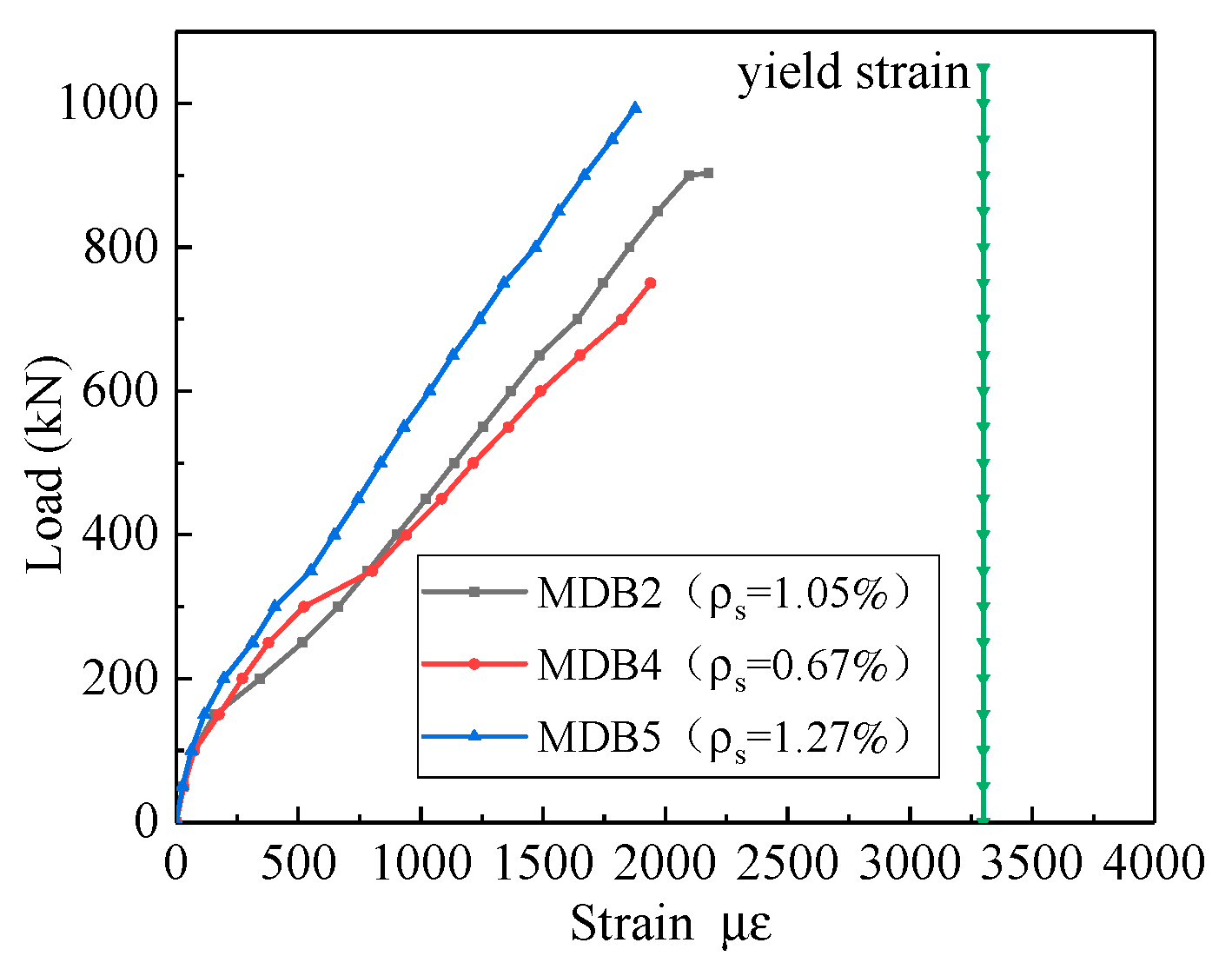
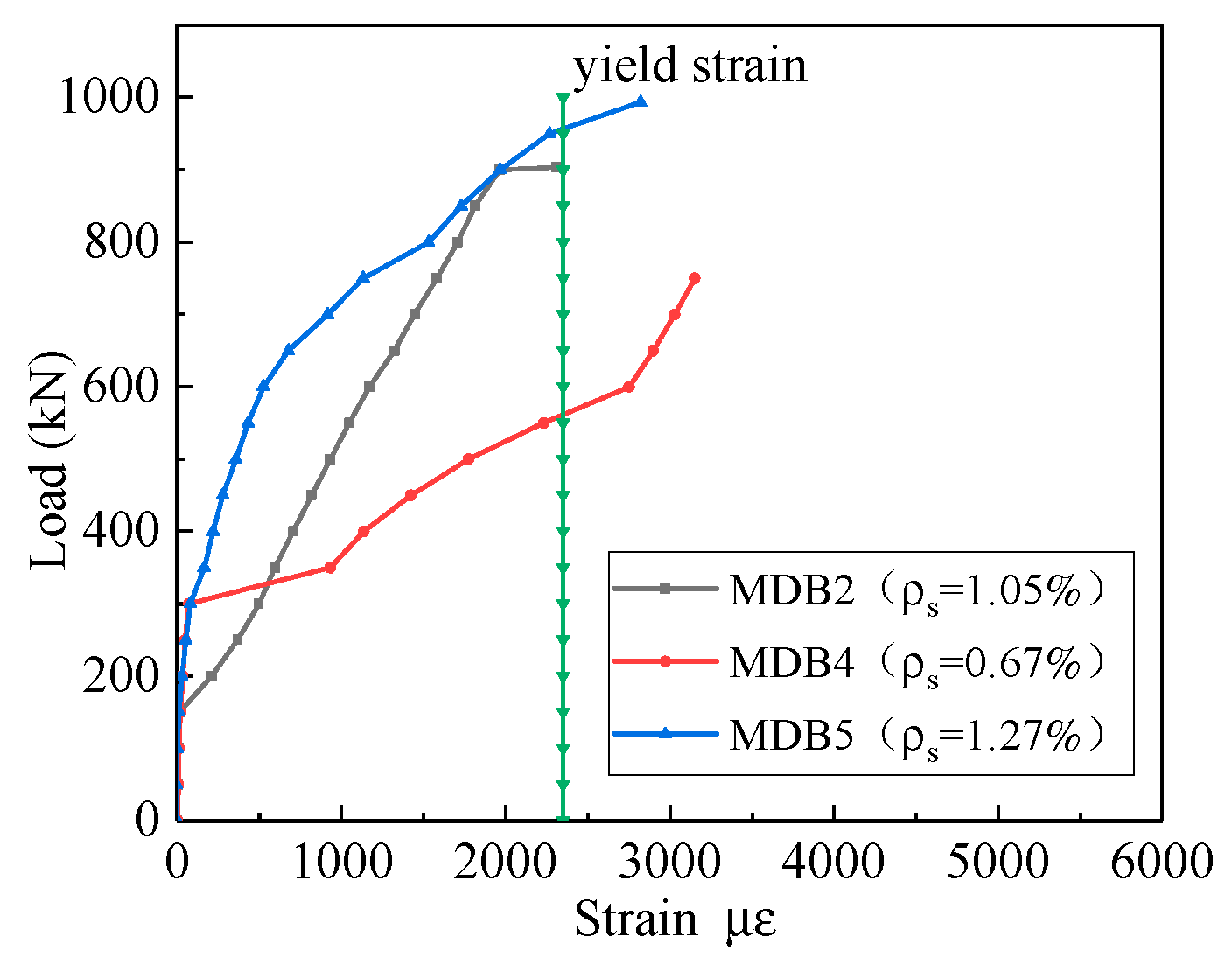
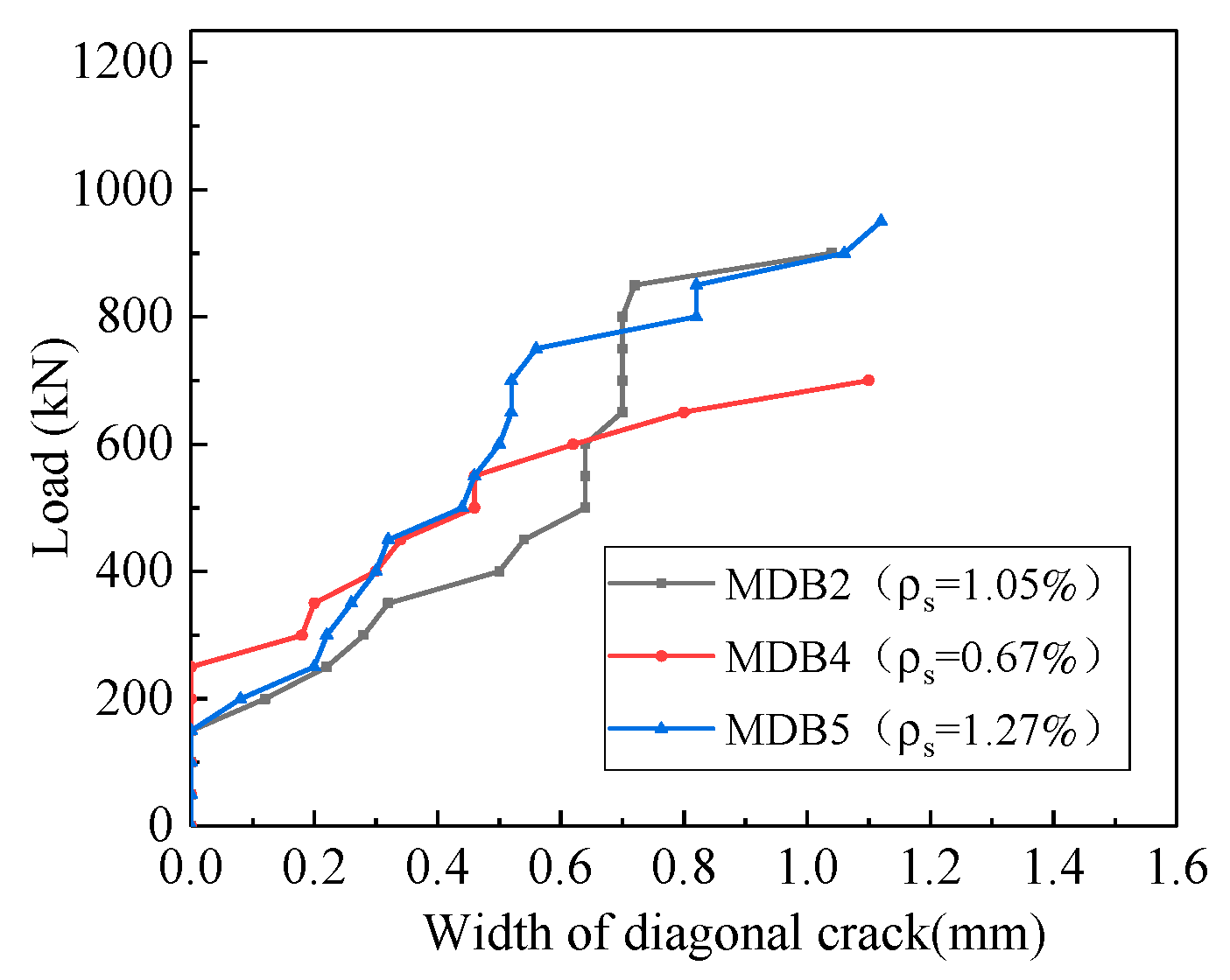
3.3.2. Longitudinal Reinforcement Ratio
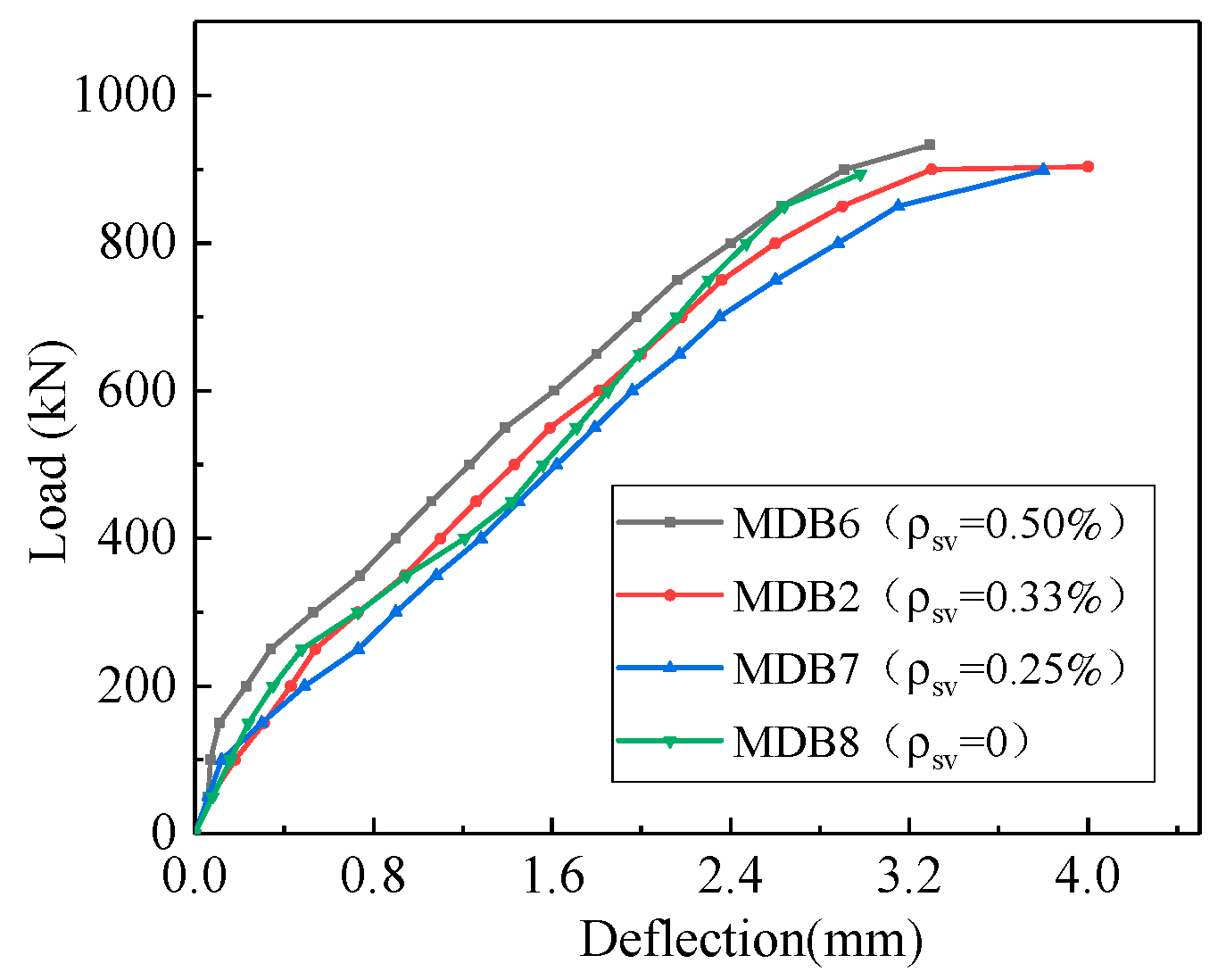
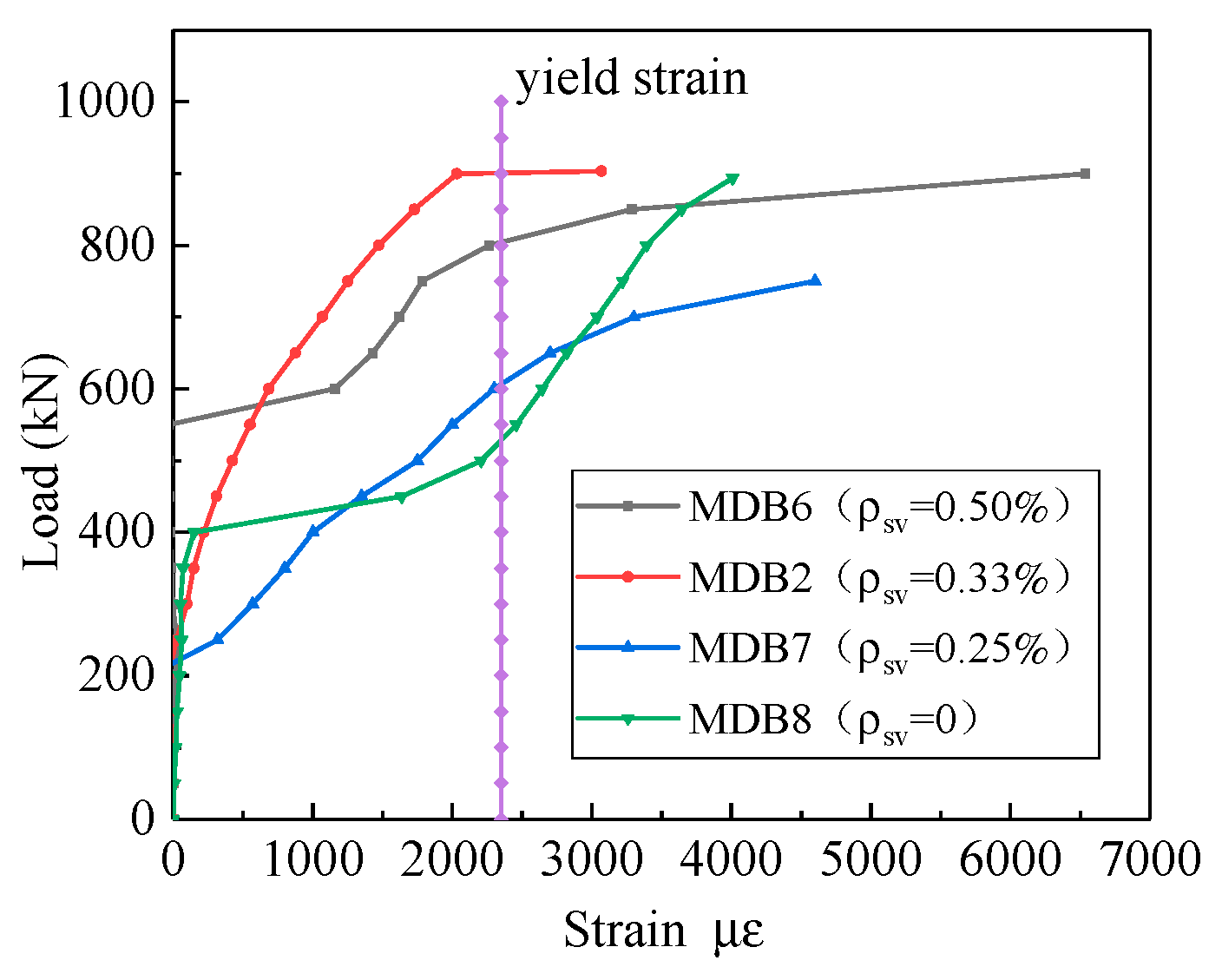
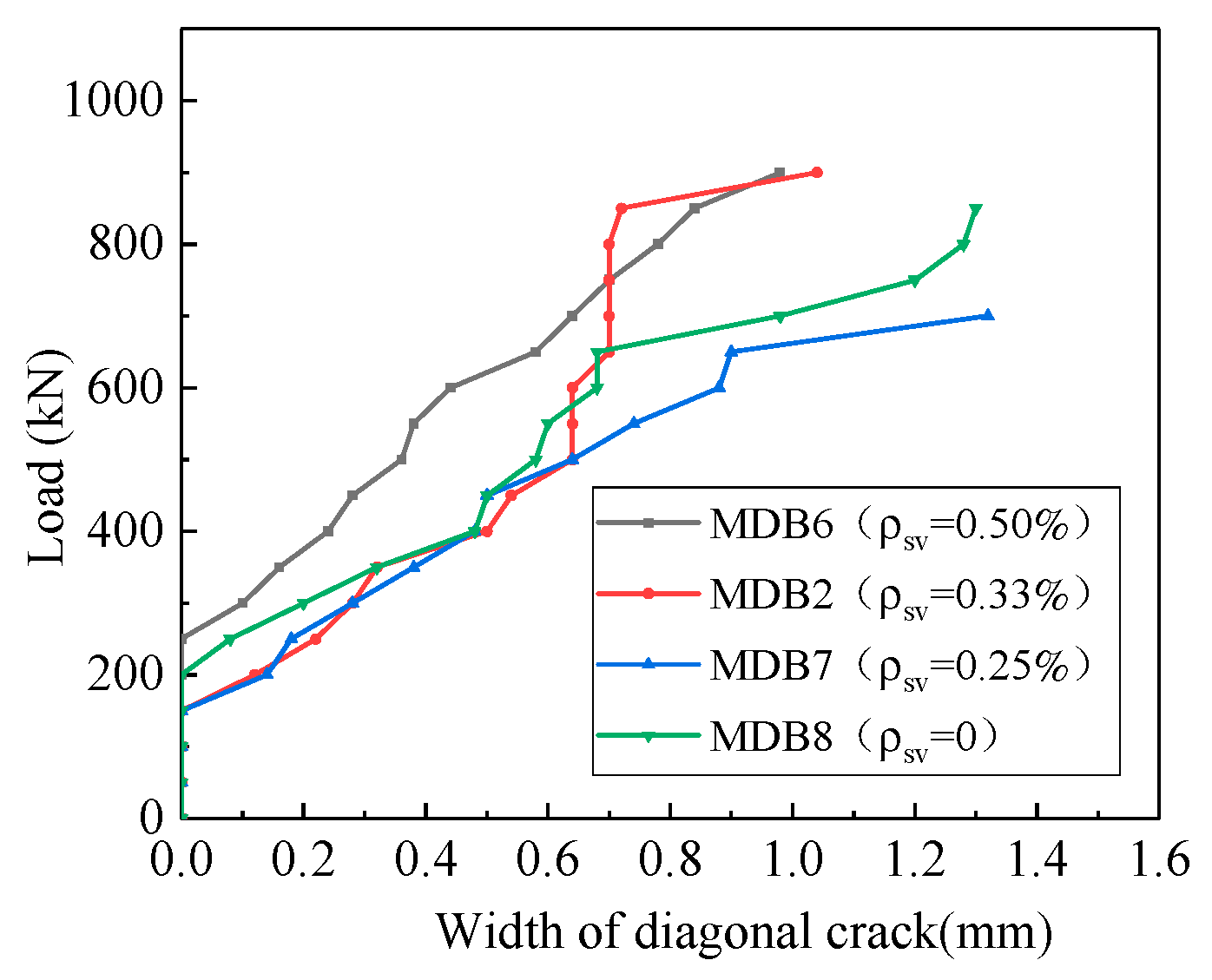
3.3.3. Vertical Stirrup Ratio
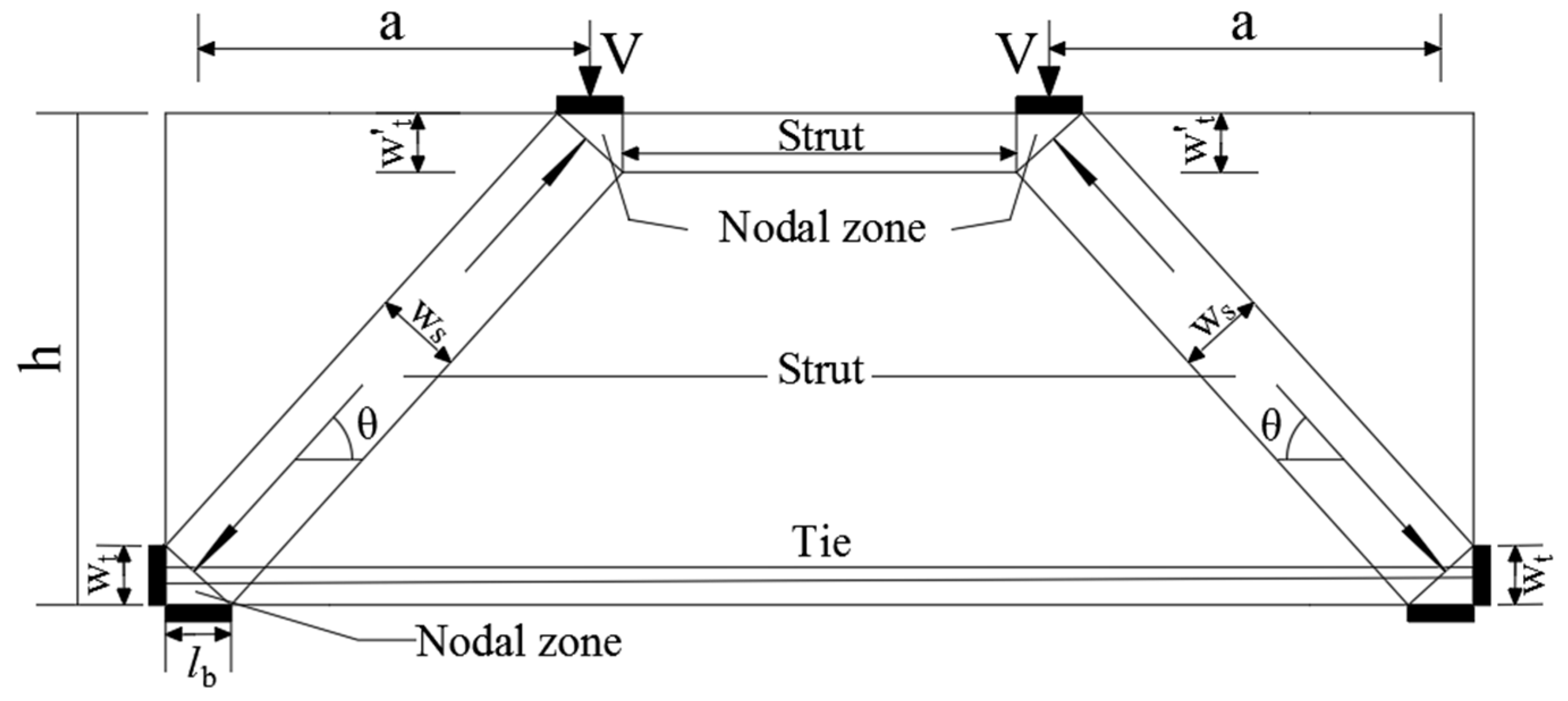
4. Design Method of Shear Capacity
4.1. China’s GB50010-2010 Code
4.2. American ACI318-14 Code
4.3. European EC Code
4.4. Canadian CSAA23.3-04 Code
4.5. Comparative Analysis of Test Results
5. Conclusions Remarks
- (1)
- The shear span–depth ratio is the most important parameter that controls behavior and shear capacity of high-strength reinforced concrete deep beams.
- (2)
- The longitudinal reinforcement ratio has no effect on the values of normal section cracking load and diagonal section cracking load of high-strength reinforced concrete deep beams, but it has a greater impact on the ultimate load. Obviously, the variation of the longitudinal reinforcement ratio applied on a beam, there will be no change of the beam’s stiffness and, therefore, the deflection will remain the same.
- (3)
- The vertical stirrup ratio has almost no effect on the normal section cracking load, diagonal section cracking load, and ultimate load of high-strength reinforced concrete deep beams. This is consistent with the view that the vertical stirrup is not considered in the calculation formula of the shear capacity of deep beams in the GB50010-2010 and the strut-and-tie model.
- (4)
- The presence of vertical shear reinforcement can control the crack propagation/opening and improve the ductile behavior of deep beams. But this effect is very limited as further increase in shear reinforcement does not enhance the shear capacity as failure is dominated by crushing of the concrete.
- (5)
- In most of the specimens, the load was supported by compression strut linking with loading point and bearing point at failure. It was destroyed after the formation of diagonal cracks parallel with the strut showing brittle fracture when the diagonal compression of strut governed the failure.
- (6)
- In the experimental results of this article, all horizontal distributing reinforcements yielded. This confirms that the horizontal distributing reinforcement is fully employed, which is consistent with the points of GB50010-2010 that the horizontal distributing reinforcement ratio is considered in the formula for calculating the shear capacity of deep beams.
- (7)
- The calculation of shear capacity of high-strength reinforced concrete deep beams implemented by EC2 code and CSSA is mostly over-conservative, and the shear equations provided by GB20010-2010 and ACI318-14 can predict results with a reasonable degree of accuracy. The results will allow an evaluation of the current code provisions and help identify their limitations.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Design Code for Concrete Structures; GB50010–2010; China Construction Industry Press: Beijing, China, 2010.
- Deep Beam Group. Experimental study on reinforced concrete deep beam. J. Build. Struct. 1987, 4, 23–35. [Google Scholar]
- Qian, G.L. Experimental study on reinforced concrete simply supported deep beams. J. Wuhan Inst. Water Resour. Electr. Power 1980, 4, 25–34. [Google Scholar]
- Liu, L.X.; Gong, S.X. Ultimate analysis of shear capacity of reinforced concrete simply supported deep beams with web openings. J. Build. Struct. 1991, 3, 44–54. [Google Scholar]
- Liu, L.X. An unified calculation method for shear capacity of reinforced concrete deep beam short beam and shallow beams. J. Build. Struct. 1995, 4, 13–21. [Google Scholar]
- Marti, P. Basic tools of reinforced concrete beam design. ACI Struct. J. 1985, 82, 46–56. [Google Scholar]
- Cook, W.D.; Mitchell, D. Studies of disturbed regions near discontinuities in reinforced concrete members. ACI Struct. J. 1988, 85, 206–216. [Google Scholar]
- Schlaich, J.; Schafer, K.; Jennewein, M. Toward a consistant design of structural concrete. Prestress. Concr. Inst. J. 1987, 32, 74–150. [Google Scholar]
- Vecchio, F.J.; Collins, M.P. The modified compression field theory for reinforced concrete elements subjected to shear. ACI J. Proc. 1986, 83, 219–231. [Google Scholar]
- Vecchio, F.J.; Collins, M.P. Compression response of cracked reinforced concrete. J. Struct. Eng. ASCE 1993, 119, 3590–3610. [Google Scholar] [CrossRef]
- Hwang, S.J.; Lu, W.Y.; Lee, H.J. Shear strength prediction for deep beams. ACI Struct. J. 2000, 97, 367–376. [Google Scholar]
- Hwang, S.J.; Lee, H.J. Strength predication for discontinuity regions by soften strut-and-tie model. J. Struct. Eng. ASCE 2002, 123, 1519–1526. [Google Scholar] [CrossRef]
- Bažant, Z.P.; Planas, J. Fracture and Size Effect in Concrete and Other Quasibrittle Materials; CRC Press: New York, NY, USA, 1998. [Google Scholar]
- Yang, K.H.; Ashour, A.F. Strut-and-tie model based on crack band theory for deep beams. J. Struct. Eng. 2010, 12, 1–33. [Google Scholar] [CrossRef]
- ACI Committee 318: Building Code Requirement for Structure Concrete (ACI 318–14) and Commentary; American Concrete Institute: Famington Hills, MI, USA, 2014.
- The European Standard EN 1992–1–1:2004, Eurocode 2, Design of Concrete Structures; British Standards Institution: Brussels, Belgium, 2004.
- Design of Concrete Structures; CSA A23.3–04; Canadian Standards Association: Mississauga, ON, Canada, 2004.
- Tang, C.Y.; Tan, K.H. Interactive mechanical model for shear strength of deep beams. J. Struct. Eng. ASCE 2004, 130, 1534–1544. [Google Scholar] [CrossRef]
- Tan, K.H.; Cheng, G.H. Size effect on shear strength of deep beams: Investigating with strut-and-tie model. J. Struct. Eng. ASCE 2006, 132, 673–685. [Google Scholar] [CrossRef]
- Liu, L.Q.; Wang, J.J.; Han, J.Y.; Zhang, G.X.; Wu, X.L. Experimental study on static performance of reinforced concrete simply-supported deep beams and analysis of compression rod model. J. Build. Struct. 2013, 34, 137–141. [Google Scholar]
- Qiu, Y.K.; Liu, X.; Lin, Y. Experimental study on simply supported reinforced concrete deep beams of strut-and-tie models. Build. Struct. 2012, 42, 91–96. [Google Scholar]
- Lu, W.Y.; Lin, I.J.; Yu, H.W. Shear strength of reinforced concrete deep beams. ACI Struct. J. 2013, 110, 671–680. [Google Scholar]
- Tan, K.H.; Cheng, G.H.; Zhang, N. Experiment to mitigate size effect on deep beams. Mag. Concr. Res. 2007, 60, 709–723. [Google Scholar] [CrossRef]
- De Dios Garay, J.; Lubell, A.S. Behavior of Concrete deep beams with high strength reinforcement. In Proceedings of the American Society of Civil Engineers, Structures Congress 2008, Vancouver, BC, Canada, 24–26 April 2008. [Google Scholar]
- Yang, K.H.; Chung, H.S.; Lee, E.T. Shear characteristics of high strength concrete deep beams without shear reinforcements. Eng. Struct. 2003, 25, 1343–1352. [Google Scholar] [CrossRef]
- Chen, H.; Yi, W.J.; Ma, Z.J.; Hwang, H.J. Shear strength of reinforced concrete simple and continuous deep beams. ACI Struct. J. 2019, 116, 31–40. [Google Scholar] [CrossRef]
- Sanabria Díaz, R.A.; Sarmiento Nova, S.J.; Teixeira da Silva, M.C.A.; Mouta Trautwein, L.; de Almeida, L.C. Reliability analysis of shear strength of reinforced concrete deep beams using NLFEA. Eng. Struct. 2020, 203, 109760. [Google Scholar] [CrossRef]
- Placidi, L.; Barchiesi, E. Energy approach to brittle fracture in strain-gradient modelling. Proc. R. Soc. A Math. Phys. Eng. Sci. 2018, 474, 20170878. [Google Scholar] [CrossRef] [PubMed]
- Placidi, L.; Barchiesi, E.; Misra, A. A strain gradient variational approach to damage: A comparison with damage gradient models and numerical results. Math. Mech. Complex Syst. 2018, 6, 77–100. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Niiranen, J. A second strain gradient damage model with a numerical implementation for quasi-brittle materials with micro-architectures. Math. Mech. Solids 2020, 25, 515–546. [Google Scholar] [CrossRef]
- Tang, X.R.; Sun, H.M. Experimental research and design suggestion on static behavior of spatial steel frame concrete simply supported deep beam. J. Build. Struct. 2010, 31, 108–116. [Google Scholar]
- Wu, T.; Wei, H.; Liu, X. Shear behavior of large-scale deep beams with lightweight-aggregate concrete. ACI Struct. J. 2020, 117, 75–89. [Google Scholar] [CrossRef]
- Gao, D.Y.; Zhao, J.; Zhu, H.T.; Zhang, Q.M. Calculation method for crack resistance of steel fiber concrete deep beams with reinforcement. J. Hydraul. Eng. 2002, 11, 124–128. [Google Scholar]
- Zhao, J.; Zhu, H.T.; Gao, D.Y. The calculating method of shear capacity steel fiber reinforced concrete deep beams. Henan Sci. 2003, 670–673. [Google Scholar]
- Ma, K.Z.; Qi, T.; Liu, H.J.; Wang, H.B. Shear behavior of hybrid fiber reinforced concrete deep beams. Materials 2018, 11, 2023. [Google Scholar] [CrossRef]
- Ferdous, W.; Almutairi, A.D.; Huang, Y.; Bai, Y. Short-term flexural behaviour of concrete filled pultruded GFRP cellular and tubular sections with pin-eye connections for modular retaining wall construction. Compos. Struct. 2018, 206, 1–10. [Google Scholar] [CrossRef]
- Ferdous, W.; Bai, Y.; Almutairi, A.D.; Satasivam, S.; Jeske, J. Modular assembly of water-retaining walls using GFRP hollow profiles: Components and connection performance. Compos. Struct. 2018, 194, 1–11. [Google Scholar] [CrossRef]
- Zhao, G.F. Advanced Reinforced Concrete Structure; China Electric Power Press: Beijing, China, 1988. [Google Scholar]
- Park, R.; Paulay, T. Reinforced Concrete Structure; Chongqing University Press: Chongqing, China, 1985. [Google Scholar]
- Ferdous, W.; Manalo, A.; Aravinthan, T. Effect of beam orientation on the static behavior of phenolic core sandwich composites with different shear span-to-depth ratios. Compos. Struct. 2017, 168, 292–304. [Google Scholar] [CrossRef]
- Yang, K.H.; Chung, H.S.; Ashour, A.F. Influence of shear reinforcement on reinforced concrete continuous deep beams. ACI Struct. J. 2007, 104, 420–429. [Google Scholar]





| fcu/MPa | fc/MPa | ft/MPa | Ec/GPa |
|---|---|---|---|
| 59.8 | 42.9 | 3.75 | 34.6 |
| Reinforcement | d/mm | fy/MPa | fu/MPa | Es/GPa |
|---|---|---|---|---|
| HTRB600 | 16 | 670 | 865 | 198.5 |
| HTRB600 | 20 | 653.7 | 823.3 | 196.6 |
| HTRB600 | 22 | 630 | 800 | 195.8 |
| HRB400E | 8 | 456.8 | 647.7 | 205.3 |
| Component Number | l × b × l /mm | Shear Span–Depth Ratio λ | Span Height Ratio l0/h | Longitudinal Reinforcement Ratio ρs (%) | Horizontal Reinforcement Ratio ρsh (%) | Vertical Stirrup Ratio ρsv (%) |
|---|---|---|---|---|---|---|
| MDB1 | 1600 × 200 × 600 | 0.3 | 2 | 1.05 | 0.33 | 0.33 |
| MDB2 | 1600 × 200 × 600 | 0.6 | 2 | 1.05 | 0.33 | 0.33 |
| MDB3 | 1600 × 200 × 600 | 0.9 | 2 | 1.05 | 0.33 | 0.33 |
| MDB4 | 1600 × 200 × 600 | 0.6 | 2 | 0.67 | 0.33 | 0.33 |
| MDB5 | 1600 × 200 × 600 | 0.6 | 2 | 1.27 | 0.33 | 0.33 |
| MDB6 | 1600 × 200 × 600 | 0.6 | 2 | 1.05 | 0.33 | 0.50 |
| MDB7 | 1600 × 200 × 600 | 0.6 | 2 | 1.05 | 0.33 | 0.25 |
| MDB8 | 1600 × 200 × 600 | 0.6 | 2 | 1.05 | 0.33 | 0 |
| Specimen | /mm | Failure Model | Failure Form | |||||
|---|---|---|---|---|---|---|---|---|
| MDB1 | 359 | 370 | 1100.0 | 32.64% | 33.64% | 3.15 | Diagonal-compression | Crushing-strut |
| MDB2 | 138 | 188 | 903.5 | 15.27% | 20.81% | 4.00 | Diagonal-compression | Crushing-strut |
| MDB3 | 99 | 149 | 785.0 | 12.61% | 18.98% | 5.99 | Diagonal-compression | Crushing-strut |
| MDB4 | 139 | 299 | 750.0 | 18.53% | 39.87% | 3.12 | Diagonal-compression | Crushing-strut |
| MDB5 | 149 | 184 | 993.7 | 14.99% | 18.52% | 3.82 | Diagonal-compression | Crushing-strut |
| MDB6 | 199 | 300 | 933.0 | 21.33% | 32.15% | 3.29 | Diagonal-compression | Crushing-strut |
| MDB7 | 145 | 199 | 899.0 | 19.33% | 22.14% | 3.80 | Diagonal-compression | Crushing-strut |
| MDB8 | 165 | 170 | 893.5 | 18.47% | 19.03% | 2.98 | Diagonal-compression | Diagonal-splitting |
| Specimen | Test Value | Predictions Vn(kN) | Vtest/Vn | ||||||
|---|---|---|---|---|---|---|---|---|---|
| China | ACI | EC2 | CSA | China | ACI | EC2 | CSA | ||
| MDB1 | 1100 | 638.54 | 620.09 | 483.46 | 659.06 | 1.723 | 1.774 | 2.275 | 1.669 |
| MDB2 | 903.5 | 638.54 | 644.37 | 502.40 | 555.24 | 1.415 | 1.402 | 1.798 | 1.627 |
| MDB3 | 785 | 638.54 | 583.68 | 455.08 | 382.33 | 1.229 | 1.345 | 1.725 | 2.053 |
| MDB4 | 750 | 640.94 | 634.49 | 494.69 | 548.45 | 1.170 | 1.182 | 1.516 | 1.367 |
| MDB5 | 993.7 | 637.34 | 649.32 | 506.26 | 558.61 | 1.559 | 1.530 | 1.963 | 1.779 |
| MDB6 | 933 | 638.54 | 644.37 | 502.40 | 555.24 | 1.461 | 1.448 | 1.857 | 1.680 |
| MDB7 | 899 | 638.54 | 644.37 | 502.40 | 555.24 | 1.408 | 1.395 | 1.789 | 1.619 |
| MDB8 | 893.5 | 638.54 | 644.37 | 502.40 | 555.24 | 1.399 | 1.387 | 1.778 | 1.609 |
| Mean | 1.421 | 1.433 | 1.838 | 1.676 | |||||
| variance | 0.027 | 0.025 | 0.041 | 0.032 | |||||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.-H.; Li, S.-S.; Xie, W.; Guo, Y.-D. Experimental Study on Shear Capacity of High Strength Reinforcement Concrete Deep Beams with Small Shear Span–Depth Ratio. Materials 2020, 13, 1218. https://doi.org/10.3390/ma13051218
Zhang J-H, Li S-S, Xie W, Guo Y-D. Experimental Study on Shear Capacity of High Strength Reinforcement Concrete Deep Beams with Small Shear Span–Depth Ratio. Materials. 2020; 13(5):1218. https://doi.org/10.3390/ma13051218
Chicago/Turabian StyleZhang, Jun-Hong, Shu-Shan Li, Wei Xie, and Yang-Dong Guo. 2020. "Experimental Study on Shear Capacity of High Strength Reinforcement Concrete Deep Beams with Small Shear Span–Depth Ratio" Materials 13, no. 5: 1218. https://doi.org/10.3390/ma13051218
APA StyleZhang, J.-H., Li, S.-S., Xie, W., & Guo, Y.-D. (2020). Experimental Study on Shear Capacity of High Strength Reinforcement Concrete Deep Beams with Small Shear Span–Depth Ratio. Materials, 13(5), 1218. https://doi.org/10.3390/ma13051218






