Study on Structural Performance of Asphalt Concrete and Hot Rolled Sheet Through Viscoelastic Characterization
Abstract
1. Introduction
2. Materials and Methods
2.1. Specimen Preparation
2.2. Marshall Stability Test
2.3. Dynamic Modulus Test
2.4. Generating Dynamic Modulus Master Curves
3. Results and Discussion
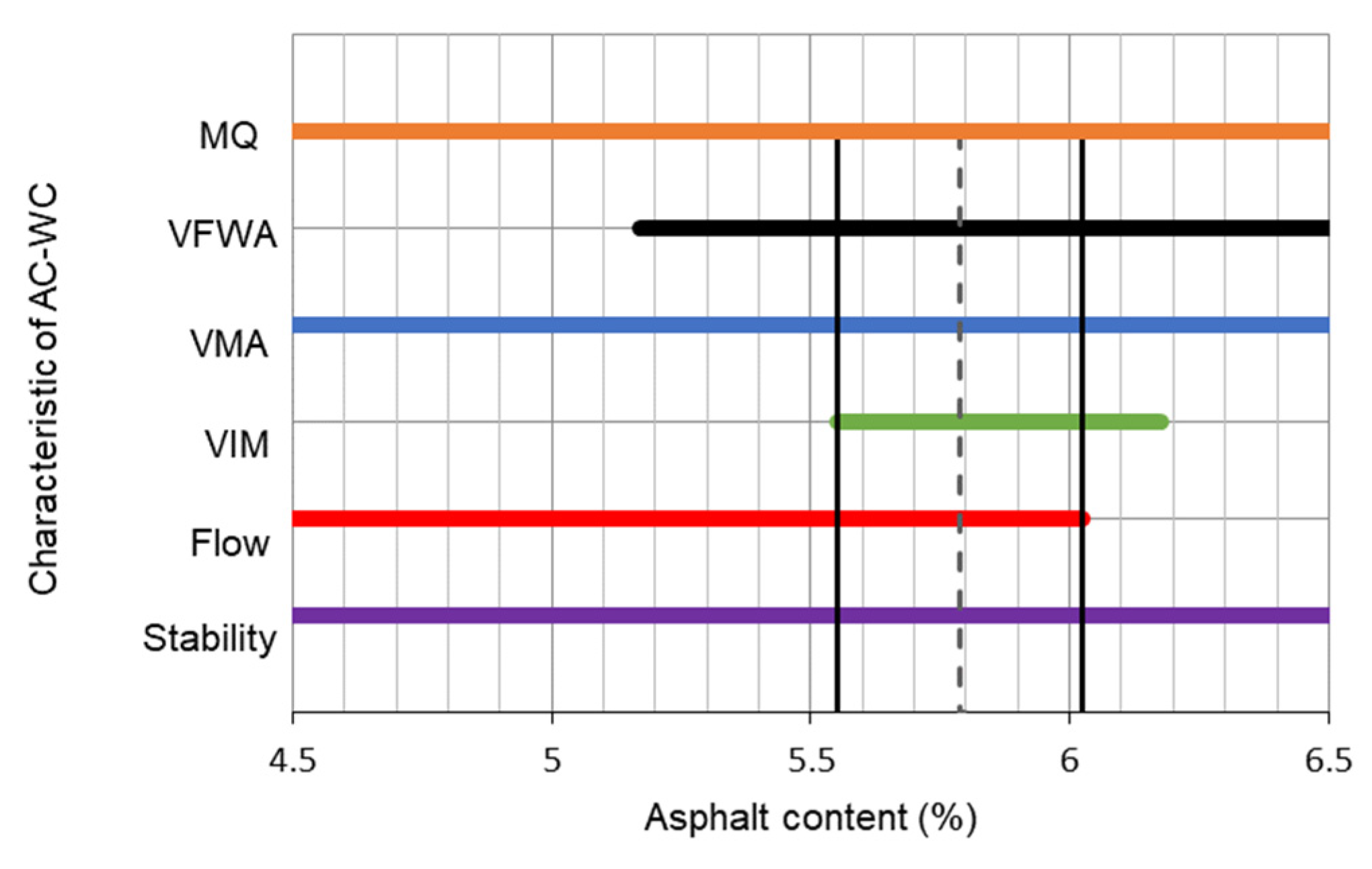
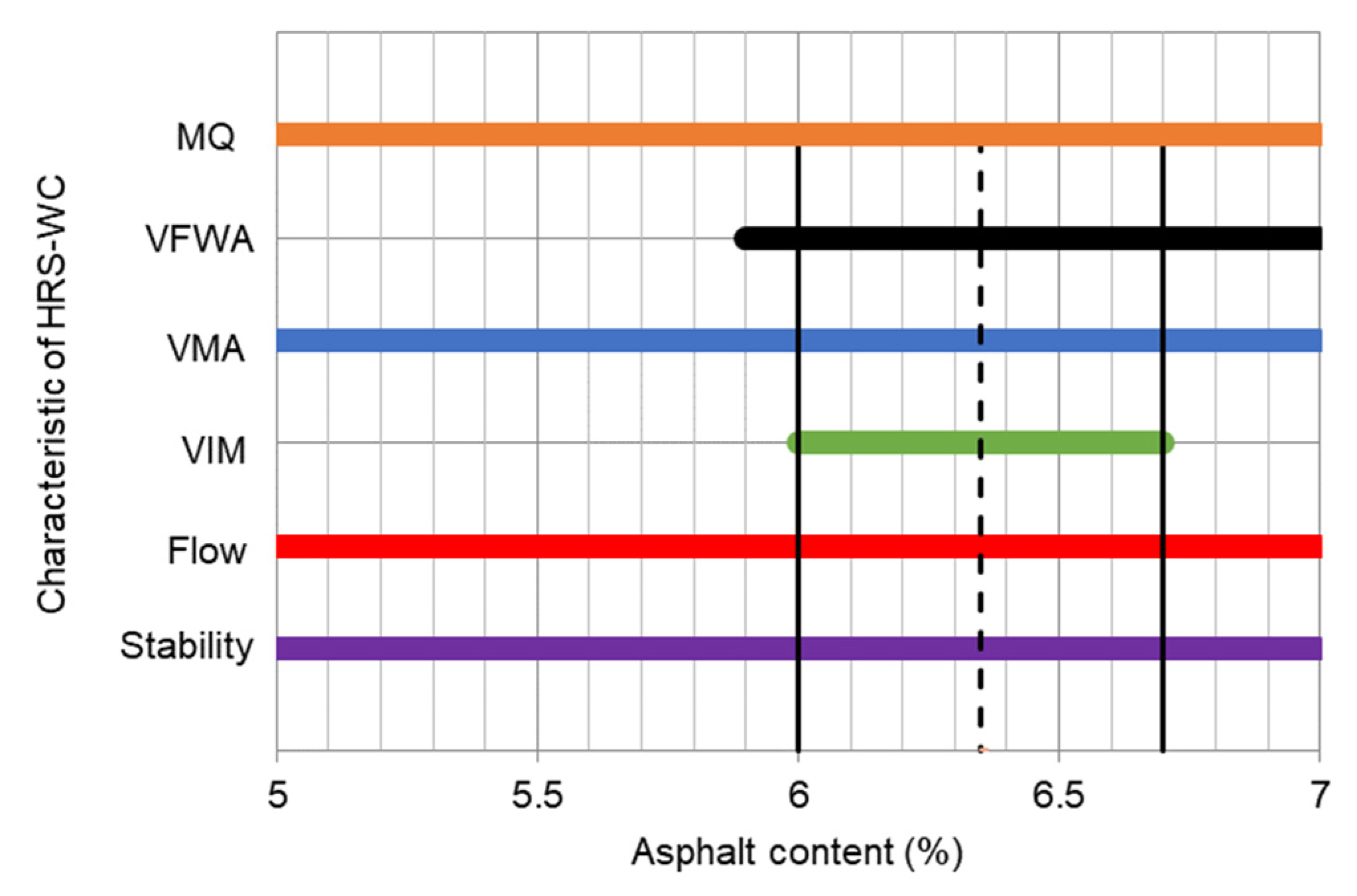
3.1. Marshall Test
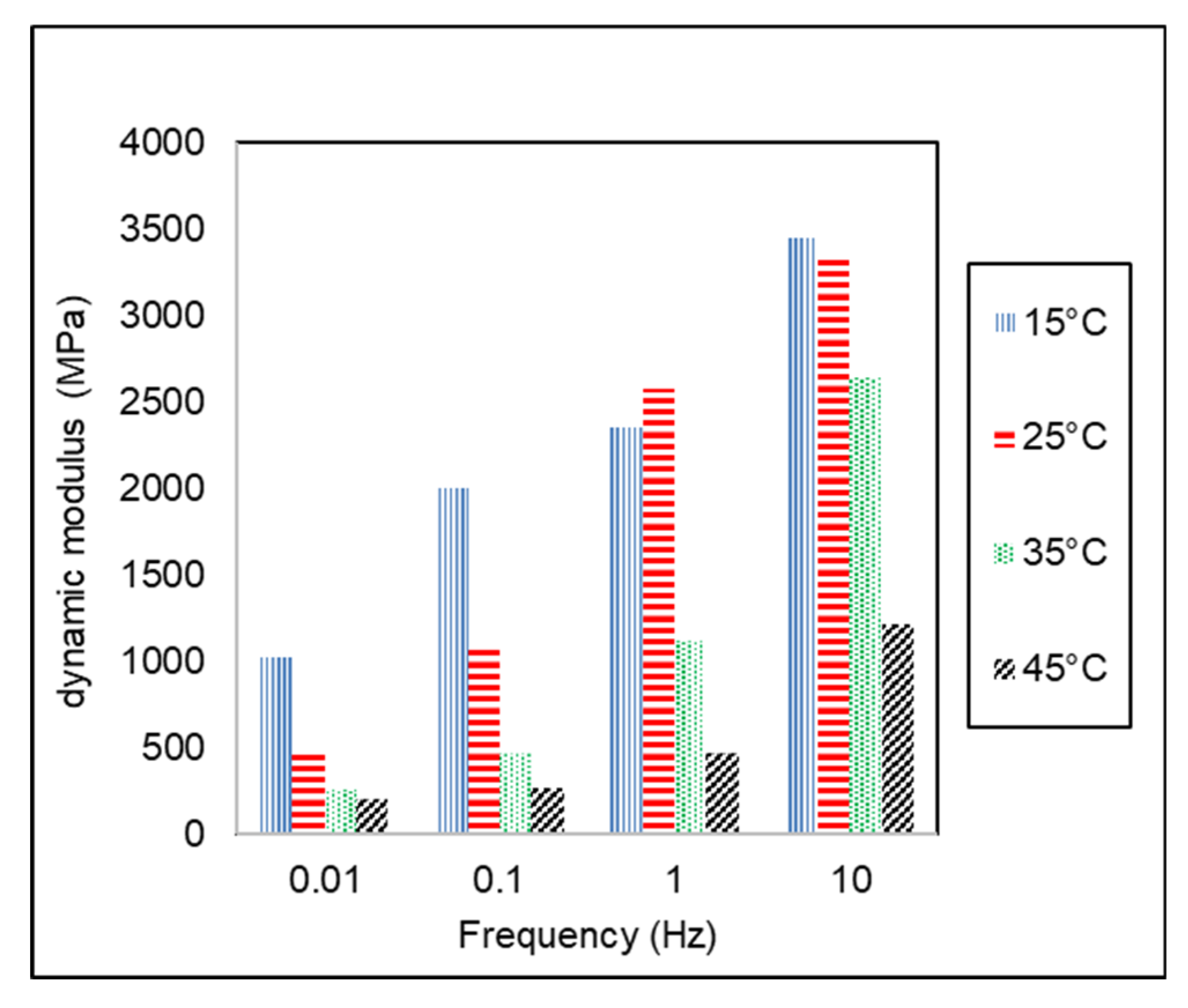
3.2. Dynamic Modulus of AC-WC and HRS-WC Asphalt Mixtures
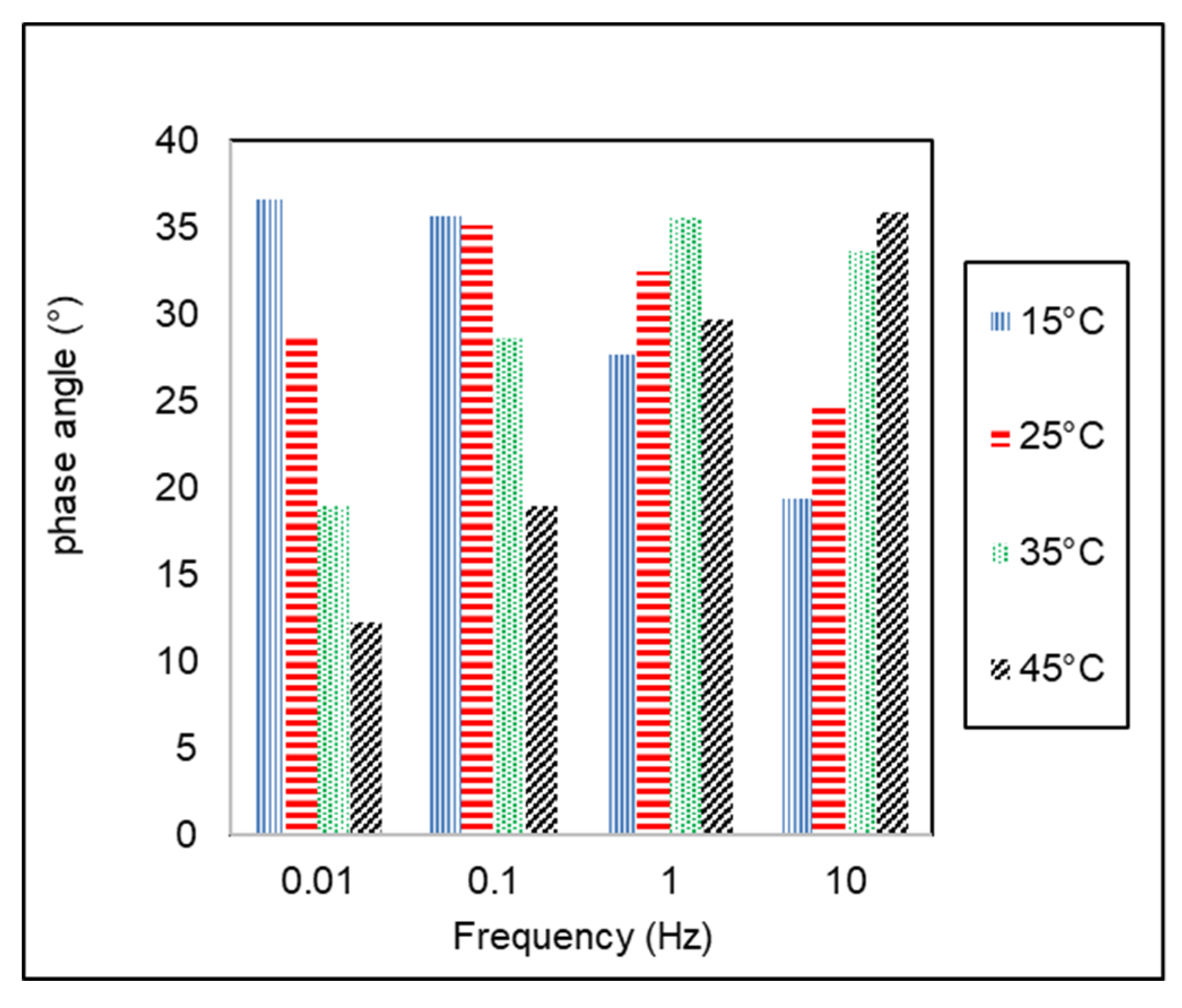
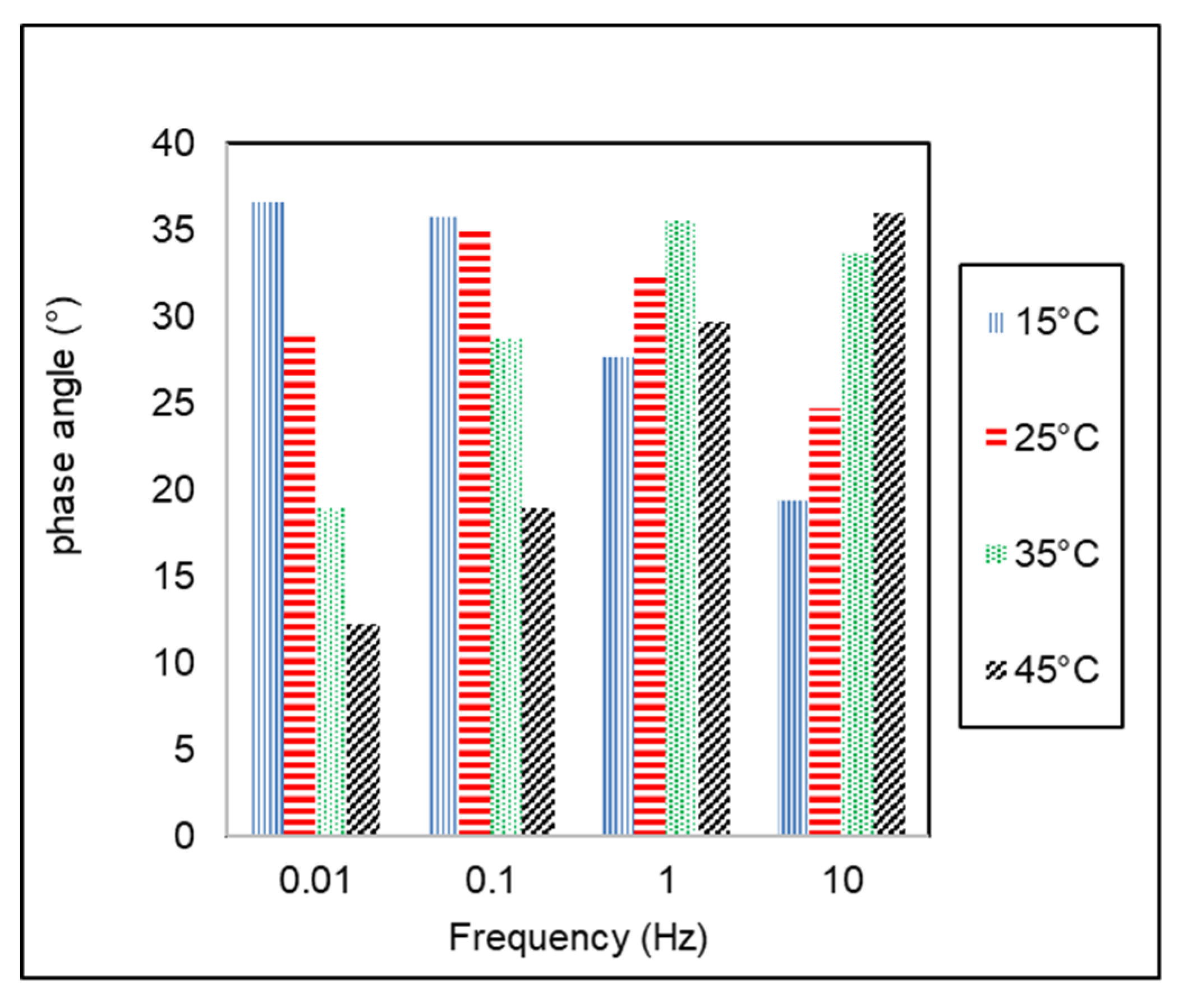
3.3. Phase Angle of AC-WC and HRS-WC Asphalt Mixtures
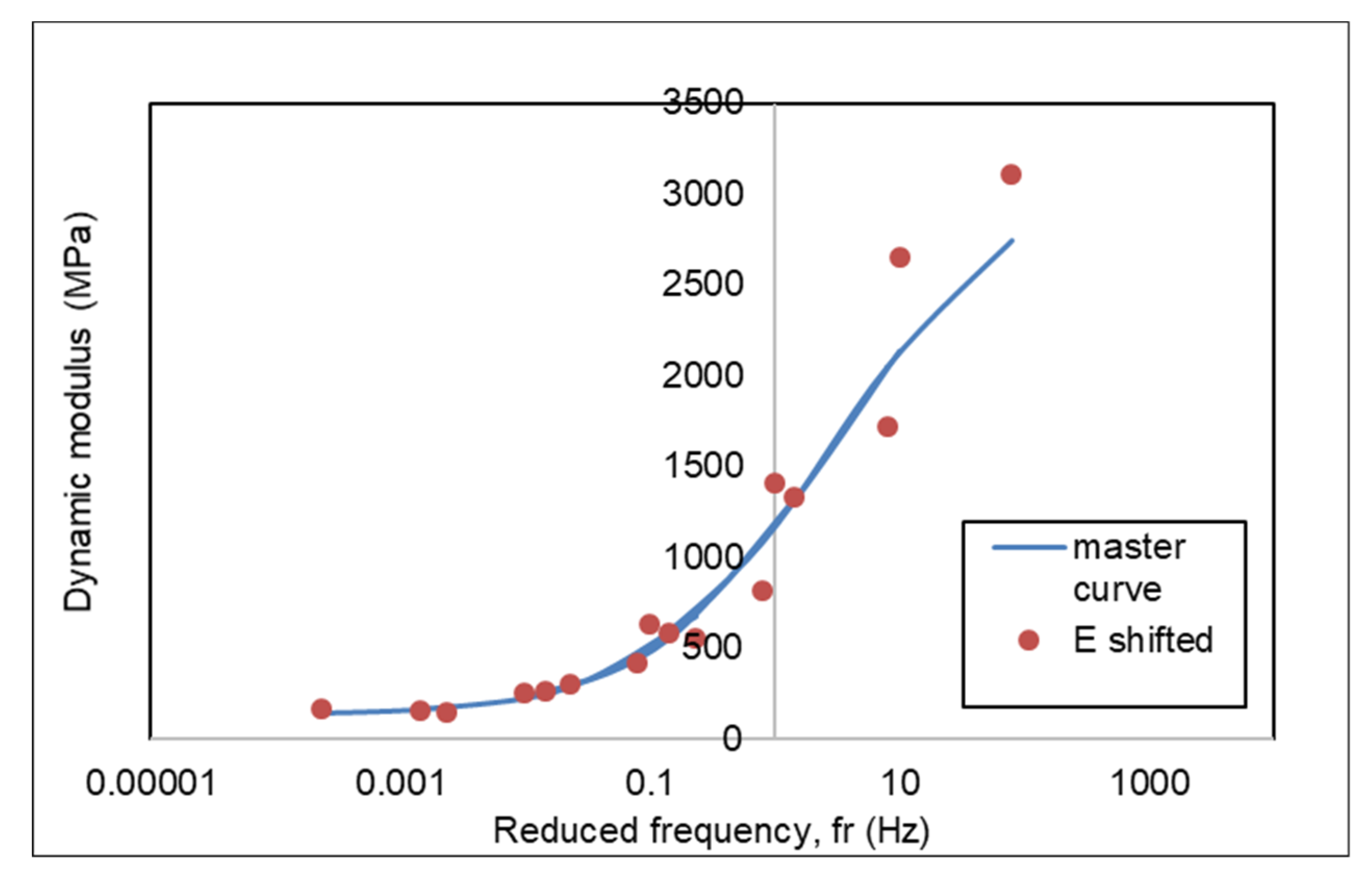
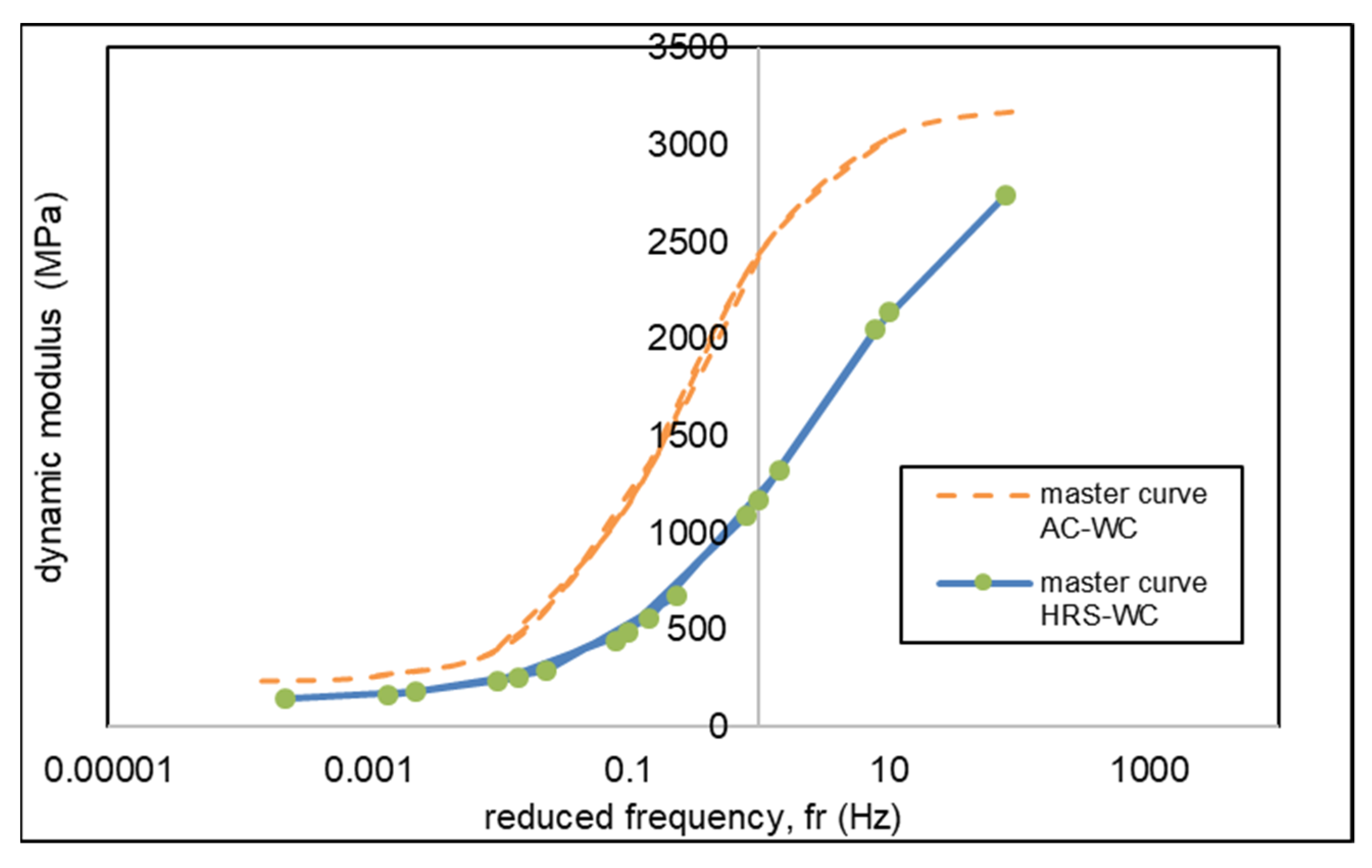
3.4. Dynamic Modulus Master Curve of AC-WC and HRS-WC Asphalt Mixtures
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jongepier, R.; Kuilman, B. Characteristics of the Rheology of Bitumens. J. Assoc. Asph. Paving Technol. 1968, 38, 98–121. [Google Scholar]
- Rahimzadeh, B. Linear and Non-Linear Viscoelastic Behavior of Binders and Asphalts. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2002. [Google Scholar]
- Read, J.; Whiteoak, D. The Shell Bitumen Handbook, 5th ed.; Thomas Telford: London, UK, 2003. [Google Scholar]
- Lamperti, R. Rheological and Energetic Characterization of Wax-Modified Asphalt Binders. Ph.D. Thesis, Universita Di Bologna, Bologna, Italy, 2011. [Google Scholar]
- Davide, L.P. Rheology and Curing of Tyre Rubber Modified Bitumen. Ph.D. Thesis, Universita Degli Studi Di Palermo, Palermo, Italy, 2011. [Google Scholar]
- Huang, Y.H. Pavement Analysis and Design; Pearson Education: Upper Saddle River, NJ, USA, 2012. [Google Scholar]
- Mashaan, N.S.; Karim, M.R. Investigating the Rheological Properties of Crumb Rubber Modified Bitumen and its Correlation with Temperature Susceptibility. Mater. Res. 2013, 16, 116–127. [Google Scholar] [CrossRef]
- Papagiannakis, A.T.; Masad, E.A. Pavement Design and Materials; John Wiley and Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Liao, Y. Viscoelastic FE Modelling of Asphalt Pavements and Its Application to US 30 Perpetual Pavement. Ph.D. Thesis, Russ College of Engineering and Technology, Athens, OH, USA, 2007. [Google Scholar]
- AASHTO. AASHTO Designation: PP 61-13. Standar Practice for Developing Dynamic Modulus Master Curves for Asphalt Mixtures Using the Asphalt Mixture Performance Tester (AMPT); AASHTO: Washington, DC, USA, 2015. [Google Scholar]
- Yoder, E.J.; Witczak, M.W. Principles of Pavement Design; John Wiley and Sons: Hoboken, NJ, USA, 1975. [Google Scholar]
- Olard, F.; Di Benedetto, H. General ‘2S2P1D’ model and relation between the linear viscoelastic behaviors of bituminous binders and mixes. Int. J. Road Mater. Pavement Des. 2003, 4, 185–224. [Google Scholar]
- Di Benedetto, H.; Corté, J.F. Road Bituminous Materials 2. Thermomechanical Properties and Components of Mixtures; Hermes-Lavoisier: Paris, France, 2005. [Google Scholar]
- Dougan, C.E.; Jack, E.; Mahoney, S.J.; Hansen, G. E*-DYNAMIC MODULUS Test Protocol—Problems and Solutions; Report Number CT-SPR-0003084-F-03-3; Connecticut Department of Transportation in 6; Cooperation with the U.S. Department of Transportation; Federal Highway Administration (FHWA): Washington DC, USA, 2003. [Google Scholar]
- Lamine, M.; Aidara, C.; Ba, M.; Carter, A. Measurement of Dynamic Modulus and Master Curve Modeling of Hot Mix Measurement of Dynamic Modulus and Master Curve Modeling of Hot Mix Asphalt from Senegal (West Africa). Stud. Eng. Technol. 2015, 2, 124–135. [Google Scholar]
- Suaryana, N. Pengembangan Model Korelasi antara Modulus Resilien dengan Modulus Dinamis untuk Campuran Stone Matrix Asphalt. J. Tek. Sipil 2014, 21, 171–178. [Google Scholar] [CrossRef]
- Bonaquist, R.; Christensen, D.W. A Practical Procedure for Developing Dynamic Modulus Master Curve for Pavement Structural Design. In Proceedings of the 84th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 19–13 January 2005. [Google Scholar]
- Lin, S.; Ashlock, J.C.; Williams, R.C. Nondestructive quality assessment of asphalt pavements based on dynamic modulus. Constr. Build. Mater. 2016, 112, 836–847. [Google Scholar] [CrossRef]
- Liu, H.; Luo, R. Development of master curve models complying with linear viscoelastic theory for complex moduli of asphalt mixtures with improved accuracy. Constr. Build. Mater. 2017, 152, 259–268. [Google Scholar] [CrossRef]
- Nobakht, M.; Sakhaeifar, M.S. Dynamic modulus and phase angle prediction of laboratory aged asphalt mixtures. Constr. Build. Mater. 2018, 190, 740–751. [Google Scholar] [CrossRef]
- Podolsky, J.H.; Williams, R.C.; Cochran, E. Effect of corn and soybean oil derived additives on polymer-modified HMA and WMA master curve construction and dynamic modulus performance. Int. J. Pavement Res. Technol. 2018, 11, 541–552. [Google Scholar] [CrossRef]
- Ruan, L.; Luo, R.; Hu, X.; Pan, P. Effect of bell-shaped loading and haversine loading on the dynamic modulus and resilient modulus of asphalt mixtures. Constr. Build. Mater. 2018, 161, 124–131. [Google Scholar] [CrossRef]
- Ali, Y.; Irfan, M.; Zeeshan, M.; Hafeez, I.; Ahmed, S. Revisiting the relationship of dynamic and resilient modulus test for asphaltic concrete mixtures. Constr. Build. Mater. 2018, 170, 698–707. [Google Scholar] [CrossRef]
- Francken, I.; Clauwaert, C. Characterization and structural assessment of bound materials for flexible road structures. In Proceedings of the 6th International Conference on Structural Design of Asphalt Pavements, Ann Arbor, MI, USA, 13–17 July 1987. [Google Scholar]
- Lytton, R.; Uzan, J.; Fernando, E.G.; Roque, R.; Hiltmen, D.; Stoffels, S. Development and Validation of Performance Prediction Models and Spesifications for Asphalt Binders and Paving Mixtures; Report No. SHRP-A-357; SHRP: Washington, DC, USA, 1993. [Google Scholar]
- Jacobs, M.M.J. Crack Growth in Asphaltic Mixes. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1995. [Google Scholar]
- Williams, M.M.J.; Landel, R.F.; Ferry, J.D. Temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Appl. Phys. 1955, 77, 3701–3706. [Google Scholar] [CrossRef]
- Walubita, L.F.; Alvarez, A.E.; Simate, G.S. Evaluating and comparing different methods and models for generating relaxation modulus master-curves for asphalt mixes. Constr. Build. Mater. 2011, 25, 2619–2626. [Google Scholar] [CrossRef]
- Ling, M.; Luo, X.; Gu, F.; Lytton, R.L. Time-temperature-aging-depth shift functions for dynamic modulus master curves of asphalt mixtures. Constr. Build. Mater. 2017, 157, 943–951. [Google Scholar] [CrossRef]
- Marga, B. General Specification of Bina Marga 2010 Divisi 6; Bina Marga: Jakarta, Indonesia, 2010. [Google Scholar]
- AASHTO. Standard Specifications for Transportation Materials and Methods of Sampling and Testing, Part 2: Tests; AASHTO: Washington, DC, USA, 2008. [Google Scholar]
- Christensen, D.W.; Pellinen, T.K.; Bonaquist, R.F. Hirsch Model for Estimating the Modulus of Asphalt Concrete. J. Assoc. Asph. Paving Technol. Lexingt. 2003, 72, 97–121. [Google Scholar]
- Nemati, R.; Dave, E.V. “Nominal property based predictive models for asphalt mixture complex modulus (dynamic modulus and phase angle). Constr. Build. Mater. 2018, 158, 308–319. [Google Scholar] [CrossRef]
- Bayane, B.M.; Yang, E.; Yanjun, Q. Dynamic Modulus Master Curve Construction Using Christensen-Anderson-Marasteanu (CAM) model. Int. J. Eng. Res. Appl. 2017, 7, 53–63. [Google Scholar] [CrossRef]
- Bhasin, A.; Button, J.W.; Chowdhurry, A. Evaluation of Simple Performance Tests on HMA Mixture from the South Central United States; Report No FHWA/TX-03/9-558-1; Texas Transportation Institute: College Station, TX, USA, 2004. [Google Scholar]
- Sabahfar, N.; Azis, S.R.; Hossain, M.; Schieber, G. Evaluation of superpave mixtures with high percentages of reclaimed asphalt pavement. In Proceedings of the Annual Meeting of the Transportation Research Board, Washington, DC, USA, 12–16 January 2014. [Google Scholar]
- Suaryana, N. Performance evaluation of stone matrix asphalt using Indonesian natural rock asphalt as stabilizer. Int. J. Pavement Res. Technol. 2016, 9, 387–392. [Google Scholar] [CrossRef]
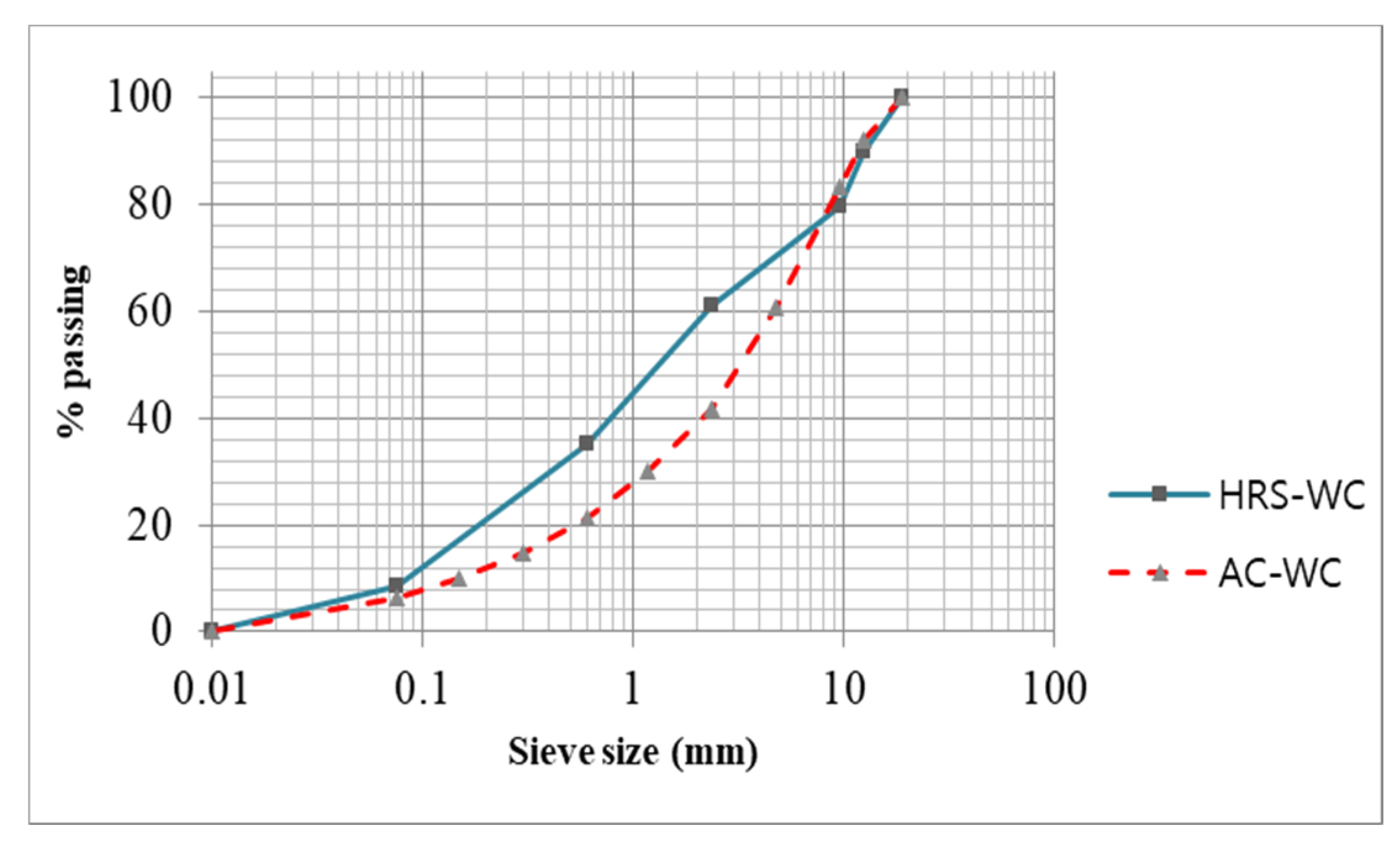



| Physical Property | Specification | Value |
|---|---|---|
| Penetration at 25 °C (0.1 mm) | 60–79 | 66 |
| Softening point (°C) | ≥48 | 53.5 |
| Ductility (mm) | ≥100 | ≥100 |
| Flash point (°C) | ≥232 | 270 |
| Specific gravity | ≥1.0 | 1.07 |
| Physical Property | Specification | Value |
|---|---|---|
| Bulk Specific Gravity | - | 2.59 |
| SSD Specific Gravity | - | 2.70 |
| Apparent Specific Gravity | - | 2.91 |
| Water Absorption | ≤5% | 4.17% |
| Sand Equivalent | ≥60% | 96.6% |
| Physical Property | Specification | Value |
|---|---|---|
| Abrasion | ≤30% | 20.90% |
| Bulk Specific Gravity | - | 2.49 |
| SSD Specific Gravity | - | 2.50 |
| Apparent Specific Gravity | - | 2.52 |
| Water Absorption | ≤3% | 0.51% |
| Marshall Properties | Unit | AC-WC | HRS-WC | ||
|---|---|---|---|---|---|
| Spec | Actual | Spec | Actual | ||
| Marshall Stability | Kg | ≥800 | 1412.31 | ≥800 | 1319.51 |
| Flow | mm | 2 ≤ 4 | 3.57 | ≥3 | 3.77 |
| VIM (Void in the mix) | % | 3 ≤ 5 | 4.54 | 4 ≤ 6 | 5.46 |
| VMA (Void in mineral aggregate) | % | ≥14 | 17.53 | ≥18 | 19.61 |
| VFWA (Void filled with asphalt) | % | ≥65 | 74.14 | ≥68 | 72.25 |
| Marshall Quotient (MQ) | Kg/mm | ≥250 | 402.03 | ≥250 | 356.37 |
| Density | gr/cm3 | 2.32 | 2.30 | ||
| |E*|, MPa (Temperature 15 °C, Frequency 10 Hz) | |E*|, MPa (Temperature 45 °C, Frequency of 0.01 Hz) | ||
|---|---|---|---|
| AC-WC | HRS-WC | AC-WC | HRS-WC |
| 6780 | 3107 | 205 | 162 |
| Rutting Factor = ǀE*ǀ/sin δ | Fatigue Factor = ǀE*ǀ × sin δ | ||||||
|---|---|---|---|---|---|---|---|
| AC-WC | HRS-WC | AC-WC | HRS-WC | ||||
| f (Hz) | f (Hz) | f (Hz) | f (Hz) | ||||
| 1 | 10 | 1 | 10 | 1 | 10 | 1 | 10 |
| 4795 | 11947 | 2623 | 6040 | 1384 | 2086 | 757 | 1161 |
| Test Temperature (°C) | f (Hz) | |
|---|---|---|
| 15 | 10 1 0.1 0.01 | 3071.6 2939.3 2365.7 1122.9 |
| 25 | 10 1 0.1 0.01 | 2938.2 2361.3 1117.6 402.3 |
| 35 | 10 1 0.1 0.01 | 2419.2 1191.1 422.3 258.3 |
| 45 | 10 1 0.1 0.01 | 1343.3 468.2 266.3 231.2 |
| Test Temperature (°C) | f (Hz) | |
|---|---|---|
| 15 | 10 1 0.1 0.01 | 2740.9 2047.9 1083.7 444.2 |
| 25 | 10 1 0.1 0.01 | 2135.4 1173.2 484.3 232 |
| 35 | 10 1 0.1 0.01 | 1322.5 557.9 254.0 166.0 |
| 45 | 10 1 0.1 0.01 | 676.3 291.3 176.8 143.8 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harnaeni, S.R.; Pramesti, F.P.; Budiarto, A.; Setyawan, A.; Khan, M.I.; Sutanto, M.H. Study on Structural Performance of Asphalt Concrete and Hot Rolled Sheet Through Viscoelastic Characterization. Materials 2020, 13, 1133. https://doi.org/10.3390/ma13051133
Harnaeni SR, Pramesti FP, Budiarto A, Setyawan A, Khan MI, Sutanto MH. Study on Structural Performance of Asphalt Concrete and Hot Rolled Sheet Through Viscoelastic Characterization. Materials. 2020; 13(5):1133. https://doi.org/10.3390/ma13051133
Chicago/Turabian StyleHarnaeni, Senja Rum, Florentina Pungky Pramesti, Arif Budiarto, Ary Setyawan, Muhammad Imran Khan, and Muslich Hartadi Sutanto. 2020. "Study on Structural Performance of Asphalt Concrete and Hot Rolled Sheet Through Viscoelastic Characterization" Materials 13, no. 5: 1133. https://doi.org/10.3390/ma13051133
APA StyleHarnaeni, S. R., Pramesti, F. P., Budiarto, A., Setyawan, A., Khan, M. I., & Sutanto, M. H. (2020). Study on Structural Performance of Asphalt Concrete and Hot Rolled Sheet Through Viscoelastic Characterization. Materials, 13(5), 1133. https://doi.org/10.3390/ma13051133





