Non-Tuned Machine Learning Approach for Predicting the Compressive Strength of High-Performance Concrete
Abstract
1. Introduction
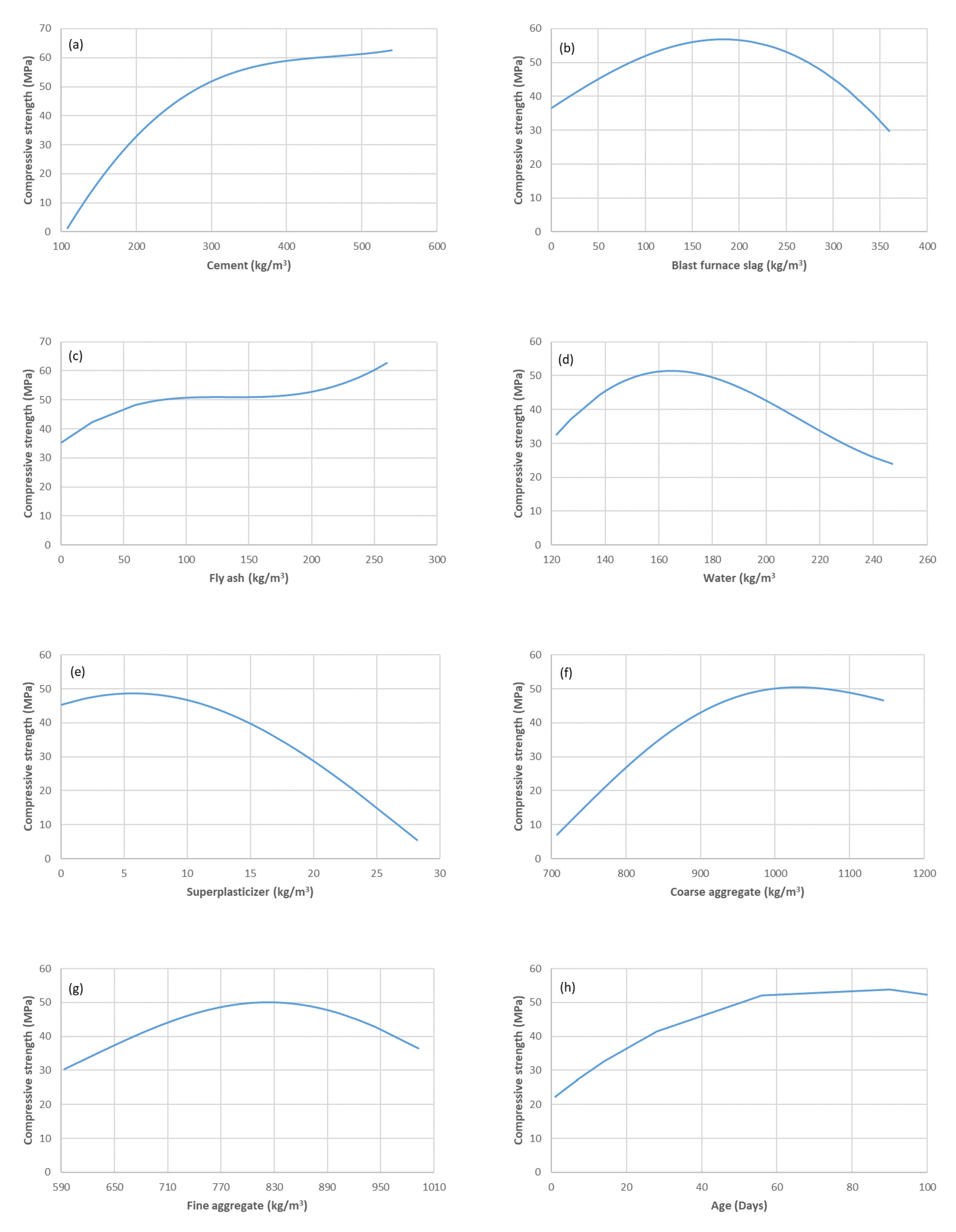
2. Experimental Dataset
3. Methods
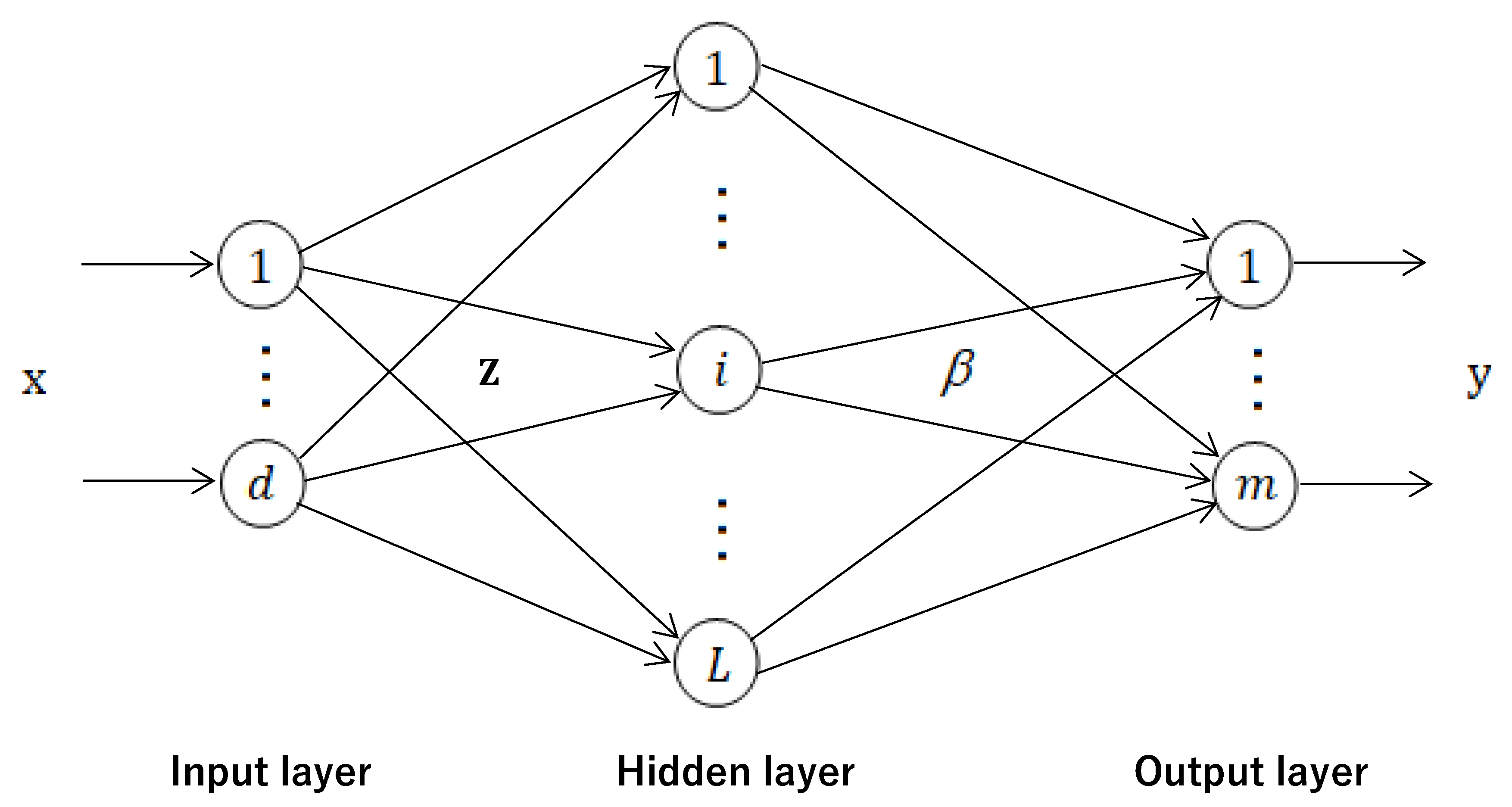
3.1. Extreme Learning Machine
3.2. Regularized Extreme Learning Machine
| Algorithm 1: Regularized extreme learning machine (RELM) Algorithm |
 |
4. Experimental Setting
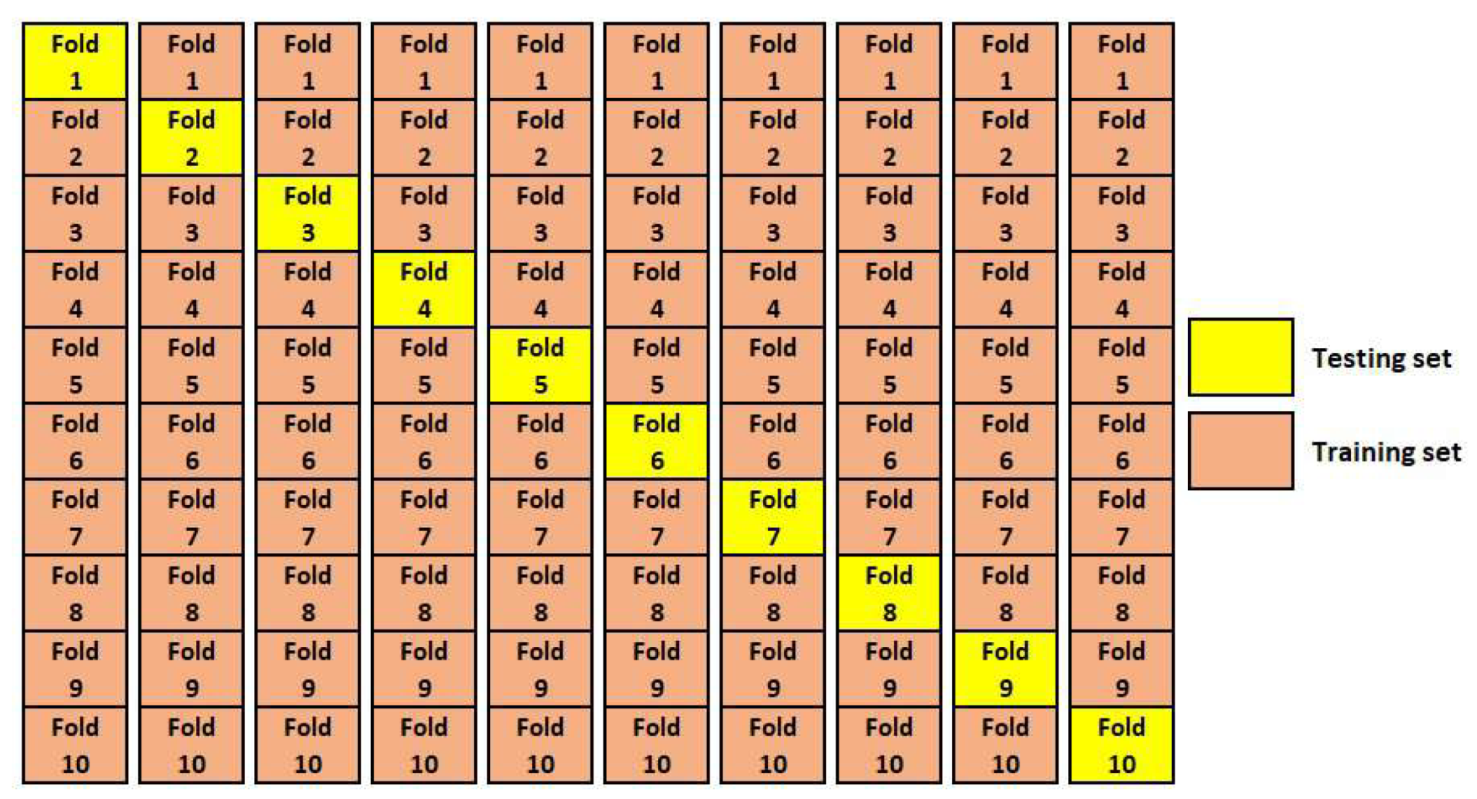
Performance-Evaluation Measures and Cross Validation
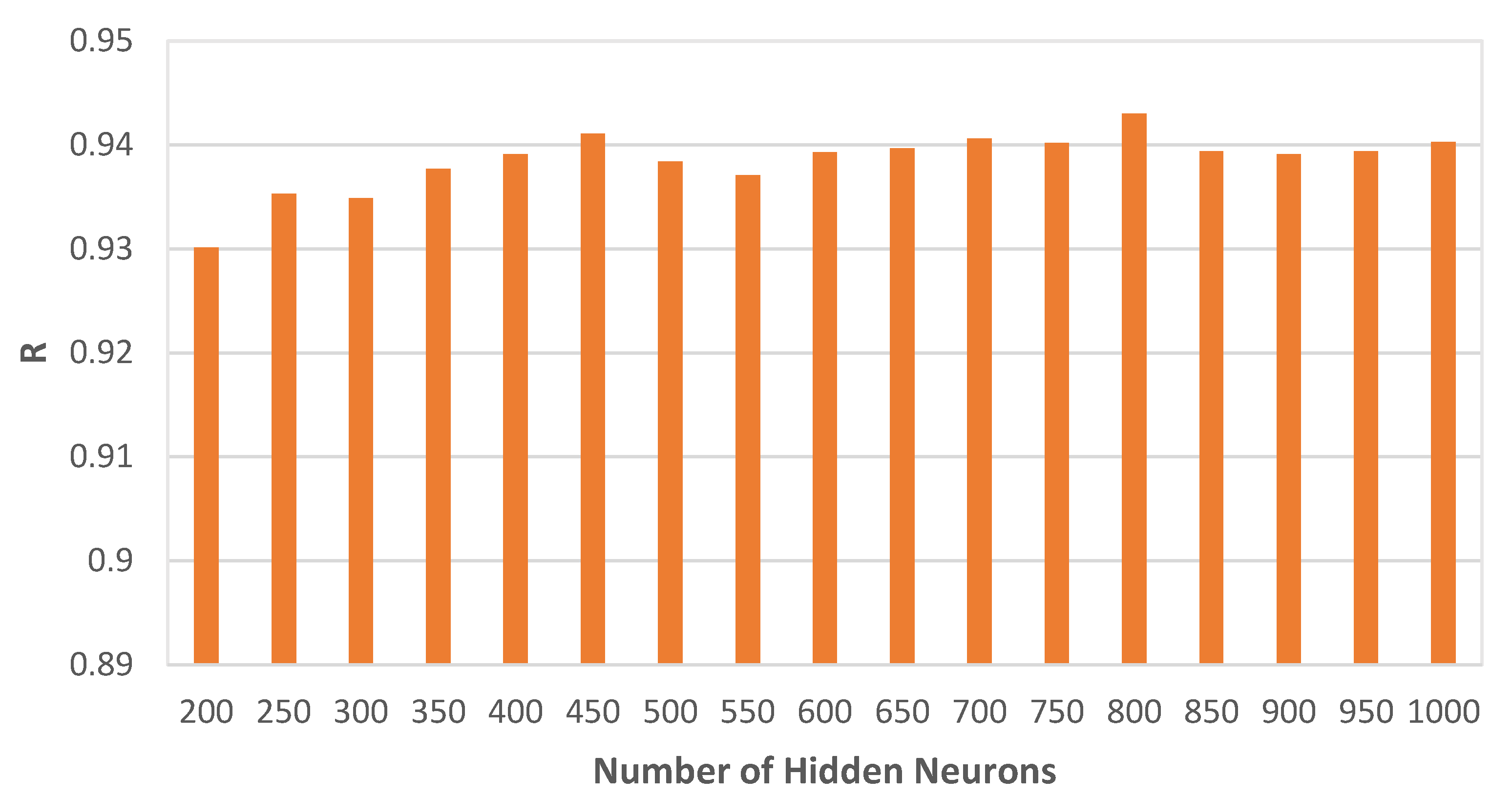
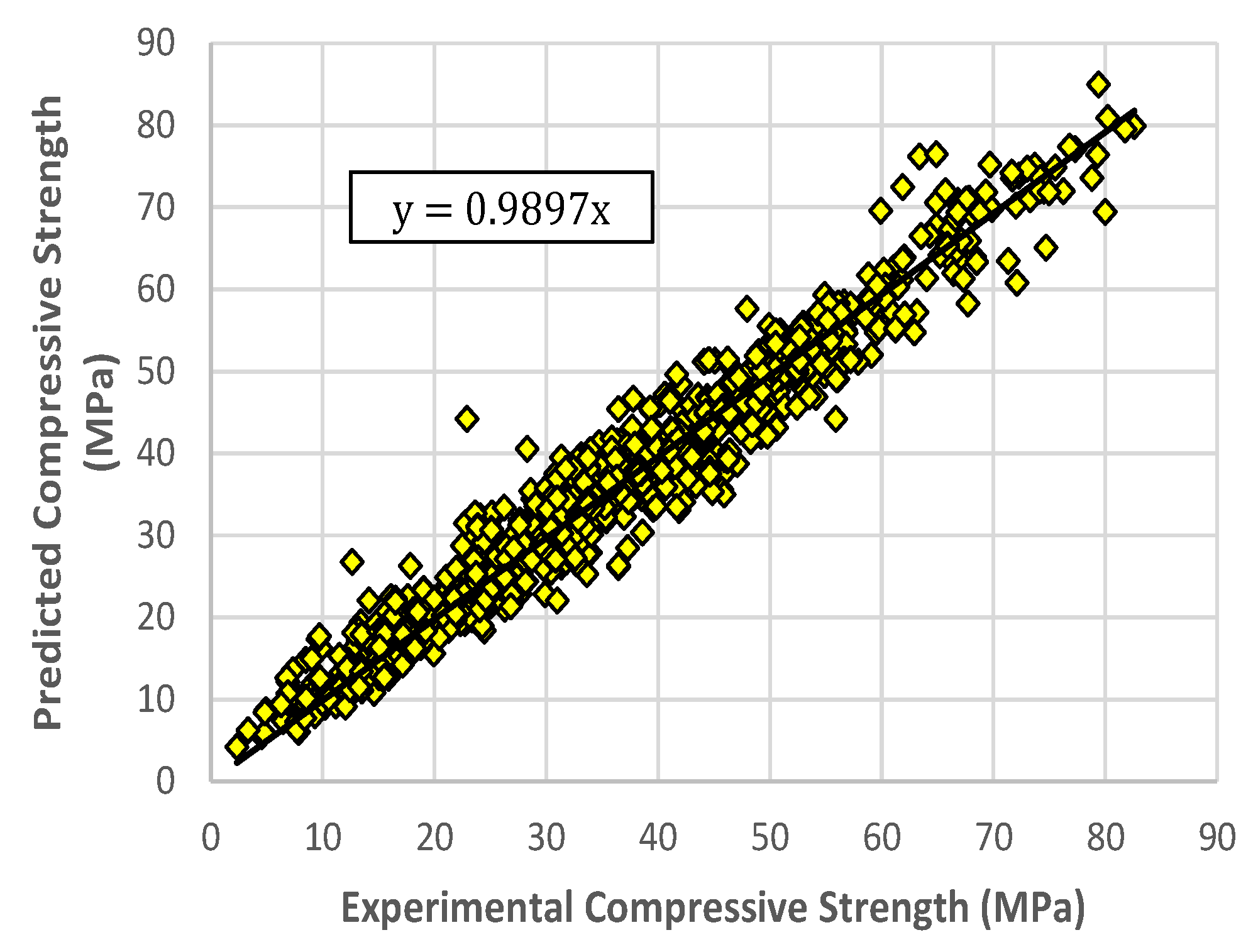
5. Results and Discussion
6. Conclusions
- Although the ELM model achieves good generalization performance (R = 0.929 on average), the RELM model performs even better.
- This research confirms that the use of regularization in ELM could prevent overfitting and improve the accuracy in estimating the HPC compressive strength.
- The RELM model can estimate the HPC compressive strength with higher accuracy than the ensemble methods presented in the literature.
- The proposed RELM model is simple, easy to implement, and has a strong potential for accurate estimation of HPC compressive strength.
- This work provides insights into the advantages of using ELM-based methods for predicting the compressive strength of concrete.
- The prediction performance of the ELM-based models can be improved by optimizing the initial input weights using optimization techniques such as harmony search, differential evolution, or other evolutionary methods.
Author Contributions
Funding
Conflicts of Interest
References
- Behnood, A.; Behnood, V.; Gharehveran, M.M.; Alyama, K.E. Prediction of the compressive strength of normal and high-performance concretes using M5P model tree algorithm. Constr. Build. Mater. 2017, 142, 199–207. [Google Scholar] [CrossRef]
- Al-Shamiri, A.K.; Kim, J.H.; Yuan, T.F.; Yoon, Y.S. Modeling the compressive strength of high-strength concrete: An extreme learning approach. Constr. Build. Mater. 2019, 208, 204–219. [Google Scholar] [CrossRef]
- Chou, J.S.; Pham, A.D. Enhanced artificial intelligence for ensemble approach to predicting high performance concrete compressive strength. Constr. Build. Mater. 2013, 49, 554–563. [Google Scholar] [CrossRef]
- Kewalramani, M.A.; Gupta, R. Concrete compressive strength prediction using ultrasonic pulse velocity through artificial neural networks. Automat. Constr. 2006, 15, 374–379. [Google Scholar] [CrossRef]
- Sobhani, J.; Najimi, M.; Pourkhorshidi, A.R.; Parhizkar, T. Prediction of the compressive strength of no-slump concrete: A comparative study of regression, neural network and ANFIS models. Constr. Build. Mater. 2010, 24, 709–718. [Google Scholar] [CrossRef]
- Naderpour, H.; Kheyroddin, A.; Amiri, G.G. Prediction of FRP-confined compressive strength of concrete using artificial neural networks. Compos. Struct. 2010, 92, 2817–2829. [Google Scholar] [CrossRef]
- Bingol, A.F.; Tortum, A.; Gul, R. Neural networks analysis of compressive strength of lightweight concrete after high temperatures. Mater. Des. 2013, 52, 258–264. [Google Scholar] [CrossRef]
- Sarıdemir, M. Prediction of compressive strength of concretes containing metakaolin and silica fume by artificial neural networks. Adv. Eng. Softw. 2009, 40, 350–355. [Google Scholar] [CrossRef]
- Yoon, J.Y.; Kim, H.; Lee, Y.J.; Sim, S.H. Prediction model for mechanical properties of lightweight aggregate concrete using artificial neural network. Materials 2019, 12, 2678. [Google Scholar] [CrossRef]
- Gilan, S.S.; Jovein, H.B.; Ramezanianpour, A.A. Hybrid support vector regression-Particle swarm optimization for prediction of compressive strength and RCPT of concretes containing metakaolin. Constr. Build. Mater. 2012, 34, 321–329. [Google Scholar] [CrossRef]
- Abd, A.M.; Abd, S.M. Modelling the strength of lightweight foamed concrete using support vector machine (SVM). Case Stud. Constr. Mater. 2017, 6, 8–15. [Google Scholar] [CrossRef]
- Erdal, H.I. Two-level and hybrid ensembles of decision trees for high performance concrete compressive strength prediction. Eng. Appl. Artif. Intell. 2013, 26, 1689–1697. [Google Scholar] [CrossRef]
- Oztas, A.; Pala, M.; Ozbay, E.; Kanca, E.; Caglar, N.; Bhatti, M.A. Predicting the compressive strength and slump of high strength concrete using neural network. Constr. Build. Mater. 2006, 20, 769–775. [Google Scholar] [CrossRef]
- Topcu, I.B.; Sarıdemir, M. Prediction of compressive strength of concrete containing fly ash using artificial neural networks and fuzzy logic. Comp. Mater. Sci. 2008, 41, 305–311. [Google Scholar] [CrossRef]
- Bilim, C.; Atis, C.D.; Tanyildizi, H.; Karahan, O. Predicting the compressive strength of ground granulated blast furnace slag concrete using artificial neural network. Adv. Eng. Softw. 2009, 40, 334–340. [Google Scholar] [CrossRef]
- Sarıdemir, M.; Topcu, I.B.; Ozcan, F.; Severcan, M.H. Prediction of long-term effects of GGBFS on compressive strength of concrete by artificial neural networks and fuzzy logic. Constr. Build. Mater. 2009, 23, 1279–1286. [Google Scholar] [CrossRef]
- Cascardi, A.; Micelli, F.; Aiello, M.A. An artificial neural networks model for the prediction of the compressive strength of FRP-confined concrete circular columns. Eng. Struct. 2017, 140, 199–208. [Google Scholar] [CrossRef]
- Duan, Z.; Kou, S.; Poon, C. Prediction of compressive strength of recycled aggregate concrete using artificial neural networks. Constr. Build. Mater. 2013, 40, 1200–1206. [Google Scholar] [CrossRef]
- Dantas, A.T.A.; Leite, M.B.; de Jesus Nagahama, K. Prediction of compressive strength of concrete containing construction and demolition waste using artificial neural networks. Constr. Build. Mater. 2013, 38, 717–722. [Google Scholar] [CrossRef]
- Sipos, T.K.; Milicevic, I.; Siddique, R. Model for mix design of brick aggregate concrete based on neural network modelling. Constr. Build. Mater. 2017, 148, 757–769. [Google Scholar] [CrossRef]
- Yu, Y.; Li, W.; Li, J.; Nguyen, T.N. A novel optimised self-learning method for compressive strength prediction of high performance concrete. Constr. Build. Mater. 2018, 148, 229–247. [Google Scholar]
- Mousavi, S.M.; Aminian, P.; Gandomi, A.H.; Alavi, A.H.; Bolandi, H. A new predictive model for compressive strength of HPC using gene expression programming. Adv. Eng. Softw. 2012, 45, 105–114. [Google Scholar] [CrossRef]
- Chithra, S.; Kumar, S.S.; Chinnaraju, K.; Ashmita, F.A. A comparative study on the compressive strength prediction models for high performance concrete containing nano silica and copper slag using regression analysis and artificial neural networks. Constr. Build. Mater. 2016, 114, 528–535. [Google Scholar] [CrossRef]
- Bui, D.K.; Nguyen, T.; Chou, J.S.; Nguyen-Xuan, H.; Ngo, T.D. A modified firefly algorithm-artificial neural network expert system for predicting compressive and tensile strength of high-performance concrete. Constr. Build. Mater. 2018, 180, 320–333. [Google Scholar] [CrossRef]
- Behnood, A.; Golafshani, E.M. Predicting the compressive strength of silica fume concrete using hybrid artificial neural network with multi-objective grey wolves. J. Clean. Prod. 2018, 202, 54–64. [Google Scholar] [CrossRef]
- Liu, G.; Zheng, J. Prediction Model of Compressive Strength Development in Concrete Containing Four Kinds of Gelled Materials with the Artificial Intelligence Method. Appl. Sci. 2019, 9, 1039. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feedforward neural networks. In Proceedings of the 2004 IEEE International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004; Volume 2, pp. 985–990. [Google Scholar]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Huang, G.B.; Chen, L.; Siew, C.K. Universal approximation using incremental constructive feedforward networks with random hidden nodes. IEEE Trans. Neural Netw. 2006, 17, 879–892. [Google Scholar] [CrossRef]
- Deng, W.; Zheng, Q.; Chen, L. Regularized extreme learning machine. In Proceedings of the 2009 IEEE Symposium on Computational Intelligence and Data Mining, Nashville, TN, USA, 30 March–2 April 2009; pp. 389–395. [Google Scholar]
- Yeh, I.C. Modeling of strength of high-performance concrete using artificial neural networks. Cem. Concr. Res. 1998, 28, 1797–1808. [Google Scholar] [CrossRef]
- Yeh, I.C. Modeling slump of concrete with fly ash and superplasticizer. Comput. Concr. 2008, 5, 559–572. [Google Scholar] [CrossRef]
- Mousavi, S.M.; Gandomi, A.H.; Alavi, A.H.; Vesalimahmood, M. Modeling of compressive strength of HPC mixes using a combined algorithm of genetic programming and orthogonal least squares. Struct. Eng. Mech. 2010, 36, 225–241. [Google Scholar] [CrossRef]
- Lan, Y.; Soh, Y.; Huang, G.B. Constructive hidden nodes selection of extreme learning machine for regression. Neurocomputing 2010, 73, 3191–3199. [Google Scholar] [CrossRef]
- Huang, G.B.; Chen, L. Convex incremental extreme learning machine. Neurocomputing 2007, 70, 3056–3062. [Google Scholar] [CrossRef]
- Huang, G.; Huang, G.B.; Song, S.; You, K. Trends in extreme learning machines: A review. Neural Netw. 2015, 61, 32–48. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.B. Learning capability and storage capacity of two-hidden-layer feedforward networks. IEEE Trans. Neural Netw. 2003, 14, 274–281. [Google Scholar] [CrossRef] [PubMed]
- Serre, D. Matrices: Theory and Applications; Springer: New York, NY, USA, 2002. [Google Scholar]
- Rao, C.R.; Mitra, S.K. Generalized Inverse of Matrices and Its Applications; Wiley: New York, NY, USA, 1971. [Google Scholar]
- Huang, G.B.; Zhou, H.; Ding, X.; Zhang, R. Extreme learning machine for regression and multiclass classification. IEEE Trans. Syst. Man Cybern. B 2012, 42, 513–529. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Luo, X.; Chang, X.; Ban, X. Regression and classification using extreme learning machine based on L1-norm and L2-norm. Neurocomputing 2016, 174, 179–186. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Zhu, Q.Y.; Qin, A.K.; Suganthan, P.N.; Huang, G.B. Evolutionary extreme learning machine. Pattern Recognit. 2005, 38, 1759–1763. [Google Scholar] [CrossRef]
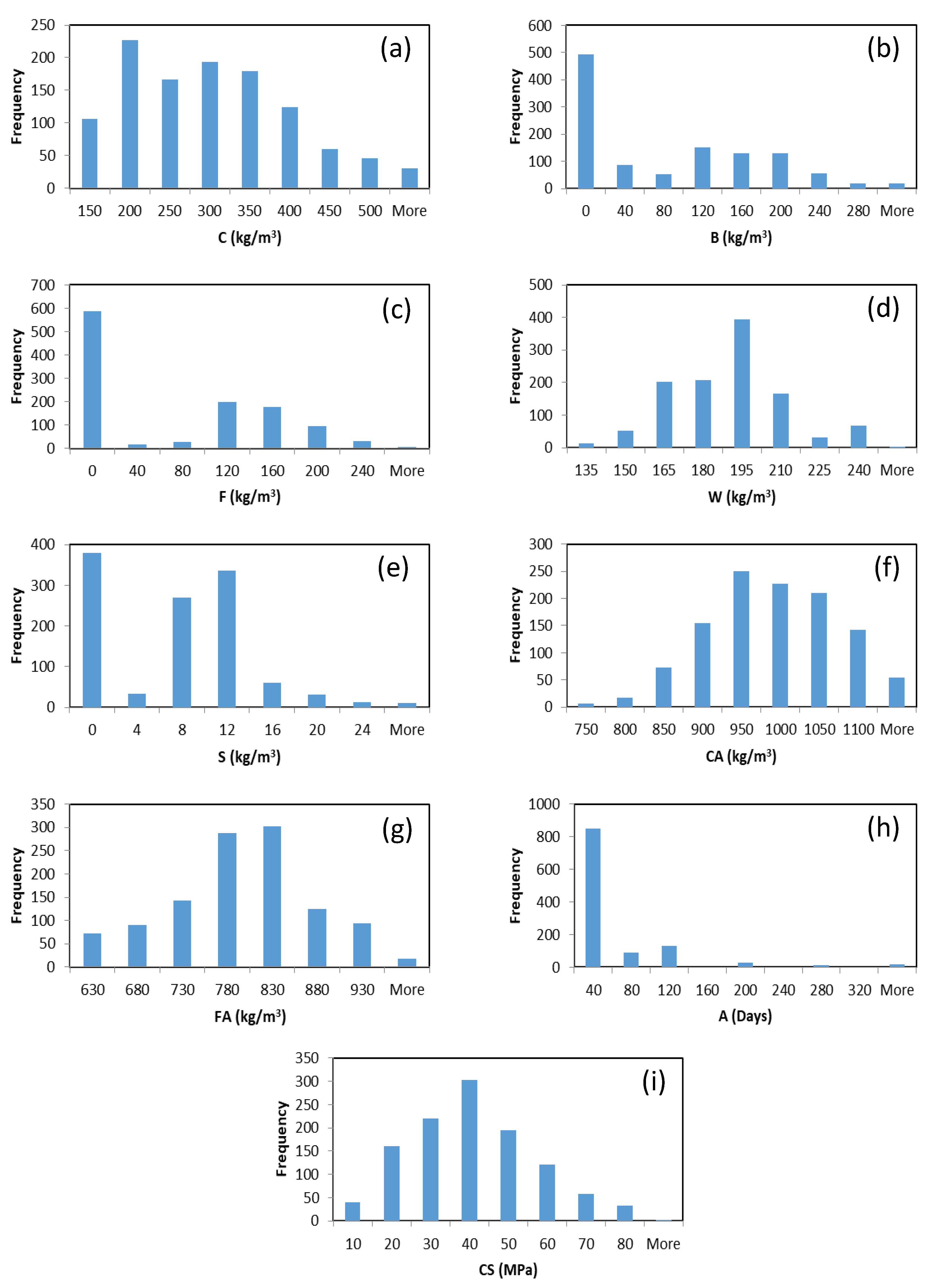



| Variable | Minimum | Maximum | Average | Standard Deviation |
|---|---|---|---|---|
| C (kg/m) | 102.00 | 540.00 | 276.51 | 103.47 |
| B (kg/m) | 0.00 | 359.40 | 74.27 | 84.25 |
| F (kg/m) | 0.00 | 260.00 | 62.81 | 71.58 |
| W (kg/m) | 121.80 | 247.00 | 182.99 | 21.71 |
| S (kg/m) | 0.00 | 32.20 | 6.42 | 5.80 |
| CA (kg/m) | 708.00 | 1145.00 | 964.83 | 82.79 |
| FA (kg/m) | 594.00 | 992.60 | 770.49 | 79.37 |
| A (Days) | 1.00 | 365.00 | 44.06 | 60.44 |
| CS (MPa) | 2.33 | 82.60 | 35.84 | 16.10 |
| Variable | C | B | F | W | S | CA | FA | A |
|---|---|---|---|---|---|---|---|---|
| C | 1.0000 | −0.2728 | −0.4204 | −0.0890 | 0.0674 | −0.0730 | −0.1859 | 0.0906 |
| B | −0.2728 | 1.0000 | −0.2889 | 0.0995 | 0.0527 | −0.2681 | −0.2760 | −0.0442 |
| F | −0.4204 | −0.2889 | 1.0000 | −0.1508 | 0.3528 | −0.1055 | −0.0062 | −0.1631 |
| W | −0.0890 | 0.0995 | −0.1508 | 1.0000 | −0.5882 | −0.2708 | −0.4247 | 0.2420 |
| S | 0.0674 | 0.0527 | 0.3528 | −0.5882 | 1.0000 | −0.2747 | 0.1985 | −0.1984 |
| CA | −0.0730 | −0.2681 | −0.1055 | −0.2708 | −0.2747 | 1.0000 | −0.1534 | 0.0233 |
| FA | −0.1859 | −0.2760 | −0.0062 | −0.4247 | 0.1985 | −0.1534 | 1.0000 | −0.1394 |
| A | 0.0906 | −0.0442 | −0.1631 | 0.2420 | −0.1984 | 0.0233 | −0.1394 | 1.0000 |
| Model | Dataset | RMSE (MPa) | MAE (MPa) | MAPE (%) | R |
|---|---|---|---|---|---|
| ELM | Training data | 4.1846 | 3.2062 | 11.3922 | 0.9656 |
| Testing data | 6.0377 | 4.4419 | 15.2558 | 0.929 | |
| All data | 4.4087 | 3.3298 | 11.7787 | 0.9617 | |
| RELM | Training data | 3.6737 | 2.7356 | 9.74 | 0.9736 |
| Testing data | 5.5075 | 3.9745 | 13.467 | 0.9403 | |
| All data | 3.8984 | 2.8595 | 10.1125 | 0.9702 |
| Model | Training Data | Testing Data | All Data |
|---|---|---|---|
| ELM | 0.1001 | 0.6739 | 0.1401 |
| RELM | 0.0405 | 0.5054 | 0.0771 |
| Method | Testing Data | |||
|---|---|---|---|---|
| RMSE (MPa) | MAE (MPa) | MAPE (%) | R | |
| ELM | 6.0377 | 4.4419 | 15.2558 | 0.929 |
| RELM | 5.5075 | 3.9745 | 13.467 | 0.9403 |
| Individual methods [3]: | ||||
| ANN | 6.329 | 4.421 | 15.3 | 0.930 |
| CART | 9.703 | 6.815 | 24.1 | 0.840 |
| CHAID | 8.983 | 6.088 | 20.7 | 0.861 |
| LR | 11.243 | 7.867 | 29.9 | 0.779 |
| GENLIN | 11.375 | 7.867 | 29.9 | 0.779 |
| SVM | 6.911 | 4.764 | 17.3 | 0.923 |
| Ensemble methods [3]: | ||||
| ANN + CHAID | 7.028 | 4.668 | 16.2 | 0.922 |
| ANN + SVM | 6.174 | 4.236 | 15.2 | 0.939 |
| CHAID + SVM | 6.692 | 4.580 | 16.3 | 0.929 |
| ANN + SVM + CHAID | 6.231 | 4.279 | 15.2 | 0.939 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Shamiri, A.K.; Yuan, T.-F.; Kim, J.H. Non-Tuned Machine Learning Approach for Predicting the Compressive Strength of High-Performance Concrete. Materials 2020, 13, 1023. https://doi.org/10.3390/ma13051023
Al-Shamiri AK, Yuan T-F, Kim JH. Non-Tuned Machine Learning Approach for Predicting the Compressive Strength of High-Performance Concrete. Materials. 2020; 13(5):1023. https://doi.org/10.3390/ma13051023
Chicago/Turabian StyleAl-Shamiri, Abobakr Khalil, Tian-Feng Yuan, and Joong Hoon Kim. 2020. "Non-Tuned Machine Learning Approach for Predicting the Compressive Strength of High-Performance Concrete" Materials 13, no. 5: 1023. https://doi.org/10.3390/ma13051023
APA StyleAl-Shamiri, A. K., Yuan, T.-F., & Kim, J. H. (2020). Non-Tuned Machine Learning Approach for Predicting the Compressive Strength of High-Performance Concrete. Materials, 13(5), 1023. https://doi.org/10.3390/ma13051023







