Hot Deformation Behavior and Microstructural Evolution of PM Ti43Al9V0.3Y with Fine Equiaxed γ and B2 Grain Microstructure
Abstract
1. Introduction
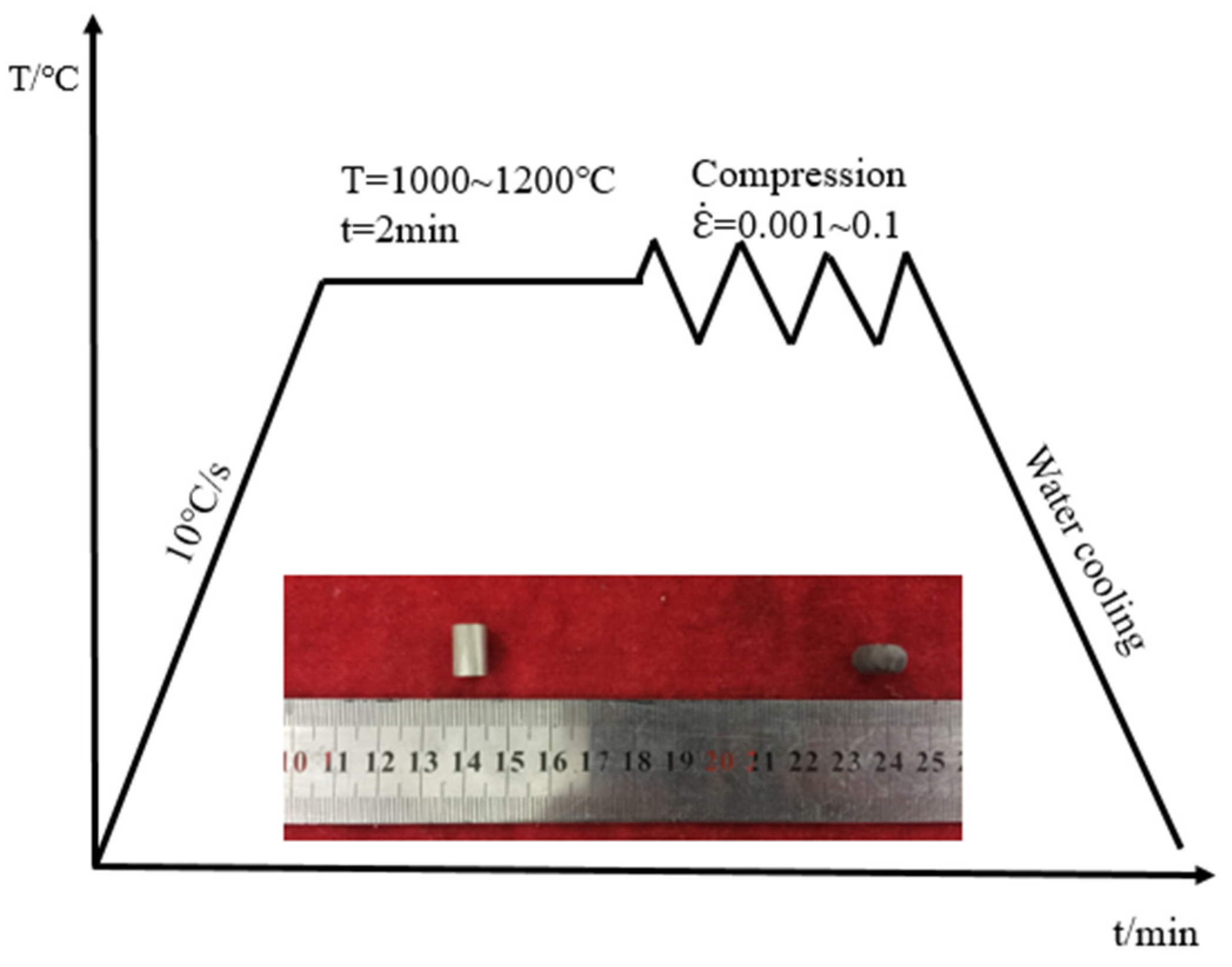
2. Materials and Experimental Procedure
3. Results and Discussion
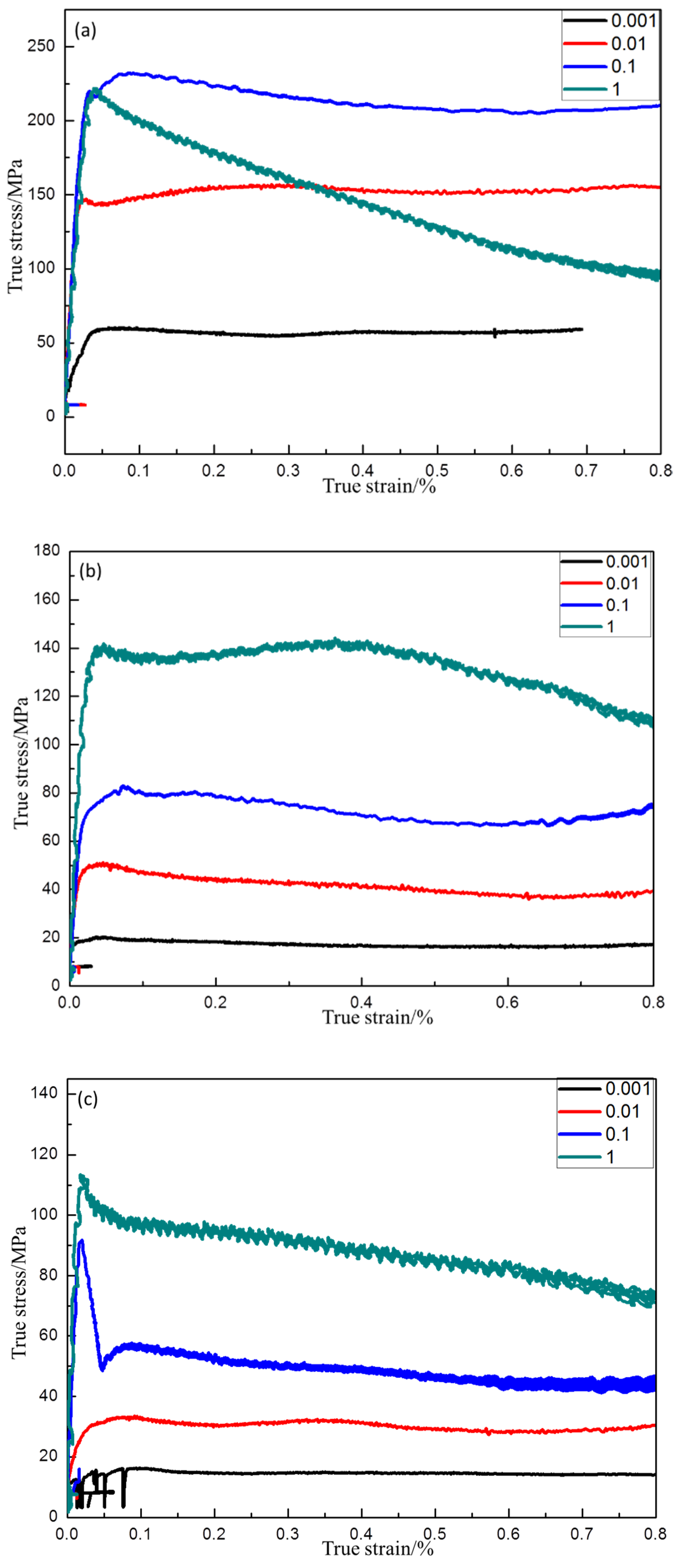
3.1. Flow Behavior
3.2. Activation Energy
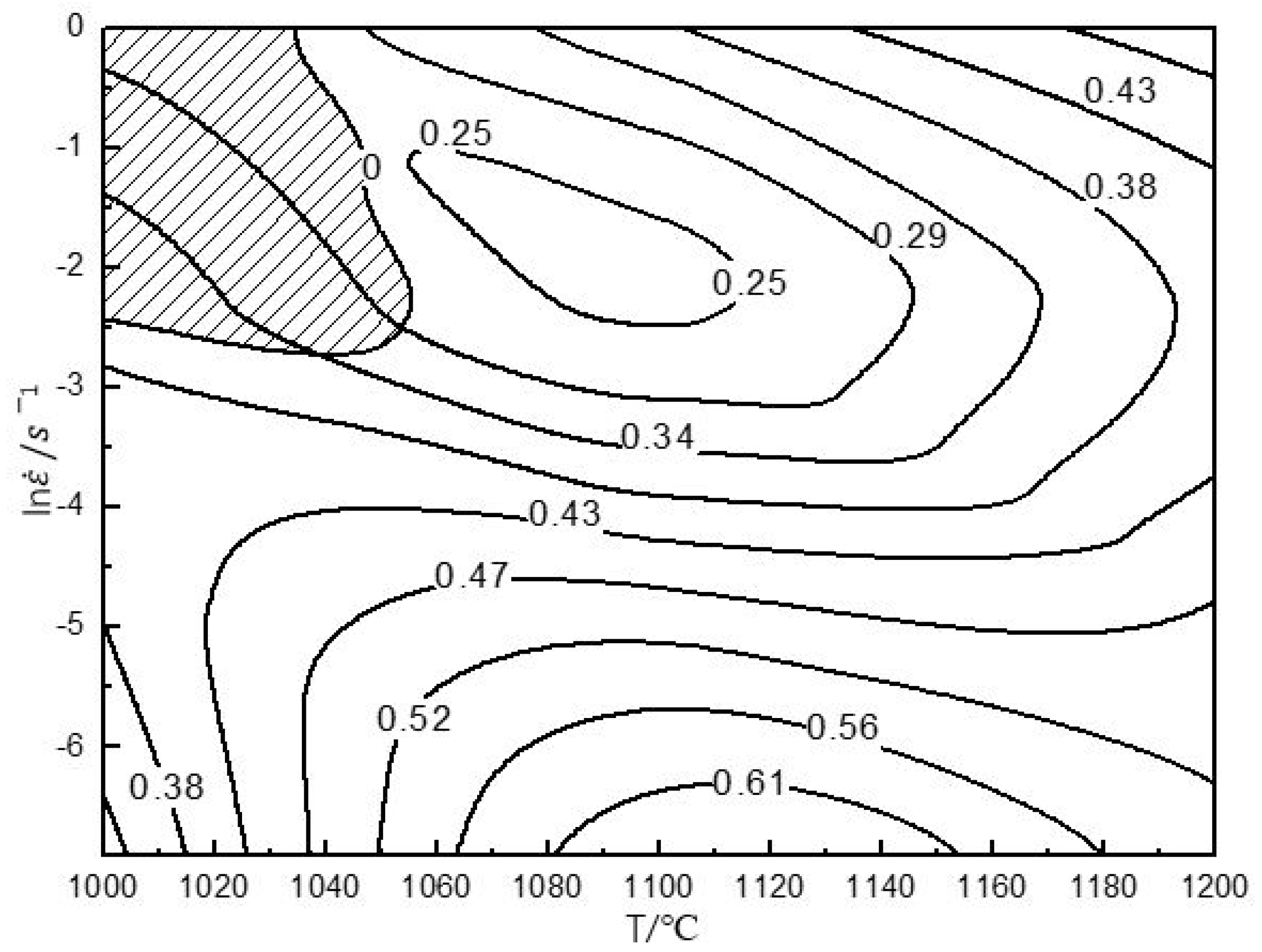
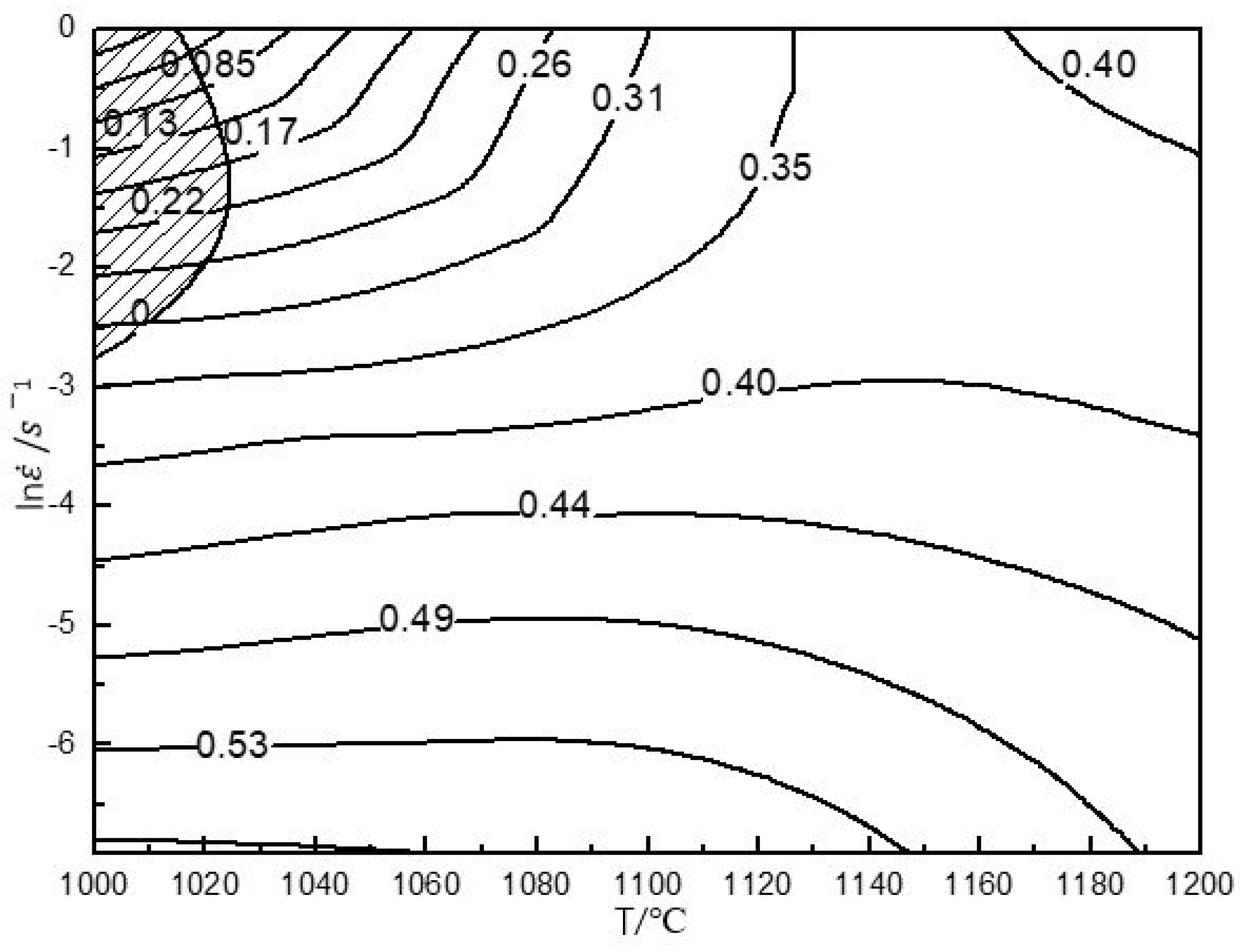
3.3. Hot Processing Map
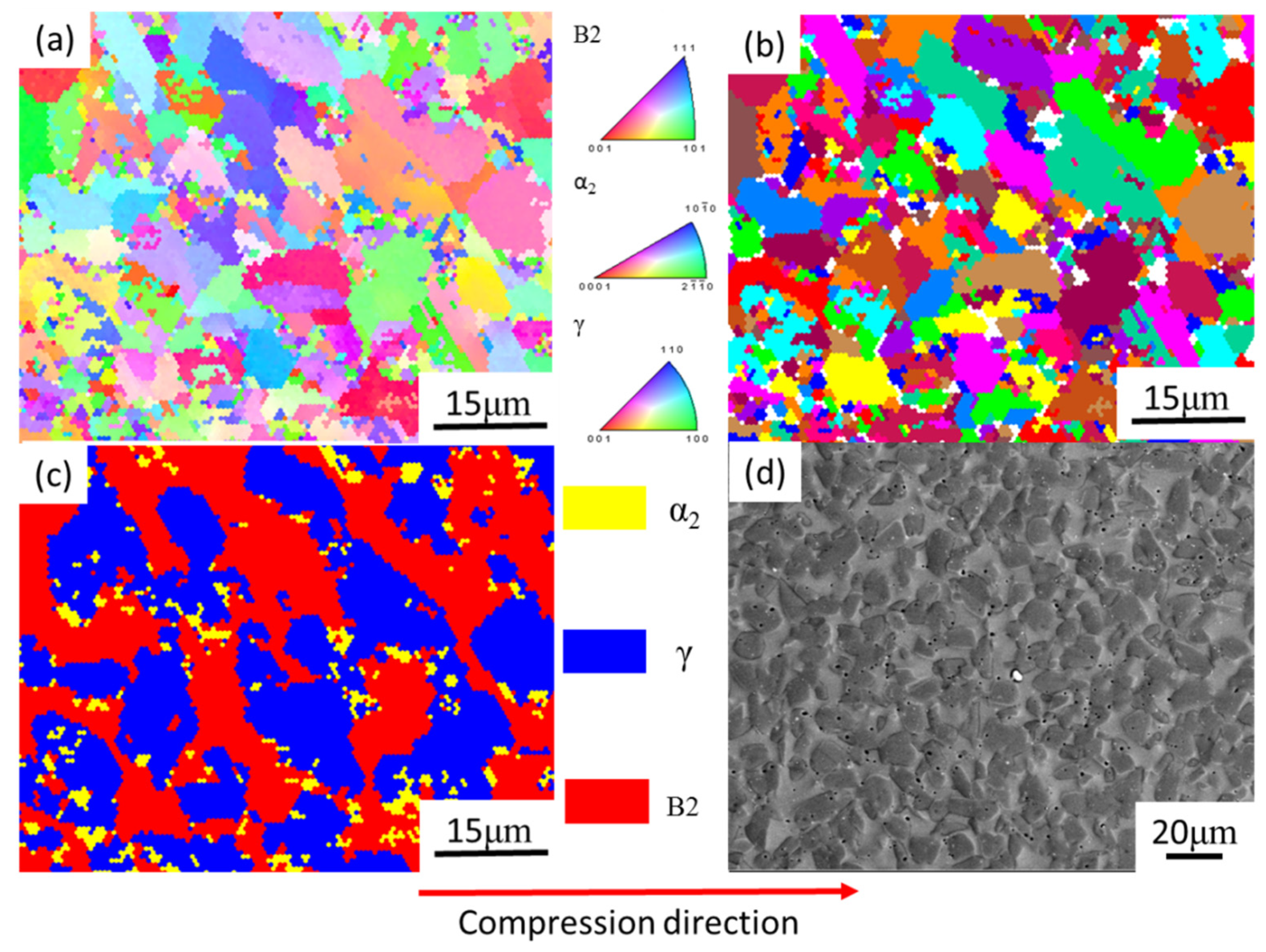
3.4. Deformed Microstructures
4. Conclusions
- The stress exponent and activation energy of PM Ti43Al9V0.3Y alloys with fine equiaxed γ and B2 grain microstructure were 2.78 and 295.86 kJ/mol, respectively.
- Reasonable hot working parameters at 80% strain were 1100–1200 °C/≤1 s−1. Furthermore, suitable hot working parameters at 50% strain were 1150–1200 °C/≤1 s−1 and 1000–1200 °C/≤0.05 s−1.
- The microstructure evolution was found to be dependent on temperature, strain, and strain rate. When the deformation temperature was 1200 °C, the α phase mainly replaced the β phase, leading to a decrease in hot workability. Increases in temperature and strain both led to a decrease in γ.
- The β phase is important for high-temperature deformation. Moreover, DRX contributes to the major deformation.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ding, X.F.; Lin, J.P.; Zhang, L.Q.; Su, Y.Q.; Chen, G.L. Microstructural control of TiAlNb alloys by directional solidification. Acta Mater. 2012, 60, 498–506. [Google Scholar] [CrossRef]
- Chen, G.; Peng, Y.B.; Zheng, G.; Qi, Z.X.; Wang, M.Z.; Yu, H.C.; Dong, C.L.; Liu, C.T. Polysynthetic twinned TiAl single crystals for high-temperature applications. Nat. Mater. 2016, 15, 876–881. [Google Scholar] [CrossRef]
- Appel, F.; Paul, J.D.H.; Oehring, M. Gamma Titanium Aluminide Alloys: Science and Technology; John Wiley & Sons: New York, NY, USA, 2011. [Google Scholar]
- Clemens, H.; Mayer, S. Design, processing, microstructure, properties, and applications of advanced intermetallic TiAl alloys. Adv. Eng. Mater. 2013, 15, 191–215. [Google Scholar] [CrossRef]
- Ning, C.; Qianqian, W.; Jin, W.; Binjiang, L.; Fantao, K. The Directional Solidification, Microstructural Characterization and Deformation Behavior of β-Solidifying TiAl Alloy. Materials 2019, 12, 1203. [Google Scholar]
- Djanarthany, S.; Viala, J.C.; Bouix, J. An overview of monolithic titanium aluminides based on Ti3Al and TiAl. Mater. Chem. Phys. 2001, 72, 301–319. [Google Scholar] [CrossRef]
- Kim, Y.W. Effects of microstructure on the deformation and fracture of γ-TiAl alloys. Mater. Sci. Eng. A 1995, 192, 519–533. [Google Scholar] [CrossRef]
- Wang, J.N.; Zhu, J.; Wu, J.S.; Du, X.W. Effects of alloying elements on creep of TiAl alloys with a fine lamellar structure. Acta Mater. 2002, 50, 13–18. [Google Scholar] [CrossRef]
- Izumi, T.; Yoshioka, T.; Hayashi, S.; Narita, T. Oxidation behavior of sulfidation processed TiAl-2 at % X (X ¼ V, Fe, Co, Cu, Nb, Mo, Ag and W) alloys at 1173 k in air. Intermetallics 2001, 9, 54–58. [Google Scholar] [CrossRef]
- Loretto, M.H.; Godfrey, A.B.; Hu, D.; Blenkinsop, P.A.; Jones, I.P.; Cheng, T.T. The influence of composition and processing on the structure and properties of TiAlbased alloys. Intermetallics 1998, 6, 6–7. [Google Scholar] [CrossRef]
- Bartels, A.; Kestler, H.; Clemens, H. Deformation behavior of differently processed g-titanium aluminides. Mater. Sci. Eng. A 2002, 62, 329–331. [Google Scholar] [CrossRef]
- Chladil, H.F.; Clemens, H.; Zickler, G.A.; Takeyama, M.; Kozeschnik, E.; Bartels, A.; Buslaps, T.; Gerling, R.; Kremmer, S.; Yeoh, L.; et al. Experimental studies and thermodynamic simulation of phase transformations in high Nb containing γ-TiAl based alloys. Int. J. Mater. Res. 2007, 98, 1131–1137. [Google Scholar] [CrossRef]
- Xu, X.J.; Lin, J.P.; Wang, Y.L.; Lin, Z.; Chen, G.L. Deformability and microstructure transformation of pilot ingot of Ti–45Al–(8–9) Nb–(W, B, Y) alloy. Mater. Sci. Eng. A 2006, 416, 98–103. [Google Scholar] [CrossRef]
- Schmoelzer, T.; Liss, K.D.; Zickler, G.A.; Watson, I.J.; Droessler, L.M.; Wallgram, W.; Buslaps, T.; Studer, A.; Clemens, H. Phase fractions, transition and ordering temperatures in TiAl–Nb–Mo alloys: An in-and exsitu study. Intermetallics 2010, 18, 1544–1552. [Google Scholar] [CrossRef]
- Niu, H.Z.; Chen, Y.Y.; Xiao, S.L.; Xu, L.J. Microstructure evolution and mechanical properties of a novel beta γ-TiAl alloy. Intermetallics 2012, 31, 225–231. [Google Scholar] [CrossRef]
- Clemens, H.; Chladil, H.F.; Wallgram, W.; Zickler, G.A.; Gerling, R.; Liss, K.D.; Kremmer, S.; Güther, V.; Smarsly, W. In and ex situ investigations of the β-phase in a Nb and Mo containing γ-TiAl based alloy. Intermetallics 2008, 16, 827–833. [Google Scholar] [CrossRef]
- Appel, F.; Oehring, M.; Paul, J.D.H. Nano-scale design of TiAl alloys based on β phase decomposition. Adv. Eng. Mater. 2006, 8, 371. [Google Scholar] [CrossRef]
- Takeyama, M.; Kobayashi, S. Physical metallurgy for wrought gamma titanium aluminides: Microstructure control through phase transformations. Intermetallics 2005, 9, 13. [Google Scholar]
- Imayev, V.; Imayev, R.; Khismatullin, T.; Guther, V.; Beck, W.; Fecht, H.J. Superplastic behavior of Ti-43Al-7(Nb, Mo)-0.2B alloy in the cast þ heat-treated condition. Scr. Mater. 2007, 6, 57. [Google Scholar]
- Witusiewicz, V.T.; Bondar, A.A.; Hecht, U.; Velikanova, T.Y. The Al-B-Nb-Ti system. IV. Experimental study and thermodynamic re-evaluation of the binary Al-Nb and ternary Al-Nb-Ti systems. J. Alloy. Compd. 2009, 472, 133–161. [Google Scholar] [CrossRef]
- Sun, F.S.; Cao, C.X.; Yan, M.G.; Kim, S.E. Alloying mechanism of beta stabilizers in a TiAl alloy. Metall. Mater. Trans. A 2001, 32, 1573–1589. [Google Scholar] [CrossRef]
- Su, Y.; Kong, F.; Chen, Y.; Gao, N.; Zhang, D. Microstructure and mechanical properties of large size Ti-43Al-9V-0.2Y alloy pancake produced by pack-forging. Intermetallics 2013, 34, 29–34. [Google Scholar] [CrossRef]
- Wei, F.; Youheng, F. High temperature deformation behavior and constitutive modeling for 20CrMnTiH steel. Mater. Des. 2014, 57, 465–471. [Google Scholar]
- Zhou, S.S.; Deng, K.K.; Li, J.C.; Nie, K.B.; Xu, F.J.; Zhou, H.F.; Fan, J.F. Hot deformation behavior and workability characteristics of bimodal size SiCp/AZ91 magnesium matrix composite with processing map. Mater. Des. 2014, 64, 177–184. [Google Scholar] [CrossRef]
- Wang, G.; Xu, L.; Tian, Y.X.; Zheng, Z.; Cui, Y.Y.; Yang, R. Flow behavior and microstructure evolution of a P/M TiAl alloy during high temperature deformation. Mater. Sci. Eng. A 2011, 528, 6754–6763. [Google Scholar] [CrossRef]
- Lin, Y.C.; Chen, X.M. A critical review of experimental results and constitutive descriptions for metals and alloys in hot working. Mater. Des. 2011, 32, 1733–1759. [Google Scholar] [CrossRef]
- Rusinek, A.; Rodrı’guez-Martı´nez, J.A.; Arias, A. A thermo-viscoplastic constitutive model for FCC metals with application to OFHC Copper. Int. J. Mech. Sci. 2010, 52, 120–135. [Google Scholar] [CrossRef]
- Shin, H.; Kim, J.B. A phenomenological constitutive equation to describe various flow stress behaviors of materials in wide strain rate and temperature regimes. J. Eng. Mater. 2010, 132, 021009. [Google Scholar] [CrossRef]
- Peng, X.N.; Guo, H.Z.; Shi, Z.F.; Qin, C.; Zhao, Z.L. Constitutive Equations for High Temperature Flow Stress of TC4-DT Alloy Incorporating Strain, Strain Rate and Temperature. Mater. Des. 2013, 50, 198–206. [Google Scholar] [CrossRef]
- Sellars, C.M.; Tegart, W.J.M. On the Mechanism of Hot Deformation. Acta Metall. 1996, 14, 1136–1138. [Google Scholar] [CrossRef]
- Rao, K.P.; Prasad, Y.V.R.K.; Suresh, K. Hot working behavior and processing map of a γ-TiAl alloy synthesized by powder metallurgy. Mater. Des. 2011, 32, 4874–4881. [Google Scholar] [CrossRef]
- Rao, K.P.; Prasad YV, R.K. Processing map and hot working mechanisms in a P/M TiAl alloy composite with in situ carbide and silicide dispersions. Mater. Sci. Eng. A 2010, 527, 6589–6595. [Google Scholar] [CrossRef]
- Zeng, Z.P.; Jonsson, S.; Zhang, Y.S. Constitutive Equations for Pure Titanium at Elevated Temperatures. Mater. Sci. Eng. A 2009, 505, 116–119. [Google Scholar] [CrossRef]
- Wang, Z.J.; Qiang, H.F.; Wang, X.R.; Wang, G. Constitutive Model for a New Kind of Metastable b Titanium Alloy During Hot Deformation. Trans. Nonferrous Met. Soc. China 2012, 22, 634–641. [Google Scholar] [CrossRef]
- Liao, C.H.; Wu, H.R.; Lee, S.Y.; Zhu, F.J.; Liu, H.C.; Wu, C.T. Strain Dependent Constitutive Analysis of Extruded AZ61 Mg Alloy Under Hot Compression. Mater. Sci. Eng. A 2013, 565, 1–8. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, L.X.; Sun, Y. Deformation Behaviour and Dynamic Recrystallization of AZ61 Magnesium Alloy. J. Alloys Compd. 2013, 580, 262–269. [Google Scholar] [CrossRef]
- Li, W.; Li, H.; Wang, Z.X.; Zheng, Z.Q. Constitutive Equations for High Temperature Flow Stress Prediction of Al-14Cu-7Ce Alloy. Mater. Sci. Eng. A 2011, 528, 4098–4103. [Google Scholar] [CrossRef]
- Lin, Y.C.; Li, Q.F.; Xia, Y.C.; Li, L.T. A Phenomenological Constit utive Model for High Temperature Flow Stress Prediction of AlCu-Mg Alloy. Mater. Sci. Eng. A 2012, 534, 654–662. [Google Scholar] [CrossRef]
- Raj, R. Development of a Processing Map for Use in Warm-Forming and Hot-Forming Processes. Metall. Trans. A 1981, 12, 1089–1097. [Google Scholar] [CrossRef]
- Prasad, Y.V.R.K.; Gegel, H.J.; Doraivelu, S.M.; Malas, J.C.; Morgan, J.T.; Lark, L.A.; Barker, D.R. Modeling of dynamic material behavior in hot deformation: Forging of Ti-6242. Metall. Trans. A 1984, 15, 1883–1892. [Google Scholar] [CrossRef]
- Zhang, D.; Liu, N.; Chen, Y.; Zhang, G.; Tian, J.; Kong, F.; Xiao, S.; Sun, J. Microstructure Evolution and Mechanical Properties of PM-Ti43Al9V0.3Y Alloy. Materials 2020, 13, 198. [Google Scholar] [CrossRef]
- Kumpfert, C. Leyens, Orthorhombic titanium aluminides: Intermetallics with improved damage tolerance. Titan. Titan. Alloy. Fundam. Appl. 2003, 2003, 59–88. [Google Scholar]
- Yamabe, Y.; Takeyama, M.; Kikuchi, M. Gamma Titanium Aluminides; Kim, Y.-W., Wagner, R., Yamaguchi, M., Eds.; TMS: Warrendale, PA, USA, 1995; p. 111. [Google Scholar]
- Uvira, J.L.; Jonas, J.J. Hot Compression of Armco Iron and Silicon Steel. Trans. Metall. Soc. AIME 1968, 242, 1619–1626. [Google Scholar]
- Ebrahimi, R.; Najafizadeh, A. A new method for evaluation of friction in bulk metal forming. J. Mater. Process. Technol. 2004, 152, 136–143. [Google Scholar] [CrossRef]
- Gnofam Jacques, T.; Dimitri, J.; Egoitz, A.; Dominique, C.; Esther, G.-O.; Franck Girot, M.; Beric, L. Analytical modeling of hot behavior of Ti-6Al-4V alloy at large strain. Mater. Des. 2019, 161, 114–123. [Google Scholar]
- Li, L.X.; Lou, Y.; Yang, L.B.; Peng, D.S.; Rao, K.P. Flow stress behavior and deformation characteristics of Ti-3Al-5V-5Mo compressed at elevated temperatures. Mater. Des. 2002, 23, 451–457. [Google Scholar] [CrossRef]
- Philippart, I.; Rack, H.J. High temperature dynamic yielding in metastable Ti–6.8Mo–4.5F–1.5Al. Mater. Sci. Eng. A 1998, 243, 196–200. [Google Scholar] [CrossRef]
- Long, M.; Rack, H.J. Proc. World Conference on Titanium, Titanium ’95; Blenkinsop, P.A., Evans, W.J., Flower, H.M., Eds.; Science and Technology, The Institute of Materials: London, UK, 1996; p. 316. [Google Scholar]
- Liu, B.; Liu, Y.; Zhang, W.; Huang, J.S. Hot deformation behavior of TiAl alloys prepared by blended elemental powders. Intermetallics 2011, 9, 19. [Google Scholar] [CrossRef]
- Kim, J.H.; Ha, T.K.; Chang, Y.W.; Lee, C.S. High temperature deformation behavior of γ-TiAl alloy-microstructural evolution and mechanisms. Metall. Mater. Trans. A 2003, 7, 34. [Google Scholar] [CrossRef]
- Huang, J.S.; Huang, L.; Liu, B.; Zhang, Y.H.; Zhang, W.; He, X.Y.; Liu, Y. Simulation of hot compression of Ti–Al alloy. Intermetallics 2007, 5, 15. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, Y.; Li, H.Z.; Li, Z.; Wang, H.; Liu, B. Constitutive modeling and processing maps for elevated temperature flow behaviors of a powder metallurgy titanium aluminide alloy. J. Mater. Proc. Technol. 2009, 70, 5363. [Google Scholar] [CrossRef]
- Jingjing, X.; Laiqi, Z.; Gengwu, G.; Junpin, L. Characterization of microstructure evolution in β-γ TiAl alloy containing high content of Niobium using constitutive equation and power dissipation map. Mater. Des. 2016, 107, 406–415. [Google Scholar]
- Fantao, K.; Ning, C.; Yuyong, C.; Xiaopeng, W.; Ningning, X. Characterization of hot deformation behavior of as-forged TiAl alloy. Intermetallics 2014, 55, 66–72. [Google Scholar]
- Haitao, Z.; Fantao, K.; Xiaopeng, W.; Yuyong, C. Hot deformation behavior and microstructural evolution of as-forged Ti-44Al-8Nb-(W, B, Y) alloy with nearly lamellar microstructure. Intermetallics 2017, 81, 62–72. [Google Scholar]
- Sriram, S.; Vasudevan, V.K.; Dimiduk, D.M. Dislocation structures and deformation behavior of Ti-50/52Al alloys between 77–1273K. Mater. Sci. Eng. 1995, 217–225. [Google Scholar] [CrossRef]
- Trivedi, P.B.; Baburaj, E.G.; Genc, A.; Ovecoglu, L.; Patankar, S.N.; Froes, F.H. Grainsize control in Ti-48Al-2Cr-2Nb with yttrium additions. Metall. Mater. Trans. A 2002, 33, 2729–2736. [Google Scholar] [CrossRef]
- Sokolovsky, V.S.; Stepanov, N.D.; Zherebtsov, S.V.; Nochovnaya, N.A.; Panin, P.V.; Zhilyakova, M.A.; Popov, A.A.; Salishchev, G.A. Hot deformation behavior and processing maps of B and Gd containing β-solidified TiAl based alloy. Intermetallics 2018, 94, 138–151. [Google Scholar] [CrossRef]
- Araki, S.; Mashima, K.; Masumura, T.; Tsuchiyama, T.; Takaki, S.; Ohmura, T. Effect of grain boundary segregation of carbon on critical grain boundary strength of ferritic steel. Scr. Mater. 2019, 169, 38–41. [Google Scholar] [CrossRef]
- Li, W.; Yang, Y.; Li, M.; Liu, J.; Cai, D.; Wei, Q.; Yan, C.; Shi, Y. Enhanced mechanical property with refined microstructure of a novel γ-TiAl/TiB2 metal matrix composite (MMC) processed via hot isostatic press. Mater. Des. 2018, 141, 57–66. [Google Scholar] [CrossRef]
- Chen, X.M.; Lin, Y.C.; Wen, D.X.; Zhang, J.L.; He, M. Dynamic recrystallization behavior of a typical nickel-based superalloy during hot deformation. Mater. Des. 2014, 57, 568–577. [Google Scholar] [CrossRef]
- Lin, Y.C.; He, D.G.; Chen, M.S.; Chen, X.M.; Zhao, C.Y.; Ma, X.; Long, Z.L. EBSD analysis of evolution of dynamic recrystallization grains and δ phase in a nickel-based superalloy during hot compressive deformation. Mater. Des. 2016, 97, 13–24. [Google Scholar] [CrossRef]
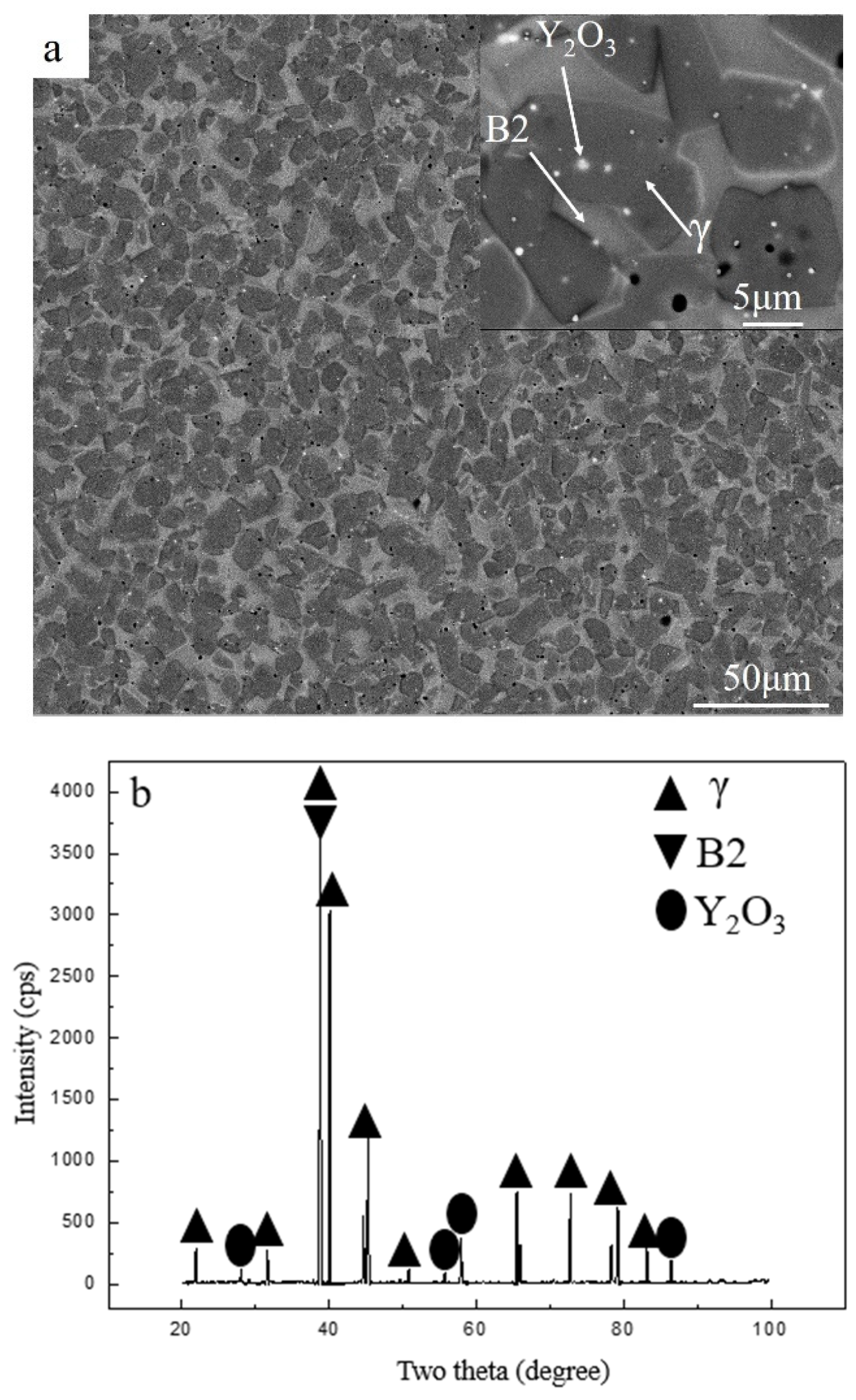








| Elements | Ti | Al | V | Y |
|---|---|---|---|---|
| Content (at.%) | 47.07 | 44.28 | 8.37 | 0.27 |
| Items | Hot Compressive Parameters |
|---|---|
| Temperature (°C) | 1000, 1100, 1200 |
| Strain rate (s−1) | 0.001, 0.010, 0.100, 1.000 |
| Reduction in height (%) | 50, 80 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Chen, Y.; Zhang, G.; Liu, N.; Kong, F.; Tian, J.; Sun, J. Hot Deformation Behavior and Microstructural Evolution of PM Ti43Al9V0.3Y with Fine Equiaxed γ and B2 Grain Microstructure. Materials 2020, 13, 896. https://doi.org/10.3390/ma13040896
Zhang D, Chen Y, Zhang G, Liu N, Kong F, Tian J, Sun J. Hot Deformation Behavior and Microstructural Evolution of PM Ti43Al9V0.3Y with Fine Equiaxed γ and B2 Grain Microstructure. Materials. 2020; 13(4):896. https://doi.org/10.3390/ma13040896
Chicago/Turabian StyleZhang, Dongdong, Yuyong Chen, Guoqing Zhang, Na Liu, Fantao Kong, Jing Tian, and Jianfei Sun. 2020. "Hot Deformation Behavior and Microstructural Evolution of PM Ti43Al9V0.3Y with Fine Equiaxed γ and B2 Grain Microstructure" Materials 13, no. 4: 896. https://doi.org/10.3390/ma13040896
APA StyleZhang, D., Chen, Y., Zhang, G., Liu, N., Kong, F., Tian, J., & Sun, J. (2020). Hot Deformation Behavior and Microstructural Evolution of PM Ti43Al9V0.3Y with Fine Equiaxed γ and B2 Grain Microstructure. Materials, 13(4), 896. https://doi.org/10.3390/ma13040896






