A Broadband Tunable Terahertz Metamaterial Absorber Based on Single-Layer Complementary Gammadion-Shaped Graphene
Abstract
1. Introduction
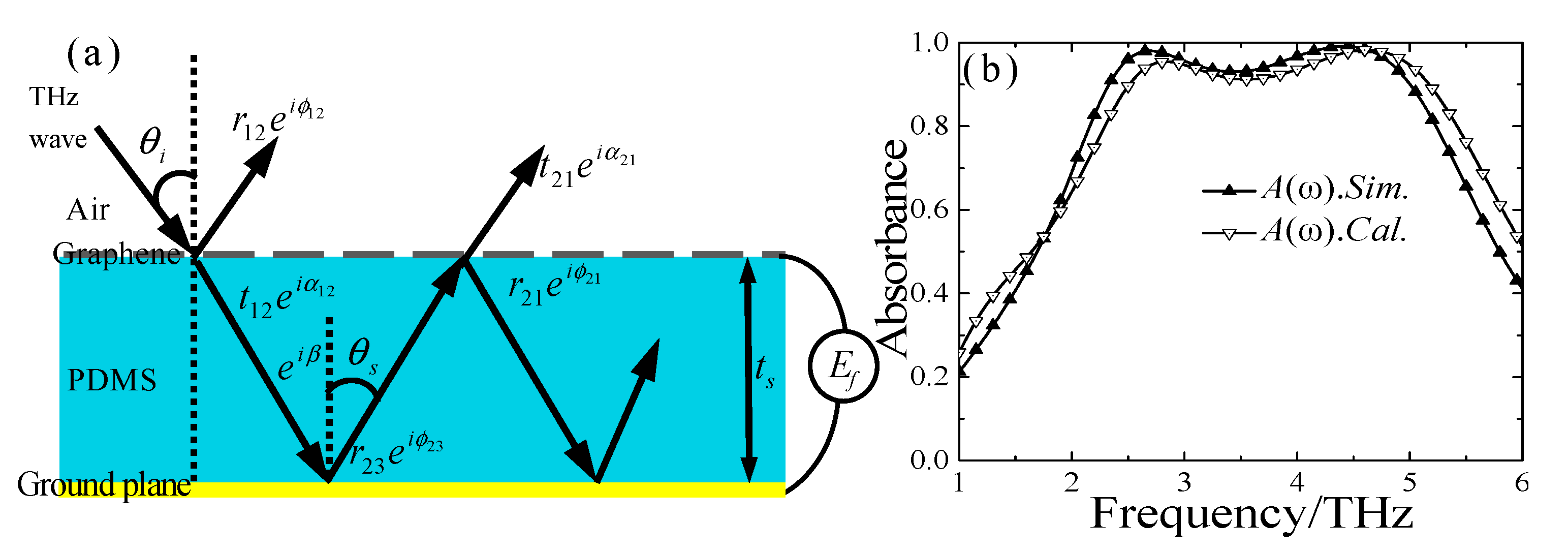
2. Structure Design, Theory, and Simulations
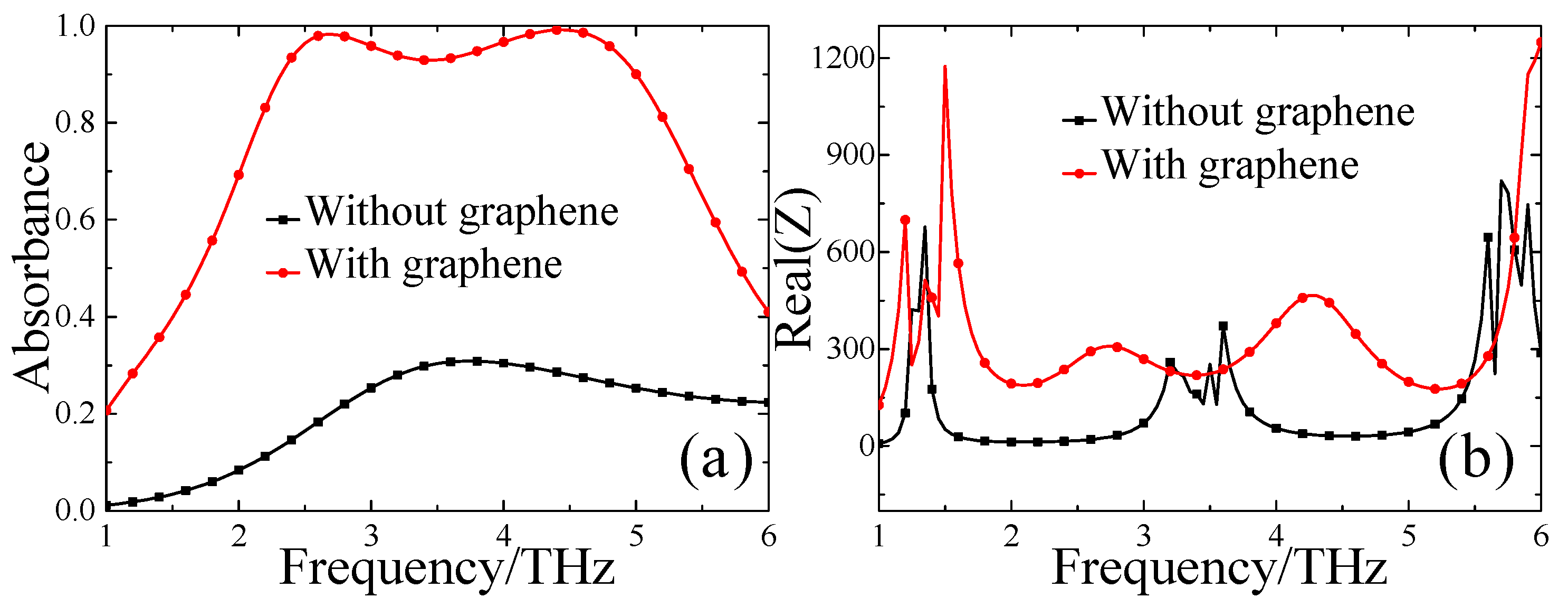
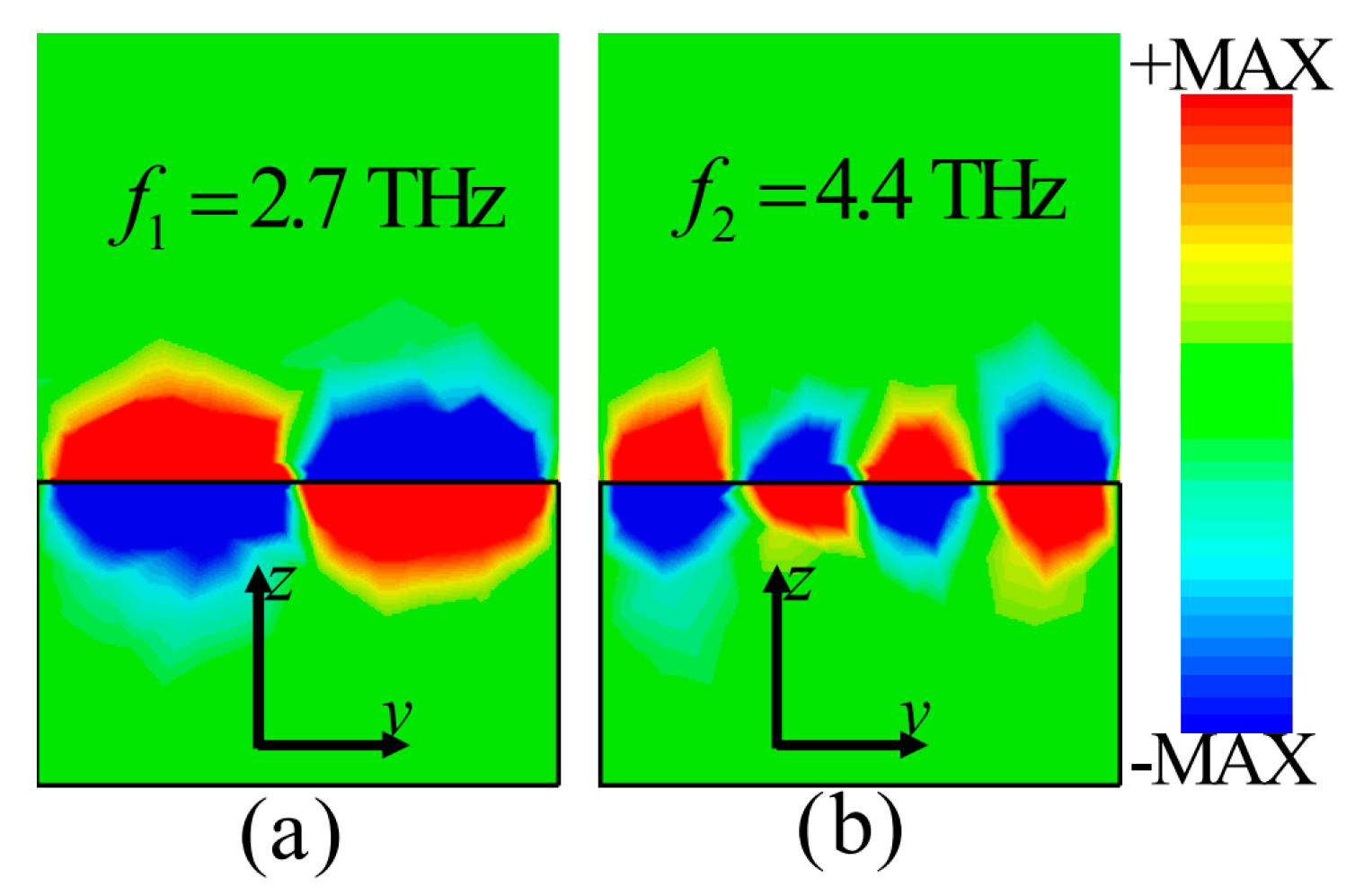
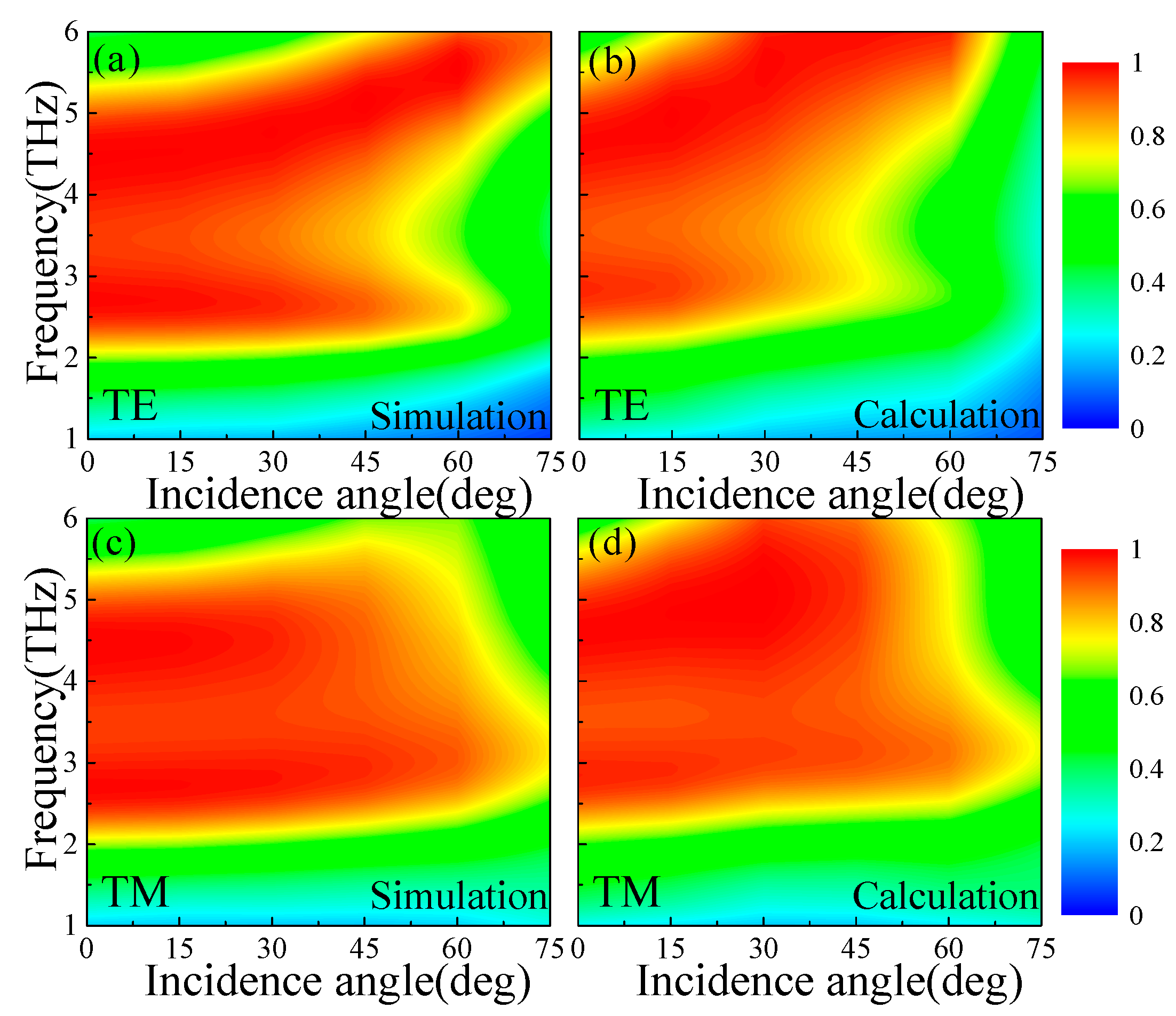
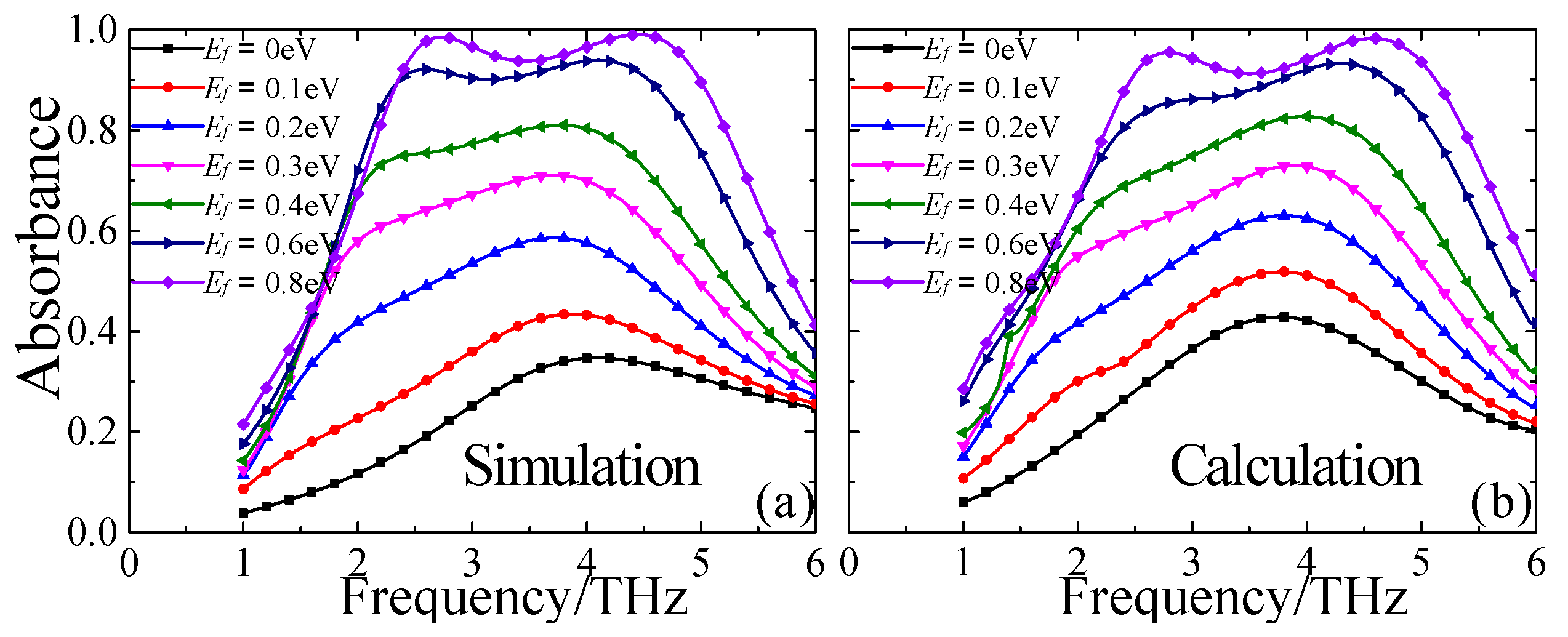
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Watts, C.M.; Liu, X.; Padilla, W.J. Metamaterial Electromagnetic Wave Absorbers. Adv. Mater. 2012, 24, 98–120. [Google Scholar] [CrossRef] [PubMed]
- Carranza, I.E.; Grant, J.P.; Gough, J.; Cumming, D. Terahertz Metamaterial Absorbers Implemented in CMOS Technology for Imaging Applications: Scaling to Large Format Focal Plane Arrays. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 1–8. [Google Scholar] [CrossRef]
- Alves, F.; Grbovic, D.; Kearney, B.; Lavrik, N.V.; Karunasiri, G. Bi-material Terahertz Sensors Using Metamaterial Structures. Opt. Express 2013, 21, 13256–13271. [Google Scholar] [CrossRef] [PubMed]
- Mittendorff, M.; Winnerl, S.; Kamann, J.; Eroms, J.; Weiss, D.; Schneider, H.; Helm, M. Ultrafast Graphene-Based Broadband THz Detector. Appl. Phys. Lett. 2013, 103, 021113. [Google Scholar] [CrossRef]
- Iwaszczuk, K.; Strikwerda, A.C.; Fan, K.; Zhang, X.; Averitt, R.D.; Jepsen, P.U. Flexible Metamaterial Absorbers for Stealth Applications at Terahertz Frequencies. Opt. Express 2012, 20, 635–643. [Google Scholar] [CrossRef]
- Nasr, M.; Richard, J.T.; Skirlo, S.A.; Heimbeck, M.S.; Joannopoulos, J.D.; Soljacic, M.; Everitt, H.O.; Domash, L. Narrowband Metamaterial Absorber for Terahertz Secure Labeling. J. Infrared, Millimeter, Terahertz Waves 2017, 38, 1120–1129. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, S.; Yang, H.; Li, J.; An, X.; Gu, C.; Tian, J. A Polarization Insensitive and Wide-Angle Dual-Band Nearly Perfect Absorber in the Infrared Regime. J. Opt. 2012, 14, 85102–85106. [Google Scholar] [CrossRef]
- Pu, M.; Wang, M.; Hu, C.; Huang, C.; Zhao, Z.; Wang, Y.; Luo, X. Engineering Heavily Doped Silicon for Broadband Absorber in the Terahertz Regime. Opt. Express 2012, 20, 25513–25519. [Google Scholar] [CrossRef]
- Cheng, Y.Z.; Huang, M.L.; Chen, H.R.; Guo, Z.Z.; Mao, X.S.; Gong, R.Z. Ultrathin Six-Band Polarization-Insensitive Perfect Metamaterial Absorber Based on a Cross-Cave Patch Resonator for Terahertz Waves. Materials 2017, 10, 591. [Google Scholar] [CrossRef]
- Cheng, Y.; Zou, H.; Yang, J.; Mao, X.; Gong, R. Dual and Broadband Terahertz Metamaterial Absorber Based on a Compact Resonator Structure. Opt. Mater. Express 2018, 8, 3104–3114. [Google Scholar] [CrossRef]
- Zou, H.; Cheng, Y. Design of a Six-Band Terahertz Metamaterial Absorber for Temperature Sensing Application. Opt. Mater. 2019, 88, 674–679. [Google Scholar] [CrossRef]
- Li, W.; Cheng, Y. Dual-Band Tunable Terahertz Perfect Metamaterial Absorber Based on Strontium Titanate (STO) Resonator Structure. Opt. Commun. 2020, 462, 125265. [Google Scholar] [CrossRef]
- Chen, H.-T. Interference Theory of Metamaterial Perfect Absorbers. Opt. Express 2012, 20, 7165–7172. [Google Scholar] [CrossRef] [PubMed]
- Huang, L.; Chen, H.T. A Brief Review on Terahertz Metamaterial Perfect Absorbers. Terahertz Sci. Technol. 2013, 6, 26–39. [Google Scholar]
- Mak, K.F.; Sfeir, M.Y.; Wu, Y.; Lui, C.H.; Misewich, J.A.; Heinz, T.F. Measurement of the Optical Conductivity of Graphene. Phys. Rev. Lett. 2008, 101, 196405. [Google Scholar] [CrossRef] [PubMed]
- Gass, M.H.; Bangert, U.; Bleloch, A.L.; Wang, P.; Nair, R.R.; Geim, A.K. Free-Standing Graphene at Atomic Resolution. Nat. Nanotechnol. 2008, 3, 676–681. [Google Scholar] [CrossRef]
- Grigorenko, A.N.; Polini, M.; Novoselov, K.S. Graphene Plasmonics. Nat. Photonics 2012, 6, 749–758. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Fal’ko, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K.A. Roadmap for Grapheme. Nature 2012, 490, 192–200. [Google Scholar] [CrossRef]
- Liu, H.; Liu, Y.; Zhu, D. Chemical Doping of Graphene. J. Mater. Chem. 2011, 21, 3335–3345. [Google Scholar] [CrossRef]
- Fang, Z.; Thongrattanasiri, S.; Schlather, A.; Liu, Z.; Ma, L.; Wang, Y.; Ajayan, P.M.; Nordlander, P.; Halas, N.J.; de Abajo, F.J.G. Gated Tunability and Hybridization of Localized Plasmons in Nanostructured Graphene. ACS Nano 2013, 7, 2388–2395. [Google Scholar] [CrossRef] [PubMed]
- Thongrattanasiri, S.; Koppens, F.H.L.; de Abajo, F.J.G. Complete Optical Absorption in Periodically Patterned Graphene. Phys. Rev. Lett. 2012, 108, 047401. [Google Scholar] [CrossRef] [PubMed]
- Alaee, R.; Farhat, M.; Rockstuhl, C.; Lederer, F. A Perfect Absorber Made of a Graphene Micro-Ribbon Metamaterial. Opt. Express 2012, 20, 28017–28024. [Google Scholar] [CrossRef] [PubMed]
- Nikitin, A.Y.; Guinea, F.; Garcia-Vidal, F.J.; Martin-Moreno, L.; Garcia-Vidal, F. Surface Plasmon Enhanced Absorption and Suppressed Transmission in Periodic Arrays of Graphene Ribbons. Phys. Rev. B 2012, 85, 081405. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, X.; Hu, Z.; Aqeeli, M.; Alburaikan, A. Design of Broadband and Tunable Terahertz Absorbers Based on Graphene Metasurface: Equivalent Circuit Model Approach. IET Microw. Antennas Propag. 2012, 9, 307–312. [Google Scholar] [CrossRef]
- Ke, S.; Wang, B.; Huang, H.; Long, H.; Wang, K.; Lu, P. Plasmonic Absorption Enhancement in Periodic Cross-Shaped Graphene Arrays. Opt. Express. 2015, 23, 8888–8900. [Google Scholar] [CrossRef]
- Ye, C.; Zhu, Z.; Xu, W.; Yuan, X.; Qin, S. Electrically Tunable Absorber Based on Nonstructured Graphene. J. Opt. 2015, 17, 125009. [Google Scholar] [CrossRef]
- Yao, G.; Ling, F.; Yue, J.; Luo, C.; Ji, J.; Yao, J. Dual-Band Tunable Perfect Metamaterial Absorber in the THz Range. Opt. Express 2016, 24, 1518–1527. [Google Scholar] [CrossRef]
- Ye, L.; Chen, Y.; Cai, G.; Liu, N.; Zhu, J.; Song, Z.; Liu, Q. Broadband absorber with periodically sinusoidally-patterned graphene layer in terahertz range. Opt. Express 2017, 25, 11223–11232. [Google Scholar] [CrossRef]
- Huang, M.; Cheng, Y.; Cheng, Z.; Chen, H.; Mao, X.; Gong, R. Based on Graphene Tunable Dual-Band Terahertz Metamaterial Absorber with Wide-Angle. Opt. Commun. 2018, 415, 194–201. [Google Scholar] [CrossRef]
- Huang, M.L.; Cheng, Y.Z.; Cheng, Z.Z.; Chen, H.R.; Mao, X.S.; Gong, R.Z. Design of a Broadband Tunable Terahertz Metamaterial Absorber Based on Complementary Structural Graphene. Materials 2018, 11, 540. [Google Scholar] [CrossRef]
- Zhou, Q.; Zha, S.; Bian, L.; Zhang, J.; Ding, L.; Liu, H.; Liu, P. Independently Controllable Dual-Band Terahertz Metamaterial Absorber Exploiting Grapheme. J. Phys. D Appl. Phys. 2019, 52, 255102. [Google Scholar] [CrossRef]
- Amin, M.; Farhat, M.; Bağcı, H. An Ultra-Broadband Multilayered Graphene Absorber. Opt. Express 2013, 21, 29938–29948. [Google Scholar] [CrossRef] [PubMed]
- Yi, S.; Zhou, M.; Shi, X.; Gan, Q.; Zi, J.; Yu, Z. A multiple-resonator approach for broadband light absorption in a single layer of nanostructured graphene. Opt. Express 2015, 23, 10081–10090. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; He, W.; Yang, F.; Ran, J.; Gao, B.; Zhang, W.-L. Polarization-Independent and Angle-Insensitive Broadband Absorber with a Target-Patterned Graphene Layer in the Terahertz Regime. Opt. Express 2018, 26, 25558–25566. [Google Scholar] [CrossRef]
- Cen, C.; Chen, Z.; Xu, D.; Jiang, L.; Chen, X.; Yi, Z.; Wu, P.; Li, G.; Yi, Y. High Quality Factor, High Sensitivity Metamaterial Graphene-Perfect Absorber Based on Critical Coupling Theory and Impedance Matching. Nanomaterials 2020, 10, 95. [Google Scholar] [CrossRef]
- Cheng, Y.; Luo, H.; Chen, F.; Gong, R. Triple Narrow-band Plasmonic Perfect Absorber for Refractive Index Sensing Applications of Optical Frequency. OSA Continuum. 2019, 2, 2113–2122. [Google Scholar] [CrossRef]
- Yang, J.; Zhu, Z.; Zhang, J.; Xu, W.; Guo, C.; Liu, K.; Zhu, M.; Chen, H.; Zhang, R.; Yuan, X.; et al. Mie Resonance Induced Broadband Near-Perfect Absorption in Nanostructured Graphene Loaded with Periodical Dielectric Wires. Opt. Express 2018, 26, 20174–20182. [Google Scholar] [CrossRef]
- Liu, Y.; Zhong, R.; Huang, J.; Lv, Y.; Han, C.; Liu, S. Independently Tunable Multi-Band and Ultra-Wide-Band Absorbers Based on Multilayer Metal-Graphene Metamaterials. Opt. Express 2019, 27, 7393–7404. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, J.; Liu, N.; Wang, Y.; Hu, P.; Wang, Z. Fast Patterned Graphene Ribbons via Soft–Lithography. Procedia CIRP 2016, 42, 428–432. [Google Scholar] [CrossRef]
- Cen, C.; Zhang, Y.; Chen, X.; Yang, H.; Yi, Z.; Yao, W.; Tang, Y.; Yi, Y.; Wang, J.; Wu, P. A Dual-Band Metamaterial Absorber for Graphene Surface Plasmon Resonance at Terahertz Frequency. Physica E 2020, 117, 113840. [Google Scholar] [CrossRef]
- Wang, X.; Shi, Y. CHAPTER 1. Fabrication Techniques of Graphene Nanostructures. In Nanoscience & Nanotechnology Series; Royal Society of Chemistry (RSC) Publishing: Cambridge, UK, 2014; pp. 1–30. [Google Scholar]
- Zhang, Y.; Shi, Y.; Liang, C.-H. Broadband Tunable Graphene-Based Metamaterial Absorber. Opt. Mater. Express 2016, 6, 3036–3044. [Google Scholar] [CrossRef]
- Hanson, G.W. Dyadic Green’s Functions and Guided Surface Waves for a Surface Conductivity Model of Grapheme. J. Appl. Phys. 2008, 103, 064302. [Google Scholar] [CrossRef]
- Hanson, G.W. Quasi-Transverse Electromagnetic Modes Supported by a Graphene Parallel-Plate Waveguide. J. Appl. Phys. 2008, 104, 084314. [Google Scholar] [CrossRef]
- Ren, L.; Zhang, Q.; Yao, J.; Sun, Z.; Kaneko, R.; Yan, Z.; Nanot, S.; Jin, Z.; Kawayama, I.; Tonouchi, M.; et al. Terahertz and Infrared Spectroscopy of Gated Large-Area Graphene. Nano Lett. 2012, 12, 3711–3715. [Google Scholar] [CrossRef] [PubMed]
- Ordal, M.A.; Long, L.L.; Bell, R.J.; Bell, S.E.; Bell, R.R.; Alexander, R.W., Jr.; Ward, C.A. Optical Properties of the Metals Al, Co, Cu, Au, Fe, Pb, Ni, Pd, Pt, Ag, Ti, and W in the Infrared and Far Infrared. Appl. Opt. 1983, 22, 1099–1119. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.Z.; Withayachumnankul, W.; Upadhyay, A.; Headland, D.; Nie, Y.; Gong, R.Z.; Bhaskaran, M.; Sriram, S.; Abbott, D. Ultrabroadband Reflective Polarization Convertor for Terahertz Waves. Appl. Phys. Lett. 2014, 105, 181111. [Google Scholar] [CrossRef]
- Li, J.-S.; Yan, D.-X.; Sun, J.-Z. Flexible Dual-Band All-Graphene-Dielectric Terahertz Absorber. Opt. Mater. Express 2019, 9, 2067–2075. [Google Scholar] [CrossRef]
- Smith, D.R.; Vier, D.C.; Koschny, T.; Soukoulis, C.M. Electromagnetic Parameter Retrieval from Inhomogeneous Metamaterials. Phys. Rev. E 2005, 71, 036617. [Google Scholar] [CrossRef]
- Wang, Y.; Qin, F.; Yi, Z.; Chen, X.; Zhou, Z.; Yang, H.; Liao, X.; Tang, Y.; Yao, W.; Yi, Y. Effect of Slit Width on Surface Plasmon Resonance. Results Phys. 2019, 15, 102711. [Google Scholar] [CrossRef]
- Qin, F.; Chen, Z.; Chen, X.; Yi, Z.; Yao, W.; Duan, T.; Wu, P.; Yang, H.; Li, G.; Yi, Y.; et al. A Tunable Triple-Band Near-Infrared Metamaterial Absorber Based on Au Nano-Cuboids Array. Nanomaterials 2020, 10, 207. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Z.; Xu, D.; Yi, Z.; Chen, X.; Chen, J.; Tang, Y.; Wu, P.; Li, G.; Yi, Y. Triple-Band Perfect Metamaterial Absorber with Good Operating Angle Polarization Tolerance Based on Split Ring Arrays. Results Phys. 2020, 16, 102951. [Google Scholar] [CrossRef]
- Chen, H.-T.; Zhou, J.; O’Hara, J.F.; Chen, F.; Azad, A.K.; Taylor, A.J. Antireflection Coating Using Metamaterials and Identification of Its Mechanism. Phys. Rev. Lett. 2010, 105, 073901. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, F.; Cheng, Y.; Luo, H. A Broadband Tunable Terahertz Metamaterial Absorber Based on Single-Layer Complementary Gammadion-Shaped Graphene. Materials 2020, 13, 860. https://doi.org/10.3390/ma13040860
Chen F, Cheng Y, Luo H. A Broadband Tunable Terahertz Metamaterial Absorber Based on Single-Layer Complementary Gammadion-Shaped Graphene. Materials. 2020; 13(4):860. https://doi.org/10.3390/ma13040860
Chicago/Turabian StyleChen, Fu, Yongzhi Cheng, and Hui Luo. 2020. "A Broadband Tunable Terahertz Metamaterial Absorber Based on Single-Layer Complementary Gammadion-Shaped Graphene" Materials 13, no. 4: 860. https://doi.org/10.3390/ma13040860
APA StyleChen, F., Cheng, Y., & Luo, H. (2020). A Broadband Tunable Terahertz Metamaterial Absorber Based on Single-Layer Complementary Gammadion-Shaped Graphene. Materials, 13(4), 860. https://doi.org/10.3390/ma13040860




