Degradation of Axial Ultimate Load-Bearing Capacity of Circular Thin-Walled Concrete-Filled Steel Tubular Stub Columns after Corrosion
Abstract
1. Introduction
2. Experimental
2.1. Raw Materials and Specimens’ Fabrication
2.2. Experimental Procedure and Testing Parameters
3. Results
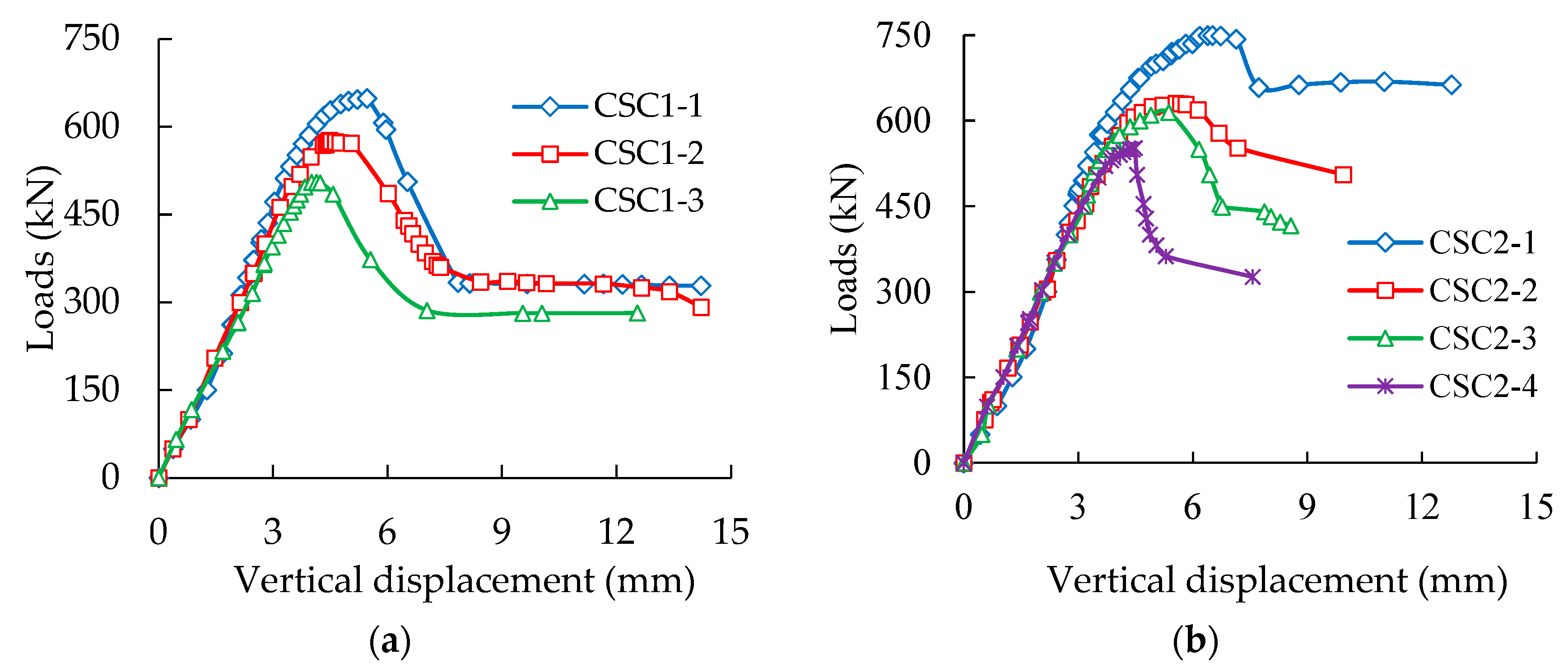
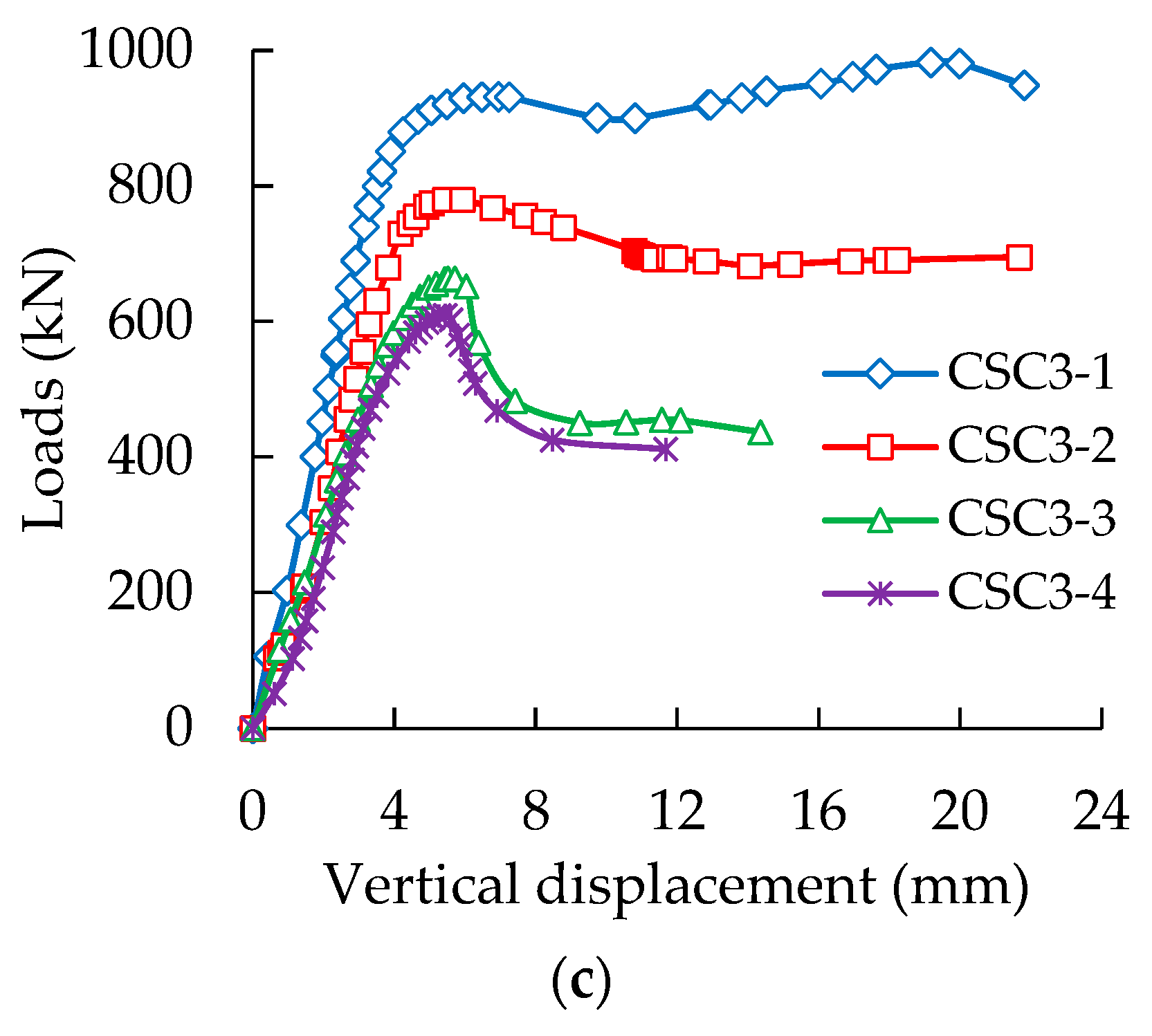
3.1. Curves of Loads Versus Displacement
3.2. Failure Modes
4. Discussion
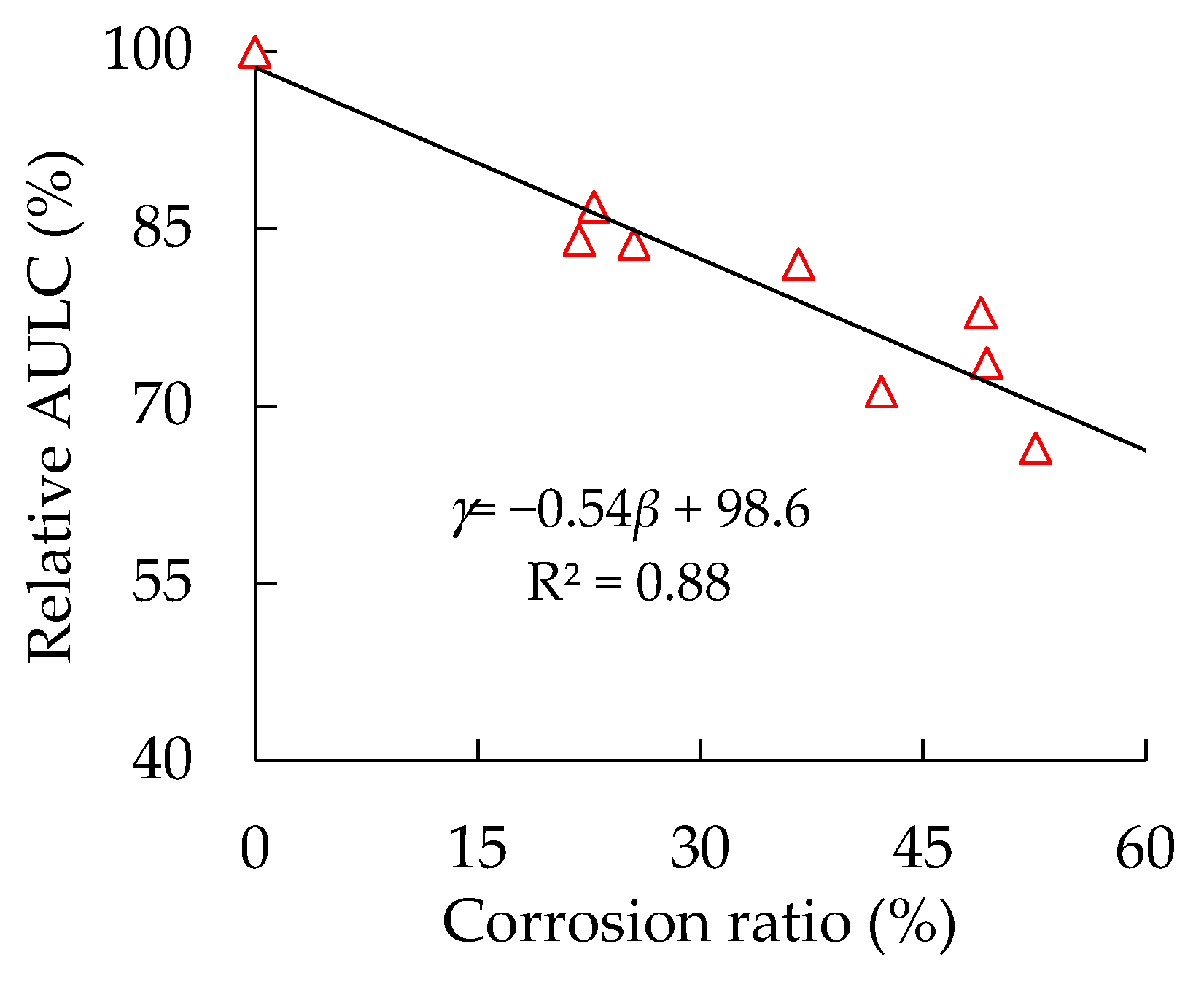
4.1. Effect of Steel Tube’s Corrosion on Specimens’ Relative AULC
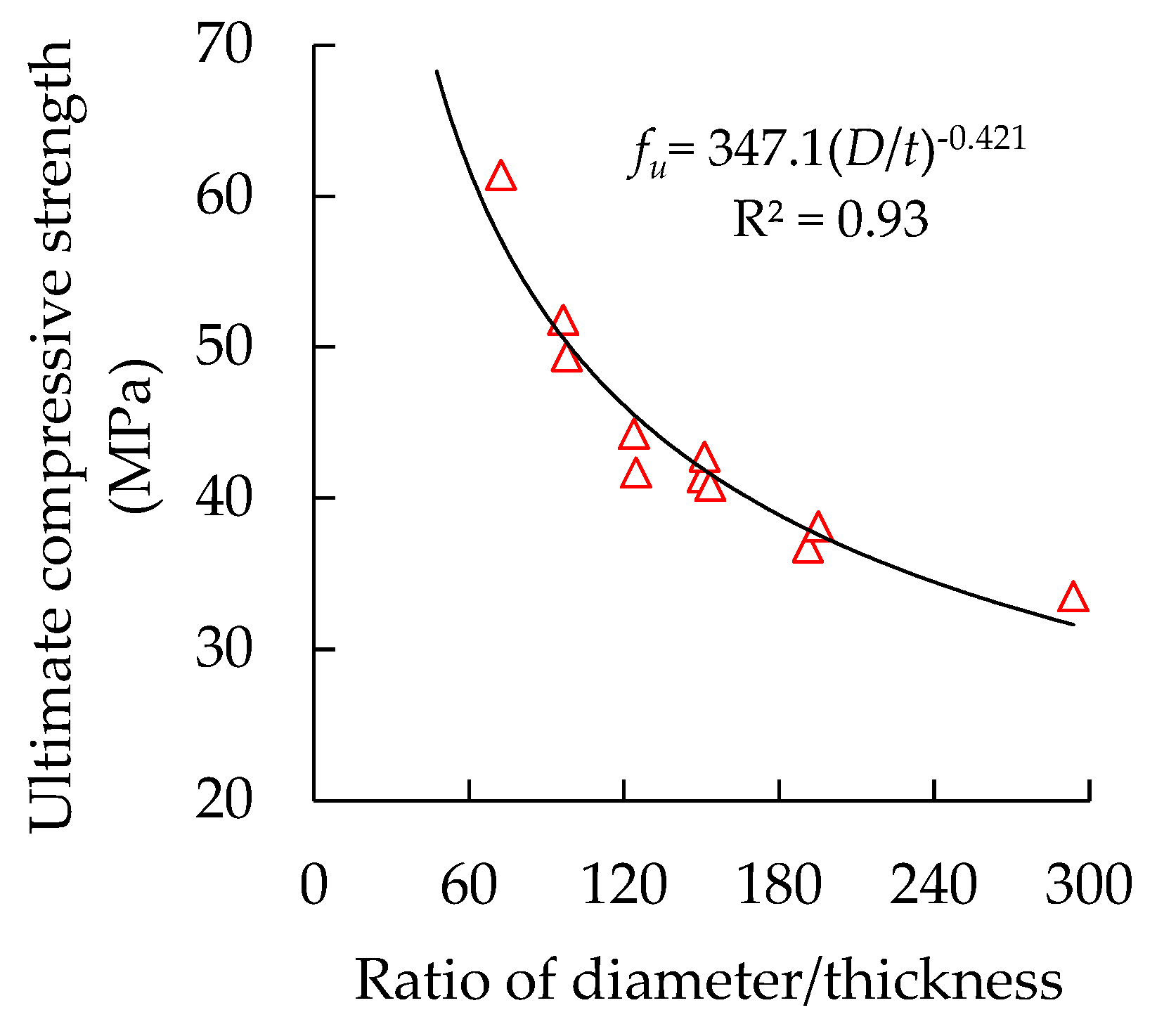
4.2. Effect of Diameter-to-Thickness Ratio on Specimens’ Ultimate Compressive Strength
4.3. Effect of Confinement Coefficient on Specimens’ Ultimate Compressive Strength
4.4. Simple AULC Prediction Model for Corroded Specimens
5. Conclusions
- The corrosion of the outer steel tube reduces the AULC and plastic deformation ability of circular thin-walled CFST stub columns, and the high corrosion ratios cause high reduction. The degradation speeds of the AULC of circular thin-walled CFST stub columns are lower than the steel tube’s corrosion rates because of the composite interaction between the steel tube and the core concrete;
- The failure modes of axial circular thin-walled CFST stub columns are mainly shear bulging with slight local outward buckling, regardless of the degree of steel tube’s corrosion because of the limited restraint action of steel tubes on core concrete. Although the core concrete failed in a brittle shear failure mode, the failure mode of the column specimens still belongs to a ductile failure because of the confinement action of the outer steel tube;
- The AULC of a corroded circular thin-walled CFST stub column is closely related to the degree of corrosion of its steel tube, its diameter/thickness ratio and effective confinement coefficient, in which the correlation with the effective confinement factor is the highest. A simple model for predicting the AULC of corroded circular thin-walled CFST stub columns was presented through a regression analysis of the experimental data.
Author Contributions
Funding
Conflicts of Interest
References
- Alostaz, Y.M.; Schneider, S.P. Analytical behavior of connections to concrete-filled steel tubes. J. Constr. Steel Res. 1996, 40, 95–127. [Google Scholar] [CrossRef]
- Shanmugam, N.E.; Lakshmi, B. State of the art report on steel–concrete composite columns. J. Constr. Steel Res. 2001, 57, 1041–1080. [Google Scholar] [CrossRef]
- Abhilash, M.; Jhanjhari, S.; Parthiban, P.; Karthikeyan, J. Axial behaviour of semi-lightweight aggregate concrete-filled steel tube columns—A DOE approach. J. Constr. Steel Res. 2019, 162. [Google Scholar] [CrossRef]
- Roeder, C.W. Overview of hybrid and composite systems for seismic design in the United States. Eng. Struct. 1998, 20, 355–363. [Google Scholar] [CrossRef]
- Kvedaras, A.K.; Sapalas, A. Research and practice of concrete-filled steel tubes in Lithuania. J. Constr. Steel Res. 1999, 49, 197–212. [Google Scholar] [CrossRef]
- Varma, A.H.; Ricles, J.M.; Sause, R.; Lu, L.-W. Seismic behavior and modeling of high-strength composite concrete-filled steel tube (CFT) beam–columns. J. Constr. Steel Res. 2002, 58, 725–758. [Google Scholar] [CrossRef]
- Han, L.-H.; Hou, C.; Wang, Q.-L. Square concrete filled steel tubular (CFST) members under loading and chloride corrosion: Experiments. J. Constr. Steel Res. 2012, 71, 11–25. [Google Scholar] [CrossRef]
- Ferdous, W.; Bai, Y.; Almutairi, A.D.; Satasivam, S.; Jeske, J. Modular assembly of water-retaining walls using GFRP hollow profiles: Components and connection performance. Compos. Struct. 2018, 194, 1–11. [Google Scholar] [CrossRef]
- Hua, Y.-X.; Han, L.-H.; Wang, Q.-L.; Hou, C. Behaviour of square CFST beam-columns under combined sustained load and corrosion: Experiments. Thin-Walled Struct. 2019, 136, 353–366. [Google Scholar] [CrossRef]
- Nour, A.I.; Güneyisi, E.M. Prediction model on compressive strength of recycled aggregate concrete filled steel tube columns. Compos. Part B Eng. 2019, 173, 106938. [Google Scholar] [CrossRef]
- Kamil, G.M.; Liang, Q.Q.; Hadi, M.N.S. Local buckling of steel plates in concrete-filled steel tubular columns at elevated temperatures. Eng. Struct. 2018, 168, 108–118. [Google Scholar] [CrossRef]
- Ferdous, W.; Almutairi, A.D.; Huang, Y.; Bai, Y. Short-term flexural behaviour of concrete filled pultruded GFRP cellular and tubular sections with pin-eye connections for modular retaining wall construction. Compos. Struct. 2018, 206, 1–10. [Google Scholar] [CrossRef]
- Ferdous, W.; Ngo, T.D.; Nguyen, K.T.Q.; Ghazlan, A.; Mendis, P.; Manalo, A. Effect of fire-retardant ceram powder on the properties of phenolic-based GFRP composites. Compos. Part B Eng. 2018, 155, 414–424. [Google Scholar] [CrossRef]
- CSCS 28:2012. Technical Specification for Concrete Filled Steel Tubular Structures; China Planning Press: Beijing, China, 2012. [Google Scholar]
- Technical Code for Concrete Filled Steel Tubular Structures; GB 50936-2014; Architecture Industrial Press of China: Beijing, China, 2014.
- Tao, Z.; Han, L.-H.; Wang, D.-Y. Experimental behaviour of concrete-filled stiffened thin-walled steel tubular columns. Thin-Walled Struct. 2007, 45, 517–527. [Google Scholar] [CrossRef]
- Petrus, C.; Abdul Hamid, H.; Ibrahim, A.; Parke, G. Experimental behaviour of concrete filled thin walled steel tubes with tab stiffeners. Journal of Constructional Steel Research 2010, 66, 915–922. [Google Scholar] [CrossRef]
- Wu, B.; Lin, L.; Zhao, J.; Yan, H. Creep behavior of thin-walled circular steel tubular columns filled with demolished concrete lumps and fresh concrete. Construction and Building Materials 2018, 187, 773–790. [Google Scholar] [CrossRef]
- Wang, Y.-l.; Cao, M.-m.; Sun, H.-j. Time-dependent reliability analysis of circular CFST stub columns under environmental corrosion. Pacific Science Review 2014, 16, 201–206. [Google Scholar] [CrossRef]
- Han, L.-H.; Hou, C.-C.; Wang, Q.-L. Behavior of circular CFST stub columns under sustained load and chloride corrosion. J. Constr. Steel Res. 2014, 103, 23–36. [Google Scholar] [CrossRef]
- Gao, S.; Peng, Z.; Li, X.; Chen, D. Tests on axial strength of circle CFST stub columns under marine atmosphere in cold region. Constr. Build. Mater. 2020, 230, 117073. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, F.; Huang, H.; Wang, C. Study on seismic performance of concrete filled square steel tubes subjected to simulated acid rain attack. J. China Railw. Soc. 2018, 40, 106–114. [Google Scholar]
- Yuan, F.; Chen, M.; Huang, H.; Xie, L.; Wang, C. Circular concrete filled steel tubular (CFST) columns under cyclic load and acid rain attack: Test simulation. Thin-Walled Struct. 2018, 122, 90–101. [Google Scholar] [CrossRef]
- Yuan, F.; Chen, M.; Huang, H. Square CFST columns under cyclic load and acid rain attack: Experiments. Steel Compos. Struct. 2019, 30, 171–183. [Google Scholar]
- Wang, J.; Shen, Q.; Wang, F.; Wang, W. Experimental and analytical studies on CFRP strengthened circular thin-walled CFST stub columns under eccentric compression. Thin-Walled Struct. 2018, 127, 102–119. [Google Scholar] [CrossRef]
- Ahmed, M.; Liang, Q.Q.; Patel, V.I.; Hadi, M.N.S. Nonlinear analysis of rectangular concrete-filled double steel tubular short columns incorporating local buckling. Eng. Struct. 2018, 175, 13–26. [Google Scholar] [CrossRef]
- Lin, H.; Zhao, Y.; Yang, J.-Q.; Feng, P.; Ozbolt, J.; Ye, H. Effects of the corrosion of main bar and stirrups on the bond behavior of reinforcing steel bar. Constr. Build. Mater. 2019, 225, 13–28. [Google Scholar] [CrossRef]
- Zhang, F.; Xia, J.; Tan, Y.; Xia, X. Application of image pixel measurement technology in the detection of the thickness of steel corrosion. Steel Constr. 2015, 30, 93–96. [Google Scholar]
- Chen, Y.; Chen, Z.; Xu, J.; Lui, E.M.; Wu, B. Performance evaluation of recycled aggregate concrete under multiaxial compression. Constr. Build. Mater. 2019, 229, 116935. [Google Scholar] [CrossRef]
- Chen, D.; Yu, X.; Liu, R.; Li, S.; Zhang, Y. Triaxial mechanical behavior of early age concrete: Experimental and modelling research. Cement Concr. Res. 2019, 115, 433–444. [Google Scholar] [CrossRef]
- Han, L. Theory and Practice of Concrete Filled Steel Tubular Structures; The Science Publishing Company: Beijing, China, 2004. [Google Scholar]
- Chen, Z.; Tan, Q.; Xue, J.; Chen, Y. Study of ultimate bearing capacity of recycled aggregate concrete-filled circle steel tube short columns under axial compression after high temperature. Ind. Constr. 2014, 44, 5–12. [Google Scholar]
- ACI. Building Code Requirements for Structural Concrete and Commentary; American Concrete Institute: Detrorit, MI, USA, 2005. [Google Scholar]
- EC4. Design of Composite Steel and Concrete Structures; European Committe for Standardisation: Brussels, Belgium, 2004. [Google Scholar]
- AIJ. Recommendation for Design and Construction of Concrete Filled Steel Tubular Structures; Architectural Institute of Japan: Tokyo, Japan, 1997. [Google Scholar]
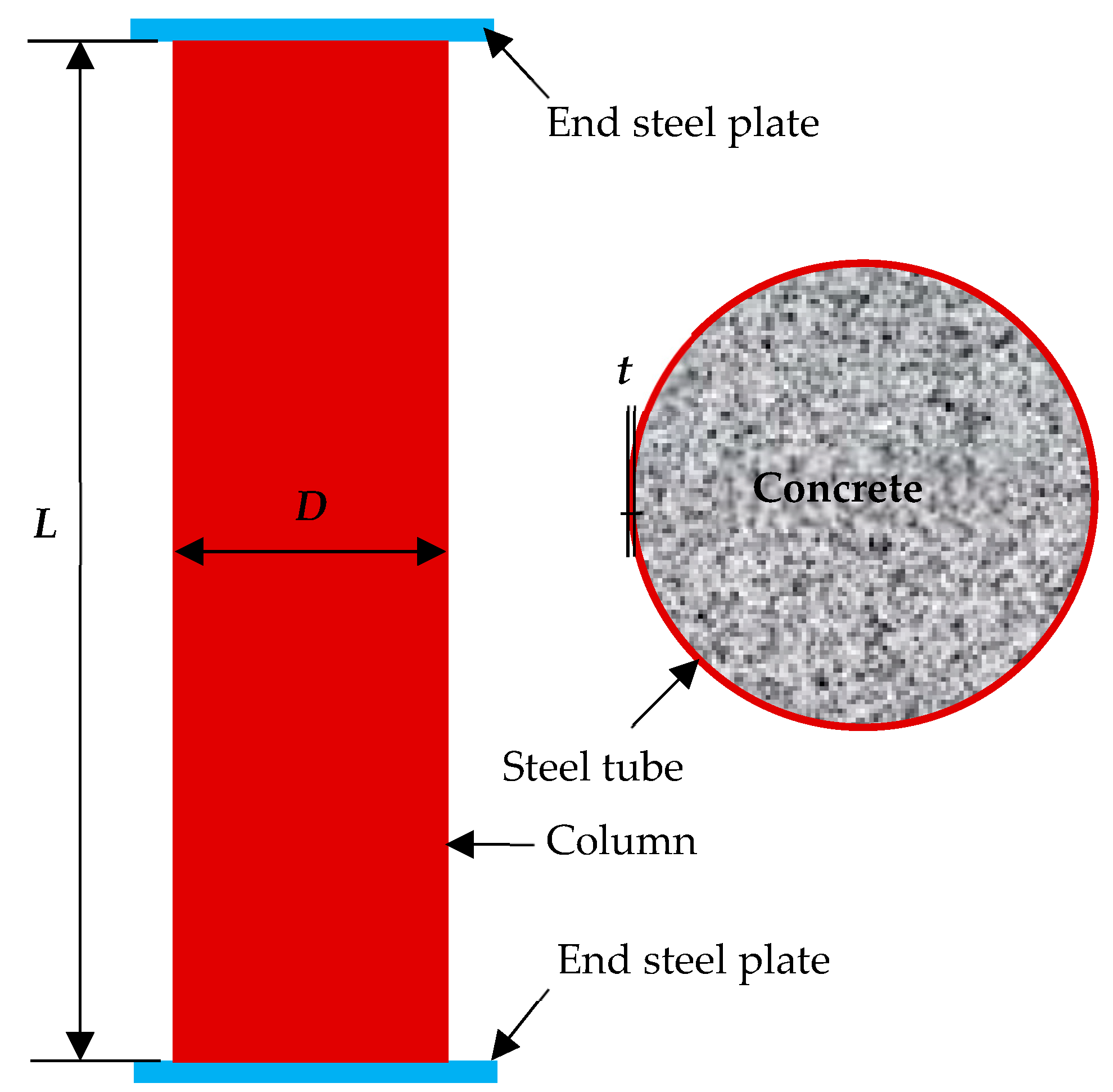
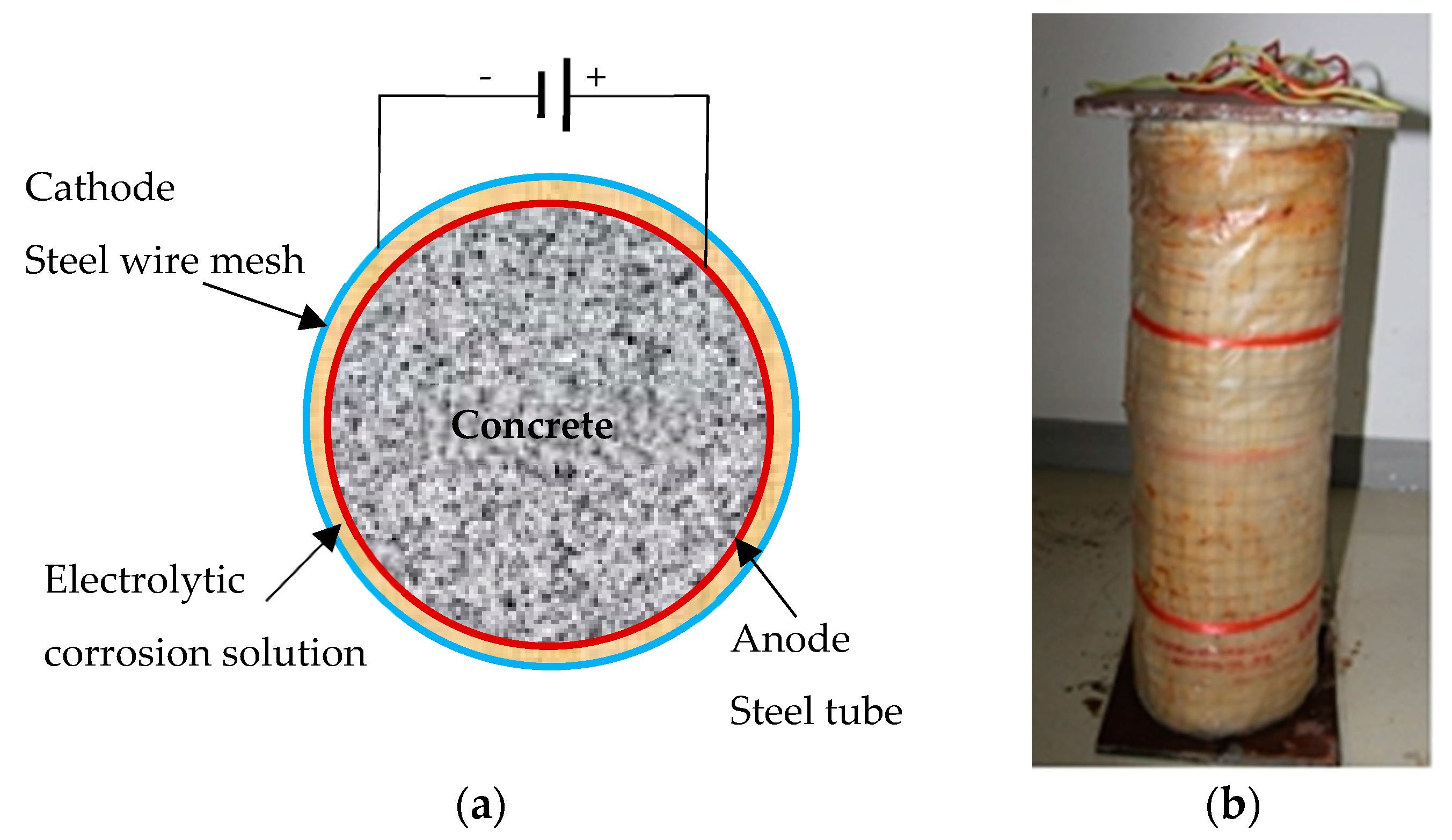




| No. | Item | t0 /mm | β /% | t0 – t /mm | Δm /g | I /A | T /h |
|---|---|---|---|---|---|---|---|
| 1 | CSC1-1 | 0.92 | 0 (0) | 0 (0) | 0 | 0 | 0 |
| 2 | CSC1-2 | 0.92 | 20 (22.8) | 0.18 (0.21) | 340.4 | 2.0 | 162.86 |
| 3 | CSC1-3 | 0.92 | 50 (48.9) | 0.46 (0.45) | 851.1 | 2.0 | 407.15 |
| 4 | CSC2-1 | 1.42 | 0 (0) | 0 (0) | 0 | 0 | 0 |
| 5 | CSC2-2 | 1.42 | 20 (21.8) | 0.28 (0.31) | 510.7 | 2.0 | 244.29 |
| 6 | CSC2-3 | 1.42 | 33.3 (36.6) | 0.47 (0.52) | 850.2 | 2.0 | 407.15 |
| 7 | CSC2-4 | 1.42 | 50 (49.3) | 0.71 (0.70) | 1276.6 | 2.0 | 586.8 |
| 8 | CSC3-1 | 1.92 | 0 (0) | 0 (0) | 0 | 0 | 0 |
| 9 | CSC3-2 | 1.92 | 25 (25.5) | 0.48 (0.49) | 851.1 | 2.0 | 407.15 |
| 10 | CSC3-3 | 1.92 | 40 (42.2) | 0.77 (0.81) | 1361.8 | 2.0 | 651.44 |
| 11 | CSC3-4 | 1.92 | 50 (52.6) | 0.96 (1.01) | 1702.2 | 2.0 | 814.30 |
| Item | Experimental Data/kN | Prediction 1/kN | Error 1/% | Prediction 2/kN | Error 2/% |
|---|---|---|---|---|---|
| CSC 1-1 | 648.8 | 624.3 | 3.8 | 529.6 | −18.4 |
| CSC 1-2 | 577.2 | 569.4 | 1.4 | 501.8 | −13.1 |
| CSC 1-3 | 505.6 | 512.0 | −1.3 | 470.1 | −7.0 |
| CSC 2-1 | 749.7 | 765.2 | −2.1 | 588.3 | −21.5 |
| CSC 2-2 | 630.2 | 670.4 | −6.4 | 547.7 | −13.1 |
| CSC 2-3 | 619.9 | 611.7 | 1.3 | 520.1 | −16.1 |
| CSC 2-4 | 552.2 | 564.9 | −2.3 | 496.5 | −10.1 |
| CSC 3-1 | 931.9 | 930.7 | 0.1 | 645.9 | −30.7 |
| CSC 3-2 | 780.4 | 760.6 | 2.5 | 582.3 | −25.4 |
| CSC 3-3 | 664.4 | 662.9 | 0.2 | 540.7 | −18.6 |
| CSC 3-4 | 619.1 | 607.2 | 1.9 | 514.7 | −16.9 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Xia, J.; Li, G.; Guo, Z.; Chang, H.; Wang, K. Degradation of Axial Ultimate Load-Bearing Capacity of Circular Thin-Walled Concrete-Filled Steel Tubular Stub Columns after Corrosion. Materials 2020, 13, 795. https://doi.org/10.3390/ma13030795
Zhang F, Xia J, Li G, Guo Z, Chang H, Wang K. Degradation of Axial Ultimate Load-Bearing Capacity of Circular Thin-Walled Concrete-Filled Steel Tubular Stub Columns after Corrosion. Materials. 2020; 13(3):795. https://doi.org/10.3390/ma13030795
Chicago/Turabian StyleZhang, Fengjie, Junwu Xia, Guo Li, Zhen Guo, Hongfei Chang, and Kejin Wang. 2020. "Degradation of Axial Ultimate Load-Bearing Capacity of Circular Thin-Walled Concrete-Filled Steel Tubular Stub Columns after Corrosion" Materials 13, no. 3: 795. https://doi.org/10.3390/ma13030795
APA StyleZhang, F., Xia, J., Li, G., Guo, Z., Chang, H., & Wang, K. (2020). Degradation of Axial Ultimate Load-Bearing Capacity of Circular Thin-Walled Concrete-Filled Steel Tubular Stub Columns after Corrosion. Materials, 13(3), 795. https://doi.org/10.3390/ma13030795








