Experimental and Analytical Study on Residual Stiffness/Strength of CFRP Tendons under Cyclic Loading
Abstract
1. Introduction
2. Experiment
2.1. Material Properties
2.2. Tension–Tension Fatigue Tests
3. Fatigue Damage Model
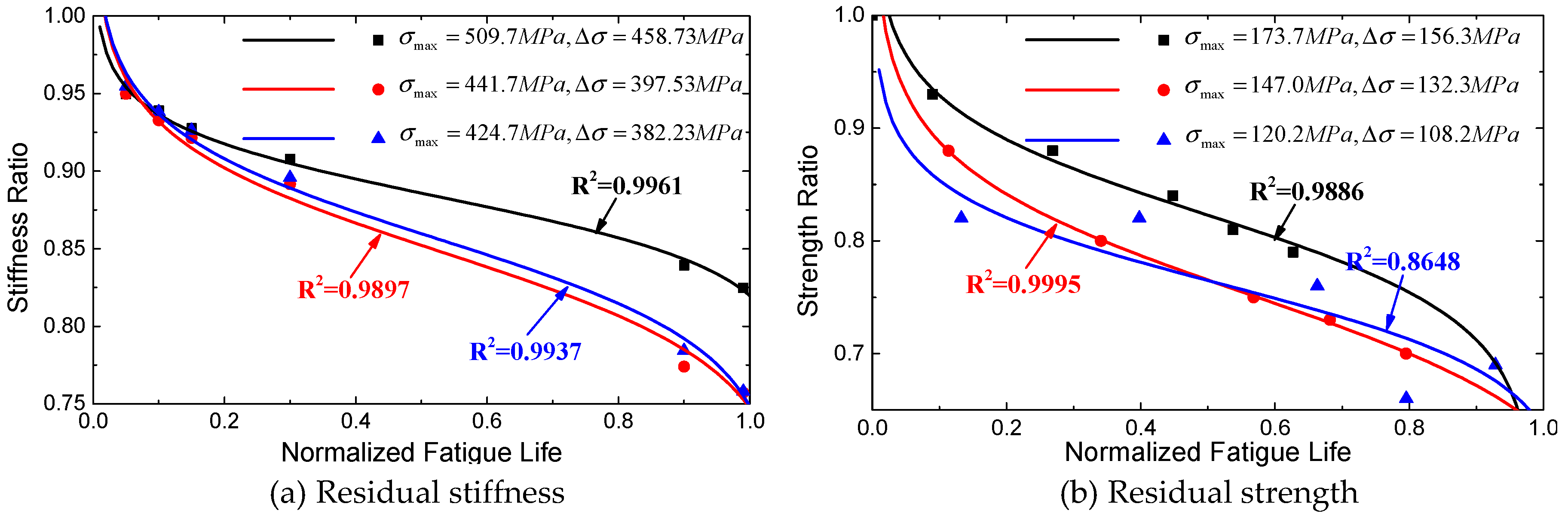
3.1. Residual Stiffness Model
3.2. Redisual Strength Model
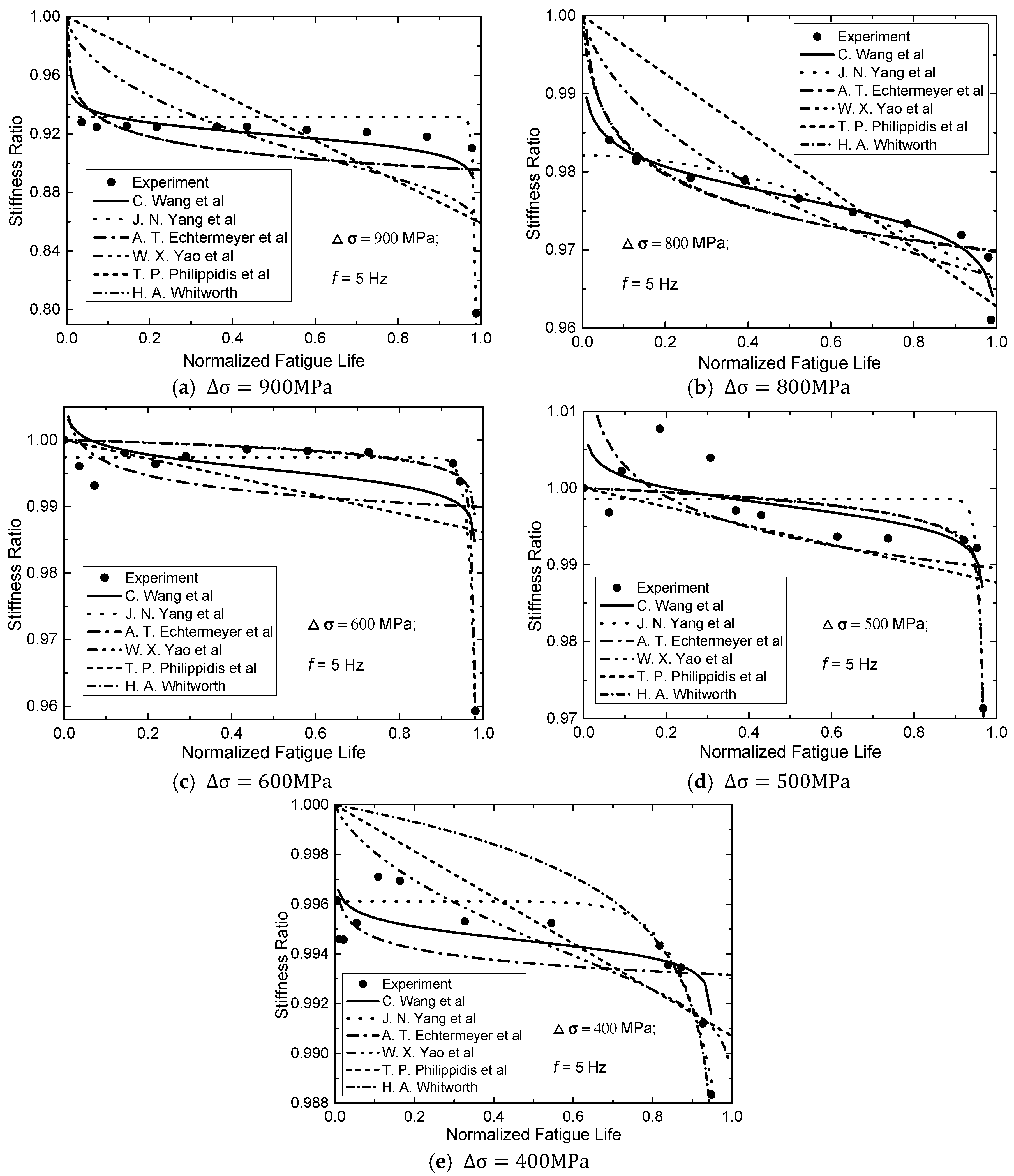
4. Discussion of Experimental Results
5. A New Proposed Fatigue Model
- (a)
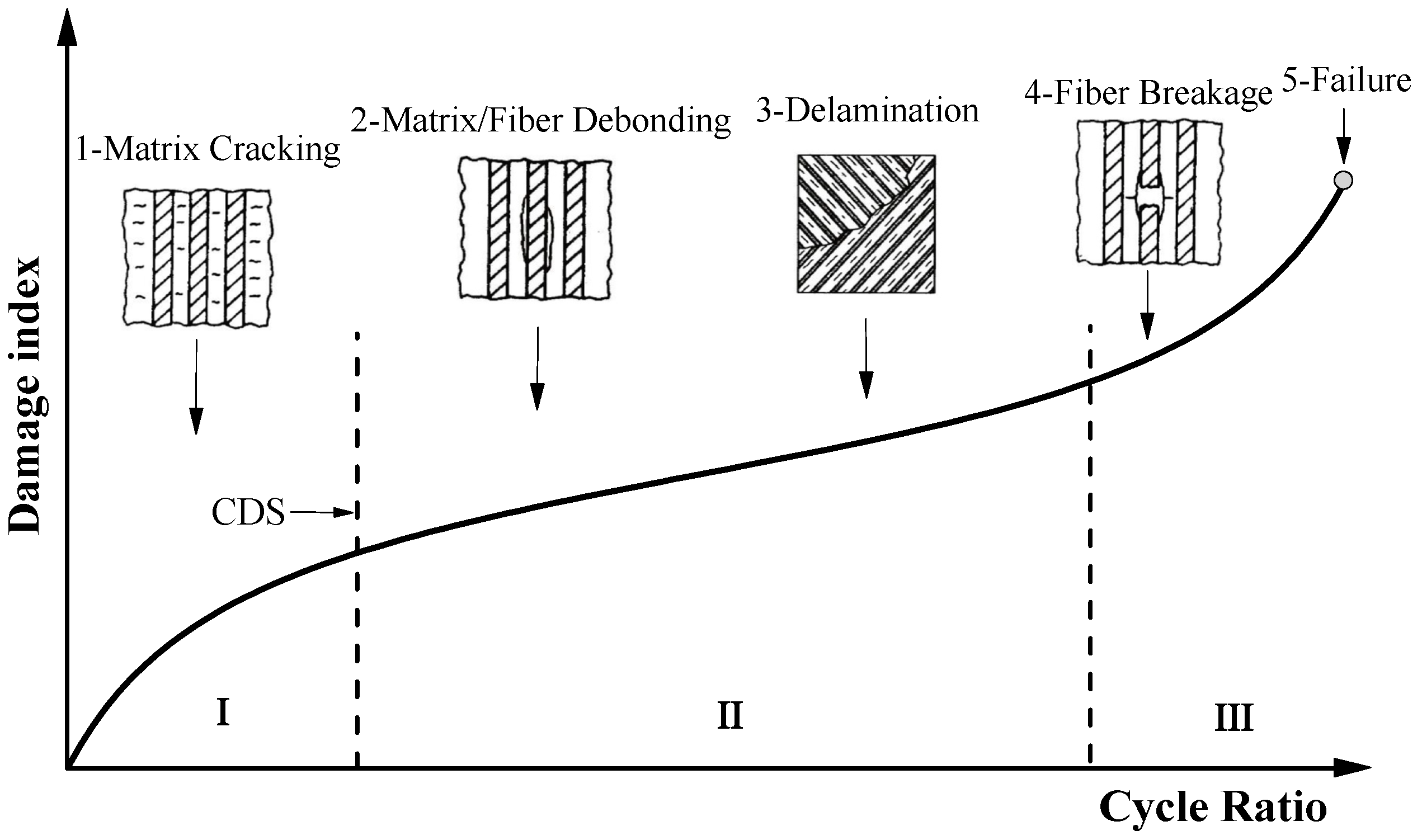
- Under cyclic loading with various stress ranges, both the stiffness and strength of CFRP tendon have three-stage degradations throughout the fatigue life cycle.
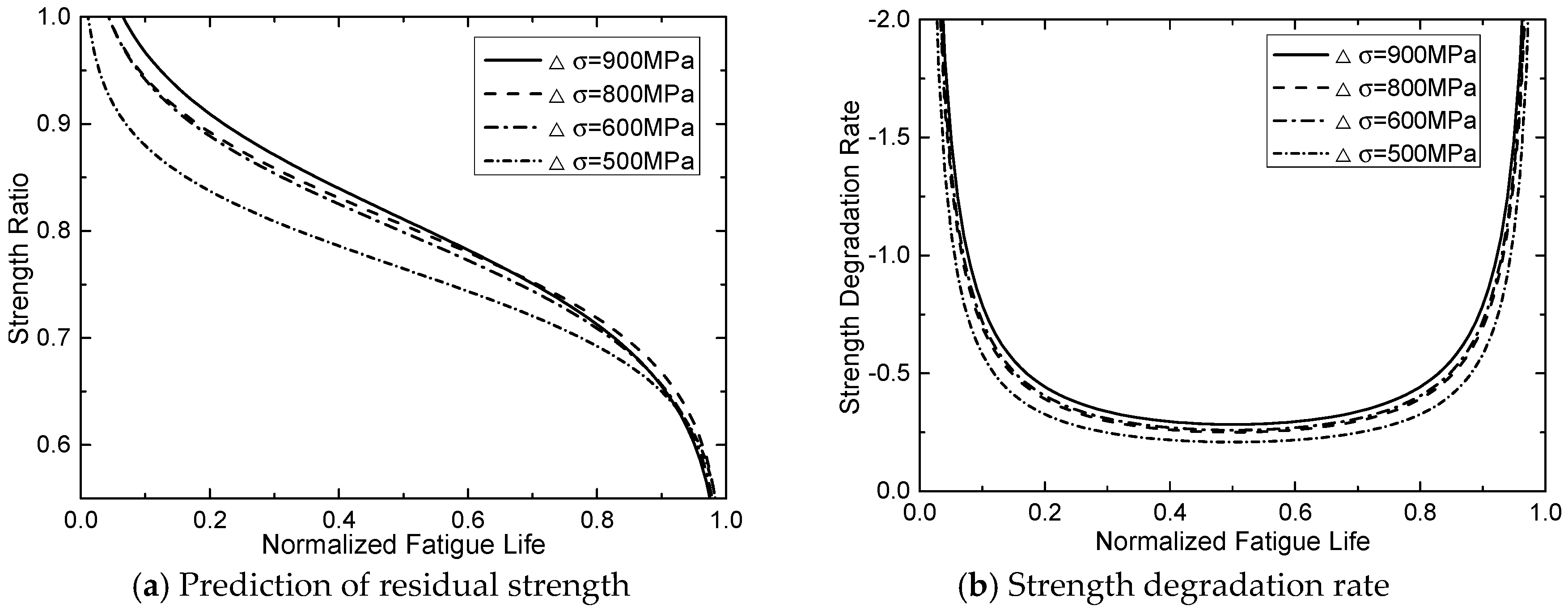
- (b)
- Stiffness/strength degradation rate of the CFRP tendon increases with the growth of stress range. This means that if the stress range gets larger, stiffness/strength degradation of the CFRP tendon become more obvious.
- (c)
- When the stress range gets smaller, the stiffness/strength degradation rates of initial stage and final stage become closer to that of the second stage.
6. Conclusions
- (a)
- Both the stiffness and strength of CFRP tendon degrade during the fatigue loading process. Also, it can be observed that as the stress range increases, stiffness and strength of CFRP tendons degrade more obviously.
- (b)
- The three-stage regularity can be observed from degradation processes of stiffness and strength when CFRP tendons and other FRP composites subjected to fatigue loading. In the first stage, transverse cracks become more saturated when CFRP tendons subjected to lower stress range. Therefore, in the first stage, mechanical property degrades more obviously at lower range. The damage mechanism in the first stage is matrix cracking and is matrix/fiber debonding in the second stage at lower stress range. However, the damage mechanism in the first and second stage becomes the mixing of matrix cracking, matrix/fiber debonding and fiber breakage at higher stress range. Therefore, the boundaries between adjacent stages become more obvious when stress range decreases.
- (c)
- The proposed fatigue damage model is applicable to predict both residual stiffness and residual strength throughout fatigue life cycle. This new proposed model has a better accuracy than the models from the literature based on the experimental results of CFRP tendons and results from the literature.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Karbhari, V.M. Use of Composite Materials in Civil Infrastructure in Japan; Word Technology Division: Baltimore, MD, USA, 1998. [Google Scholar]
- Grace, N.F.; Navarre, F.C.; Nacey, R.B.; Bonus, W.; Collavino, L. Design-construction of bridge street bridge-first CFRP bridge in the United States. Pci J. 2002, 47, 20–35. [Google Scholar] [CrossRef]
- Lu, Z.; Mei, K. First application of CFRP cables for a cable-stayed bridge in China. Tumu Gongcheng Xuebao (China Civ. Eng. J.) 2007, 40, 54–59. [Google Scholar]
- Degrieck, J.; Paepegem, W.V. Fatigue damage modeling of fibre-reinforced composite materials: Review. Appl. Mech. Rev. 2001, 54, 279–299. [Google Scholar] [CrossRef]
- Whitworth, H.A. Modeling Stiffness Reduction of Graphite/Epoxy Composite Laminates. J. Compos. Mater. 1987, 21, 362–372. [Google Scholar] [CrossRef]
- Yang, J.N.; Jones, D.L.; Yang, S.H.; Meskini, A. A Stiffness Degradation Model for Graphite/Epoxy Laminates. J. Compos. Mater. 1990, 24, 753–769. [Google Scholar] [CrossRef]
- Yang, J.N.; Lee, L.J.; Sheu, D.Y. Modulus reduction and fatigue damage of matrix dominated composite laminates. Compos. Struct. 1992, 21, 91–100. [Google Scholar] [CrossRef]
- Echtermeyer, A.T.; Engh, B.; Buene, L. Lifetime and Young’s modulus changes of glass/phenolic and glass/polyester composites under fatigue. Composites 1995, 26, 10–16. [Google Scholar] [CrossRef]
- Philippidis, T.P.; Vassilopoulos, A.P. Fatigue design allowables for GRP laminates based on stiffness degradation measurements. Compos. Ence Technol. 2000, 60, 2819–2828. [Google Scholar] [CrossRef]
- Lian, W.; Yao, W. Residual stiffness-residual strength coupled model of composite laminates. Fuhe Cailiao Xuebao/Acta Mater. Compos. Sin. 2008, 25, 151–156. [Google Scholar]
- Yao, W.; Zong, J.; Lian, W. Residual Stiffness Method for Monitoring Life of Composite Laminates. Nanjing Hangkong Hangtian Daxue Xuebao/J. Nanjing Univ. Aeronaut. Astronaut. 2012, 44, 677–682. [Google Scholar]
- Ye, L. On fatigue damage accumulation and material degradation in composite materials. Compos. Ence Technol. 1989, 36, 339–350. [Google Scholar] [CrossRef]
- Liu, B.; Lessard, L.B. Fatique and damage-tolerance analysis of composite laminates: Stiffness loss, damage-modelling, and life prediction. Compos. Sci. Technol. 1994, 51, 43–51. [Google Scholar] [CrossRef]
- Zhang, D.; Sandor, B.I. Damage evaluation in composite materials using thermographic stress analysis. In Advances in Fatigue Lifetime Predictive Techniques; ASTM International: West Conshohocken, PA, USA, 1992. [Google Scholar]
- Varvani-Farahani, A.; Shirazi, A. A Fatigue Damage Model for (0/90) FRP Composites based on Stiffness Degradation of 0 and 90 Composite Plies. J. Rnforced Plast. Compos. 2007, 26, 1319–1336. [Google Scholar] [CrossRef]
- Ramakrishnan, V.; Jayaraman, N. Mechanistically based fatigue-damage evolution model for brittle matrix fibre-reinforced composites. J. Mater. Sci. 1993, 28, 5592–5602. [Google Scholar] [CrossRef]
- Hwang, W.; Han, K.S. Fatigue of Composites–Fatigue Modulus Concept and Life Prediction. J. Compos. Mater. 1986, 20, 154–165. [Google Scholar] [CrossRef]
- Wu, F.; Yao, W. A fatigue damage model of composite materials. Int. J. Fatigue 2010, 32, 134–138. [Google Scholar] [CrossRef]
- Cadavid, M.O.; Al-Khudairi, O.; Hadavinia, H.; Goodwin, D.; Liaghat, G.H. Experimental Studies of Stiffness Degradation and Dissipated Energy in Glass Fibre Reinforced Polymer Composite under Fatigue Loading. Polym. Polym. Compos. 2017, 25, 435–446. [Google Scholar] [CrossRef]
- Gao, J.; Yuan, Y. Probabilistic modeling of stiffness degradation for fiber reinforced polymer under fatigue loading. Eng. Fail. Anal. 2020. [Google Scholar] [CrossRef]
- Chen, J.; Yao, W.; Zong, J.; Chen, P. Probability Model fo residual stiffness of composite materials. J. Nanjing Univ. Aeronaut. Astronautics. 2019, 51, 534–539. [Google Scholar]
- Broutman, L.J.; Sahu, S. A new theory to predict cumulative fatigue damage in fiberglass reinforced plastics. In Proceedings of In Composite materials: Testing and Design (Second Conference); ASTM International: West Conshohocken, PA, USA, 1972. [Google Scholar]
- Yao, W.X.; Himmel, N. A new cumulative fatigue damage model for fibre-reinforced plastics. Compos. Ence Technol. 2000, 60, 59–64. [Google Scholar] [CrossRef]
- Schaff, J.R.; Davidson, B.D. Life Prediction Methodology for Composite Structures. Part I—Constant Amplitude and Two-Stress Level Fatigue. J. Compos. Mater. 1997, 31, 128–157. [Google Scholar] [CrossRef]
- Stojković, N.; Folić, R.; Pasternak, H. Mathematical model for the prediction of strength degradation of composites subjected to constant amplitude fatigue. Int. J. Fatigue 2017, 103, 478–487. [Google Scholar] [CrossRef]
- Yang, J.N.; Liu, M.D. Residual Strength Degradation Model and Theory of Periodic Proof Tests for Graphite/Epoxy Laminates. J. Compos. Mater. 1977, 11, 176–203. [Google Scholar] [CrossRef]
- Yang, J.N. Fatigue and Residual Strength Degradation for Graphite/Epoxy Composites Under Tension-Compression Cyclic Loadings. J. Compos. Mater. 1978, 12, 19–39. [Google Scholar] [CrossRef]
- Hashin, Z. Cumulative damage theory for composite materials: Residual life and residual strength methods. Compos. Ence Technol. 1985, 23, 1–19. [Google Scholar] [CrossRef]
- Halpin, J.C.; Johnson, T.A.; Waddoups, M.E. Kinetic fracture models and structural reliability. Int. J. Fract. Mech. 1972, 8, 465–468. [Google Scholar] [CrossRef]
- Owen, M.J.; Howe, R.J. The accumulation of damage in a glass-reinforced plastic under tensile and fatigue loading. J. Phys. D Appl. Phys. 2002, 5, 1637. [Google Scholar] [CrossRef]
- Revuelta, D.; Cuartero, J.; Miravete, A.; Clemente, R. A new approach to fatigue analysis in composites based on residual strength degradation. Compos. Struct. 2000, 48, 183–186. [Google Scholar] [CrossRef]
- Cremona, C. Probabilistic approach for cable residual strength assessment. Eng. Struct. 2003, 25, 377–384. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, X.; Wu, Z.; Zhu, Z. Fatigue behavior and failure mechanism of basalt FRP composites under long-term cyclic loads. Int. J. Fatigue 2016, 88, 58–67. [Google Scholar] [CrossRef]
- Möller, M.; Blaurock, J.; Ziegmann, G.; Esderts, A. Residual strength prediction for multi-directional composites subjected to arbitrary fatigue loads. In Proceedings of the 6th European Conference on Computational Mechanics (Solids, Structures and Coupled Problems), 7th European Conference on Computational Fluid Mechanics, Glasgow, UK, 11–15 June 2018; pp. 3825–3836. [Google Scholar]
- D’Amore, A.; Grassia, L. A method to predict the fatigue life and the residual strength of composite materials subjected to variable amplitude (VA) loadings. Compos. Struct. 2019, 228, 111338. [Google Scholar] [CrossRef]
- ASTM. Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials; ASTM International: West Conshohocken, PA, USA, 2017. [Google Scholar]
- ASTM. Standard Test Method for Tension-Tension Fatigue of Polymer Matrix Composite Materials; ASTM International: West Conshohocken, PA, USA, 2012. [Google Scholar]
- Barron, V.; Buggy, M.; Mckenna, N.H. Frequency effects on the fatigue behaviour on carbon fibre reinforced polymer laminates. J. Mater. Sci. 2001, 36, 1755–1761. [Google Scholar] [CrossRef]
- Reifsnider, K.L.; Henneke, E.G.; Stinchcomb, W.W.; Duke, J.C. Damage mechanics and NDE of composite laminates. In Mechanics of Composite Materials: Recent Advances; Hashin, Z., Herakovich, C.T., Eds.; Pergamon Press Ltd: New York, NY, USA, 1983; pp. 399–420. [Google Scholar]
- Philippidis, T.P.; Passipoularidis, V.A. Residual strength after fatigue in composites: Theory vs. experiment. Int. J. Fatigue 2007, 29, 2104–2116. [Google Scholar] [CrossRef]
- Jianxin, X.; Zhenyu, F. Experimental Study on the Stiffness Degradation of Composite Laminates under Constant Amplitude Loading. Mech. Sci. Technol. 2005, 9, 1060–1070,1102. [Google Scholar]
- Post, N.L.; Cain, J.; Mcdonald, K.J.; Case, S.W.; Lesko, J.J. Residual strength prediction of composite materials: Random spectrum loading. Eng. Fract. Mech. 2008, 75, 2707–2724. [Google Scholar] [CrossRef]
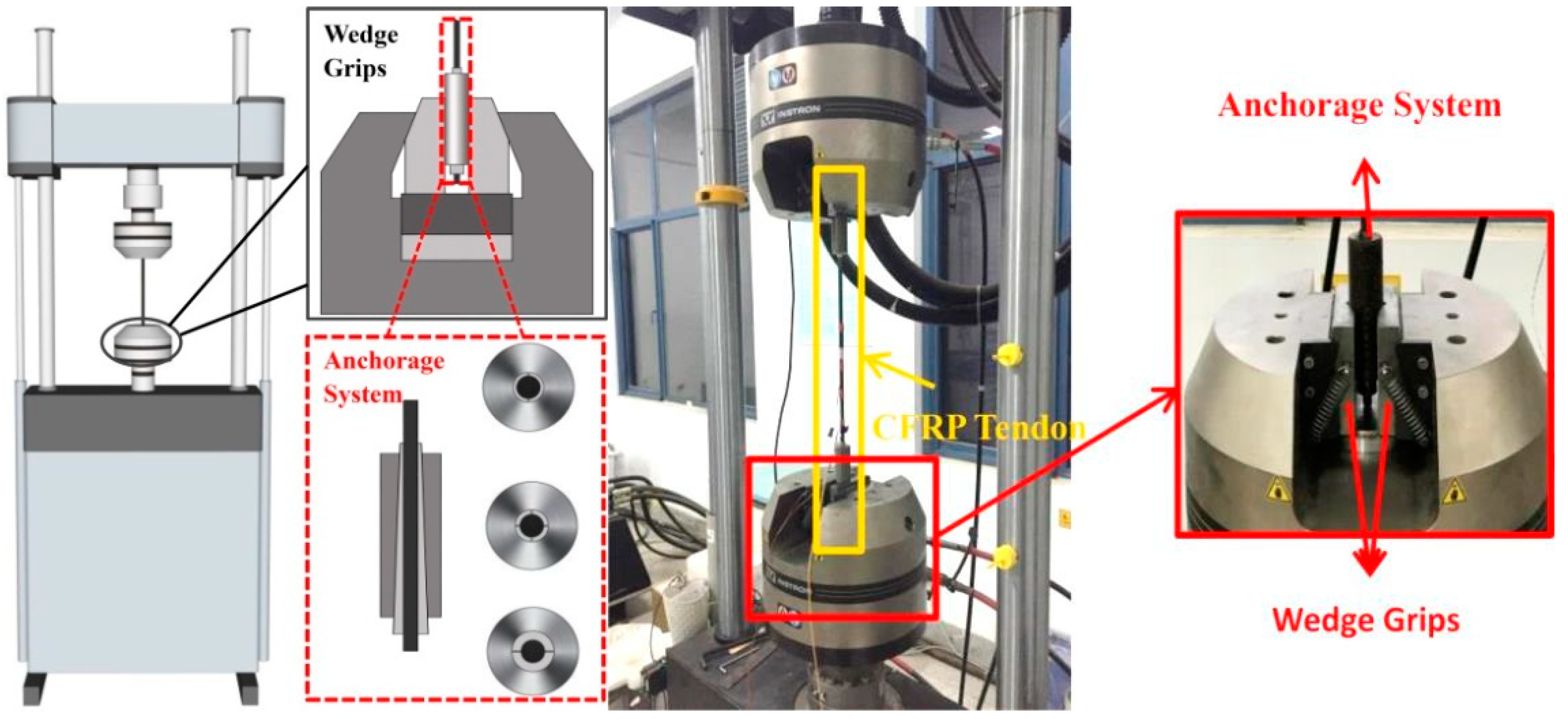



| Specimen | Young’s Modulus, E (GPa) | Ultimate Strength, (MPa) | (Gpa) | (Mpa) |
|---|---|---|---|---|
| S1 | 155.4 | 2064.9 | 155.9 | 2084.0 |
| S2 | 162.1 | 2104.4 | ||
| S3 | 159.5 | 2142.4 | ||
| S4 | 149.7 | 2049.2 | ||
| S5 | 152.6 | 2059.3 |
| Stress Range | Residual Stiffness | Residual Strength | ||||||
|---|---|---|---|---|---|---|---|---|
| 900 | −0.00605 | 0.98912 | 0.91945 | 0.862 | −0.07095 | 0.99923 | 0.81094 | 0.823 |
| 800 | −0.00276 | 0.98483 | 0.97684 | 0.945 | −0.06266 | 0.99941 | 0.80541 | 0.776 |
| 600 | −0.00165 | 0.98125 | 0.99557 | 0.721 | −0.06482 | 0.99968 | 0.79876 | 0.768 |
| 500 | −0.00175 | 0.96750 | 0.99769 | 0.746 | −0.05227 | 0.99971 | 0.76475 | 0.794 |
| 400 | −0.00042 | 0.94790 | 0.99454 | 0.693 | N/A | |||
| Residual Stiffness | Stress Level | Residual Strength | Stress Level | ||||
|---|---|---|---|---|---|---|---|
| Ⅰ | Ⅱ | Ⅲ | Ⅰ | Ⅱ | Ⅲ | ||
| Whitworth | 0.9674 | 0.9799 | 0.9814 | Brountman | 0.9975 | 0.9849 | 0.7920 |
| Yang | 0.9917 | 0.9841 | 0.9934 | Scaff | 0.9859 | 0.9921 | 0.6712 |
| Echtermeyer | 0.9377 | 0.9223 | 0.9203 | Yao | 0.9714 | 0.9888 | 0.6005 |
| Philippidis | 0.9946 | 0.9586 | 0.9675 | Philippidis | 0.9849 | 0.9109 | 0.5772 |
| Yao | 0.9958 | 0.9845 | 0.9897 | Stojković | 0.9856 | 0.9224 | 0.5820 |
| New model | 0.9961 | 0.9897 | 0.9937 | New model | 0.9886 | 0.9995 | 0.8648 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Zhang, J. Experimental and Analytical Study on Residual Stiffness/Strength of CFRP Tendons under Cyclic Loading. Materials 2020, 13, 5653. https://doi.org/10.3390/ma13245653
Wang C, Zhang J. Experimental and Analytical Study on Residual Stiffness/Strength of CFRP Tendons under Cyclic Loading. Materials. 2020; 13(24):5653. https://doi.org/10.3390/ma13245653
Chicago/Turabian StyleWang, Chao, and Jiwen Zhang. 2020. "Experimental and Analytical Study on Residual Stiffness/Strength of CFRP Tendons under Cyclic Loading" Materials 13, no. 24: 5653. https://doi.org/10.3390/ma13245653
APA StyleWang, C., & Zhang, J. (2020). Experimental and Analytical Study on Residual Stiffness/Strength of CFRP Tendons under Cyclic Loading. Materials, 13(24), 5653. https://doi.org/10.3390/ma13245653




